Emergence of Classical Random Walk from Non-Hermitian Effects in Quantum Kicked Rotor
Abstract
1. Introduction
2. Realization of Quantum Walk with Spinor Kicked Rotor Model
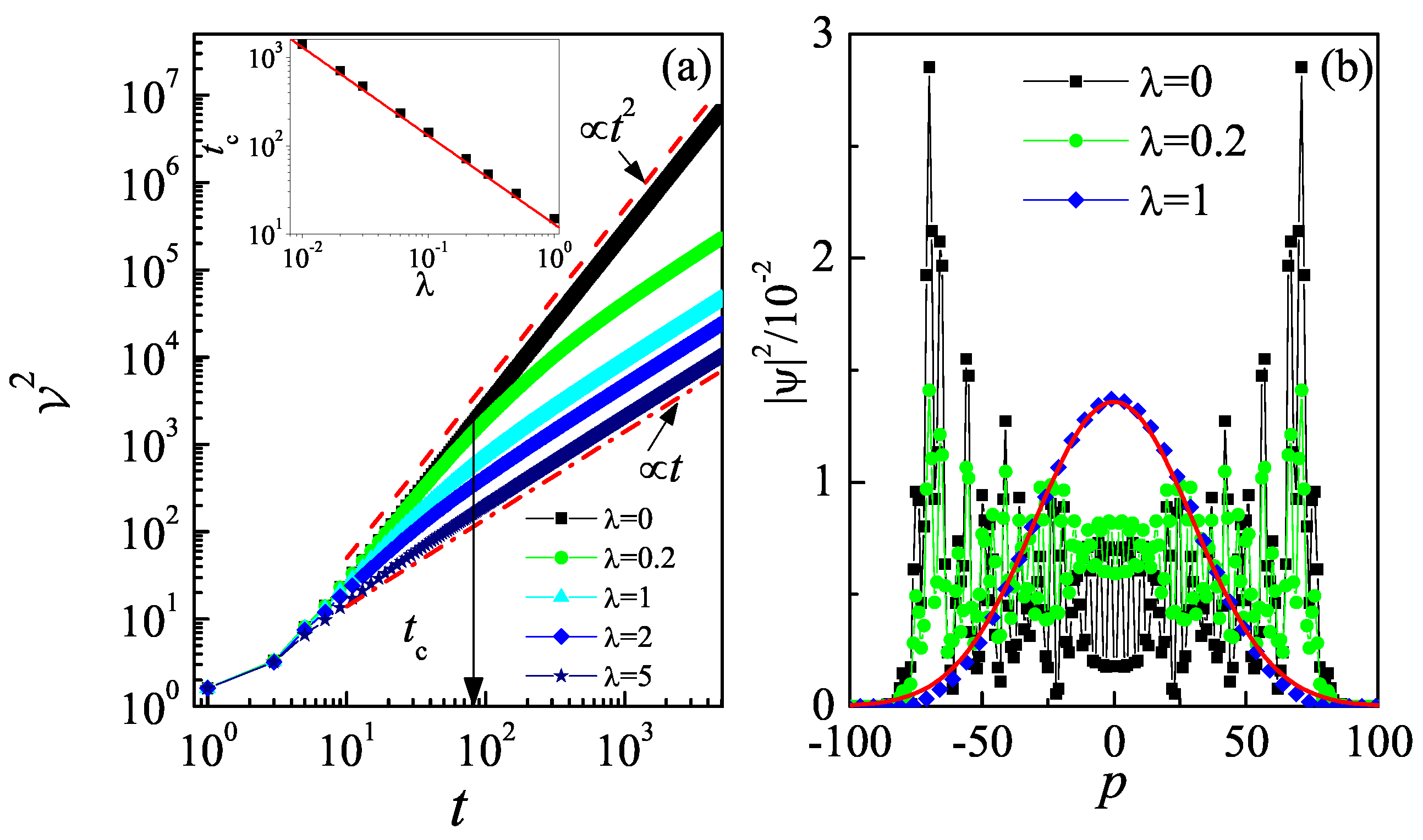
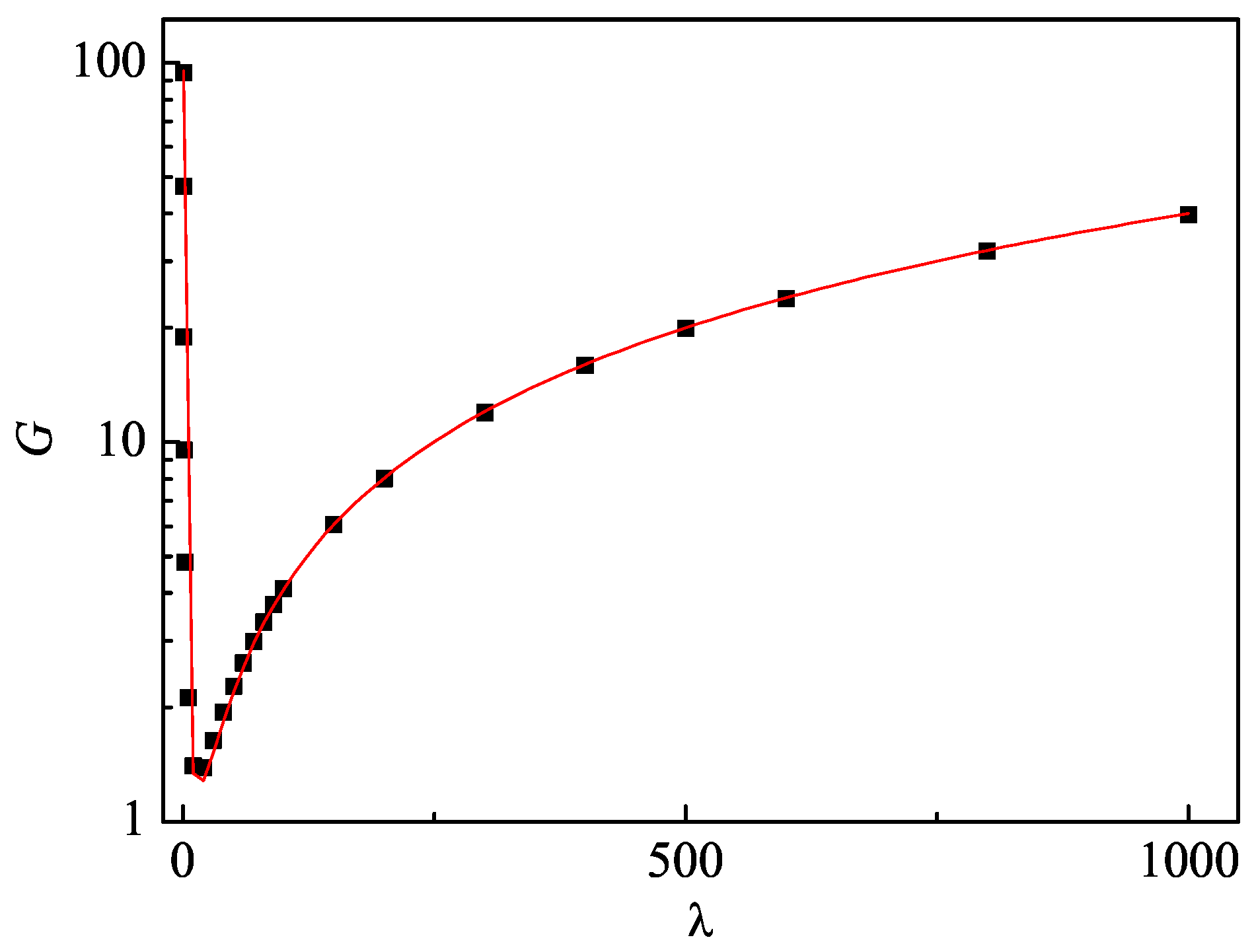
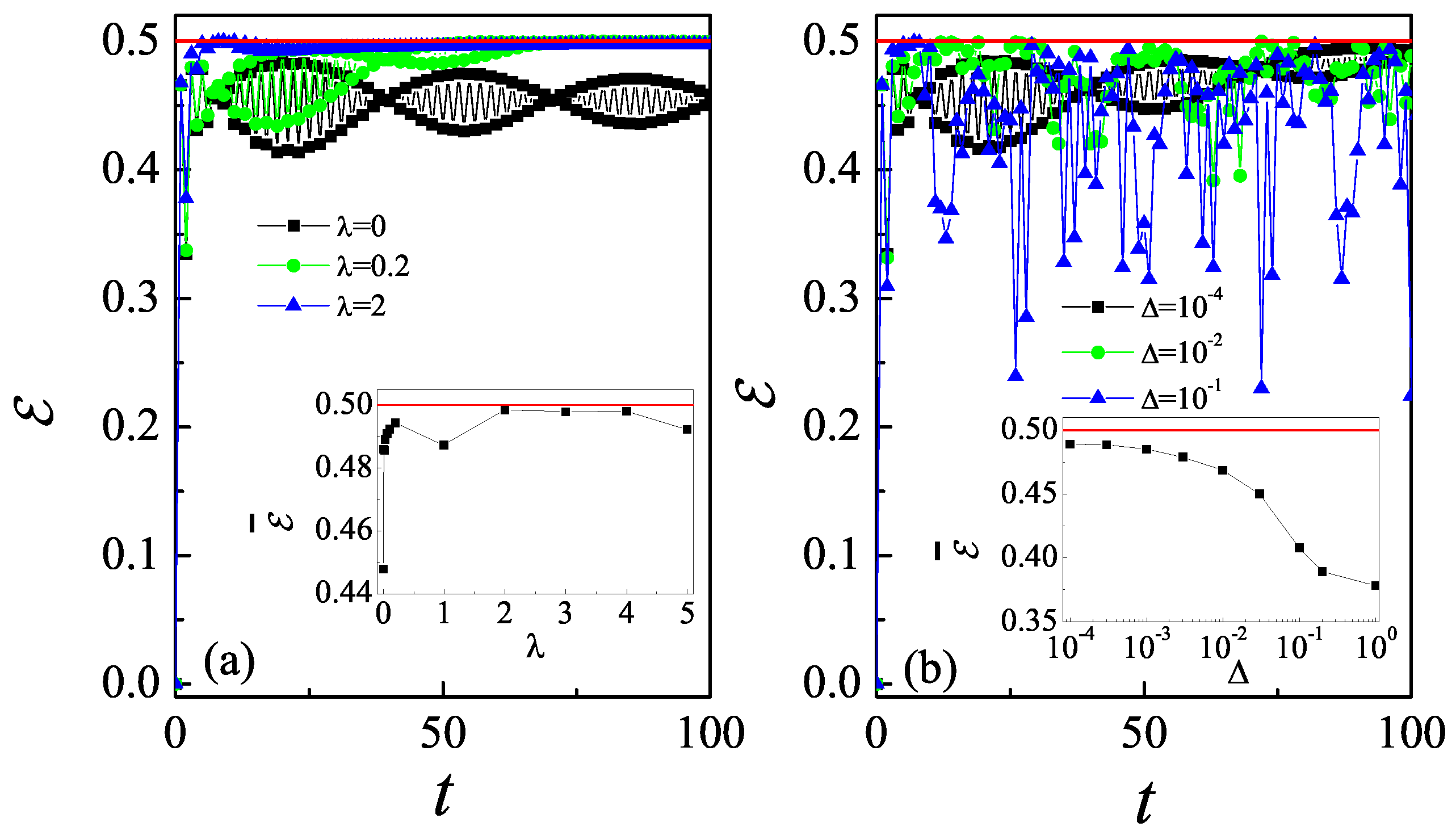
3. Classical Random Walk Induced by Non-Hermiticity
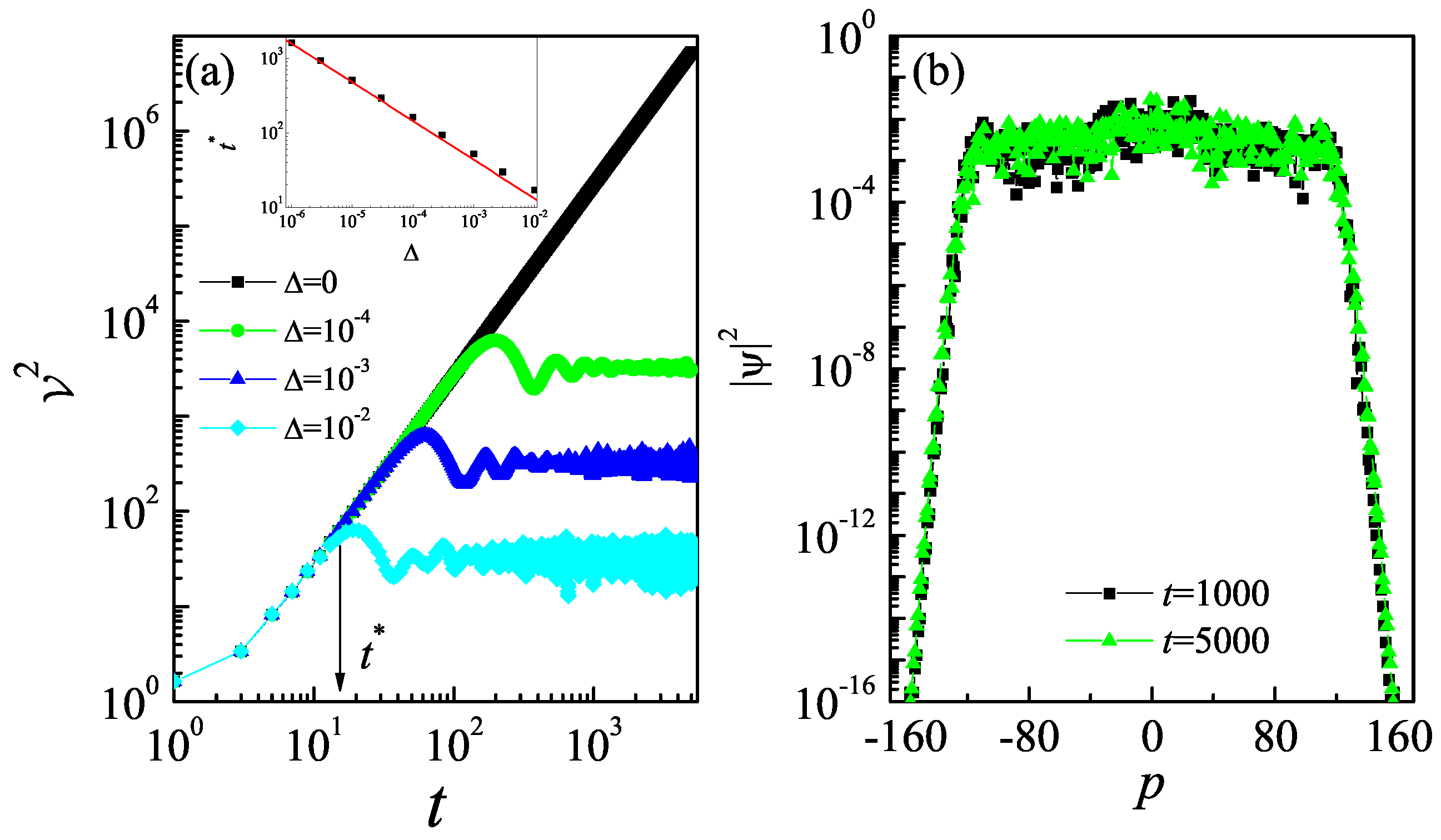
4. Dynamical Localization of Quantum Walk in Quantum Non-Resonance Condition
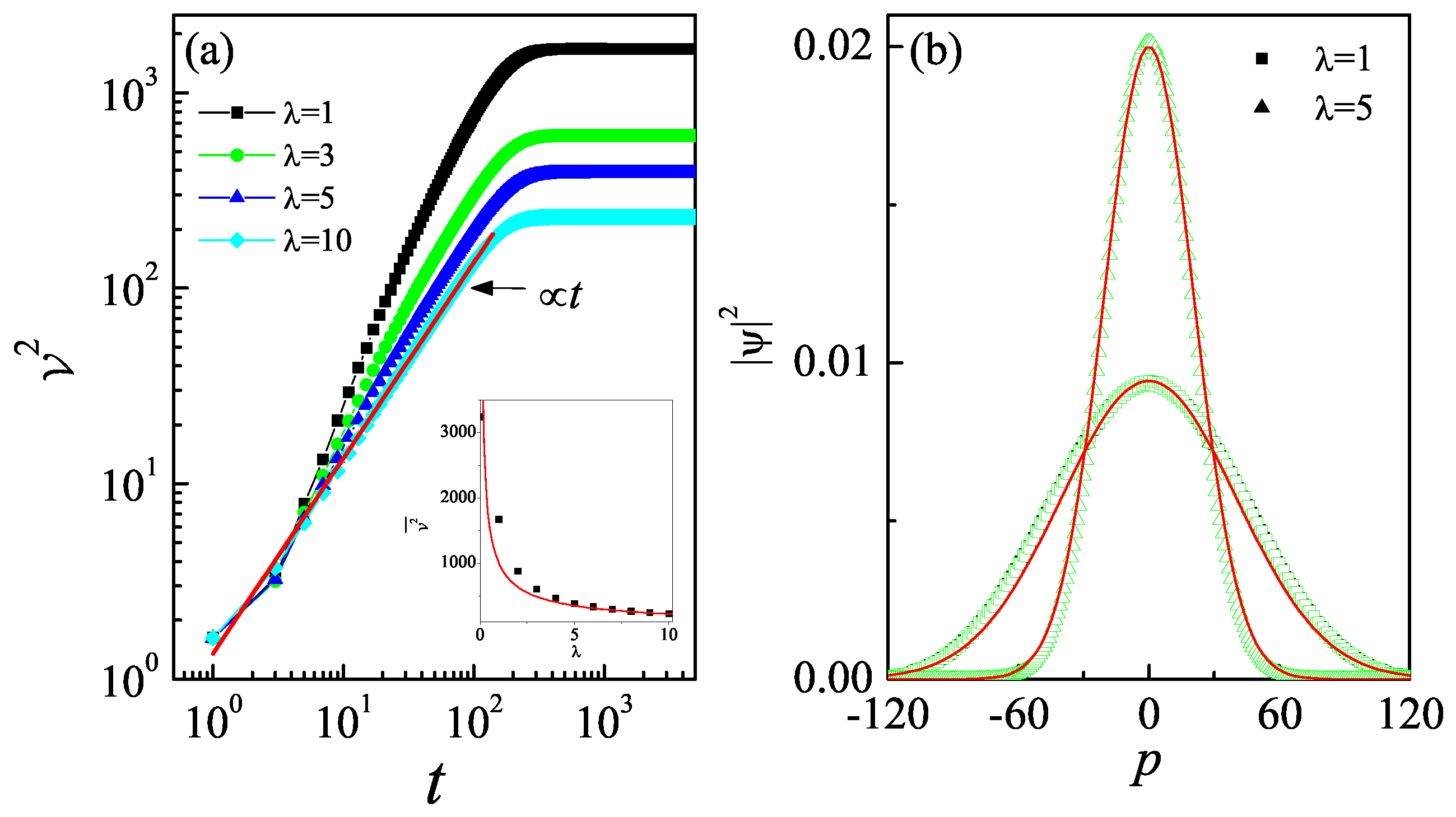
5. Quantum Entanglement
6. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687. [Google Scholar] [CrossRef] [PubMed]
- Vieira, R.; Amorim, E.P.M.; Rigolin, G. Entangling power of disordered quantum walks. Phys. Rev. A 2014, 89, 042307. [Google Scholar] [CrossRef]
- Qiang, X.G.; Ma, S.X.; Song, H.J. Review on Quantum Walk Computing: Theory, Implementation, and Application. arXiv 2024, arXiv:2404.04178. [Google Scholar]
- Mackay, T.D.; Bartlett, S.D.; Stephenson, L.T.; Sanders, B.C. Quantum walks in higher dimensions. J. Phys. A Math. Gen. 2002, 35, 2745. [Google Scholar] [CrossRef]
- Feng, D.; Pang, S.S. Multi-particle quantum walks in one-dimensional lattice. arXiv 2022, arXiv:2212.05452. [Google Scholar]
- Frigerio, M.; Benedetti, C.; Olivares, S.; Paris, M.G.A. Generalized quantum-classical correspondence for random walks on graphs. Phys. Rev. A 2021, 104, L030201. [Google Scholar] [CrossRef]
- Lovett, N.B.; Cooper, S.; Everitt, M.; Trevers, M.; Kendon, V. Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 2010, 81, 042330. [Google Scholar] [CrossRef]
- Duda, R.; Ivaki, M.N.; Sahlberg, I.; Pöyhönen, K.; Ojanen, T. Quantum walks on random lattices: Diffusion, localization, and the absence of parametric quantum speedup. Phys. Rev. Res. 2023, 5, 023150. [Google Scholar] [CrossRef]
- Potoček, V.; Gábris, A.; Kiss, T.; Jex, I. Optimized quantum random-walk search algorithms on the hypercube. Phys. Rev. A 2009, 79, 012325. [Google Scholar] [CrossRef]
- Obuse, H.; Kawakami, N. Topological phases and delocalization of quantum walks in random environments. Phys. Rev. B 2011, 84, 195139. [Google Scholar] [CrossRef]
- Kitagawa, T. Topological phenomena in quantum walks. Quantum Inf. Process. 2012, 11, 1107. [Google Scholar] [CrossRef]
- Zhou, L.W.; Gong, J. Floquet topological phases in a spin-double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef]
- Groh, T.; Brakhane, S.; Alt, W.; Meschede, D.; Asbóth, J.K.; Alberti, A. Robustness of topologically protected edge states in quantum walk experiments with neutral atoms. Phys. Rev. A 2016, 94, 013620. [Google Scholar] [CrossRef]
- Chen, C.; Ding, X.; Qin, J.; He, Y.; Luo, Y.H.; Chen, M.C.; Liu, C.; Wang, X.L.; Zhang, W.J.; Li, H.; et al. Observation of Topologically Protected Edge States in a Photonic Two-Dimensional Quantum Walk. Phys. Rev. Lett. 2018, 121, 100502. [Google Scholar] [CrossRef]
- Vakulchyk, I.; Fistul, M.V.; Flach, S. Wave Packet Spreading with Disordered Nonlinear Discrete-Time Quantum Walks. Phys. Rev. Lett. 2019, 122, 040501. [Google Scholar] [CrossRef] [PubMed]
- Ezawa, M. Electric-circuit simulation of the Schrö dinger equation and non-Hermitian quantum walks. Phys. Rev. B 2019, 100, 165419. [Google Scholar] [CrossRef]
- Yang, H.; Song, L.; Cao, Y.; Yan, P. Circuit realization of topological physics. Phys. Rep. 2024, 1093, 1–54. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Quantum Walk in Momentum Space with a Bose-Einstein Condensate. Phys. Rev. Lett. 2018, 121, 070402. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Experimental realization of a momentum-space quantum walk. Phys. Rev. A 2019, 99, 043617. [Google Scholar] [CrossRef]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-hermitian physics. Adv. Phys. 2020, 69, 249. [Google Scholar]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex Extension of Quantum Mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gong, J. Non-Hermitian Floquet topological phases with arbitrarily many real-quasienergy edge states. Phys. Rev. B 2018, 98, 205417. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Q.; Wang, H.; Gong, J. Dynamical quantum phase transitions in non-Hermitian lattices. Phys. Rev. A 2018, 98, 022129. [Google Scholar] [CrossRef]
- Li, H.C.; Luo, C.; Zhang, T.L.; Zhou, X.; Xu, J.W.; Xu, J.W.; Duan, S.X.; Deng, X.H.; Shen, Y. Non-Hermitian total-loss high-order topological insulator based on 1D Su-Schrieffer-Heeger (SSH). Phys. Condens. Matter 2023, 650, 414570. [Google Scholar] [CrossRef]
- Shen, Y.; Ji, J.; Li, H.C.; Zhang, L.; Yu, X.; Yan, S.B.; Rasmussen, M.; Shen, Q.; Madhi, D.; Zhou, B.B.; et al. Realization of Photonic Topological Insulators at Terahertz Frequencies Characterized by Time-Domain Spectroscopy. Phys. Rev. Appl. 2022, 18, 064025. [Google Scholar] [CrossRef]
- Li, H.C.; Luo, C.; Zhang, T.L.; Xu, J.W.; Zhou, X.; Shen, Y.; Deng, X.H. Topological Refraction in Kagome Split-Ring Photonic Insulators. Nanomaterials 2022, 12, 1493. [Google Scholar] [CrossRef]
- Gong, Z.; Ashida, Y.; Kawabata, K.; Takasan, K.; Higashikawa, S.; Ueda, M. Topological Phases of Non-Hermitian Systems. Phys. Rev. X 2018, 8, 031079. [Google Scholar] [CrossRef]
- Kawabata, K.; Shiozaki, K.; Ueda, M.; Sato, M. Symmetry and Topology in Non-Hermitian Physics. Phys. Rev. X 2019, 9, 041015. [Google Scholar] [CrossRef]
- Shen, H.; Zhen, B.; Fu, L. Topological band theory for non-Hermitian Hamiltonians. Phys. Rev. Lett. 2018, 120, 146402. [Google Scholar] [CrossRef]
- Zhao, W.L.; Liu, J. Superexponential behaviors of out-of-time ordered correlators and Loschmidt echo in a non-Hermitian interacting system. arXiv 2023, arXiv:2305.1215. [Google Scholar]
- Zhao, W.L.; Zhou, L.W.; Liu, J.; Tong, P.Q.; Huang, K.Q. Super-exponential diffusion in nonlinear non-Hermitian systems. Phys. Rev. A 2020, 102, 062213. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.F.; Chen, T. Non-Hermiticity-induced quantum control of localization in quantum walks. Phys. Rev. A 2020, 102, 022218. [Google Scholar] [CrossRef]
- Wang, B.; Chen, T.; Zhang, X. Observation of Novel Robust Edge States in Dissipative Non-Hermitian Quantum Walks. Laser Photonics Rev. 2020, 14, 2000092. [Google Scholar] [CrossRef]
- Xiao, L.; Xue, W.T.; Song, F.; Hu, Y.M.; Yi, W.; Wang, Z.; Xue, P. Observation of non-Hermitian edge burst in quantum dynamics. Phys. Rev. Lett. 2024, 133, 070801. [Google Scholar] [CrossRef]
- Xue, P.; Lin, Q.; Wang, K.; Xiao, L.; Longhi, S.; Yi, W. Self acceleration from spectral geometry in dissipative quantum-walk dynamics. Nat. Commun. 2024, 15, 4381. [Google Scholar] [CrossRef]
- Xue, P.; Qiu, X.Z.; Wang, K.K.; Sanders, B.C.; Yi, W. Observation of dark edge states in parity-time-symmetric quantum dynamics. Natl. Sci. Rev. 2023, 10, nwad005. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Yi, W.; Xue, P. Manipulating directional flow in a two-dimensional photonic quantum walk under a synthetic magnetic field. Nat. Commun. 2023, 14, 6283. [Google Scholar] [CrossRef]
- Fishman, S.; Grempel, D.R.; Prange, R.E. Chaos, quantum recurrences, and Anderson localization. Phys. Rev. Lett. 1982, 49, 509. [Google Scholar] [CrossRef]
- Grempel, D.R.; Prange, R.E.; Fishman, S. Quantum dynamics of a nonintegrable system. Phys. Rev. A 1984, 29, 1639. [Google Scholar] [CrossRef]
- Shepelyansky, D.L. Localization of quasienergy eigenfunctions in action space. Phys. Rev. Lett. 1986, 56, 677. [Google Scholar] [CrossRef] [PubMed]
- Casati, G.; Ford, J.; Guarneri, I.; Vivaldi, F. Search for randomness in the kicked quantum rotator. Phys. Rev. A 1986, 34, 1413. [Google Scholar] [CrossRef] [PubMed]
- Summy, G.; Wimberger, S. Quantum random walk of a Bose-Einstein condensate in momentum space. Phys. Rev. A 2016, 93, 023638. [Google Scholar] [CrossRef]
- Brun, T.A.; Carteret, H.A.; Ambainis, A. Quantum to Classical Transition for Random Walks. Phys. Rev. Lett. 2003, 91, 130602. [Google Scholar] [CrossRef]
- Zhao, W.L.; Liu, J. Quantum criticality at the boundary of the non-Hermitian regime of a Floquet system. Phys. Rev. A 2024, 109, 052215. [Google Scholar] [CrossRef]
- Zhao, W.L.; Li, G.L.; Liu, J. Phase modulation of directed transport, energy diffusion and quantum scrambling in a Floquet non-Hermitian system. Phys. Rev. Res. 2024, 6, 033249. [Google Scholar] [CrossRef]
- Cohen, D.; Fishman, S. Quantum dissipation for the kicked particle. Phys. Rev. A 1989, 39, 6478. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, T.; Graham, R. Long time behavior in the quantized standard map with dissipation. Ann. Phys. (NY) 1990, 200, 363. [Google Scholar] [CrossRef]
- Kolovsky, A. A remark on the problem of quantum-classical correspondence in the case of chaotic dynamics. Europhys. Lett. 1994, 27, 79. [Google Scholar] [CrossRef]
- Kendon, V. Decoherence in quantum walks-a review. Math. Struct. Comp. Sci. 2007, 17, 1169. [Google Scholar] [CrossRef]
- Schreiber, A.; Cassemiro, K.N.; Potocek, V.; Gábris, A.; Jex, I.; Silberhorn, C. Decoherence and disorder in quantumwalks: From ballistic spread to localization. Phys. Rev. Lett. 2011, 106, 180403. [Google Scholar] [CrossRef] [PubMed]
- Chirikov, B.V. Chaos and Quantum Mechanics, Les Houches Lecture Series; Giannoni, M.-J., Voros, A., Zinn-Justin, J., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1991; Volume 52, pp. 443–545. [Google Scholar]
- Paul, S.; Kannan, J.B.; Santhanam, M.S. Interaction-induced directed transport in quantum chaotic subsystems. Phys. Rev. E 2023, 108, 044208. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299. [Google Scholar] [CrossRef]
- Santhanam, M.S.; Paul, S.; Kannan, J.B. Quantum kicked rotor and its variants: Chaos, localization and beyond. Phys. Rep. 2022, 956, 1–87. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F.; Zelevinsky, V.G. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef]
- Wang, W.G.; He, L.W.; Gong, J.B. Preferred States of Decoherence under Intermediate System-Environment Coupling. Phys. Rev. Lett. 2012, 108, 070403. [Google Scholar] [CrossRef]
- Paul, S.; Kannan, J.B.; Santhanam, M.S. Faster entanglement driven by quantum resonance in many-body kicked rotors. Phys. Rev. B 2024, 110, 144301. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, L.W.; Ma, W.C.; Kong, X.; Wang, P.F.; Qin, X.; Rong, X.; Wang, Y.; Shi, F.Z.; Gong, J.B.; et al. Floquet dynamical quantum phase transitions. Phys. Rev. B 2019, 100, 085308. [Google Scholar] [CrossRef]
- Zhou, L.W.; Pan, J. Non-Hermitian Floquet topological phases in the double-kicked rotor. Phys. Rev. A 2019, 100, 053608. [Google Scholar] [CrossRef]
- Zhou, L.W.; Gu, Y.; Gong, J. Dual topological characterization of non-Hermitian Floquet phases. Phys. Rev. B 2021, 103, L041404. [Google Scholar] [CrossRef]
- Chen, F.X.; Fang, P. System Symmetry and the Classification of Out-of-Time-Ordered Correlator Dynamics in Quantum Chaos. arXiv 2024, arXiv:2410.04712. [Google Scholar]
- Zhao, W.L.; Wang, R.R.; Ke, H.; Liu, J. Scaling laws of the out-of-time-order correlators at the transition to the spontaneous PT-symmetry breaking in a Floquet system. Phys. Rev. A 2023, 107, 062201. [Google Scholar] [CrossRef]
- Zhao, W.L. Quantization of Out-of-Time-Ordered Correlators in non-Hermitian Chaotic Systems. Phys. Rev. Res. 2022, 4, 023004. [Google Scholar] [CrossRef]
- Sharma, K.; Sahu, H.; Mukerjee, S. Quantum chaos in PT symmetric quantum systems. arXiv 2024, arXiv:2401.07215. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Zhang, J.; Hua, L.; Xiong, Z.; Zhao, W. Emergence of Classical Random Walk from Non-Hermitian Effects in Quantum Kicked Rotor. Entropy 2025, 27, 288. https://doi.org/10.3390/e27030288
Song W, Zhang J, Hua L, Xiong Z, Zhao W. Emergence of Classical Random Walk from Non-Hermitian Effects in Quantum Kicked Rotor. Entropy. 2025; 27(3):288. https://doi.org/10.3390/e27030288
Chicago/Turabian StyleSong, Wenxuan, Jiaming Zhang, Lihao Hua, Zhihua Xiong, and Wenlei Zhao. 2025. "Emergence of Classical Random Walk from Non-Hermitian Effects in Quantum Kicked Rotor" Entropy 27, no. 3: 288. https://doi.org/10.3390/e27030288
APA StyleSong, W., Zhang, J., Hua, L., Xiong, Z., & Zhao, W. (2025). Emergence of Classical Random Walk from Non-Hermitian Effects in Quantum Kicked Rotor. Entropy, 27(3), 288. https://doi.org/10.3390/e27030288






