A Revisit of Large-Scale Patterns in Middle Stratospheric Circulation Variations
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Eigen Microstate Approach
2.3. Temporal Correlation Coefficient
2.4. Linear Prediction Model
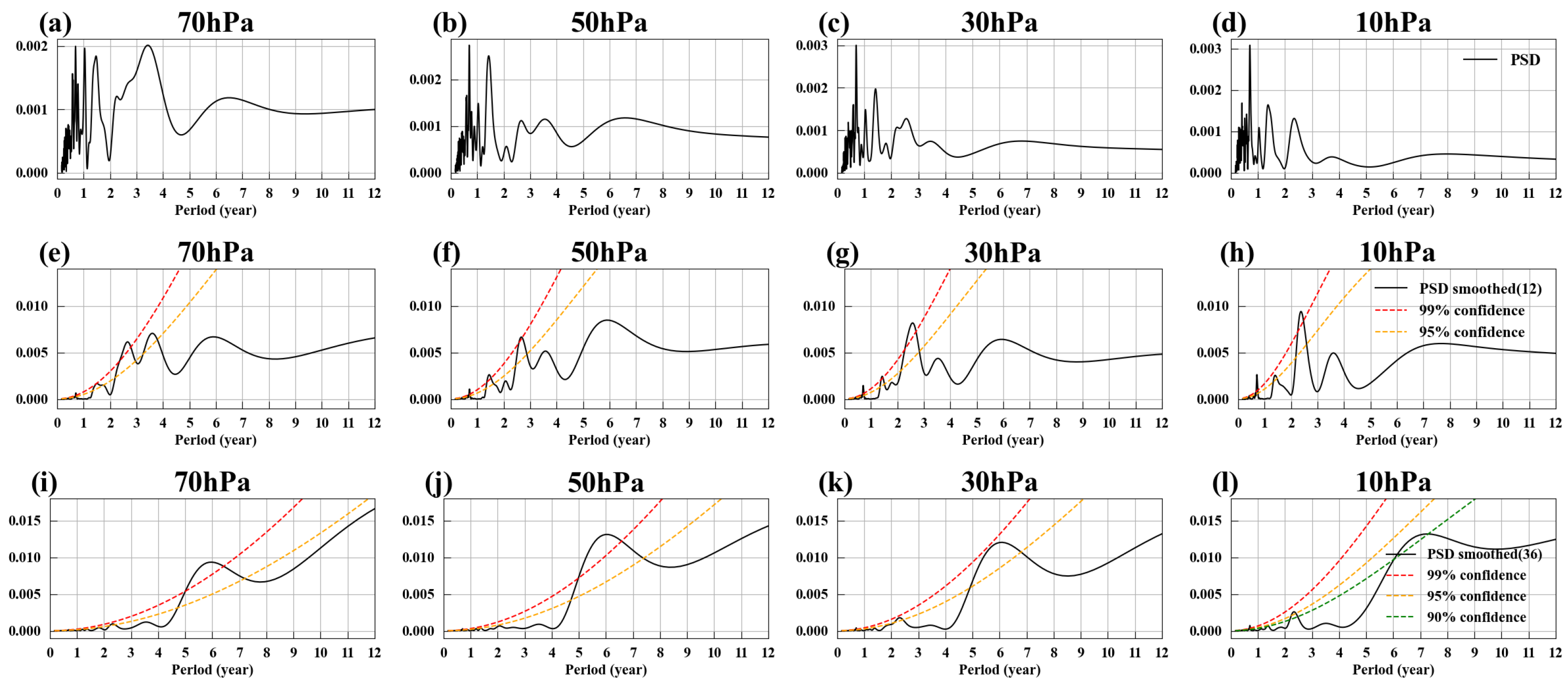
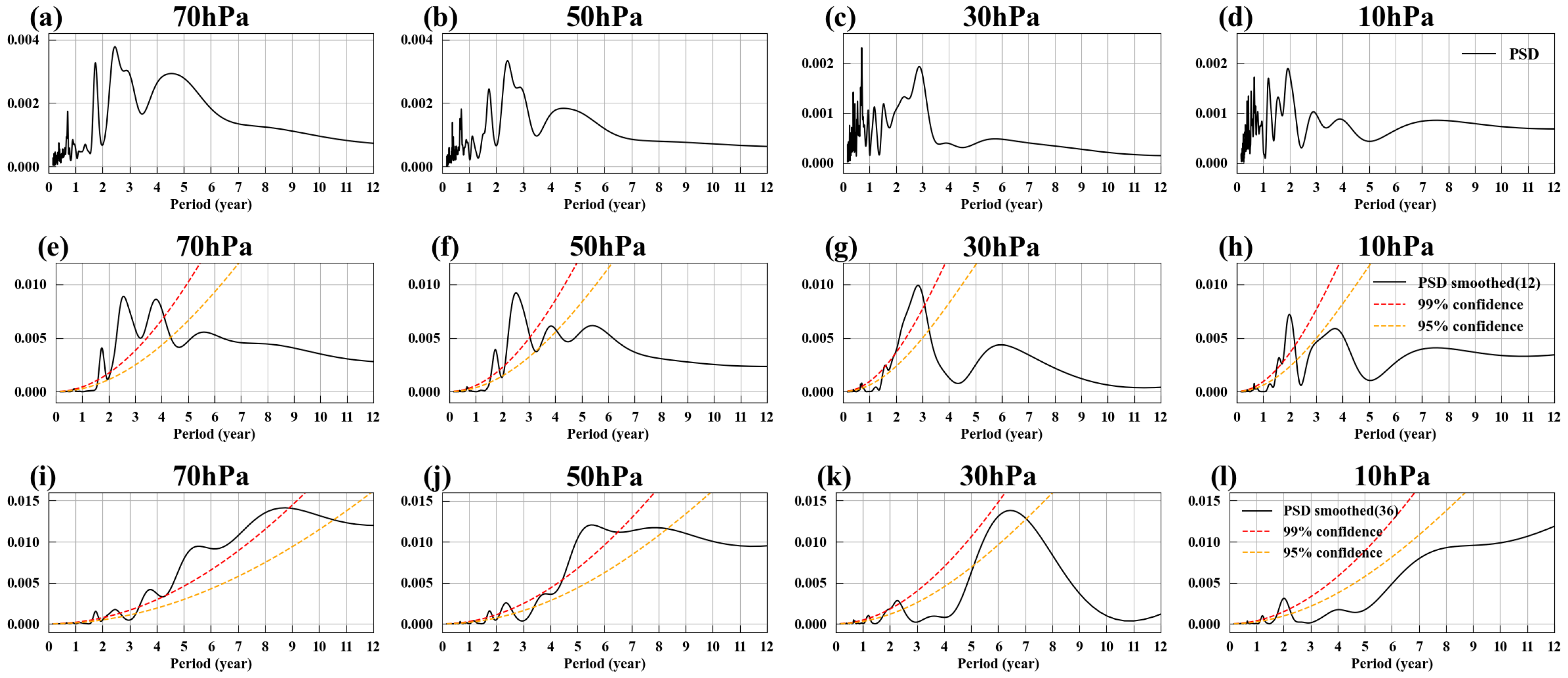
2.5. Spectral Peak Significance Test
- Calculate the power spectrum of the signal.
- Estimate the power spectrum of red noise based on the signal’s lag-1 autocorrelation.
- Calculate the ratio of the signal’s power spectrum to the red noise power spectrum.
- Perform a significance test on the ratio using the F-statistic.
3. Results
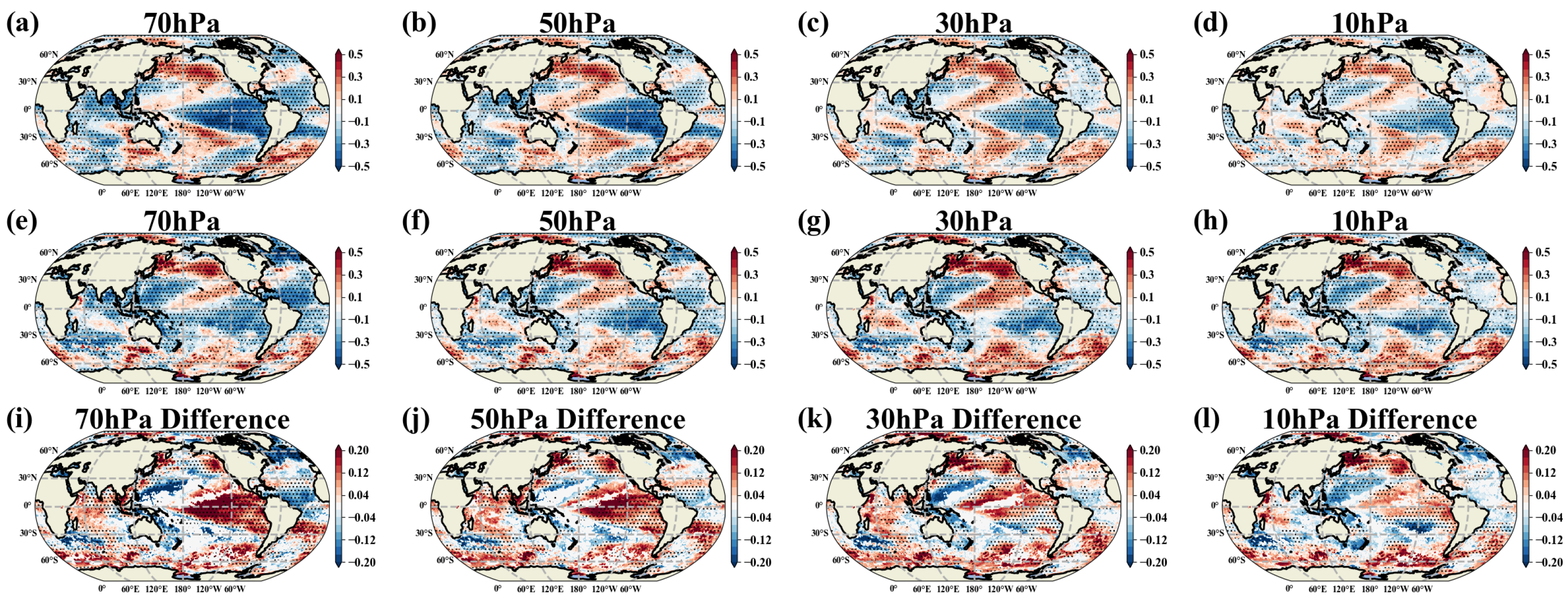
3.1. EM1 and Its Relationship with QBO
3.2. EM2 and the Arctic Polar Vortex Variations
3.3. EM3 and the Antarctic Polar Vortex Variations
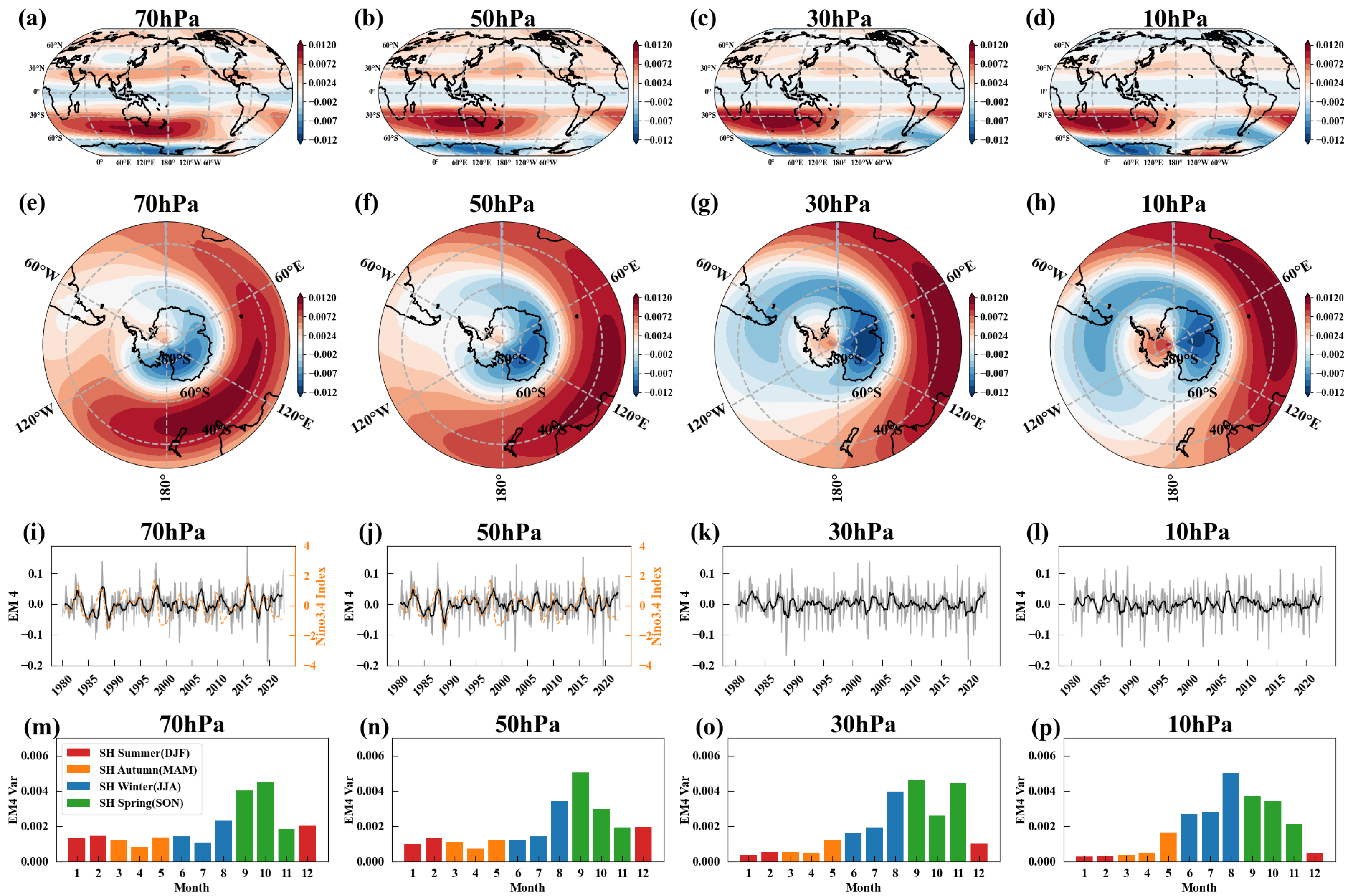
3.4. EM4: The Southern Hemisphere Dipole Mode
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Example of EMA



References
- Baldwin, M.P.; Dunkerton, T.J. Stratospheric harbingers of anomalous weather regimes. Science 2001, 294, 581–584. [Google Scholar] [CrossRef] [PubMed]
- Domeisen, D.I.; Butler, A.H.; Charlton-Perez, A.J.; Ayarzagüena, B.; Baldwin, M.P.; Dunn-Sigouin, E.; Furtado, J.C.; Garfinkel, C.I.; Hitchcock, P.; Karpechko, A.Y.; et al. The role of the stratosphere in subseasonal to seasonal prediction: 2. Predictability arising from stratosphere-troposphere coupling. J. Geophys. Res. Atmos. 2020, 125, e2019JD030923. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Birner, T.; Brasseur, G.; Burrows, J.; Butchart, N.; Garcia, R.; Geller, M.; Gray, L.; Hamilton, K.; Harnik, N.; et al. 100 years of progress in understanding the stratosphere and mesosphere. Meteorol. Monogr. 2019, 59, 27.1-27.62. [Google Scholar]
- Brewer, A. Evidence for a world circulation provided by the measurements of helium and water vapour distribution in the stratosphere. Q. J. R. Meteorol. Soc. 1949, 75, 351–363. [Google Scholar] [CrossRef]
- Dobson, G.M.B. Origin and distribution of the polyatomic molecules in the atmosphere. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 236, 187–193. [Google Scholar]
- Butchart, N. The Brewer-Dobson circulation. Rev. Geophys. 2014, 52, 157–184. [Google Scholar] [CrossRef]
- Scherhag, R. Die explosionsartige Stratosphärenerwärmung des Späitwinters 1951/52. In Berichte des Deutschen Wetterdienstes in der US-Zone; Deutscher Wetterdienst in der US-Zone: Bad Kissingen, Germany, 1952; Volume 38, pp. 51–63. [Google Scholar]
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Labitzke, K. Stratospheric-mesospheric midwinter disturbances: A summary of observed characteristics. J. Geophys. Res. Oceans 1981, 86, 9665–9678. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Ayarzagüena, B.; Birner, T.; Butchart, N.; Butler, A.H.; Charlton-Perez, A.J.; Domeisen, D.I.; Garfinkel, C.I.; Garny, H.; Gerber, E.P.; et al. Sudden stratospheric warmings. Rev. Geophys. 2021, 59, e2020RG000708. [Google Scholar] [CrossRef]
- Ebdon, R. Notes on the wind flow at 50 mb in tropical and sub-tropical regions in January 1957 and January 1958. Q. J. R. Meteorol. Soc. 1960, 86, 540–542. [Google Scholar] [CrossRef]
- Reed, R.J.; Campbell, W.J.; Rasmussen, L.A.; Rogers, D.G. Evidence of a downward-propagating, annual wind reversal in the equatorial stratosphere. J. Geophys. Res. 1961, 66, 813–818. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Holton, J.R. A theory of the quasi-biennial oscillation. J. Atmos. Sci. 1968, 25, 1095–1107. [Google Scholar] [CrossRef]
- Holton, J.R.; Lindzen, R.S. An updated theory for the quasi-biennial cycle of the tropical stratosphere. J. Atmos. Sci. 1972, 29, 1076–1080. [Google Scholar] [CrossRef]
- Baldwin, M.; Gray, L.; Dunkerton, T.; Hamilton, K.; Haynes, P.; Randel, W.; Holton, J.; Alexander, M.; Hirota, I.; Horinouchi, T.; et al. The quasi-biennial oscillation. Rev. Geophys. 2001, 39, 179–229. [Google Scholar] [CrossRef]
- Eliassen, A. On the transfer of energy in stationary mountain waves. Geofys. Publ. 1961, 22, 1–23. [Google Scholar]
- Andrews, D.; McIntyre, M. An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 1978, 89, 609–646. [Google Scholar] [CrossRef]
- Boyd, J.P. The noninteraction of waves with the zonally averaged flow on a spherical earth and the interrelationships on eddy fluxes of energy, heat and momentum. J. Atmos. Sci. 1976, 33, 2285–2291. [Google Scholar] [CrossRef]
- Marks, C.J.; Eckermann, S.D. A three-dimensional nonhydrostatic ray-tracing model for gravity waves: Formulation and preliminary results for the middle atmosphere. J. Atmos. Sci. 1995, 52, 1959–1984. [Google Scholar] [CrossRef]
- Alexander, M.J. A model of non-stationary gravity waves in the stratosphere and comparison to observations. In Gravity Wave Processes: Their Parameterization in Global Climate Models; Springer: Berlin/Heidelberg, Germany, 1997; pp. 153–168. [Google Scholar]
- Alexander, M.; Dunkerton, T. A spectral parameterization of mean-flow forcing due to breaking gravity waves. J. Atmos. Sci. 1999, 56, 4167–4182. [Google Scholar] [CrossRef]
- Geller, M.A.; Alexander, M.J.; Love, P.T.; Bacmeister, J.; Ern, M.; Hertzog, A.; Manzini, E.; Preusse, P.; Sato, K.; Scaife, A.A.; et al. A comparison between gravity wave momentum fluxes in observations and climate models. J. Clim. 2013, 26, 6383–6405. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Birner, T.; Ayarzagüena, B. Tropospheric amplification of stratosphere–troposphere coupling. Q. J. R. Meteorol. Soc. 2024, 150, 5188–5205. [Google Scholar] [CrossRef]
- Hall, T.M.; Plumb, R.A. Age as a diagnostic of stratospheric transport. J. Geophys. Res. Atmos. 1994, 99, 1059–1070. [Google Scholar] [CrossRef]
- Dobson, G. A photoelectric spectrophotometer for measuring the amount of atmospheric ozone. Proc. Phys. Soc. 1931, 43, 324. [Google Scholar] [CrossRef]
- Bates, D.R.; Nicolet, M. The photochemistry of atmospheric water vapor. J. Geophys. Res. 1950, 55, 301–327. [Google Scholar] [CrossRef]
- Crutzen, P.J. The Influence of Nitrogen Oxides on Atmospheric Ozone Content. Q. J. R. Meteorol. Soc. 1970, 96, 320–325. [Google Scholar] [CrossRef]
- Stolarski, R.S.; Cicerone, R.J. Stratospheric chlorine: A possible sink for ozone. Can. J. Chem. 1974, 52, 1610–1615. [Google Scholar] [CrossRef]
- Wofsy, S.C.; McElroy, M.B.; Yung, Y.L. The chemistry of atmospheric bromine. Geophys. Res. Lett. 1975, 2, 215–218. [Google Scholar] [CrossRef]
- Johnston, H. Reduction of stratospheric ozone by nitrogen oxide catalysts from supersonic transport exhaust. Science 1971, 173, 517–522. [Google Scholar] [CrossRef]
- Molina, M.J.; Rowland, F.S. Stratospheric sink for chlorofluoromethanes: Chlorine atom-catalysed destruction of ozone. Nature 1974, 249, 810–812. [Google Scholar] [CrossRef]
- Crutzen, P.J.; Arnold, F. Nitric acid cloud formation in the cold Antarctic stratosphere: A major cause for the springtime ‘ozone hole’. Nature 1986, 324, 651–655. [Google Scholar] [CrossRef]
- Toon, O.B.; Hamill, P.; Turco, R.P.; Pinto, J. Condensation of HNO3 and HCl in the winter polar stratospheres. Geophys. Res. Lett. 1986, 13, 1284–1287. [Google Scholar] [CrossRef]
- Solomon, S.; Garcia, R.R.; Rowland, F.S.; Wuebbles, D.J. On the depletion of Antarctic ozone. Nature 1986, 321, 755–758. [Google Scholar] [CrossRef]
- McElroy, M.B.; Salawitch, R.J.; Wofsy, S.C.; Logan, J.A. Reductions of Antarctic ozone due to synergistic interactions of chlorine and bromine. Nature 1986, 321, 759–762. [Google Scholar] [CrossRef]
- Tung, K.K.; Ko, M.K.; Rodriguez, J.M.; Dak Sze, N. Are Antarctic ozone variations a manifestation of dynamics or chemistry? Nature 1986, 322, 811–814. [Google Scholar] [CrossRef]
- Molina, L.T.; Molina, M.J. Production of chlorine oxide (Cl2O2) from the self-reaction of the chlorine oxide (ClO) radical. J. Phys. Chem. 1987, 91, 433–436. [Google Scholar] [CrossRef]
- Ruffini, R.; Wheeler, J.A. Introducing the black hole. Phys. Today 1971, 24, 30–41. [Google Scholar] [CrossRef]
- Castelvecchi, D. Gravitational wave detection wins physics Nobel. Nature 2017, 550, 19. [Google Scholar] [CrossRef]
- Wright, A. Nobel Prize 2013: Englert and Higgs. Nat. Phys. 2013, 9, 692. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef]
- Pfeffer, R.L. Wave-mean flow interactions in the atmosphere. J. Atmos. Sci. 1981, 38, 1340–1359. [Google Scholar] [CrossRef]
- Anderson, P.W. More Is Different: Broken symmetry and the nature of the hierarchical structure of science. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Hu, G.; Zhang, Y.; Lu, B.; Lu, Z.; Fan, J.; Li, X.; Deng, Q.; Chen, X. Eigen microstates and their evolutions in complex systems. Commun. Theor. Phys. 2021, 73, 065603. [Google Scholar] [CrossRef]
- Hu, G.; Liu, T.; Liu, M.; Chen, W.; Chen, X. Condensation of eigen microstate in statistical ensemble and phase transition. Sci. China Phys. Mech. Astron. 2019, 62, 990511. [Google Scholar] [CrossRef]
- Li, X.; Xue, T.; Sun, Y.; Fan, J.; Li, H.; Liu, M.; Han, Z.; Di, Z.; Chen, X. Discontinuous and continuous transitions of collective behaviors in living systems. Chin. Phys. B 2021, 30, 128703. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Hu, G.; Liu, T.; Chen, X. Eigen microstates in self-organized criticality. Phys. Rev. E 2024, 109, 044130. [Google Scholar] [CrossRef]
- Hu, G.; Liu, M.; Chen, X. Quantum phase transition and eigen microstate condensation in the quantum Rabi model. Phys. A Stat. Mech. Its Appl. 2023, 630, 129210. [Google Scholar] [CrossRef]
- Li, X.; Xiang, X.; Xue, T.; Wang, L.; Chen, X. Exploring multiple phases and first-order phase transitions in Kármán Vortex Street. Sci. China Phys. Mech. Astron. 2024, 67, 110511. [Google Scholar] [CrossRef]
- Ma, X.; Liang, R.; Chen, X.; Xie, F.; Zuo, J.; Sun, C.; Ding, R. Increased predictability of extreme El Niño from decadal interbasin interaction. Geophys. Res. Lett. 2024, 51, e2024GL110943. [Google Scholar]
- Wang, X.; Fan, H.; Chen, X.; Xie, Y.; Wang, H. Holistic evolution of ecosystem in Heihe River Basin from the perspective of eigen microstates. Ecol. Indic. 2024, 159, 111689. [Google Scholar] [CrossRef]
- Chen, X.; Ying, N.; Chen, D.; Zhang, Y.; Lu, B.; Fan, J.; Chen, X. Eigen microstates and their evolution of global ozone at different geopotential heights. Chaos 2021, 31, 071102. [Google Scholar] [CrossRef]
- Chen, X.; Ren, H.; Tang, Z.; Zhou, K.; Zhou, L.; Zuo, Z.; Cui, X.; Chen, X.; Liu, Z.; He, Y.; et al. Leading basic modes of spontaneous activity drive individual functional connectivity organization in the resting human brain. Commun. Biol. 2023, 6, 892. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Monthly Averaged Data on Pressure Levels from 1940 to Present, 2023. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-pressure-levels-monthly-means?tab=overview (accessed on 3 May 2023).
- Liang, Z.; Rao, J.; Guo, D.; Lu, Q.; Shi, C. Northern winter stratospheric polar vortex regimes and their possible influence on the extratropical troposphere. Clim. Dyn. 2023, 60, 3167–3186. [Google Scholar] [CrossRef]
- Yamazaki, K.; Nakamura, T.; Ukita, J.; Hoshi, K. A tropospheric pathway of the stratospheric quasi-biennial oscillation (QBO) impact on the boreal winter polar vortex. Atmos. Chem. Phys. 2020, 20, 5111–5127. [Google Scholar] [CrossRef]
- Luo, F.; Luo, J.; Xie, F.; Tian, W.; Hu, Y.; Yuan, L.; Zhang, R.; Wang, T. The Key Role of the Vertical Structure of the Stratospheric Quasi-Biennial Oscillation in the Variations of Asian Precipitation in Summer. Geophys. Res. Lett. 2023, 50, e2023GL105863. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Ross, S.M. Introductory Statistics; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Guez, O.C.; Gozolchiani, A.; Havlin, S. Influence of autocorrelation on the topology of the climate network. Phys. Rev. E 2014, 90, 062814. [Google Scholar] [CrossRef]
- Lancaster, G.; Iatsenko, D.; Pidde, A.; Ticcinelli, V.; Stefanovska, A. Surrogate data for hypothesis testing of physical systems. Phys. Rep. 2018, 748, 1–60. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Gilman, D.L.; Fuglister, F.J.; Mitchell, J.’M. On the Power Spectrum of “Red Noise”. J. Atmos. Sci. 1963, 20, 182–184. [Google Scholar] [CrossRef]
- Mohanakumar, K. Stratosphere Troposphere Interactions: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Kawatani, Y.; Watanabe, S.; Sato, K.; Dunkerton, T.J.; Miyahara, S.; Takahashi, M. The roles of equatorial trapped waves and internal inertia–gravity waves in driving the quasi-biennial oscillation. Part I: Zonal mean wave forcing. J. Atmos. Sci. 2010, 67, 963–980. [Google Scholar] [CrossRef]
- Richter, J.H.; Solomon, A.; Bacmeister, J.T. On the simulation of the quasi-biennial oscillation in the Community Atmosphere Model, version 5. J. Geophys. Res. Atmos. 2014, 119, 3045–3062. [Google Scholar]
- Kim, Y.H.; Chun, H.Y. Momentum forcing of the quasi-biennial oscillation by equatorial waves in recent reanalyses. Atmos. Chem. Phys. 2015, 15, 6577–6587. [Google Scholar]
- Kim, Y.H.; Chun, H.Y. Contributions of equatorial wave modes and parameterized gravity waves to the tropical QBO in HadGEM2. J. Geophys. Res. Atmos. 2015, 120, 1065–1090. [Google Scholar]
- Pahlavan, H.A.; Fu, Q.; Wallace, J.M.; Kiladis, G.N. Revisiting the quasi-biennial oscillation as seen in ERA5. Part I: Description and momentum budget. J. Atmos. Sci. 2021, 78, 673–691. [Google Scholar] [CrossRef]
- Ern, M.; Ploeger, F.; Preusse, P.; Gille, J.; Gray, L.; Kalisch, S.; Mlynczak, M.; Russell, J., III; Riese, M. Interaction of gravity waves with the QBO: A satellite perspective. J. Geophys. Res. Atmos. 2014, 119, 2329–2355. [Google Scholar]
- Newman, P.; Coy, L.; Pawson, S.; Lait, L. The anomalous change in the QBO in 2015–2016. Geophys. Res. Lett. 2016, 43, 8791–8797. [Google Scholar]
- Saunders, M.A.; Lea, A.S.; Smallwood, J.R. The quasi-biennial oscillation: A second disruption in four years. ESS Open Archive 2020. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, J.; Lu, Y.; Ju, Z.; Yang, J.; Luo, J. A revisit and comparison of the quasi-biennial oscillation (QBO) disruption events in 2015/16 and 2019/20. Atmos. Res. 2023, 294, 106970. [Google Scholar]
- Osprey, S.M.; Butchart, N.; Knight, J.R.; Scaife, A.A.; Hamilton, K.; Anstey, J.A.; Schenzinger, V.; Zhang, C. An unexpected disruption of the atmospheric quasi-biennial oscillation. Science 2016, 353, 1424–1427. [Google Scholar]
- Kang, M.J.; Chun, H.Y.; Son, S.W.; Garcia, R.R.; An, S.I.; Park, S.H. Role of tropical lower stratosphere winds in quasi-biennial oscillation disruptions. Sci. Adv. 2022, 8, eabm7229. [Google Scholar]
- Anstey, J.A.; Banyard, T.P.; Butchart, N.; Coy, L.; Newman, P.A.; Osprey, S.; Wright, C.J. Prospect of increased disruption to the QBO in a changing climate. Geophys. Res. Lett. 2021, 48, e2021GL093058. [Google Scholar] [CrossRef]
- Holton, J.R.; Tan, H.C. The influence of the equatorial quasi-biennial oscillation on the global circulation at 50 mb. J. Atmos. Sci. 1980, 37, 2200–2208. [Google Scholar] [CrossRef]
- Anstey, J.A.; Shepherd, T.G. High-latitude influence of the quasi-biennial oscillation. Q. J. R. Meteorol. Soc. 2014, 140, 1–21. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Schwartz, C.; Domeisen, D.I.; Son, S.W.; Butler, A.H.; White, I.P. Extratropical atmospheric predictability from the quasi-biennial oscillation in subseasonal forecast models. J. Geophys. Res. Atmos. 2018, 123, 7855–7866. [Google Scholar] [CrossRef]
- Rao, J.; Garfinkel, C.I.; White, I.P. Impact of the quasi-biennial oscillation on the northern winter stratospheric polar vortex in CMIP5/6 models. J. Clim. 2020, 33, 4787–4813. [Google Scholar]
- Randel, W.J.; Wu, F. Isolation of the ozone QBO in SAGE II data by singular-value decomposition. J. Atmos. Sci. 1996, 53, 2546–2559. [Google Scholar]
- Rao, J.; Yu, Y.; Guo, D.; Shi, C.; Chen, D.; Hu, D. Evaluating the Brewer–Dobson circulation and its responses to ENSO, QBO, and the solar cycle in different reanalyses. Earth Planet. Phys. 2019, 3, 166–181. [Google Scholar]
- Garfinkel, C.I.; Hartmann, D.L. The influence of the quasi-biennial oscillation on the troposphere in winter in a hierarchy of models. Part II: Perpetual winter WACCM runs. J. Atmos. Sci. 2011, 68, 2026–2041. [Google Scholar]
- Wang, J.; Kim, H.M.; Chang, E.K. Interannual modulation of Northern Hemisphere winter storm tracks by the QBO. Geophys. Res. Lett. 2018, 45, 2786–2794. [Google Scholar] [CrossRef]
- Martin, Z.; Son, S.W.; Butler, A.; Hendon, H.; Kim, H.; Sobel, A.; Yoden, S.; Zhang, C. The influence of the quasi-biennial oscillation on the Madden–Julian oscillation. Nat. Rev. Earth Environ. 2021, 2, 477–489. [Google Scholar] [CrossRef]
- Anstey, J.A.; Osprey, S.M.; Alexander, J.; Baldwin, M.P.; Butchart, N.; Gray, L.; Kawatani, Y.; Newman, P.A.; Richter, J.H. Impacts, processes and projections of the quasi-biennial oscillation. Nat. Rev. Earth Environ. 2022, 3, 588–603. [Google Scholar]
- Zhang, R.; Zhou, W.; Tian, W.; Zhang, Y.; Zhang, J.; Luo, J. A stratospheric precursor of East Asian summer droughts and floods. Nat. Commun. 2024, 15, 247. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Tippett, M.K.; Sobel, A.H.; Martin, Z.K.; Vitart, F. Impact of the QBO on prediction and predictability of the MJO convection. J. Geophys. Res. Atmos. 2019, 124, 11766–11782. [Google Scholar] [CrossRef]
- Naujokat, B. An update of the observed quasi-biennial oscillation of the stratospheric winds over the tropics. J. Atmos. Sci. 1986, 43, 1873–1877. [Google Scholar]
- Dunkerton, T.J.; Delisi, D.P. Climatology of the equatorial lower stratosphere. J. Atmos. Sci. 1985, 42, 376–396. [Google Scholar]
- Xu, W.; Ren, H.L. A CEOF-based method for measuring amplitude and phase properties of the QBO. Clim. Dyn. 2023, 61, 923–937. [Google Scholar] [CrossRef]
- Waugh, D.W.; Sobel, A.H.; Polvani, L.M. What is the polar vortex and how does it influence weather? Bull. Am. Meteorol. Soc. 2017, 98, 37–44. [Google Scholar]
- Zuev, V.V.; Savelieva, E.; Borovko, I.V.; Krupchatnikov, V.N. Influence of the subtropical stratosphere on the Antarctic polar vortex during spring 2019. In Proceedings of the 27th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics, SPIE, Moscow, Russia, 5–9 July 2021; Volume 11916, pp. 1539–1544. [Google Scholar]
- Schoeberl, M.R.; Hartmann, D.L. The dynamics of the stratospheric polar vortex and its relation to springtime ozone depletions. Science 1991, 251, 46–52. [Google Scholar]
- Roy, R.; Kuttippurath, J. The dynamical evolution of Sudden Stratospheric Warmings of the Arctic winters in the past decade 2011–2021. SN Appl. Sci. 2022, 4, 105. [Google Scholar] [CrossRef]
- Thompson, D.W.; Baldwin, M.P.; Wallace, J.M. Stratospheric connection to Northern Hemisphere wintertime weather: Implications for prediction. J. Clim. 2002, 15, 1421–1428. [Google Scholar]
- Lim, E.P.; Hendon, H.H.; Boschat, G.; Hudson, D.; Thompson, D.W.; Dowdy, A.J.; Arblaster, J.M. Australian hot and dry extremes induced by weakenings of the stratospheric polar vortex. Nat. Geosci. 2019, 12, 896–901. [Google Scholar]
- Kolstad, E.W.; Breiteig, T.; Scaife, A.A. The association between stratospheric weak polar vortex events and cold air outbreaks in the Northern Hemisphere. Q. J. R. Meteorol. Soc. 2010, 136, 886–893. [Google Scholar] [CrossRef]
- Overland, J.; Hall, R.; Hanna, E.; Karpechko, A.; Vihma, T.; Wang, M.; Zhang, X. The polar vortex and extreme weather: The Beast from the East in winter 2018. Atmosphere 2020, 11, 664. [Google Scholar] [CrossRef]
- Yu, Y.; Cai, M.; Shi, C.; Ren, R. On the linkage among strong stratospheric mass circulation, stratospheric sudden warming, and cold weather events. Mon. Weather. Rev. 2018, 146, 2717–2739. [Google Scholar]
- Rao, J.; Ren, R.; Chen, H.; Yu, Y.; Zhou, Y. The stratospheric sudden warming event in February 2018 and its prediction by a climate system model. J. Geophys. Res. Atmos. 2018, 123, 13–332. [Google Scholar]
- Bao, M.; Tan, X.; Hartmann, D.L.; Ceppi, P. Classifying the tropospheric precursor patterns of sudden stratospheric warmings. Geophys. Res. Lett. 2017, 44, 8011–8016. [Google Scholar]
- Ma, C.; Yang, P.; Tan, X.; Bao, M. Possible causes of the occurrence of a rare Antarctic sudden stratospheric warming in 2019. Atmosphere 2022, 13, 147. [Google Scholar] [CrossRef]
- Wei, K.; Chen, W.; Huang, R. Dynamical diagnosis of the breakup of the stratospheric polar vortex in the Northern Hemisphere. Sci. China Ser. D Earth Sci. 2007, 50, 1369–1379. [Google Scholar] [CrossRef]
- Lu, H.; Bracegirdle, T.J.; Phillips, T.; Bushell, A.; Gray, L. Mechanisms for the Holton-Tan relationship and its decadal variation. J. Geophys. Res. Atmos. 2014, 119, 2811–2830. [Google Scholar]
- Yang, S.; Li, Z.; Yu, J.Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern Oscillation and its impact in the changing climate. Natl. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Domeisen, D.I.; Garfinkel, C.I.; Butler, A.H. The teleconnection of El Niño Southern Oscillation to the stratosphere. Rev. Geophys. 2019, 57, 5–47. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.; Grinsted, A. Oceanic and atmospheric transport of multiyear El Nino–Southern Oscillation (ENSO) signatures to the polar regions. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Hu, D.; Guan, Z.; Tian, W.; Ren, R. Recent strengthening of the stratospheric Arctic vortex response to warming in the central North Pacific. Nat. Commun. 2018, 9, 1697. [Google Scholar] [PubMed]
- Li, Y.; Tian, W.; Xie, F.; Wen, Z.; Zhang, J.; Hu, D.; Han, Y. The connection between the second leading mode of the winter North Pacific sea surface temperature anomalies and stratospheric sudden warming events. Clim. Dyn. 2018, 51, 581–595. [Google Scholar]
- Xie, F.; Li, J.; Tian, W.; Fu, Q.; Jin, F.F.; Hu, Y.; Zhang, J.; Wang, W.; Sun, C.; Feng, J.; et al. A connection from Arctic stratospheric ozone to El Niño-Southern oscillation. Environ. Res. Lett. 2016, 11, 124026. [Google Scholar]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Komitov, B. About the Possible Solar Nature of the ∼200 yr (de Vries/Suess) and ∼2000–2500 yr (Hallstadt) Cycles and Their Influences on the Earth’s Climate: The Role of Solar-Triggered Tectonic Processes in General “Sun–Climate” Relationship. Atmosphere 2024, 15, 612. [Google Scholar] [CrossRef]
- Komitov, B.; Kaftan, V. Danjon Effect, Solar Activity, and Volcanism. Geomagn. Aeron. 2022, 62, 1117–1122. [Google Scholar]
- Komitov, B.; Kaftan, V. The Lower Ionosphere and Tectonic Processes on Earth. Geomagn. Aeron. 2023, 63, 1038–1046. [Google Scholar]
- Khain, V.; Khalilov, E. About possible influence of solar activity on seismic and volcanic activities: Long-term forecast. Sci. Without Bord. 2009, 316. [Google Scholar]
- Qu, W.Z.; Huang, F.; Du, L.; Zhao, J.P.; Deng, S.G.; Cao, Y. The periodicity of volcano activity and its reflection in some climate factors. Chin. J. Geophys. 2011, 54, 135–149. [Google Scholar]
- Yamazaki, K.; Nakamura, T. The stratospheric QBO affects antarctic sea ice through the tropical convection in early austral winter. Polar Sci. 2021, 28, 100674. [Google Scholar]
- Rao, J.; Garfinkel, C.I.; Ren, R.; Wu, T.; Lu, Y.; Chu, M. Projected strengthening impact of the Quasi-Biennial Oscillation on the Southern Hemisphere by CMIP5/6 models. J. Clim. 2023, 36, 5461–5476. [Google Scholar]
- Butler, A.H.; Domeisen, D.I. The wave geometry of final stratospheric warming events. Weather. Clim. Dyn. 2021, 2, 453–474. [Google Scholar]
- Zambri, B.; Solomon, S.; Thompson, D.W.; Fu, Q. Emergence of Southern Hemisphere stratospheric circulation changes in response to ozone recovery. Nat. Geosci. 2021, 14, 638–644. [Google Scholar]
- Zuev, V.V.; Savelieva, E. The cause of the spring strengthening of the Antarctic polar vortex. Dyn. Atmos. Oceans 2019, 87, 101097. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, N.; Chen, X.; Xie, F.; Zhang, Y.; Xia, Y.; Ma, X.; Huang, H.; Wang, H. A Revisit of Large-Scale Patterns in Middle Stratospheric Circulation Variations. Entropy 2025, 27, 327. https://doi.org/10.3390/e27040327
Tao N, Chen X, Xie F, Zhang Y, Xia Y, Ma X, Huang H, Wang H. A Revisit of Large-Scale Patterns in Middle Stratospheric Circulation Variations. Entropy. 2025; 27(4):327. https://doi.org/10.3390/e27040327
Chicago/Turabian StyleTao, Ningning, Xiaosong Chen, Fei Xie, Yongwen Zhang, Yan Xia, Xuan Ma, Han Huang, and Hongyu Wang. 2025. "A Revisit of Large-Scale Patterns in Middle Stratospheric Circulation Variations" Entropy 27, no. 4: 327. https://doi.org/10.3390/e27040327
APA StyleTao, N., Chen, X., Xie, F., Zhang, Y., Xia, Y., Ma, X., Huang, H., & Wang, H. (2025). A Revisit of Large-Scale Patterns in Middle Stratospheric Circulation Variations. Entropy, 27(4), 327. https://doi.org/10.3390/e27040327





