A New Analytical Formulation for the Electrophoretic Mobility of a Colloidal Sphere
Abstract
1. Introduction
2. Definitions
- The Reynolds number is small so that the inertial terms in the Navier–Stokes equations can be ignored.
- The fluid is incompressible.
- The applied electric field is weak compared to the local electric field around the particle so that higher-order terms in can be neglected.
2.1. The Double Layer
2.2. The Electrochemical Potential
2.3. The Ionic Flux
2.4. The Velocity
2.5. Variable Definitions
3. The Poisson–Boltzmann Equation
3.1. Boundary Conditions at
3.2. Boundary Conditions Far Away
4. The Conservation of Mass Law (Nernst–Planck)
4.1. Boundary Conditions at
4.2. Boundary Conditions Far Away
5. Navier–Stokes
5.1. Boundary Conditions at
5.2. Boundary Conditions Far Away
6. Analytical Solutions
6.1. Full Solution as Function of Integrals
6.2. Approximated Analytical Solution
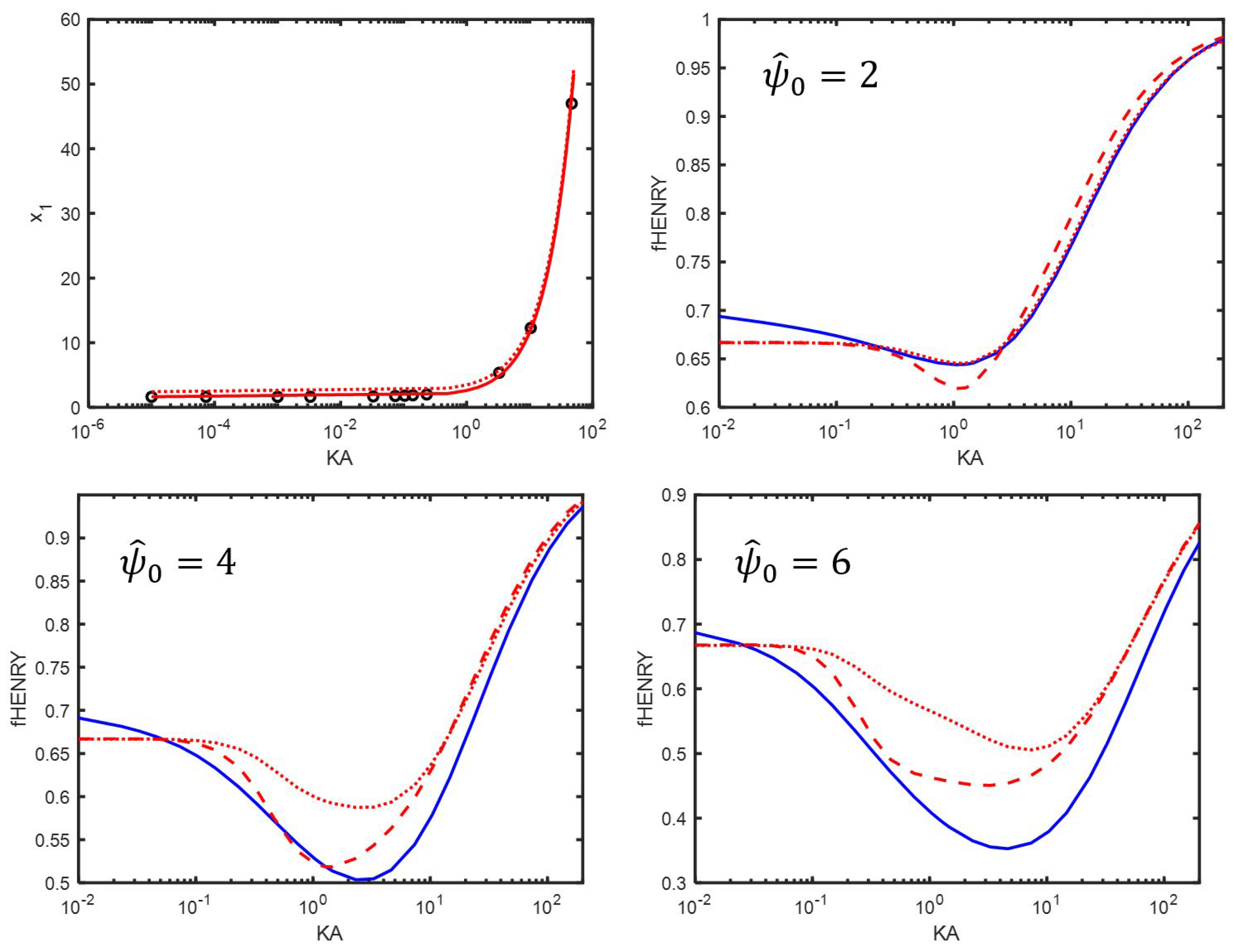
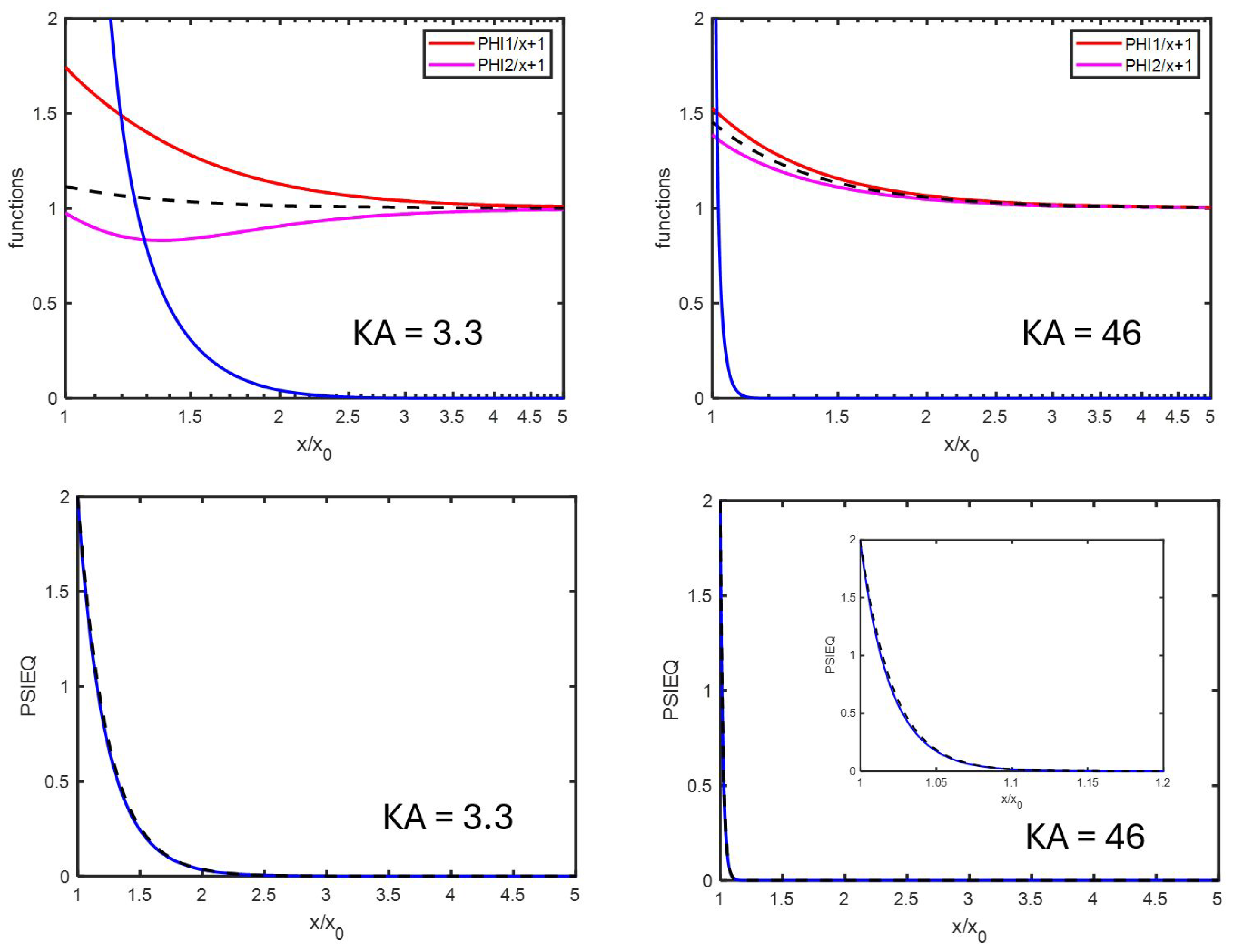
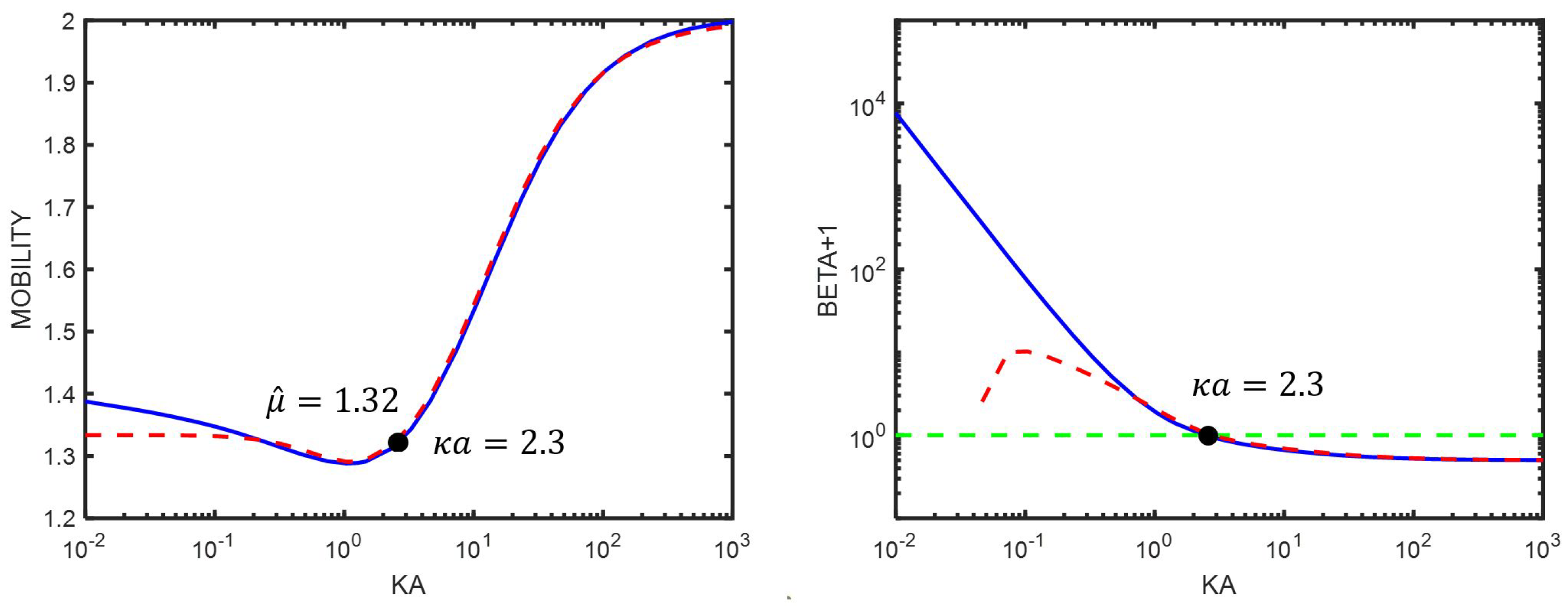
7. Comparison Between the Use of Equations (76) and (77)
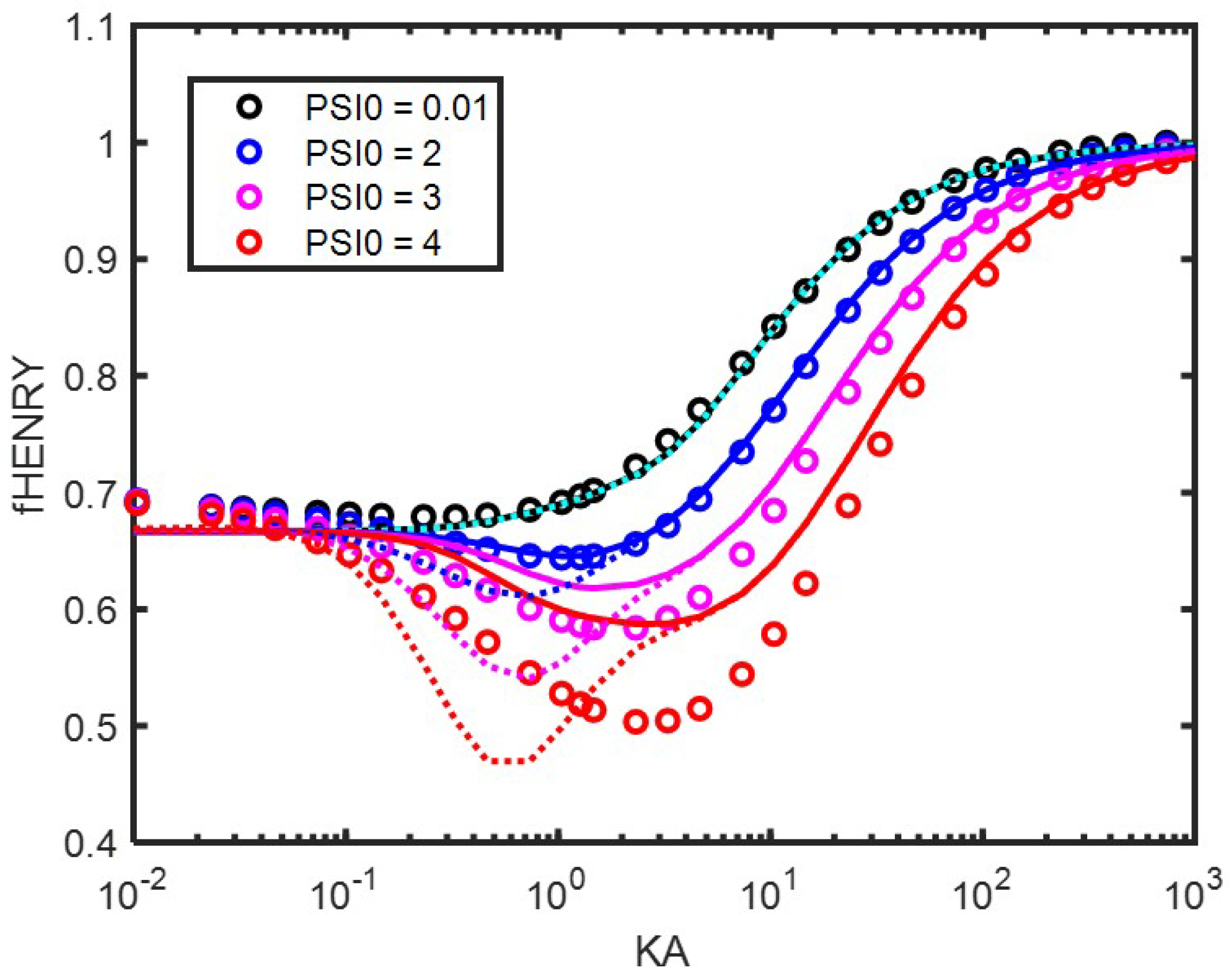
8. The Electrophoretic Mobility for Different
8.1. The Role of the Double Layer
8.1.1. Hückel’s Approximation ()
8.1.2. Smoluchowski’ s Approximation ()
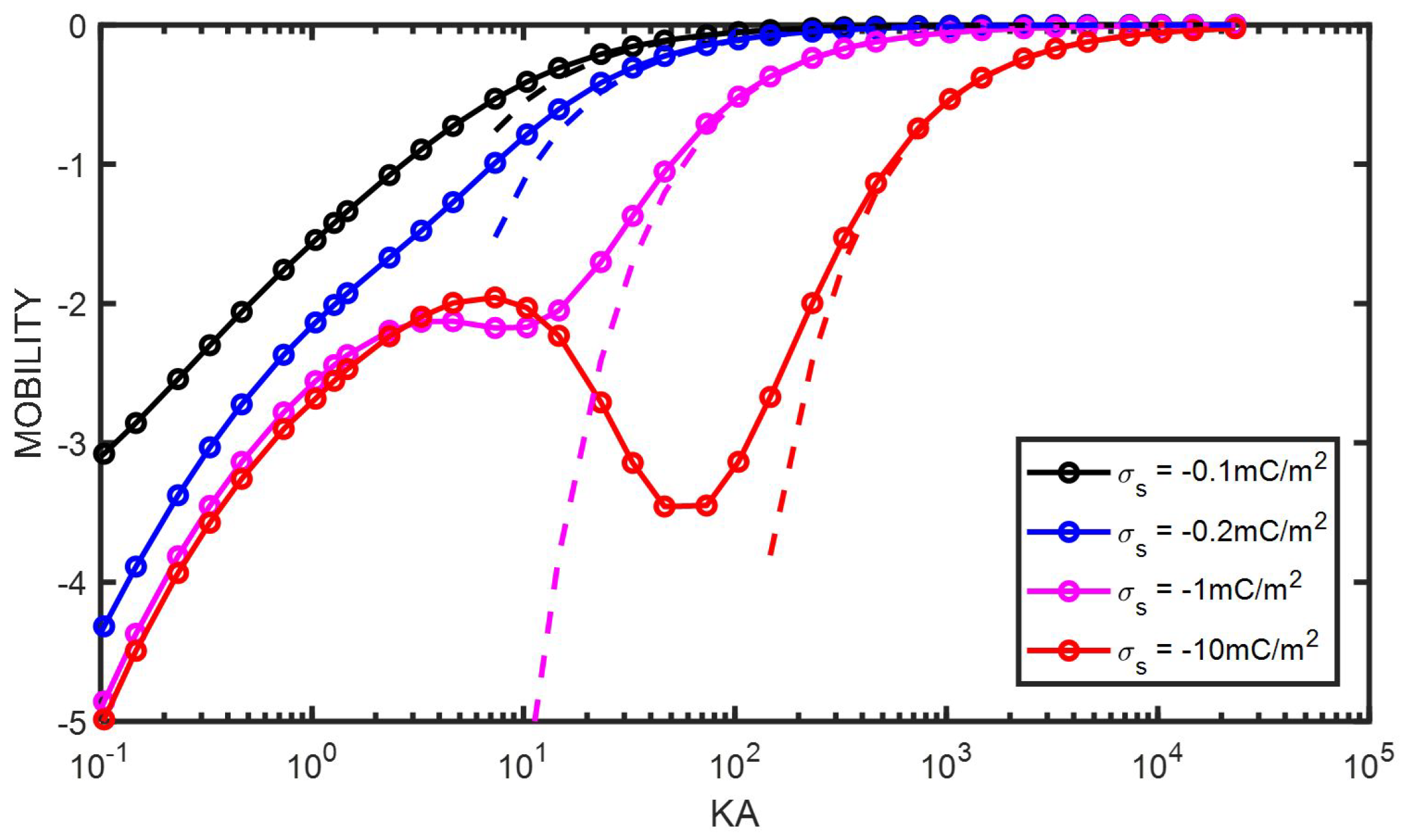
9. Particle with a Constant Surface Charge
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Equivalence with Previous Work
Appendix B. An Analytical Expression for β
Appendix B.1. Low
Appendix B.2. High
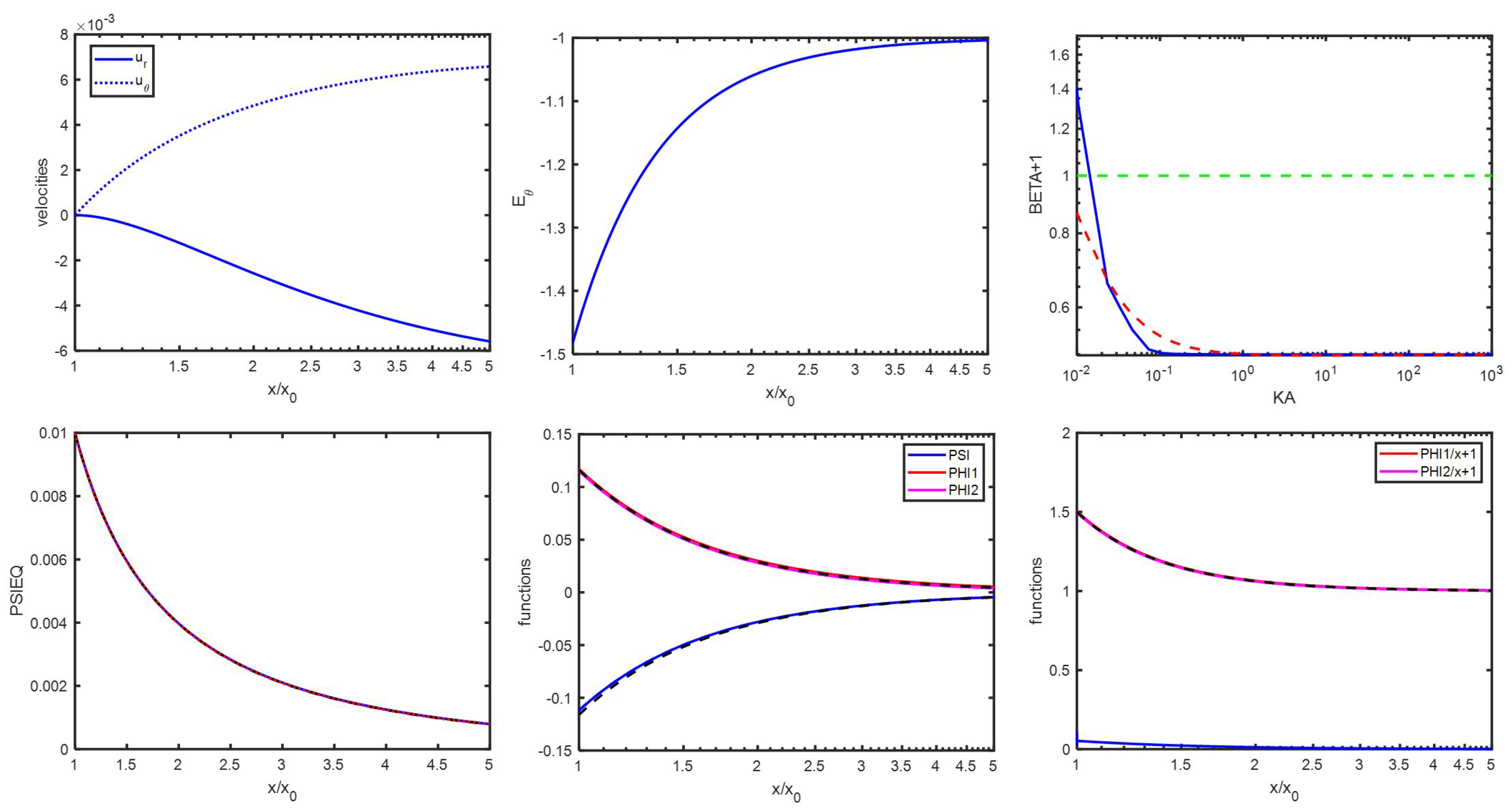
Appendix C. An Estimation of x1
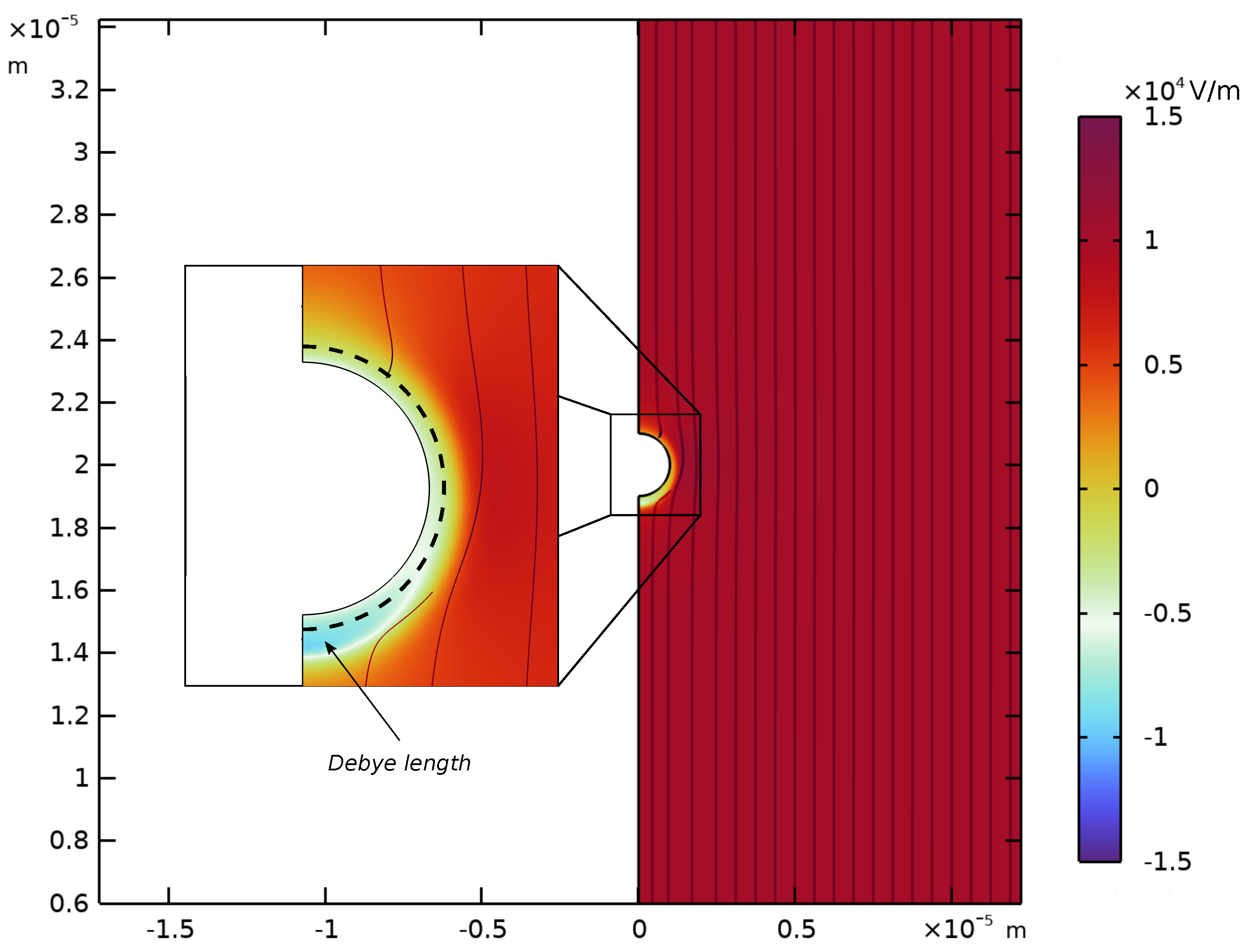
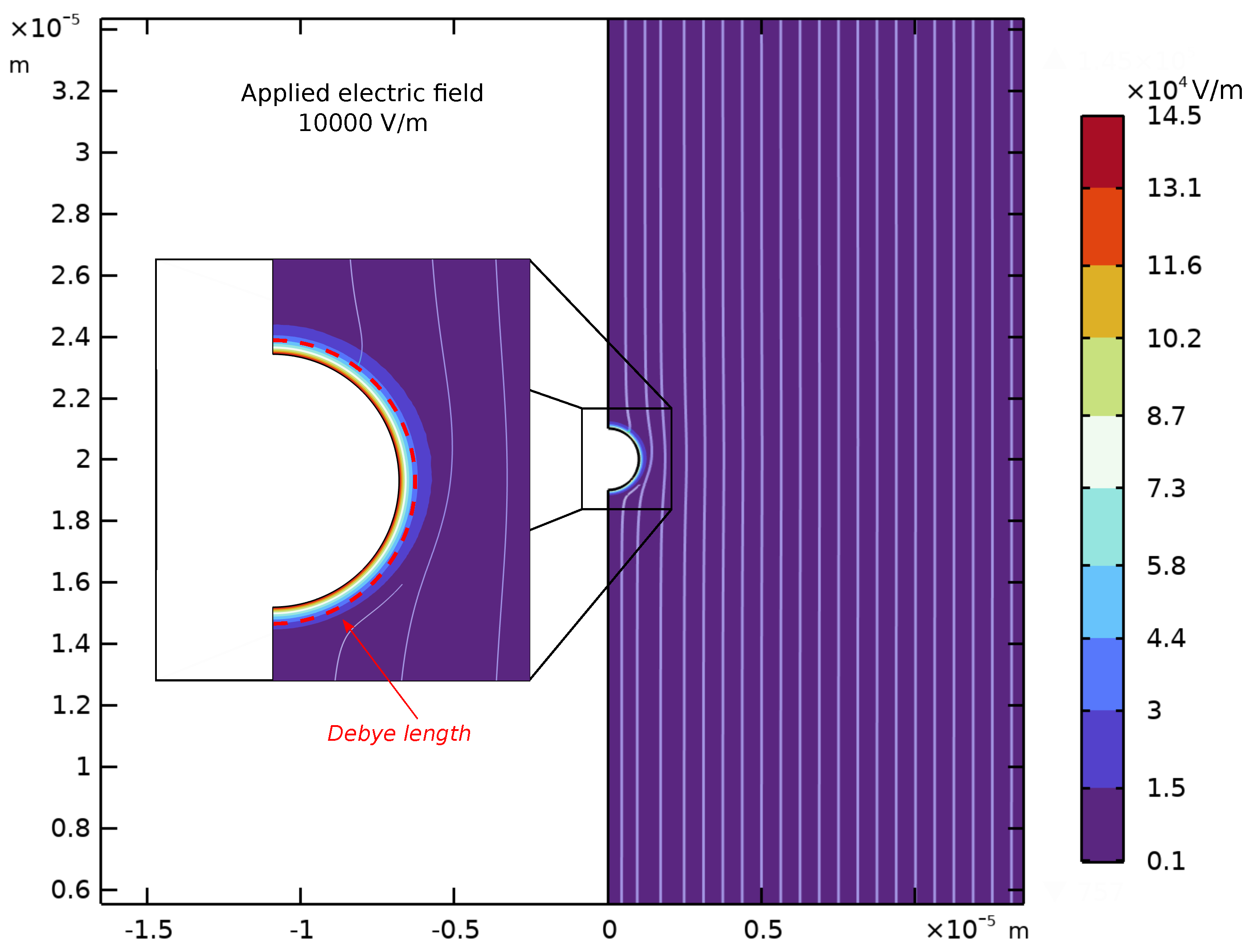
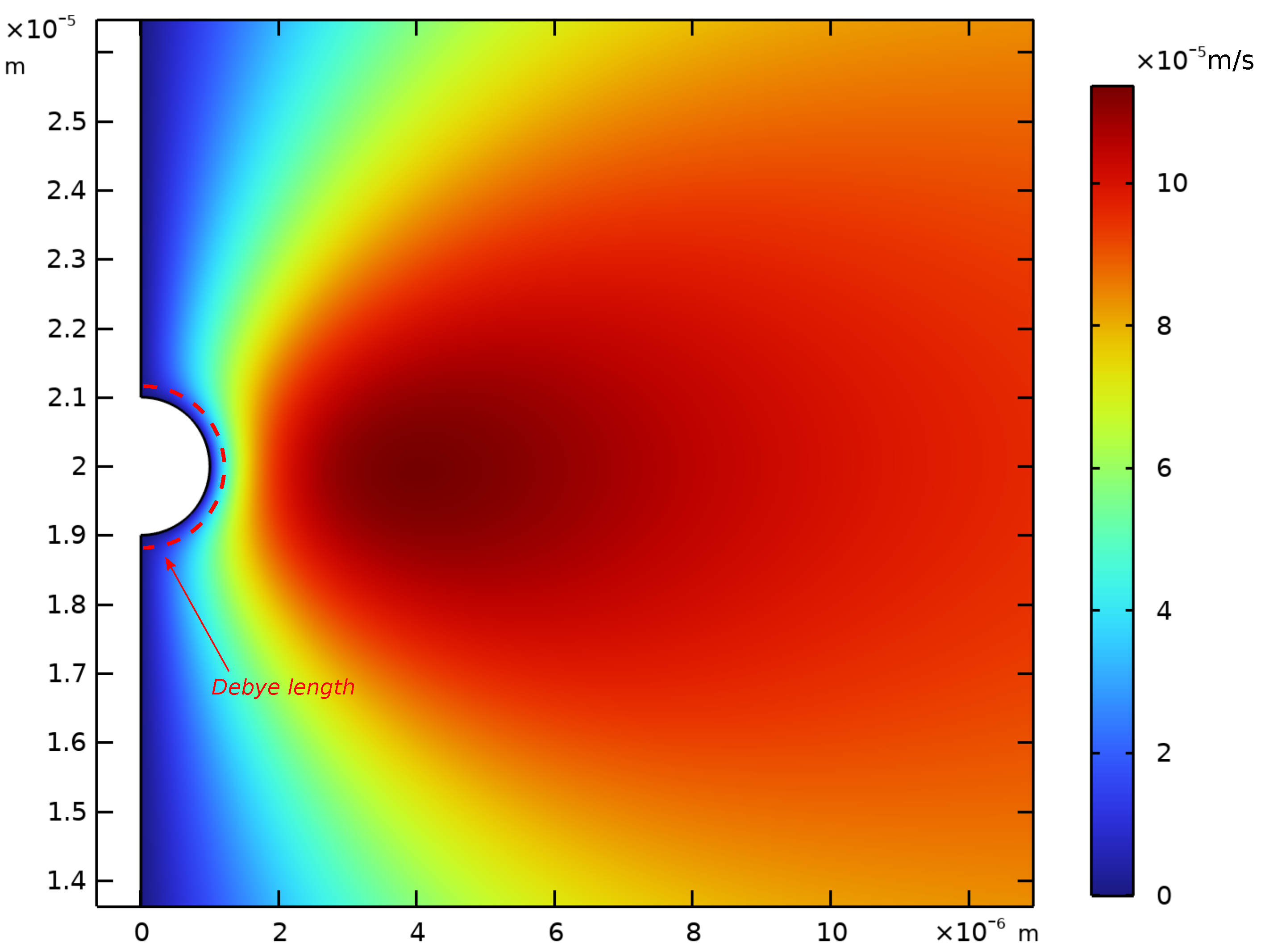
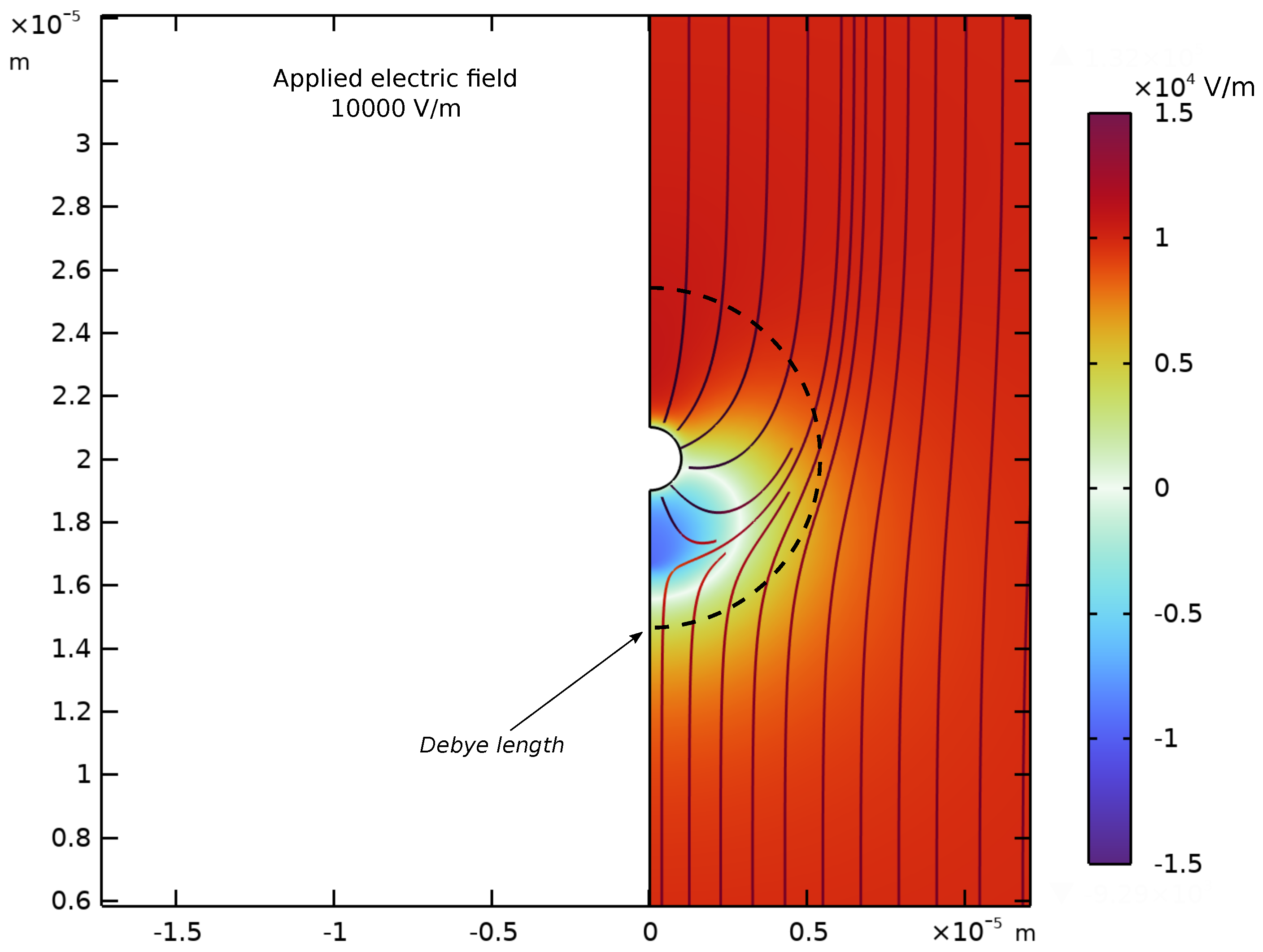
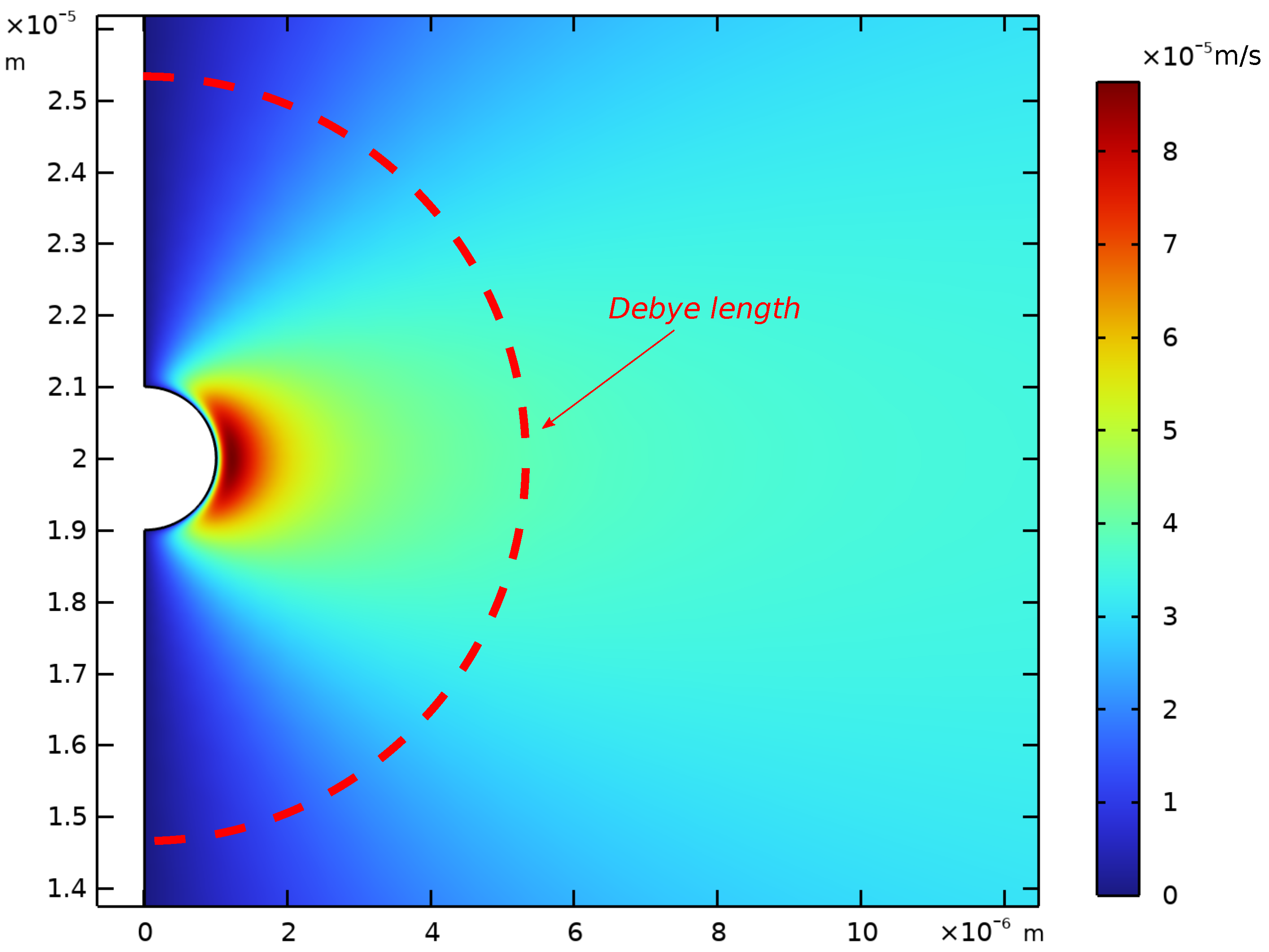
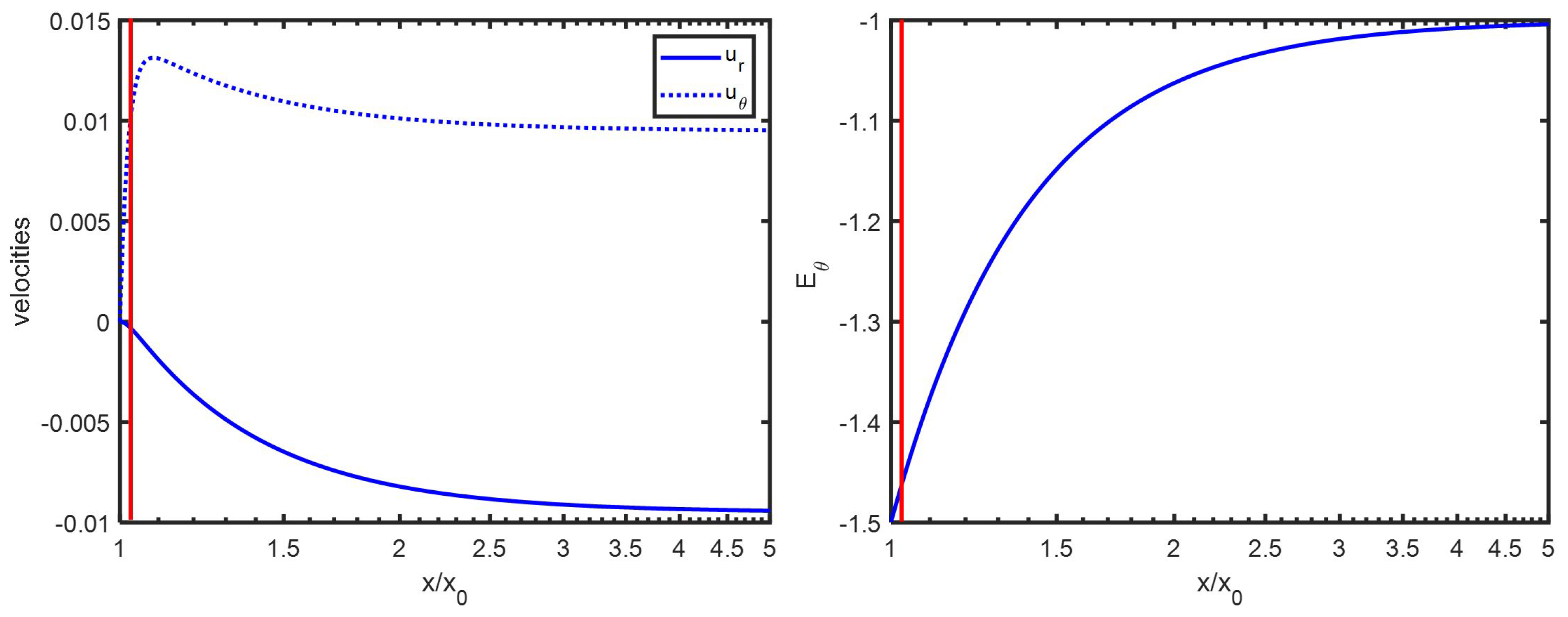
Appendix D. Spatial Representation



References
- Ohshima, H. Theory of Colloid and Interfacial Electric Phenomena; Elsevier: Amsterdam, The Netherlands, 2006; Volume 12. [Google Scholar]
- O’Brien, R.W.; White, L.R. Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Trans. Mol. Chem. Phys. 1978, 74, 1607–1626. [Google Scholar] [CrossRef]
- Jayaraman, A.S.; Klaseboer, E.; Chan, D.Y. The unusual fluid dynamics of particle electrophoresis. J. Colloid Interface Sci. 2019, 553, 845–863. [Google Scholar] [CrossRef] [PubMed]
- Chassagne, C.; Bedeaux, D. The dielectric response of a colloidal spheroid. J. Colloid Interface Sci. 2008, 326, 240–253. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, C.J.F.; van Belle, O.C.; Bordewijk, P.; Rip, A.; Yue, D.D. Theory of Electric Polarization; American Elsevier PubIishing Co., Inc.: New York, NY, USA, 1973. [Google Scholar]
- Chassagne, C.; Ibanez, M. Electrophoretic mobility of latex nanospheres in electrolytes: Experimental challenges. Pure Appl. Chem. 2012, 85, 41–51. [Google Scholar] [CrossRef]
- Döpke, M.F.; Hartkamp, R. The importance of specifically adsorbed ions for electrokinetic phenomena: Bridging the gap between experiments and MD simulations. J. Chem. Phys. 2021, 154, 094701. [Google Scholar] [CrossRef] [PubMed]
- Chassagne, C.; Dubois, E.; Jiménez, M.L.; van Der Ploeg, J.M.; Van Turnhout, J. Compensating for electrode polarization in dielectric spectroscopy studies of colloidal suspensions: Theoretical assessment of existing methods. Front. Chem. 2016, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Klaseboer, E.; Chan, D.Y. On the derivation of the Smoluchowski result of electrophoretic mobility. J. Colloid Interface Sci. 2020, 568, 176–184. [Google Scholar] [CrossRef] [PubMed]
- Jeffrey, A.; Dai, H.H. Handbook of Mathematical Formulas and Integrals; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Ohshima, H.; Healy, T.W.; White, L.R. Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1983, 79, 1613–1628. [Google Scholar] [CrossRef]
- Chassagne, C. Dielectric response of a charged prolate spheroid in an electrolyte solution. Int. J. Thermophys. 2013, 34, 1239–1254. [Google Scholar] [CrossRef]
- COMSOL Multiphysics v. 6.3. COMSOL AB, Stockholm, Sweden. Available online: www.comsol.com (accessed on 28 February 2025).
- Henry, D.C. The cataphoresis of suspended particles. Part I.—The equation of cataphoresis. Proc. R. Soc. Lond. Ser. A 1931, 133, 106–129. [Google Scholar]
- Overbeek, J.T.G.; Wiersema, P.H. The Interpretation of Electrophoretic Mobilities; Academic Press: New York, NY, USA, 1967; Volume 2, pp. 1–52. [Google Scholar]
- Overbeek, J.T.G.; Loeb, A.L.; Wiersema, P.H. Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid Interface Sci. 1966, 22, 78–99. [Google Scholar]
- Kobayashi, M. Electrophoretic mobility of latex spheres in the presence of divalent ions: Experiments and modeling. Colloid Polym. Sci. 2008, 286, 935–940. [Google Scholar] [CrossRef]
- Kaya, A.; Yukselen, Y. Zeta potential of clay minerals and quartz contaminated by heavy metals. Can. Geotech. J. 2005, 42, 1280–1289. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casarella, A.; Gourdin-Bertin, S.; Chassagne, C. A New Analytical Formulation for the Electrophoretic Mobility of a Colloidal Sphere. Entropy 2025, 27, 336. https://doi.org/10.3390/e27040336
Casarella A, Gourdin-Bertin S, Chassagne C. A New Analytical Formulation for the Electrophoretic Mobility of a Colloidal Sphere. Entropy. 2025; 27(4):336. https://doi.org/10.3390/e27040336
Chicago/Turabian StyleCasarella, Angela, Simon Gourdin-Bertin, and Claire Chassagne. 2025. "A New Analytical Formulation for the Electrophoretic Mobility of a Colloidal Sphere" Entropy 27, no. 4: 336. https://doi.org/10.3390/e27040336
APA StyleCasarella, A., Gourdin-Bertin, S., & Chassagne, C. (2025). A New Analytical Formulation for the Electrophoretic Mobility of a Colloidal Sphere. Entropy, 27(4), 336. https://doi.org/10.3390/e27040336







