Kinetic Description of Viral Capsid Self-Assembly Using Mesoscopic Non-Equilibrium Thermodynamics
Abstract
:1. Introduction
2. Kinetic Aspects of Viral Capsid Self-Assembly
3. Continuum Description of the Free Energy Landscape of Viral Capsid Self-Assembly
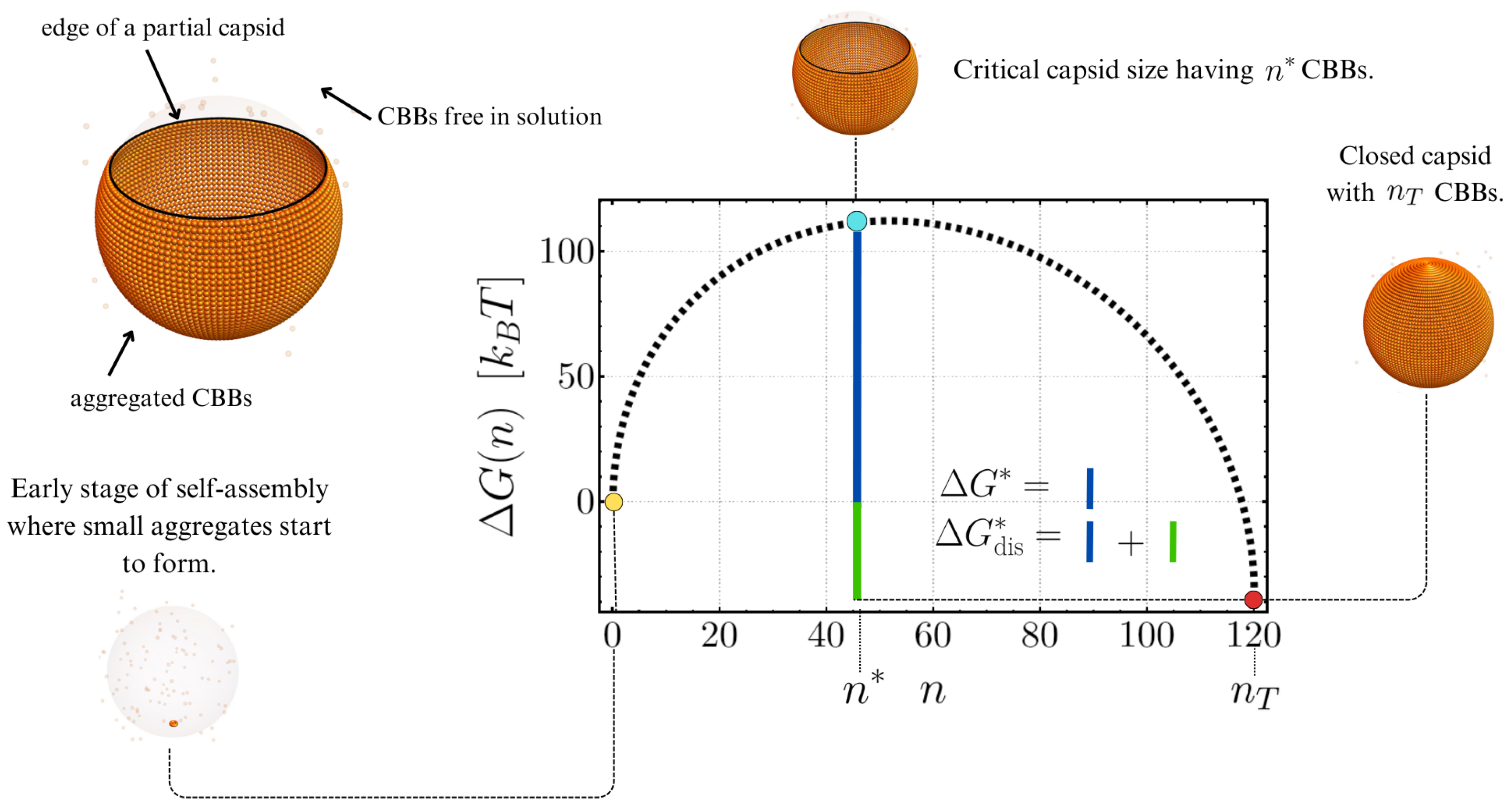
Extensions of Classical Nucleation Theory of Viral Capsids Incorporating Elastic Contributions
4. General Framework for Mesoscopic Non-Equilibrium Thermodynamics
Entropy as the Key to the Time Evolution of an Out-of-Equilibrium System
5. Kinetics of Viral Capsid Self-Assembly from MNET
5.1. The Case of One Degree of Freedom: The Assembly of a Spherical Capsid with a Fixed Radius
5.2. Two Degrees of Freedom
5.3. Three Degrees of Freedom: The Assembly of Tubes with Arbitrary Line Tension
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.-Z.; Shi, M.; Holmes, E.C. Using Metagenomics to Characterize an Expanding Virosphere. Cell 2018, 172, 1168–1172. [Google Scholar] [CrossRef] [PubMed]
- French, R.K.; Holmes, E.C. An Ecosystems Perspective on Virus Evolution and Emergence. Trends Microbiol. 2020, 28, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Suttle, C.A. Viruses in the sea. Nature 2005, 437, 356–361. [Google Scholar] [CrossRef] [PubMed]
- Pearce, D.A.; Wilson, W.H. Viruses in Antarctic ecosystems. Antarct. Sci. 2003, 15, 319–331. [Google Scholar] [CrossRef]
- Lopez-Simon, J.; Vila-Nistal, M.; Rosenova, A.; De Corte, D.; Baltar, F.; Martinez-Garcia, M. Viruses under the Antarctic Ice Shelf are active and potentially involved in global nutrient cycles. Nat. Commun. 2023, 14, 8295. [Google Scholar] [CrossRef]
- Le Romancer, M.; Gaillard, M.; Geslin, C.; Prieur, D. Viruses in extreme environments. Rev. Environ. Sci. Biotechnol. 2007, 6, 17–31. [Google Scholar] [CrossRef]
- Gil, J.F.; Mesa, V.; Estrada-Ortiz, N.; Lopez-Obando, M.; Gómez, A.; Plácido, J. Viruses in Extreme Environments, Current Overview, and Biotechnological Potential. Viruses 2021, 13, 81. [Google Scholar] [CrossRef]
- Rachel, R.; Bettstetter, M.; Hedlund, B.P.; Häring, M.; Kessler, A.; Stetter, K.O.; Prangishvili, D. Remarkable morphological diversity of viruses and virus-like particles in hot terrestrial environments. Arch. Virol. 2002, 147, 2419–2429. [Google Scholar] [CrossRef]
- Jiang, S.; Steward, G.; Jellison, R.; Chu, W.; Choi, S. Abundance, Distribution, and Diversity of Viruses in Alkaline, Hypersaline Mono Lake, California. Microb. Ecol. 2004, 47, 9–17. [Google Scholar] [CrossRef]
- Oren, A.; Bratbak, G.; Heldal, M. Occurrence of virus-like particles in the Dead Sea. Extremophiles 1997, 1, 143–149. [Google Scholar] [CrossRef]
- Breitbart, M.; Rohwer, F. Here a virus, there a virus, everywhere the same virus? Trends Microbiol. 2005, 13, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Edwards, R.A.; Rohwer, F. Viral metagenomics. Nat. Rev. Microbiol. 2005, 3, 504–510. [Google Scholar] [CrossRef] [PubMed]
- Cobian Guemes, A.G.; Youle, M.; Cantu, V.A.; Felts, B.; Nulton, J.; Rohwer, F. Viruses as Winners in the Game of Life. Annu. Rev. Virol. 2016, 3, 197–214. [Google Scholar] [CrossRef]
- Stanley, W.M. Properties of Viruses. Medicine 1939, 18, 4. Available online: https://journals.lww.com/md-journal/fulltext/1939/12000/properties_of_viruses.1.aspx (accessed on 20 December 2024). [CrossRef]
- Pollard, E.C. The Physics of Viruses. Sci. Am. 1954, 191, 62–71. [Google Scholar] [CrossRef]
- Stockley, P.; Twarock, R. (Eds.) Emerging Topics in Physical Virology; Imperial College Press: London, UK, 2010. [Google Scholar]
- Khaykelson, D.; Raviv, U. Studying Viruses Using Solution X-ray Scattering. Biophys. Rev. 2020, 12, 41–48. [Google Scholar] [CrossRef]
- Mateu, M.G. (Ed.) Structure and Physics of Viruses: An Integrated Textbook; Springer: Dordrecht, The Netherlands, 2024. [Google Scholar]
- Kushner, D.J. Self-assembly of biological structures. Bacteriol. Rev. 1969, 33, 302–345. [Google Scholar] [CrossRef]
- Bancroft, J.B. The Self-Assembly of Spherical Plant Viruses. In Advances in Virus Research; Smith, K.M., Lauffer, M.A., Bang, F.B., Eds.; Academic Press: New York, NY, 1970; Volume 16, pp. 99–134. [Google Scholar] [CrossRef]
- Rong, J.; Niu, Z.; Lee, L.A.; Wang, Q. Self-assembly of viral particles. Curr. Opin. Colloid Interface Sci. 2011, 16, 441–450. [Google Scholar] [CrossRef]
- Panahandeh, S.; Li, S.; Dragnea, B.; Zandi, R. Virus Assembly Pathways Inside a Host Cell. ACS Nano 2022, 16, 317–327. [Google Scholar] [CrossRef]
- Sun, S.; Rao, V.B.; Rossmann, M.G. Genome packaging in viruses. Curr. Opin. Struct. Biol. 2010, 20, 114–120. [Google Scholar] [CrossRef]
- Rossmann, M.G.; Rao, V.B. (Eds.) Viral Molecular Machines; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Garmann, R.F.; Goldfain, A.M.; Tanimoto, C.R.; Beren, C.E.; Vasquez, F.F.; Villarreal, D.A.; Knobler, C.M.; Gelbart, W.M.; Manoharan, V.N. Single-Particle Studies of the Effects of RNA–Protein Interactions on the Self-Assembly of RNA Virus Particles. Proc. Natl. Acad. Sci. USA 2022, 119, e2206292119. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, S.M.; Li, F.; Briani, F.; Cingolani, G. Viral Genome Delivery Across Bacterial Cell Surfaces. Annu. Rev. Microbiol. 2024, 78, 125–145. [Google Scholar] [CrossRef] [PubMed]
- Perham, R.N.; Phillips, D.C.; Radda, G.K. Self-assembly of biological macromolecules. Philos. Trans. R. Soc. B Biol. Sci. 1975, 272, 123–136. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-Assembly at All Scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef]
- Fang, H.; Tyukodi, B.; Rogers, W.B.; Hagan, M.F. Polymorphic self-assembly of helical tubules is kinetically controlled. Soft Matter 2022, 18, 6716–6728. [Google Scholar] [CrossRef]
- Tyukodi, B.; Mohajerani, F.; Hall, D.M.; Grason, G.M.; Hagan, M.F. Thermodynamic Size Control in Curvature-Frustrated Tubules: Self-Limitation with Open Boundaries. ACS Nano 2022, 16, 9077–9085. [Google Scholar] [CrossRef]
- Pinto, D.E.P.; Šulc, P.; Sciortino, F.; Russo, J. Design strategies for the self-assembly of polyhedral shells. Proc. Natl. Acad. Sci. USA 2023, 120, e2219458120. [Google Scholar] [CrossRef]
- Mohajerani, F.; Sayer, E.; Neil, C.; Inlow, K.; Hagan, M.F. Mechanisms of Scaffold-Mediated Microcompartment Assembly and Size Control. ACS Nano 2021, 15, 4197–4212. [Google Scholar] [CrossRef]
- Li, Y.; Kennedy, N.W.; Li, S.; Mills, C.E.; Tullman-Ercek, D.; Olvera de la Cruz, M. Computational and Experimental Approaches to Controlling Bacterial Microcompartment Assembly. ACS Cent. Sci. 2021, 7, 658–670. [Google Scholar] [CrossRef]
- Caspar, D.L.D.; Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef]
- Zlotnick, A. To build a virus capsid: An equilibrium model of the self-assembly of polyhedral protein complexes. J. Mol. Biol. 1994, 241, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Bruinsma, R.F.; Gelbart, W.M.; Reguera, D.; Rudnick, J.; Zandi, R. Viral self-assembly as a thermodynamic process. Phys. Rev. Lett. 2003, 90, 248101. [Google Scholar] [CrossRef] [PubMed]
- Zlotnick, A.; Stray, S.J. How does your virus grow? Understanding and interfering with virus assembly. Trends Biotechnol. 2003, 21, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Zandi, R.; Reguera, D.; Bruinsma, R.F.; Gelbart, W.M.; Rudnick, J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA 2004, 101, 15556–15560. [Google Scholar] [CrossRef]
- Zandi, R.; Reguera, D. Mechanical properties of viral capsids. Phys. Rev. E 2005, 72, 021917. [Google Scholar] [CrossRef]
- Twarock, R. Mathematical virology: A novel approach to the structure and assembly of viruses. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 3357–3373. [Google Scholar] [CrossRef]
- Roos, W.H.; Ivanovska, I.L.; Evilevitch, A.; Wuite, G.J.L. Viral capsids: Mechanical characteristics, genome packaging and delivery mechanisms. Cell. Mol. Life Sci. 2007, 64, 1484–1497. [Google Scholar] [CrossRef]
- Stephanidis, B.; Adichtchev, S.; Gouet, P.; McPherson, A.; Mermet, A. Elastic properties of viruses. Biophys. J. 2007, 93, 1354–1359. [Google Scholar] [CrossRef]
- Angelescu, D.G.; Linse, P. Viruses as supramolecular self-assemblies: Modelling of capsid formation and genome packaging. Soft Matter 2008, 4, 1981–1990. [Google Scholar] [CrossRef]
- Elrad, O.M.; Hagan, M.F. Encapsulation of a polymer by an icosahedral virus. Phys. Biol. 2010, 7, 045003. [Google Scholar] [CrossRef]
- Luque, A.; Reguera, D.; Morozov, A.; Rudnick, J.; Bruinsma, R. Physics of shell assembly: Line tension, hole implosion, and closure catastrophe. J. Chem. Phys. 2012, 136, 184507. [Google Scholar] [CrossRef] [PubMed]
- Baschek, J.E.; Klein, H.C.R.; Schwarz, U.S. Stochastic Dynamics of Virus Capsid Formation: Direct Versus Hierarchical Self-Assembly. BMC Biophys. 2012, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Boettcher, M.A.; Klein, H.C.R.; Schwarz, U.S. Role of Dynamic Capsomere Supply for Viral Capsid Self-Assembly. Phys. Biol. 2015, 12, 016014. [Google Scholar] [CrossRef]
- Garmann, R.F.; Comas-Garcia, M.; Knobler, C.M.; Gelbart, W.M. Physical principles in the self-assembly of a simple spherical virus. Acc. Chem. Res. 2016, 49, 48–55. [Google Scholar] [CrossRef]
- Hagan, M.; Zandi, R. Recent advances in coarse-grained modeling of virus assembly. Curr. Opin. Virol. 2016, 18, 36–43. [Google Scholar] [CrossRef]
- Moerman, P.; van der Schoot, P.; Kegel, W. Kinetics versus Thermodynamics in Virus Capsid Polymorphism. J. Phys. Chem. B 2016, 120, 6003–6009. [Google Scholar] [CrossRef]
- Chaudhary, A.; Yadav, R.D. A review on virus protein self-assembly. J. Nanopart. Res. 2019, 21, 254. [Google Scholar] [CrossRef]
- Marchetti, M.; Kamsma, D.; Cazares Vargas, E.; Hernandez García, A.; van der Schoot, P.; de Vries, R.; Wuite, G.J.L.; Roos, W.H. Real-Time Assembly of Viruslike Nucleocapsids Elucidated at the Single-Particle Level. Nano Lett. 2019, 19, 5746–5753. [Google Scholar] [CrossRef] [PubMed]
- Garmann, R.F.; Goldfain, A.M.; Manoharan, V.N. Measurements of the self-assembly kinetics of individual viral capsids around their RNA genome. Proc. Natl. Acad. Sci. USA 2019, 116, 22485–22490. [Google Scholar] [CrossRef]
- Zandi, R.; Dragnea, B.; Travesset, A.; Podgornik, R. On virus growth and form. Phys. Rep. 2020, 847, 1–102. [Google Scholar] [CrossRef]
- Buzón, P.; Maity, S.; Roos, W.H. Physical virology: From virus self-assembly to particle mechanics. WIREs Nanomed. Nanobiotechnol. 2020, 12, e1613. [Google Scholar] [CrossRef] [PubMed]
- van Rosmalen, M.G.M.; Kamsma, D.; Biebricher, A.S.; Li, C.; Zlotnick, A.; Roos, W.H.; Wuite, G.J.L. Revealing in Real-Time a Multistep Assembly Mechanism for SV40 Virus-Like Particles. Sci. Adv. 2020, 6, eaaz1639. [Google Scholar] [CrossRef] [PubMed]
- Bruinsma, R.F.; Wuite, G.J.L.; Roos, W.H. Physics of Viral Dynamics. Nat. Rev. Phys. 2021, 3, 76–91. [Google Scholar] [CrossRef]
- Kra, K.; Li, S.; Gargowitsch, L.; Degrouard, J.; Pérez, J.; Zandi, R.; Bressanelli, S.; Tresset, G. Energetics and Kinetic Assembly Pathways of Hepatitis B Virus Capsids in the Presence of Antivirals. ACS Nano 2023, 17, 12723–12733. [Google Scholar] [CrossRef]
- Li, S.; Tresset, G.; Zandi, R. Switchable Conformation in Protein Subunits: Unveiling Assembly Dynamics of Icosahedral Viruses. arXiv 2024, arXiv:2409.00226. [Google Scholar] [CrossRef]
- Lostroh, P. Molecular and Cellular Biology of Viruses, 1st ed.; Garland Science: New York, NY, USA, 2019. [Google Scholar]
- Flint, J.; Racaniello, V.R.; Rall, G.F.; Hatziioannou, T.; Skalka, A.M. Principles of Virology, 5th ed.; ASM Press: Washington, DC, USA, 2020; ISBN 978-1-683-67358-3. [Google Scholar]
- Bancroft, J.B.; Bracker, C.E.; Wagner, G.W. Structures derived from cowpea chlorotic mottle and brome mosaic virus protein. Virology 1969, 38, 324–335. [Google Scholar] [CrossRef]
- Phillips, B.A. In vitro assembly of poliovirus: II. Evidence for the self-assembly of 14 S particles into empty capsids. Virology 1971, 44, 307–316. [Google Scholar] [CrossRef]
- Xie, Z.; Hendrix, R.W. Assembly in vitro of bacteriophage HK97 proheads. J. Mol. Biol. 1995, 253, 74–85. [Google Scholar] [CrossRef]
- Gross, I.; Hohenberg, H.; Kräusslich, H.G. In vitro assembly properties of purified bacterially expressed capsid proteins of human immunodeficiency virus. Eur. J. Biochem. 1997, 249, 592–600. [Google Scholar] [CrossRef]
- Ceres, P.; Zlotnick, A. Weak Protein-Protein Interactions Are Sufficient to Drive Assembly of Hepatitis B Virus Capsids. Biochemistry 2002, 41, 11525–11531. [Google Scholar] [CrossRef]
- Kegel, W.; van der Schoot, P. Competing hydrophobic and screened-coulomb interactions in hepatitis B virus capsid assembly. Biophys. J. 2004, 86, 3905–3913. [Google Scholar] [CrossRef] [PubMed]
- Li, T.-C.; Takeda, N.; Miyamura, T.; Matsuura, Y.; Wang, J.C.Y.; Engvall, H.; Hammar, L.; Xing, L.; Cheng, R.H. Essential Elements of the Capsid Protein for Self-Assembly into Empty Virus-like Particles of Hepatitis E Virus. J. Virol. 2005, 79, 12999–13006. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Thorsteinsson, M.V.; Johnston, L.B.; DePhillips, P.A.; Zlotnick, A. A quantitative description of in vitro assembly of human papillomavirus 16 virus-like particles. J. Mol. Biol. 2008, 381, 229–237. [Google Scholar] [CrossRef]
- Shoemaker, G.K.; van Duijn, E.; Crawford, S.E.; Uetrecht, C.; Baclayon, M.; Roos, W.H.; Wuite, G.J.L.; Estes, M.K.; Prasad, B.V.V.; Heck, A.J.R. Norwalk Virus Assembly and Stability Monitored by Mass Spectrometry. Mol. Cell. Proteom. 2010, 9, 1742–1751. [Google Scholar] [CrossRef]
- Salunke, D.M.; Caspar, D.L.D.; Garcea, R.L. Polymorphism in the assembly of polyomavirus capsid protein VP1. Biophys. J. 1989, 56, 887–900. [Google Scholar] [CrossRef] [PubMed]
- Kanesashi, S.; Ishizu, K.; Kawano, M.; Han, S.; Tomita, S.; Watanabe, H.; Kataoka, K.; Handa, H. Simian virus 40 VP1 capsid protein forms polymorphic assemblies in vitro. J. Gen. Virol. 2003, 84, 1899–1905. [Google Scholar] [CrossRef]
- Casini, G.L.; Graham, D.; Heine, D.; Garcea, R.L.; Wu, D.T. In vitro papillomavirus capsid assembly analyzed by light scattering. Virology 2004, 325, 320–327. [Google Scholar] [CrossRef]
- Bajaj, S.; Banerjee, M. In vitro assembly of polymorphic virus-like particles from the capsid protein of a nodavirus. Virology 2016, 496, 106–115. [Google Scholar] [CrossRef]
- Pierson, E.E.; Keifer, D.Z.; Kukreja, A.A.; Wang, J.C.-Y.; Zlotnick, A.; Jarrold, M.F. Charge Detection Mass Spectrometry Identifies Preferred Non-Icosahedral Polymorphs in the Self-Assembly of Woodchuck Hepatitis Virus Capsids. J. Mol. Biol. 2016, 428, 292–300. [Google Scholar] [CrossRef]
- Patterson, A.; Young, K.; Biever, M.P.; Klein, S.M.; Huang, S.-Y.; DePhillips, P.A.; Jacobson, S.C.; Jarrold, M.F.; Zlotnick, A. Heterogeneity of HPV16 virus-like particles indicates a complex assembly energy surface. Virology 2024, 600, 110211. [Google Scholar] [CrossRef]
- Zlotnick, A.; Aldrich, R.; Johnson, J.M.; Ceres, P.; Young, M.J. Mechanism of Capsid Assembly for an Icosahedral Plant Virus. Virology 2000, 277, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Elrad, O.M.; Hagan, M.F. Mechanisms of Size Control and Polymorphism in Viral Capsid Assembly. Nano Lett. 2008, 8, 3850–3857. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Brooks, C.L. Generalized Structural Polymorphism in Self-Assembled Viral Particles. Nano Lett. 2008, 8, 4574–4581. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Reddy, V.S.; Brooks, C.L., III. Invariant Polymorphism in Virus Capsid Assembly. J. Am. Chem. Soc. 2009, 131, 2606–2614. [Google Scholar] [CrossRef]
- Aznar, M.; Reguera, D. Physical Ingredients Controlling Stability and Structural Selection of Empty Viral Capsids. J. Phys. Chem. B 2016, 120, 6147–6159. [Google Scholar] [CrossRef] [PubMed]
- Grime, J.M.A.; Dama, J.F.; Ganser-Pornillos, B.K.; Woodward, C.L.; Jensen, G.J.; Yeager, M.J.; Voth, G.A. Coarse-grained simulation reveals key features of HIV-1 capsid self-assembly. Nat. Commun. 2016, 7, 11568. [Google Scholar] [CrossRef] [PubMed]
- Waltmann, C.; Asor, R.; Raviv, U.; Olvera de la Cruz, M. Assembly and Stability of Simian Virus 40 Polymorphs. ACS Nano 2020, 14, 4430–4443. [Google Scholar] [CrossRef]
- Spiriti, J.; Conway, J.F.; Zuckerman, D.M. Should Virus Capsids Assemble Perfectly? Theory and Observation of Defects. Biophys. J. 2020, 119, 1781–1790. [Google Scholar] [CrossRef]
- Mohajerani, F.; Tyukodi, B.; Schlicksup, C.J.; Hadden-Perilla, J.A.; Zlotnick, A.; Hagan, M.F. Multiscale Modeling of Hepatitis B Virus Capsid Assembly and Its Dimorphism. ACS Nano 2022, 16, 13845–13859. [Google Scholar] [CrossRef]
- Seitz, I.; Saarinen, S.; Kumpula, E.-P.; McNeale, D.; Anaya-Plaza, E.; Lampinen, V.; Hytönen, V.P.; Sainsbury, F.; Cornelissen, J.J.L.M.; Linko, V.; et al. DNA-origami-directed virus capsid polymorphism. Nat. Nanotechnol. 2023, 18, 1205–1212. [Google Scholar] [CrossRef]
- Zandi, R.; van der Shoot, P.; Reguera, D.; Kegel, W.; Reiss, H. Classical nucleation theory of virus capsids. Biophys. J. 2006, 90, 1929–1948. [Google Scholar] [CrossRef]
- Luque, A.; Reguera, D. Theoretical Studies on Assembly, Physical Stability, and Dynamics of Viruses. Subcell. Biochem. 2024, 105, 693–741. [Google Scholar] [CrossRef] [PubMed]
- Law-Hine, D.; Zeghal, M.; Bressanelli, S.; Constantin, D.; Tresset, G. Identification of a major intermediate along the self-assembly pathway of an icosahedral viral capsid by using an analytical model of a spherical patch. Soft Matter 2016, 12, 6728–6736. [Google Scholar] [CrossRef]
- Timmermans, S.B.P.E.; Ramezani, A.; Montalvo, T.; Nguyen, M.; van der Schoot, P.; van Hest, J.C.M.; Zandi, R. The Dynamics of Viruslike Capsid Assembly and Disassembly. J. Am. Chem. Soc. 2022, 144, 12608–12612. [Google Scholar] [CrossRef] [PubMed]
- Endres, D.; Zlotnick, A. Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys. J. 2002, 83, 1217–1230. [Google Scholar] [CrossRef] [PubMed]
- Khaykelson, D.; Asor, R.; Zhao, Z.; Schlicksup, C.J.; Zlotnick, A.; Raviv, U. Guanidine Hydrochloride-Induced Hepatitis B Virus Capsid Disassembly Hysteresis. Biochemistry 2024, 63, 1543–1552. [Google Scholar] [CrossRef]
- Singh, S.; Zlotnick, A. Observed Hysteresis of Virus Capsid Disassembly Is Implicit in Kinetic Models of Assembly. J. Biol. Chem. 2003, 278, 18249–18255. [Google Scholar] [CrossRef]
- Starr, C.A.; Barnes, L.F.; Jarrold, M.F.; Zlotnick, A. Hysteresis in Hepatitis B Virus (HBV) Requires Assembly of Near-Perfect Capsids. Biochemistry 2022, 61, 505–513. [Google Scholar] [CrossRef]
- Herrmann, E.; Neumann, A.U.; Schmidt, J.M.; Zeuzem, S. Hepatitis C Virus Kinetics. Antivir. Ther. 2000, 5, 85–90. [Google Scholar] [CrossRef]
- Chen, C.; Kao, C.C.; Dragnea, B. Self-Assembly of Brome Mosaic Virus Capsids: Insights from Shorter Time-Scale Experiments. J. Phys. Chem. A 2008, 112, 9405–9412. [Google Scholar] [CrossRef]
- Perlmutter, J.D.; Hagan, M.F. Mechanisms of Virus Assembly. Annu. Rev. Phys. Chem. 2015, 66, 217–239. [Google Scholar] [CrossRef] [PubMed]
- Peña, J. Virología Física: Teoría de Autoensamblaje de Cápsides Virales. Master’s Thesis, Universidad Autónoma Metropolitana-Iztapalapa, CDMX, México, 2024. Available online: https://ixtlan.izt.uam.mx/leo/wp-content/uploads/2024/10/tesis_maestria_jason_pena.pdf (accessed on 15 November 2024).
- Mendoza, C.; Reguera, D. Shape selection and mis-assembly in viral capsid formation by elastic frustration. eLife 2020, 9, e52525. [Google Scholar] [CrossRef]
- Hagan, M.; Grason, G.M. Equilibrium mechanisms of self-limiting assembly. Rev. Mod. Phys. 2021, 93, 025008. [Google Scholar] [CrossRef]
- Peña, J.; Dagdug, L.; Reguera, D. On the Influence of Bending Energy on the Assembly of Spherical Viral Capsids; Universidad Autónoma Metropolitana-Iztapalapa: Mexico City, Mexico; Universitat de Barcelona: Barcelona, Spain, 2025; status (manuscript in preparation; to be submitted). [Google Scholar]
- Seung, H.S.; Nelson, D.R. Defects in flexible membranes with crystalline order. Phys. Rev. A 1988, 38, 1005–1018. [Google Scholar] [CrossRef] [PubMed]
- Lidmar, J.; Mirny, L.; Nelson, D.R. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E 2003, 68, 051910. [Google Scholar] [CrossRef]
- Meng, G.; Paulose, J.; Nelson, D.R.; Manoharan, V.N. Elastic Instability of a Crystal Growing on a Curved Surface. Science 2014, 343, 634–637. [Google Scholar] [CrossRef] [PubMed]
- Helfrich, W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. Naturforsch. C J. Biosci. 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Bruinsma, R.F.; Gelbart, W.M. Elasticity theory and shape transitions of viral shells. Phys. Rev. E 2005, 72, 051923. [Google Scholar] [CrossRef]
- Klug, W.S.; Bruinsma, R.F.; Michel, J.-P.; Knobler, C.M.; Ivanovska, I.L.; Schmidt, C.F.; Wuite, G.J.L. Failure of Viral Shells. Phys. Rev. Lett. 2006, 97, 228101. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Bruinsma, R.F.; Gelbart, W.M. Continuum Theory of Retroviral Capsids. Phys. Rev. Lett. 2006, 96, 078102. [Google Scholar] [CrossRef]
- Zhao, Y.; Ge, Z.; Fang, J. Elastic modulus of viral nanotubes. Phys. Rev. E 2008, 78, 031914. [Google Scholar] [CrossRef] [PubMed]
- Buenemann, M.; Lenz, P. Elastic properties and mechanical stability of chiral and filled viral capsids. Phys. Rev. E 2008, 78, 051924. [Google Scholar] [CrossRef] [PubMed]
- Roos, W.H.; Gibbons, M.M.; Arkhipov, A.; Uetrecht, C.; Watts, N.R.; Wingfield, P.T.; Steven, A.C.; Heck, A.J.R.; Schulten, K.; Klug, W.S.; et al. Squeezing Protein Shells: How Continuum Elastic Models, Molecular Dynamics Simulations, and Experiments Coalesce at the Nanoscale. Biophys. J. 2010, 99, 1175–1181. [Google Scholar] [CrossRef] [PubMed]
- Grason, G.M. Perspective: Geometrically frustrated assemblies. J. Chem. Phys. 2016, 145, 110901. [Google Scholar] [CrossRef]
- Castelnovo, M. Viral self-assembly pathway and mechanical stress relaxation. Phys. Rev. E 2017, 95, 052405. [Google Scholar] [CrossRef]
- Mendoza, C.I.; Reguera, D. Assembly of Tubes in the Stretching-Dominated Limit; Universidad Nacional Autónoma de México (UNAM): Mexico City, Mexico; Universitat de Barcelona: Barcelona, Spain, 2025; status (manuscript in preparation; to be submitted). [Google Scholar]
- Luque, A. Structure, Mechanical Properties, and Self-Assembly of Virus Capsids. Ph.D. Thesis, Departament de Física Fonamental, Universitat de Barcelona, Barcelona, Spain, 2011. [Google Scholar]
- Reguera, D.; Rubí, J.M.; Vilar, J.M.G. The Mesoscopic Dynamics of Thermodynamic Systems. J. Phys. Chem. B 2005, 109, 21502–21515. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Parts 1 and 2; Pergamon Press: New York, NY, USA, 1980. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D.; Johannessen, E.; Gross, J.; Wilhelmsen, O. Non-Equilibrium Thermodynamics for Engineering Applications; World Scientific Publishing Company: Singapore, 2024. [Google Scholar]
- Reguera, D.; Rubí, J.M. Kinetic equations for diffusion in the presence of entropic barriers. Phys. Rev. E 2001, 64, 061106. [Google Scholar] [CrossRef]
- Gomila, G.; Pérez-Madrid, A.; Rubí, J.M. Non-equilibrium thermodynamics of thermionic emission processes in abrupt semiconductor junctions, including the effects of surface states. Phys. A 1996, 233, 208–220. [Google Scholar] [CrossRef]
- Pagonabarraga, I.; Pérez-Madrid, A.; Rubí, J.M. Fluctuating hydrodynamics approach to chemical reactions. Phys. A 1997, 237, 205–219. [Google Scholar] [CrossRef]
- Reguera, D.; Rubí, J.M. Homogeneous nucleation in inhomogeneous media. I. Nucleation in a temperature gradient. J. Chem. Phys. 2003, 119, 9877–9887. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Rubí, J.M.; Pagonabarraga, I.; Bedeaux, D. Mesoscopic non-equilibrium thermodynamic analysis of molecular motors. Phys. Chem. Chem. Phys. 2013, 15, 19405–19414. [Google Scholar] [CrossRef] [PubMed]
- Zandi, R.; Reguera, D.; Rudnick, J.; Gelbart, W.M. What drives the translocation of stiff chains? Proc. Natl. Acad. Sci. USA 2003, 100, 8649–8653. [Google Scholar] [CrossRef] [PubMed]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Vehkamäki, H. Classical Nucleation Theory in Multicomponent Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kalikmanov, V.I. Nucleation Theory; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña, J.; Dagdug, L.; Reguera, D. Kinetic Description of Viral Capsid Self-Assembly Using Mesoscopic Non-Equilibrium Thermodynamics. Entropy 2025, 27, 281. https://doi.org/10.3390/e27030281
Peña J, Dagdug L, Reguera D. Kinetic Description of Viral Capsid Self-Assembly Using Mesoscopic Non-Equilibrium Thermodynamics. Entropy. 2025; 27(3):281. https://doi.org/10.3390/e27030281
Chicago/Turabian StylePeña, Jason, Leonardo Dagdug, and David Reguera. 2025. "Kinetic Description of Viral Capsid Self-Assembly Using Mesoscopic Non-Equilibrium Thermodynamics" Entropy 27, no. 3: 281. https://doi.org/10.3390/e27030281
APA StylePeña, J., Dagdug, L., & Reguera, D. (2025). Kinetic Description of Viral Capsid Self-Assembly Using Mesoscopic Non-Equilibrium Thermodynamics. Entropy, 27(3), 281. https://doi.org/10.3390/e27030281





