The Dynamics of Shannon Entropy in Analyzing Climate Variability for Modeling Temperature and Precipitation Uncertainty in Poland
Abstract
1. Introduction
- Agriculture—for drought forecasting, optimizing irrigation systems, and managing agricultural production [12];
- Water management—for predicting water resource availability, managing retention, and implementing flood protection strategies [13];
- Energy—for assessing water availability for cooling power plants and forecasting energy demand [14];
- Spatial planning—in evaluating flood risks and protecting infrastructure [12];
- Medicine and public health—for anticipating the effects of heatwaves and humidity changes on human health [15].
2. Data Preparation for Analysis
3. Methodology
- First, the use of monthly values ensures greater statistical stability, appropriate frequency for assessing periodicity, and improved detection of seasonal cycles. Statistical stability is especially critical in long-term studies, where excessive data variability may lead to erroneous interpretations and suboptimal decision-making [57].
- Second, analyzing average values increases the number of usable observations, making the results more representative of long-term trends [58].
- Furthermore, this approach better reflects the underlying climate reality, as it focuses on typical conditions rather than isolated extremes, which may distort the broader picture of climate variability. Mean values enhance statistical robustness and capture a wider range of observations, thereby increasing the accuracy of long-term trend assessment. Such an approach is essential for informed decision-making and effective climate adaptation planning [34,56].
4. Bootstrap Resampling Technique
5. Fitting the Normal and Gamma Distribution
6. Fitting the Copula Clayton Function
7. Shannon Entropy
- Sensitivity to measurement scale: Entropy calculations are affected by the scale of measurement. The units used can significantly impact the computed entropy, necessitating precise definitions and appropriate scaling.
- Assumption of uniform distribution: In meteorological data, assuming a uniform distribution of all outcomes can be problematic—especially since variables like precipitation are naturally bounded. This can lead to underestimation of entropy.
- Neglect of inter-variable correlation: Ignoring correlations between variables such as temperature and precipitation can result in oversimplified models that fail to capture the true complexity of the system.
- Data discretization: The process of binning or categorizing data influences entropy calculations. The chosen discretization method must align with the nature of the data to ensure accurate entropy estimation.
- Standardization of measurement units;
- Careful selection of marginal distribution parameters;
- Application of a uniform discretization methodology across all datasets.
8. Statistical Tests Used
9. Analysis of Shannon’s Entropy Trend Variation
10. Results of the Analyses and Discussion
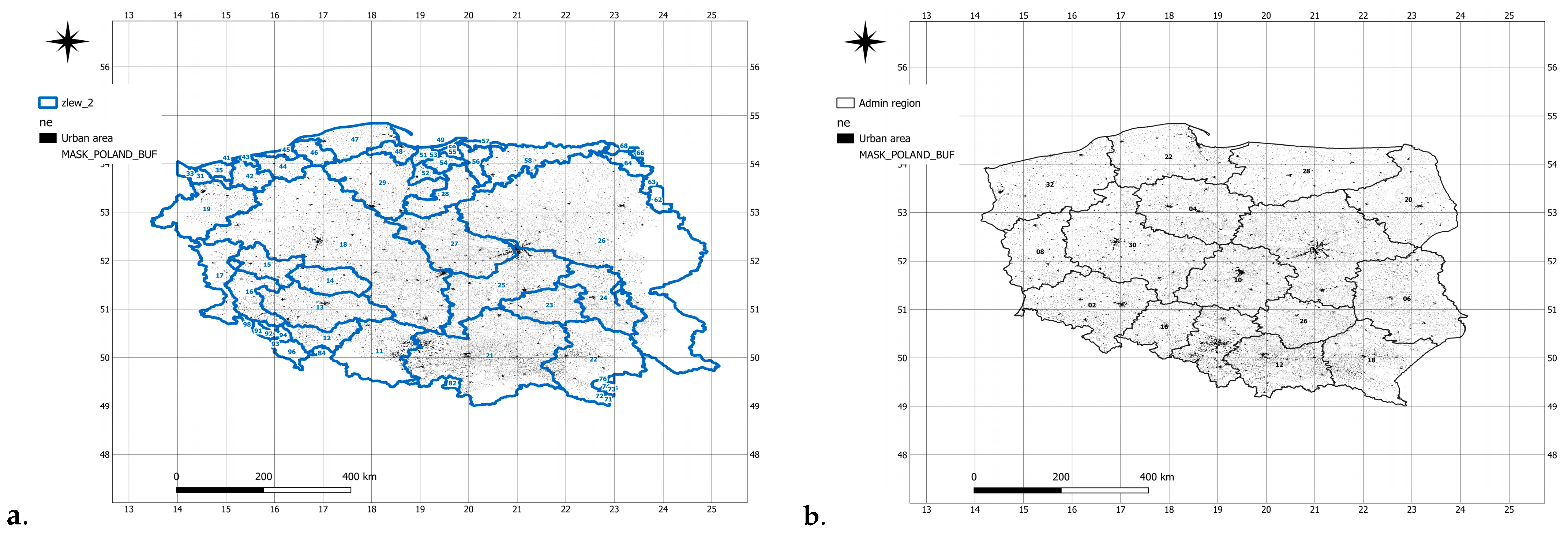
10.1. Analysis of Shannon Entropy Values in Second-Order River Basins
10.2. Analysis of Shannon Entropy Values in the Context of Public Administration Activities
10.3. Recommendations for Public Administration in the Context of Drought and Flood Protection and Climate Change Adaptation
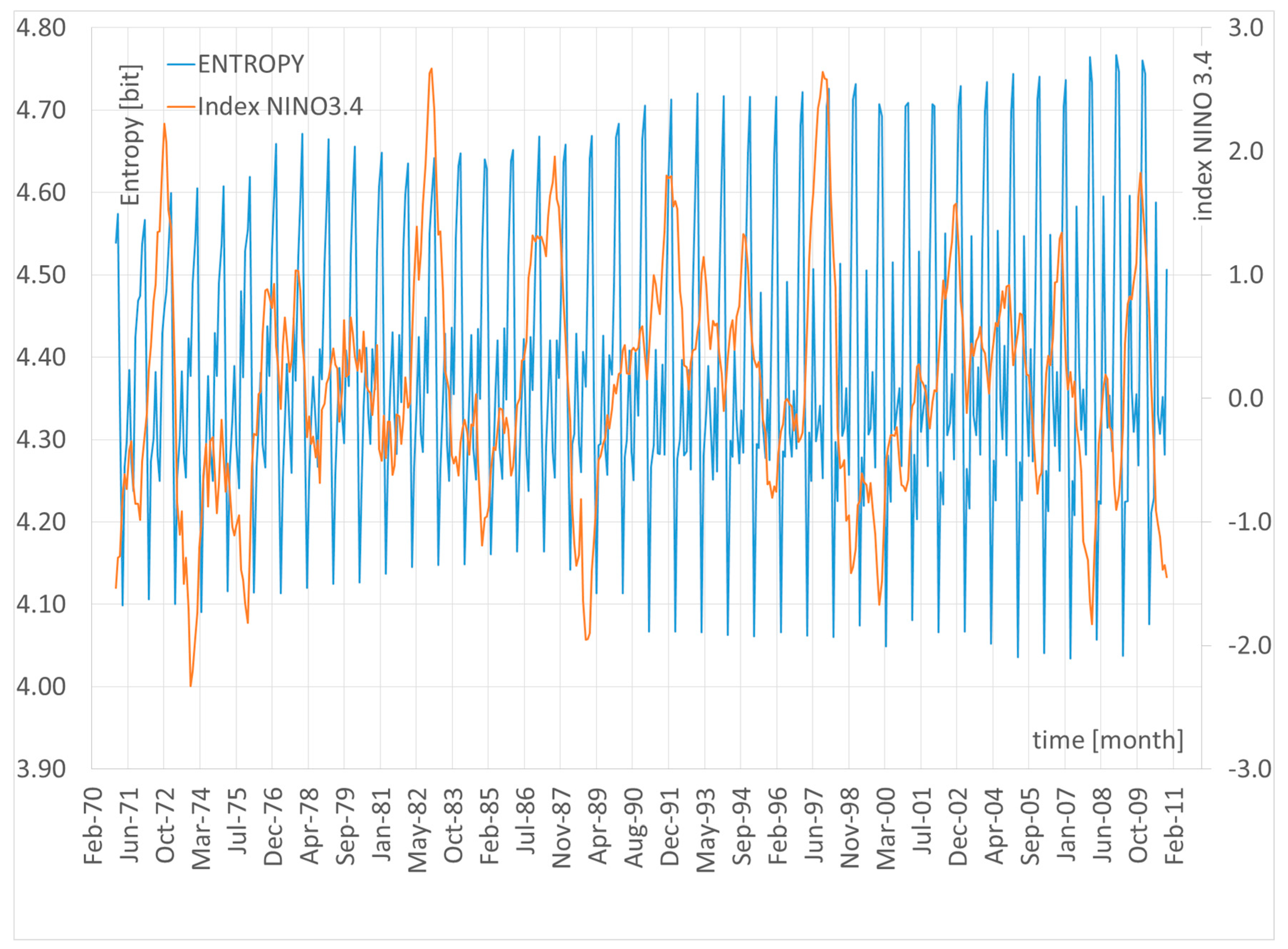
11. Trend and Seasonal Variability of Shannon Entropy in the Context of Climate Change
11.1. The Relationship Between Climate Variability and Global Climate Change Through the Lens of Shannon Entropy
11.2. Attractor of the Mean Shannon Entropy
12. Summary
Funding
Data Availability Statement
Conflicts of Interest
References
- Lucarini, V.; Fraedrich, K.; Lunkeit, F. Thermodynamics of climate change: Generalized sensitivities. Atmos. Chem. Phys. 2010, 10, 9729–9737. [Google Scholar] [CrossRef]
- Bannon, P.R. Entropy production and climate efficiency. J. Atmos. Sci. 2015, 72, 3268–3280. [Google Scholar] [CrossRef]
- Pitt, M.A. Increased Temperature and Entropy Production in the Earth’s Atmosphere: Effect on Wind, Precipitation, Chemical Reactions, Freezing and Melting of Ice and Electrical Activity. J. Mod. Phys. 2019, 10, 966–973. [Google Scholar] [CrossRef]
- Gibbins, G.; Haigh, J.D. Entropy production rates of the climate. J. Atmos. Sci. 2020, 77, 3551–3566. [Google Scholar] [CrossRef]
- Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Costa, Á.M. Analysis and comparison of spatial-temporal entropy variability of tehran city microclimate based on climate change scenarios. Entropy 2019, 21, 13. [Google Scholar] [CrossRef]
- Atieh, M.; Rudra, R.; Gharabaghi, B. Investigation of spatial and temporal variability of precipitation using an entropy theory. In ASABE 1st Climate Change Symposium: Adaptation and Mitigation Conference Proceedings; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2015; pp. 191–194. [Google Scholar] [CrossRef]
- da Silva, V.D.P.R.; Belo Filho, A.F.; Almeida, R.S.R.; de Holanda, R.M.; da Cunha Campos, J.H.B. Shannon information entropy for assessing space-time variability of rainfall and streamflow in semiarid region. Sci. Total Environ. 2016, 544, 330–338. [Google Scholar] [CrossRef]
- Lewis, S.C.; King, A.D. Evolution of mean, variance and extremes in 21st century temperatures. Weather Clim. Extrem. 2017, 15, 1–10. [Google Scholar] [CrossRef]
- Pfleiderer, P.; Schleussner, C.F.; Mengel, M.; Rogelj, J. Global mean temperature indicators linked to warming levels avoiding climate risks. Environ. Res. Lett. 2018, 13, 064015. [Google Scholar] [CrossRef]
- Miętus, M. Climate of Poland 2022. 2023. Available online: www.imgw.pl (accessed on 20 February 2025).
- Yang, X.L.; Xu, L.R.; Liu, K.K.; Li, C.H.; Hu, J.; Xia, X.H. Trends in Temperature and Precipitation in the Zhangweinan River Basin during the last 53 Years. Procedia Environ. Sci. 2012, 13, 1966–1974. [Google Scholar] [CrossRef][Green Version]
- Mesbahzadeh, T.; Miglietta, M.M.; Mirakbari, M.; Soleimani Sardoo, F.; Abdolhoseini, M. Joint Modeling of Precipitation and Temperature Using Copula Theory for Current and Future Prediction under Climate Change Scenarios in Arid Lands (Case Study, Kerman Province, Iran). Adv. Meteorol. 2019, 2019, 6848049. [Google Scholar] [CrossRef]
- Chen, L.; Guo, S. Copulas and Its Application in Hydrology and Water Resources; Springer: Singapore, 2019. [Google Scholar]
- Tu, Y.X.; Kubatko, O.; Piven, V.; Sotnyk, I.; Kurbatova, T. Determinants of Renewable Energy Development: Evidence from the EU Countries. Energies 2022, 15, 7093. [Google Scholar] [CrossRef]
- Dankers, R.; Hiederer, R. Extreme Temperatures and Precipitation in Europe: Analysis of a High-Resolution Climate Change Scenario; JRC Scientific and Technical Reports; Joint Research Centre: Luxembourg, 2008; p. 82. [Google Scholar]
- Rawat, A.; Kumar, D.; Khati, B.S. A review on climate change impacts, models, and its consequences on different sectors: A systematic approach. J. Water Clim. Chang. 2024, 15, 104–126. [Google Scholar] [CrossRef]
- Vinod, H.D.; López-de-Lacalle, J. Maximum entropy bootstrap for time series: The meboot R package. J. Stat. Softw. 2009, 29, 1–19. [Google Scholar] [CrossRef]
- Hao, Z. Application of Entropy Theory in Hydrologic Analysis and Simulation. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2012. [Google Scholar]
- Saha, S.; Chattopadhyay, S. Exploring of the summer monsoon rainfall around the Himalayas in time domain through maximization of Shannon entropy. Theor. Appl. Climatol. 2020, 141, 133–141. [Google Scholar] [CrossRef]
- Guntu, R.K.; Agarwal, A. Investigation of Precipitation Variability and Extremes Using Information Theory. Environ. Sci. Proc. 2021, 4, 14. [Google Scholar] [CrossRef]
- Varbanov, P.S.; Wang, B.; Ocłoń, P.; Radziszewska-Zielina, E.; Ma, T.; Klemeš, J.J.; Jia, X. Efficiency measures for energy supply and use aiming for a clean circular economy. Energy 2023, 283, 129035. [Google Scholar] [CrossRef]
- Staffas, L.; Gustavsson, M.; McCormick, K. Strategies and policies for the bioeconomy and bio-based economy: An analysis of official national approaches. Sustainability 2013, 5, 2751–2769. [Google Scholar] [CrossRef]
- Marosz, M.; Miętus, M.; Biernacik, D. Features of Multiannual Air Temperature Variability in Poland (1951–2021). Atmosphere 2023, 14, 282. [Google Scholar] [CrossRef]
- Cebulska, M.; Szczepanek, R.; Twardosz, R. Rozkład Przestrzenny Opadów Atmosferycznych w Dorzeczu Górnej Wisły; Politechnika Krakowska im. T. Kościuszki, Wydział Inżynierii Środowiska, Instytut Geografii i Gospodarki Przestrzennej Uniwersytetu Jagiellońskiego: Kraków, Poland, 2013. [Google Scholar]
- Cebulska, M.; Twardosz, R. the Distribution of Extreme Monthly Precipitation Totals in the Polish Western Carpathians and Their Foreland Over the Year. Prz. Geofiz. 2020, 65, 55–68. [Google Scholar] [CrossRef]
- Młyński, D.; Cebulska, M.; Wałȩga, A. Trends, variability, and seasonality of maximum annual daily precipitation in the Upper Vistula Basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef]
- Ziernicka-Wojtaszek, A.; Zawora, T. Thermal regions in light of contemporary climate change in Poland. Pol. J. Environ. Stud. 2011, 20, 1627–1632. [Google Scholar]
- Struzewska, J.; Kaminski, J.W.; Jefimow, M. Changes in Temperature and Precipitation Trends in Selected Polish Cities Based on the Results of Regional EURO-CORDEX Climate Models in the 2030–2050 Horizon. Appl. Sci. 2024, 14, 9. [Google Scholar] [CrossRef]
- Venegas-Cordero, N.; Kundzewicz, Z.W.; Jamro, S.; Piniewski, M. Detection of trends in observed river floods in Poland. J. Hydrol. Reg. Stud. 2022, 41, 101098. [Google Scholar] [CrossRef]
- Christensen, J.H.; Kanikicharla, K.K.; Aldrian, E.; An, S.I.; Albuquerque Cavalcanti, I.F.; de Castro, M.; Dong, W.; Goswami, P.; Hall, A.; Kanyanga, J.K.; et al. Climate phenomena and their relevance for future regional climate change. In Climate Change 2013–The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013; Volume 9781107057, pp. 1217–1308. [Google Scholar] [CrossRef]
- Easterling, D.R.; Kunkel, K.E.; Wehner, M.F.; Sun, L. Detection and attribution of climate extremes in the observed record. Weather Clim. Extrem. 2016, 11, 17–27. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Shen, X.; Zhang, J. A comprehensive wind speed prediction system based on Monte Carlo and artificial intelligence algorithms. Appl. Energy 2022, 305, 117815. [Google Scholar] [CrossRef]
- Młyński, D.; Wałȩga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating maximum daily precipitation in the Upper Vistula Basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef]
- Stocker, T.F.; Clarke, G.K.C.; Le Treut, H.; Lindzen, R.S.; Meleshko, V.P.; Mugara, R.K.; Palmer, T.N.; Pierrehumbert, R.T.; Sellers, P.J.; Trenberth, K.E.; et al. Physical Climate Processes and Feedbacks. In IPCC, 2001: Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; p. 881. [Google Scholar]
- Beillouin, D.; Schauberger, B.; Bastos, A.; Ciais, P.; Makowski, D. Impact of extreme weather conditions on European crop production in 2018: Random forest—Yield anomalies. Philos. Trans. R. Soc. B Biol. Sci. 2020, 375, 20190510. [Google Scholar] [CrossRef]
- Twaróg, B. Application of Shannon Entropy in Assessing Changes in Precipitation Conditions and Temperature Based on Long-Term Sequences Using the Bootstrap Method. Atmosphere 2024, 15, 898. [Google Scholar] [CrossRef]
- Falarz, M.; Opała-Owczarek, M.; Niedźwiedź, T.; Bielec-Bąkowska, Z.; Wojkowski, J.; Matuszko, D.; Filipiak, J.; Ustrnul, Z.; Wypych, A.; Lisowska, M.; et al. Initial Research of Climate Change in Poland. In Climate Change in Poland: Past, Present, Future; Falarz, M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 9–27. [Google Scholar]
- Falarz, M.; Przybylak, R.; Filipiak, J.; Wypych, A.; Szwed, M. Introduction. In Climate Change in Poland: Past, Present, Future; Falarz, M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 3–8. [Google Scholar]
- Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data. World Climate Programme—Water. 2000; p. 158. Available online: http://water.usgs.gov/osw/wcp-water/detecting-trend.pdf (accessed on 19 February 2025).
- Łupikasza, E.; Małarzewski, Ł. Precipitation Change. In Climate Change in Poland: Past, Present, Future; Falarz, M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 349–373. [Google Scholar]
- Ustrnul, Z.; Wypych, A.; Czekierda, D. Air Temperature Change. In Climate Change in Poland: Past, Present, Future; Falarz, M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 275–330. [Google Scholar]
- Silva, V.D.P.R.D.; Belo Filho, A.F.; Singh, V.P.; Almeida, R.S.R.; Silva, B.B.D.; de Sousa, I.F.; Holanda, R.M.D. Entropy theory for analysing water resources in northeastern region of Brazil. Hydrol. Sci. J. 2017, 62, 1029–1038. [Google Scholar] [CrossRef]
- Nelsen, R.B.; Quesada-Molina, J.J.; Rodríguez-Lallena, J.A.; Úbeda-Flores, M. Kendall distribution functions. Stat. Probab. Lett. 2003, 65, 263–268. [Google Scholar] [CrossRef]
- Rank, J. Copulas in Financial Risk Management. Mathematical Finance. Diploma Thesis, University of Oxford, Oxford, UK, 2000. [Google Scholar]
- Vavrus, S.J.; Notaro, M.; Lorenz, D.J. Interpreting climate model projections of extreme weather events. Weather Clim. Extrem. 2015, 10, 10–28. [Google Scholar] [CrossRef]
- Lorenz, M.O. Methods of Measuring the Concentration of Wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Bhattacharya, K. The climate attractor. Proc. Indian Acad. Sci. Earth Planet. Sci. 1993, 102, 113–120. [Google Scholar] [CrossRef]
- Silva, A.S.A.; Menezes, R.S.C.; Rosso, O.A.; Stosic, B.; Stosic, T. Complexity entropy-analysis of monthly rainfall time series in northeastern Brazil. Chaos Solitons Fractals 2021, 143, 110623. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An overview of the global historical climatology network-daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Domínguez-Castro, F.; Reig, F.; Vicente-Serrano, S.M.; Aguilar, E.; Peña-Angulo, D.; Noguera, I.; Revuelto, J.; van der Schrier, G.; El Kenawy, A.M. A multidecadal assessment of climate indices over Europe. Sci. Data 2020, 7, 125. [Google Scholar] [CrossRef]
- Twaróg, B. Assessing Polarisation of Climate Phenomena Based on Long-Term Precipitation and Temperature Sequences. Sustainability 2024, 16, 8311. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Climatological Practices 2018 Edition; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Allan, R.P.; Soden, B.J. Atmospheric warming and the amplification of precipitation extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef] [PubMed]
- Labriet, M.; Espegren, K.; Giannakidis, G.; Ó Gallachóir, B. Aligning the Energy Transition with the Sustainable Development Goals: Key Insights from Energy System Modelling; Springer: Cham, Switzerland, 2024; Volume 101. [Google Scholar]
- Asadieh, B.; Krakauer, N.Y. Global trends in extreme precipitation: Climate models versus observations. Hydrol. Earth Syst. Sci. 2015, 19, 877–891. [Google Scholar] [CrossRef]
- Hou, W.; Yan, P.; Feng, G.; Zuo, D. A 3D Copula Method for the Impact and Risk Assessment of Drought Disaster and an Example Application. Front. Phys. 2021, 9, 656253. [Google Scholar] [CrossRef]
- DeDeo, S.; Hawkins, R.X.D.; Klingenstein, S.; Hitchcock, T. Bootstrap methods for the empirical study of decision-making and information flows in social systems. Entropy 2013, 15, 2246–2276. [Google Scholar] [CrossRef]
- Ng, J.L.; Abd Aziz, S.; Huang, Y.F.; Mirzaei, M.; Wayayok, A.; Rowshon, M.K. Uncertainty analysis of rainfall depth duration frequency curves using the bootstrap resampling technique. J. Earth Syst. Sci. 2019, 128, 113. [Google Scholar] [CrossRef]
- De Michele, C.; Avanzi, F. Superstatistical distribution of daily precipitation extremes: A worldwide assessment. Sci. Rep. 2018, 8, 14204. [Google Scholar] [CrossRef]
- Huser, R.; Davison, A.C. Space-time modelling of extreme events. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 439–461. [Google Scholar] [CrossRef]
- Gurmu, S.; Dagne, G.A. Bayesian approach to zero-inflated bivariate ordered probit regression model, with an application to tobacco use. J. Probab. Stat. 2012, 2012, 617678. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, 5th ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ogwang, T. Calculating a standard error for the Gini coefficient: Some further results: Reply. Oxf. Bull. Econ. Stat. 2004, 66, 435–437. [Google Scholar] [CrossRef]
- Samson, P.; Carlen, E. Concentration of measure principle and entropy-inequalities. In Convexity and Concentration; Springer: New York, NY, USA, 2017. [Google Scholar]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Najjari, V.; Unsal, M.G. An Application of Archimedean Copulas for Meteorological Data. Gazi Univ. J. Sci. 2012, 25, 417–424. [Google Scholar]
- Frees, E.W.; Valdez, E.A. Understanding Relationships Using Copulas. N. Am. Actuar. J. 1997, 2, 1–25. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall and runoff analysis using entropy and copula theories. Entropy 2012, 14, 1784–1812. [Google Scholar] [CrossRef]
- Cherubini, U.; Luciano, E. Copula Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Panchenko, V. Goodness-of-fit test for copulas. Phys. A Stat. Mech. Its Appl. 2005, 355, 176–182. [Google Scholar] [CrossRef]
- Fermanian, J.D. Goodness-of-fit tests for copulas. J. Multivar. Anal. 2005, 95, 119–152. [Google Scholar] [CrossRef]
- Belov, D.I.; Armstrong, R.D. Distributions of the Kullback-Leibler divergence with applications. Br. J. Math. Stat. Psychol. 2011, 64, 291–309. [Google Scholar] [CrossRef]
- Christianto, V.; Smarandache, F. A Thousand Words: How Shannon Entropy Perspective Provides Link between Exponential Data Growth, Average Temperature of the Earth and Declining Earth Magnetic Field. Bull. Pure Appl. Sci. Geol. 2019, 38, 225–231. [Google Scholar] [CrossRef]
- Chakrabarti, C.G.; Chakrabarty, I. Shannon entropy: Axiomatic characterization and application. Int. J. Math. Math. Sci. 2005, 2005, 2847–2854. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Silini, R.; Masoller, C. Fast and effective pseudo transfer entropy for bivariate data-driven causal inference. Sci. Rep. 2021, 11, 8423. [Google Scholar] [CrossRef]
- Karmeshu, N. Trend Detection in Annual Temperature & Precipitation Using the Mann Kendall Test—A Case Study to Assess Climate Change on Select States in the Northeastern United States. Master’s Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2015. Volume 66, pp. 1–6. Available online: http://repository.upenn.edu/mes_capstones/47 (accessed on 20 February 2025).
- Wibig, J.; Glowicki, B. Trends of minimum and maximum temperature in Poland. Clim. Res. 2002, 20, 123–133. [Google Scholar] [CrossRef]
- Conte, L.C.; Bayer, D.M.; Bayer, F.M. Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil. Hydrol. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Krakauer, N.Y. It Is Normal: The Probability Distribution of Temperature Extremes. Climate 2024, 12, 204. [Google Scholar] [CrossRef]
- Mesbahzadeh, T.; Mirakbari, M.; Mohseni Saravi, M.; Soleimani Sardoo, F.; Miglietta, M.M. Meteorological drought analysis using copula theory and drought indicators under climate change scenarios (RCP). Meteorol. Appl. 2020, 27, e1856. [Google Scholar] [CrossRef]
- Viner, D.; Ekstrom, M.; Hulbert, M.; Warner, N.K.; Wreford, A.; Zommers, Z. Understanding the dynamic nature of risk in climate change assessments—A new starting point for discussion. Atmos. Sci. Lett. 2020, 21, e958. [Google Scholar] [CrossRef]
- Sillmann, J.; Thorarinsdottir, T.; Keenlyside, N.; Schaller, N.; Alexander, L.V.; Hegerl, G.; Seneviratne, S.I.; Vautard, R.; Zhang, X.; Zwiers, F.W. Understanding, modeling and predicting weather and climate extremes: Challenges and opportunities. Weather Clim. Extrem. 2017, 18, 65–74. [Google Scholar] [CrossRef]
- Froyland, G.; Giannakis, D.; Lintner, B.R.; Pike, M.; Slawinska, J. Spectral analysis of climate dynamics with operator-theoretic approaches. Nat. Commun. 2021, 12, 6570. [Google Scholar] [CrossRef]
- Essex, C.; Lookman, T.; Nerenberg, M.A.H. The climate attractor over short timescales. Nature 1987, 326, 64–66. [Google Scholar] [CrossRef]
- Kovács, T. How can contemporary climate research help understand epidemic dynamics? Ensemble approach and snapshot attractors. J. R. Soc. Interface 2020, 17, 20200648. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, M.; Ragon, C. Attractors and bifurcation diagrams in complex climate models. Phys. Rev. E 2023, 107, 054214. [Google Scholar] [CrossRef]
| Bivariate Copula Function | |
|---|---|
| (4) | |
| Kendall’s τ | |
| (5) | |
| Month | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.361 | 0.180 | 0.091 | 0.045 | 0.041 | 0.033 | 0.025 | 0.037 | 0.016 | 0.066 | 0.295 | 0.293 |
| CODE | NAME | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 24 | Nysa Kłodzka | 4.620 | 4.663 | 4.389 | 3.996 | 4.334 | 4.286 | 4.730 | 4.498 | 4.463 | 4.384 | 4.183 | 4.249 |
| 28 | Barycz | 4.664 | 4.641 | 4.368 | 3.726 | 4.043 | 3.986 | 4.628 | 4.107 | 4.054 | 4.179 | 4.039 | 4.461 |
| 35 | Cieśnina Dziwna | 4.812 | 4.785 | 4.319 | 3.925 | 3.956 | 3.822 | 4.395 | 4.045 | 4.083 | 4.144 | 4.078 | 4.370 |
| 44 | Parsęta | 4.970 | 4.916 | 4.590 | 4.077 | 4.033 | 4.031 | 4.643 | 4.285 | 4.550 | 4.411 | 4.347 | 4.745 |
| 45 | Odra od Baryczy do Bobru (l) | 4.769 | 4.780 | 4.395 | 3.898 | 4.130 | 4.008 | 4.722 | 4.199 | 4.166 | 4.166 | 4.095 | 4.485 |
| 45 | Przymorze od Parsęty do Wieprzy | 4.900 | 4.859 | 4.434 | 4.069 | 4.488 | 4.277 | 4.729 | 4.543 | 4.466 | 4.564 | 4.405 | 4.607 |
| 46 | Wieprza | 4.879 | 4.823 | 4.450 | 3.979 | 4.140 | 4.052 | 4.562 | 4.332 | 4.437 | 4.468 | 4.359 | 4.690 |
| 51 | Odra od Bobru do Warty (p) | 4.817 | 4.813 | 4.375 | 4.059 | 4.181 | 4.061 | 4.674 | 4.208 | 4.122 | 4.176 | 4.084 | 4.472 |
| 51 | Zalew Wiślany do Nogatu | 4.787 | 4.917 | 4.296 | 3.886 | 4.171 | 4.128 | 4.464 | 4.357 | 4.421 | 4.411 | 4.319 | 4.881 |
| 52 | Nogat | 4.911 | 4.769 | 4.247 | 3.809 | 4.078 | 4.094 | 4.392 | 4.191 | 4.417 | 4.132 | 4.175 | 4.687 |
| 55 | Zalew Wiślany od Elbląga do Pasłęki | 4.903 | 4.959 | 4.369 | 3.851 | 4.155 | 4.102 | 4.455 | 4.336 | 4.467 | 4.480 | 4.392 | 4.949 |
| 62 | Świsłocz (l) | 4.681 | 4.613 | 4.357 | 4.018 | 4.130 | 4.159 | 4.634 | 4.304 | 4.137 | 4.237 | 4.118 | 4.355 |
| 64 | Bóbr | 5.103 | 5.012 | 4.620 | 4.293 | 4.397 | 4.205 | 4.853 | 4.443 | 4.461 | 4.533 | 4.365 | 4.682 |
| 64 | Czarna Hańcza (l) | 4.711 | 4.638 | 4.373 | 3.980 | 4.076 | 4.188 | 4.733 | 4.425 | 4.178 | 4.351 | 4.230 | 4.345 |
| 72 | Lechnawa | 4.551 | 4.643 | 4.606 | 4.189 | 4.286 | 4.290 | 4.442 | 4.243 | 4.479 | 4.534 | 4.404 | 4.756 |
| 77 | Odra do Nysy Kłodzkiej (l) | 4.504 | 4.624 | 4.307 | 4.013 | 4.285 | 4.193 | 4.619 | 4.204 | 4.328 | 4.343 | 4.189 | 4.340 |
| 84 | Rega | 5.070 | 4.962 | 4.606 | 4.137 | 4.112 | 3.962 | 4.567 | 4.331 | 4.386 | 4.433 | 4.364 | 4.667 |
| 91 | Odra od Nysy Kłodzkiej do Baryczy (p) | 4.602 | 4.642 | 4.280 | 3.899 | 4.227 | 4.130 | 4.704 | 4.272 | 4.196 | 4.260 | 4.092 | 4.340 |
| 92 | Wisła od Sanu do Wieprza (p) | 4.666 | 4.731 | 4.544 | 4.152 | 4.099 | 4.323 | 4.588 | 4.298 | 4.220 | 4.278 | 4.335 | 4.466 |
| 96 | Orlica (Dzika Orlica) | 4.605 | 4.600 | 4.257 | 4.173 | 4.330 | 4.159 | 4.702 | 4.447 | 4.311 | 4.302 | 4.089 | 4.362 |
| 96 | Martwa Wisła | 4.683 | 4.608 | 4.046 | 3.925 | 4.121 | 3.984 | 4.433 | 4.401 | 4.333 | 4.340 | 4.176 | 4.592 |
| 112 | Drwęca | 4.780 | 4.876 | 4.311 | 3.831 | 4.108 | 4.228 | 4.579 | 4.176 | 4.401 | 4.243 | 4.188 | 4.760 |
| 112 | Pasłęka | 5.015 | 5.019 | 4.546 | 3.944 | 4.175 | 4.256 | 4.493 | 4.388 | 4.549 | 4.491 | 4.387 | 5.022 |
| 114 | Odra od Warty do ujścia | 4.842 | 4.837 | 4.254 | 3.963 | 4.017 | 4.031 | 4.460 | 4.032 | 4.035 | 4.142 | 4.011 | 4.337 |
| 144 | Wieprz | 4.657 | 4.669 | 4.560 | 4.027 | 4.021 | 4.187 | 4.427 | 4.175 | 4.135 | 4.236 | 4.265 | 4.460 |
| 174 | Wisła od Drwęcy do ujścia | 4.850 | 4.773 | 4.356 | 3.895 | 4.085 | 4.125 | 4.609 | 4.157 | 4.341 | 4.250 | 4.226 | 4.698 |
| 175 | Wisła od Wieprza do Narwi (p) | 4.686 | 4.655 | 4.482 | 3.942 | 4.127 | 4.192 | 4.566 | 4.097 | 4.117 | 4.127 | 4.260 | 4.461 |
| 188 | Przymorze od Wieprzy do Martwej Wisły | 4.865 | 4.815 | 4.344 | 3.976 | 4.162 | 3.995 | 4.576 | 4.400 | 4.398 | 4.454 | 4.382 | 4.692 |
| 198 | San | 4.552 | 4.649 | 4.619 | 4.173 | 4.270 | 4.284 | 4.468 | 4.156 | 4.354 | 4.387 | 4.317 | 4.578 |
| 243 | Wisła od Narwi do Drwęcy (l) | 4.641 | 4.694 | 4.224 | 3.890 | 4.160 | 4.247 | 4.641 | 4.116 | 4.174 | 4.145 | 4.259 | 4.593 |
| 348 | Pregoła | 4.900 | 4.845 | 4.521 | 3.907 | 4.057 | 4.214 | 4.576 | 4.418 | 4.429 | 4.388 | 4.365 | 4.711 |
| 357 | Wisła do Sanu | 4.776 | 4.841 | 4.731 | 4.281 | 4.363 | 4.389 | 4.682 | 4.274 | 4.491 | 4.460 | 4.467 | 4.524 |
| 486 | Warta | 4.687 | 4.743 | 4.374 | 3.849 | 4.142 | 4.172 | 4.665 | 4.127 | 4.207 | 4.237 | 4.171 | 4.527 |
| 1014 | Narew | 4.705 | 4.707 | 4.389 | 3.925 | 4.088 | 4.196 | 4.498 | 4.229 | 4.186 | 4.232 | 4.194 | 4.462 |
| CODE | NAME_ | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Dolnośląskie | 4.781 | 4.782 | 4.418 | 4.073 | 4.317 | 4.192 | 4.769 | 4.372 | 4.318 | 4.373 | 4.213 | 4.461 |
| 4 | Kujawsko-Pomorskie | 4.683 | 4.746 | 4.231 | 3.786 | 4.079 | 4.228 | 4.680 | 4.168 | 4.237 | 4.130 | 4.147 | 4.618 |
| 6 | Lubelskie | 4.660 | 4.669 | 4.576 | 4.040 | 4.026 | 4.197 | 4.441 | 4.160 | 4.147 | 4.242 | 4.271 | 4.471 |
| 8 | Lubuskie | 4.816 | 4.825 | 4.404 | 3.976 | 4.155 | 4.065 | 4.694 | 4.182 | 4.151 | 4.180 | 4.113 | 4.512 |
| 10 | Łódzkie | 4.609 | 4.680 | 4.350 | 3.904 | 4.252 | 4.225 | 4.670 | 4.086 | 4.162 | 4.216 | 4.310 | 4.484 |
| 12 | Małopolskie | 4.733 | 4.808 | 4.692 | 4.286 | 4.366 | 4.383 | 4.647 | 4.277 | 4.492 | 4.428 | 4.400 | 4.510 |
| 14 | Mazowieckie | 4.689 | 4.671 | 4.325 | 3.921 | 4.066 | 4.205 | 4.503 | 4.190 | 4.136 | 4.150 | 4.227 | 4.510 |
| 16 | Opolskie | 4.499 | 4.609 | 4.257 | 3.896 | 4.213 | 4.120 | 4.593 | 4.117 | 4.293 | 4.297 | 4.071 | 4.365 |
| 18 | Podkarpackie | 4.605 | 4.672 | 4.669 | 4.172 | 4.292 | 4.314 | 4.494 | 4.191 | 4.383 | 4.391 | 4.334 | 4.612 |
| 20 | Podlaskie | 4.685 | 4.674 | 4.374 | 3.910 | 4.081 | 4.168 | 4.579 | 4.305 | 4.167 | 4.284 | 4.173 | 4.359 |
| 22 | Pomorskie | 4.840 | 4.774 | 4.293 | 3.926 | 4.127 | 4.039 | 4.524 | 4.301 | 4.384 | 4.356 | 4.276 | 4.695 |
| 24 | Śląskie | 4.689 | 4.807 | 4.561 | 4.185 | 4.360 | 4.324 | 4.780 | 4.226 | 4.386 | 4.450 | 4.449 | 4.484 |
| 26 | Swiętokrzyskie | 4.745 | 4.780 | 4.610 | 4.106 | 4.231 | 4.321 | 4.711 | 4.128 | 4.366 | 4.304 | 4.344 | 4.449 |
| 28 | Warmińsko-Mazurskie | 4.880 | 4.895 | 4.503 | 3.896 | 4.095 | 4.218 | 4.504 | 4.338 | 4.469 | 4.386 | 4.333 | 4.834 |
| 30 | Wielkopolskie | 4.660 | 4.697 | 4.333 | 3.753 | 4.111 | 4.135 | 4.633 | 4.116 | 4.175 | 4.217 | 4.098 | 4.524 |
| 32 | Zachodniopomorskie | 4.919 | 4.878 | 4.456 | 4.022 | 4.073 | 4.014 | 4.571 | 4.186 | 4.294 | 4.316 | 4.234 | 4.568 |
| Regional Water Management Strategies | |
|---|---|
| Provinces with High Winter Entropy (e.g., Zachodniopomorskie, Warmińsko-Mazurskie). | Expansion of retention systems and flood-control reservoirs to mitigate the impact of sudden snowmelt and rainfall. Modernization of flood embankments and drainage infrastructure in areas most at risk of inundation. Implementation of smart water management systems to monitor river levels and forecast flood risks. |
| Provinces with High Summer Entropy (e.g., Dolnośląskie, śląskie, Swiętokrzyskie, Lubelskie). | Development of small-scale water retention programs, including the construction of ponds and reservoirs to store water during drought periods. Grants for rainwater harvesting systems for households and businesses. Support for agriculture through drip irrigation systems and water-saving technologies. |
| Provinces with Low Spring Entropy (e.g., Kujawsko-Pomorskie, Wielkopolskie). | Monitoring of prolonged dry spells and implementation of field irrigation systems. Development of local-level water management plans, adapted to specific soil and climatic conditions. Combating soil degradation by expanding green spaces and protecting forested areas. |
| Development of Monitoring and Forecasting Systems | |
| Modern Early Warning Systems for Extreme Weather Events. | Installation of precipitation and water level sensors in regions with high climatic variability. Deployment of AI-based forecasting systems capable of predicting heavy rainfall and drought periods. Improvement of hydrological models by incorporating Shannon entropy data for enhanced emergency response planning. |
| Spatial and Urban Adaptation | |
| Climate-Resilient Urban Planning. | Limiting urban sealing through green roofs and permeable surfaces. Expansion of urban green spaces to reduce the urban heat island effect and improve stormwater infiltration. Development of flood risk maps based on entropy analysis to guide infrastructure planning. |
| Education and Public Engagement | |
| Raising Public Awareness of Climate Change Impacts. | Educational campaigns on water conservation and efficiency. Subsidy programs for households to install rainwater storage and management systems. Promotion of sustainable agricultural practices in drought-prone areas. |
| Interregional Cooperation and Administrative Integration | |
| Coordination Between National and Local Authorities. | Establishment of regional crisis management centers to analyze entropy and climatic variability data. Inter-voivodeship cooperation among regions with similar climate conditions, e.g., joint investments in water systems. Integration of water policy with regional development strategies, ensuring alignment of investments with projected climate scenarios. |
| Period | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1901–1971 | 4.539 | 4.574 | 4.342 | 4.099 | 4.267 | 4.297 | 4.385 | 4.272 | 4.237 | 4.425 | 4.469 | 4.474 |
| 1902–1972 | 4.537 | 4.566 | 4.335 | 4.106 | 4.274 | 4.301 | 4.382 | 4.280 | 4.249 | 4.430 | 4.459 | 4.480 |
| 1903–1973 | 4.528 | 4.599 | 4.333 | 4.100 | 4.253 | 4.303 | 4.383 | 4.282 | 4.254 | 4.423 | 4.377 | 4.489 |
| 1904–1974 | 4.543 | 4.605 | 4.326 | 4.090 | 4.250 | 4.294 | 4.377 | 4.292 | 4.250 | 4.429 | 4.377 | 4.490 |
| 1905–1975 | 4.536 | 4.607 | 4.353 | 4.116 | 4.264 | 4.324 | 4.389 | 4.293 | 4.241 | 4.480 | 4.376 | 4.529 |
| 1906–1976 | 4.555 | 4.619 | 4.354 | 4.114 | 4.267 | 4.319 | 4.382 | 4.294 | 4.266 | 4.438 | 4.377 | 4.532 |
| 1907–1977 | 4.594 | 4.659 | 4.346 | 4.114 | 4.253 | 4.320 | 4.392 | 4.316 | 4.260 | 4.447 | 4.371 | 4.523 |
| 1908–1978 | 4.590 | 4.671 | 4.359 | 4.120 | 4.250 | 4.322 | 4.376 | 4.317 | 4.267 | 4.410 | 4.373 | 4.514 |
| 1909–1979 | 4.583 | 4.665 | 4.359 | 4.125 | 4.258 | 4.327 | 4.387 | 4.329 | 4.296 | 4.408 | 4.365 | 4.524 |
| 1910–1980 | 4.598 | 4.656 | 4.369 | 4.127 | 4.244 | 4.340 | 4.412 | 4.331 | 4.295 | 4.410 | 4.361 | 4.530 |
| 1911–1981 | 4.607 | 4.648 | 4.372 | 4.137 | 4.269 | 4.348 | 4.430 | 4.327 | 4.283 | 4.427 | 4.346 | 4.530 |
| 1912–1982 | 4.598 | 4.636 | 4.395 | 4.145 | 4.266 | 4.347 | 4.425 | 4.307 | 4.285 | 4.448 | 4.357 | 4.550 |
| 1913–1983 | 4.592 | 4.642 | 4.389 | 4.148 | 4.263 | 4.350 | 4.429 | 4.293 | 4.250 | 4.436 | 4.355 | 4.544 |
| 1914–1984 | 4.633 | 4.648 | 4.388 | 4.149 | 4.276 | 4.348 | 4.427 | 4.289 | 4.252 | 4.435 | 4.350 | 4.529 |
| 1915–1985 | 4.640 | 4.629 | 4.368 | 4.161 | 4.278 | 4.361 | 4.420 | 4.290 | 4.252 | 4.435 | 4.349 | 4.521 |
| 1916–1986 | 4.639 | 4.652 | 4.346 | 4.164 | 4.283 | 4.358 | 4.422 | 4.283 | 4.238 | 4.425 | 4.360 | 4.509 |
| 1917–1987 | 4.603 | 4.668 | 4.347 | 4.164 | 4.292 | 4.349 | 4.420 | 4.285 | 4.254 | 4.421 | 4.375 | 4.498 |
| 1918–1988 | 4.637 | 4.658 | 4.353 | 4.142 | 4.295 | 4.307 | 4.428 | 4.295 | 4.260 | 4.406 | 4.364 | 4.502 |
| 1919–1989 | 4.642 | 4.669 | 4.357 | 4.114 | 4.293 | 4.295 | 4.426 | 4.289 | 4.257 | 4.402 | 4.379 | 4.489 |
| 1920–1990 | 4.667 | 4.683 | 4.368 | 4.113 | 4.280 | 4.299 | 4.408 | 4.285 | 4.250 | 4.406 | 4.329 | 4.490 |
| 1921–1991 | 4.665 | 4.706 | 4.381 | 4.067 | 4.267 | 4.293 | 4.409 | 4.283 | 4.283 | 4.391 | 4.282 | 4.485 |
| 1922–1992 | 4.621 | 4.713 | 4.366 | 4.067 | 4.277 | 4.301 | 4.397 | 4.281 | 4.286 | 4.385 | 4.263 | 4.479 |
| 1923–1993 | 4.614 | 4.720 | 4.377 | 4.066 | 4.281 | 4.333 | 4.389 | 4.330 | 4.252 | 4.362 | 4.261 | 4.469 |
| 1924–1994 | 4.625 | 4.717 | 4.363 | 4.063 | 4.299 | 4.279 | 4.408 | 4.325 | 4.271 | 4.336 | 4.284 | 4.489 |
| 1925–1995 | 4.649 | 4.716 | 4.391 | 4.061 | 4.295 | 4.290 | 4.479 | 4.319 | 4.277 | 4.349 | 4.275 | 4.500 |
| 1926–1996 | 4.646 | 4.717 | 4.393 | 4.066 | 4.286 | 4.279 | 4.491 | 4.308 | 4.279 | 4.359 | 4.289 | 4.508 |
| 1927–1997 | 4.682 | 4.722 | 4.402 | 4.062 | 4.308 | 4.250 | 4.507 | 4.298 | 4.315 | 4.341 | 4.253 | 4.521 |
| 1928–1998 | 4.705 | 4.726 | 4.389 | 4.061 | 4.297 | 4.226 | 4.514 | 4.305 | 4.314 | 4.363 | 4.257 | 4.500 |
| 1929–1999 | 4.713 | 4.732 | 4.402 | 4.074 | 4.278 | 4.220 | 4.506 | 4.307 | 4.313 | 4.382 | 4.266 | 4.505 |
| 1930–2000 | 4.707 | 4.692 | 4.398 | 4.049 | 4.281 | 4.225 | 4.515 | 4.312 | 4.334 | 4.362 | 4.268 | 4.508 |
| 1931–2001 | 4.704 | 4.709 | 4.427 | 4.081 | 4.282 | 4.203 | 4.529 | 4.310 | 4.333 | 4.366 | 4.268 | 4.515 |
| 1932–2002 | 4.708 | 4.705 | 4.422 | 4.066 | 4.260 | 4.222 | 4.550 | 4.305 | 4.320 | 4.380 | 4.276 | 4.525 |
| 1933–2003 | 4.706 | 4.729 | 4.414 | 4.067 | 4.265 | 4.216 | 4.547 | 4.330 | 4.306 | 4.388 | 4.282 | 4.529 |
| 1934–2004 | 4.699 | 4.735 | 4.413 | 4.052 | 4.275 | 4.226 | 4.554 | 4.347 | 4.300 | 4.414 | 4.281 | 4.506 |
| 1935–2005 | 4.698 | 4.744 | 4.414 | 4.036 | 4.273 | 4.226 | 4.547 | 4.344 | 4.280 | 4.410 | 4.274 | 4.482 |
| 1936–2006 | 4.714 | 4.741 | 4.413 | 4.041 | 4.262 | 4.213 | 4.548 | 4.352 | 4.293 | 4.382 | 4.262 | 4.498 |
| 1937–2007 | 4.705 | 4.737 | 4.425 | 4.034 | 4.250 | 4.208 | 4.583 | 4.386 | 4.312 | 4.361 | 4.281 | 4.522 |
| 1938–2008 | 4.764 | 4.733 | 4.421 | 4.057 | 4.225 | 4.222 | 4.596 | 4.383 | 4.314 | 4.353 | 4.286 | 4.515 |
| 1939–2009 | 4.767 | 4.747 | 4.430 | 4.038 | 4.225 | 4.225 | 4.597 | 4.362 | 4.309 | 4.355 | 4.269 | 4.512 |
| 1940–2010 | 4.760 | 4.744 | 4.425 | 4.076 | 4.211 | 4.229 | 4.588 | 4.331 | 4.307 | 4.352 | 4.281 | 4.506 |
| Month | Entropy Change (1940–2010)—(1901–1971) | Average Growth Rate (per Decade) |
|---|---|---|
| [bits] | [bits/10 years] | |
| JAN | +0.221 (4.760–4.539) | 0.055 |
| FEB | +0.170 (4.744–4.574) | 0.043 |
| MAR | +0.083 (4.425–4.342) | 0.021 |
| APR | −0.023 (4.076–4.099) | −0.006 |
| MAY | −0.056 (4.211–4.267) | −0.014 |
| JUN | −0.068 (4.229–4.297) | −0.017 |
| JUL | +0.203 (4.588–4.385) | 0.051 |
| AUG | +0.059 (4.331–4.272) | 0.015 |
| SEP | +0.070 (4.307–4.237) | 0.018 |
| OCT | −0.073 (4.352–4.425) | −0.018 |
| NOV | −0.188 (4.281–4.469) | −0.047 |
| DEC | +0.032 (4.506–4.474) | 0.008 |
| CODE | Name_ | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Dolnośląskie | 1988 | 1987 | 1991 | 1990 | 1990 | 1989 | 1992 | 1994 | 1991 | 1989 | 1989 | 1989 |
| 4 | Kujawsko-Pomorskie | 1994 | 1989 | 1990 | 1990 | 1993 | 1996 | 1994 | 1988 | 1992 | 1984 | 1990 | 1996 |
| 6 | Lubelskie | 1992 | 1989 | 1991 | 1989 | 1990 | 1994 | 1996 | 1991 | 1988 | 1989 | 1989 | 1994 |
| 8 | Lubuskie | 1995 | 1990 | 1993 | 1992 | 1990 | 1992 | 1993 | 1994 | 1991 | 1990 | 1991 | 1990 |
| 10 | Łódzkie | 1989 | 1991 | 1991 | 1988 | 1997 | 1993 | 1996 | 1989 | 1993 | 1988 | 1988 | 1994 |
| 12 | Małopolskie | 1992 | 1989 | 1985 | 1989 | 1991 | 1991 | 1992 | 1990 | 1984 | 1988 | 1987 | 1989 |
| 14 | Mazowieckie | 1995 | 1989 | 1988 | 1990 | 1995 | 1993 | 1994 | 1992 | 1994 | 1987 | 1990 | 1996 |
| 16 | Opolskie | 1992 | 1987 | 1990 | 1988 | 1990 | 1989 | 1993 | 1992 | 1989 | 1990 | 1989 | 1985 |
| 18 | Podkarpackie | 1991 | 1987 | 1990 | 1992 | 1991 | 1991 | 1994 | 1992 | 1985 | 1990 | 1991 | 1995 |
| 20 | Podlaskie | 1984 | 1991 | 1986 | 1989 | 1994 | 1992 | 1994 | 1994 | 1990 | 1988 | 1990 | 1989 |
| 22 | Pomorskie | 1991 | 1990 | 1996 | 1991 | 1991 | 1992 | 1995 | 1992 | 1990 | 1987 | 1990 | 1993 |
| 24 | Śląskie | 1983 | 1989 | 1991 | 1990 | 1988 | 1995 | 1994 | 1991 | 1991 | 1990 | 1989 | 1991 |
| 26 | Świętokrzyskie | 1990 | 1991 | 1987 | 1987 | 1996 | 1987 | 1996 | 1994 | 1982 | 1988 | 1983 | 1989 |
| 28 | Warmińsko-Mazurskie | 1988 | 1991 | 1992 | 1989 | 1995 | 1994 | 1994 | 1989 | 1992 | 1985 | 1990 | 1996 |
| 30 | Wielkopolskie | 1992 | 1990 | 1993 | 1990 | 1992 | 1992 | 1994 | 1991 | 1992 | 1989 | 1990 | 1991 |
| 32 | Zachodniopomorskie | 1995 | 1990 | 1993 | 1990 | 1995 | 1989 | 1994 | 1989 | 1987 | 1988 | 1989 | 1986 |
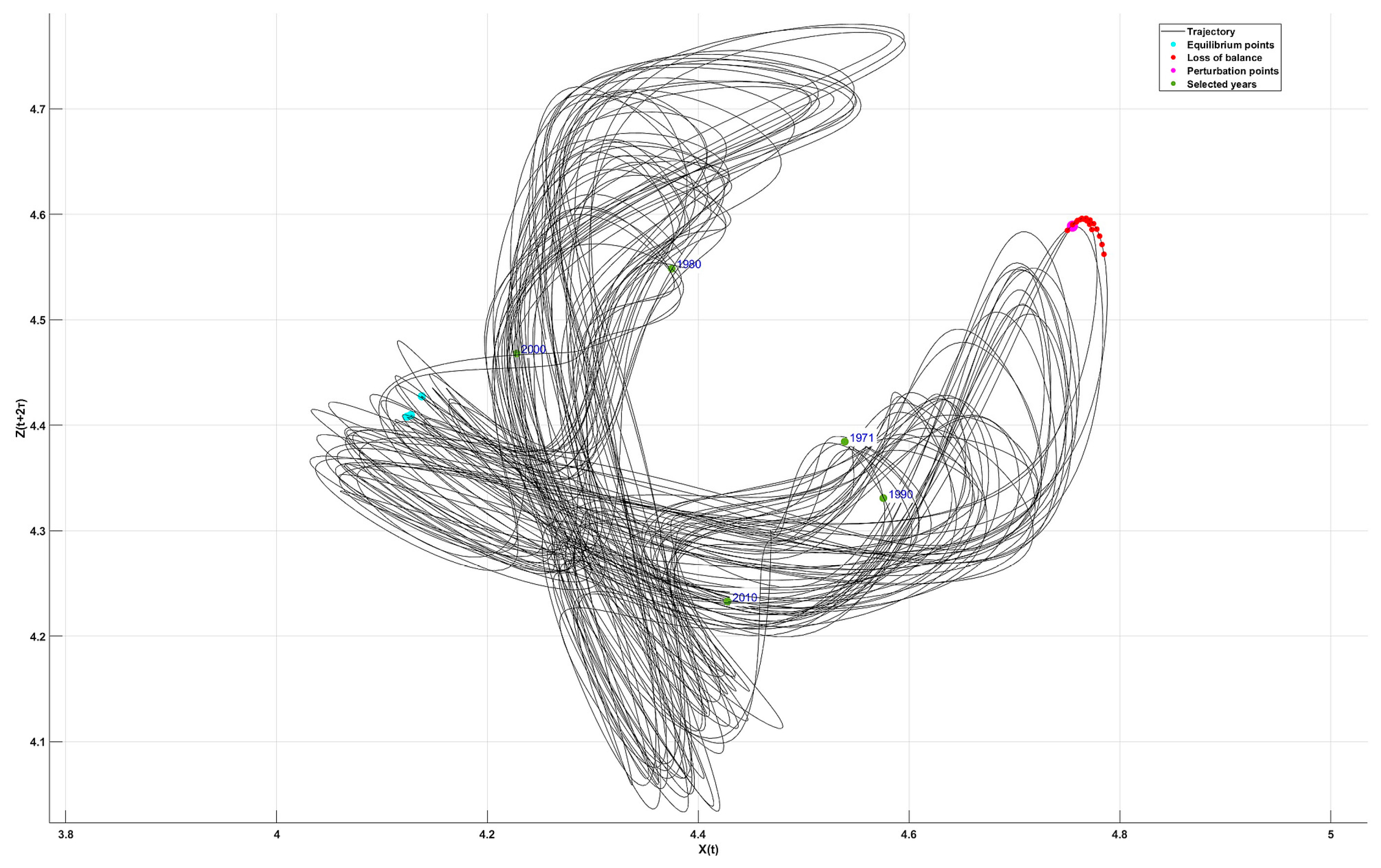
| No. | Continent | X(t) | Y(t + τ) | Z(t + 2τ) |
|---|---|---|---|---|
| 1 | Equilibrium Points | 4.124 | 4.387 | 4.408 |
| 4.127 | 4.413 | 4.410 | ||
| 4.138 | 4.431 | 4.428 | ||
| 3 | Unstable Points | 4.768 | 4.053 | 4.588 |
| 4 | Perturbation Points | 4.755 | 4.056 | 4.589 |
| Selected Years | ||||
| 5 | 1971 | 4.539 | 4.099 | 4.3845 |
| 6 | 1980 | 4.598 | 4.127 | 4.412 |
| 7 | 1990 | 4.667 | 4.113 | 4.408 |
| 8 | 2000 | 4.707 | 4.049 | 4.515 |
| 9 | 2010 | 4.760 | 4.076 | 4.588 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Twaróg, B. The Dynamics of Shannon Entropy in Analyzing Climate Variability for Modeling Temperature and Precipitation Uncertainty in Poland. Entropy 2025, 27, 398. https://doi.org/10.3390/e27040398
Twaróg B. The Dynamics of Shannon Entropy in Analyzing Climate Variability for Modeling Temperature and Precipitation Uncertainty in Poland. Entropy. 2025; 27(4):398. https://doi.org/10.3390/e27040398
Chicago/Turabian StyleTwaróg, Bernard. 2025. "The Dynamics of Shannon Entropy in Analyzing Climate Variability for Modeling Temperature and Precipitation Uncertainty in Poland" Entropy 27, no. 4: 398. https://doi.org/10.3390/e27040398
APA StyleTwaróg, B. (2025). The Dynamics of Shannon Entropy in Analyzing Climate Variability for Modeling Temperature and Precipitation Uncertainty in Poland. Entropy, 27(4), 398. https://doi.org/10.3390/e27040398







