A Constrained Talagrand Transportation Inequality with Applications to Rate-Distortion-Perception Theory
Abstract
1. Introduction
- 1.
- We prove a variant of Talagrand’s transportation inequality, where the reference distribution is Gaussian and the other distribution is subject to constraints on its first- and second-order statistics.
- 2.
- This inequality is then used to establish a connection between the Gaussian distortion-rate-perception functions with limited common randomness under the Kullback–Leibler divergence-based and squared Wasserstein-2 distance-based perception measures. We leverage this connection as an organizational framework to assess existing bounds on these functions. In particular, it is shown that the best-known bounds of Xie et al. [22] are nonredundant when examined through this connection.
2. A Constrained Talagrand Transportation Inequality
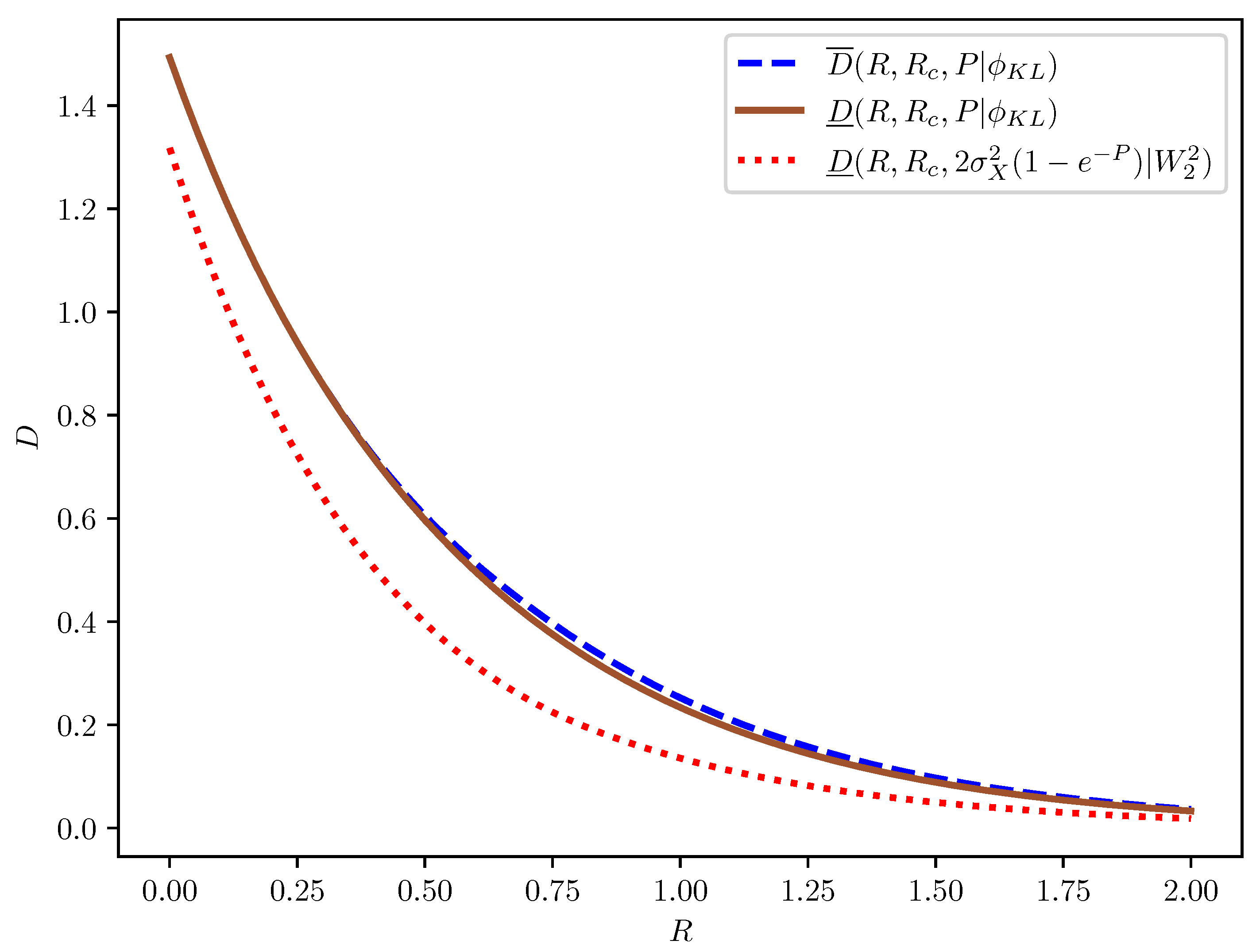
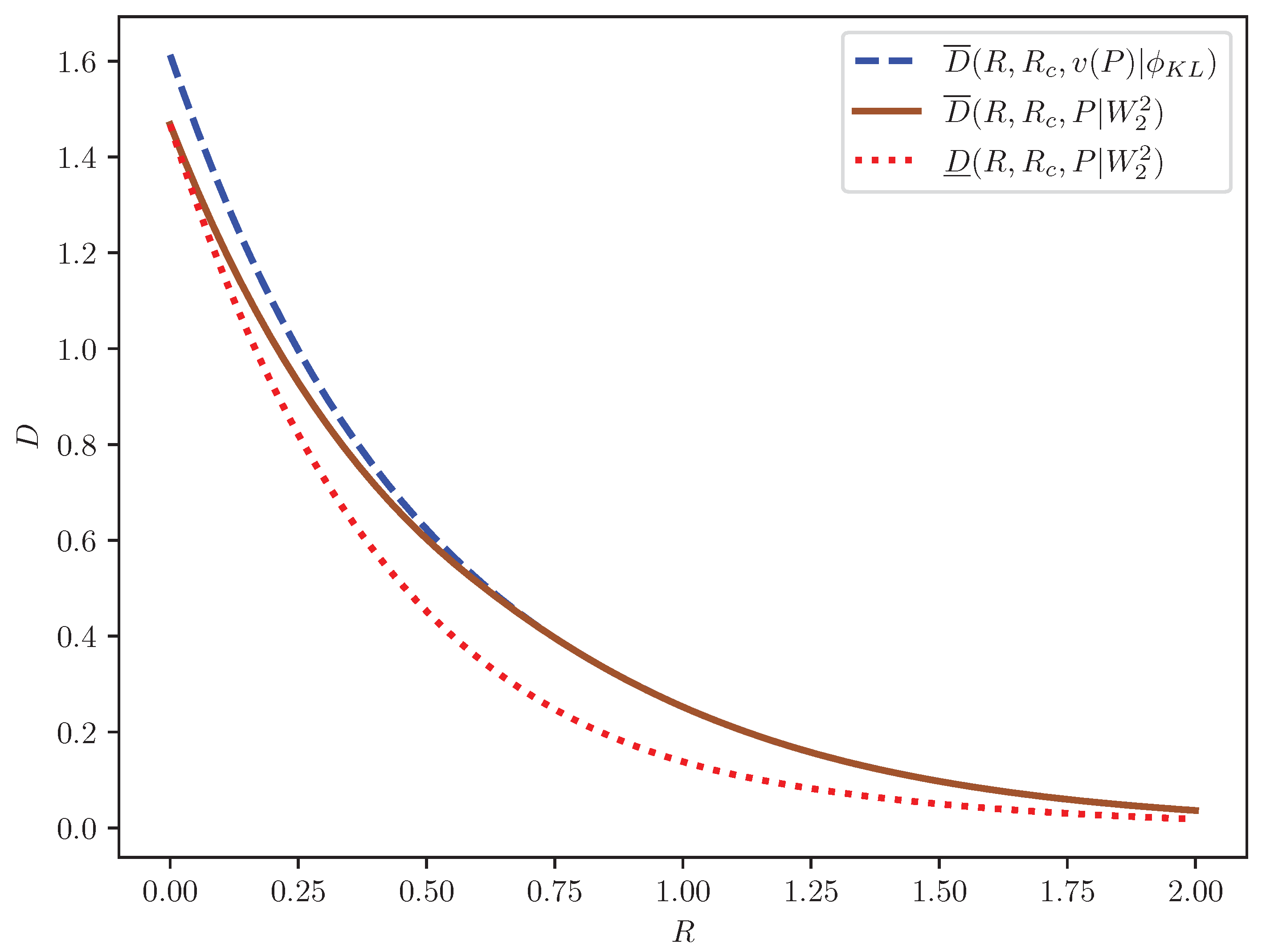
3. Application to Rate-Distortion-Perception Theory
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Blau, Y.; Michaeli, T. The perception-distortion tradeoff. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 6228–6237. [Google Scholar]
- Li, M.; Klejsa, J.; Kleijn, W.B. Distribution preserving quantization with dithering and transformation. IEEE Signal Process. Lett. 2010, 17, 1014–1017. [Google Scholar] [CrossRef]
- Klejsa, J.; Zhang, G.; Li, M.; Kleijn, W.B. Multiple description distribution preserving quantization. IEEE Trans. Signal Process. 2013, 61, 6410–6422. [Google Scholar] [CrossRef]
- Saldi, N.; Linder, T.; Yüksel, S. Randomized quantization and source coding with constrained output distribution. IEEE Trans. Inf. Theory 2015, 61, 91–106. [Google Scholar] [CrossRef]
- Saldi, N.; Linder, T.; Yüksel, S. Output constrained lossy source coding with limited common randomness. IEEE Trans. Inf. Theory 2015, 61, 4984–4998. [Google Scholar] [CrossRef]
- Blau, Y.; Michaeli, T. Rethinking lossy compression: The rate-distortion-perception tradeoff. Proc. Mach. Learn. Res. 2019, 97, 675–685. [Google Scholar]
- Matsumoto, R. Introducing the perception-distortion tradeoff into the rate-distortion theory of general information sources. IEICE Comm. Express 2018, 7, 427–431. [Google Scholar] [CrossRef]
- Matsumoto, R. Rate-distortion-perception tradeoff of variable-length source coding for general information sources. IEICE Comm. Express 2019, 8, 38–42. [Google Scholar] [CrossRef]
- Yan, Z.; Wen, F.; Ying, R.; Ma, C.; Liu, P. On perceptual lossy compression: The cost of perceptual reconstruction and an optimal training framework. Proc. Mach. Learn. Res. 2021, 139, 11682–11692. [Google Scholar]
- Zhang, G.; Qian, J.; Chen, J.; Khisti, A. Universal rate-distortion-perception representations for lossy compression. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; pp. 11517–11529. [Google Scholar]
- Freirich, D.; Michaeli, T.; Meir, R. A theory of the distortion-perception tradeoff in Wasserstein space. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; pp. 25661–25672. [Google Scholar]
- Yan, Z.; Wen, F.; Liu, P. Optimally controllable perceptual lossy compression. In Proceedings of the ICMLC 2022: 2022 14th International Conference on Machine Learning and Computing, Guangzhou, China, 18–21 February 2022; pp. 24911–24928. [Google Scholar]
- Theis, L.; Agustsson, E. On the advantages of stochastic encoders. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, 3–7 May 2021; pp. 1–8. [Google Scholar]
- Wagner, A.B. The rate-distortion-perception tradeoff: The role of common randomness. arXiv 2022, arXiv:2202.04147. [Google Scholar]
- Chen, J.; Yu, L.; Wang, J.; Shi, W.; Ge, Y.; Tong, W. On the rate-distortion-perception function. IEEE J. Sel. Areas Inf. Theory 2022, 3, 664–673. [Google Scholar] [CrossRef]
- Hamdi, Y.; Wagner, A.B.; Gündxuxz, D. The rate-distortion-perception trade-off: The role of private randomness. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT 2024), Athens, Greece, 7–12 July 2024; pp. 1083–1088. [Google Scholar]
- Theis, L.; Wagner, A.B. A coding theorem for the rate-distortion-perception function. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, 3–7 May 2021; pp. 1–5. [Google Scholar]
- Freirich, D.; Weinberger, N.; Meir, R. Characterization of the distortion-perception tradeoff for finite channels with arbitrary metrics. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT 2024), Athens, Greece, 7–12 July 2024; pp. 238–243. [Google Scholar]
- Serra, G.; Stavrou, P.A.; Kountouris, M. On the computation of the Gaussian rate–distortion–perception function. IEEE J. Sel. Areas Inf. Theory 2024, 5, 314–330. [Google Scholar] [CrossRef]
- Qian, J.; Salehkalaibar, S.; Chen, J.; Khisti, A.; Yu, W.; Shi, W.; Ge, Y.; Tong, W. Rate-distortion-perception tradeoff for vector Gaussian sources. IEEE J. Sel. Areas Inf. Theory 2025, 6, 1–17. [Google Scholar] [CrossRef]
- Xie, L.; Li, L.; Chen, J.; Zhang, Z. Output-constrained lossy source coding with application to rate-distortion-perception theory. IEEE Trans. Commun. 2025, 73, 1801–1815. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, Q.; Li, Y.; He, D.; Wang, Z.; Wang, Y.; Qin, H.; Wang, Y.; Liu, J.; Zhang, Y.-Q. Conditional perceptual quality preserving image compression. arXiv 2023, arXiv:2308.08154. [Google Scholar]
- Niu, X.; Gündüz, D.; Bai, B.; Han, W. Conditional rate-distortion-perception trade-off. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; pp. 1068–1073. [Google Scholar]
- Qiu, Y.; Wagner, A.B.; Ballé, J.; Theis, L. Wasserstein distortion: Unifying fidelity and realism. In Proceedings of the 2024 58th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 11–13 March 2024; pp. 1–6. [Google Scholar]
- Qiu, Y.; Wagner, A.B. Low-rate, low-distortion compression with Wasserstein distortion. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT 2024), Athens, Greece, 7–12 July 2024; pp. 855–860. [Google Scholar]
- Salehkalaibar, S.; Chen, J.; Khisti, A.; Yu, W. Rate-distortion-perception tradeoff based on the conditional-distribution perception measure. IEEE Trans. Inf. Theory 2024, 70, 8432–8454. [Google Scholar] [CrossRef]
- Zhou, C.; Lu, G.; Li, J.; Chen, X.; Cheng, Z.; Song, L.; Zhang, W. Controllable distortion-perception tradeoff through latent diffusion for neural image compression. In Proceedings of the 2025 AAAI Conference on Artificial Intelligence, Dubai, United Arab Emirates, 20–22 May 2025; pp. 10725–10733. [Google Scholar]
- Niu, X.; Bai, B.; Guo, N.; Zhang, W.; Han, W. Rate–distortion–perception trade-off in information theory, generative models, and intelligent communications. Entropy 2025, 27, 373. [Google Scholar] [CrossRef]
- Gunlu, O.; Skorski, M.; Poor, H.V. Low-latency Rate-distortion-perception Trade-Off: A Randomized Distributed Function Computation Application. 2025. Cryptology ePrint Archive. Paper 2025/613. Available online: https://eprint.iacr.org/2025/613 (accessed on 12 March 2025).
- Tan, K.; Dai, J.; Liu, Z.; Wang, S.; Qin, X.; Xu, W.; Niu, K.; Zhang, P. Rate-distortion-perception controllable joint source-channel coding for high-fidelity generative semantic communications. IEEE Trans. Cogn. Commun. Netw. 2025, 11, 672–686. [Google Scholar] [CrossRef]
- Lei, E.; Hassani, H.; Bidokhti, S.S. Optimal neural compressors for the rate-distortion-perception tradeoff. arXiv 2025, arXiv:2503.17558. [Google Scholar]
- Talagrand, M. Transportation cost for Gaussian and other product measures. Geom. Funct. Anal. 1996, 6, 587–600. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, X.; Özgür, A. Information constrained optimal transport: From Talagrand, to Marton, to Cover. IEEE Trans. Inf. Theory 2023, 69, 2059–2073. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Li, L.; Chen, J.; Yu, L.; Zhang, Z. A Constrained Talagrand Transportation Inequality with Applications to Rate-Distortion-Perception Theory. Entropy 2025, 27, 441. https://doi.org/10.3390/e27040441
Xie L, Li L, Chen J, Yu L, Zhang Z. A Constrained Talagrand Transportation Inequality with Applications to Rate-Distortion-Perception Theory. Entropy. 2025; 27(4):441. https://doi.org/10.3390/e27040441
Chicago/Turabian StyleXie, Li, Liangyan Li, Jun Chen, Lei Yu, and Zhongshan Zhang. 2025. "A Constrained Talagrand Transportation Inequality with Applications to Rate-Distortion-Perception Theory" Entropy 27, no. 4: 441. https://doi.org/10.3390/e27040441
APA StyleXie, L., Li, L., Chen, J., Yu, L., & Zhang, Z. (2025). A Constrained Talagrand Transportation Inequality with Applications to Rate-Distortion-Perception Theory. Entropy, 27(4), 441. https://doi.org/10.3390/e27040441





