Non-Trivial Solutions of Non-Autonomous Nabla Fractional Difference Boundary Value Problems
Abstract
:1. Introduction
2. Preliminaries
- (A0)
- α, β, γ, , , and .
- (1)
- for all ;
- (2)
- for all ;
- (3)
- , where
3. Green’s Function and Its Properties
- (A1)
- There exists such that
4. Existence of Solutions
- (A2)
- is continuous;
- (A3)
- f satisfies the Lipschitz condition with respect to the second variable with the Lipschitz constant L on . That is, for all , , the following inequality holds:
- (A4)
- There exists a continuous function and a continuous nondecreasing function such that
- (A5)
- .
- (1)
- F has a fixed point in .
- (2)
- There exist and with ,
- (1)
- F has a fixed point in , or
- (2)
- there is a and with .
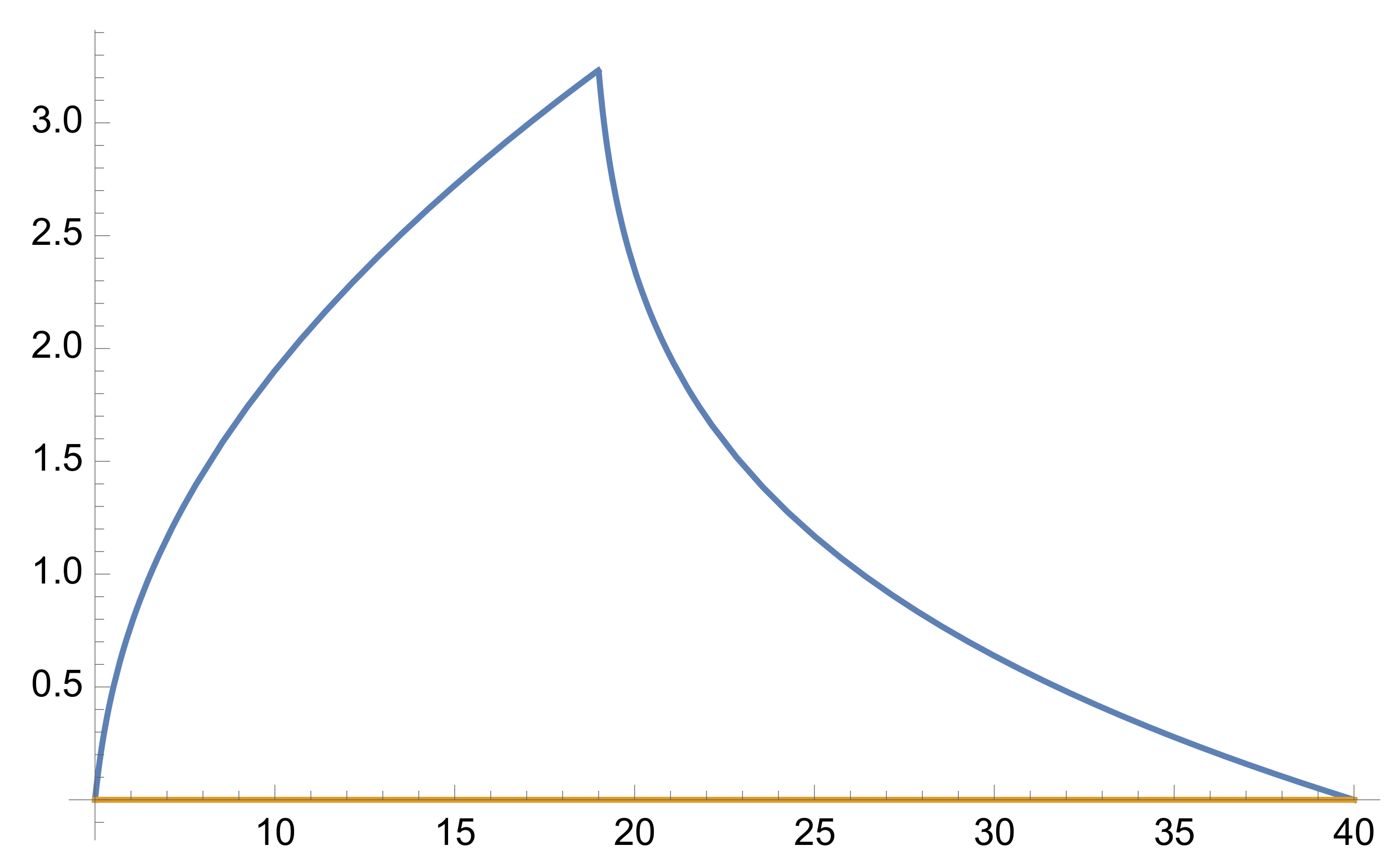
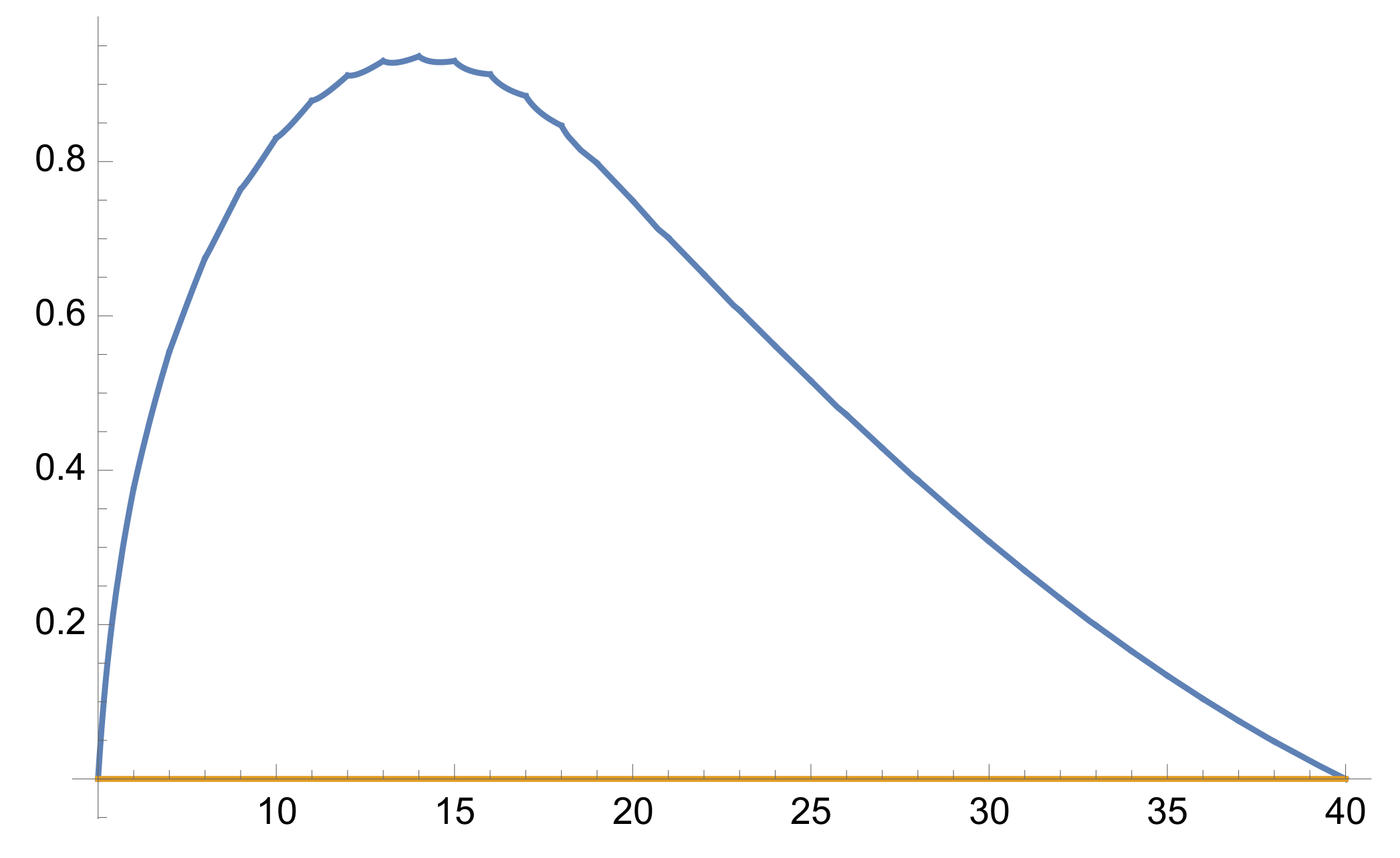
5. Examples
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gray, H.L.; Zhang, N.F. On a new definition of the fractional difference. Math. Comput. 1988, 50, 513–529. [Google Scholar] [CrossRef]
- Atıcı, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 12. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Nabla discrete fractional calculus and nabla inequalities. Math. Comput. Model. 2010, 51, 562–571. [Google Scholar] [CrossRef] [Green Version]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Hill, G.W. On the part of the motion of the lunar perigee which is a function of the mean motions of the Sun and the Moon. Acta Math. 1886, 8, 1–36. [Google Scholar] [CrossRef]
- Cabada, A.; Cid, J.Á.; López-Somoza, L. Maximum Principles for the Hill’s Equation; Academic Press: London, UK, 2018; 238p. [Google Scholar]
- Magnus, W.; Winkler, S. Hill’s Equation; Corrected Reprint of the 1966 Edition; Dover Publications, Inc.: New York, NY, USA, 1979; 129p. [Google Scholar]
- Brackins, A. Boundary Value Problems of Nabla Fractional Difference Equations. Ph.D. Thesis, The University of Nebraska-Lincoln, Lincoln, NE, USA, 2014; 92p. [Google Scholar]
- Ahrendt, K.; Kissler, C. Cameron Green’s function for higher-order boundary value problems involving a nabla Caputo fractional operator. J. Differ. Equ. Appl. 2019, 25, 788–800. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Bohner, M.; Jia, B. Existence and uniqueness of solutions for nonlinear Caputo fractional difference equations. Turk. J. Math. 2020, 44, 857–869. [Google Scholar] [CrossRef]
- Gholami, Y.; Ghanbari, K. Coupled systems of fractional ∇-difference boundary value problems. Differ. Equ. Appl. 2016, 8, 459–470. [Google Scholar] [CrossRef] [Green Version]
- Goodrich, C.S. Existence of a positive solution to a class of fractional differential equations. Appl. Math. Lett. 2010, 23, 1050–1055. [Google Scholar] [CrossRef] [Green Version]
- Goodrich, C.S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions. Comput. Math. Appl. 2011, 61, 191–202. [Google Scholar] [CrossRef]
- Ikram, A. Lyapunov inequalities for nabla Caputo boundary value problems. J. Differ. Equ. Appl. 2019, 25, 757–775. [Google Scholar] [CrossRef] [Green Version]
- Baoguo, J.; Erbe, L.; Goodrich, C.; Peterson, A. The relation between nabla fractional differences and nabla integer differences. Filomat 2017, 31, 1741–1753. [Google Scholar] [CrossRef]
- Jonnalagadda, J.M. On two-point Riemann-Liouville type nabla fractional boundary value problems. Adv. Dyn. Syst. Appl. 2018, 13, 141–166. [Google Scholar]
- Liu, X.; Jia, B.; Gensler, S.; Erbe, L.; Peterson, A. Convergence of approximate solutions to nonlinear Caputo nabla fractional difference equations with boundary conditions. Electron. J. Differ. Equ. 2020, 2020, 1–19. [Google Scholar]
- St. Goar, J. A Caputo Boundary Value Problem in Nabla Fractional Calculus. Ph.D. Thesis, The University of Nebraska-Lincoln, Lincoln, NE, USA, 2016; 112p. [Google Scholar]
- Graef, J.R.; Kong, L.; Kong, Q.; Wang, M. Existence and uniqueness of solutions for a fractional boundary value problem with Dirichlet boundary condition. Electron. J. Qual. Theory Differ. Equ. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Cabada, A.; Dimitrov, N. Non-trivial solutions of non-autonomous Dirichlet fractional discrete problems. Fract. Calc. Appl. Anal. 2020, 23, 980–995. [Google Scholar] [CrossRef]
- Jonnalagadda, J.M. Existence results for solutions of nabla fractional boundary value problems with general boundary conditions. Adv. Theory Nonlinear Anal. Appl. 2020, 4, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Jonnalagadda, J.M. On a nabla fractional boundary value problem with general boundary conditions. AIMS Math. 2020, 5, 204–215. [Google Scholar] [CrossRef]
- Zeidler, E. Nonlinear Functional Analysis and Its Applications. I. Fixed-Point Theorems; Wadsack, P.R., Translator; Springer: New York, NY, USA, 1986. [Google Scholar]
- Agarwal, R.P.; Meehan, M.; O’regan, D. Fixed Point Theory and Applications. Cambridge Tracts in Mathematics; Cambridge University Press: Cambridge, UK, 2001; Volume 141. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabada, A.; Dimitrov, N.D.; Jonnalagadda, J.M. Non-Trivial Solutions of Non-Autonomous Nabla Fractional Difference Boundary Value Problems. Symmetry 2021, 13, 1101. https://doi.org/10.3390/sym13061101
Cabada A, Dimitrov ND, Jonnalagadda JM. Non-Trivial Solutions of Non-Autonomous Nabla Fractional Difference Boundary Value Problems. Symmetry. 2021; 13(6):1101. https://doi.org/10.3390/sym13061101
Chicago/Turabian StyleCabada, Alberto, Nikolay D. Dimitrov, and Jagan Mohan Jonnalagadda. 2021. "Non-Trivial Solutions of Non-Autonomous Nabla Fractional Difference Boundary Value Problems" Symmetry 13, no. 6: 1101. https://doi.org/10.3390/sym13061101
APA StyleCabada, A., Dimitrov, N. D., & Jonnalagadda, J. M. (2021). Non-Trivial Solutions of Non-Autonomous Nabla Fractional Difference Boundary Value Problems. Symmetry, 13(6), 1101. https://doi.org/10.3390/sym13061101






