Insights into the Structure and Energy of DNA Nanoassemblies §
Abstract
1. Introduction
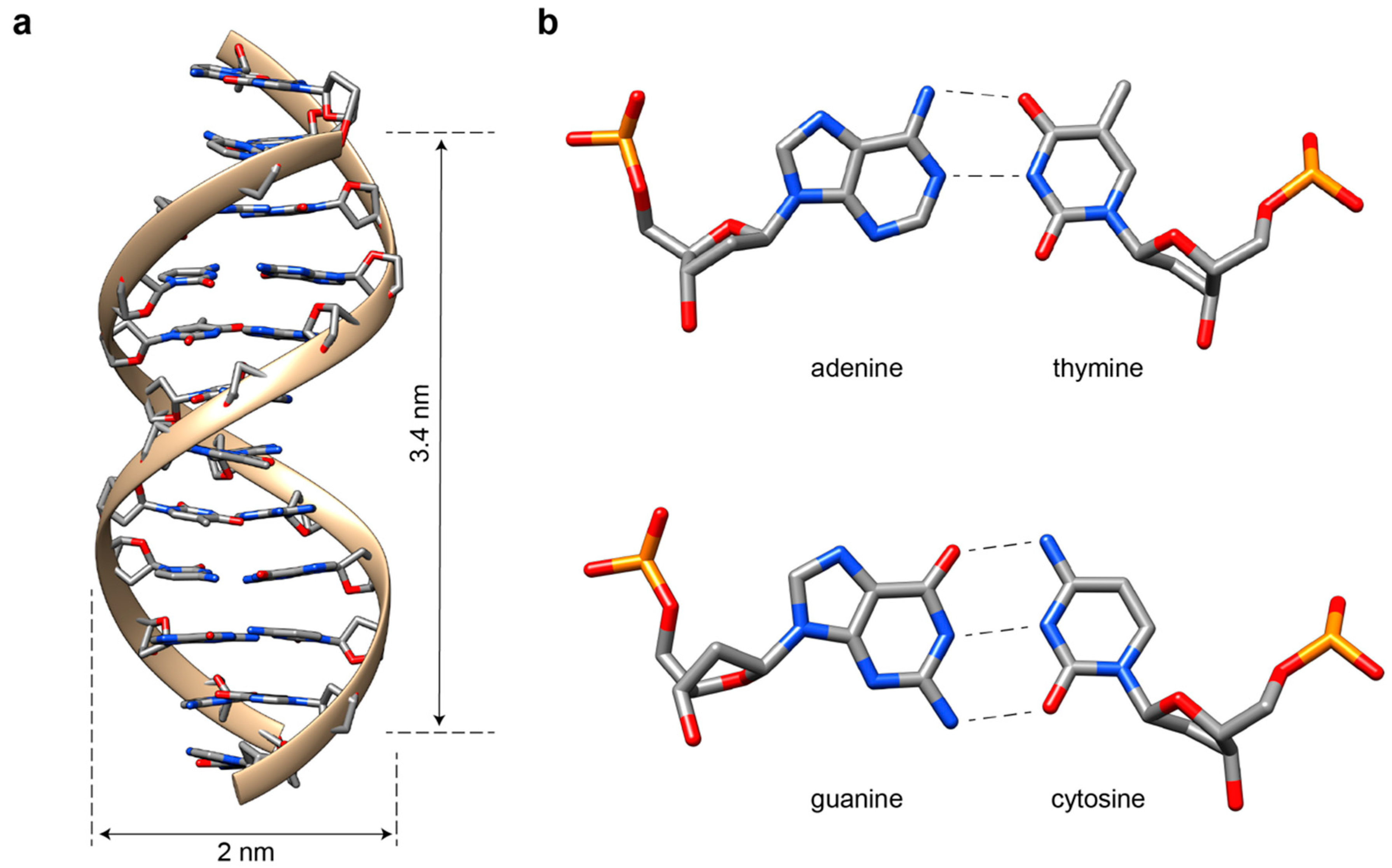
2. The Double Helix
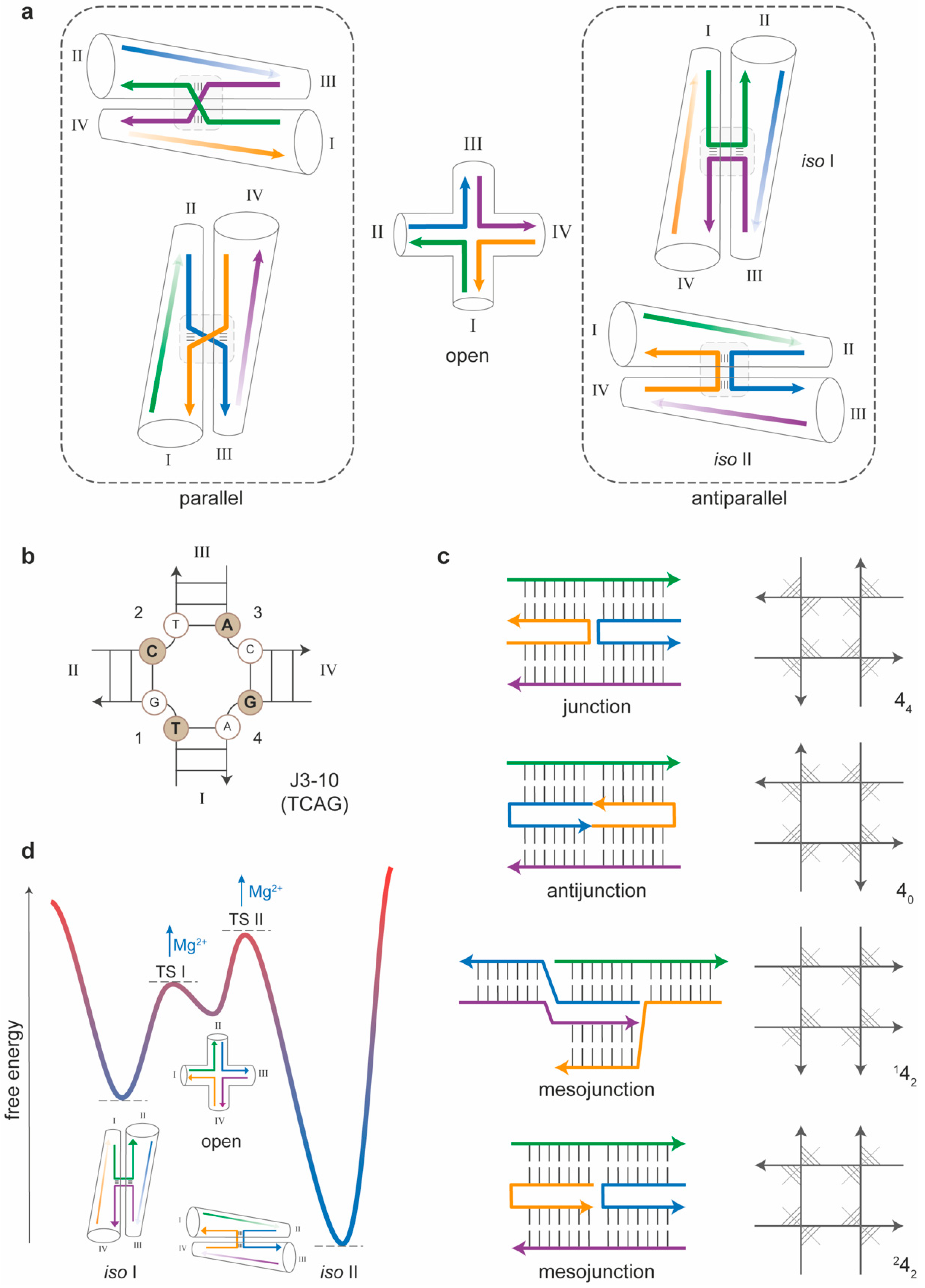
3. The Four-Arm Junction
3.1. Sequence-Dependent Properties of Four-Arm Junctions
3.2. Topology-Dependent Properties of Four-Arm Junctions
3.3. Thermal Stability and Isomerization of Four-Arm Junctions
4. The Multi-Stranded Approach
4.1. Multi-Branched DNA Tiles
4.2. Structural Properties of Multi-Stranded Nanostructures
4.3. On the Thermal Assembly of Multi-Branched DNA Tiles and Their Extended Nanostructures
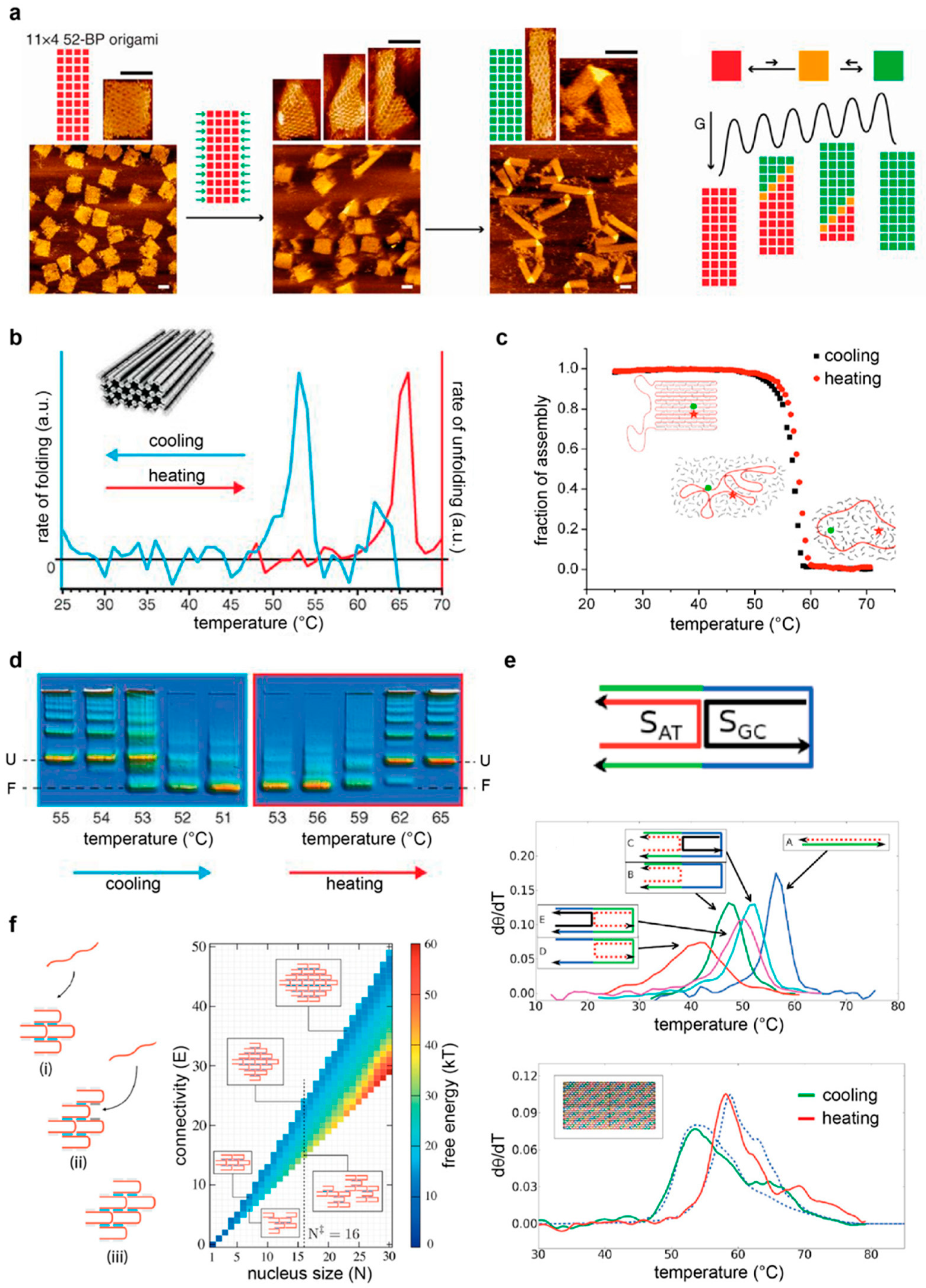
5. The Scaffold-Based Approach
5.1. Structural Properties of Scaffold-Based Assemblies
5.2. Thermal Assembly and Disassembly of DNA Origami Structures
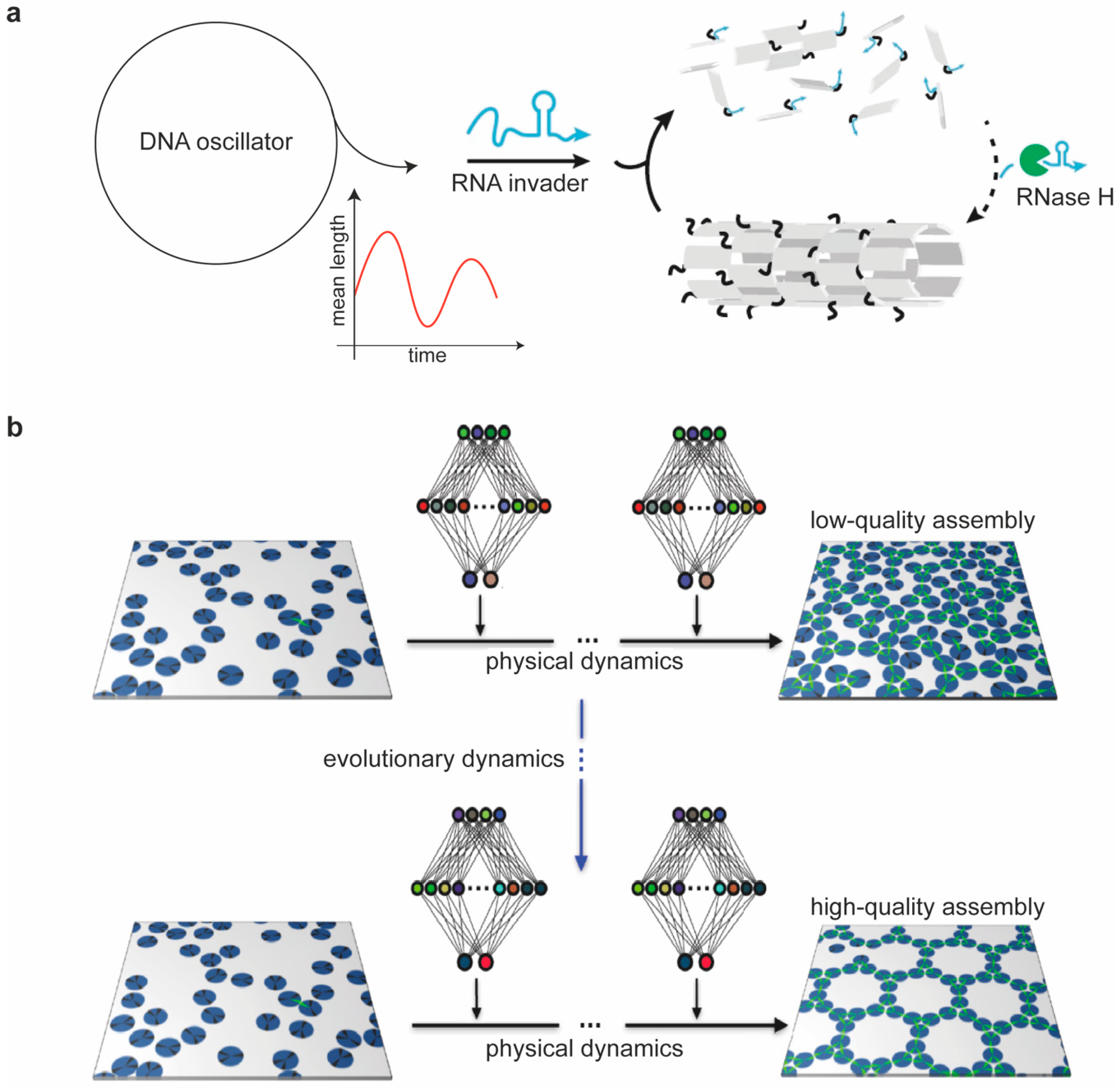
6. Proposed Models of DNA Nanostructures’ Assembly
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.D.; Crick, F.H.C. Genetical Implications of the Structure of Deoxyribonucleic Acid. Nature 1953, 171, 964–967. [Google Scholar] [CrossRef] [PubMed]
- Seeman, N.C. Nucleic acid junctions and lattices. J. Theor. Biol. 1982, 99, 237–247. [Google Scholar] [CrossRef]
- Seeman, N.C. DNA in a material world. Nature 2003, 421, 427–431. [Google Scholar] [CrossRef]
- Rothemund, P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed]
- Douglas, S.M.; Dietz, H.; Liedl, T.; Högberg, B.; Graf, F.; Shih, W.M. Self-assembly of DNA into nanoscale three-dimensional shapes. Nature 2009, 459, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Dietz, H.; Douglas, S.M.; Shih, W.M. Folding DNA into twisted and curved nanoscale shapes. Science 2009, 325, 725–730. [Google Scholar] [CrossRef] [PubMed]
- Saccà, B.; Niemeyer, C.M. DNA origami: The art of folding DNA. Angew. Chem. Int. Ed. 2012, 51, 58–66. [Google Scholar] [CrossRef]
- Hong, F.; Zhang, F.; Liu, Y.; Yan, H. DNA origami: Scaffolds for creating higher order structures. Chem. Rev. 2017, 117, 12584–12640. [Google Scholar] [CrossRef]
- Tørring, T.; Voigt, N.V.; Nangreave, J.; Yan, H.; Gothelf, K.V. DNA origami: A quantum leap for self-assembly of complex structures. Chem. Soc. Rev. 2011, 40, 5636–5646. [Google Scholar] [CrossRef]
- Mao, C.; Sun, W.; Shen, Z.; Seeman, N.C. A nanomechanical device based on the B-Z transition of DNA. Nature 1999, 397, 144–146. [Google Scholar] [CrossRef] [PubMed]
- Bhanjadeo, M.M.; Nayak, A.K.; Subudhi, U. Cerium chloride stimulated controlled conversion of B-to-Z DNA in self-assembled nanostructures. Biochem. Biophys. Res. Commun. 2017, 482, 916–921. [Google Scholar] [CrossRef]
- Simmel, F.C.; Yurke, B.; Singh, H.R. Principles and applications of nucleic acid strand displacement reactions. Chem. Rev. 2019, 119, 6326–6369. [Google Scholar] [CrossRef] [PubMed]
- SantaLucia, J. A unified view of polymer, dumbbell and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA 1998, 95, 1460–1465. [Google Scholar] [CrossRef] [PubMed]
- Wetmur, J.G.; Davidson, N. Kinetics of renaturation of DNA. J. Mol. Biol. 1968, 31, 349–370. [Google Scholar] [CrossRef]
- Zhang, J.X.; Fang, J.Z.; Duan, W.; Wu, L.R.; Zhang, A.W.; Dalchau, N.; Yordanov, B.; Petersen, R.; Phillips, A.; Zhang, D.Y. Predicting DNA hybridization kinetics from sequence. Nat. Chem. 2018, 10, 91–98. [Google Scholar] [CrossRef]
- Xiao, S.; Sharpe, D.J.; Chakraborty, D.; Wales, D.J. Energy landscapes and hybridization pathways for DNA hexamer duplexes. J. Phys. Chem. Lett. 2019, 10, 6771–6779. [Google Scholar] [CrossRef]
- Wyer, J.A.; Kristensen, M.B.; Jones, N.C.; Hoffmann, S.V.; Nielsen, S.B. Kinetics of DNA duplex formation: A-tracts versus AT-tracts. Phys. Chem. Chem. Phys. 2014, 16, 18827–18839. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Šulc, P.; Romano, F.; Doye, J.P.K.; Louis, A.A. DNA hybridization kinetics: Zippering, internal displacement and sequence dependence. Nucleic Acids Res. 2013, 41, 8886–8895. [Google Scholar] [CrossRef]
- Morrison, L.E.; Stols, L.M. Sensitive fluorescence-based thermodynamic and kinetic measurements of DNA hybridization in solution. Biochemistry 1993, 32, 3095–3104. [Google Scholar] [CrossRef]
- Eichhorn, G.L.; Shin, Y.A. Interaction of metal ions with polynucleotides and related compounds. XII. The relative effect of various metal ions on DNA helicity. J. Am. Chem. Soc. 1968, 90, 7323–7328. [Google Scholar] [PubMed]
- Kriegel, F.; Ermann, N.; Forbes, R.; Dulin, D.; Dekker, N.H.; Lipfert, J. Probing the salt dependence of the torsional stiffness of DNA by multiplexed magnetic torque tweezers. Nucleic Acids Res. 2017, 45, 5920–5929. [Google Scholar] [CrossRef]
- Seeman, N.C.; Kallenbach, N.R. DNA branched junctions. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 53–86. [Google Scholar] [CrossRef] [PubMed]
- Matos, J.; West, S.C. Holliday junction resolution: Regulation in space and time. DNA Repair 2014, 19, 176–181. [Google Scholar] [CrossRef] [PubMed]
- Lilley, D.M. The interaction of four-way DNA junctions with resolving enzymes. Biochem. Soc. Trans. 2010, 38, 399–403. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Altona, C. Classification of nucleic acid junctions. J. Mol. Biol. 1996, 263, 568–581. [Google Scholar] [CrossRef]
- Cooper, J.P.; Hagerman, P.J. Gel electrophoretic analysis of the geometry of a DNA four-way junction. J. Mol. Biol. 1987, 198, 711–719. [Google Scholar] [CrossRef]
- Murchie, A.I.H.; Clegg, R.M.; Von Krtzing, E.; Duckett, D.R.; Diekmann, S.; Lilley, D.M.J. Fluorescence energy transfer shows that the four-way DNA junction is a right-handed cross of antiparallel molecules. Nature 1989, 341, 763–766. [Google Scholar] [CrossRef]
- Du, S.M.; Zhang, S.; Seeman, N.C. DNA junctions, antijunctions, and mesojunctions. Biochemistry 1992, 31, 10955–10963. [Google Scholar] [CrossRef]
- Marky, L.A.; Kallenbach, N.R.; McDonough, K.A.; Seeman, N.C.; Breslauer, K.J. The melting behavior of a DNA junction structure: A calorimetric and spectroscopic study. Biopolymers 1987, 26, 1621–1634. [Google Scholar] [CrossRef]
- Clegg, R.M.; Murchie, A.I.; Lilley, D.M. The solution structure of the four-way DNA junction at low-salt conditions: A fluorescence resonance energy transfer analysis. Biophys. J. 1994, 66, 99–109. [Google Scholar] [CrossRef]
- Luan, B.; Aksimentiev, A. DNA attraction in monovalent and divalent electrolytes. J. Am. Chem. Soc. 2008, 130, 15754–15755. [Google Scholar] [CrossRef] [PubMed]
- McKinney, S.A.; Déclais, A.-C.; Lilley, D.M.; Ha, T. Structural dynamics of individual Holliday junctions. Nat. Struct. Biol. 2003, 10, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Hohng, S.; Zhou, R.; Nahas, M.K.; Yu, J.; Schulten, K.; Lilley, D.M.J.; Ha, T. Fluorescence-force spectroscopy maps two-dimensional reaction landscape of the holliday junction. Science 2007, 318, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Kallenbach, N.R.; Ma, R.-I.; Seeman, N.C. An immobile nucleic acid junction constructed from oligonucleotides. Nature 1983, 305, 829–831. [Google Scholar] [CrossRef]
- Seeman, N.C.; Kallenbach, N.R. Design of immobile nucleic acid junctions. Biophys. J. 1983, 44, 201–209. [Google Scholar] [CrossRef]
- Ma, R.-I.; Kallenbach, N.R.; Sheardy, R.D.; Petrillo, M.L.; Seeman, N.C. Three-arm nucleic acid junctions are flexible. Nucleic Acids Res. 1986, 14, 9745–9753. [Google Scholar] [CrossRef]
- Wang, Y.; Mueller, J.E.; Kemper, B.; Seeman, N.C. Assembly and characterization of five-arm and six-arm DNA branched junctions. Biochemistry 1991, 30, 5667–5674. [Google Scholar] [CrossRef]
- Wang, X.; Seeman, N.C. Assembly and characterization of 8-arm and 12-arm DNA branched junctions. J. Am. Chem. Soc. 2007, 129, 8169–8176. [Google Scholar] [CrossRef]
- Chen, J.H.; Kallenbach, N.R.; Seeman, N.C. A specific quadrilateral synthesized from DNA branched junctions. J. Am. Chem. Soc. 1989, 111, 6402–6407. [Google Scholar] [CrossRef]
- Chen, J.H.; Seeman, N.C. Synthesis from DNA of a molecule with the connectivity of a cube. Nature 1991, 350, 631–633. [Google Scholar] [CrossRef] [PubMed]
- Seeman, N.C. Macromolecular design, nucleic acid junctions, and crystal formation. J. Biomol. Struct. Dyn. 1985, 3, 11–34. [Google Scholar] [CrossRef] [PubMed]
- Fu, T.J.; Seeman, N.C. DNA double-crossover molecules. Biochemistry 1993, 32, 3211–3220. [Google Scholar] [CrossRef] [PubMed]
- Winfree, E.; Liu, F.; Wenzler, L.A.; Seeman, N.C. Design and self-assembly of two-dimensional DNA crystals. Nature 1998, 394, 539–544. [Google Scholar] [CrossRef] [PubMed]
- LaBean, T.H.; Yan, H.; Kopatsch, J.; Liu, F.R.; Winfree, E.; Reif, J.H.; Seeman, N.C. Construction, analysis, ligation, and self-assembly of DNA triple crossover complexes. J. Am. Chem. Soc. 2000, 122, 1848–1860. [Google Scholar] [CrossRef]
- Mao, C.; Sun, A.W.; Seeman, N.C. Designed two-dimensional DNA holliday junction arrays visualized by atomic force microscopy. J. Am. Chem. Soc. 1999, 121, 5437–5443. [Google Scholar] [CrossRef]
- Yan, H.; Park, S.H.; Finkelstein, G.; Reif, J.; LaBean, T.H. DNA-templated self-assembly of protein arrays and highly conductive nanowires. Science 2003, 301, 1882–1884. [Google Scholar] [CrossRef]
- Constantinou, P.E.; Wang, T.; Kopatsch, J.; Israel, L.B.; Zhang, X.; Ding, B.; Sherman, W.B.; Wang, X.; Zheng, J.; Sha, R.; et al. Double cohesion in structural DNA nanotechnology. Org. Biomol. Chem. 2006, 4, 3414–3419. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Liu, H.; Ribbe, A.A.E.; Mao, C. Self-assembly of hexagonal DNA two-dimensional (2D) arrays. J. Am. Chem. Soc. 2005, 127, 12202–12203. [Google Scholar] [CrossRef]
- Wei, B.; Dai, M.; Yin, P. Complex shapes self-assembled from single-stranded DNA tiles. Nature 2012, 485, 623–626. [Google Scholar] [CrossRef]
- Saccà, B.; Meyer, R.; Feldkamp, U.; Schroeder, H.; Niemeyer, C.M. High-throughput, real-time monitoring of the self-assembly of DNA nanostructures by FRET spectroscopy. Angew. Chem. Int. Ed. 2008, 47, 2135–2137. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, S.; Li, W.; Hunt, A.; Liu, Y.; Yan, H. Self-assembly of complex DNA tessellations by using low-symmetry multi-arm DNA tiles. Angew. Chem. Int. Ed. 2016, 55, 8860–8863. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Tian, Y.; Chen, Y.; Deng, Z.; Ribbe, A.E.; Mao, C. Sequence symmetry as a tool for designing DNA nanostructures. Angew. Chem. Int. Ed. 2005, 44, 6694–6696. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Ye, T.; Su, M.; Zhang, C.; Ribbe, A.E.; Jiang, W.; Mao, C. Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature 2008, 452, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Grünbaum, B.; Shephard, G.C. Tilings by regular polygons. Patterns in the plane from Kepler to the present, including recent results and unsolved problems. Math. Mag. 1977, 50, 227–247. [Google Scholar]
- He, Y.; Tian, Y.; Ribbe, A.A.E.; Mao, C. Highly connected two-dimensional crystals of DNA six-point-stars. J. Am. Chem. Soc. 2006, 128, 15978–15979. [Google Scholar] [CrossRef]
- Chhabra, R.; Sharma, J.; Ke, Y.; Liu, Y.; Rinker, S.; Lindsay, S.; Yan, H. Spatially addressable multiprotein nanoarrays templated by aptamer-tagged DNA nanoarchitectures. J. Am. Chem. Soc. 2007, 129, 10304–10305. [Google Scholar] [CrossRef] [PubMed]
- Park, S.H.; Yin, P.; Liu, Y.; Reif, J.H.; LaBean, T.H.; Yan, H. Programmable DNA self-assemblies for nanoscale organization of ligands and proteins. Nano Lett. 2005, 5, 729–733. [Google Scholar] [CrossRef]
- Lin, C.; Liu, A.Y.; Yan, H. Self-assembled combinatorial encoding nanoarrays for multiplexed biosensing. Nano Lett. 2007, 7, 507–512. [Google Scholar] [CrossRef]
- Lund, K.; Liu, Y.; Lindsay, S.; Yan, H. Self-assembling a molecular pegboard. J. Am. Chem. Soc. 2005, 127, 17606–17607. [Google Scholar] [CrossRef]
- Ke, Y.; Ong, L.L.; Shih, W.M.; Yin, P. Three-dimensional structures self-assembled from DNA bricks. Science 2012, 338, 1177–1183. [Google Scholar] [CrossRef] [PubMed]
- Mergny, J.-L.; Lacroix, L. Analysis of thermal melting curves. Oligonucleotides 2003, 13, 515–537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Fu, T.J.; Seeman, N.C. Symmetric immobile DNA branched junctions. Biochemistry 1993, 32, 8062–8067. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Yan, H.; Wang, T.; Seeman, N.C. Paranemic crossover DNA: A generalized holliday structure with applications in nanotechnology. J. Am. Chem. Soc. 2004, 126, 1666–1674. [Google Scholar] [CrossRef] [PubMed]
- Saccà, B.; Meyer, R.; Niemeyer, C.M. Analysis of the self-assembly of 4×4 DNA tiles by temperature-dependent FRET spectroscopy. ChemPhysChem 2009, 10, 3239–3248. [Google Scholar] [CrossRef]
- Ke, Y.; Sharma, J.; Liu, M.; Jahn, K.; Liu, Y.; Yan, H. Scaffolded DNA origami of a DNA tetrahedron molecular container. Nano Lett. 2009, 9, 2445–2447. [Google Scholar] [CrossRef]
- Andersen, E.S.; Dong, M.; Nielsen, M.M.; Jahn, K.; Subramani, R.; Mamdouh, W.; Golas, M.M.; Sander, B.; Stark, H.; Oliveira, C.L.P.; et al. Self-assembly of a nanoscale DNA box with a controllable lid. Nature 2009, 459, 73–76. [Google Scholar] [CrossRef]
- Endo, M.; Hidaka, K.; Kato, T.; Namba, K.; Sugiyama, H. DNA prism structures constructed by folding of multiple rectangular arms. J. Am. Chem. Soc. 2009, 131, 15570–15571. [Google Scholar] [CrossRef]
- Kuzuya, A.; Komiyama, M. Design and construction of a box-shaped 3D-DNA origami. Chem. Commun. 2009, 4182–4184. [Google Scholar] [CrossRef]
- Sprengel, A.; Lill, P.; Stegemann, P.; Bravo-Rodriguez, K.; Schöneweiß, E.-C.; Merdanovic, M.; Gudnason, D.; Aznauryan, M.; Gamrad, L.; Barcikowski, S.; et al. Tailored protein encapsulation into a DNA host using geometrically organized supramolecular interactions. Nat. Commun. 2017, 8, 14472. [Google Scholar] [CrossRef]
- Ke, Y.; Douglas, S.M.; Liu, M.; Sharma, J.; Cheng, A.; Leung, A.; Liu, Y.; Shih, W.M.; Yan, H. Multilayer DNA origami packed on a square lattice. J. Am. Chem. Soc. 2009, 131, 15903–15908. [Google Scholar] [CrossRef] [PubMed]
- Liedl, T.; Högberg, B.; Tytell, J.D.; Ingber, D.E.; Shih, W.M. Self-assembly of three-dimensional prestressed tensegrity structures from DNA. Nat. Nanotechnol. 2010, 5, 520–524. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, S.; Wu, S.; Li, Y.; Mao, C.; Liu, Y.; Yan, H. Complex wireframe DNA origami nanostructures with multi-arm junction vertices. Nat. Nanotechnol. 2015, 10, 779–785. [Google Scholar] [CrossRef] [PubMed]
- Benson, E.; Mohammed, A.; Gardell, J.; Masich, S.; Czeizler, E.; Orponen, P.; Högberg, B. DNA rendering of polyhedral meshes at the nanoscale. Nature 2015, 523, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Hong, F.; Jiang, S.; Wang, T.; Liu, Y.; Yan, H. 3D Framework DNA origami with layered crossovers. Angew Chem. Int. Ed. Engl. 2016, 55, 12832–12835. [Google Scholar] [CrossRef] [PubMed]
- Bryngelson, J.D.; Wolynes, P.G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 7524–7528. [Google Scholar] [CrossRef]
- Pfitzner, E.; Wachauf, C.; Kilchherr, F.; Pelz, B.; Shih, W.M.; Rief, M.; Dietz, H. Rigid DNA beams for high-resolution single-molecule mechanics. Angew. Chem. Int. Ed. 2013, 52, 7766–7771. [Google Scholar] [CrossRef]
- Woodside, M.T.; Anthony, P.C.; Behnke-Parks, W.M.; Larizadeh, K.; Herschlag, D.; Block, S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science 2006, 314, 1001–1004. [Google Scholar] [CrossRef]
- Ma, H.; Wan, C.; Wu, A.; Zewail, A.H. DNA folding and melting observed in real time redefine the energy landscape. Proc. Natl. Acad. Sci. USA 2007, 104, 712–716. [Google Scholar] [CrossRef]
- Shrestha, P.; Jonchhe, S.; Emura, T.; Hidaka, K.; Endo, M.; Sugiyama, H.; Mao, H. Confined space facilitates G-quadruplex formation. Nat. Nanotechnol. 2017, 12, 582–588. [Google Scholar] [CrossRef]
- Song, J.; Arbona, J.-M.; Zhang, Z.; Liu, L.; Xie, E.; Elezgaray, J.; Aime, J.-P.; Gothelf, K.V.; Besenbacher, F.; Dong, M. Direct visualization of transient thermal response of a DNA origami. J. Am. Chem. Soc. 2012, 134, 9844–9847. [Google Scholar] [CrossRef] [PubMed]
- Wah, J.L.T.; David, C.; Rudiuk, S.; Baigl, D.; Estevez-Torres, A. Observing and controlling the folding pathway of DNA origami at the nanoscale. ACS Nano 2016, 10, 1978–1987. [Google Scholar] [PubMed]
- Endo, M.; Yamamoto, S.; Emura, T.; Hidaka, K.; Morone, N.; Heuser, J.E.; Sugiyama, H. Helical DNA origami tubular structures with various sizes and arrangements. Angew. Chem. Int. Ed. 2014, 53, 7484–7490. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Chen, R.; Kai, M.; Wang, Y.; Mi, Y.; Wei, B. Versatile DNA origami nanostructures in simplified and modular designing framework. ACS Nano 2017, 11, 8199–8206. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Li, Z.; Wang, P.; Meyer, T.; Mao, C.; Ke, Y. Reconfiguration of DNA molecular arrays driven by information relay. Science 2017, 357, eaan3377. [Google Scholar] [CrossRef] [PubMed]
- Dunn, K.E.; Dannenberg, F.; Ouldridge, T.E.; Kwiatkowska, M.; Turberfield, A.J.; Bath, J. Guiding the folding pathway of DNA origami. Nature 2015, 525, 82–86. [Google Scholar] [CrossRef]
- Kosinski, R.; Mukhortava, A.; Pfeifer, W.; Candelli, A.; Rauch, P.; Saccà, B. Sites of high local frustration in DNA origami. Nat. Commun. 2019, 10, 1061. [Google Scholar] [CrossRef]
- Arbona, J.-M.; Aimé, J.-P.; Elezgaray, J. Cooperativity in the annealing of DNA origamis. J. Chem. Phys. 2013, 138, 015105. [Google Scholar] [CrossRef]
- Sobczak, J.-P.J.; Martin, T.G.; Gerling, T.; Dietz, H. Rapid folding of DNA into nanoscale shapes at constant temperature. Science 2012, 338, 1458–1461. [Google Scholar] [CrossRef]
- Wei, X.; Nangreave, J.; Jiang, S.; Yan, H.; Liu, Y. Mapping the thermal behavior of DNA origami nanostructures. J. Am. Chem. Soc. 2013, 135, 6165–6176. [Google Scholar] [CrossRef]
- Schneider, F.; Möritz, N.; Dietz, H. The sequence of events during folding of a DNA origami. Sci. Adv. 2019, 5, eaaw1412. [Google Scholar] [CrossRef] [PubMed]
- Kielar, C.; Xin, Y.; Shen, B.; Kostiainen, M.A.; Grundmeier, G.; Linko, V.; Keller, A. On the stability of DNA origami nanostructures in low-magnesium buffers. Angew. Chem. Int. Ed. 2018, 57, 9470–9474. [Google Scholar] [CrossRef] [PubMed]
- Majikes, J.M.; Nash, J.A.; LaBean, T.H. Competitive annealing of multiple DNA origami: Formation of chimeric origami. New J. Phys. 2016, 18, 115001. [Google Scholar] [CrossRef]
- Fonseca, P.; Romano, F.; Schreck, J.S.; Ouldridge, T.E.; Doye, J.P.K.; Louis, A.A. Multi-scale coarse-graining for the study of assembly pathways in DNA-brick self-assembly. J. Chem. Phys. 2018, 148, 134910. [Google Scholar] [CrossRef] [PubMed]
- Arbona, J.-M.; Aimé, J.-P.; Elezgaray, J. Modeling the mechanical properties of DNA nanostructures. Phys. Rev. E 2012, 86, 051912. [Google Scholar] [CrossRef]
- Dannenberg, F.; Dunn, K.E.; Bath, J.; Kwiatkowska, M.; Turberfield, A.J.; Ouldridge, T.E. Modelling DNA origami self-assembly at the domain level. J. Chem. Phys. 2015, 143, 165102. [Google Scholar] [CrossRef]
- Majikes, J.M.; Patrone, P.N.; Schiffels, D.; Zwolak, M.; Kearsley, A.J.; Forry, S.P.; Liddle, J.A. Revealing thermodynamics of DNA origami folding via affine transformations. Nucleic Acids Res. 2020, 48, 5268–5280. [Google Scholar] [CrossRef]
- Halverson, J.D.; Tkachenko, A.V. DNA-programmed mesoscopic architecture. Phys. Rev. E 2013, 87, 062310. [Google Scholar] [CrossRef]
- Reinhardt, A.; Frenkel, D. Numerical evidence for nucleated self-assembly of DNA brick structures. Phys. Rev. Lett. 2014, 112, 238103. [Google Scholar] [CrossRef]
- Jacobs, W.M.; Reinhardt, A.; Frenkel, D. Rational design of self-assembly pathways for complex multicomponent structures. Proc. Natl. Acad. Sci. USA 2015, 112, 6313–6318. [Google Scholar] [CrossRef]
- Reinhardt, A.; Frenkel, D. DNA brick self-assembly with an off-lattice potential. Soft Matter 2016, 12, 6253–6260. [Google Scholar] [CrossRef] [PubMed]
- Ouldridge, T.E.; Louis, A.A.; Doye, J.P.K. DNA nanotweezers studied with a coarse-grained model of DNA. Phys. Rev. Lett. 2010, 104, 178101. [Google Scholar] [CrossRef] [PubMed]
- Myhrvold, C.; Dai, M.; Silver, P.A.; Yin, P. Isothermal self-assembly of complex DNA structures under diverse and biocompatible conditions. Nano Lett. 2013, 13, 4242–4248. [Google Scholar] [CrossRef] [PubMed]
- Green, L.N.; Subramanian, H.K.K.; Mardanlou, V.; Kim, J.; Hariadi, R.F.; Franco, E. Autonomous dynamic control of DNA nanostructure self-assembly. Nat. Chem. 2019, 11, 510–520. [Google Scholar] [CrossRef]
- Whitelam, S.; Tamblyn, I. Learning to grow: Control of material self-assembly using evolutionary reinforcement learning. Phys. Rev. E 2020, 101, 052604. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaekel, A.; Lill, P.; Whitelam, S.; Saccà, B. Insights into the Structure and Energy of DNA Nanoassemblies. Molecules 2020, 25, 5466. https://doi.org/10.3390/molecules25235466
Jaekel A, Lill P, Whitelam S, Saccà B. Insights into the Structure and Energy of DNA Nanoassemblies. Molecules. 2020; 25(23):5466. https://doi.org/10.3390/molecules25235466
Chicago/Turabian StyleJaekel, Andreas, Pascal Lill, Stephen Whitelam, and Barbara Saccà. 2020. "Insights into the Structure and Energy of DNA Nanoassemblies" Molecules 25, no. 23: 5466. https://doi.org/10.3390/molecules25235466
APA StyleJaekel, A., Lill, P., Whitelam, S., & Saccà, B. (2020). Insights into the Structure and Energy of DNA Nanoassemblies. Molecules, 25(23), 5466. https://doi.org/10.3390/molecules25235466





