Being Uncertain in Chromatographic Calibration—Some Unobvious Details in Experimental Design
Abstract
:1. Introduction
2. Theory
2.1. Classical Formulation of Simple Linear Regression
- The modeled equation must match the real calibration dependence. This assumption is not valid when a straight line is fitted to a curvilinear dataset (instead of quadratic or cubic equation). Then, the residuals contain the whole nonlinearity pattern instead of a random error. It causes the introduction of a strong systematic error to the predicted values: the fitted equation does not estimate anything serious. The most frequently used validation criteria: Pearson’s correlation coefficient r, as well as coefficient of determination R2 are only measures of the error’s magnitude [13]: the randomness of the error is neglected by them. Therefore, when their value is close to 1, it does not indicate that the model is sufficient to describe the calibration dependence and that all assumptions are fulfilled [14].
- There is no error in x: concentrations are known without any uncertainty. This cannot be achieved in practice, so calibration samples should be prepared as carefully, as possible. There are some approaches that include this error into the model [15,16]. It substantially makes the mathematical background much more complex, so they did not reach much attention in practice.
- The error is homoscedastic (the variance of the error does not depend on the concentration of analyzed compound). This can be checked with visual inspection of residuals plot, as well as by Bartlett test on residual groups. In case of heteroscedascity, appropriate weights should be used in regression [17,18]. The most reasonable weighting is the reciprocal of the concentration, as the error is proportional to it. This is frequently a case in chromatography, when the injection volume remains the same, but calibration is done with increasing concentrations. When standard addition is performed, the error distribution change—this topic lies beyond the area of the current paper, and interested readers can be referred to [19,20]. Another important factor is also the use of certified reference materials [21].
- The distribution of residuals should be as similar as possible to that of normal distribution. The attention should be put especially when the results were transformed. Although the logarithmic transformation seems to be good solution to deal with nonlinearity, it also transforms the errors [22,23]. Therefore, in most cases, quadratic regression is better than the combination of the linear regression and the transformation.
2.2. Uncertainty of the Regression Estimates
- To minimize the slope uncertainty, one should take concentrations with as large variance, as possible. The ideal solution would be to make the first half measurements at zero and the second half at the highest concentration [24].
- To minimize the intercept uncertainty, one should measure one observation at the highest concentration and the other measurements should be done at concentration equal to zero. More reasonable solutions are available only when it is allowed to use negative concentrations, which does not happen in practice.
- It is possible to get rid of the covariance between uncertainties—to achieve this goal, the concentrations should be symmetrical around zero (with mean equal to zero). Without negative concentrations, the lowest covariance is achieved in the same case as in (2).
2.3. Design Optimality
- D-optimality, which minimizes the determinant , (which is equal to maximizing determinant of ). Optimizing experiment in this way forces us to use the same strange design as when minimizing slope uncertainty.
- C-optimality, minimizing the uncertainty of some linear combination of fitted coefficients, for example the uncertainty of the root of fitted line (such a parameter is often computed in lipophilicity measurements). In linear regression, the mean of x values must be equal to the place of the root. Not so useful idea-we are led again to the paradox, as we must know the answer before designing the experiment.
- A-optimality, minimizing the trace (sum of diagonal values) of . It can be seen, that this idea ends with the same solution, as minimizing the uncertainty of the intercept.
- T-optimality (maximizing the trace of ), as well as E-optimality (maximizing the minimum eigenvalue of ), leading to measurement of all but one points at maximum concentration and the remaining point at zero (reverse idea than the intercept case).
2.4. Uncertainty in Quadratic Regression
- D-optimal design puts equal (1/3) number of measurements to these three points
- To minimize the uncertainty of intercept, one should measure one sample at maximum, one in the middle, then the rest at zero (this also minimizes covariance between uncertainties of the intercept and the linear coefficient).
- Minimizing the uncertainty of the linear coefficient needs placing half of the samples in the middle and about 1/8 at the maximum concentration.
- To minimize quadratic coefficient error, half of the samples should still lie in the middle, but the rest divided equally (1/4) to zero and the maximum concentration (this is also very close to A-optimality).
- A totally different design should be used to minimize the covariances between quadratic coefficient and both other ones: one zero, one in the middle, all other at maximum concentration.
2.5. Fedorov Nonuniform D-Optimal Designs
2.6. Uncertainty of Prediction
- G-optimality minimizes the maximal value of the hat matrix diagonal (thus minimizing the maximal uncertainty)
- I-optimality minimizes the average uncertainty (expressed for example as the trace of hat matrix)
- V-optimality minimizes the average uncertainty for the specific range or set of concentrations.
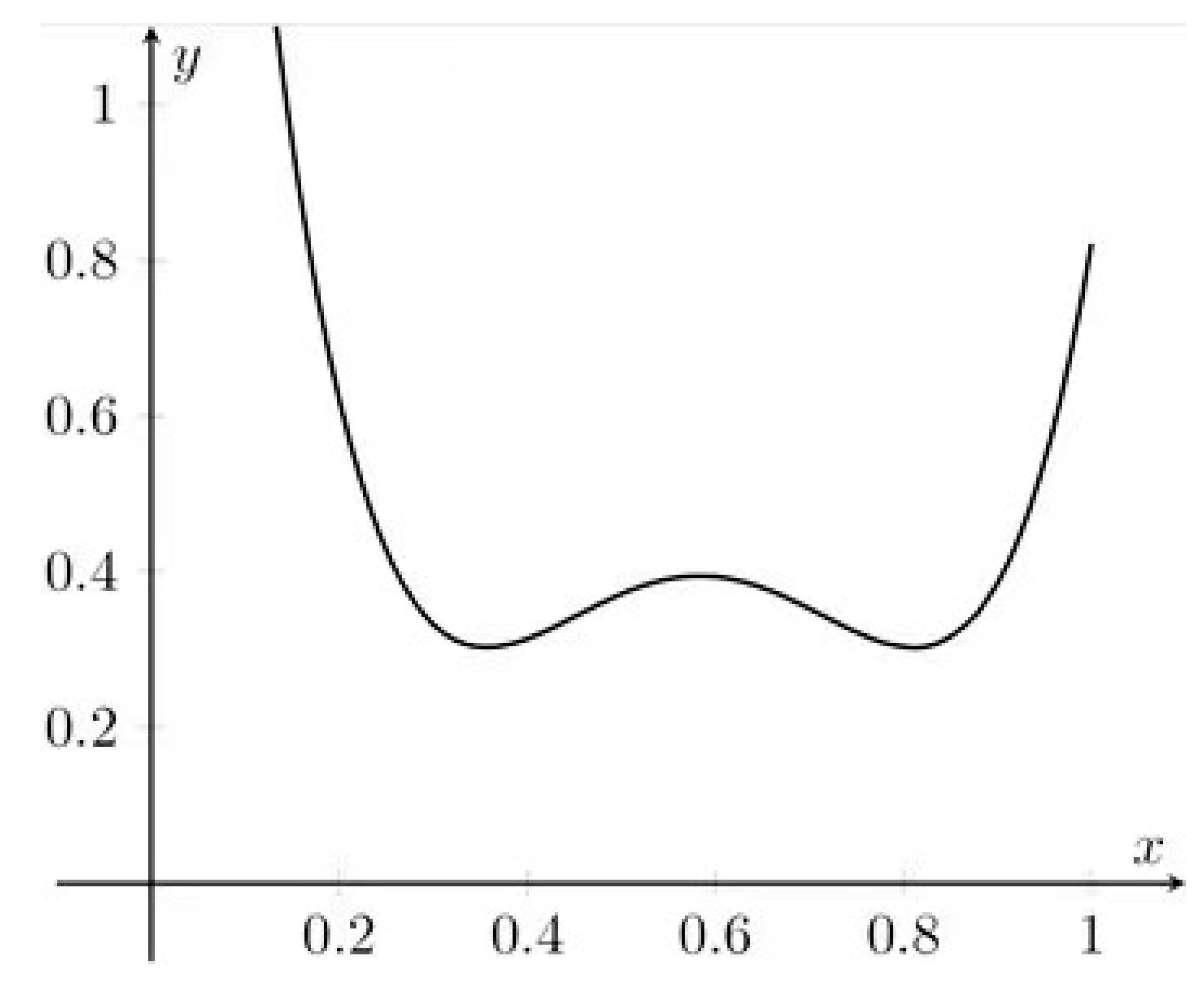
- The prediction uncertainty is modeled by quadratic (parabolic) dependence, so it is symmetric and unimodal (having exactly one optimal minimum)
- The minimum occurs when is equal to zero. This occurs for the arithmetic mean of all calibration concentrations
- To minimize prediction error (across the whole calibration range) we should maximize . Again, we end up with half of points located at zero, the other at the maximal concentration.
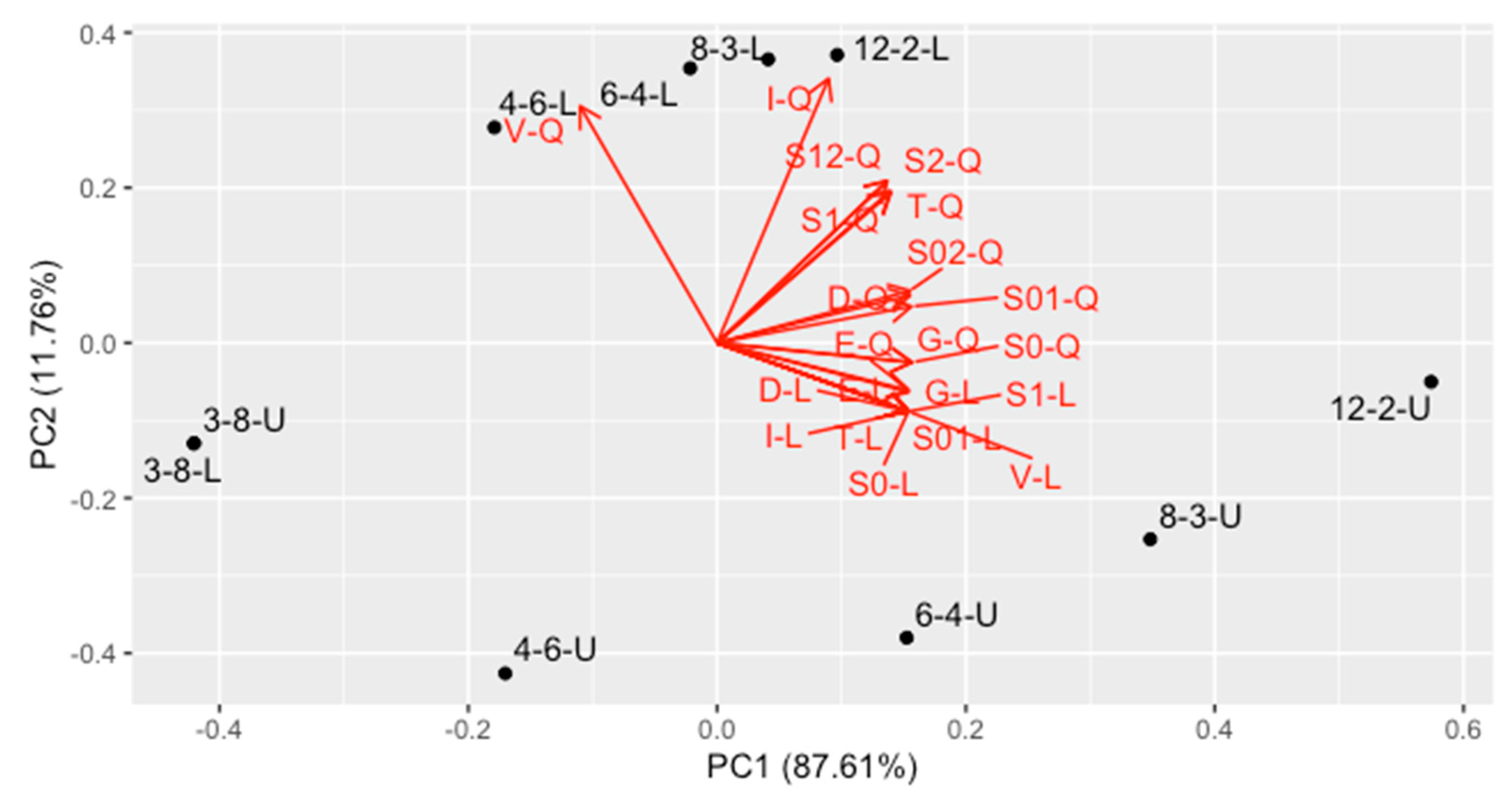
3. Putting All Together in a Comparison
- The second PC, containing 11.76% of variance, represents mainly the V-, T- and I-optimality for quadratic regression, together with uncertainty of linear and quadratic coefficient in quadratic regression, as well as covariance between them. They are quite intercorrelated. Designs located at the bottom of the plot are the best ones in this trend.
- The first PC contains the average optimality for all the other criteria (87.61% variance). This trend contains all criteria for linear model and intercept term for the quadratic one, as well as correlation of the intercept with linear and quadratic term in quadratic regression. Designs located at the left side are the best ones regarding this trend.
- In general, contrary to the intuitive perception, a design is better when it uses less concentrations and more replicates. The best one is 3–8 design (in the bottom-left corner).
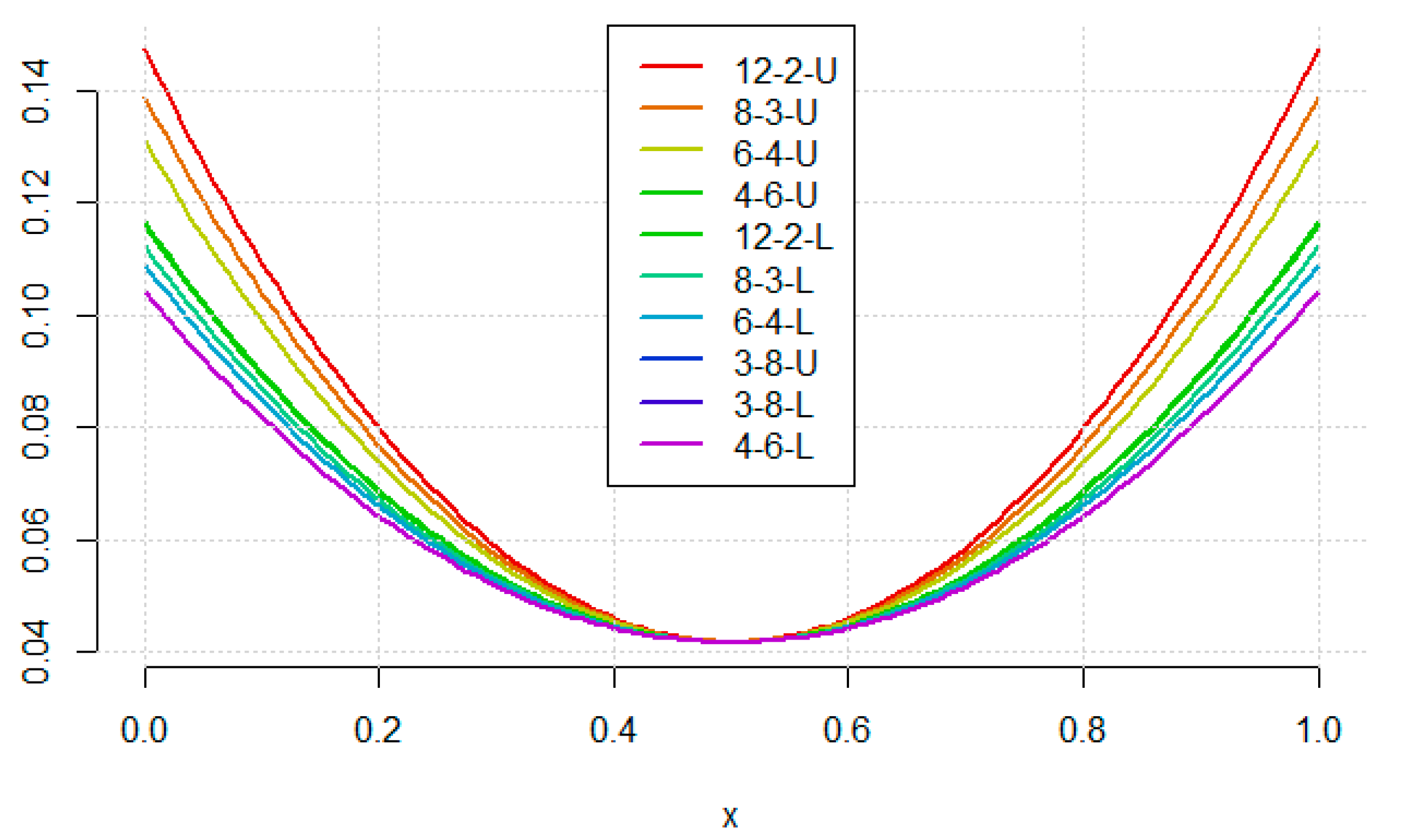
- The difference between uniform and nonuniform version of each design changes with number of concentrations.
- For 4 concentrations, the difference is almost vertical, and they are located at the left side of the graph. Therefore, they perform equally well for linear model, but for quadratic model the uniform design is significantly better.
- For 6 concentrations, the difference for linear model appears, so nonuniform design is visibly better in this case, the difference on vertical axis is analogous.
- For 8 and 12 concentrations, the difference is more horizontal, and the nonuniform design is much more better than the uniform one.
- The worst among the considered designs is 12–2-U.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Karnes, H.T.; Shiu, G.; Shah, V.P. Validation of Bioanalytical Methods. Pharm. Res. 1991, 8, 421–426. [Google Scholar] [CrossRef] [PubMed]
- Cuadros-Rodríguez, L.; Gámiz-Gracia, L.; Almansa-López, E.M.; Bosque-Sendra, J.M. Calibration in Chemical Measurement Processes. II. A Methodological Approach. TrAC Trends Anal. Chem. 2001, 20, 620–636. [Google Scholar] [CrossRef]
- Rozet, E.; Marini, R.D.; Ziemons, E.; Boulanger, B.; Hubert, P. Advances in Validation, Risk and Uncertainty Assessment of Bioanalytical Methods. J. Pharm. Biomed. Anal. 2011, 55, 848–858. [Google Scholar] [CrossRef]
- Olivieri, A.C. Analytical Figures of Merit: From Univariate to Multiway Calibration. Chem. Rev. 2014, 114, 5358–5378. [Google Scholar] [CrossRef] [PubMed]
- Olivieri, A.C. Practical Guidelines for Reporting Results in Single- and Multi-Component Analytical Calibration: A Tutorial. Anal. Chim. Acta 2015, 868, 10–22. [Google Scholar] [CrossRef]
- Kościelniak, P.; Wieczorek, M. Univariate Analytical Calibration Methods and Procedures. A Review. Anal. Chim. Acta 2016, 944, 14–28. [Google Scholar] [CrossRef] [PubMed]
- Baumann, K.; Wätzig, H. Regression and Calibration for Analytical Separation Techniques. Part I: Design Considerations. Process Control Qual. 1997, 1–2, 59–73. [Google Scholar]
- Baumann, K. Regression and Calibration for Analytical Separation Techniques. Part II: Validation, Weighted and Robust Regression. Process Control Qual. 1997, 10, 75–112. [Google Scholar]
- Lee, K.R.; McAllister, P.R. Helping Analytical Scientists Apply Statistics. Drug Dev. Ind. Pharm. 1996, 22, 891–908. [Google Scholar] [CrossRef]
- Scheffe, H. A Statistical Theory of Calibration. Ann. Stat. 1973, 1, 1–37. [Google Scholar] [CrossRef]
- John, R.C.; Draper, N.R. D-Optimality for Regression Designs: A Review. Technometrics 1975, 17, 15–23. [Google Scholar] [CrossRef]
- Raposo, F. Evaluation of Analytical Calibration Based on Least-Squares Linear Regression for Instrumental Techniques: A Tutorial Review. TrAC Trends Anal. Chem. 2016, 77, 167–185. [Google Scholar] [CrossRef]
- Tellinghuisen, J.; Bolster, C.H. Using R2 to Compare Least-Squares Fit Models: When It Must Fail. Chemom. Intell. Lab. Syst. 2011, 105, 220–222. [Google Scholar] [CrossRef]
- Raposo, F.; Barceló, D. Assessment of Goodness-of-Fit for the Main Analytical Calibration Models: Guidelines and Case Studies. TrAC Trends Anal. Chem. 2021, 143, 116373. [Google Scholar] [CrossRef]
- Hyk, W.; Stojek, Z. Quantifying Uncertainty of Determination by Standard Additions and Serial Dilutions Methods Taking into Account Standard Uncertainties in Both Axes. Anal. Chem. 2013, 85, 5933–5939. [Google Scholar] [CrossRef] [PubMed]
- Tellinghuisen, J. Least Squares in Calibration: Dealing with Uncertainty in x. Analyst 2010, 135, 1961. [Google Scholar] [CrossRef]
- Allegrini, F.; Olivieri, A.C. Recent Advances in Analytical Figures of Merit: Heteroscedasticity Strikes Back. Anal. Methods 2017, 9, 739–743. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Weighted Least-Squares in Calibration: What Difference Does It Make? Analyst 2007, 132, 536. [Google Scholar] [CrossRef]
- Andersen, J.E.T. The Standard Addition Method Revisited. TrAC Trends Anal. Chem. 2017, 89, 21–33. [Google Scholar] [CrossRef]
- Ellison, S.L.R.; Thompson, M. Standard Additions: Myth and Reality. Analyst 2008, 133, 992–997. [Google Scholar] [CrossRef]
- Świtaj-Zawadka, A.; Konieczka, P.; Przyk, E.; Namieśnik, J. Calibration in Metrological Approach. Anal. Lett. 2005, 38, 353–376. [Google Scholar] [CrossRef]
- Kong, D.; Zhao, J.; Tang, S.; Shen, W.; Lee, H.K. Logarithmic Data Processing Can Be Used Justifiably in the Plotting of a Calibration Curve. Anal. Chem. 2021, 93, 12156–12161. [Google Scholar] [CrossRef] [PubMed]
- Tellinghuisen, J. Least Squares with Non-Normal Data: Estimating Experimental Variance Functions. Analyst 2008, 133, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Kitsos, C.P. The Simple Linear Calibration Problem as an Optimal Experimental Design. Commun. Stat. - Theory Methods 2002, 31, 1167–1177. [Google Scholar] [CrossRef]
- O’Brien, T.E.; Funk, G.M. A Gentle Introduction to Optimal Design for Regression Models. Am. Stat. 2003, 57, 265–267. [Google Scholar] [CrossRef] [Green Version]
- McGree, J.M.; Eccleston, J.A.; Duffull, S.B. Compound Optimal Design Criteria for Nonlinear Models. J. Biopharm. Stat. 2008, 18, 646–661. [Google Scholar] [CrossRef]
- Bogacka, B.; Wright, F. Comparison of Two Design Optimality Criteria Applied to a Nonlinear Model. J. Biopharm. Stat. 2004, 14, 909–930. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P.; Lucas, H.L. Design of Experiments in Non-Linear Situations. Biometrika 1959, 46, 77–90. [Google Scholar] [CrossRef]
- Imhof, L.; Krafft, O.; Schaefer, M. D-Optimal Exact Designs for Parameter Estimation in A Quadratic Model. Sankhyā Indian J. Stat. Ser. B 2002, 62, 266–275. [Google Scholar]
- Hajiyev, C. Determination of Optimum Measurement Points via A-Optimality Criterion for the Calibration of Measurement Apparatus. Measurement 2010, 43, 563–569. [Google Scholar] [CrossRef]
- Smucker, B.; Krzywinski, M.; Altman, N. Optimal Experimental Design. Nat. Methods 2018, 15, 559–560. [Google Scholar] [CrossRef] [PubMed]
- Gaffke, N. On D-Optimality of Exact Linear Regression Designs with Minimum Support. J. Stat. Plan. Inference 1986, 15, 189–204. [Google Scholar] [CrossRef]
- Fedorov, V.V. Theory of Optimal Experiments.; Elsevier Science: Saint Louis, MO, USA, 2014; ISBN 978-0-323-16246-3. [Google Scholar]
- Antille, G.; Allen, A.W. D-Optimal Design for Polynomial Regression: Choice of Degree and Robustness. Appl. Econom. 2007, 8, 55–66. [Google Scholar]
- Cook, R.D.; Nachtsheim, C.J. A Comparison of Algorithms for Constructing Exact D-Optimal Designs. Technometrics 1980, 22, 315–324. [Google Scholar] [CrossRef]
- Barlow, R.E.; Mensing, R.W.; Smiriga, N.G. Computing the Optimal Design for a Calibration Experiment. J. Stat. Plan. Inference 1991, 29, 5–19. [Google Scholar] [CrossRef]
- O’Hagan, A.; Kingman, J.F.C. Curve Fitting and Optimal Design for Prediction. J. R. Stat. Soc. Ser. B (Methodol.) 1978, 40, 1–42. [Google Scholar] [CrossRef]
- Brooks, R.J. On the Choice of an Experiment for Prediction in Linear Regression. Biometrika 1974, 61, 303–311. [Google Scholar] [CrossRef]
- Gaylor, D.W.; Sweeny, H.C. Design for Optimal Prediction in Simple Linear Regression. J. Am. Stat. Assoc. 1965, 60, 205–216. [Google Scholar] [CrossRef]
- Guest, P.G. The Spacing of Observations in Polynomial Regression. Ann. Math. Stat. 1958, 29, 294–299. [Google Scholar] [CrossRef]
- Dette, H.; O’Brien, T.E. Optimality Criteria for Regression Models Based on Predicted Variance. Biometrika 1999, 86, 93–106. [Google Scholar] [CrossRef]
- Kiefer, J. General Equivalence Theory for Optimum Designs (Approximate Theory). Ann. Stat. 1974, 2, 849–879. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Buonaccorsi, J.P. Design Considerations for Calibration. Technometrics 1986, 28, 149–155. [Google Scholar] [CrossRef]
- Dette, H. Optimal Designs for Identifying the Degree of a Polynomial Regression. Ann. Stat. 1995, 23, 1248–1266. [Google Scholar] [CrossRef]

| Concentrations | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 1 | |||||||
| 3 | 0 | 0.5000 | 1 | ||||||
| 4 | 0 | 0.2764 | 0.7236 | 1 | |||||
| 5 | 0 | 0.1727 | 0.5000 | 0.8273 | 1 | ||||
| 6 | 0 | 0.1175 | 0.3574 | 0.6426 | 0.8825 | 1 | |||
| 7 | 0 | 0.0849 | 0.2656 | 0.5000 | 0.7344 | 0.9151 | 1 | ||
| 8 | 0 | 0.0641 | 0.2041 | 0.3954 | 0.6046 | 0.7959 | 0.9359 | 1 | |
| 9 | 0 | 0.0501 | 0.1614 | 0.3184 | 0.5000 | 0.6816 | 0.8386 | 0.9499 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komsta, Ł.; Wicha-Komsta, K.; Kocki, T. Being Uncertain in Chromatographic Calibration—Some Unobvious Details in Experimental Design. Molecules 2021, 26, 7035. https://doi.org/10.3390/molecules26227035
Komsta Ł, Wicha-Komsta K, Kocki T. Being Uncertain in Chromatographic Calibration—Some Unobvious Details in Experimental Design. Molecules. 2021; 26(22):7035. https://doi.org/10.3390/molecules26227035
Chicago/Turabian StyleKomsta, Łukasz, Katarzyna Wicha-Komsta, and Tomasz Kocki. 2021. "Being Uncertain in Chromatographic Calibration—Some Unobvious Details in Experimental Design" Molecules 26, no. 22: 7035. https://doi.org/10.3390/molecules26227035
APA StyleKomsta, Ł., Wicha-Komsta, K., & Kocki, T. (2021). Being Uncertain in Chromatographic Calibration—Some Unobvious Details in Experimental Design. Molecules, 26(22), 7035. https://doi.org/10.3390/molecules26227035







