Influence of Liquid Crystallinity and Mechanical Deformation on the Molecular Relaxations of an Auxetic Liquid Crystal Elastomer
Abstract
:1. Introduction
2. Results and Discussion
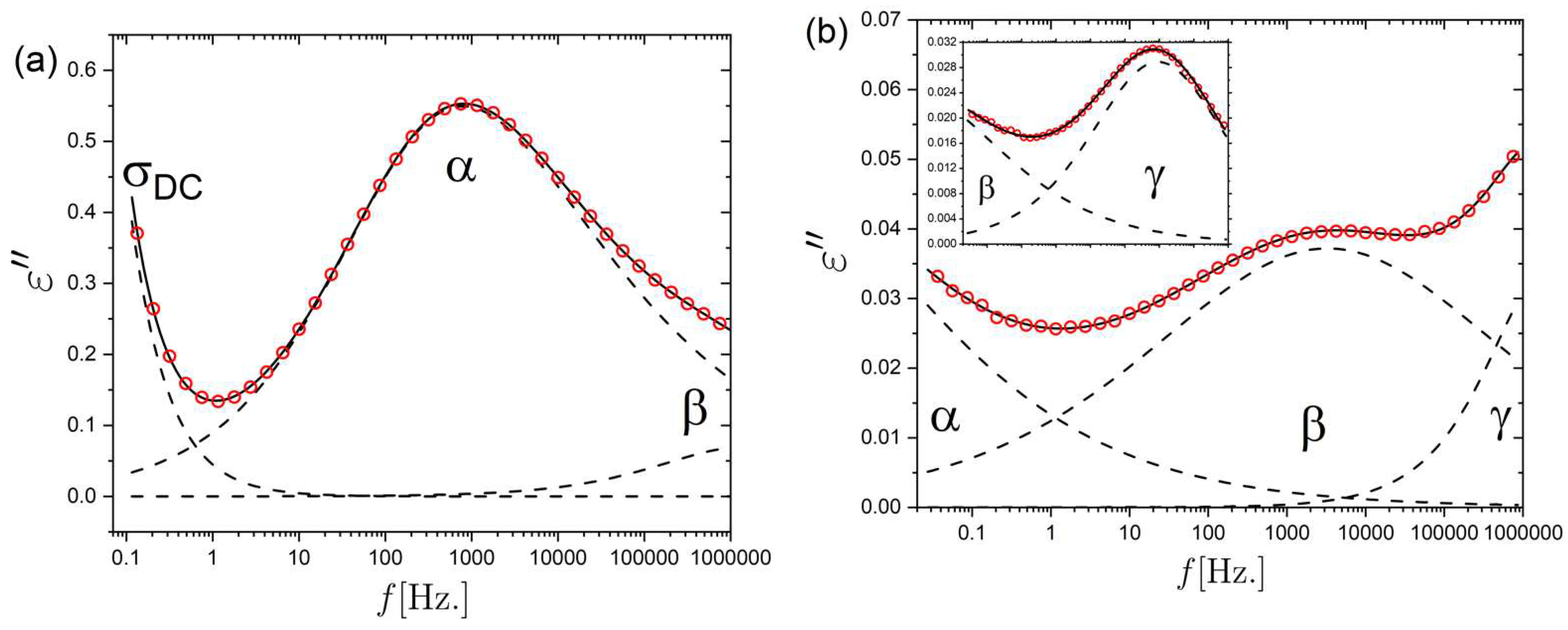
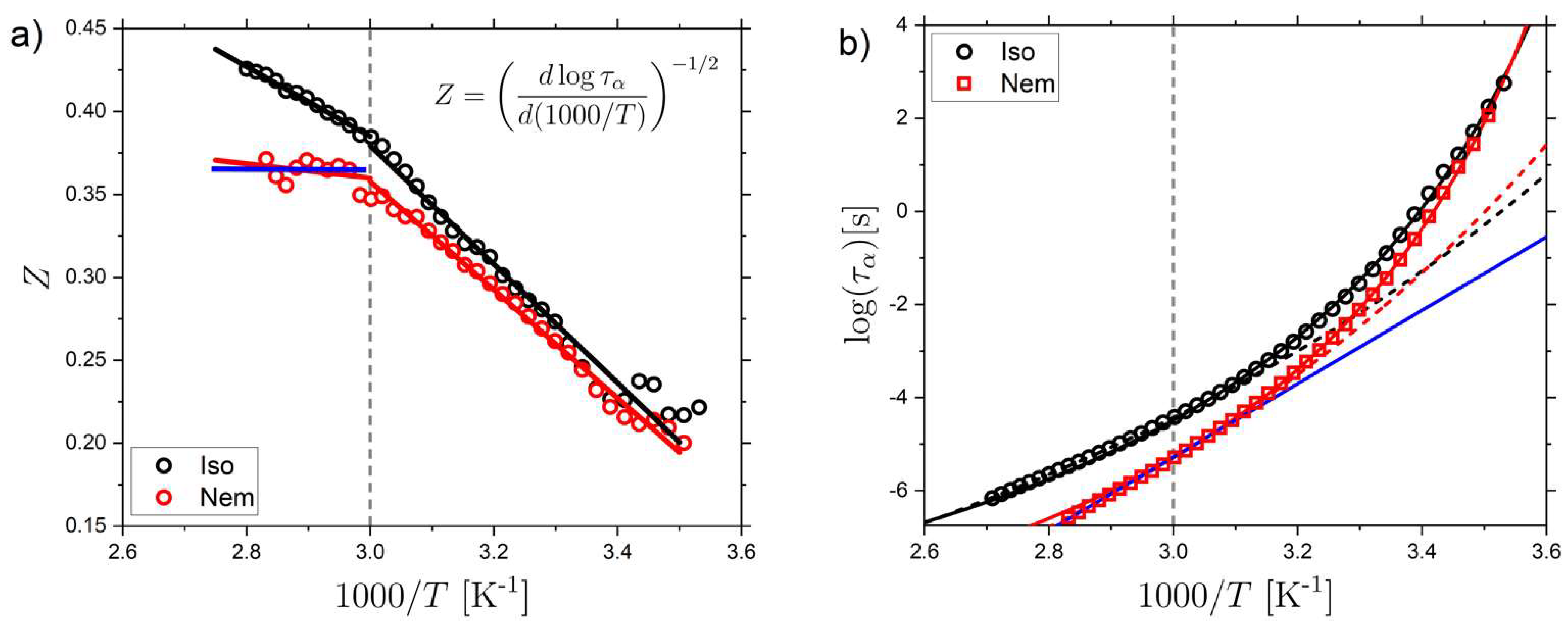
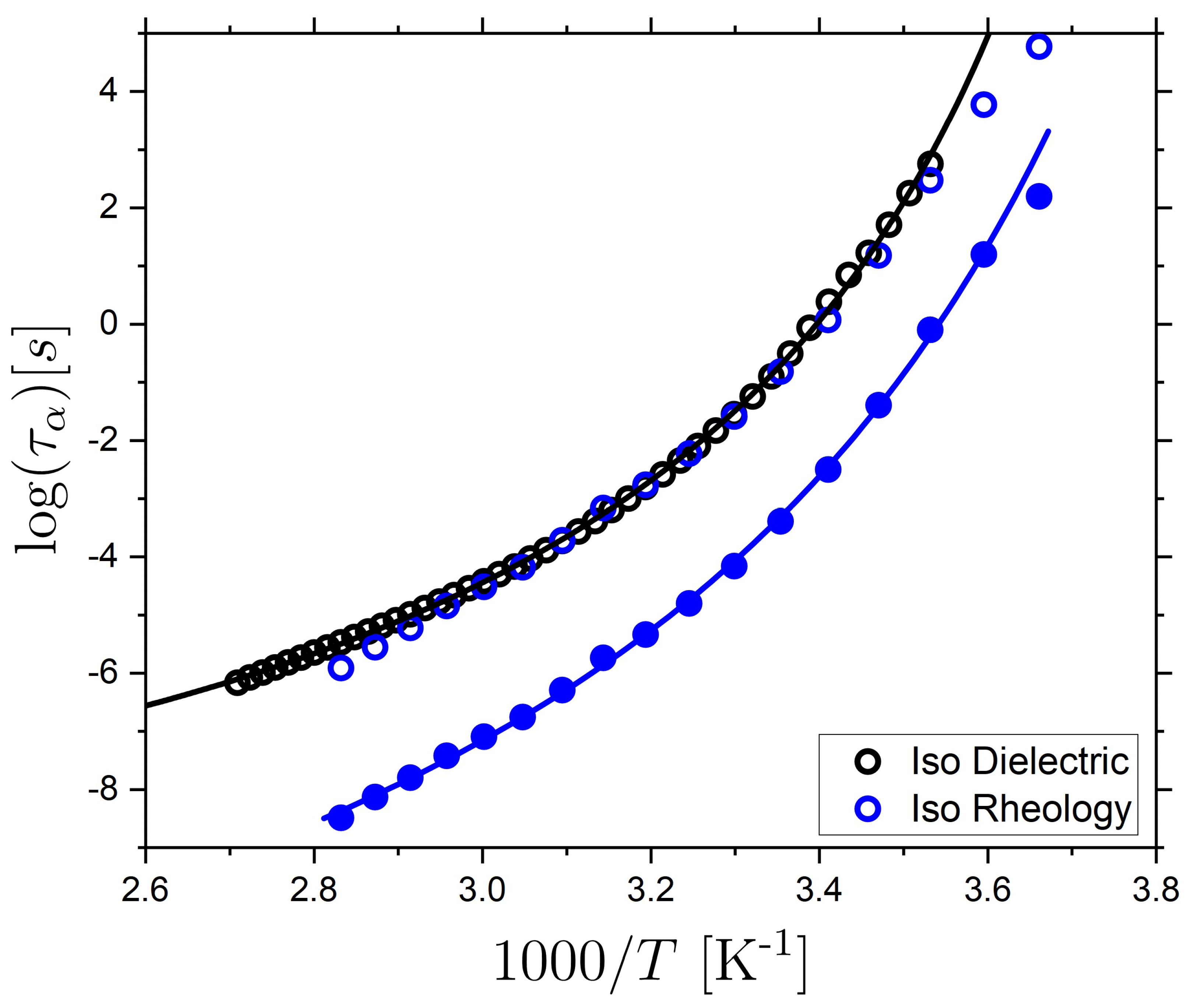
2.1. Relaxation Dynamics of the Isotropic and Nematic LCE
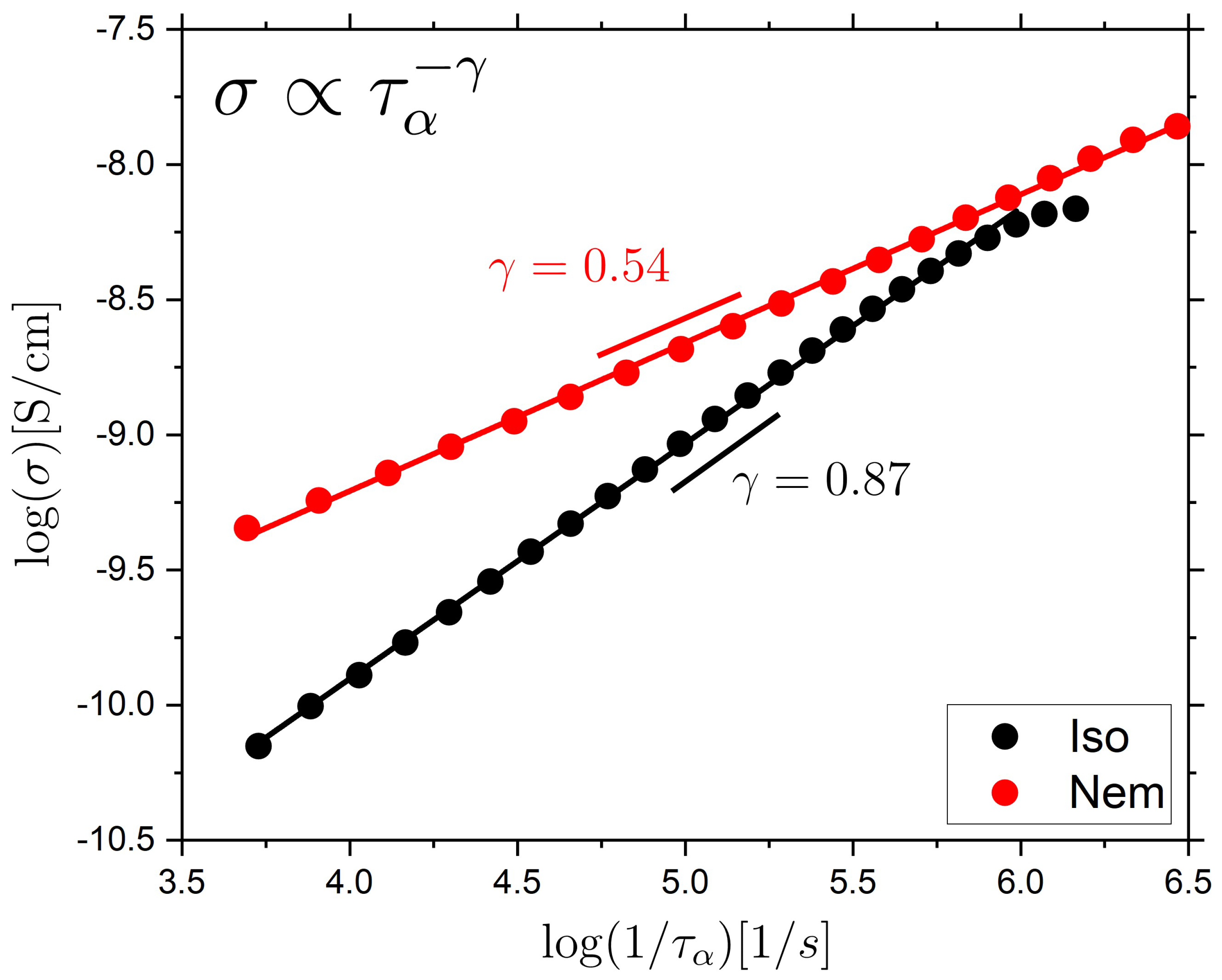
2.2. Ionic Conductivity Behavior of the Isotropic and Nematic LCE
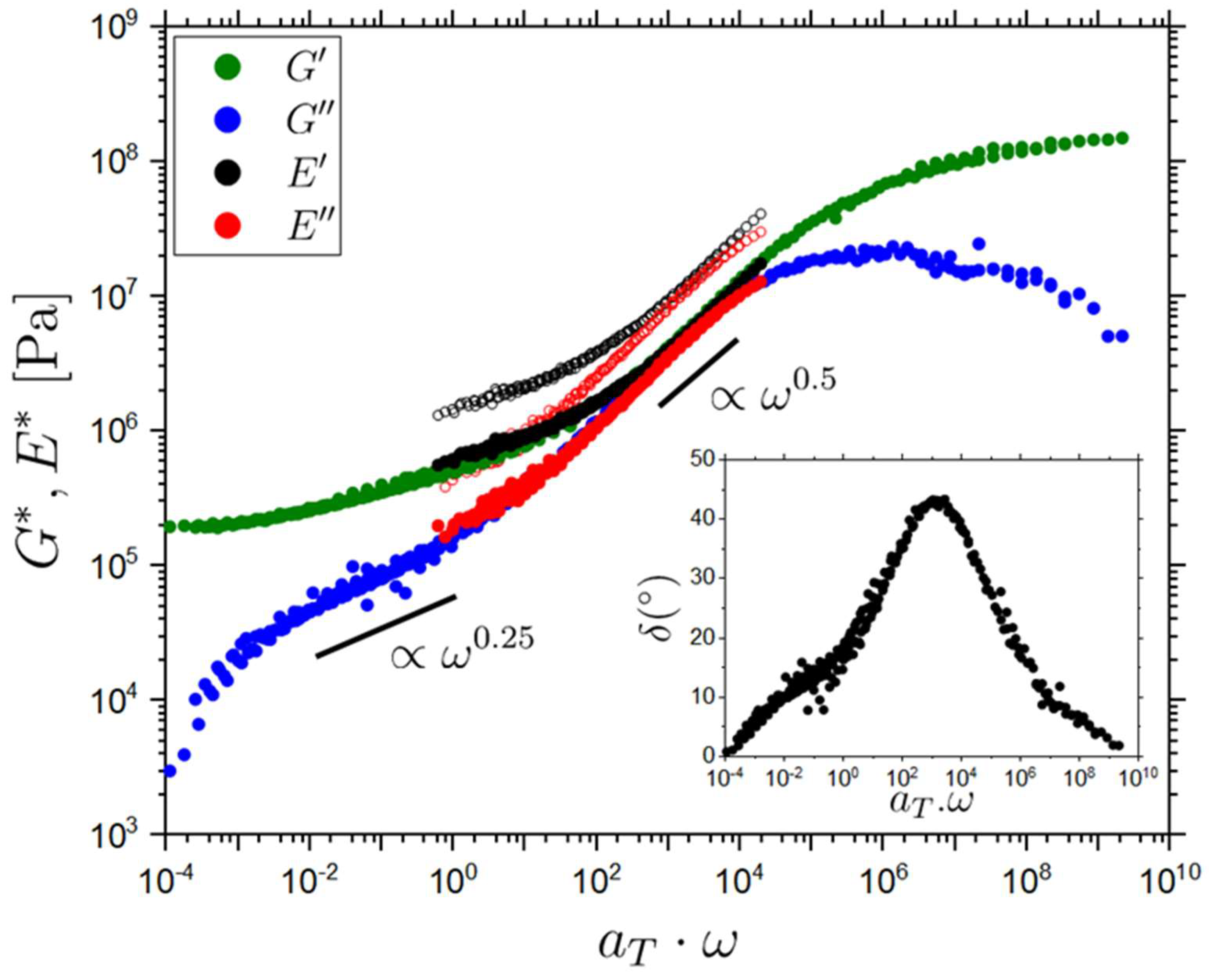
2.3. Rheology of the Isotropic LCE Sample
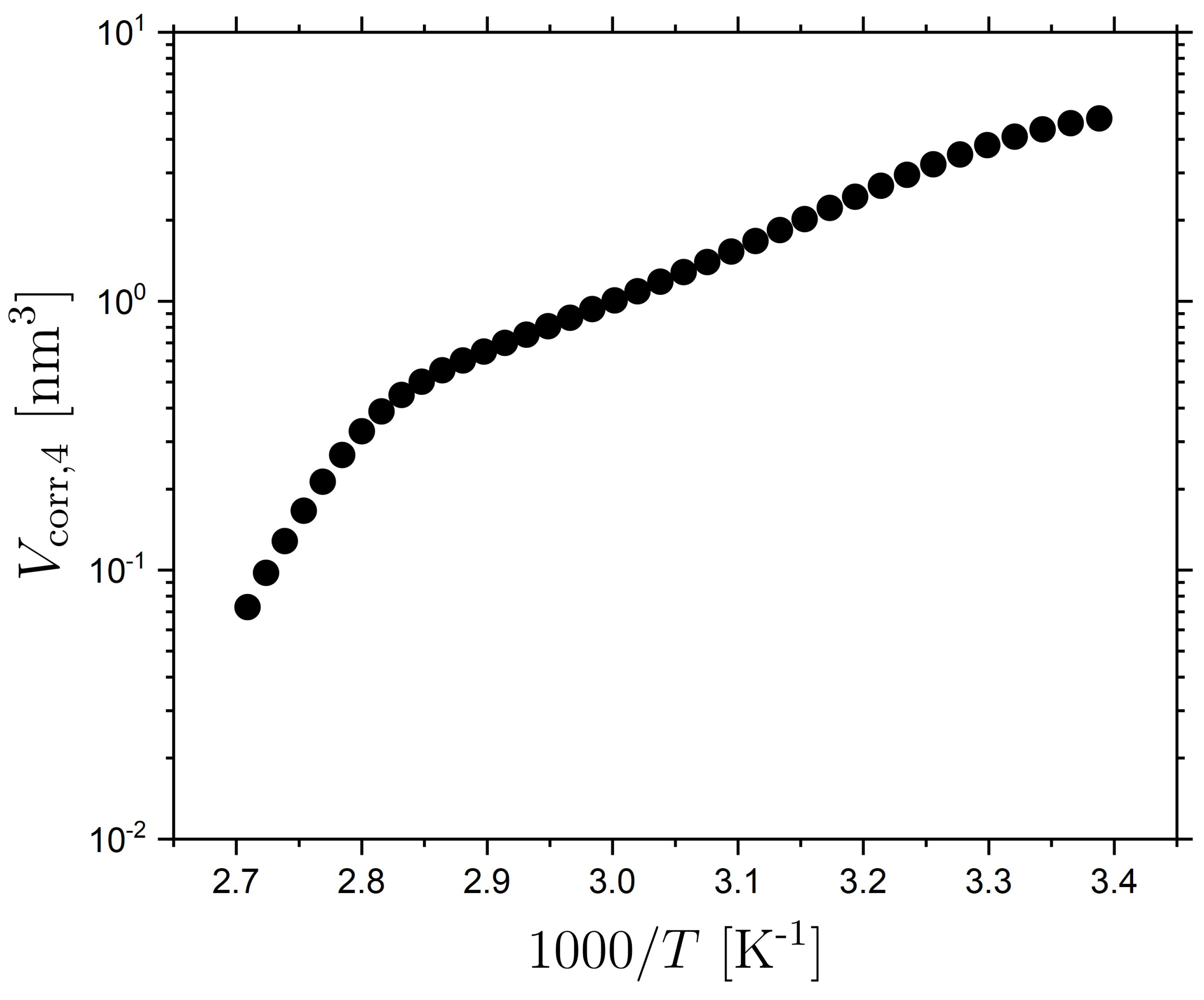
2.4. Volume of Correlated Motions in the Isotropic LCE
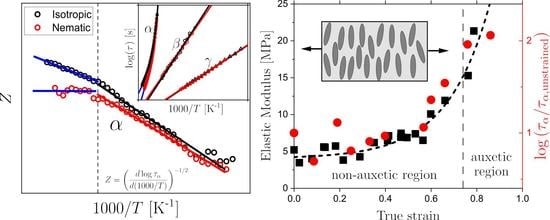
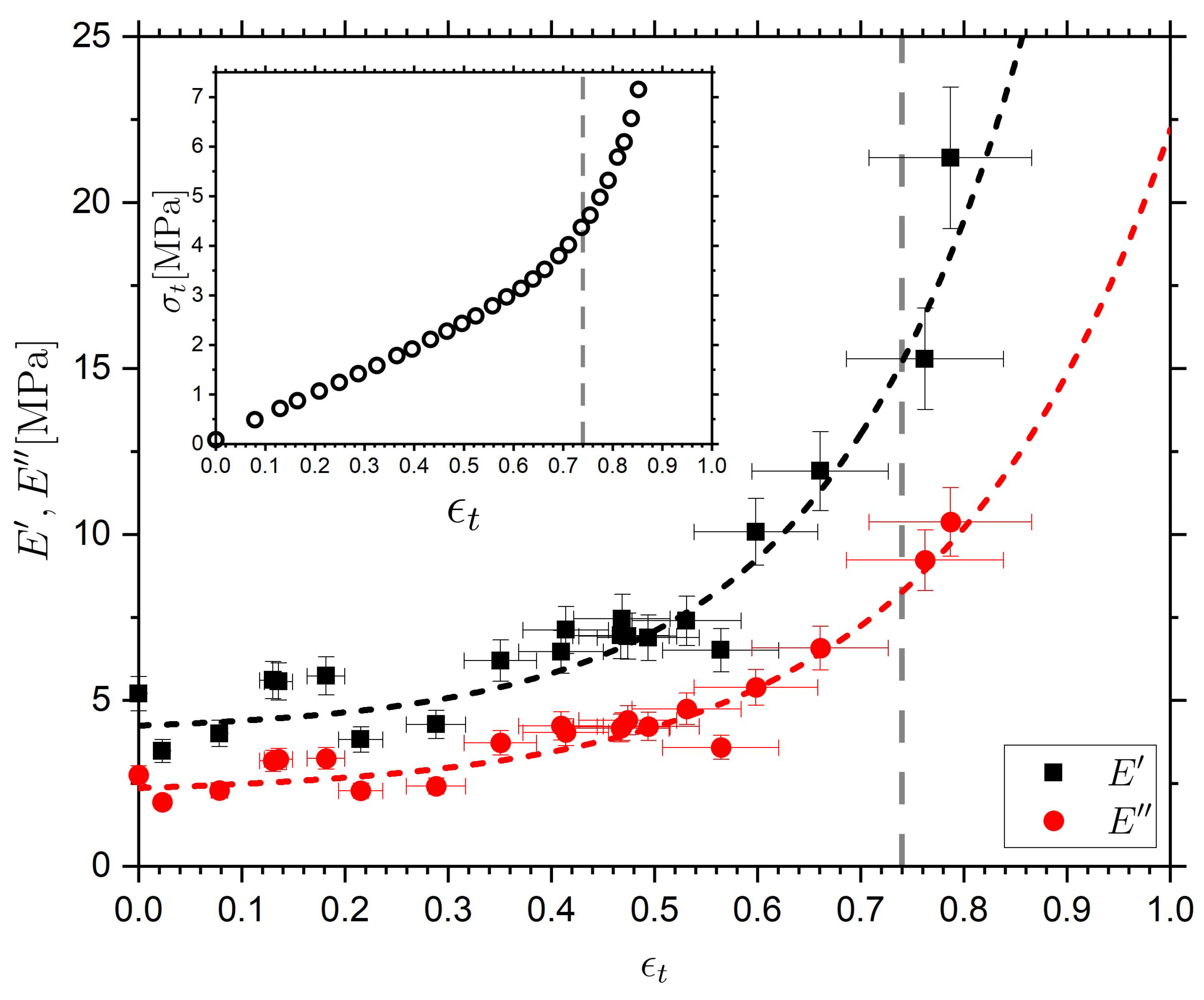
2.5. Effect of Strain on the Dielectric and Rheological Behaviors of the Nematic Sample
3. Materials and Methods
3.1. Synthesis of the Liquid Crystalline Elastomer
3.2. Broadband Dielectric Spectroscopy
3.3. Rheology
3.4. Differential Scanning Calorimetry and Modulated Differential Scanning Calorimetry
3.5. Determining the Correlation Volume from Broadband Dielectric Relaxation Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Zeng, H.; Wani, O.M.; Wasylczyk, P.; Priimagi, A. Light-Driven, Caterpillar-Inspired Miniature Inching Robot. Macromol. Rapid Commun. 2018, 39, 1700224. [Google Scholar] [CrossRef]
- Boothby, J.M.; Kim, H.; Ware, T.H. Shape Changes in Chemoresponsive Liquid Crystal Elastomers. Sens. Actuators B Chem. 2017, 240, 511–518. [Google Scholar] [CrossRef]
- Mistry, D.; Nikkhou, M.; Raistrick, T.; Hussain, M.; Jull, E.I.L.; Gleeson, H.F. Isotropic Liquid Crystal Elastomers as Exceptional Photoelastic Strain Sensors. Macromolecules 2020, 53, 3709–3718. [Google Scholar] [CrossRef]
- Kundler, I.; Finkelmann, H. Strain-Induced Director Reorientation in Nematic Liquid Single Crystal Elastomers. Macromol. Rapid Commun. 1995, 16, 679–686. [Google Scholar] [CrossRef]
- Hussain, M.; Jull, E.I.L.; Mandle, R.J.; Raistrick, T.; Hine, P.J.; Gleeson, H.F. Liquid Crystal Elastomers for Biological Applications. Nanomaterials 2021, 11, 813. [Google Scholar] [CrossRef] [PubMed]
- Merkel, D.R.; Traugutt, N.A.; Visvanathan, R.; Yakacki, C.M.; Frick, C.P. Thermomechanical Properties of Monodomain Nematic Main-Chain Liquid Crystal Elastomers. Soft Matter 2018, 14, 6024–6036. [Google Scholar] [CrossRef]
- Yin, H.; Chapala, P.; Bermeshev, M.; Schönhals, A.; Böhning, M. Molecular Mobility and Physical Aging of a Highly Permeable Glassy Polynorbornene as Revealed by Dielectric Spectroscopy. ACS Macro Lett. 2017, 6, 813–818. [Google Scholar] [CrossRef]
- Lee, H.; Fragiadakis, D.; Martin, D.; Milne, A.; Milne, J.; Runt, J. Dynamics of Uniaxially Oriented Elastomers Using Broadband Dielectric Spectroscopy. Macromolecules 2010, 43, 3125–3127. [Google Scholar] [CrossRef] [Green Version]
- Riggleman, R.A.; Lee, H.-N.; Ediger, M.D.; Pablo, J.J. de Heterogeneous Dynamics during Deformation of a Polymer Glass. Soft Matter 2010, 6, 287–291. [Google Scholar] [CrossRef]
- Lee, H.-N.; Paeng, K.; Swallen, S.F.; Ediger, M.D.; Stamm, R.A.; Medvedev, G.A.; Caruthers, J.M. Molecular Mobility of Poly(Methyl Methacrylate) Glass during Uniaxial Tensile Creep Deformation. J. Polym. Sci. Part B Polym. Phys. 2009, 47. [Google Scholar] [CrossRef]
- Bending, B.; Christison, K.; Ricci, J.; Ediger, M.D. Measurement of Segmental Mobility during Constant Strain Rate Deformation of a Poly(Methyl Methacrylate) Glass. Macromolecules 2014, 47, 800–806. [Google Scholar] [CrossRef] [Green Version]
- Ratner, M.A.; Johansson, P.; Shriver, D.F. Polymer Electrolytes: Ionic Transport Mechanisms and Relaxation Coupling. MRS Bull. 2000, 25, 31–37. [Google Scholar] [CrossRef]
- Mistry, D.; Gleeson, H.F. Mechanical Deformations of a Liquid Crystal Elastomer at Director Angles between 0° and 90°: Deducing an Empirical Model Encompassing Anisotropic Nonlinearity. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 1367–1377. [Google Scholar] [CrossRef] [Green Version]
- Drozd-Rzoska, A. Heterogeneity-Related Dynamics in Isotropic n-Pentylcyanobiphenyl. Phys. Rev. E 2006, 73, 022501. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A. Glassy Dynamics of Liquid Crystalline 4′-n-Pentyl-4-Cyanobiphenyl in the Isotropic and Supercooled Nematic Phases. J. Chem. Phys. 2009, 130, 234910. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Paluch, M.; Pawlus, S.; Zioło, J.; Santangelo, P.G.; Roland, C.M.; Czupryński, K.; Dąbrowski, R. Mode Coupling Behavior in Glass-Forming Liquid Crystalline Isopentylcyanobiphenyl. Phys. Rev. E 2005, 71, 011508. [Google Scholar] [CrossRef] [Green Version]
- Mistry, D.; Connell, S.D.; Mickthwaite, S.L.; Morgan, P.B.; Clamp, J.H.; Gleeson, H.F. Coincident Molecular Auxeticity and Negative Order Parameter in a Liquid Crystal Elastomer. Nat. Commun. 2018, 9, 5095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raistrick, T.; Zhang, Z.; Mistry, D.; Mattsson, J.; Gleeson, H.F. Understanding the Physics of the Auxetic Response in a Liquid Crystal Elastomer. Phys. Rev. Res. 2021, 3, 023191. [Google Scholar] [CrossRef]
- Mistry, D.; Morgan, P.B.; Clamp, J.H.; Gleeson, H.F. New Insights into the Nature of Semi-Soft Elasticity and “Mechanical-Fréedericksz Transitions” in Liquid Crystal Elastomers. Soft Matter 2018, 14, 1301–1310. [Google Scholar] [CrossRef] [Green Version]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled Liquids and the Glass Transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef]
- Kremer, F.; Schönhals, A. (Eds.) Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-642-62809-2. [Google Scholar]
- Roland, C.M. Relaxation Phenomena in Vitrifying Polymers and Molecular Liquids. Macromolecules 2010, 43, 7875–7890. [Google Scholar] [CrossRef]
- Casalini, R.; Roland, C.M.; Capaccioli, S. Effect of Chain Length on Fragility and Thermodynamic Scaling of the Local Segmental Dynamics in Poly(Methylmethacrylate). J. Chem. Phys. 2007, 126, 184903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ngai, K.L.; Lunkenheimer, P. Nature and Properties of the Johari–Goldstein β-Relaxation in the Equilibrium Liquid State of a Class of Glass-Formers. J. Chem. Phys. 2001, 115, 9. [Google Scholar] [CrossRef] [Green Version]
- Ngai, K.; Capaccioli, S. Relation between the Activation Energy of the Johari-Goldstein β Relaxation and Tg of Glass Formers. Phys. Rev. E 2004, 69, 031501. [Google Scholar] [CrossRef] [PubMed]
- Kudlik, A.; Tschirwitz, C.; Benkhof, S.; Blochowicz, T.; Rössler, E. Slow Secondary Relaxation Process in Supercooled Liquids. EPL 1997, 40, 649. [Google Scholar] [CrossRef]
- Paluch, M.; Roland, C.M.; Pawlus, S.; Zioło, J.; Ngai, K.L. Does the Arrhenius Temperature Dependence of the Johari-Goldstein Relaxation Persist above Tg? Phys. Rev. Lett. 2003, 91, 115701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.-M.; Angell, C.A.; Richert, R. Fragility and Thermodynamics in Nonpolymeric Glass-Forming Liquids. J. Chem. Phys. 2006, 125, 074505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novikov, V.N.; Sokolov, A.P. Universality of the Dynamic Crossover in Glass-Forming Liquids: A “Magic” Relaxation Time. Phys. Rev. E 2003, 67, 031507. [Google Scholar] [CrossRef] [PubMed]
- Stickel, F.; Fischer, E.W.; Richert, R. Dynamics of Glass-forming Liquids. II. Detailed Comparison of Dielectric Relaxation, Dc-conductivity, and Viscosity Data. J. Chem. Phys. 1996, 104, 2043–2055. [Google Scholar] [CrossRef]
- Goldstein, M. Viscous Liquids and the Glass Transition: A Potential Energy Barrier Picture. J. Chem. Phys. 1969, 51, 3728–3739. [Google Scholar] [CrossRef] [Green Version]
- Baker, D.L.; Reynolds, M.; Masurel, R.; Olmsted, P.D.; Mattsson, J. Chain-Length, Flexibility and the Glass Transition of Polymers. arXiv 2019, arXiv:1911.13278. [Google Scholar]
- Colmenero, J. Are Polymers Standard Glass-Forming Systems? The Role of Intramolecular Barriers on the Glass-Transition Phenomena of Glass-Forming Polymers. J. Phys. Condens. Matter 2015, 27, 103101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mattsson, J.; Bergman, R.; Jacobsson, P.; Börjesson, L. Chain-Length-Dependent Relaxation Scenarios in an Oligomeric Glass-Forming System: From Merged to Well-Separated α and β Loss Peaks. Phys. Rev. Lett. 2003, 90, 075702. [Google Scholar] [CrossRef]
- Schroeder, M.J.; Roland, C.M. Segmental Relaxation in End-Linked Poly(Dimethylsiloxane) Networks. Macromolecules 2002, 35, 2676–2681. [Google Scholar] [CrossRef] [Green Version]
- Lal, S.; Tripathi, S.K.; Sood, N.; Khosla, S. Study of Dielectric Parameters of Liquid Crystal Elastomer. Liq. Cryst. 2014, 41, 1402–1409. [Google Scholar] [CrossRef]
- Brömmel, F.; Stille, W.; Finkelmann, H.; Hoffmann, A. Molecular Dynamics and Biaxiality of Nematic Polymers and Elastomers. Soft Matter 2011, 7, 2387–2401. [Google Scholar] [CrossRef]
- Shenoy, D.; Filippov, S.; Aliev, F.; Keller, P.; Thomsen, D.; Ratna, B. Vogel-Fulcher Dependence of Relaxation Rates in a Nematic Monomer and Elastomer. Phys. Rev. E 2000, 62, 8100–8105. [Google Scholar] [CrossRef] [PubMed]
- Schönhals, A. Hans-eckartcarius Dielectric Properties of Thermotropic Polymer Liquid Crystals. Int. J. Polym. Mater. 2000, 45, 239–276. [Google Scholar] [CrossRef]
- Zentel, R.; Strobl, G.R.; Ringsdorf, H. Dielectric Relaxation of Liquid Crystalline Polyacrylates and Polymethacrylates. Macromolecules 1985, 18, 960–965. [Google Scholar] [CrossRef]
- Schönhals, A.; Wolff, D.; Springer, J. Temperature Dependence of the Relaxation Rates of α and δ Relaxation in Liquid-Crystalline Side-Group Polymethacrylates. Macromolecules 1998, 31, 9019–9025. [Google Scholar] [CrossRef]
- Salehli, F.; Yildiz, S.; Ozbek, H.; Uykur, E.; Gursel, Y.H.; Durmaz, Y.Y. Peculiarities of δ- and α-Relaxations in Thermotropic Side Chain Liquid Crystalline Polymers with and without Nematic Reentrant Phase. Polymer 2010, 51, 1450–1456. [Google Scholar] [CrossRef]
- Ngai, K.L.; Schönhals, A. Interpretation of the Observed Influence of Mesophase Structures on the β-Relaxation in Side Chain Liquid Crystal Polymers. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 1927–1934. [Google Scholar] [CrossRef]
- Vallerien, S.U.; Kremer, F.; Boeffel, C. Broadband Dielectric Spectroscopy on Side Group Liquid Crystal Polymers. Liq. Cryst. 1989, 4, 79–86. [Google Scholar] [CrossRef]
- Turky, G.; Wolff, D.; Schönhals, A. Confinement Effects on the Molecular Dynamics of Liquid-Crystalline Polymethacrylates—A Broadband Dielectric Spectroscopy Study. Macromol. Chem. Phys. 2012, 213, 2420–2431. [Google Scholar] [CrossRef]
- Verwey, G.C.; Warner, M.; Terentjev, E.M. Elastic Instability and Stripe Domains in Liquid Crystalline Elastomers. J. Phys. II Fr. 1996, 6, 1273–1290. [Google Scholar] [CrossRef]
- Stein, P.; Aßfalg, N.; Finkelmann, H.; Martinoty, P. Shear Modulus of Polydomain, Mono-Domain and Non-Mesomorphic Side-Chain Elastomers: Influence of the Nematic Order. Eur. Phys. J. E 2001, 4, 255–262. [Google Scholar] [CrossRef]
- Rogez, D.; Francius, G.; Finkelmann, H.; Martinoty, P. Shear Mechanical Anisotropy of Side Chain Liquid-Crystal Elastomers: Influence of Sample Preparation. Eur. Phys. J. E 2006, 20, 369–378. [Google Scholar] [CrossRef]
- Weilepp, J.; Zanna, J.J.; Assfalg, N.; Stein, P.; Hilliou, L.; Mauzac, M.; Finkelmann, H.; Brand, H.R.; Martinoty, P. Rheology of Liquid Crystalline Elastomers in Their Isotropic and Smectic A State. Macromolecules 1999, 32, 4566–4574. [Google Scholar] [CrossRef]
- Roberts, P.M.S.; Mitchell, G.R.; Davis, F.J. A Single Director Switching Mode for Monodomain Liquid Crystal Elastomers. J. Phys. II Fr. 1997, 7, 1337–1351. [Google Scholar] [CrossRef]
- Bladon, P.; Warner, M.; Terentjev, E.M. Orientational Order in Strained Nematic Networks. Macromolecules 1994, 27, 7067–7075. [Google Scholar] [CrossRef]
- Wübbenhorst, M.; van Turnhout, J. Analysis of Complex Dielectric Spectra. I. One-Dimensional Derivative Techniques and Three-Dimensional Modelling. J. Non-Cryst. Solids 2002, 305, 40–49. [Google Scholar] [CrossRef]
- Gedde, U.W.; Liu, F.; Hult, A.; Sahlén, F.; Boyd, R.H. Dielectric Relaxation of Liquid Crystalline Side-Chain Poly(Vinyl Ether)s. Polymer 1994, 35, 2056–2062. [Google Scholar] [CrossRef]
- Martínez-Felipe, A.; Santonja-Blasco, L.; Badia, J.D.; Imrie, C.T.; Ribes-Greus, A. Characterization of Functionalized Side-Chain Liquid Crystal Methacrylates Containing Nonmesogenic Units by Dielectric Spectroscopy. Ind. Eng. Chem. Res. 2013, 52, 8722–8731. [Google Scholar] [CrossRef]
- Stickel, F.; Fischer, E.W.; Richert, R. Dynamics of Glass-forming Liquids. I. Temperature-derivative Analysis of Dielectric Relaxation Data. J. Chem. Phys. 1995, 102, 6251–6257. [Google Scholar] [CrossRef]
- Schick, C.; Sukhorukov, D.; Schönhals, A. Comparison of the Molecular Dynamics of a Liquid Crystalline Side Group Polymer Revealed from Temperature Modulated DSC and Dielectric Experiments in the Glass Transition Region. Macromol. Chem. Phys. 2001, 202, 1398–1404. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, W.; Gao, Y.; Zhang, C.; Yang, H. Polysiloxane-Based Side Chain Liquid Crystal Polymers: From Synthesis to Structure–Phase Transition Behavior Relationships. Polymers 2018, 10, 794. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Fan, F.; Agapov, A.L.; Yu, X.; Hong, K.; Mays, J.; Sokolov, A.P. Design of Superionic Polymers—New Insights from Walden Plot Analysis. Solid State Ion. 2014, 262, 782–784. [Google Scholar] [CrossRef]
- Agapov, A.L.; Sokolov, A.P. Decoupling Ionic Conductivity from Structural Relaxation: A Way to Solid Polymer Electrolytes? Macromolecules 2011, 44, 4410–4414. [Google Scholar] [CrossRef]
- Bocharova, V.; Sokolov, A.P. Perspectives for Polymer Electrolytes: A View from Fundamentals of Ionic Conductivity. Macromolecules 2020, 53, 4141–4157. [Google Scholar] [CrossRef]
- Funahashi, M.; Shimura, H.; Yoshio, M.; Kato, T. Functional Liquid-Crystalline Polymers for Ionic and Electronic Conduction. In Liquid Crystalline Functional Assemblies and Their Supramolecular Structures; Kato, T., Ed.; Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2008; pp. 151–179. ISBN 978-3-540-77867-7. [Google Scholar]
- Kishimoto, K.; Suzawa, T.; Yokota, T.; Mukai, T.; Ohno, H.; Kato, T. Nano-Segregated Polymeric Film Exhibiting High Ionic Conductivities. J. Am. Chem. Soc. 2005, 127, 15618–15623. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Rajapaksha, C.P.H.; Cedillo, J.M.; Piedrahita, C.; Cao, J.; Kaphle, V.; Lüssem, B.; Kyu, T.; Jákli, A. Electroresponsive Ionic Liquid Crystal Elastomers. Macromol. Rapid Commun. 2019, 40, 1900299. [Google Scholar] [CrossRef] [PubMed]
- Chambers, M.; Zalar, B.; Remškar, M.; Kovač, J.; Finkelmann, H.; Žumer, S. Investigations on an Integrated Conducting Nanoparticle–Liquid Crystal Elastomer Layer. Nanotechnology 2007, 18, 415706. [Google Scholar] [CrossRef]
- Wang, Y.; Agapov, A.L.; Fan, F.; Hong, K.; Yu, X.; Mays, J.; Sokolov, A.P. Decoupling of Ionic Transport from Segmental Relaxation in Polymer Electrolytes. Phys. Rev. Lett. 2012, 108, 088303. [Google Scholar] [CrossRef]
- Do, C.; Lunkenheimer, P.; Diddens, D.; Götz, M.; Weiß, M.; Loidl, A.; Sun, X.-G.; Allgaier, J.; Ohl, M. Li+ Transport in Poly(Ethylene Oxide) Based Electrolytes: Neutron Scattering, Dielectric Spectroscopy, and Molecular Dynamics Simulations. Phys. Rev. Lett. 2013, 111, 018301. [Google Scholar] [CrossRef] [Green Version]
- Golodnitsky, D.; Strauss, E.; Peled, E.; Greenbaum, S. Review—On Order and Disorder in Polymer Electrolytes. J. Electrochem. Soc. 2015, 162, A2551. [Google Scholar] [CrossRef]
- Dyre, J.C. Colloquium: The Glass Transition and Elastic Models of Glass-Forming Liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef] [Green Version]
- Price, H.C.; Mattsson, J.; Murray, B.J. Sucrose Diffusion in Aqueous Solution. Phys. Chem. Chem. Phys. 2016, 18, 19207–19216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollack, G.L. Atomic Test of the Stokes-Einstein Law: Diffusion and Solubility of Xe. Phys. Rev. A 1981, 23, 2660–2663. [Google Scholar] [CrossRef]
- Ediger, M.D.; Harrowell, P.; Yu, L. Crystal Growth Kinetics Exhibit a Fragility-Dependent Decoupling from Viscosity. J. Chem. Phys. 2008, 128, 034709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ediger, M.D. Can Density or Entropy Fluctuations Explain Enhanced Translational Diffusion in Glass-Forming Liquids? J. Non-Cryst. Solids 1998, 235–237, 10–18. [Google Scholar] [CrossRef]
- Ediger, M.D.; Angell, C.A.; Nagel, S.R. Supercooled Liquids and Glasses. J. Phys. Chem. 1996, 100, 13200–13212. [Google Scholar] [CrossRef]
- Yu, H.B.; Wang, W.H.; Bai, H.Y.; Samwer, K. The β-Relaxation in Metallic Glasses. Natl. Sci. Rev. 2014, 1, 429–461. [Google Scholar] [CrossRef] [Green Version]
- Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.J.; Kralj, S. Nanoparticle-Controlled Glassy Dynamics in Nematogen-Based Nanocolloids. Phys. Rev. E 2019, 99, 052703. [Google Scholar] [CrossRef] [PubMed]
- Andreev, Y.G.; Bruce, P.G. Polymer Electrolyte Structure and Its Implications. Electrochim. Acta 2000, 45, 1417–1423. [Google Scholar] [CrossRef]
- Zanna, J.J.; Stein, P.; Marty, J.D.; Mauzac, M.; Martinoty, P. Influence of Molecular Parameters on the Elastic and Viscoelastic Properties of Side-Chain Liquid Crystalline Elastomers. Macromolecules 2002, 35, 5459–5465. [Google Scholar] [CrossRef]
- van Gurp, M.; Palmen, J. Time-Temperature Superposition for Polymeric Blends. Rheol. Bull. 1998, 67, 5–8. [Google Scholar]
- Ren, W.; McMullan, P.J.; Griffin, A.C. Stress–Strain Behavior in Main Chain Liquid Crystalline Elastomers: Effect of Crosslinking Density and Transverse Rod Incorporation on “Poisson’s Ratio”. Phys. Status Solidi 2009, 246, 2124–2130. [Google Scholar] [CrossRef]
- Ren, W.; McMullan, P.J.; Griffin, A.C. Poisson’s Ratio of Monodomain Liquid Crystalline Elastomers. Macromol. Chem. Phys. 2008, 209, 1896–1899. [Google Scholar] [CrossRef]
- Vandoolaeghe, W.L.; Terentjev, E.M. Constrained Rouse Model of Rubber Viscoelasticity. J. Chem. Phys. 2005, 123, 034902. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R. (Eds.) Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Gallani, J.L.; Hilliou, L.; Martinoty, P.; Doublet, F.; Mauzac, M. Mechanical Behavior of Side-Chain Liquid Crystalline Networks. J. Phys. II 1996, 6, 443–452. [Google Scholar] [CrossRef]
- Urayama, K.; Yokoyama, K.; Kohjiya, S. Viscoelastic Relaxation of Guest Linear Poly(Dimethylsiloxane) in End-Linked Poly(Dimethylsiloxane) Networks. Macromolecules 2001, 34, 4513–4518. [Google Scholar] [CrossRef]
- Yamazaki, H.; Takeda, M.; Kohno, Y.; Ando, H.; Urayama, K.; Takigawa, T. Dynamic Viscoelasticity of Poly(Butyl Acrylate) Elastomers Containing Dangling Chains with Controlled Lengths. Macromolecules 2011, 44, 8829–8834. [Google Scholar] [CrossRef]
- Agudelo, D.C.; Roth, L.E.; Vega, D.A.; Vallés, E.M.; Villar, M.A. Dynamic Response of Transiently Trapped Entanglements in Polymer Networks. Polymer 2014, 55, 1061–1069. [Google Scholar] [CrossRef]
- Jakobsen, B.; Niss, K.; Maggi, C.; Olsen, N.B.; Christensen, T.; Dyre, J.C. Beta Relaxation in the Shear Mechanics of Viscous Liquids: Phenomenology and Network Modeling of the Alpha-Beta Merging Region. J. Non-Cryst. Solids 2011, 357, 267–273. [Google Scholar] [CrossRef] [Green Version]
- Dalle-Ferrier, C.; Thibierge, C.; Alba-Simionesco, C.; Berthier, L.; Biroli, G.; Bouchaud, J.-P.; Ladieu, F.; L’Hôte, D.; Tarjus, G. Spatial Correlations in the Dynamics of Glassforming Liquids: Experimental Determination of Their Temperature Dependence. Phys. Rev. E 2007, 76, 041510. [Google Scholar] [CrossRef] [Green Version]
- Tracht, U.; Wilhelm, M.; Heuer, A.; Feng, H.; Schmidt-Rohr, K.; Spiess, H.W. Length Scale of Dynamic Heterogeneities at the Glass Transition Determined by Multidimensional Nuclear Magnetic Resonance. Phys. Rev. Lett. 1998, 81, 2727–2730. [Google Scholar] [CrossRef]
- Donth, E. The Size of Cooperatively Rearranging Regions at the Glass Transition. J. Non-Cryst. Solids 1982, 53, 325–330. [Google Scholar] [CrossRef]
- Stevenson, J.D.; Schmalian, J.; Wolynes, P.G. The Shapes of Cooperatively Rearranging Regions in Glass-Forming Liquids. Nat. Phys. 2006, 2, 268–274. [Google Scholar] [CrossRef] [Green Version]
- Hempel, E.; Hempel, G.; Hensel, A.; Schick, C.; Donth, E. Characteristic Length of Dynamic Glass Transition near Tg for a Wide Assortment of Glass-Forming Substances. J. Phys. Chem. B 2000, 104, 2460–2466. [Google Scholar] [CrossRef]
- Berthier, L. Direct Experimental Evidence of a Growing Length Scale Accompanying the Glass Transition. Science 2005, 310, 1797–1800. [Google Scholar] [CrossRef] [Green Version]
- Capaccioli, S.; Ruocco, G.; Zamponi, F. Dynamically Correlated Regions and Configurational Entropy in Supercooled Liquids. J. Phys. Chem. B 2008, 112, 10652–10658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krich, J.J.; Romanowsky, M.B.; Collings, P.J. Correlation Length and Chirality of the Fluctuations in the Isotropic Phase of Nematic and Cholesteric Liquid Crystals. Phys. Rev. E 2005, 71, 051712. [Google Scholar] [CrossRef] [Green Version]
- Brand, H.R.; Kawasaki, K. On the Macroscopic Consequences of Frozen Order in Liquid Single Crystal Elastomers. Macromol. Rapid Commun. 1994, 15, 251–257. [Google Scholar] [CrossRef]
- Petridis, L.; Terentjev, E.M. Nematic-Isotropic Transition with Quenched Disorder. Phys. Rev. E 2006, 74, 051707. [Google Scholar] [CrossRef] [Green Version]
- Rzoska, S.J.; Drozd-Rzoska, A.; Mukherjee, P.K.; Lopez, D.O.; Martinez-Garcia, J.C. Distortion-Sensitive Insight into the Pretransitional Behavior of 4-n-Octyloxy-4′-Cyanobiphenyl (8OCB). J. Phys. Condens. Matter 2013, 25, 245105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rzoska, S.J.; Starzonek, S.; Łoś, J.; Drozd-Rzoska, A.; Kralj, S. Dynamics and Pretransitional Effects in C60 Fullerene Nanoparticles and Liquid Crystalline Dodecylcyanobiphenyl (12CB) Hybrid System. Nanomaterials 2020, 10, 2343. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Hay, J.L.; Swindeman, J.E.; Oliver, W.C. Continuous Dynamic Analysis: Evolution of Elastic Properties with Strain. MRS Commun. 2014, 4, 25–29. [Google Scholar] [CrossRef]
- Lv, Z.; Ren, J.; Lin, S.; Pei, Y.; Shao, Z.; Ling, S. Understanding the Continuous Dynamic Mechanical Behavior of Animal Silk. Macromolecules 2021, 54, 249–258. [Google Scholar] [CrossRef]
- Meinecke, E.A. Dynamisches Verhalten von Elastomeren bei großen Dehnungen überlagerten kleinen Schwingungen. Rheol. Acta 1971, 10, 302–309. [Google Scholar] [CrossRef]
- Suphadon, N.; Thomas, A.G.; Busfield, J.J.C. Viscoelastic Behavior of Rubber under a Complex Loading. J. Appl. Polym. Sci. 2009, 113, 693–699. [Google Scholar] [CrossRef]
- Mason, P. The Viscoelastic Behavior of Rubber in Extension. J. Appl. Polym. Sci. 1959, 1, 63–69. [Google Scholar] [CrossRef]
- Choi, T.; Fragiadakis, D.; Roland, C.M.; Runt, J. Microstructure and Segmental Dynamics of Polyurea under Uniaxial Deformation. Macromolecules 2012, 45, 3581–3589. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.-N.; Paeng, K.; Swallen, S.F.; Ediger, M.D. Direct Measurement of Molecular Mobility in Actively Deformed Polymer Glasses. Science 2009, 323, 231–234. [Google Scholar] [CrossRef] [Green Version]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Roland, C.M.; Hensel-Bielowka, S.; Paluch, M.; Casalini, R. Supercooled Dynamics of Glass-Forming Liquids and Polymers under Hydrostatic Pressure. Rep. Prog. Phys. 2005, 68, 1405–1478. [Google Scholar] [CrossRef] [Green Version]
- Havriliak, S.; Havriliak, S.J. Results from an Unbiased Analysis of Nearly 1000 Sets of Relaxation Data. J. Non-Cryst. Solids 1994, 172–174, 297–310. [Google Scholar] [CrossRef]
- Plazek, D.J. 1995 Bingham Medal Address: Oh, Thermorheological Simplicity, Wherefore Art Thou? J. Rheol. 1996, 40, 987–1014. [Google Scholar] [CrossRef]



| Sample | Process | |||||
|---|---|---|---|---|---|---|
| Isotropic | - | 5.0 | 243 | 286 | ||
| - | - | - | ||||
| - | - | - | ||||
| Nematic | - | 5.6 | 243 | 285 | ||
| - | - | - | ||||
| - | - | - |
| Sample | ||||||
|---|---|---|---|---|---|---|
| Isotropic | - | 16.6 | 183 | 270 | ||
| - | 5.4 | 241 | 286 | |||
| Nematic | - | 17.2 | 193 | 275 | ||
| 151.0 | - | - | - | |||
| - | 5.1 | 245 | 285 |
| 8.3 | 227 | 276 |
| Chemical Name | Mol% of Monomer Mixture |
| A6OCB | 14.6 |
| RM82 | 7.1 |
| 6OCB | 55.9 |
| EHA | 20.9 |
| MBF | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raistrick, T.; Reynolds, M.; Gleeson, H.F.; Mattsson, J. Influence of Liquid Crystallinity and Mechanical Deformation on the Molecular Relaxations of an Auxetic Liquid Crystal Elastomer. Molecules 2021, 26, 7313. https://doi.org/10.3390/molecules26237313
Raistrick T, Reynolds M, Gleeson HF, Mattsson J. Influence of Liquid Crystallinity and Mechanical Deformation on the Molecular Relaxations of an Auxetic Liquid Crystal Elastomer. Molecules. 2021; 26(23):7313. https://doi.org/10.3390/molecules26237313
Chicago/Turabian StyleRaistrick, Thomas, Matthew Reynolds, Helen F. Gleeson, and Johan Mattsson. 2021. "Influence of Liquid Crystallinity and Mechanical Deformation on the Molecular Relaxations of an Auxetic Liquid Crystal Elastomer" Molecules 26, no. 23: 7313. https://doi.org/10.3390/molecules26237313