Characterization of Nano-Scale Parallel Lamellar Defects in RDX and HMX Single Crystals by Two-Dimension Small Angle X-ray Scattering
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Single Crystals
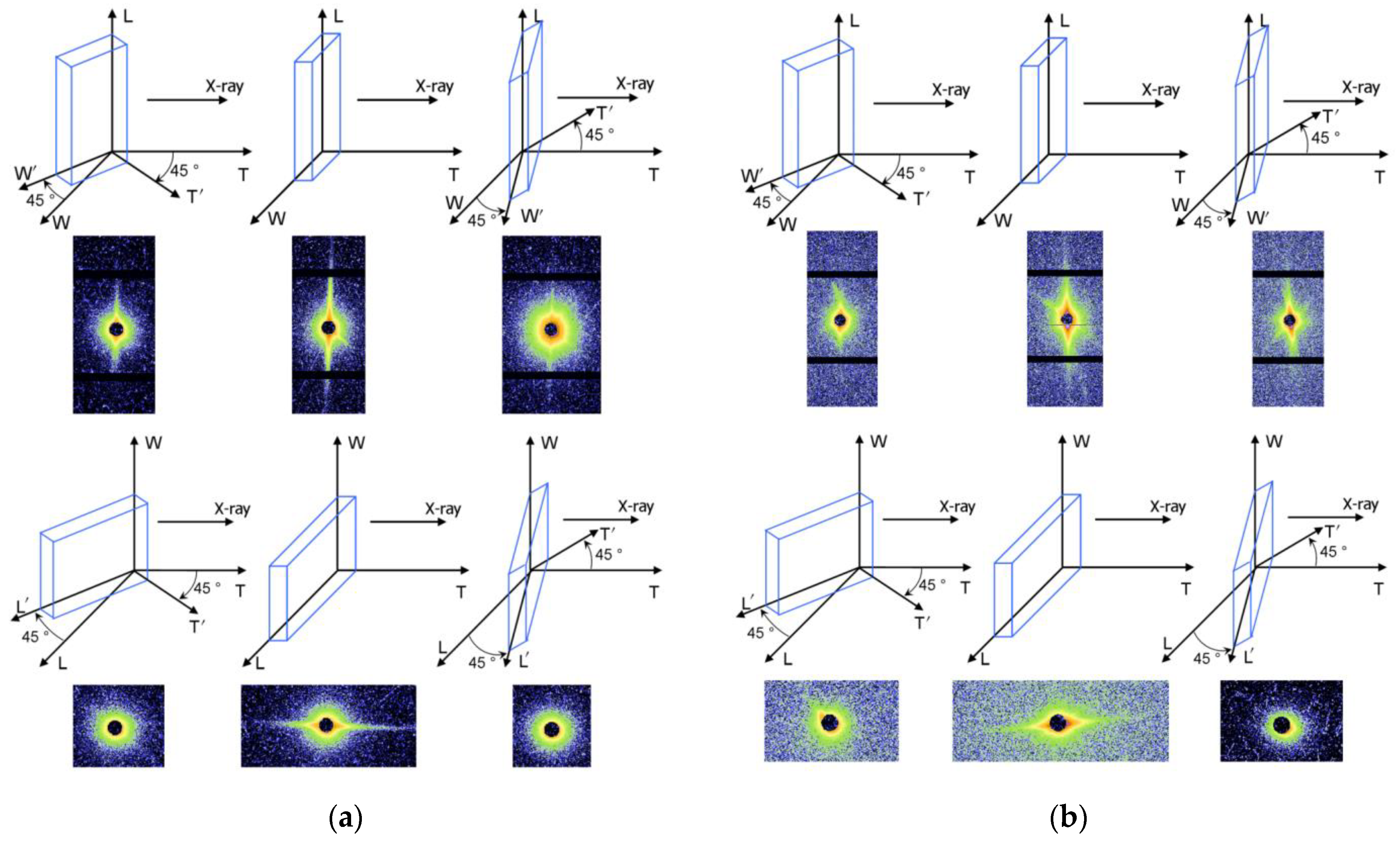
2.2. Characterization Methods
2.3. Theoretic Calculation
3. Results and Discussion
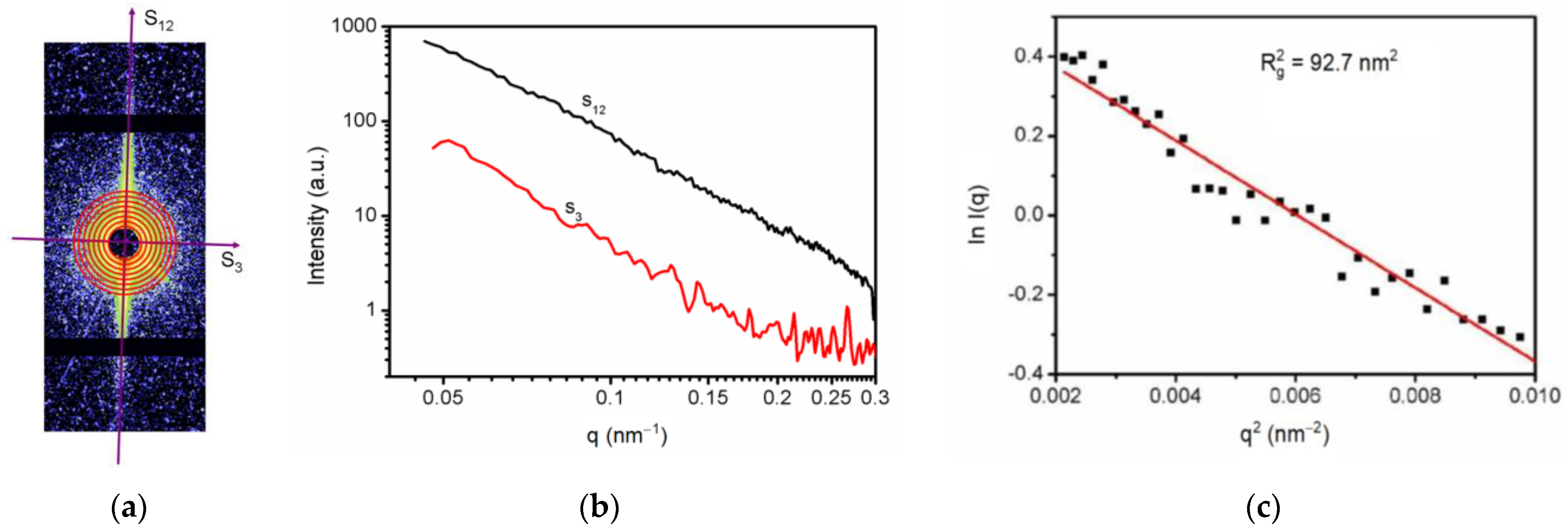
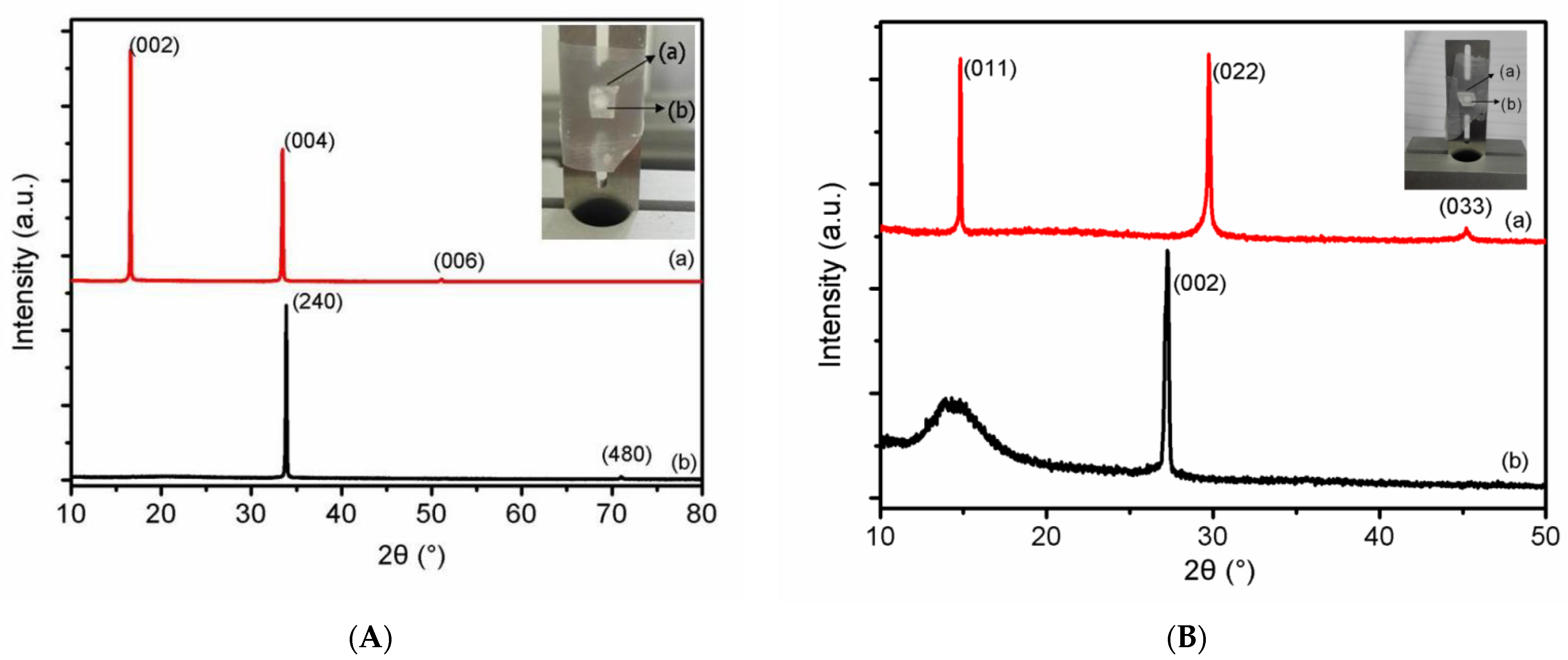
3.1. Nano-Scale Defect Structure of RDX and HMX Single Crystal
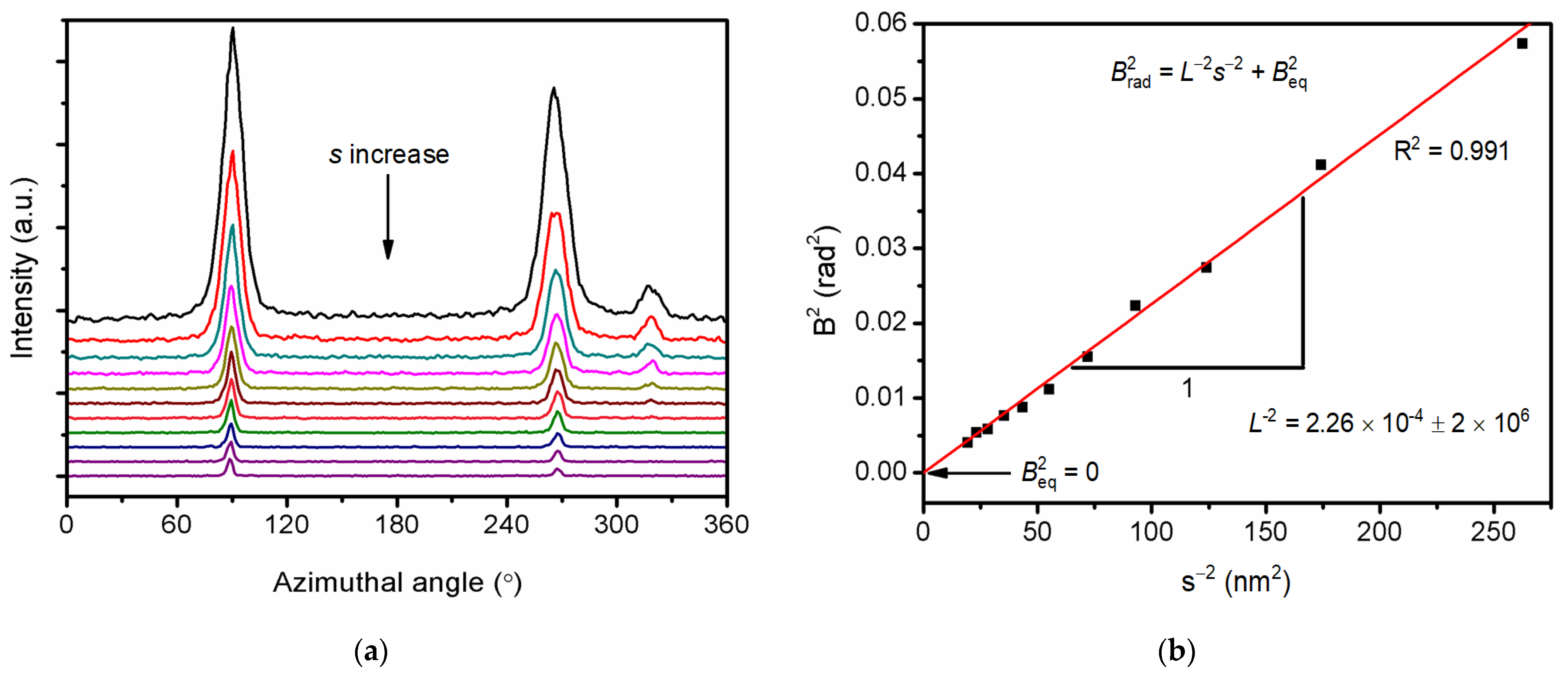
3.2. Orientation of the Nano-Scale Lamellar Defects
3.3. Mechanism of the Nano-Scale Defects Orientation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Badgujar, D.M.; Talawar, M.B.; Asthana, S.N.; Mahulikar, P.P. Advances in science and technology of modern energetic materials: An overview. J. Hazard. Mater. 2008, 151, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Larin, A.A.; Fershtat, L.L. High-energy hydroxytetrazoles: Design, synthesis and performance. Energetic Mater. Front. 2021, 2, 3–13. [Google Scholar] [CrossRef]
- Talawar, M.B.; Sivabalan, R.; Mukundan, T.; Muthurajan, H.; Sikder, A.K.; Gandhe, B.R.; Rao, A.S. Environmentally compatible next generation green energetic materials (GEMs). J. Hazard. Mater. 2009, 161, 589–607. [Google Scholar] [CrossRef]
- Huang, X.; Qiao, Z.; Dai, X.; Zhang, K.; Li, M.; Pei, G.; Wen, Y. Effects of different types of defects on ignition mechanisms in shocked p-cyclotetramethylene tetranitramine crystals: A molecular dynamics study based on ReaxFF-Ig force field. J. Appl. Phys. 2019, 125, 195101. [Google Scholar] [CrossRef]
- Yan, F.; Zhu, P.; Zhao, S.; Shi, J.; Mu, Y.; Xia, H.; Shen, R. Microfluidic strategy for coating and modification of polymer-bonded nano-HNS explosives. Chem. Eng. J. 2022, 428, 131096. [Google Scholar] [CrossRef]
- Bellitto, V.J.; Melnik, M.I.; Sorensen, D.N.; Chang, J.C. Predicting the shock sensitivity of cyclotrimethylene-trinitramine. J. Therm. Anal. Calorim. 2010, 102, 557–562. [Google Scholar] [CrossRef]
- Zong, H.; Xiao, L.; Hao, Y.; Gao, X.; Wang, W.; Yang, Y.; Liu, Q.; Hao, G.; Jiang, W. The effect of micro-nano TKX-50 particle gradation on the properties of TNT based castable explosives. J. Energetic Mater. 2021, in press. [Google Scholar] [CrossRef]
- Tan, K.-Y.; Liu, R.-Q.; Deng, C.; Guo, F.; Huang, X.-N.; Han, Y.; Wen, Y.-S.; Dai, X.-G.; Huang, F.-L.; Li, M. Impacts of defect distribution on the ignition of crystalline explosives: An insight from the overlapping effect. Energetic Mater. Front. 2022, in press. [Google Scholar] [CrossRef]
- Zaug, J.M.; Austin, R.A.; Armstrong, M.R.; Crowhurst, J.C.; Goldman, N.; Ferranti, L.; Saw, C.K.; Swan, R.A.; Gross, R.; Fried, L.E. Ultrafast dynamic response of single-crystal β-HMX (octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine). J. Appl. Phys. 2018, 123, 205902. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Huang, X.; Suo, T.; Li, Y. Numerical modeling of crack growth in polymer-bonded explosive with cavity subject to compression. Adv. Mech. Eng. 2019, 11, 1687814019856954. [Google Scholar] [CrossRef]
- Nesterov, E.; Bobrov, D. Research of cracking in case of explosion on outburst-hazardous dolomite rocks. In Engineering and Mining Geophysics 2020; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, W.B.; Huang, H.; Tian, Y.; Dai, B. Characterization of RDX-Based Thermosetting Plastic-Bonded Explosive by Cone-Beam Microfocus Computed Tomography. J. Energetic Mater. 2012, 30, 196–208. [Google Scholar] [CrossRef]
- Shang, H.L.; Xiao, M.A.; Cheng, F.; Tao, L.I.; Hua, F.U. Coupling Properties of Crack Penetration Driven by Explosive Burning Products. Chin. J. Energetic Mater. 2019, 27, 819–823. [Google Scholar]
- Duarte, C.A.; Kohler, R.; Koslowski, M. Dynamic fracture and frictional heating due to periodic excitation in energetic materials. J. Appl. Phys. 2018, 124, 165109. [Google Scholar] [CrossRef]
- Berghout, H.L.; Son, S.F.; Skidmore, C.B.; Idar, D.J.; Asay, B.W. Combustion of damaged PBX 9501 explosive. Thermochim. Acta 2002, 384, 261–277. [Google Scholar] [CrossRef]
- Stepanov, V.; Willey, T.M.; Ilavsky, J.; Gelb, J.; Qiu, H. Structural Characterization of RDX-Based Explosive Nanocomposites. Propellants Explos. Pyrotech. 2013, 38, 386–393. [Google Scholar] [CrossRef]
- Trevor, M.W.; Mark, H.D.; Tony, V.B.; Lisa, L.; Richard, H.G.; Amitesh, M.; George, E.O.; Laurence, E.F.; Jan, I. The Microstructure of TATB-Based Explosive Formulations During Temperature Cycling Using Ultra-Small-Angle X-Ray Scattering. Propellants Explos. Pyrotech. 2010, 34, 406–414. [Google Scholar]
- Yan, G.Y.; Tian, Q.; Liu, J.H. Small-angle X-ray analysis of the effect of grain size on the thermal damage of octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7 tetrazocine-based plastic-bounded expolsives. Chin. Phys. B 2014, 23, 560–564. [Google Scholar] [CrossRef]
- Yan, G.Y.; Tian, Q.; Huang, C.Q.; Gu, X.M.; Sun, G.A.; Bo, C.; Ming, H.; Nie, F.D.; Yi, L.; Li, X.H. A small-angle X-ray scattering study of micro-defects in thermally treated HMX. Acta Phys. Sin. 2012, 61, 331–337. [Google Scholar]
- Mang, J.; Hjelm, R.; Francois, E. Measurement of Porosity in a Composite High Explosive as a Function of Pressing Conditions by Ultra-Small-Angle Neutron Scattering with Contrast Variation. Propellants Explos. Pyrotech. 2010, 35, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Mang, J.T.; Hjelm, R.P. Small-Angle Neutron Scattering and Contrast Variation Measurement of the Interfacial Surface Area in PBX 9501 as a Function of Pressing Intensity. Propellants Explos. Pyrotech. 2011, 36, 439–445. [Google Scholar] [CrossRef]
- Mang, J.T.; Hjelm, R.P. Fractal Networks of Inter-Granular Voids in Pressed TATB. Propellants Explos. Pyrotech. 2013, 38, 831–840. [Google Scholar] [CrossRef]
- Peterson, P.D.; Mang, J.T.; Asay, B.W. Quantitative analysis of damage in an octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazonic-based composite explosive subjected to a linear thermal gradient. J. Appl. Phys. 2005, 97, 261–1068. [Google Scholar] [CrossRef]
- Willey, T.M.; Lauderbach, L.; Gagliardi, F.; van Buuren, T.; Glascoe, E.A.; Tringe, J.W.; Lee, J.R.I.; Springer, H.K.; Ilavsky, J. Mesoscale evolution of voids and microstructural changes in HMX-based explosives during heating through the beta-delta phase transition. J. Appl. Phys. 2015, 118, 055901–055906. [Google Scholar] [CrossRef]
- Stoltz, C.A.; Mason, B.P.; Hooper, J. Neutron scattering study of internal void structure in RDX. J. Appl. Phys. 2010, 107, 2362. [Google Scholar] [CrossRef]
- Mang, J.T.; Skidmore, C.B.; Hjelm, R.P.; Howe, P.M. Application of small-angle neutron scattering to the study of porosity in energetic materials. J. Mater. Res. 2000, 15, 1199–1208. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Sun, S.; Liu, Y.; Zhu, C.; Li, J.; Sun, J.; Wang, S.; Zhang, H. Characterization of crystal microstructure based on small angle X-ray scattering (SAXS) Technique. Molecules 2020, 25, 443. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Zhang, S.; Liu, Q.; Li, X.; Frost, R.L. The molecular structure of kaolinite–potassium acetate intercalation complexes: A combined experimental and molecular dynamic simulation study. Appl. Clay Sci. 2015, 116–117, 273–280. [Google Scholar] [CrossRef]
- Sun, H.; Ren, P.; Fried, J.R. The COMPASS force field: Parameterization and validation for phosphazenes. Comput. Theor. Polym. Sci. 1998, 8, 229–246. [Google Scholar] [CrossRef]
- Guinier, A.; Fournet, G.; Walker, C.B. Small-Angle Scattering of X-Rays. J. Phys. Today 1956, 9, 38. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.Z.; Liu, X.F.; Yu, X.L.; Zhao, N.; Liu, J.H.; Xu, J. A small-angle X-ray scattering study and molecular dynamics simulation of microvoid evolution during the tensile deformation of carbon fibers. Carbon 2012, 50, 235–243. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Pöselt, E.; Eling, B.; Wang, Z. Melting behavior of polymorphic MDI/BD-block TPU investigated by using in-situ SAXS/WAXS and FTIR techniques. Hydrogen bonding formation causing the inhomogeneous melt. Polym. Test. 2021, 96, 107065. [Google Scholar] [CrossRef]


| Sample | Crystal Face | E (kcal/mol) | E (eV) | ∆E (eV) | A (nm) | B (nm) | Θ (°) | S (nm2) | ∆E/S (eV·nm−2) |
|---|---|---|---|---|---|---|---|---|---|
| RDX | (100) | −101,929.85 | −4428.33 | 54.57 | 4.630 | 4.284 | 90.000 | 19.83 | 2.75 |
| (010) | −102,290.94 | −4444.02 | 38.88 | 4.284 | 5.273 | 90.000 | 22.59 | 1.72 | |
| (001) | −102,367.25 | −4447.33 | 35.56 | 5.273 | 4.630 | 90.000 | 24.41 | 1.46 | |
| (110) | −101,806.89 | −4422.99 | 59.91 | 4.284 | 7.017 | 90.000 | 30.06 | 1.99 | |
| (101) | −101,784.11 | −4422.00 | 60.90 | 6.794 | 4.630 | 90.000 | 31.45 | 1.94 | |
| (011) | −101,940.71 | −4428.80 | 54.09 | 5.273 | 6.307 | 90.000 | 33.26 | 1.63 | |
| (111) | −101,543.49 | −4411.54 | 71.35 | 6.793 | 6.307 | 64.645 | 38.72 | 1.84 | |
| (210) | −101,373.64 | −4404.16 | 78.73 | 4.284 | 10.655 | 90.000 | 45.64 | 1.72 | |
| HMX | (100) | −33,128.81 | −1439.28 | 28.04 | 2.940 | 4.413 | 90.000 | 12.98 | 2.16 |
| (010) | −33,322.18 | −1447.68 | 19.64 | 4.413 | 2.613 | 90.000 | 11.53 | 1.70 | |
| (001) | −33,500.61 | −1455.43 | 11.89 | 2.613 | 2.940 | 77.320 | 7.50 | 1.59 | |
| (110) | −32,957.35 | −1431.83 | 35.49 | 4.413 | 3.479 | 90.000 | 15.35 | 2.31 | |
| (101) | −33,129.62 | −1439.31 | 28.00 | 5.129 | 2.940 | 83.578 | 14.99 | 1.87 | |
| (011) | −33,342.86 | −1448.58 | 18.74 | 2.613 | 5.303 | 83.009 | 13.75 | 1.36 | |
| (1 0) | −32,973.36 | −1432.52 | 34.79 | 4.341 | 4.413 | 90.000 | 19.16 | 1.82 | |
| (111) | −32,901.97 | −1429.42 | 37.89 | 3.479 | 5.129 | 73.248 | 17.08 | 2.22 | |
| (1) | −32,834.41 | −1426.49 | 40.83 | 4.341 | 5.129 | 67.514 | 20.57 | 1.98 | |
| (210) | −32,457.30 | −1410.10 | 57.21 | 4.413 | 5.888 | 90.000 | 25.98 | 2.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, J.; Li, S.; Sun, J.; Wang, X. Characterization of Nano-Scale Parallel Lamellar Defects in RDX and HMX Single Crystals by Two-Dimension Small Angle X-ray Scattering. Molecules 2022, 27, 3871. https://doi.org/10.3390/molecules27123871
Zhang H, Xu J, Li S, Sun J, Wang X. Characterization of Nano-Scale Parallel Lamellar Defects in RDX and HMX Single Crystals by Two-Dimension Small Angle X-ray Scattering. Molecules. 2022; 27(12):3871. https://doi.org/10.3390/molecules27123871
Chicago/Turabian StyleZhang, Haobin, Jinjiang Xu, Shichun Li, Jie Sun, and Xiaolin Wang. 2022. "Characterization of Nano-Scale Parallel Lamellar Defects in RDX and HMX Single Crystals by Two-Dimension Small Angle X-ray Scattering" Molecules 27, no. 12: 3871. https://doi.org/10.3390/molecules27123871
APA StyleZhang, H., Xu, J., Li, S., Sun, J., & Wang, X. (2022). Characterization of Nano-Scale Parallel Lamellar Defects in RDX and HMX Single Crystals by Two-Dimension Small Angle X-ray Scattering. Molecules, 27(12), 3871. https://doi.org/10.3390/molecules27123871






