Analysis of Conformational Preferences in Caffeine
Abstract
:1. Introduction
2. Methods
- Hyperconjugation effects on electronic energies:
- (a)
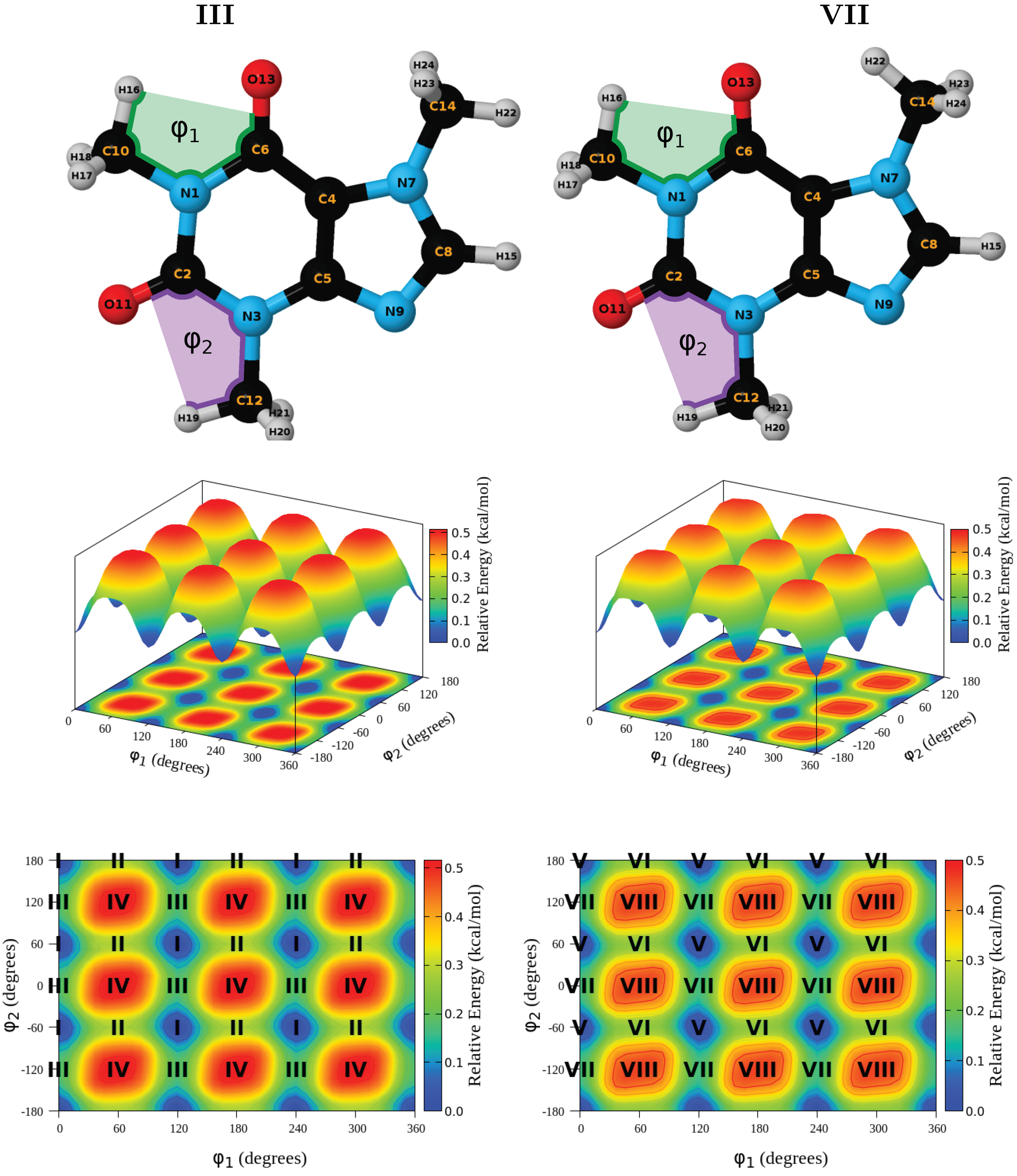
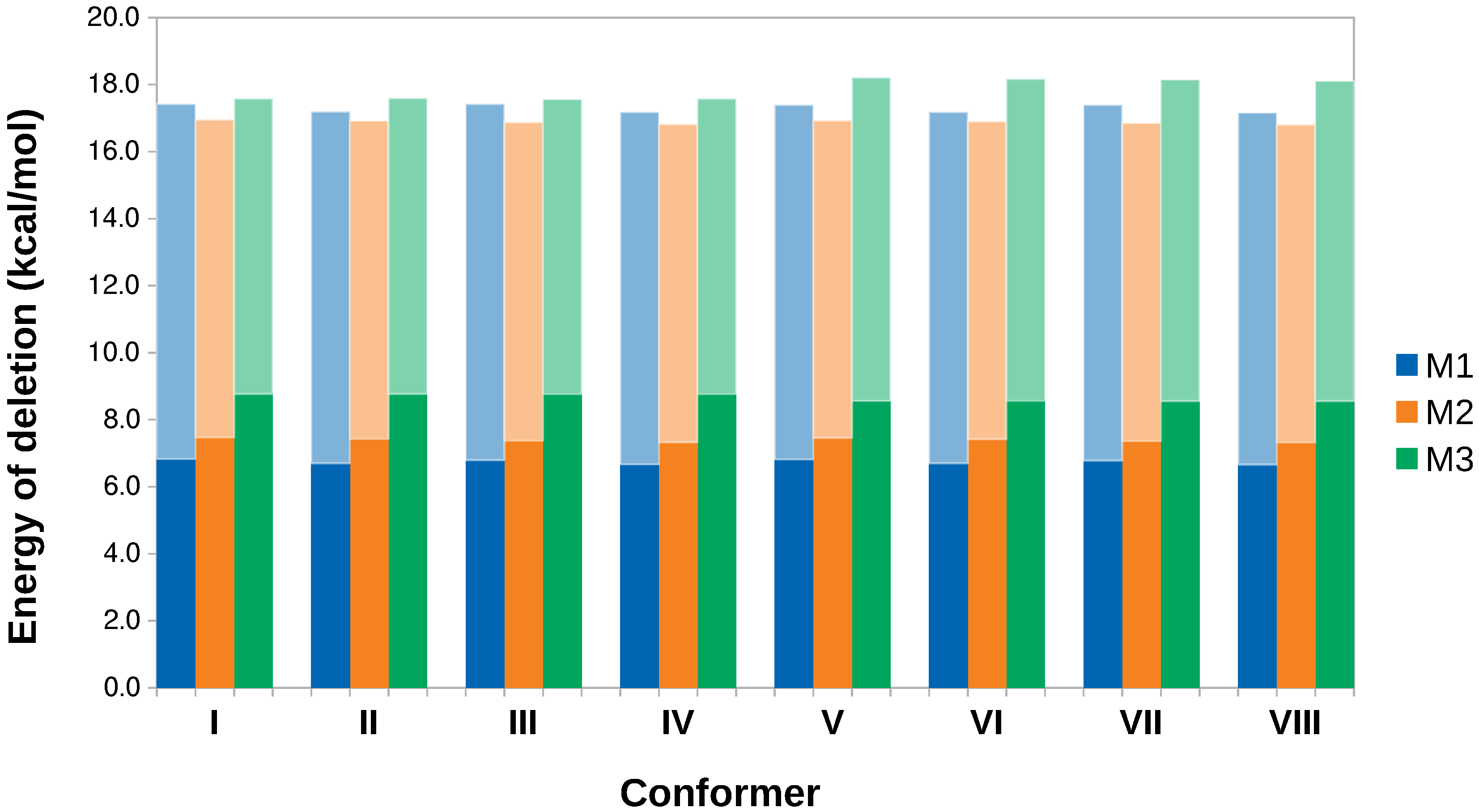
- The energy of a localized Lewis structure was constructed by deleting all non–Lewis orbitals from the Fock matrix and then the hyperconjugative contributions are obtained as the difference between the full and localized structures. This procedure was repeated for each one of the eight conformers located in this work as shown in Figure 2 and for the relaxed scans involving interconversion of I via the two lowest energy paths afforded by the structural analysis, namely I→II→I and I→III→I.
- (b)
- Specific hyperconjugative contributions from the methyl groups to the eight conformers in Figure 2 were obtained by deletion of all donor→acceptor interactions involving the methyl groups.
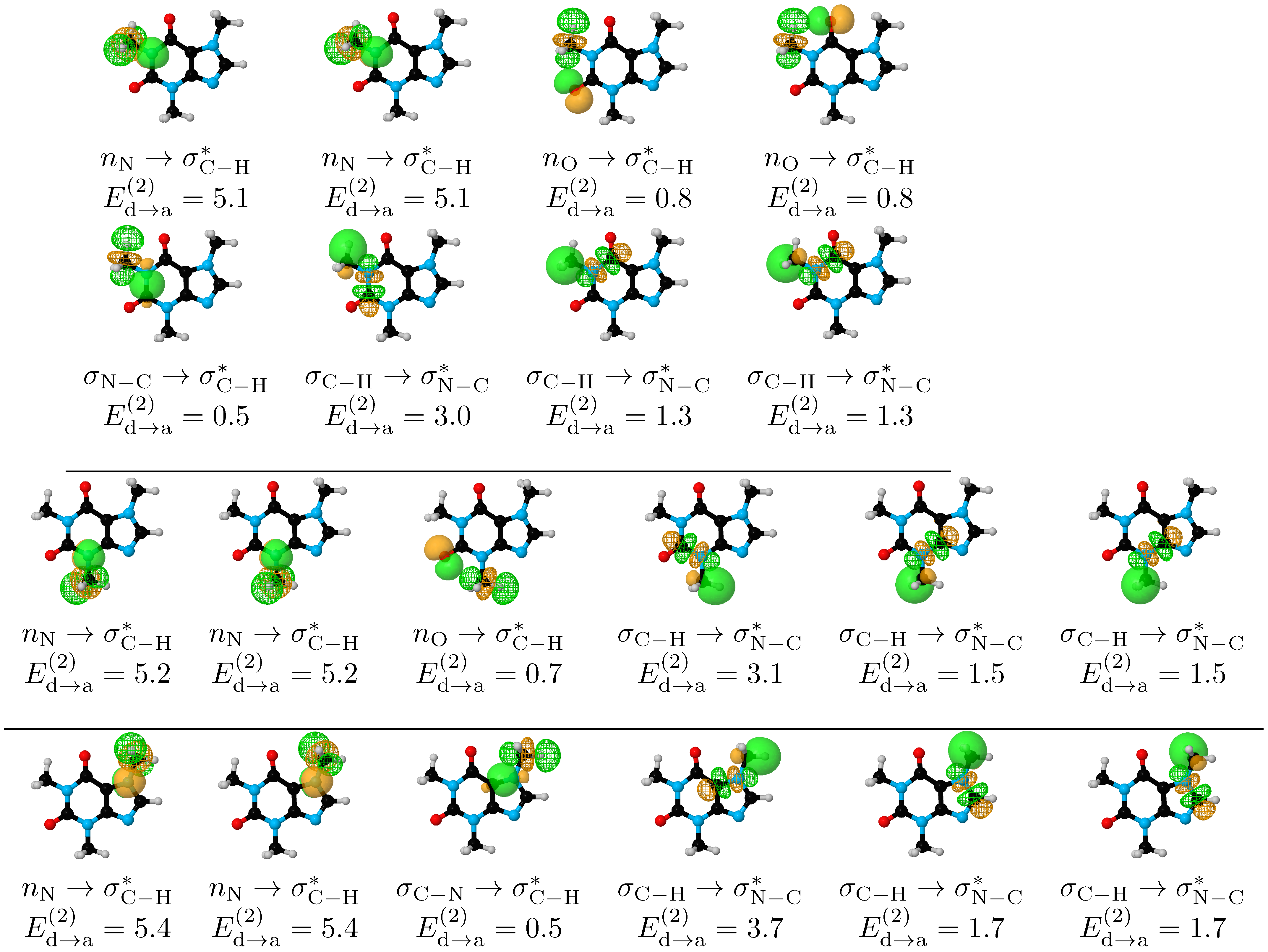
- Hyperconjugation effects on molecular geometries: following a strategy suggested elsewhere [29,78,79,80,81,82], geometry optimizations for the rotations of the methyl groups within the lowest energy structure were carried out by deleting all hyperconjugative interactions involving each methyl group separately and then involving all methyl groups simultaneously.
3. Results and Discussion
3.1. Validation of the Calculations
3.2. Aromaticity
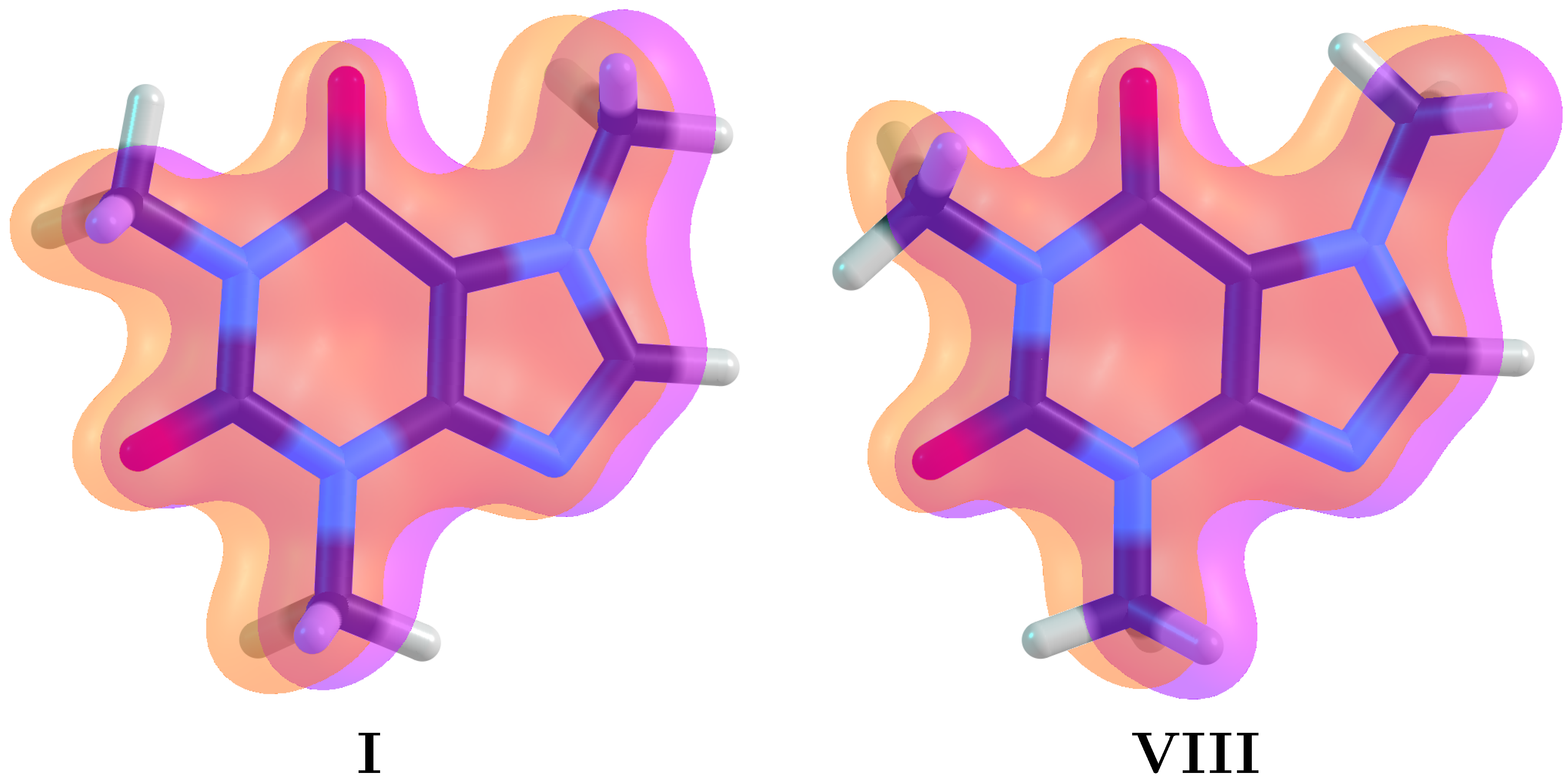
3.3. Structures and Energies
3.4. Hyperconjugation Effects on Electronic Energies
3.5. Hyperconjugation Effects on Molecular Geometries
3.6. QTAIM and NCI Analysis
- Within the respective thresholds, both QTAIM and NCI fail to detect any intramolecular interactions associated to the stabilization of the eclipsed C–H/C–H conformations (Structures I–IV, Figure 2) while NBO clearly identifies bidirectional –CH aromatic charge transfer as the mechanism behind this conformational preference (bottom row of Figure 5).
- Bonding paths are obtained only for the M3⋯Carbonyl interactions (Structures V-VII, Figure 2). Thus, QTAIM suggests a wrong conformation for M3 favoring the 1,4-allylic effect over the C-H/C-H eclipsing and even over the 1,3-allylic effect while saying nothing about the conformational preferences of M1 and M2. The very small accumulation of electron density at the bond critical points, a. u., about half that of the water dimer [43,44], a well studied weakly bonded system, is a good descriptor of the tiny rotational barriers.
- NCI affords green (with a small amount of red) surfaces for all conformations of M1 and M2, and only for the M3 conformation which eclipses a carbonyl group (Figure 2). However, the sizes of the surfaces suggest that the wrong conformation of M3 should be preferred since nothing can be inferred from structure I–IV.
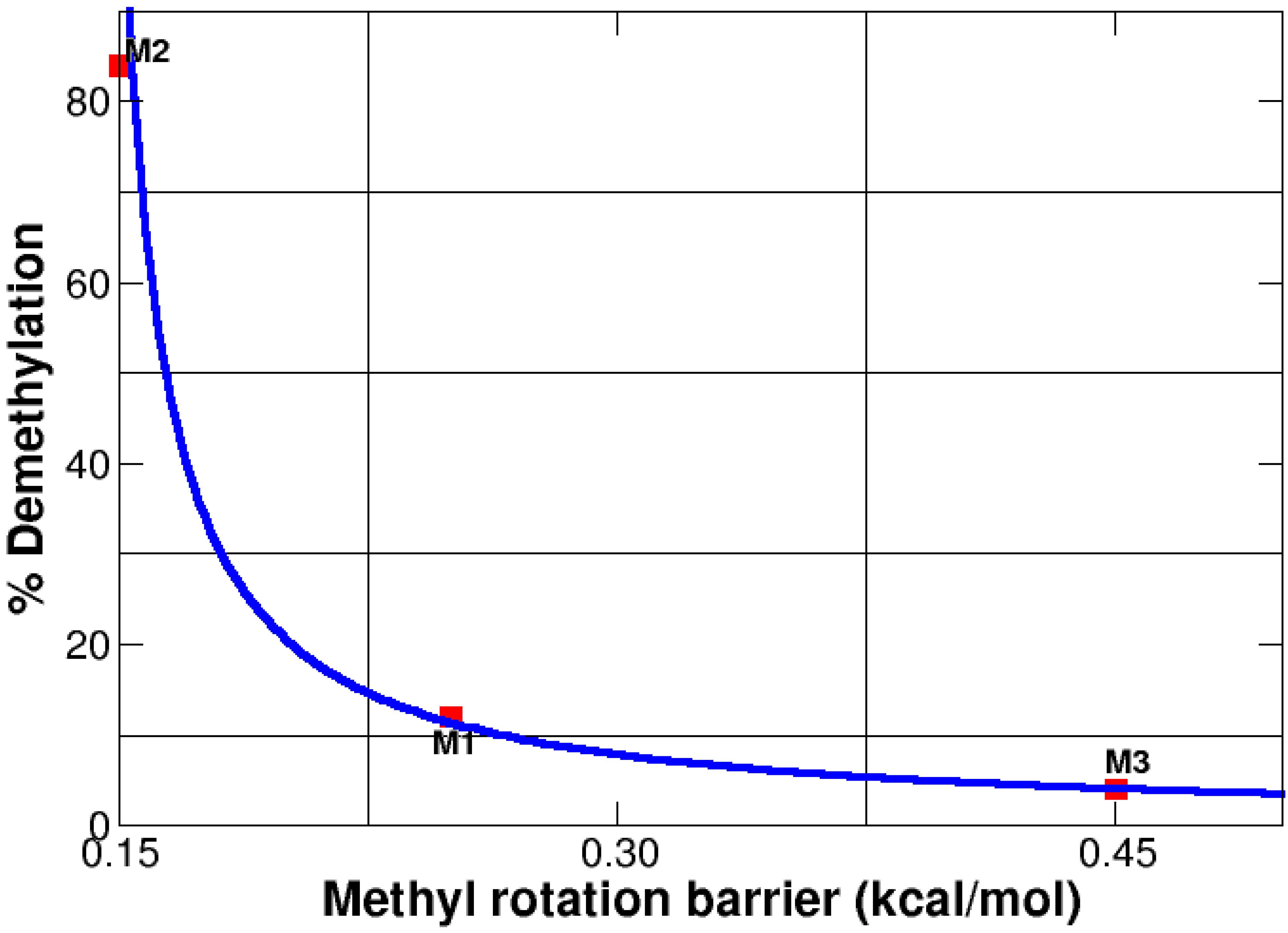
3.7. Methyl Rotation and Biological Activity
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NBO | Natural Bond Orbitals |
| NL | Non–Lewis Orbitals |
| DFT | Density Functional Theory |
| DLPNO–CCSD(T) | domain-based local pair natural orbital coupled-cluster |
| QTAIM | Quantum Theory of Atoms in Molecules |
| NCI | Non–Covalent Interactions |
References
- Rosenfeld, L.S.; Mihalov, J.J.; Carlson, S.J.; Mattia, A. Regulatory status of caffeine in the United States. Nutr. Rev. 2014, 72, 23–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zajac, M.A.; Zakrzewski, A.G.; Kowal, M.G.; Narayan, S. A Novel Method of Caffeine Synthesis from Uracil. Synth. Commun. 2003, 33, 3291–3297. [Google Scholar] [CrossRef]
- Callahan, M.P.; Gengeliczki, Z.; Svadlenak, N.; Valdes, H.; Hobza, P.; de Vries, M.S. Non-standard base pairing and stacked structures in methyl xanthine clusters. Phys. Chem. Chem. Phys. 2008, 10, 2819–2826. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.K.; Singh, V.B. Ab initio and DFT studies of the structure and vibrational spectra of anhydrous caffeine. Spectrochim. Acta Part Mol. Biomol. Spectrosc. 2013, 115, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Poltev, V.; Grokhlina, T.; González, E.; Deriabina, A.; Cruz, A.; Gorb, L.; Leszczynski, J.; Djimant, L.; Veselkov, A. The study of three-dimensional structure of caffeine associates using computational and experimental methods. J. Mol. Struct. THEOCHEM 2004, 709, 123–128. [Google Scholar] [CrossRef]
- Coquis, C.; Richaud, A.; Méndez, F. Effect of methyl substituents in the reactivity of methylxanthines. J. Mol. Model. 2018, 24, 331. [Google Scholar] [CrossRef]
- Faudone, G.; Arifi, S.; Merk, D. The Medicinal Chemistry of Caffeine. J. Med. Chem. 2021, 64, 7156–7178. [Google Scholar] [CrossRef]
- Heckman, M.A.; Weil, J.; De Mejia, E.G. Caffeine (1, 3, 7-trimethylxanthine) in Foods: A Comprehensive Review on Consumption, Functionality, Safety, and Regulatory Matters. J. Food Sci. 2010, 75, R77–R87. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kurpiewski, J.; Igielska, M.; Kamińska, B. Quantitative description of bond lengths alternation for caffeine-effects of ionization, proton-transfer, and noncovalent interaction. Comput. Theor. Chem. 2020, 1180, 112811. [Google Scholar] [CrossRef]
- Jovanović, S.; Puchta, R.; Klisurić, O.; Živadin, D. Bugarčić. Crystal structure of K[PtCl3(caffeine)] and its interactions with important nitrogen-donor ligands. J. Coord. Chem. 2016, 69, 735–747. [Google Scholar] [CrossRef]
- Gibson, C.M.; Fowler, P.W. Aromaticity of caffeine, xanthine and the dimethyl xanthines. Tetrahedron Lett. 2014, 55, 2078–2081. [Google Scholar] [CrossRef]
- Senthilnithy, R.; Weerasingha, M.; Dissanayake, D. Interaction of caffeine dimers with water molecules. Comput. Theor. Chem. 2014, 1028, 60–64. [Google Scholar] [CrossRef]
- Bach, T.; Jödicke, K.; Kather, K.; Fröhlich, R. 1,3-Allylic Strain as a Control Element in the Paterno-Buchi Reaction of Chiral Silyl Enol Ethers: Synthesis of Diastereomerically Pure Oxetanes Containing Four Contiguous Stereogenic Centers. J. Am. Chem. Soc. 1997, 119, 2437–2445. [Google Scholar] [CrossRef]
- Hoffmann, R.W. Allylic 1,3-strain as a controlling factor in stereoselective transformations. Chem. Rev. 1989, 89, 1841–1860. [Google Scholar] [CrossRef]
- Suezawa, H.; Yoshida, T.; Hirota, M.; Takahashi, H.; Umezawa, Y.; Honda, K.; Tsuboyama, S.; Nishio, M. The CH⋯π interaction as an important factor in the crystal packing and in determining the structure of clathrates. J. Chem. Soc. Perkin Trans. 2 2001, 2053–2058. [Google Scholar] [CrossRef]
- Rengifo, E.; Gómez, S.; Arce, J.C.; Weinhold, F.; Restrepo, A. The role of hyperconjugation in the unusual conformation of thymine: A natural bond orbital analysis. Comput. Theor. Chem. 2018, 1130, 58–62. [Google Scholar] [CrossRef]
- Utzat, K.; Restrepo, A.A.; Bohn, R.K.; Michels, H.H. Conformational studies of benzyl alcohol and benzyl fluoride. Int. J. Quantum Chem. 2004, 100, 964–972. [Google Scholar] [CrossRef]
- Sutor, D.J. The structures of the pyrimidines and purines. VII. The crystal structure of caffeine. Acta Crystallogr. 1958, 11, 453–458. [Google Scholar] [CrossRef] [Green Version]
- Edwards, H.G.M.; Lawson, E.; de Matas, M.; Shields, L.; York, P. Metamorphosis of caffeine hydrate and anhydrous caffeine. J. Chem. Soc. Perkin Trans. 2 1997, 1985–1990. [Google Scholar] [CrossRef]
- Gerdil, R.; Marsh, R. On the arrangement of the water molecules in the crystal structure of caffeine. Acta Crystallogr. 1960, 13, 166–167. [Google Scholar] [CrossRef]
- Prager, M.; Pawlukojc, A.; Wischnewski, A.; Wuttke, J. Inelastic neutron scattering study of methyl groups rotation in some methylxanthines. J. Chem. Phys. 2007, 127, 214509. [Google Scholar] [CrossRef] [PubMed]
- Egawa, T.; Kamiya, A.; Takeuchi, H.; Konaka, S. Molecular structure of caffeine as determined by gas electron diffraction aided by theoretical calculations. J. Mol. Struct. 2006, 825, 151–157. [Google Scholar] [CrossRef] [Green Version]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; Wiley-VCH: Hoboken, NJ, USA, 2012; 319p. [Google Scholar]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree–Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.; Glendening, E. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F.; Curtiss, L.A.; Pochatko, D.J. Natural bond orbital analysis of molecular interactions: Theoretical studies of binary complexes of HF, H2O, NH3, N2, O2, F2, CO, and CO2 with HF, H2O, and NH3. J. Chem. Phys. 1986, 84, 5687–5705. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Jiao, Y.; Weinhold, F. NBO/NRT Two-State Theory of Bond-Shift Spectral Excitation. Molecules 2020, 25, 4052. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F. A new twist on molecular shape. Nature 2001, 411, 539–541. [Google Scholar] [CrossRef]
- Suidan, L.; Badenhoop, J.K.; Glendening, E.D.; Weinhold, F. Common Textbook and Teaching Misrepresentations of Lewis Structures. J. Chem. Educ. 1995, 72, 583. [Google Scholar] [CrossRef]
- Weinhold, F.; Klein, R.A. Anti-Electrostatic Hydrogen Bonds. Angew. Chem. Int. Ed. 2014, 53, 11214–11217. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F. Natural bond critical point analysis: Quantitative relationships between natural bond orbital-based and QTAIM-based topological descriptors of chemical bonding. J. Comput. Chem. 2012, 33, 2440–2449. [Google Scholar] [CrossRef] [PubMed]
- Pophristic, V.; Goodman, L. Hyperconjugation not steric repulsion leads to the staggered structure of ethane. Nature 2001, 411, 565–568. [Google Scholar] [CrossRef] [PubMed]
- Rojas-Valencia, N.; Ibargüen, C.; Restrepo, A. Molecular interactions in the microsolvation of dimethylphosphate. Chem. Phys. Lett. 2015, 635, 301–305. [Google Scholar] [CrossRef]
- Acelas, N.; Flórez, E.; Hadad, C.; Merino, G.; Restrepo, A. A Comprehensive Picture of the Structures, Energies, and Bonding in [SO4(H2O)n]2–, n = 1–6. J. Phys. Chem. A 2019, 123, 8650–8656. [Google Scholar] [CrossRef]
- Rojas-Valencia, N.; Gómez, S.; Montillo, S.; Manrique-Moreno, M.; Cappelli, C.; Hadad, C.; Restrepo, A. Evolution of Bonding during the Insertion of Anionic Ibuprofen into Model Cell Membranes. J. Phys. Chem. B 2020, 124, 79–90. [Google Scholar] [CrossRef]
- Rojas-Valencia, N.; Gómez, S.; Guerra, D.; Restrepo, A. A detailed look at the bonding interactions in the microsolvation of monoatomic cations. Phys. Chem. Chem. Phys. 2020, 22, 13049–13061. [Google Scholar] [CrossRef]
- Gómez, S.; Osorio, E.; Dzib, E.; Islas, R.; Restrepo, A.; Merino, G. Revisiting the Rearrangement of Dewar Thiophenes. Molecules 2020, 25, 284. [Google Scholar] [CrossRef] [Green Version]
- Gómez, S.; Ramírez-Malule, H.; Cardona-G, W.; Osorio, E.; Restrepo, A. Double-Ring Epimerization in the Biosynthesis of Clavulanic Acid. J. Phys. Chem. A 2020, 124, 9413–9426. [Google Scholar] [CrossRef]
- Rojas-Valencia, N.; Gómez, S.; Núñez-Zarur, F.; Cappelli, C.; Hadad, C.; Restrepo, A. Thermodynamics and Intermolecular Interactions during the Insertion of Anionic Naproxen into Model Cell Membranes. J. Phys. Chem. B 2021, 125, 10383–10391. [Google Scholar] [CrossRef]
- Gómez, S.A.; Rojas-Valencia, N.; Gómez, S.; Egidi, F.; Cappelli, C.; Restrepo, A. Binding of SARS-CoV-2 to Cell Receptors: A Tale of Molecular Evolution. ChemBioChem 2021, 22, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Gómez, S.; Rojas-Valencia, N.; Gómez, S.A.; Cappelli, C.; Merino, G.; Restrepo, A. A molecular twist on hydrophobicity. Chem. Sci. 2021, 12, 9233–9245. [Google Scholar] [CrossRef] [PubMed]
- Gomez, S.A.; Rojas-Valencia, N.; Gomez, S.; Cappelli, C.; Restrepo, A. The role of spike protein mutations in the infectious power of SARS-COV-2 variants: A molecular interaction perspective. ChemBioChem 2021. [Google Scholar] [CrossRef] [PubMed]
- David, J.; Gomez, S.; Guerra, D.; Guerra, D.; Restrepo, A. A Comprehensive Picture of the Structures, Energies, and Bonding in the Alanine Dimers. ChemPhysChem 2021, 22, 2401–2412. [Google Scholar] [CrossRef]
- Tobón, P.; Gómez, S.; Restrepo, A.; Núñez-Zarur, F. Role of Substrate Substituents in Alkene Metathesis Mediated by a Ru Alkylidene Catalyst. Organometallics 2021, 40, 119–133. [Google Scholar] [CrossRef]
- Uribe, L.; Gómez, S.; Giovannini, T.; Egidi, F.; Restrepo, A. An efficient and robust procedure to calculate absorption spectra of aqueous charged species applied to NO2−. Phys. Chem. Chem. Phys. 2021, 23, 14857–14872. [Google Scholar] [CrossRef]
- Giraldo, C.; Gómez, S.; Weinhold, F.; Restrepo, A. Insight into the Mechanism of the Michael Reaction. ChemPhysChem 2016, 17, 2022–2034. [Google Scholar] [CrossRef]
- Farfán, P.; Gómez, S.; Restrepo, A. Dissection of the Mechanism of the Wittig Reaction. J. Org. Chem. 2019, 84, 14644–14658. [Google Scholar] [CrossRef]
- Farfán, P.; Echeverri, A.; Diaz, E.; Tapia, J.D.; Gómez, S.; Restrepo, A. Dimers of formic acid: Structures, stability, and double proton transfer. J. Chem. Phys. 2017, 147, 044312. [Google Scholar] [CrossRef]
- Gómez, S.; Oueis, Y.; Restrepo, A.; Wasserman, A. Partition potential for hydrogen bonding in formic acid dimers. Int. J. Quantum Chem. 2019, 119, e25814. [Google Scholar] [CrossRef] [Green Version]
- Llano, S.; Gómez, S.; Londoño, J.; Restrepo, A. Antioxidant activity of curcuminoids. Phys. Chem. Chem. Phys. 2019, 21, 3752–3760. [Google Scholar] [CrossRef]
- Zapata-Escobar, A.D.; Murillo-López, J.A.; Hadad, C.; Restrepo, A. Understanding the nature of bonding interactions in the carbonic acid dimers. J. Mol. Model. 2019, 25, 20. [Google Scholar] [CrossRef] [PubMed]
- Gómez, S.; Restrepo, A.; Hadad, C.Z. Theoretical tools to distinguish O-ylides from O-ylidic complexes in carbene–solvent interactions. Phys. Chem. Chem. Phys. 2015, 17, 31917–31930. [Google Scholar] [CrossRef] [PubMed]
- Coa, J.C.; Cardona-Galeano, W.; Restrepo, A. Fe3+ chelating quinoline–hydrazone hybrids with proven cytotoxicity, leishmanicidal, and trypanocidal activities. Phys. Chem. Chem. Phys. 2018, 20, 20382–20390. [Google Scholar] [CrossRef] [PubMed]
- Florez, E.; Acelas, N.; Ramírez, F.; Hadad, C.; Restrepo, A. Microsolvation of F-. Phys. Chem. Chem. Phys. 2018, 20, 8909–8916. [Google Scholar] [CrossRef]
- Moreno, N.; Restrepo, A.; Hadad, C. Exotic species with explicit noble metal–noble gas–noble metal linkages. Phys. Chem. Chem. Phys. 2018, 20, 5036–5045. [Google Scholar] [CrossRef] [PubMed]
- Zapata-Escobar, A.D.; Cárcamo-Camacho, T.; Hadad, C.; Restrepo, A. On the nature of the trimer, tetramer, and pentamer of ammonia borane. Theor. Chem. Accounts 2016, 135, 95. [Google Scholar] [CrossRef]
- Flórez, E.; Acelas, N.; Ibargüen, C.; Mondal, S.; Cabellos, J.L.; Merino, G.; Restrepo, A. Microsolvation of NO3−: Structural exploration and bonding analysis. RSC Adv. 2016, 6, 71913–71923. [Google Scholar] [CrossRef]
- Echeverri, A.; Moreno, N.; Restrepo, A.; Hadad, C. Exotic noble gas carbene-like ions. Chem. Phys. Lett. 2014, 615, 16–20. [Google Scholar] [CrossRef]
- Kim, D.; Yang, K.Y.; Kim, H.M.; Kim, T.R.; Kim, N.J.; Shin, S.; Kim, S.K. Site-dependent effects of methylation on the electronic spectra of jet-cooled methylated xanthine compounds. Phys. Chem. Chem. Phys. 2017, 19, 22375–22384. [Google Scholar] [CrossRef]
- Gómez, S.; Giovannini, T.; Cappelli, C. Absorption spectra of xanthines in aqueous solution: A computational study. Phys. Chem. Chem. Phys. 2020, 22, 5929–5941. [Google Scholar] [CrossRef] [PubMed]
- Edwards, Q.A.; Lunat, I.; Neale, L.; Kulikov, S.M. Distribution of caffeine between selected water-organic solvent media. Int. J. Chem. Sci. 2015, 13, 1218–1226. [Google Scholar]
- Shalmashi, A.; Golmohammad, F. Solubility of caffeine in water, ethyl acetate, ethanol, carbon tetrachloride, methanol, chloroform, dichloromethane, and acetone between 298 and 323 K. Lat. Am. Appl. Res. 2010, 40, 283. [Google Scholar]
- Liakos, D.G.; Sparta, M.; Kesharwani, M.K.; Martin, J.M.L.; Neese, F. Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
- Sandler, I.; Chen, J.; Taylor, M.; Sharma, S.; Ho, J. Accuracy of DLPNO-CCSD(T): Effect of Basis Set and System Size. J. Phys. Chem. A 2021, 125, 1553–1563. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Bader, R. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Keith, T. AIMALL (Version 19.10.12); TK Gristmill Software: Overland Park, KS, USA, 2019; Available online: aim.tkgristmill.com (accessed on 28 October 2021).
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Sinha, R.K. Ab initio and NBO studies of methyl internal rotation in 1-methyl-2 (1H)-quinolinone: Effect of aromatic substitution to 1-methyl-2 (1H)-pyridone. J. Mol. Model. 2020, 26, 92. [Google Scholar] [CrossRef] [PubMed]
- Wood, B.M.; Forse, A.C.; Persson, K.A. Aromaticity as a Guide to Planarity in Conjugated Molecules and Polymers. J. Phys. Chem. C 2020, 124, 5608–5612. [Google Scholar] [CrossRef]
- Pros, G.J.; Bloomfield, A.J. Why do N-alkylated anilides bend over? The factors dictating the divergent conformational preferences of 2 and 3 N-aryl amides. J. Phys. Chem. A 2019, 123, 7609–7618. [Google Scholar] [CrossRef] [PubMed]
- Nagesh, J. Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif. Molecules 2021, 26, 1533. [Google Scholar] [CrossRef] [PubMed]
- Alabugin, I.V.; Kuhn, L.; Krivoshchapov, N.V.; Mehaffy, P.; Medvedev, M.G. Anomeric effect, hyperconjugation and electrostatics: Lessons from complexity in a classic stereoelectronic phenomenon. Chem. Soc. Rev. 2021, 50, 10212–10252. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, A.A.; Bohn, R.K. Alkyl chains with CN and CCH substituents prefer gauche conformations. J. Mol. Struct. 2007, 833, 189–196. [Google Scholar] [CrossRef]
- Kot, M.; Daniel, W.A. Caffeine as a marker substrate for testing cytochrome P450 activity in human and rat. Pharmacol. Rep. 2008, 60, 789. [Google Scholar]
- Begas, E.; Kouvaras, E.; Tsakalof, A.; Papakosta, S.; Asprodini, E. In vivo evaluation of CYP1A2, CYP2A6, NAT-2 and xanthine oxidase activities in a Greek population sample by the RP-HPLC monitoring of caffeine metabolic ratios. Biomed. Chromatogr. 2007, 21, 190–200. [Google Scholar] [CrossRef]
- Benowitz, N.L.; Jacob, P., III.; Mayan, H.; Denaro, C. Sympathomimetic effects of paraxanthine and caffeine in humans. Clin. Pharmacol. Ther. 1995, 58, 684–691. [Google Scholar] [CrossRef]
- Thorn, C.F.; Aklillu, E.; McDonagh, E.M.; Klein, T.E.; Altman, R.B. PharmGKB summary: Caffeine pathway. Pharmacogenet. Genom. 2012, 22, 389. [Google Scholar] [CrossRef] [Green Version]


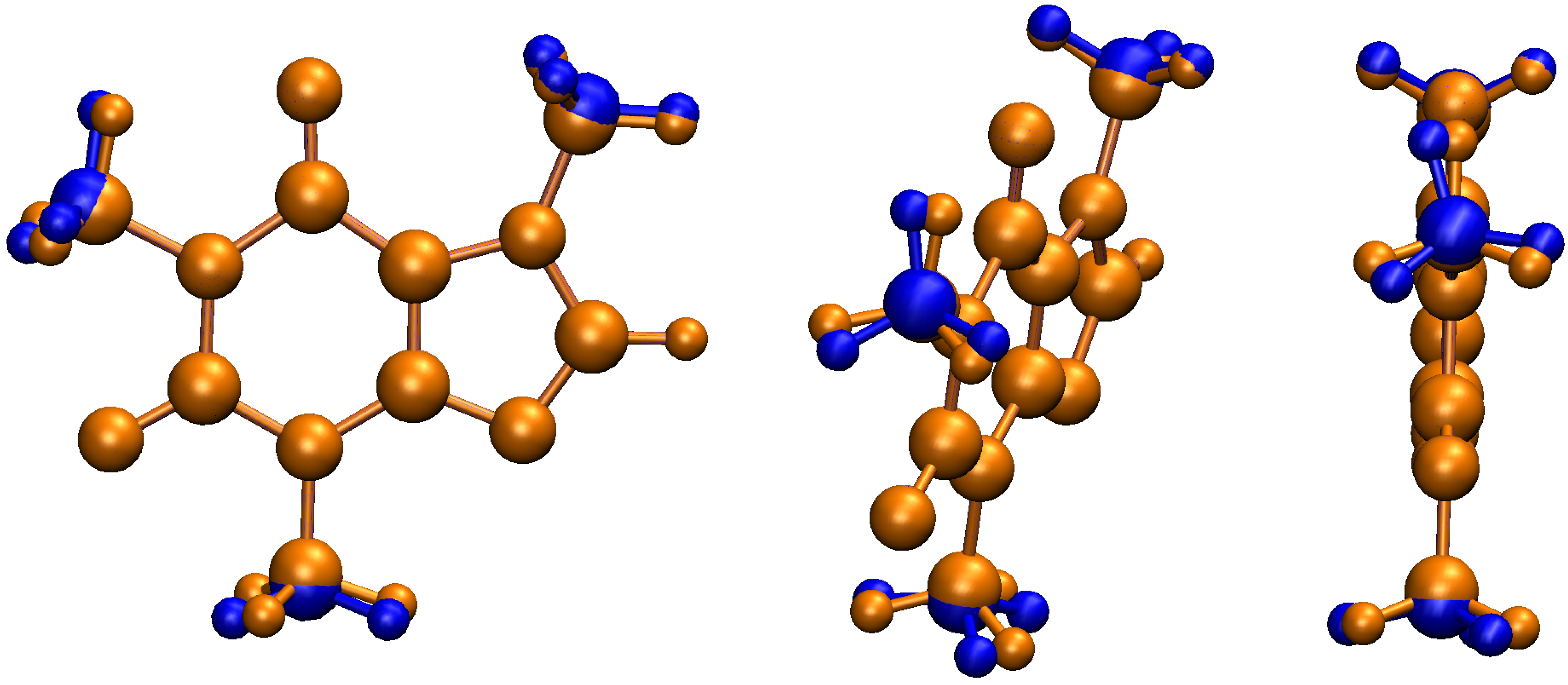
| Conformer | Dihedral | CCSD(T) | B3LYP–D3 | Water | Acetone | Acetonitrile | Chloroform | Dichloromethane | Toluene | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | E | E | E | G | E | G | E | G | E | G | E | G | E | G | E | G | ||||
| I | 0 | 180 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| II | 60 | 180 | 1 | 0.3 | 0.2 | 0.3 | 0.2 | 1.1 | 0.2 | 1.0 | 0.2 | 0.9 | 0.2 | 1.0 | 0.2 | 0.9 | 0.2 | 0.9 | 0.2 | 0.9 |
| III | 0 | 120 | 1 | 0.4 | 0.3 | 0.2 | 0.1 | 0.8 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 1.0 |
| IV | 60 | 120 | 2 | 0.8 | 0.6 | 0.5 | 0.3 | 2.2 | 0.3 | 1.9 | 0.3 | 1.9 | 0.3 | 1.9 | 0.3 | 1.9 | 0.3 | 1.8 | 0.3 | 0.3 |
| V | 0 | 180 | 1 | 0.8 | 0.8 | 0.4 | 0.4 | 2.1 | 0.6 | 1.2 | 0.6 | 1.2 | 0.6 | 1.2 | 0.6 | 1.4 | 0.6 | 1.3 | 0.6 | 1.6 |
| VI | 60 | 180 | 1 | 1.1 | 1.0 | 0.7 | 0.6 | 1.8 | 0.8 | 2.3 | 0.8 | 2.3 | 0.8 | 2.3 | 0.8 | 1.1 | 0.8 | 0.8 | 0.7 | 1.4 |
| VII | 0 | 0 | 2 | 1.1 | 1.1 | 0.6 | 0.5 | 3.1 | 0.8 | 2.3 | 0.7 | 2.3 | 0.8 | 2.3 | 0.7 | 2.3 | 0.7 | 2.3 | 0.7 | 2.6 |
| VIII | 180 | 0 | 2 | 1.5 | 1.3 | 0.9 | 0.7 | 2.6 | 0.9 | 3.2 | 0.9 | 3.2 | 0.9 | 3.2 | 0.9 | 2.1 | 0.9 | 1.9 | 0.9 | 2.3 |
| Conformer | (L) | (NL) | M1 | M2 | M3 | |||
|---|---|---|---|---|---|---|---|---|
| Donor | Acceptor | Donor | Acceptor | Donor | Acceptor | |||
| I | 0.0 | 0.0 | 6.8 | 10.6 | 7.5 | 9.5 | 8.8 | 8.8 |
| II | −0.4 | 0.7 | 6.7 | 10.5 | 7.4 | 9.5 | 8.8 | 8.8 |
| III | 0.6 | −0.4 | 6.8 | 10.6 | 7.4 | 9.5 | 8.8 | 8.8 |
| IV | 0.1 | 0.5 | 6.7 | 10.5 | 7.3 | 9.5 | 8.8 | 8.8 |
| V | −0.8 | 1.2 | 6.8 | 10.6 | 7.5 | 9.5 | 8.6 | 9.6 |
| VI | −1.2 | 1.8 | 6.7 | 10.5 | 7.4 | 9.5 | 8.6 | 9.6 |
| VII | −0.2 | 0.8 | 6.8 | 10.6 | 7.4 | 9.5 | 8.6 | 9.6 |
| VIII | −0.6 | 1.5 | 6.7 | 10.5 | 7.3 | 9.5 | 8.6 | 9.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, S.; Rojas-Valencia, N.; Restrepo, A. Analysis of Conformational Preferences in Caffeine. Molecules 2022, 27, 1937. https://doi.org/10.3390/molecules27061937
Gómez S, Rojas-Valencia N, Restrepo A. Analysis of Conformational Preferences in Caffeine. Molecules. 2022; 27(6):1937. https://doi.org/10.3390/molecules27061937
Chicago/Turabian StyleGómez, Sara, Natalia Rojas-Valencia, and Albeiro Restrepo. 2022. "Analysis of Conformational Preferences in Caffeine" Molecules 27, no. 6: 1937. https://doi.org/10.3390/molecules27061937
APA StyleGómez, S., Rojas-Valencia, N., & Restrepo, A. (2022). Analysis of Conformational Preferences in Caffeine. Molecules, 27(6), 1937. https://doi.org/10.3390/molecules27061937






