Combined Description of the Equation of State and Diffusion Coefficient of Liquid Water Using a Two-State Sanchez–Lacombe Approach
Abstract
1. Introduction
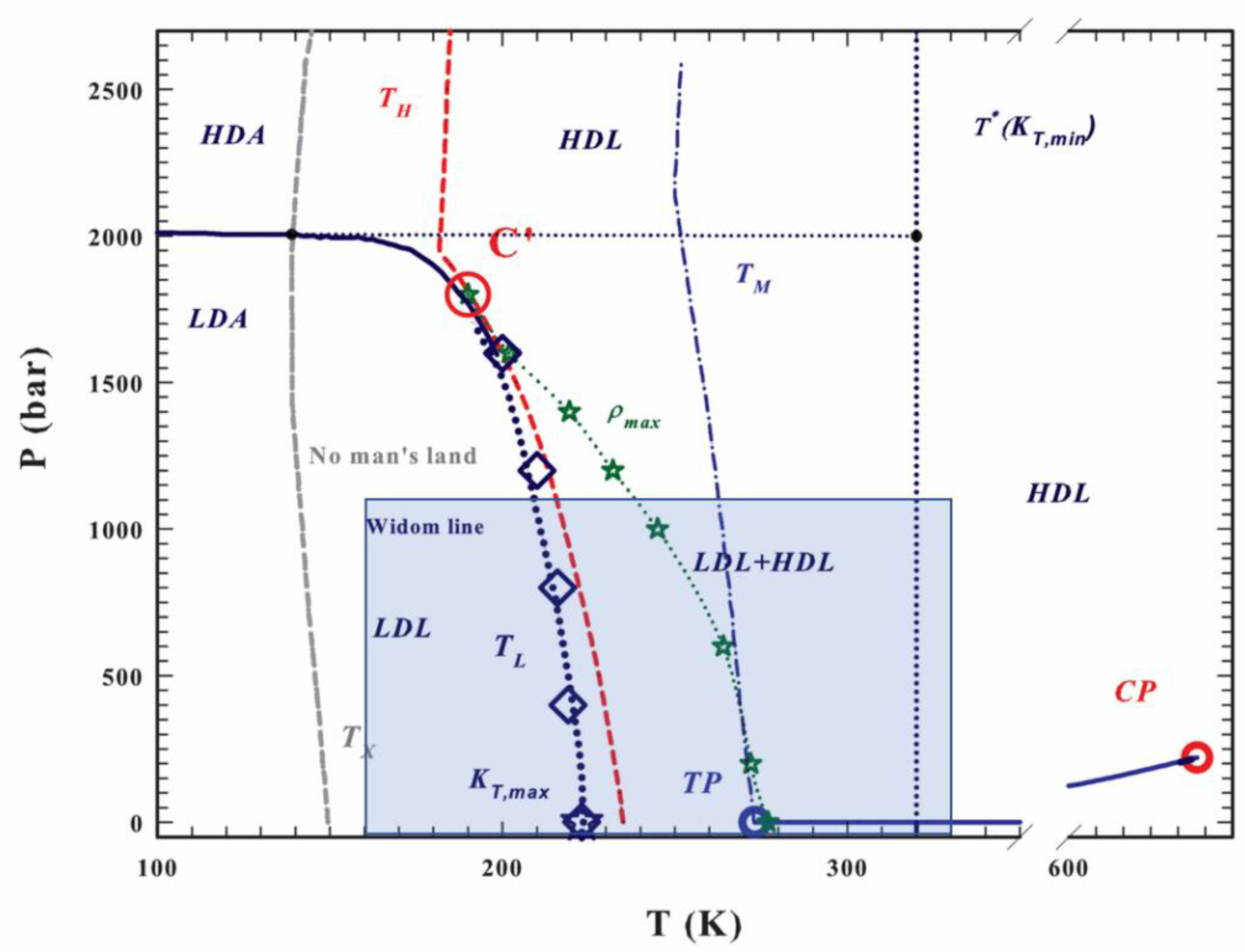
2. Results
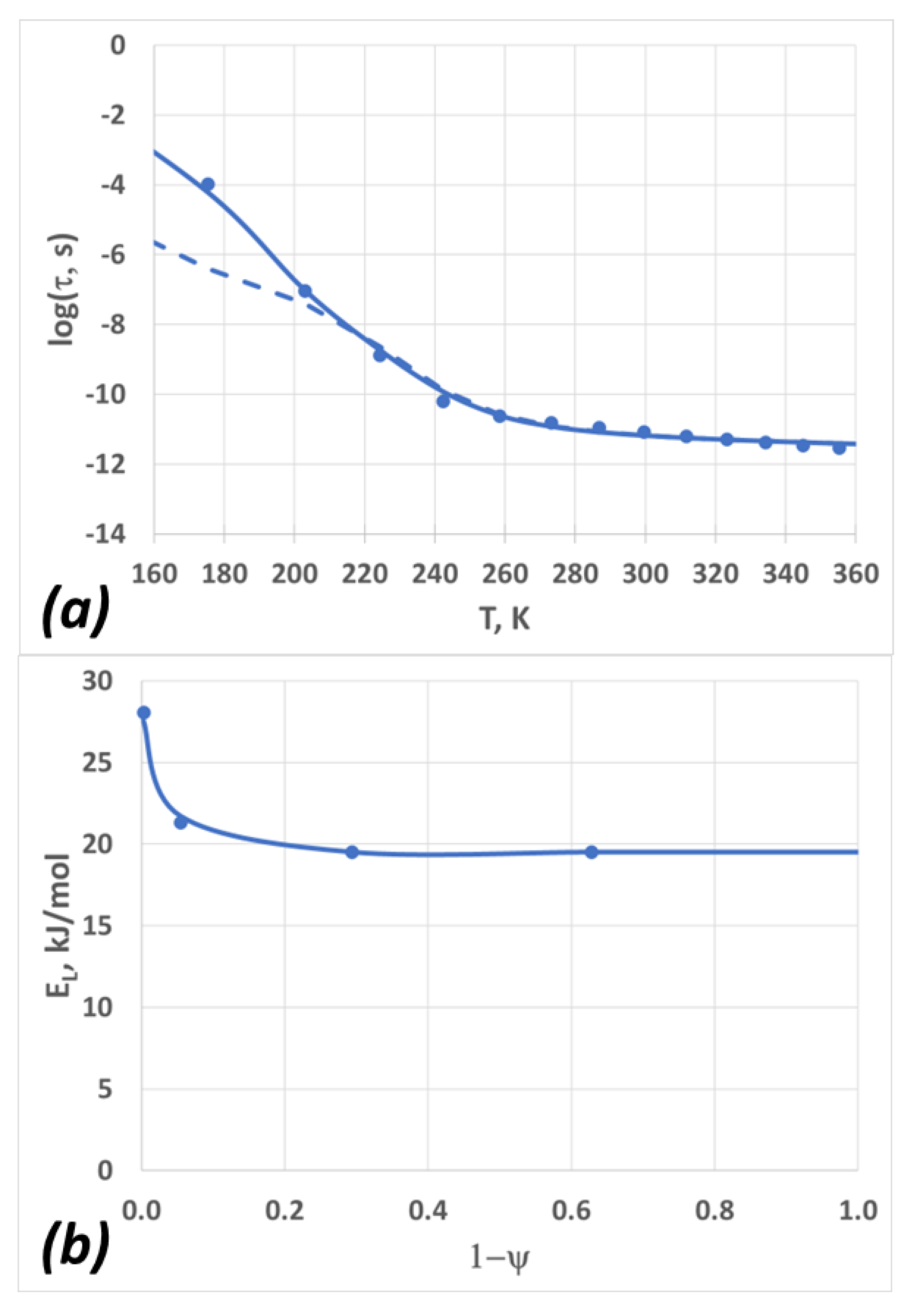
2.1. Master Curves and Scaling
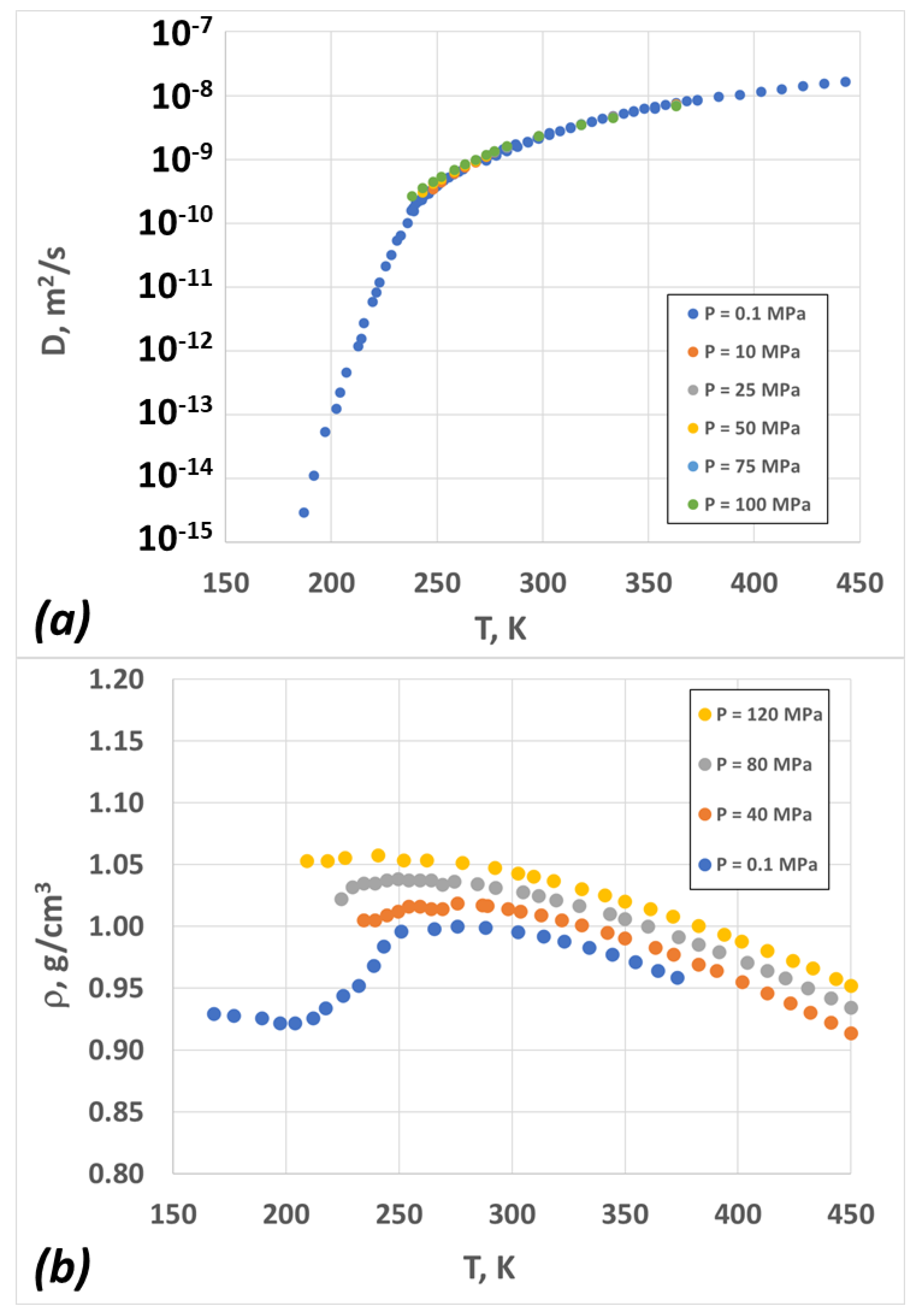
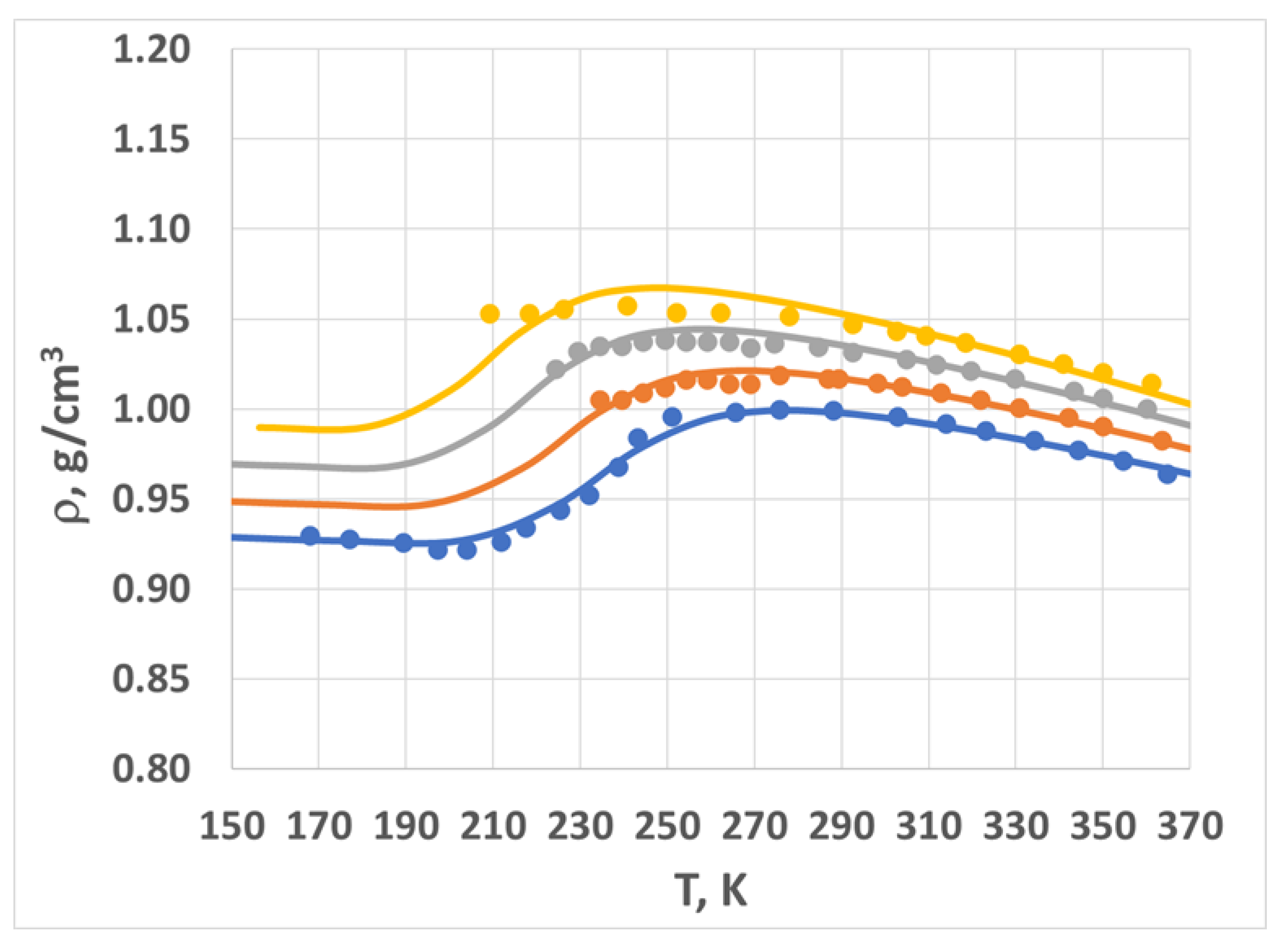
2.2. Density vs. Temperature and Pressure—Model and Experiment
2.3. Diffusion Coefficient vs. Temperature and Pressure—Model and Experiment
3. Discussion
4. Materials and Methods
4.1. The Model Density and Specific Volume
4.2. The Model’s Relaxation Time and Diffusion
4.3. The Dynamic “τTV” Scaling
4.4. Experimental Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pettersson, L.G.M.; Henchman, R.H.; Nilsson, A. Water—The Most Anomalous Liquid. Chem. Rev. 2016, 116, 7459–7462. [Google Scholar] [CrossRef]
- Gallo, P.; Amann-Winkel, K.; Angell, C.A.; Anisimov, M.A.; Caupin, F.; Chakravarty, C.; Lascaris, E.; Loerting, T.; Panagiotopoulos, A.Z.; Russo, J.; et al. Water: A Tale of Two Liquids. Chem. Rev. 2016, 116, 7463–7500. [Google Scholar] [CrossRef] [PubMed]
- Cai, R.; Glinel, K.; de Smet, D.; Vanneste, M.; Mannu, N.; Kartheuser, B.; Nysten, B.; Jonas, A.M. Environmentally Friendly Super-Water-Repellent Fabrics Prepared from Water-Based Suspensions. ACS Appl. Mater. Interfaces 2018, 10, 15346–15351. [Google Scholar] [CrossRef]
- Pettersson, L.G.M. A Two-State Picture of Water and the Funnel of Life. In Proceedings of the International Conference Physics of Liquid Matter: Modern Problems, Kyiv, Ukraine, 18–22 May 2018; pp. 3–39. [Google Scholar]
- Corsaro, C.; Mallamace, D.; Neri, G.; Fazio, E. Hydrophilicity and Hydrophobicity: Key Aspects for Biomedical and Technological Purposes. Phys. A Stat. Mech. Its Appl. 2021, 580, 126189. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Fasano, M.; Asinari, P.; Decuzzi, P. Scaling Behaviour for the Water Transport in Nanoconfined Geometries. Nat. Commun. 2014, 5, 3565. [Google Scholar] [CrossRef]
- Shi, R.; Russo, J.; Tanaka, H. Common Microscopic Structural Origin for Water’s Thermodynamic and Dynamic Anomalies. J. Chem. Phys. 2018, 149, 224502. [Google Scholar] [CrossRef]
- Ceriotti, M.; Cuny, J.; Parrinello, M.; Manolopoulos, D.E. Nuclear Quantum Effects and Hydrogen Bond Fluctuations in Water. Proc. Natl. Acad. Sci. USA 2013, 110, 15591–15596. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Stanley, H.E. A Singular Thermodynamically Consistent Temperature at the Origin of the Anomalous Behavior of Liquid Water. Sci. Rep. 2012, 2, 993. [Google Scholar] [CrossRef]
- Morawietz, T.; Singraber, A.; Dellago, C.; Behler, J. How van Der Waals Interactions Determine the Unique Properties of Water. Proc. Natl. Acad. Sci. USA 2016, 113, 8368–8373. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Buldyrev, S.V.; Angell, C.A.; Stanley, H.E. Thermodynamics and Dynamics of the Two-Scale Spherically Symmetric Jagla Ramp Model of Anomalous Liquids. Phys. Rev. E 2006, 74, 31108. [Google Scholar] [CrossRef]
- Starr, F.W.; Angell, C.A.; la Nave, E.; Sastry, S.; Scala, A.; Sciortino, F.; Stanley, H.E. Recent Results on the Connection between Thermodynamics and Dynamics in Supercooled Water. Biophys. Chem. 2003, 105, 573–583. [Google Scholar] [CrossRef]
- Stanley, H.E.; Kumar, P.; Xu, L.; Yan, Z.; Mazza, M.G.; Buldyrev, S.V.; Chen, S.-H.; Mallamace, F. The Puzzling Unsolved Mysteries of Liquid Water: Some Recent Progress. Phys. A Stat. Mech. Its Appl. 2007, 386, 729–743. [Google Scholar] [CrossRef]
- Maestro, L.M.; Marqués, M.I.; Camarillo, E.; Jaque, D.; Solé, J.G.; Gonzalo, J.A.; Jaque, F.; del Valle, J.C.; Mallamace, F.; Stanley, H.E. On the Existence of Two States in Liquid Water: Impact on Biological and Nanoscopic Systems. Int. J. Nanotechnol. 2016, 13, 667–677. [Google Scholar] [CrossRef]
- Tanaka, H. Bond Orientational Order in Liquids: Towards a Unified Description of Water-like Anomalies, Liquid-Liquid Transition, Glass Transition, and Crystallization. Eur. Phys. J. E 2012, 35, 1–84. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. A New Scenario of the Apparent Fragile-to-Strong Transition in Tetrahedral Liquids: Water as an Example. J. Phys. Condens. Matter 2003, 15, L703. [Google Scholar] [CrossRef]
- Shi, R.; Tanaka, H. The Anomalies and Criticality of Liquid Water. Proc. Natl. Acad. Sci. USA 2020, 117, 26591–26599. [Google Scholar] [CrossRef] [PubMed]
- Yagasaki, T.; Matsumoto, M.; Tanaka, H. Spontaneous Liquid-Liquid Phase Separation of Water. Phys. Rev. E 2014, 89, 20301. [Google Scholar] [CrossRef] [PubMed]
- Murata, K.; Tanaka, H. Liquid–Liquid Transition without Macroscopic Phase Separation in a Water–Glycerol Mixture. Nat. Mater. 2012, 11, 436–443. [Google Scholar] [CrossRef]
- Shi, R.; Russo, J.; Tanaka, H. Origin of the Emergent Fragile-to-Strong Transition in Supercooled Water. Proc. Natl. Acad. Sci. USA 2018, 115, 9444–9449. [Google Scholar] [CrossRef]
- Koga, K.; Tanaka, H.; Zeng, X.C. First-Order Transition in Confined Water between High-Density Liquid and Low-Density Amorphous Phases. Nature 2000, 408, 564–567. [Google Scholar] [CrossRef] [PubMed]
- Cisneros, G.A.; Wikfeldt, K.T.; Ojamäe, L.; Lu, J.; Xu, Y.; Torabifard, H.; Bartók, A.P.; Csányi, G.; Molinero, V.; Paesani, F. Modeling Molecular Interactions in Water: From Pairwise to Many-Body Potential Energy Functions. Chem. Rev. 2016, 116, 7501–7528. [Google Scholar] [CrossRef] [PubMed]
- Cerveny, S.; Mallamace, F.; Swenson, J.; Vogel, M.; Xu, L. Confined Water as Model of Supercooled Water. Chem. Rev. 2016, 116, 7608–7625. [Google Scholar] [CrossRef]
- Neophytou, A.; Chakrabarti, D.; Sciortino, F. Topological Nature of the Liquid–Liquid Phase Transition in Tetrahedral Liquids. Nat. Phys. 2022, 18, 1248–1253. [Google Scholar] [CrossRef]
- Gartner, T.E.; Piaggi, P.M.; Car, R.; Panagiotopoulos, A.Z.; Debenedetti, P.G. Liquid-Liquid Transition in Water from First Principles. Phys. Rev. Lett. 2022, 129, 255702. [Google Scholar] [CrossRef]
- Simões, M.; Yamaguti, K.; Cobo, R.F.; Steudel, A.; Amaral, R.; Santos, A.P.R. An Analytical Approach to the Anomalous Density of Water. Phys. Fluids 2022, 34, 74111. [Google Scholar] [CrossRef]
- Mandumpal, J.B. A Journey Through Water: A Scientific Exploration of The Most Anomalous Liquid on Earth; Bentham Science Publishers: Sharjah, United Arab Emirates, 2017. [Google Scholar]
- Mallamace, D.; Corsaro, C.; Mallamace, F.; Stanley, H.E. Experimental Tests for a Liquid-Liquid Critical Point in Water. Sci. China Phys. Mech. Astron. 2020, 63, 1–42. [Google Scholar] [CrossRef]
- Tanaka, H. Phase Behaviors of Supercooled Water: Reconciling a Critical Point of Amorphous Ices with Spinodal Instability. J. Chem. Phys. 1996, 105, 5099–5111. [Google Scholar] [CrossRef]
- Poole, P.H.; Sciortino, F.; Essmann, U.; Stanley, H.E. Phase Behaviour of Metastable Water. Nature 1992, 360, 324–328. [Google Scholar] [CrossRef]
- Vega, C.; Abascal, J.L.F.; Sanz, E.; MacDowell, L.G.; McBride, C. Can Simple Models Describe the Phase Diagram of Water? J. Phys. Condens. Matter 2005, 17, S3283–S3288. [Google Scholar] [CrossRef]
- Salzmann, C.G. Advances in the Experimental Exploration of Water’s Phase Diagram. J. Chem. Phys. 2019, 150, 60901. [Google Scholar] [CrossRef]
- Weis, J.; Sciortino, F.; Panagiotopoulos, A.Z.; Debenedetti, P.G. Liquid–Liquid Criticality in the WAIL Water Model. J. Chem. Phys. 2022, 157, 24502. [Google Scholar] [CrossRef] [PubMed]
- Debenedetti, P.G.; Sciortino, F.; Zerze, G.H. Second Critical Point in Two Realistic Models of Water. Science 2020, 369, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. Supercooled Water: Two Phases? Nat. Mater. 2014, 13, 673–675. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. Glass Transition Dynamics in Water and Other Tetrahedral Liquids: ‘Order–Disorder’ Transitions versus ‘Normal’ Glass Transitions. J. Phys. Condens. Matter 2007, 19, 205112. [Google Scholar] [CrossRef]
- Angell, C.A. Water II Is a ”Strong” Liquid. J. Phys. Chem. 1993, 97, 6339–6341. [Google Scholar] [CrossRef]
- Angell, C.A. Liquid Fragility and the Glass Transition in Water and Aqueous Solutions. Chem. Rev. 2002, 102, 2627–2650. [Google Scholar] [CrossRef]
- Angell, C.A. Relaxation in Liquids, Polymers and Plastic Crystals—Strong/Fragile Patterns and Problems. J. Non Cryst. Solids 1991, 131, 13–31. [Google Scholar] [CrossRef]
- Yue, Y.; Angell, C.A. Clarifying the Glass-Transition Behaviour of Water by Comparison with Hyperquenched Inorganic Glasses. Nature 2004, 427, 717–720. [Google Scholar] [CrossRef]
- Ito, K.; Moynihan, C.T.; Angell, C.A. Thermodynamic Determination of Fragility in Liquids and a Fragile-to-Strong Liquid Transition in Water. Nature 1999, 398, 492–495. [Google Scholar] [CrossRef]
- Corsaro, C.; Fazio, E. From Critical Point to Critical Point: The Two-States Model Describes Liquid Water Self-Diffusion from 623 to 126 K. Molecules 2021, 26, 5899. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, X.; Yu, H.-B.; Douglas, J.F. Dynamic Heterogeneity, Cooperative Motion, and Johari–Goldstein β-Relaxation in a Metallic Glass-Forming Material Exhibiting a Fragile-to-Strong Transition. Eur. Phys. J. E 2021, 44, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V. A Simple Mean-Field Model of Glassy Dynamics and Glass Transition. Soft Matter 2020, 16, 810–825. [Google Scholar] [CrossRef]
- Ginzburg, V. Combined Description of Polymer PVT and Relaxation Data Using a Dynamic “SL-TS2” Mean-Field Lattice Model. Soft Matter 2021, 17, 9094–9106. [Google Scholar] [CrossRef]
- Ginzburg, V. Modeling the Glass Transition and Glassy Dynamics of Random Copolymers Using the TS2 Mean-Field Approach. Macromolecules 2021, 54, 2774–2782. [Google Scholar] [CrossRef]
- Ginzburg, V. Modeling the Glass Transition of Free-Standing Polymer Thin Films Using the “SL-TS2” Mean-Field Approach. Macromolecules 2022, 55, 873–882. [Google Scholar] [CrossRef]
- Ginzburg, V.V.; Zaccone, A.; Casalini, R. Combined Description of Pressure-Volume-Temperature and Dielectric Relaxation of Several Polymeric and Low-Molecular-Weight Organic Glass-Formers Using’SL-TS2’Mean-Field Approach. Soft Matter 2022, 18, 8456–8466. [Google Scholar] [CrossRef]
- Casalini, R.; Roland, C.M. Thermodynamical Scaling of the Glass Transition Dynamics. Phys. Rev. E 2004, 69, 62501. [Google Scholar] [CrossRef]
- Casalini, R.; Roland, C.M. Determination of the Thermodynamic Scaling Exponent for Relaxation in Liquids from Static Ambient-Pressure Quantities. Phys. Rev. Lett. 2014, 113, 85701. [Google Scholar] [CrossRef] [PubMed]
- Casalini, R.; Mohanty, U.; Roland, C.M. Thermodynamic Interpretation of the Scaling of the Dynamics of Supercooled Liquids. J. Chem. Phys. 2006, 125, 14505. [Google Scholar] [CrossRef]
- Roland, C.M.; Bair, S.; Casalini, R. Thermodynamic Scaling of the Viscosity of van Der Waals, H-Bonded, and Ionic Liquids. J. Chem. Phys. 2006, 125, 124508. [Google Scholar] [CrossRef]
- Casalini, R.; Bair, S.S.; Roland, C.M. Density Scaling and Decoupling in O-Terphenyl, Salol, and Dibutyphthalate. J. Chem. Phys. 2016, 145, 64502. [Google Scholar] [CrossRef]
- Roland, C.M.; Hensel-Bielowka, S.; Paluch, M.; Casalini, R. Supercooled Dynamics of Glass-Forming Liquids and Polymers under Hydrostatic Pressure. Rep. Prog. Phys. 2005, 68, 1405. [Google Scholar] [CrossRef]
- Ngai, K.L.; Casalini, R.; Capaccioli, S.; Paluch, M.; Roland, C.M. Do Theories of the Glass Transition, in Which the Structural Relaxation Time Does Not Define the Dispersion of the Structural Relaxation, Need Revision? J. Phys. Chem. B 2005, 109, 17356–17360. [Google Scholar] [CrossRef] [PubMed]
- Maimbourg, T.; Dyre, J.; Costigliola, L. Density Scaling of Generalized Lennard-Jones Fluids in Different Dimensions. SciPost Phys. 2020, 9, 90. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Fazio, E.; Chen, S.-H. Some Considerations on the Water Polymorphism and the Liquid-Liquid Transition by the Density Behavior in the Liquid Phase. J. Chem. Phys. 2019, 151, 44504. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Chen, Y.; Xu, L. Liquid-Liquid Phase Transition in Water. Sci. China Phys. Mech. Astron. 2014, 57, 810–818. [Google Scholar] [CrossRef]
- Lucas, P.; Pries, J.; Wei, S.; Wuttig, M. The Glass Transition of Water, Insight from Phase Change Materials. J. Non-Cryst. Solids X 2022, 14, 100084. [Google Scholar] [CrossRef]
- Bertolini, D.; Cassettari, M.; Salvetti, G. The Dielectric Relaxation Time of Supercooled Water. J. Chem. Phys. 1982, 76, 3285–3290. [Google Scholar] [CrossRef]
- Buchner, R.; Barthel, J.; Stauber, J. The Dielectric Relaxation of Water between 0 C and 35 C. Chem. Phys. Lett. 1999, 306, 57–63. [Google Scholar] [CrossRef]
- Xu, L.; Kumar, P.; Buldyrev, S.V.; Chen, S.-H.; Poole, P.H.; Sciortino, F.; Stanley, H.E. Relation between the Widom Line and the Dynamic Crossover in Systems with a Liquid–Liquid Phase Transition. Proc. Natl. Acad. Sci. USA 2005, 102, 16558–16562. [Google Scholar] [CrossRef]
- Lacombe, R.H.; Sanchez, I.C. Statistical Thermodynamics of Fluid Mixtures. J. Phys. Chem. 1976, 80, 2568–2580. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical Thermodynamics of Polymer Solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An Elementary Molecular Theory of Classical Fluids. Pure Fluids. J. Phys. Chem. 1976, 80, 2352–2362. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Cho, J.; Chen, W.J. Universal Response of Polymers, Solvents, and Solutions to Pressure. Macromolecules 1993, 26, 4234–4241. [Google Scholar] [CrossRef]
- Condo, P.D.; Sanchez, I.C.; Panayiotou, C.G.; Johnston, K.P. Glass Transition Behavior Including Retrograde Vitrification of Polymers with Compressed Fluid Diluents. Macromolecules 1992, 25, 6119–6127. [Google Scholar] [CrossRef]
- Giovambattista, N.; Angell, C.A.; Sciortino, F.; Stanley, H.E. Glass-Transition Temperature of Water: A Simulation Study. Phys. Rev. Lett. 2004, 93, 47801. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Matubayasi, N.; Nakahara, M. Self-Diffusion Coefficients for Water and Organic Solvents at High Temperatures along the Coexistence Curve. J. Chem. Phys. 2008, 129, 214501. [Google Scholar] [CrossRef]
- Simpson, J.H.; Carr, H.Y. Diffusion and Nuclear Spin Relaxation in Water. Phys. Rev. 1958, 111, 1201–1202. [Google Scholar] [CrossRef]
- Price, W.S.; Ide, H.; Arata, Y. Self-Diffusion of Supercooled Water to 238 K Using PGSE NMR Diffusion Measurements. J. Phys. Chem. A 1999, 103, 448–450. [Google Scholar] [CrossRef]
- Xu, Y.; Petrik, N.G.; Smith, R.S.; Kay, B.D.; Kimmel, G.A. Growth Rate of Crystalline Ice and the Diffusivity of Supercooled Water from 126 to 262 K. Proc. Natl. Acad. Sci. USA 2016, 113, 14921–14925. [Google Scholar] [CrossRef] [PubMed]
- Price, W.S. Pulsed-Field Gradient Nuclear Magnetic Resonance as a Tool for Studying Translational Diffusion: Part 1. Basic Theory. Concepts Magn. Reson. 1997, 9, 299–336. [Google Scholar] [CrossRef]
- Jackson, K.A. The Interface Kinetics of Crystal Growth Processes. Interface Sci. 2002, 10, 159–169. [Google Scholar] [CrossRef]
- Prielmeier, F.X.; Lang, E.W.; Speedy, R.J.; Lüdemann, H.-D. The Pressure Dependence of Self Diffusion in Supercooled Light and Heavy Water. Ber. Bunsenges. Phys. Chem. 1988, 92, 1111–1117. [Google Scholar] [CrossRef]
- Weingärtner, H. Self Diffusion in Liquid Water. A Reassessment. Z. Phys. Chem. 1982, 132, 129–149. [Google Scholar] [CrossRef]
- Tyrrell, H.J.V.; Harris, K.R. Diffusion in Liquids: A Theoretical and Experimental Study; Elsevier Ltd.: Amsterdam, The Netherlands, 1984; ISBN 978-0-408-17591-3. [Google Scholar]
- Grindley, T.; Lind, J.E. PVT Properties of Water and Mercury. J. Chem. Phys. 1971, 54, 3983–3989. [Google Scholar] [CrossRef]
- Kell, G.S.; Whalley, E. Reanalysis of the Density of Liquid Water in the Range 0–150 °C and 0–1 Kbar. J. Chem. Phys. 1975, 62, 3496–3503. [Google Scholar] [CrossRef]
- Hare, D.E.; Sorensen, C.M. Densities of Supercooled H2O and D2O in 25 μ Glass Capillaries. J. Chem. Phys. 1986, 84, 5085–5089. [Google Scholar] [CrossRef]
- Mallamace, F.; Branca, C.; Broccio, M.; Corsaro, C.; Mou, C.-Y.; Chen, S.-H. The Anomalous Behavior of the Density of Water in the Range 30 K < T < 373 K. Proc. Natl. Acad. Sci. USA 2007, 104, 18387–18391. [Google Scholar] [CrossRef] [PubMed]
- Erko, M.; Wallacher, D.; Hoell, A.; Hauß, T.; Zizak, I.; Paris, O. Density Minimum of Confined Water at Low Temperatures: A Combined Study by Small-Angle Scattering of X-Rays and Neutrons. Phys. Chem. Chem. Phys. 2012, 14, 3852–3858. [Google Scholar] [CrossRef]
- Wilson, W.D. Speed of Sound in Distilled Water as a Function of Temperature and Pressure. J. Acoust. Soc. Am. 1959, 31, 1067–1072. [Google Scholar] [CrossRef]
- Mishima, O. Volume of Supercooled Water under Pressure and the Liquid-Liquid Critical Point. J. Chem. Phys. 2010, 133, 144503. [Google Scholar] [CrossRef] [PubMed]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]

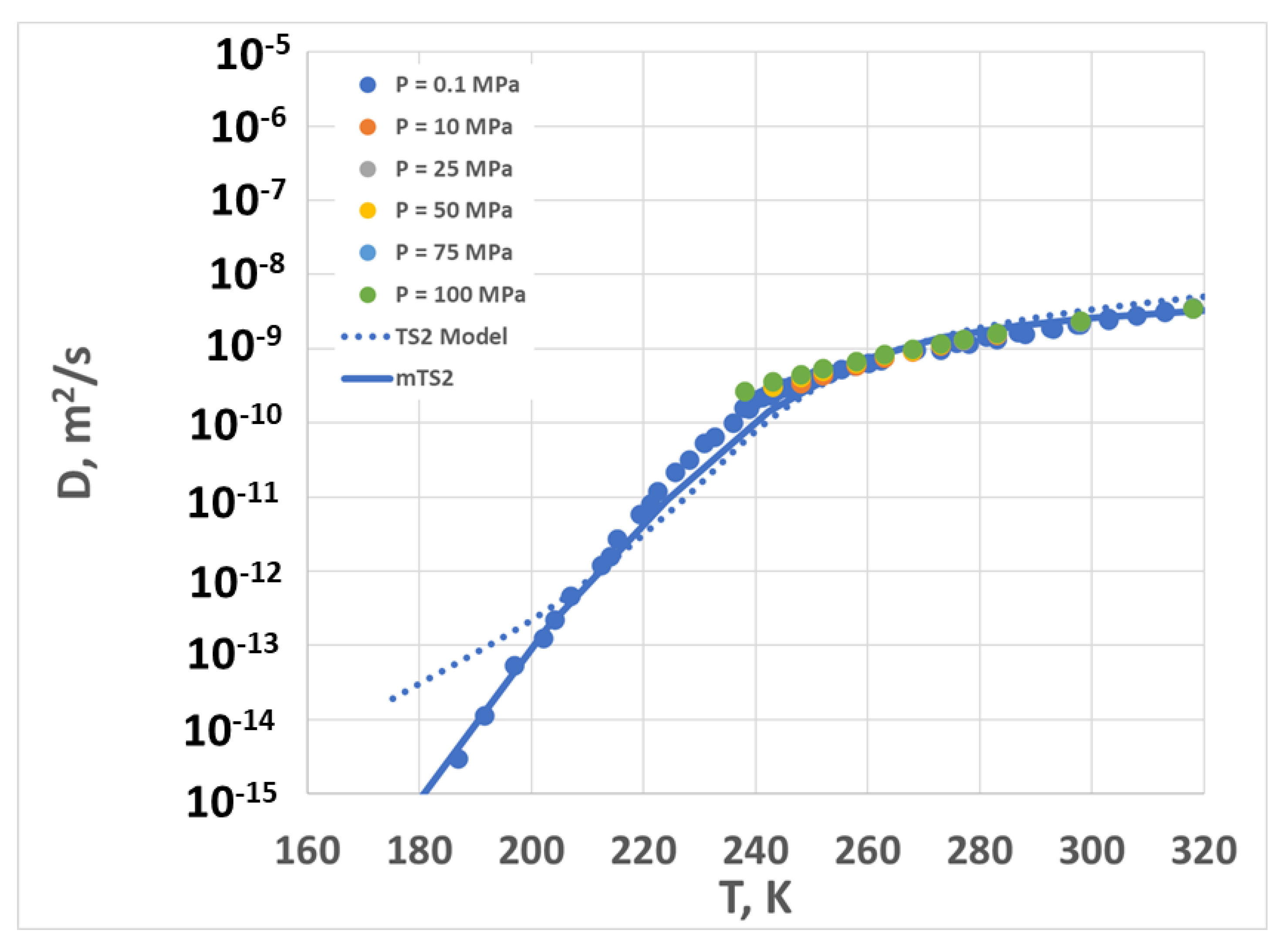
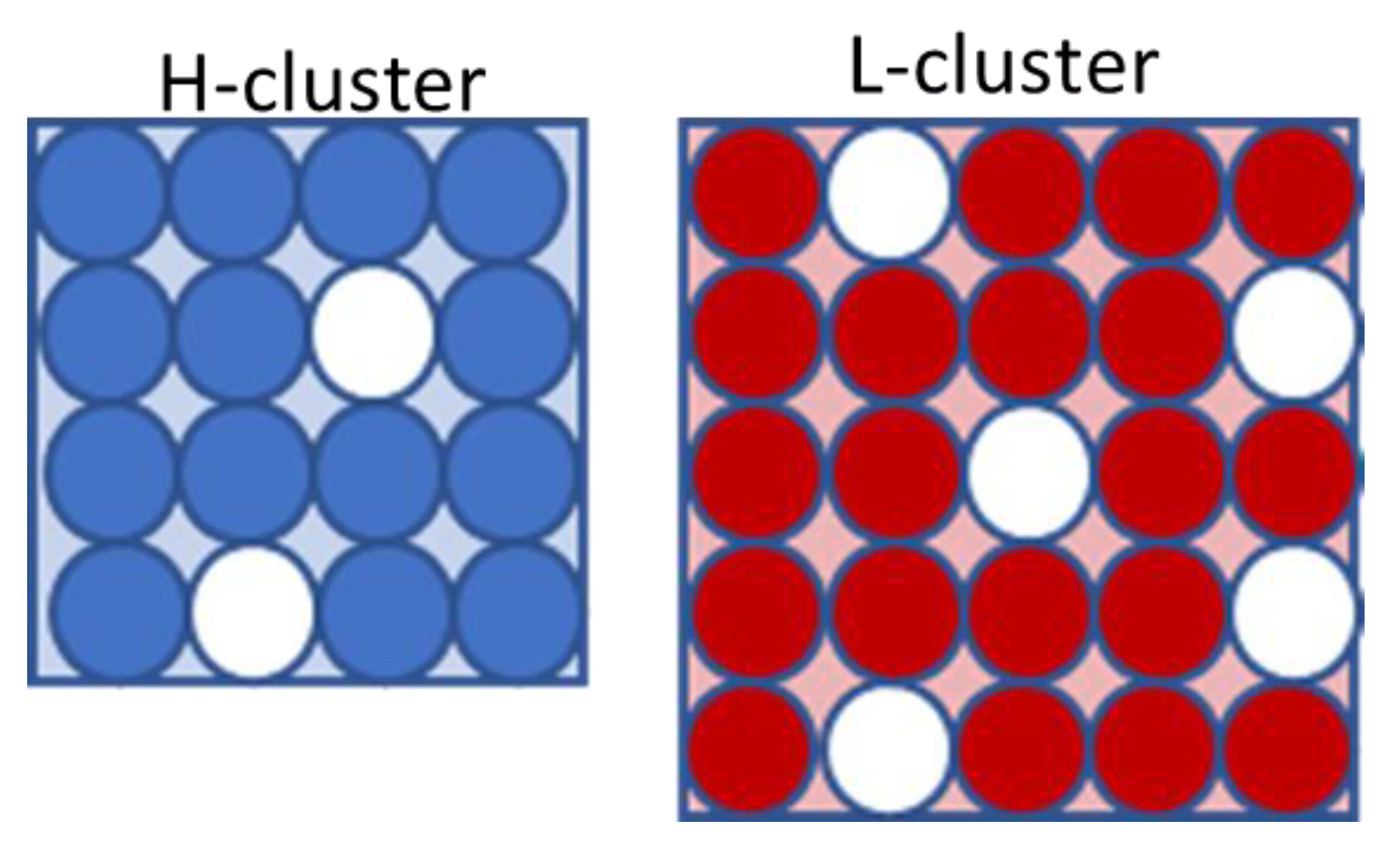
| Parameter | Units | Value |
|---|---|---|
| ar | (MPa)−1 | 5.48 × 10−4 |
| aT | (MPa)−1 | 9.35 × 10−4 |
| aD | (MPa)−1 | 7.78 × 10−3 |
| Parameter | Units | Value |
|---|---|---|
| T* | K | 734.1 |
| rL | 56.5 | |
| rH | 50.6 | |
| αHH | 1.0 | |
| αHΛ | 1.0 | |
| ΔSH | 18.5 | |
| Vsp,0 | cm3/g | 1.073 |
| Parameter | Units | Value |
|---|---|---|
| τ∞ | s | 4.0 × 10−13 |
| EH | kJ/mol | 6.7 |
| TS2 | ||
| EL | kJ/mol | 20.1 |
| mTS2 | ||
| EL,min | kJ/mol | 19.5 |
| EL,max | kJ/mol | 28.1 |
| k | 25.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginzburg, V.V.; Fazio, E.; Corsaro, C. Combined Description of the Equation of State and Diffusion Coefficient of Liquid Water Using a Two-State Sanchez–Lacombe Approach. Molecules 2023, 28, 2560. https://doi.org/10.3390/molecules28062560
Ginzburg VV, Fazio E, Corsaro C. Combined Description of the Equation of State and Diffusion Coefficient of Liquid Water Using a Two-State Sanchez–Lacombe Approach. Molecules. 2023; 28(6):2560. https://doi.org/10.3390/molecules28062560
Chicago/Turabian StyleGinzburg, Valeriy V., Enza Fazio, and Carmelo Corsaro. 2023. "Combined Description of the Equation of State and Diffusion Coefficient of Liquid Water Using a Two-State Sanchez–Lacombe Approach" Molecules 28, no. 6: 2560. https://doi.org/10.3390/molecules28062560
APA StyleGinzburg, V. V., Fazio, E., & Corsaro, C. (2023). Combined Description of the Equation of State and Diffusion Coefficient of Liquid Water Using a Two-State Sanchez–Lacombe Approach. Molecules, 28(6), 2560. https://doi.org/10.3390/molecules28062560








