Influence of the Hubbard U Correction on the Electronic Properties and Chemical Bands of the Cubic (Pm
Abstract
1. Introduction
2. Results and Discussion
2.1. Geometry Optimization
2.1.1. Appropriate Pseudopotential Methods, K-Points, and Cut-Off Energy
2.1.2. Hubbard Potential Correction
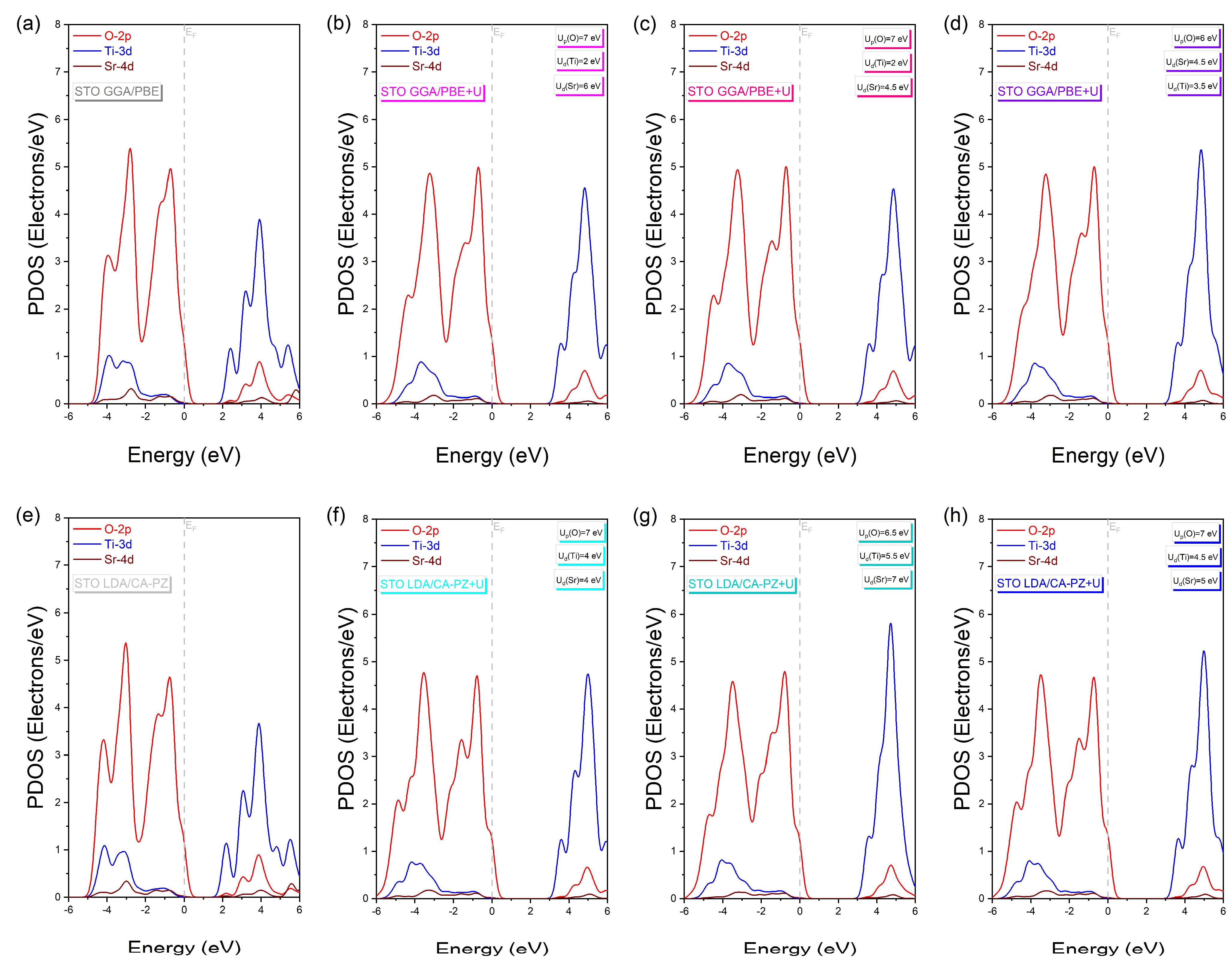
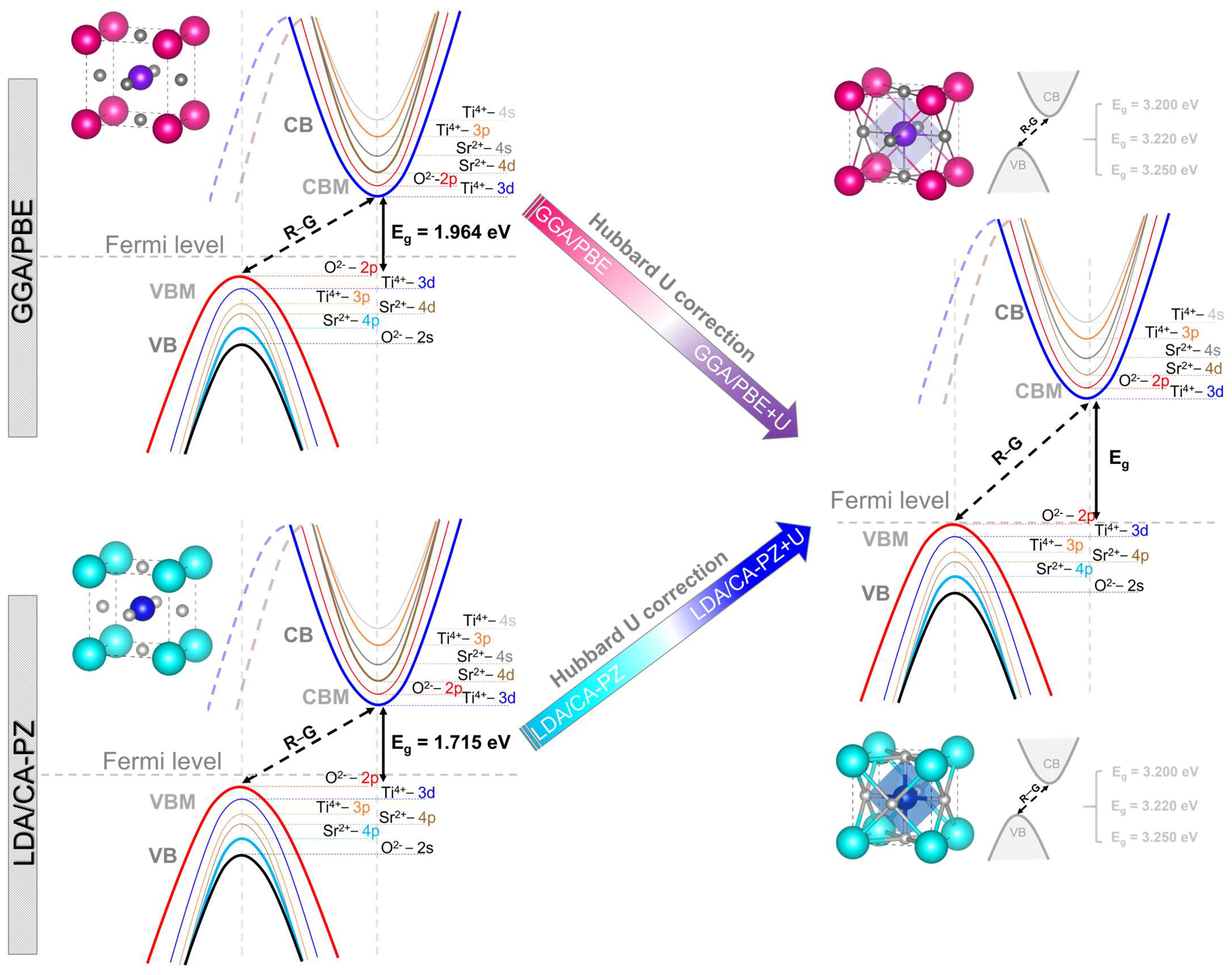
2.2. Electronic Properties
Band Structure and Density of States
2.3. Chemical Bonds
2.3.1. Electron Charges Density
2.3.2. Bond Lengths, Population, Mulliken Charges, and Effective Valence Charges
3. Computational Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, H.; Song, Y.; Gu, H.; Wang, P.; Xi, Y. A high-permittivity SrTiO3-based grain boundary barrier layer capacitor material single-fired under low temperature. Mater. Lett. 2002, 56, 802–805. [Google Scholar] [CrossRef]
- Ortmann, J.E.; Duncan, M.A.; Demkov, A.A. Designing near-infrared electro-optical devices from the SrTiO3/LaAlO3 materials system. Opt. Mater. Express 2019, 9, 2982. [Google Scholar] [CrossRef]
- Qin, L.; Li, Q.; Wu, S.; Wang, J.; Wang, Z.; Wang, L.; Wang, Q. All-Optical Reconfigurable Electronic Memory in a Graphene/SrTiO3 Heterostructure. ACS Omega 2022, 7, 15841–15845. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Tan, O.K.; Cao, W.; Zhu, W. A low temperature nano-structured SrTiO3 thick film oxygen gas sensor. Ceram. Int. 2004, 30, 1819–1822. [Google Scholar] [CrossRef]
- Trabelsi, H.; Bejar, M.; Dhahri, E.; Valente, M.A.; Graça, M.P.F. Oxygen-vacancy-related giant permittivity and ethanol sensing response in SrTiO3-δ ceramics. Phys. E Low Dimens. Syst. Nanostruct. 2019, 108, 317–325. [Google Scholar] [CrossRef]
- Chang, C.-W.; Hu, C. Graphene oxide-derived carbon-doped SrTiO3 for highly efficient photocatalytic degradation of organic pollutants under visible light irradiation. Chem. Eng. J. 2020, 383, 123116. [Google Scholar] [CrossRef]
- Deshmukh, V.V.; Ravikumar, C.R.; Kumar, M.R.A.; Ghotekar, S.; Kumar, A.N.; Jahagirdar, A.A.; Murthy, H.C.A. Structure, morphology and electrochemical properties of SrTiO3 perovskite: Photocatalytic and supercapacitor applications. Environ. Chem. Ecotoxicol. 2021, 3, 241–248. [Google Scholar] [CrossRef]
- Opoku, F.; Govender, K.K.; van Sittert, C.G.C.E.; Govender, P.P. Enhancing Charge Separation and Photocatalytic Activity of Cubic SrTiO3 with Perovskite-Type Materials MTaO3 (M=Na, K) for Environmental Remediation: A First-Principles Study. ChemistrySelect 2017, 2, 6304–6316. [Google Scholar] [CrossRef]
- Morgenbesser, M.; Schmid, A.; Viernstein, A.; de Dios Sirvent, J.; Chiabrera, F.; Bodenmüller, N.; Taibl, S.; Kubicek, M.; Baiutti, F.; Tarancon, A.; et al. SrTiO3 based high temperature solid oxide solar cells: Photovoltages, photocurrents and mechanistic insight. Solid State Ion. 2021, 368, 115700. [Google Scholar] [CrossRef]
- Reunchan, P.; Ouyang, S.; Umezawa, N.; Xu, H.; Zhang, Y.; Ye, J. Theoretical design of highly active SrTiO3-based photocatalysts by a codoping scheme towards solar energy utilization for hydrogen production. J. Mater. Chem. A 2013, 1, 4221. [Google Scholar] [CrossRef]
- Kawasaki, S.; Nakatsuji, K.; Yoshinobu, J.; Komori, F.; Takahashi, R.; Lippmaa, M.; Mase, K.; Kudo, A. Epitaxial Rh-doped SrTiO3 thin film photocathode for water splitting under visible light irradiation. Appl. Phys. Lett. 2012, 101, 033910. [Google Scholar] [CrossRef]
- Yamada, Y.; Kanemitsu, Y. Photoluminescence spectra of perovskite oxide semiconductors. J. Lumin. 2013, 133, 30–34. [Google Scholar] [CrossRef]
- van Benthem, K.; Elsässer, C.; French, R.H. Bulk electronic structure of SrTiO3: Experiment and theory. J. Appl. Phys. 2001, 90, 6156–6164. [Google Scholar] [CrossRef]
- Muhamad, N.F.; Osman, R.A.M.; Idris, M.S.; Yasin, M.N.M. Physical and electrical properties of SrTiO3 and SrZrO3. EPJ Web Conf. 2017, 162, 01052. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, H.; Inoue, T.; Yao, Q. Band gap engineering of SrTiO3 for water splitting under visible light irradiation. Int. J. Hydrogen Energy 2014, 39, 12507–12514. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Popov, A.I. Systematic trends in (0 0 1) surface ab initio calculations of ABO3 perovskites. J. Saudi Chem. Soc. 2018, 22, 459–468. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Purans, J.; Jia, R. Comparative Hybrid Hartree-Fock-DFT Calculations of WO2-Terminated Cubic WO3 as Well as SrTiO3, BaTiO3, PbTiO3 and CaTiO3 (001) Surfaces. Crystals 2021, 11, 455. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Purans, J.; Popov, A.I.; Bocharov, D.; Chekhovska, A.; Jia, R. Ab Initio Computations of O and AO as well as ReO2, WO2 and BO2-Terminated ReO3, WO3, BaTiO3, SrTiO3 and BaZrO3 (001) Surfaces. Symmetry 2022, 14, 1050. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Piskunov, S.; Heifets, E.; Kotomin, E.A.; Borstel, G. Ab initio study of the SrTiO3, BaTiO3 and PbTiO3 (001) surfaces. Ceram. Int. 2004, 30, 1989–1992. [Google Scholar] [CrossRef]
- Cappellini, G.; Bouette-Russo, S.; Amadon, B.; Noguera, C.; Finocchi, F. Structural properties and quasiparticle energies of cubic SrO, MgO and SrTiO3. J. Phys. Condens. Matter. 2000, 12, 3671–3688. [Google Scholar] [CrossRef]
- Kimura, S.; Yamauchi, J.; Tsukada, M.; Watanabe, S. First-principles study on electronic structure of the (001) surface of SrTiO3. Phys. Rev. B 1995, 51, 11049–11054. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, J.; Li, C. Effect of Metal Doping on Electronic Structure and Visible Light Absorption of SrTiO3 and NaTaO3 (Metal = Mn, Fe, and Co). J. Phys. Chem. C 2011, 115, 8305–8311. [Google Scholar] [CrossRef]
- Kang, G.; Kang, Y.; Han, S. Influence of wave-function updates in G W calculations on titanates. Phys. Rev. B 2015, 91, 155141. [Google Scholar] [CrossRef]
- Bhandari, C.; van Schilfgaarde, M.; Kotani, T.; Lambrecht, W.R. All-electron quasiparticle self-consistent GW band structures for SrTiO3 including lattice polarization corrections in different phases. Phys. Rev. Mater. 2018, 2, 013807. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef] [PubMed]
- Derkaoui, I.; Achehboune, M.; Boukhoubza, I.; El Adnani, Z.; Rezzouk, A. Improved first-principles electronic band structure for cubic (Pmm) and tetragonal (P4mm, P4/mmm) phases of BaTiO3 using the Hubbard U correction. Comput. Mater. Sci. 2023, 217, 111913. [Google Scholar] [CrossRef]
- Dompablo, M.E.A.-D.; Morales-García, A.; Taravillo, M. DFT+ U calculations of crystal lattice, electronic structure, and phase stability under pressure of TiO2 polymorphs. J. Chem. Phys. 2011, 135, 054503. [Google Scholar] [CrossRef]
- Issam, D.; Achehboune, M.; Boukhoubza, I.; Hatel, R.; El Adnani, Z.; Rezzouk, A. Investigation of the crystal structure, electronic and optical properties of Cr-doped BaTiO3 on the Ti site using first principles calculations. J. Phys. Chem. Solids 2023, 175, 111209. [Google Scholar] [CrossRef]
- Abramov, Y.A.; Tsirelson, V.G.; Zavodnik, V.E.; Ivanov, S.A.; Brown, I.D. The chemical bond and atomic displacements in SrTiO3 from X-ray diffraction analysis. Acta Crystallogr. B Struct. Sci. 1995, 51, 942–951. [Google Scholar] [CrossRef]
- Longo, V.M.; Costa, M.D.G.S.; Simões, A.Z.; Rosa, I.L.V.; Santos, C.O.P.; Andrés, J.; Longo, E.; Varela, J.A. On the photoluminescence behavior of samarium-doped strontium titanate nanostructures under UV light. A structural and electronic understanding. Phys. Chem. Chem. Phys. 2010, 12, 7566. [Google Scholar] [CrossRef]
- Piskunov, S.; Heifets, E.; Eglitis, R.I.; Borstel, G. Bulk properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: An ab initio HF/DFT study. Comput. Mater. Sci. 2004, 29, 165–178. [Google Scholar] [CrossRef]
- Tinte, S.; Stachiotti, M.G.; Rodriguez, C.O.; Novikov, D.L.; Christensen, N.E. Applications of the generalized gradient approximation to ferroelectric perovskites. Phys. Rev. B 1998, 58, 11959–11963. [Google Scholar] [CrossRef]
- Lopez-Candales, G.; Tang, Z.; Xia, W.; Jia, F.; Zhang, P. Quasiparticle band structure of SrTiO3 and BaTiO3: A combined LDA+ U and G0W0 approach. Phys. Rev. B 2021, 103, 035128. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Blokhin, E.; Gryaznov, D.; Kotomin, E.A.; Maier, J. Phonon calculations in cubic and tetragonal phases of SrTiO3: A comparative LCAO and plane-wave study. Phys. Rev. B 2011, 83, 134108. [Google Scholar] [CrossRef]
- Jauch, W.; Reehuis, M. Electron-density distribution in cubic SrTiO3: A comparative γ-ray diffraction study. Acta Crystallogr. A Found. Crystallogr. 2005, 61, 411–417. [Google Scholar] [CrossRef] [PubMed]
- Weyrich, K.-H.; Siems, R. Deformation charge distribution and total energy for perowskites. Z. Physik. B Condens. Matter. 1985, 61, 63–68. [Google Scholar] [CrossRef]
- Xiao, W.; Yoo, K.; Kim, J.H.; Xu, H. Breaking Barriers to High-Practical Li-S Batteries with Isotropic Binary Sulfiphilic Electrocatalyst: Creating a Virtuous Cycle for Favorable Polysulfides Redox Environments. Adv. Sci. 2023, 10, 2303916. [Google Scholar] [CrossRef]
- Guan, D.; Xu, H.; Zhang, Q.; Huang, Y.; Shi, C.; Chang, Y.; Xu, X.; Tang, J.; Gu, Y.; Pao, C.; et al. Identifying a universal activity descriptor and a unifying mechanism concept on perovskite oxides for green hydrogen production. Adv. Mater. 2023, 35, 2305074. [Google Scholar] [CrossRef] [PubMed]
- Guan, D.; Shi, C.; Xu, H.; Gu, Y.; Zhong, J.; Sha, Y.; Hu, Z.; Ni, M.; Shao, Z. Simultaneously mastering operando strain and reconstruction effects via phase-segregation strategy for enhanced oxygen-evolving electrocatalysis. J. Energy Chem. 2023, 82, 572–580. [Google Scholar] [CrossRef]
- Wei, W.; Dai, Y.; Jin, H.; Huang, B. Density functional characterization of the electronic structure and optical properties of Cr-doped SrTiO3. J. Phys. D Appl. Phys. 2009, 42, 055401. [Google Scholar] [CrossRef]
- Li, N.; Yao, K.L. The electronic and optical properties of carbon-doped SrTiO3: Density functional characterization. AIP Adv. 2012, 2, 032135. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]

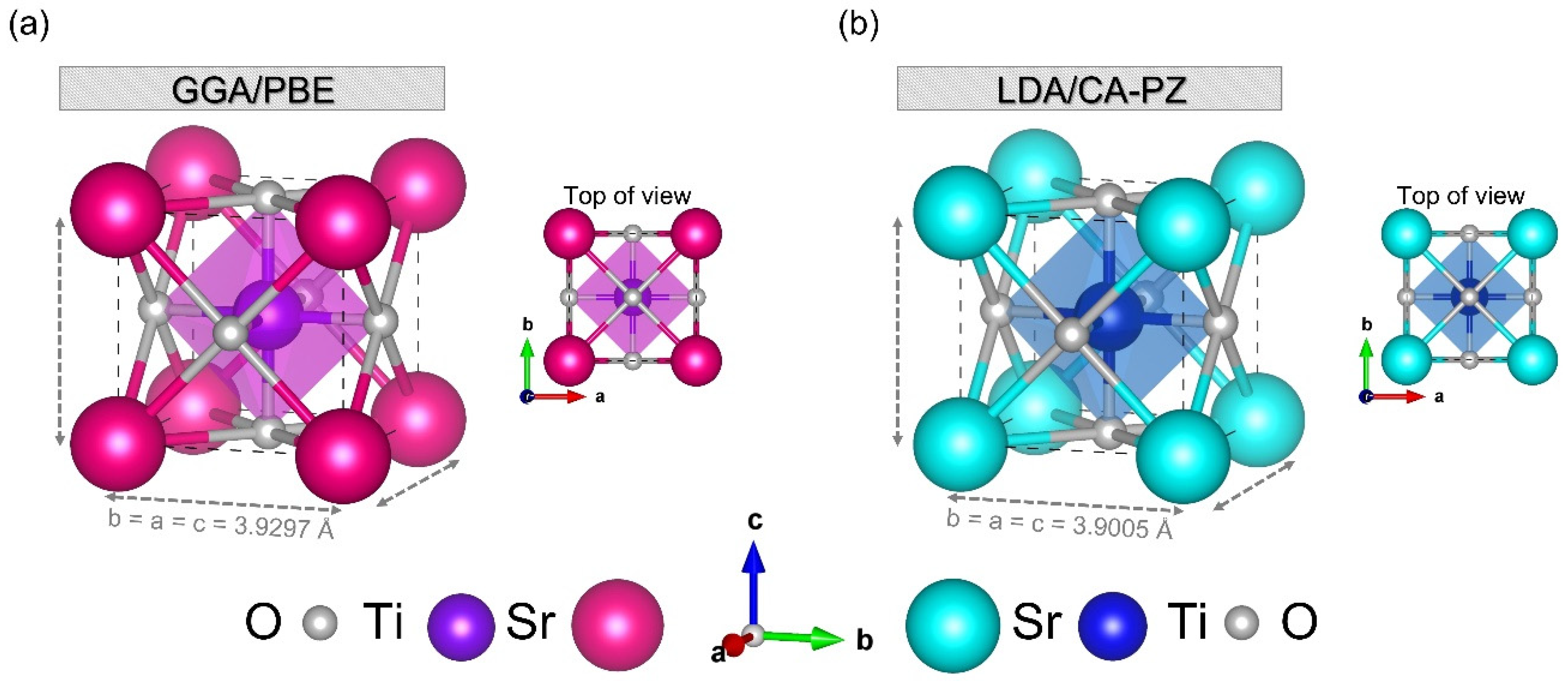

| Methods | K-Points | Cut-Off (eV) | ai = bi = ci (Å) | af = bf = cf (Å) | Deviation (%) | Vi (Å3) | Vf (Å3) | Deviation (%) |
|---|---|---|---|---|---|---|---|---|
| STO: (Pmm) [Pseudopotential methods: OTFG Ultrasoft (GGA/PBE), OTFG norm-conserving (LDA/CA-PZ)] | ||||||||
| GGA/PBE | 2 × 2 × 2 | 800 | 3.901 [a] | 3.9297 | 0.7303 | 59.365 [a] | 60.687 | 2.1783 |
| LDA/CA-PZ | 3 × 3 × 3 | 570 | 3.901 [a] | 3.9005 | −0.0128 | 59.365 [a] | 59.344 | −0.0353 |
| Structure | This Calculation | Experimental Data | Previous Theoretical Results (DFT Functional) | |
|---|---|---|---|---|
| DFT Functional | a = b = c | |||
| STO | GGA/PBE | 3.9297 | 3.901 [29], 3.907 [20]. | 3.850 (LDA) [20], 3.86 (LDA), 3.95 (PWGGA), 3.94 (PBE), 3.98 (BLYP), 3.90 (P3PW), 3.94 (P3LYP), 3.92 (HF) [31], 3.862 (LSDA), 3.947 (PBE-GGA) [32]. |
| Methods | Up(O) | Ud(Ti) | Ud(Sr) | Eg (eV) | Deviations (%) | |
|---|---|---|---|---|---|---|
| This Cal. | Exp Data. | |||||
| GGA/PBE | 0 | 0 | 0 | 1.964 | - | - |
| 5 | 4.5 | 6.5 | 3.195 | 3.20 [11] | −0.156 | |
| 5.5 | 3.5 | 0 | 3.203 | 0.093 | ||
| 5.5 | 4 | 7 | 3.196 | −0.125 | ||
| 6.5 | 2.5 | 4 | 3.203 | 0.093 | ||
| 6.5 | 3 | 8.5 | 3.193 | −0.219 | ||
| 6 | 3 | 2 | 3.203 | 0.093 | ||
| 6 | 3.5 | 7.5 | 3.199 | −0.031 | ||
| 6 | 4 | 10 | 3.206 | 0.187 | ||
| 7 | 2 | 6 | 3.200 | 0 | ||
| 7 | 2.5 | 9 | 3.201 | 0.031 | ||
| 7.5 | 1 | 3 | 3.199 | −0.031 | ||
| 5.5 | 4 | 5.5 | 3.222 | 3.22 [12] | 0.062 | |
| 6 | 3 | 0 | 3.220 | 0 | ||
| 6 | 3.5 | 6.5 | 3.219 | −0.031 | ||
| 6 | 4 | 9.5 | 3.224 | 0.124 | ||
| 6.5 | 2.5 | 2 | 3.223 | 0.093 | ||
| 6.5 | 3 | 7 | 3.227 | 0.216 | ||
| 6.5 | 3.5 | 10 | 3.221 | 0.031 | ||
| 7 | 2 | 4 | 3.226 | 0.185 | ||
| 7 | 2 | 4.5 | 3.220 | 0 | ||
| 7 | 2.5 | 8 | 3.227 | 0.216 | ||
| 7.5 | 2 | 9 | 3.225 | 0.155 | ||
| 5 | 4.5 | 2 | 3.256 | 3.25 [13] | 0.184 | |
| 5.5 | 4 | 3 | 3.255 | 0.153 | ||
| 6 | 3.5 | 4 | 3.257 | 0.214 | ||
| 6 | 3.5 | 4.5 | 3.250 | 0 | ||
| 6 | 4 | 8.5 | 3.254 | 0.122 | ||
| 6.5 | 3 | 5.5 | 3.254 | 0.122 | ||
| 6.5 | 3.5 | 9 | 3.254 | 0.122 | ||
| 7 | 2 | 1 | 3.255 | 0.153 | ||
| 7 | 2 | 1.5 | 3.251 | 0.030 | ||
| 7 | 2,5 | 6.5 | 3.258 | 0.245 | ||
| 7 | 3 | 9.5 | 3.256 | 0.184 | ||
| LDA/CA-PZ | 0 | 0 | 0 | 1.715 | - | - |
| 5.5 | 6.5 | 6 | 3.209 | 3.20 [11] | 0.280 | |
| 6.5 | 5.5 | 7.5 | 3.191 | −0.282 | ||
| 7 | 4 | 4 | 3.200 | 0 | ||
| 7 | 5 | 8 | 3.197 | −0.093 | ||
| 6.5 | 5.5 | 7 | 3.224 | 3.22 [12] | 0.124 | |
| 7 | 4 | 1.5 | 3.227 | 0.216 | ||
| 7 | 4 | 2.5 | 3.214 | −0.186 | ||
| 7.5 | 4 | 7 | 3.226 | 0.185 | ||
| 5.5 | 6.5 | 5.5 | 3.259 | 3.25 [13] | 0.276 | |
| 6 | 6 | 5 | 3.251 | 0.030 | ||
| 6.5 | 5.5 | 6 | 3.259 | 0.276 | ||
| 7 | 4.5 | 5 | 3.250 | 0 | ||
| These Calculations (eV) | Exp. Data (eV) | Previous Theoretical Results (eV) Indirect Band Gaps (Without U) | |||
|---|---|---|---|---|---|
| Without U | With U | ||||
| Methods | Methods | ||||
| GGA/PBE | LDA/CA-PZ | GGA/PBE | LDA/CA-PZ | ||
| 1.964 [R-G] | 1.715 [M-G] | 3.200 [R-G] | 3.200 [R-G] | 3.20 [11] | 1.89 [R-Γ] (LDA) [13], 1.90 [R-Γ] (LDA) [20], 1.79 [R-Γ] (LDA PW) [21], 1.73 (GGA) [22], 2.04 [R-Γ] (LDA), 1.97 [R-Γ] (PWGGA), 1.99 [R-Γ] (PBE) [31], 1.8 (LCAO/PBE), 1.8 (PW/PBE) [34]. |
| 3.220 [R-G] | 3.224 [R-G] | 3.22 [12] | |||
| 3.250 [R-G] | 3.250 [R-G] | 3.25 [13] | |||
| ] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Species | Mulliken Charges (e) | Effective Valence Charges (e) | ||||||
| Eg = 1.964 (eV) | Eg = 3.200 (eV) | Eg = 3.220 (eV) | Eg = 3.250 (eV) | Eg = 1.964 (eV) | Eg = 3.200 (eV) | Eg = 3.220 (eV) | Eg = 3.250 (eV) | ||
| GGA/PBE | Sr | 1.37 | 1.61 | 1.58 | 1.56 | 0.57 | 0.36 | 0.39 | 0.40 |
| Ti | 0.85 | 1.02 | 1.03 | 1.03 | 2.24 | 1.93 | 1.93 | 1.92 | |
| O1=O2=O3 | −0.74 | −0.88 | −0.87 | −0.87 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Method | Species | Mulliken charges (e) | Effective valence charges (e) | ||||||
| Eg = 1.715 (eV) | Eg = 3.200 (eV) | Eg = 3.224 (eV) | Eg = 3.250 (eV) | Eg = 1.715 (eV) | Eg = 3.200 (eV) | Eg = 3.224 (eV) | Eg = 3.250 (eV) | ||
| LDA/CA-PZ | Sr | 1.35 | 1.57 | 1.66 | 1.60 | 0.65 | 0.45 | 0.34 | 0.42 |
| Ti | 0.84 | 1.06 | 1.06 | 1.07 | 2.17 | 1.80 | 1.76 | 1.78 | |
| O1=O2=O3 | −0.73 | −0.88 | −0.90 | −0.89 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Method | Bond | Population | Lengths (Å) | ||||||
| Eg = 1.964 (eV) | Eg = 3.200 (eV) | Eg = 3.220 (eV) | Eg = 3.250 (eV) | Eg = 1.964 (eV) | Eg = 3.200 (eV) | Eg = 3.220 (eV) | Eg = 3.250 (eV) | ||
| GGA/PBE | O-Sr | 0.13 | 0.04 | 0.05 | 0.06 | 2.778 | 2.791 | 2.782 | 2.792 |
| O-Ti | 0.86 | 0.92 | 0.92 | 0.91 | 1.964 | 1.973 | 1.967 | 1.974 | |
| O-O | −0.14 | −0.13 | −0.13 | −0.13 | 2.778 | 2.791 | 2.782 | 2.792 | |
| Method | Bond | Population | Lengths (Å) | ||||||
| Eg = 1.715 (eV) | Eg = 3.200 (eV) | Eg = 3.224 (eV) | Eg = 3.250 (eV) | Eg = 1.715 (eV) | Eg = 3.200 (eV) | Eg = 3.224 (eV) | Eg = 3.250 (eV) | ||
| LDA/CA-PZ | O-Sr | 0.10 | 0.03 | 0.01 | 0.02 | 2.748 | 2.760 | 2.797 | 2.773 |
| O-Ti | 0.90 | 0.96 | 0.98 | 0.97 | 1.943 | 1.952 | 1.978 | 1.960 | |
| O-O | −0.16 | −0.15 | −0.14 | −0.14 | 2.748 | 2.760 | 2.797 | 2.773 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derkaoui, I.; Achehboune, M.; Eglitis, R.I.; Popov, A.I.; Boukhoubza, I.; Basyooni-M. Kabatas, M.A.; Rezzouk, A.
Influence of the Hubbard U Correction on the Electronic Properties and Chemical Bands of the Cubic (Pm
Derkaoui I, Achehboune M, Eglitis RI, Popov AI, Boukhoubza I, Basyooni-M. Kabatas MA, Rezzouk A.
Influence of the Hubbard U Correction on the Electronic Properties and Chemical Bands of the Cubic (Pm
Derkaoui, Issam, Mohamed Achehboune, Roberts I. Eglitis, Anatoli I. Popov, Issam Boukhoubza, Mohamed A. Basyooni-M. Kabatas, and Abdellah Rezzouk.
2024. "Influence of the Hubbard U Correction on the Electronic Properties and Chemical Bands of the Cubic (Pm
Derkaoui, I., Achehboune, M., Eglitis, R. I., Popov, A. I., Boukhoubza, I., Basyooni-M. Kabatas, M. A., & Rezzouk, A.
(2024). Influence of the Hubbard U Correction on the Electronic Properties and Chemical Bands of the Cubic (Pm









