The Effects of External Interfaces on Hydrophobic Interactions I: Smooth Surface
Abstract
:1. Introduction
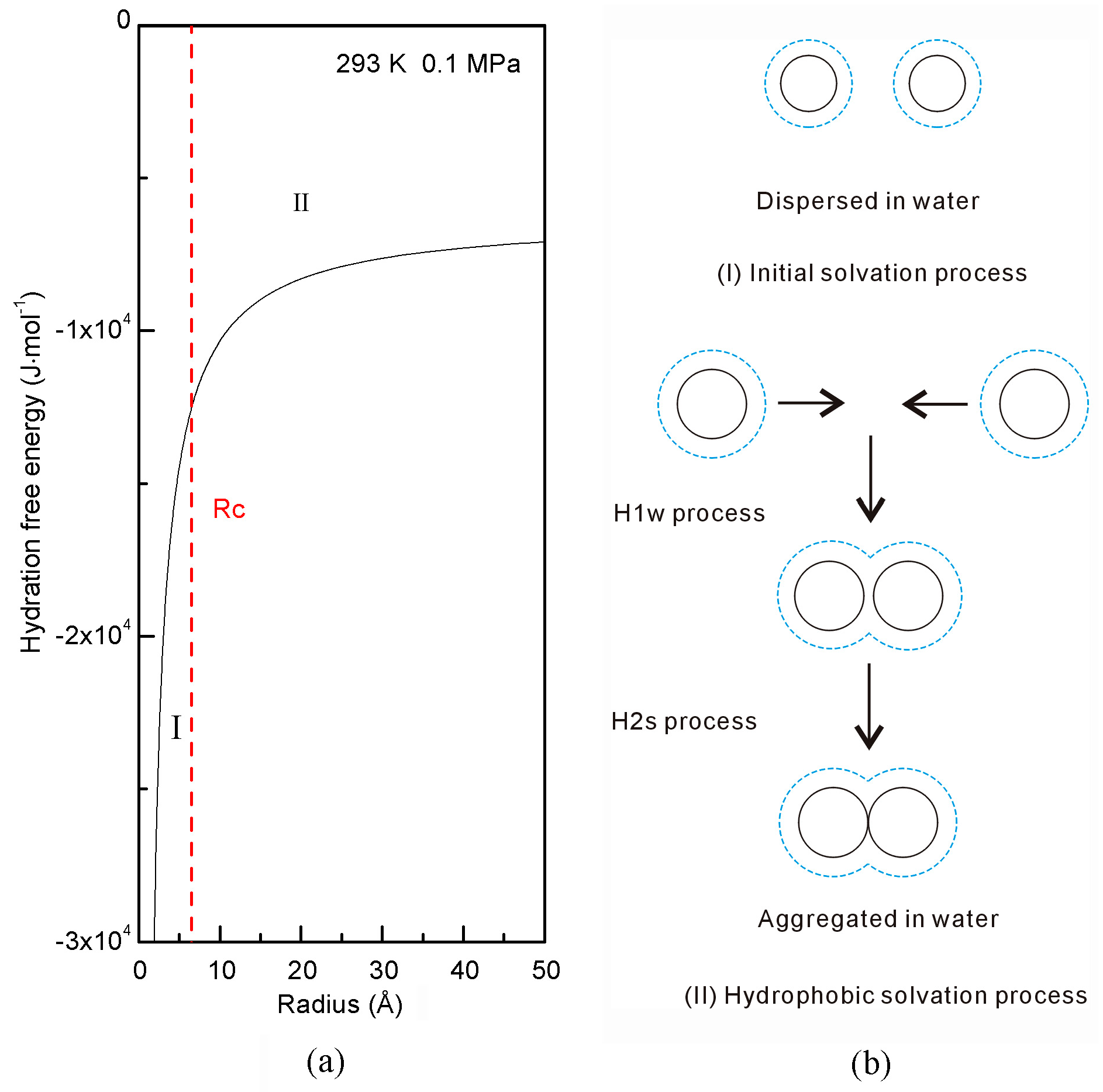
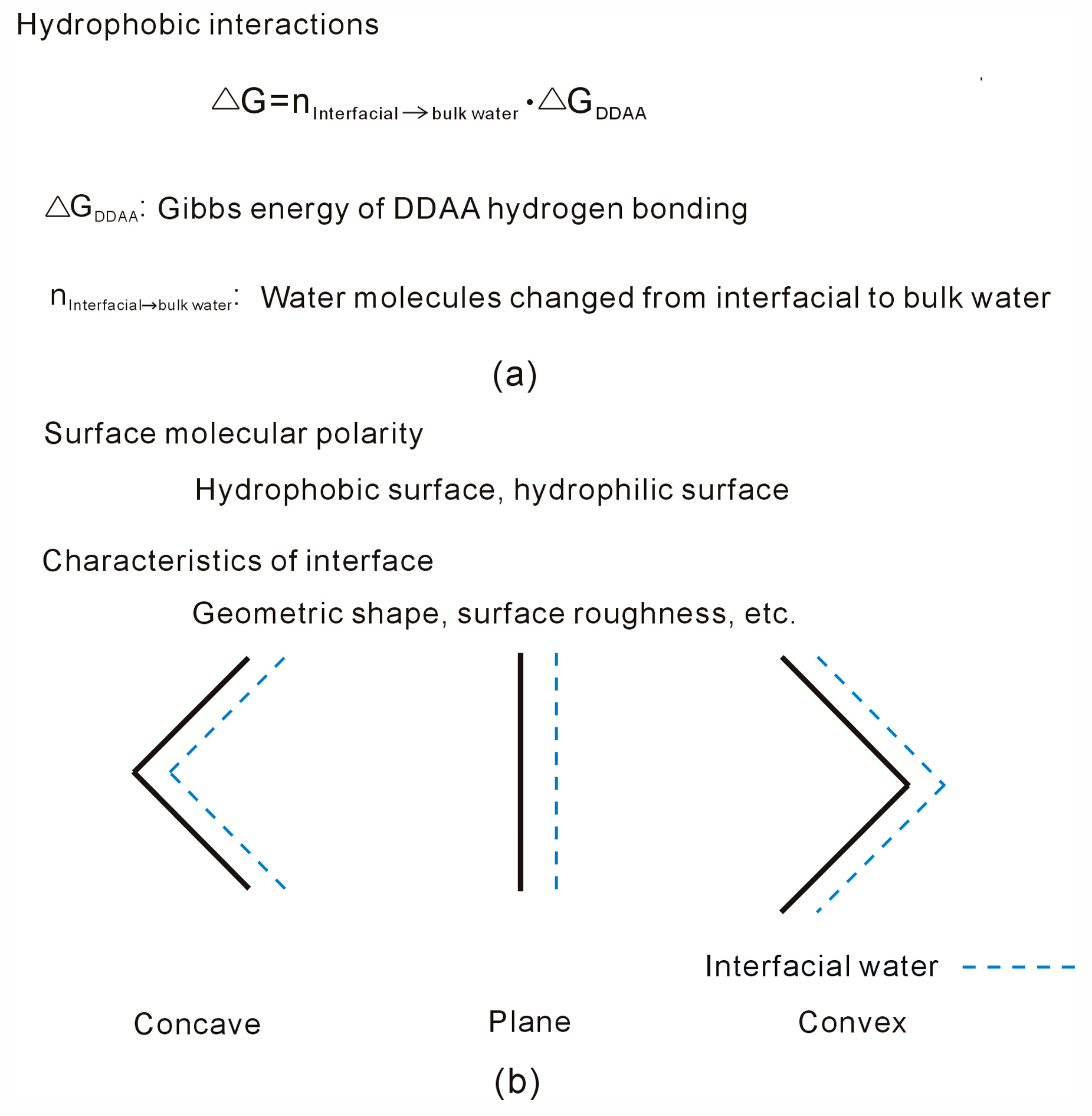
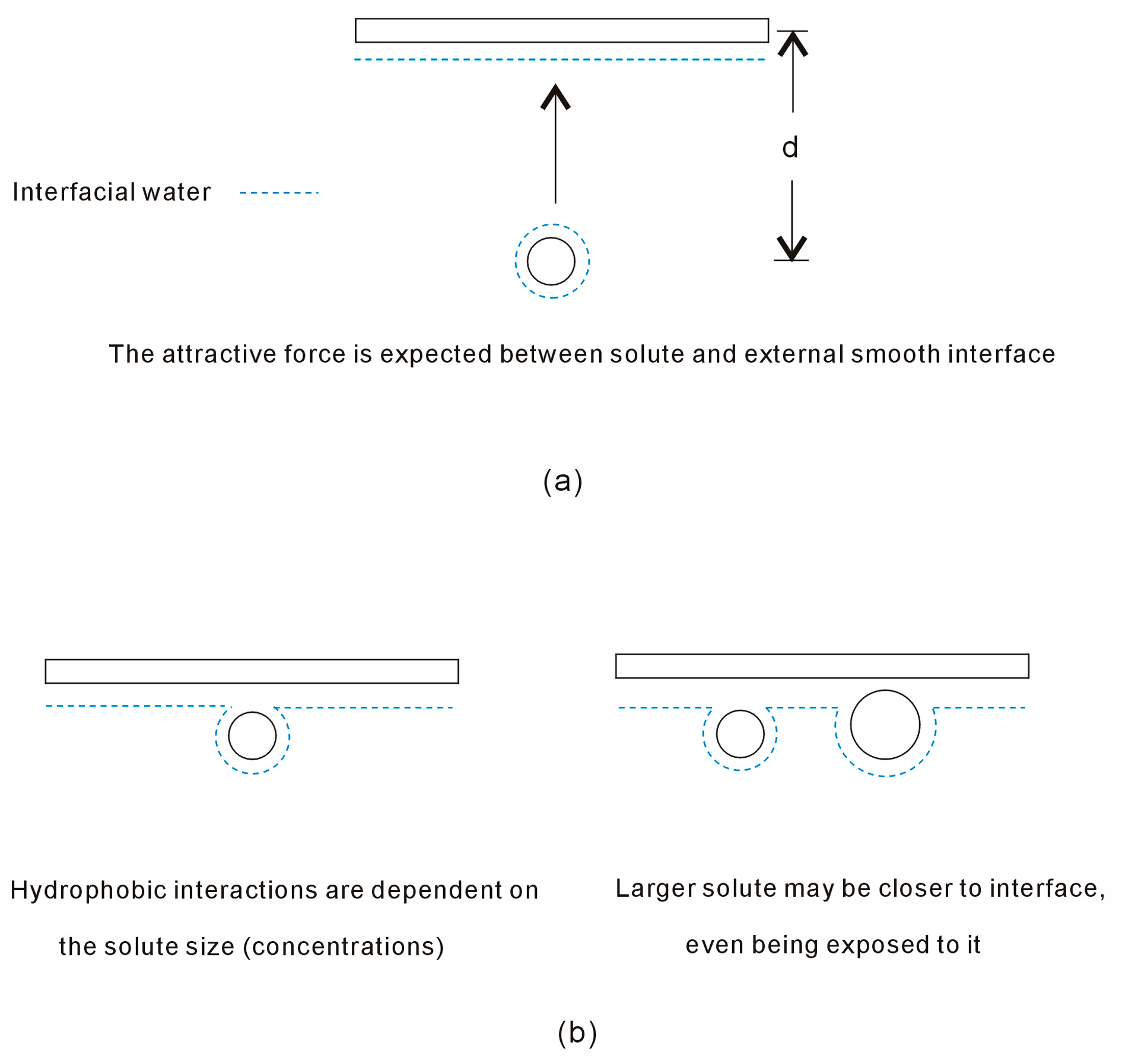
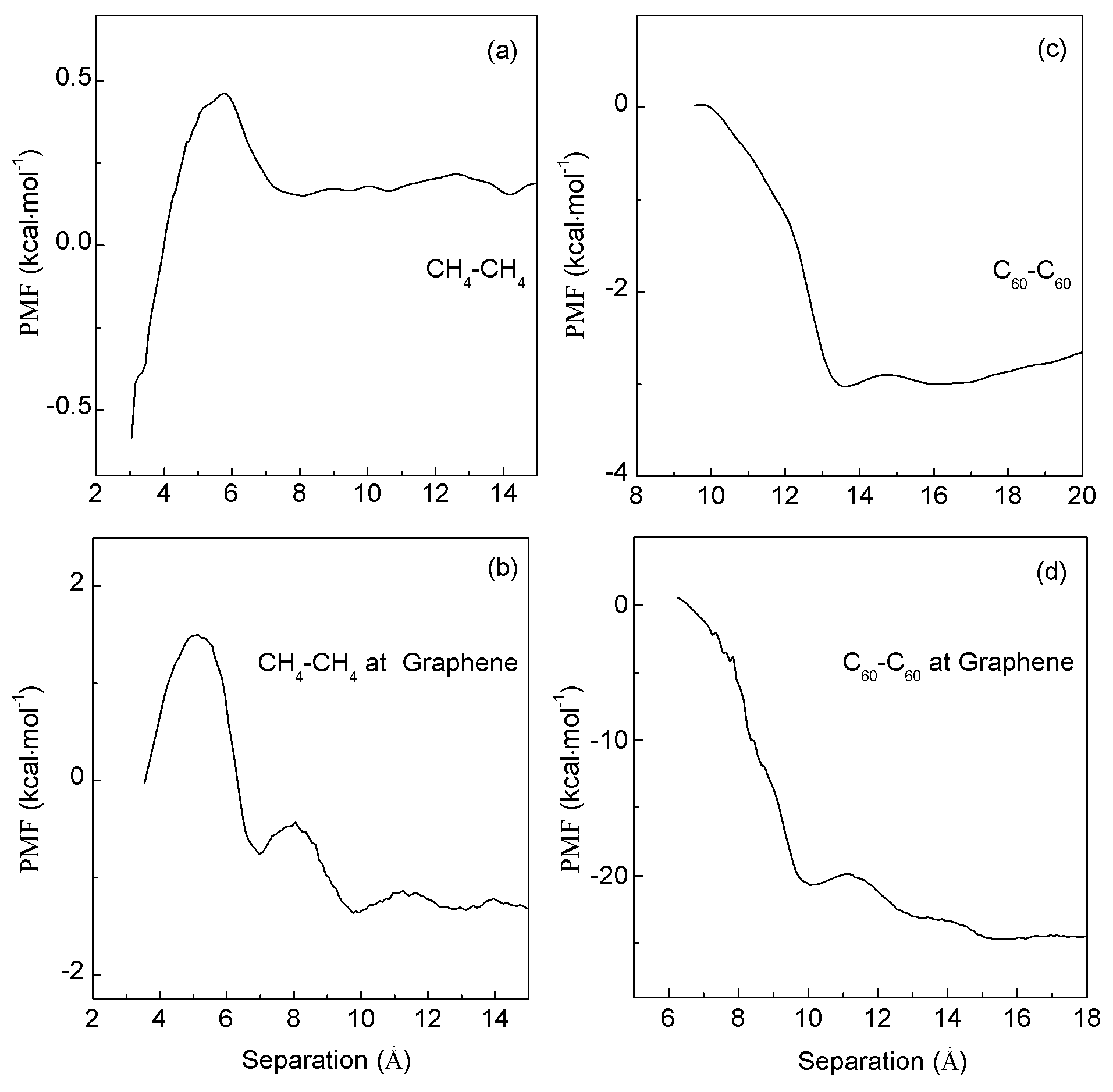
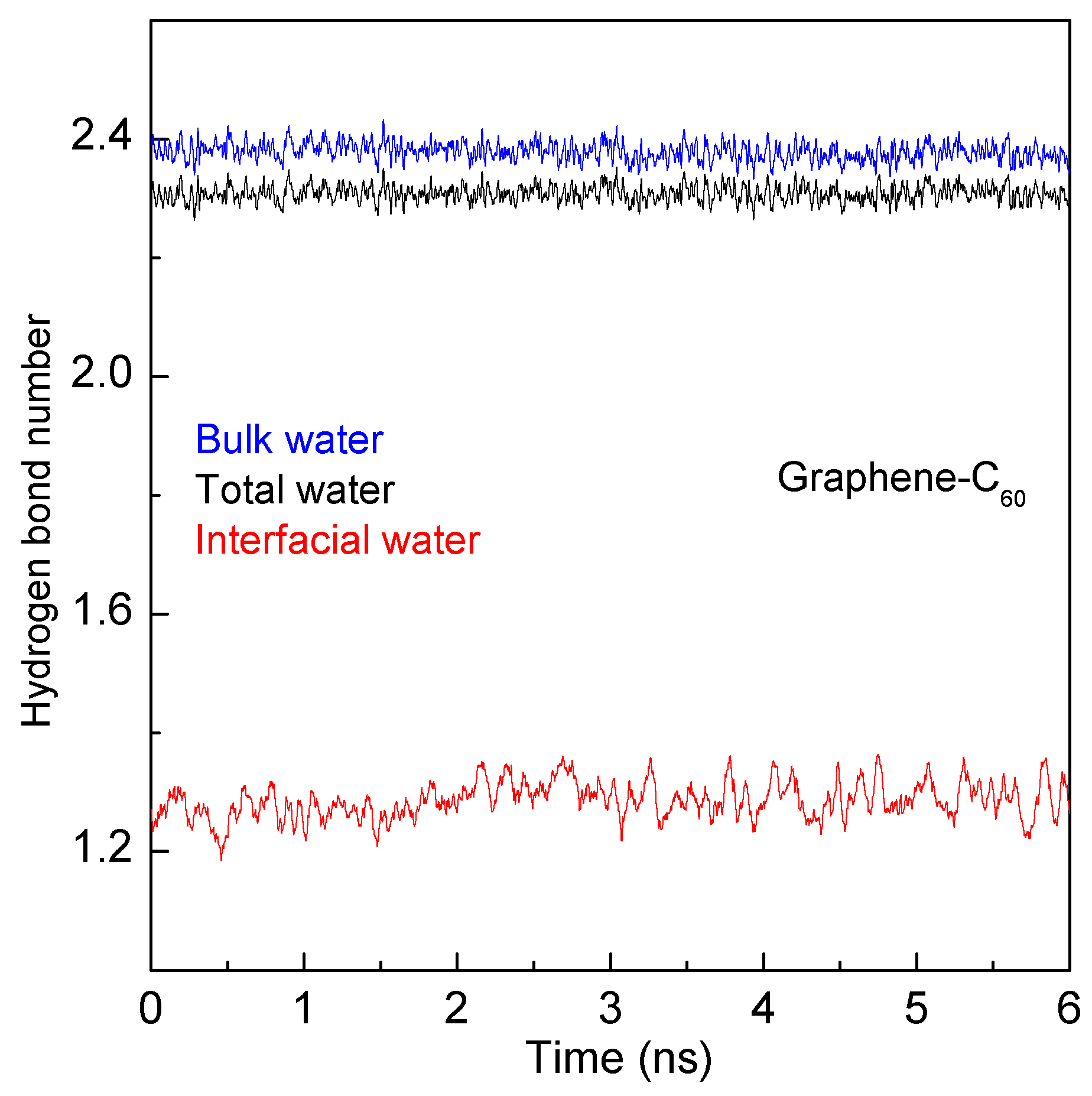
2. Results and Discussion
2.1. Thermodynamic Analysis
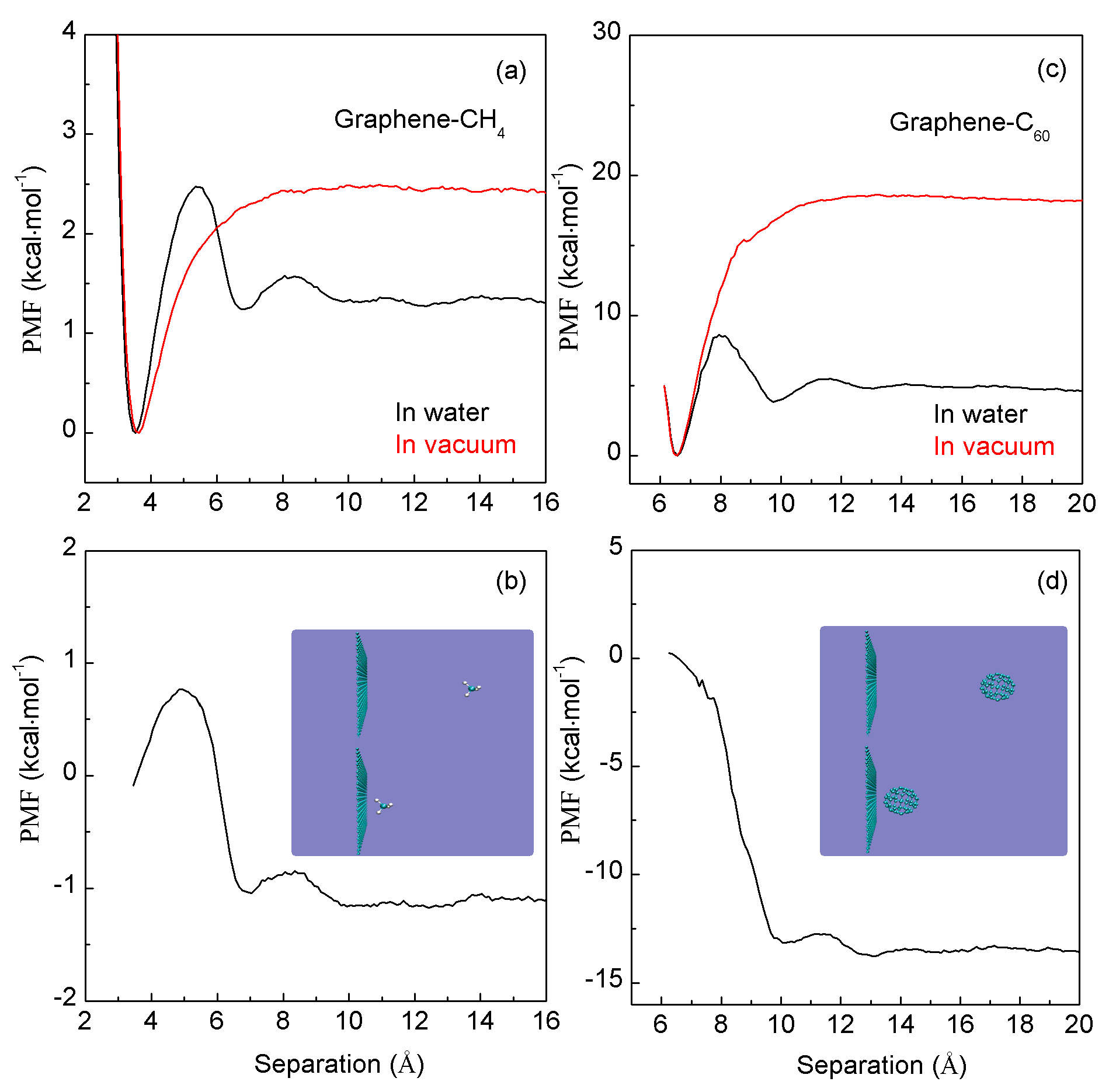
2.2. MD Simulations
3. Methods
3.1. MD Simulations
3.2. PMF Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grigolato, F.; Arosio, P. The role of surfaces on amyloid formation. Biophys. Chem. 2021, 270, 106533. [Google Scholar] [CrossRef]
- Morinaga, A.; Hasegawa, K.; Nomura, R.; Ookoshi, T.; Ozawa, D.; Goto, Y.; Yamada, M.; Naiki, H. Critical role of interfaces and agitation on the nucleation of Aβ amyloid fibrils at low concentrations of Aβ monomers. Biochim. Biophys. Acta 2010, 1804, 986–995. [Google Scholar] [CrossRef]
- Jean, L.; Lee, C.F.; Vaux, D.J. Enrichment of amyloidogenesis at an air-water interface. Biophys. J. 2012, 102, 1154–1162. [Google Scholar] [CrossRef]
- Itoh, S.G.; Yagi-Utsumi, M.; Kato, K.; Okumura, H. Effects of a hydrophilic/hydrophobic interface on amyloid-β peptides studied by molecular dynamics simulations and NMR experiments. J. Phys. Chem. B 2019, 123, 160–169. [Google Scholar] [CrossRef]
- Yagi-Utsumi, M.; Kato, K.; Nishimura, K. Membrane-induced dichotomous conformation of amyloid β with the disordered N-terminal segment followed by the stable C-terminal β structure. PLoS ONE 2016, 11, e0146405. [Google Scholar] [CrossRef]
- Fantini, J.; Yahi, N. Molecular insights into amyloid regulation by membrane cholesterol and sphingolipids: Common mechanisms in neurodegenerative diseases. Expert Rev. Mol. Med. 2010, 12, e27. [Google Scholar] [CrossRef]
- Kakio, A.; Nishimoto, S.; Yanagisawa, K.; Kozutsumi, Y. Interactions of amyloid β-protein with various gangliosides in raft-like membranes: Importance of GM1 ganglioside-bound form as an endogenous seed for Alzheimer amyloid. Biochemistry 2002, 41, 7385–7390. [Google Scholar] [CrossRef]
- Somorjai, G.A.; Rupprechter, G. Molecular studies of catalytic reactions on crystal surfaces at high pressures and high temperatures by infrared-visible sum frequency generation (SFG) surface vibrational spectroscopy. J. Phys. Chem. B 1999, 103, 1623–1638. [Google Scholar] [CrossRef]
- Li, X.; Rupprechter, G. Sum frequency generation spectroscopy in heterogeneous model catalysis: A minireview of co-related processes. Catal. Sci. Technol. 2021, 11, 12–26. [Google Scholar] [CrossRef]
- Wellen, B.A.; Lach, E.A.; Allen, H.C. Surface pK a of octanoic, nonanoic, and decanoic fatty acids at the air–water interface: Applications to atmospheric aerosol chemistry. Phys. Chem. Chem. Phys. 2017, 19, 26551–26558. [Google Scholar] [CrossRef]
- Jubb, A.M.; Hua, W.; Allen, H.C. Organization of water and atmospherically relevant ions and solutes: Vibrational sum frequency spectroscopy at the vapor/liquid and liquid/solid interfaces. Acc. Chem. Res. 2012, 45, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Patrow, J.G.; Sorenson, S.A.; Dawlaty, J.M. Direct spectroscopic measurement of interfacial electric fields near an electrode under polarizing or current-carrying conditions. J. Phys. Chem. C 2017, 121, 11585–11592. [Google Scholar] [CrossRef]
- Kato, M.; Oyaizu, N.; Shimazu, K.; Yagi, I. Oxygen reduction reaction catalyzed by self-assembled monolayers of copper-based electrocatalysts on a polycrystalline gold surface. J. Phys. Chem. C 2016, 120, 15814–15822. [Google Scholar] [CrossRef]
- Gonella, G.; Backus, E.H.G.; Nagata, Y.; Bonthuis, D.J.; Loche, P.; Schlaich, A.; Netz, R.R.; Kühnle, A.; McCrum, I.T.; Koper, M.T.M.; et al. Water at charged interfaces. Nat. Rev. Chem. 2021, 5, 466–485. [Google Scholar] [CrossRef] [PubMed]
- Knipping, E.M.; Lakin, M.J.; Foster, K.L.; Jungwirth, P.; Tobias, D.J.; Gerber, R.B.; Dabdub, D.; Finlayson-pitts, B.J. Experiments and simulations of ion-enhanced interfacial chemistry on aqueous nacl aerosols. Science 2000, 288, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, P.; Tobias, D.J. Surface effects on aqueous ionic solvation: A molecular dynamics simulation study of NaCl at the air/water interface from infinite dilution to saturation. J. Phys. Chem. B 2000, 104, 7702–7706. [Google Scholar] [CrossRef]
- Ghosal, S.; Hemminger, J.C.; Bluhm, H.; Mun, B.S.; Hebenstreit, E.L.D.; Ketteler, G.; Ogletree, D.F.; Requejo, F.G.; Salmeron, M. Electron spectroscopy of aqueous solution interfaces reveals surface enhancement of halides. Science 2005, 307, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Petersen, P.; Saykally, R. On the nature of ions at the liquid water surface. Annu. Rev. Phys. Chem. 2006, 57, 333–364. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, P.; Tobias, D.J. Specific ion effects at the air/water interface. Chem. Rev. 2006, 106, 1259–1281. [Google Scholar] [CrossRef]
- Caleman, C.; van der Spoel, D. Evaporation from water clusters containing singly charged ions. Phys. Chem. Chem. Phys. 2007, 9, 5105–5111. [Google Scholar] [CrossRef]
- Collins, K.D.; Washabaugh, M.W. The Hofmeister effect and the behavior of water at interfaces. Q. Rev. Biophys. 1985, 18, 323–422. [Google Scholar] [CrossRef] [PubMed]
- Wick, C.D.; Kuo, I.F.W.; Mundy, C.J.; Dang, L.X. The effect of polarizability for understanding the molecular structure of aqueous interfaces. J. Chem. Theory Comput. 2007, 3, 2002–2010. [Google Scholar] [CrossRef] [PubMed]
- Levin, Y.; dos Santos, A.P.; Diehl, A. Ions at the air-water interface: An end to a hundred-year-old mystery? Phys. Rev. Lett. 2009, 103, 257802. [Google Scholar] [CrossRef]
- Levin, Y. Polarizable ions at interfaces. Phys. Rev. Lett. 2009, 102, 147803. [Google Scholar] [CrossRef] [PubMed]
- Kunz, W.; Henle, J.; Ninham, B.W. For the study of the effect of salts: Franz Hofmeister’s historical papers (Translated from German). Curr. Opin. Colloid Interface Sci. 2004, 9, 19–37. [Google Scholar] [CrossRef]
- Bostrom, M.; Ninham, B.W. Dispersion self-free energies and interaction free energies of finite-sized ions. Langmuir 2004, 20, 7569–7574. [Google Scholar] [CrossRef] [PubMed]
- Noah-Vanhoucke, J.; Geissler, P.L. On the fluctuations that drive small ions toward, and away from, interfaces between polar liquids and their vapors. Proc. Natl. Acad. Sci. USA 2009, 106, 15125–15130. [Google Scholar] [CrossRef]
- Caleman, C.; Hub, J.S.; van Maaren, P.J.; van der Spoel, D. Atomistic simulation of ion solvation in water explains surface preference of halides. Proc. Natl. Acad. Sci. USA 2011, 108, 6838–6842. [Google Scholar] [CrossRef]
- Colussi, A.J.; Cheng, J.; Hoffmann, M.R. Anion fractionation and reactivity at air/water: Methanol interfaces. Implications for the origin of Hofmeister effects. J. Phys. Chem. B 2008, 112, 7157–7161. [Google Scholar]
- Ruiz-Lopez, M.F.; Francisco, J.S.; Martins-Costa, M.T.C.; Anglada, J.M. Molecular reactions at aqueous interfaces. Nat. Rev. Chem. 2020, 4, 459–475. [Google Scholar] [CrossRef]
- Narayan, S.; Muldoon, J.; Finn, M.G.; Fokin, V.V.; Kolb, H.C.; Sharpless, K.B. “On water”: Unique reactivity of organic compounds in aqueous suspension. Angew. Chem. Int. Ed. 2005, 44, 3275–3279. [Google Scholar] [CrossRef]
- Frank, H.S.; Evans, M.W. Free volume and entropy in condensed systems III. Entropy in binary liquid mixtures; partial molal entropy in dilute solutions; structure and thermodynamics in aqueous electrolytes. J. Chem. Phys. 1945, 13, 507–532. [Google Scholar] [CrossRef]
- Kauzmann, W. Some factors in the interpretation of protein denaturation. Adv. Protein Chem. 1959, 14, 1–63. [Google Scholar]
- Davis, J.G.; Gierszal, K.P.; Wang, P.; Ben-Amotz, D. Water structural transformation at molecular hydrophobic interfaces. Nature 2012, 491, 582–585. [Google Scholar] [CrossRef]
- Galamba, N. Water’s structure around hydrophobic solutes and the iceberg model. J. Phys. Chem. B 2013, 117, 2153–2159. [Google Scholar] [CrossRef]
- Raschke, T.M.; Levitt, M. Nonpolar solutes enhance water structure within hydration shells while reducing interactions between them. Proc. Natl. Acad. Sci. USA 2005, 102, 6777–6782. [Google Scholar] [CrossRef]
- Rezus, Y.L.A.; Bakker, H.J. Observation of immobilized water molecules around hydrophobic groups. Phys. Rev. Lett. 2007, 99, 148301. [Google Scholar] [CrossRef]
- Turner, J.; Soper, A.K.; Finney, J.L. A neutron-diffraction study of tetramethylammonium chloride in aqueous solution. Mol. Phys. 1990, 70, 679–700. [Google Scholar] [CrossRef]
- Qvist, J.; Halle, B. Thermal signature of hydrophobic hydration dynamics. J. Am. Chem. Soc. 2008, 130, 10345–10353. [Google Scholar] [CrossRef]
- Buchanan, P.; Aldiwan, N.; Soper, A.K.; Creek, J.L.; Koh, C.A. Decreased structure on dissolving methane in water. Chem. Phys. Lett. 2005, 415, 89–93. [Google Scholar] [CrossRef]
- Bakulin, A.A.; Liang, C.; Jansen, T.L.; Wiersma, D.A.; Bakker, H.J.; Pshenichnikov, M.S. Hydrophobic solvation: A 2D IR spectroscopic inquest. Acc. Chem. Res. 2009, 42, 1229–1238. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q. The effects of dissolved hydrophobic and hydrophilic groups on water structure. J. Solution Chem. 2020, 49, 1473–1484. [Google Scholar] [CrossRef]
- Stillinger, F.H. Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled particle theory. J. Solution Chem. 1973, 2, 141–158. [Google Scholar] [CrossRef]
- Huang, D.M.; Geissler, P.L.; Chandler, D. Scaling of hydrophobic solvation free energies. J. Phys. Chem. B 2001, 105, 6704–6709. [Google Scholar] [CrossRef]
- Lum, K.; Chandler, D.; Weeks, J.D. Hydrophobicity at small and large length scales. J. Phys. Chem. B 1999, 103, 4570–4577. [Google Scholar] [CrossRef]
- Chandler, D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q. The physical origin of hydrophobic effects. Chem. Phys. Lett. 2017, 672, 21–25. [Google Scholar] [CrossRef]
- Sun, Q.; Su, X.W.; Cheng, C.B. The dependence of hydrophobic interactions on the solute size. Chem. Phys. 2019, 516, 199–205. [Google Scholar] [CrossRef]
- Sun, Q. The hydrophobic effects: Our current understanding. Molecules 2022, 27, 7009. [Google Scholar] [CrossRef]
- Ball, P. Water as an active constituent in cell biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
- Ball, P. Water is an active matrix of life for cell and molecular biology. Proc. Natl. Acad. Sci. USA 2017, 114, 13327–13335. [Google Scholar] [CrossRef] [PubMed]
- Vembanur, S.; Patel, A.J.; Sarupria, S.; Garde, S. On the thermodynamics and kinetics of hydrophobic interactions at interfaces. J. Phys. Chem. B 2013, 117, 10261–10270. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q. The Raman OH stretching bands of liquid water. Vib. Spectrosc. 2009, 51, 213–217. [Google Scholar] [CrossRef]
- Sun, Q. Local statistical interpretation for water structure. Chem. Phys. Lett. 2013, 568, 90–94. [Google Scholar] [CrossRef]
- Stanley, H.E.; Teixeira, J. Interpretation of the unusual behavior of H2O and D2O at low temperatures: Tests of a percolation model. J. Chem. Phys. 1980, 73, 3404–3422. [Google Scholar] [CrossRef]
- Nilsson, A.; Pettersson, L.G.M. Perspective on the structure of liquid water. Chem. Phys. 2011, 389, 1–34. [Google Scholar] [CrossRef]
- Russo, J.; Tanaka, H. Understanding water’s anomalies with locally favoured structures. Nat. Commun. 2014, 5, 3556. [Google Scholar] [CrossRef] [PubMed]
- Hamm, P. Markov state model of the two-state behaviour of water. J. Chem. Phys. 2016, 145, 134501. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Tanaka, H. Microscopic structural descriptor of liquid water. J. Chem. Phys. 2018, 148, 124503. [Google Scholar] [CrossRef] [PubMed]
- Hura, G.; Sorenson, J.M.; Glaeser, R.M.; Head-Gordon, T. A high-quality X-ray scattering experiment on liquid water at ambient conditions. J. Chem. Phys. 2000, 113, 9140. [Google Scholar] [CrossRef]
- Sun, Q.; Guo, Y. Vibrational sum frequency generation spectroscopy of the air/water interface. J. Mol. Liq. 2016, 213, 28–32. [Google Scholar] [CrossRef]
- Dorsey, N.E. Properties of Ordinary Water Substance; ACS Monograph No. 81; Reinhold: New York, NY, USA, 1940. [Google Scholar]
- Bresme, F.; Chacón, E.; Tarazona, P.; Tay, K. Intrinsic structure of hydrophobic surfaces: The oil-water interface. Phys. Rev. Lett. 2008, 101, 056102. [Google Scholar] [CrossRef] [PubMed]
- Willard, A.P.; Chandler, D. The molecular structure of the interface between water and a hydrophobic substrate is liquid-vapor like. J. Chem. Phys. 2014, 141, 18C519. [Google Scholar] [CrossRef] [PubMed]
- Mchedlov-Petrossyan, N.O. Fullerenes in liquid media: An unsettling intrusion into the solution chemistry. Chem. Rev. 2013, 113, 5149–5193. [Google Scholar] [CrossRef] [PubMed]
- Li, L.W.; Bedrov, D.; Smith, G.D. Water-induced interactions between carbon nanoparticles. J. Phys. Chem. B 2006, 110, 10509–10513. [Google Scholar] [CrossRef] [PubMed]
- Li, L.W.; Bedrov, D.; Smith, G.D. A molecular-dynamics simulation study of solvent-induced repulsion between C60 fullerenes in water. J. Chem. Phys. 2005, 123, 204504. [Google Scholar] [CrossRef] [PubMed]
- Li, L.W.; Bedrov, D.; Smith, G.D. Repulsive solvent-induced interaction between C60 fullerenes in water. Phys. Rev. E 2005, 71, 011502. [Google Scholar] [CrossRef]
- Zangi, R. Are buckyballs hydrophobic? J. Phys. Chem. B 2014, 118, 12263–12270. [Google Scholar] [CrossRef]
- Kim, H.; Bedrov, D.; Smith, G.D. Molecular dynamics simulation study of the influence of cluster geometry on formation of C60 fullerene clusters in aqueous solution. J. Chem. Theory Comput. 2008, 4, 335–340. [Google Scholar] [CrossRef]
- Sobolewski, E.; Makowski, M.; Ołdziej, S.; Czaplewski, C.; Liwo, A.; Scheraga, H.A. Towards temperature-dependent coarse-grained potentials of side-chain interactions for protein folding simulations. I: Molecular dynamics study of a pair of methane molecules in water at various temperatures. Protein Eng. Des. Sel. 2009, 22, 547–552. [Google Scholar] [CrossRef]
- Collins, K.D.; Neilson, G.W.; Enderby, J.E. Ions in water: Characterizing the forces that control chemical processes and biological structure. Biophys. Chem. 2007, 128, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Cappa, C.D.; Smith, J.D.; Messer, B.M.; Cohen, R.C.; Saykally, R.J. Effects of cations on the hydrogen bond network of liquid water: New results from X-ray absorption spectroscopy of liquid microjets. J. Phys. Chem. B 2006, 110, 5301–5309. [Google Scholar] [CrossRef] [PubMed]
- Moilanen, D.E.; Fenn, E.E.; Wong, D.; Fayer, M.D. Water dynamics in large and small reverse micelles: From two ensembles to collective behavior. J. Chem. Phys. 2009, 131, 014704. [Google Scholar] [CrossRef] [PubMed]
- Omta, A.W.; Kropman, M.F.; Woutersen, S.; Bakker, H.J. Influence of ions on the hydrogen-bond structure in liquid water. J. Chem. Phys. 2003, 119, 12457–12461. [Google Scholar] [CrossRef]
- Turton, D.A.; Hunger, J.; Hefter, G.; Buchner, R.; Wynne, K. Glasslike behavior in aqueous electrolyte solutions. J. Chem. Phys. 2008, 128, 161102. [Google Scholar] [CrossRef] [PubMed]
- Thompson, H.; Soper, A.K.; Ricci, M.A.; Bruni, F.; Skipper, N.T. The three-dimensional structure of water confined in nanoporous vycor glass. J. Phys. Chem. B 2007, 111, 5610–5620. [Google Scholar] [CrossRef] [PubMed]
- Giri, A.K.; Teixeira, F.; Cordeiro, M.N.D.S. Structure and kinetics of water in highly confined conditions: A molecular dynamics simulation study. J. Mol. Liquids. 2018, 268, 625–636. [Google Scholar] [CrossRef]
- Kumar, R.; Schmidt, J.R.; Skinner, J.L. Hydrogen bonding definitions and dynamics in liquid water. J. Chem. Phys. 2007, 126, 204107. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD-Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.; Brooks III, C.L. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald-an NlogN method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. Mu1tidimensional free-energy calculations using the weighted histogram analysis method. J. Comput. Chem. 1995, 16, 1339–1350. [Google Scholar] [CrossRef]
- Souaille, M.; Roux, B. Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 2001, 135, 40–57. [Google Scholar] [CrossRef]
- GrossField, A. WHAM: An Implementation of the Weighted Histogram Analysis Method. Version 2.0.10. Available online: http://membrane.urmc.rochester.edu/content/wham/ (accessed on 7 June 2024).





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Chen, Y.-N.; Liu, Y.-Z. The Effects of External Interfaces on Hydrophobic Interactions I: Smooth Surface. Molecules 2024, 29, 3128. https://doi.org/10.3390/molecules29133128
Sun Q, Chen Y-N, Liu Y-Z. The Effects of External Interfaces on Hydrophobic Interactions I: Smooth Surface. Molecules. 2024; 29(13):3128. https://doi.org/10.3390/molecules29133128
Chicago/Turabian StyleSun, Qiang, Yan-Nan Chen, and Yu-Zhen Liu. 2024. "The Effects of External Interfaces on Hydrophobic Interactions I: Smooth Surface" Molecules 29, no. 13: 3128. https://doi.org/10.3390/molecules29133128
APA StyleSun, Q., Chen, Y.-N., & Liu, Y.-Z. (2024). The Effects of External Interfaces on Hydrophobic Interactions I: Smooth Surface. Molecules, 29(13), 3128. https://doi.org/10.3390/molecules29133128





