Large Number of Direct or Pseudo-Direct Band Gap Semiconductors among A3TrPn2 Compounds with A = Li, Na, K, Rb, Cs; Tr = Al, Ga, In; Pn = P, As
Abstract
:1. Introduction
2. Results and Discussion
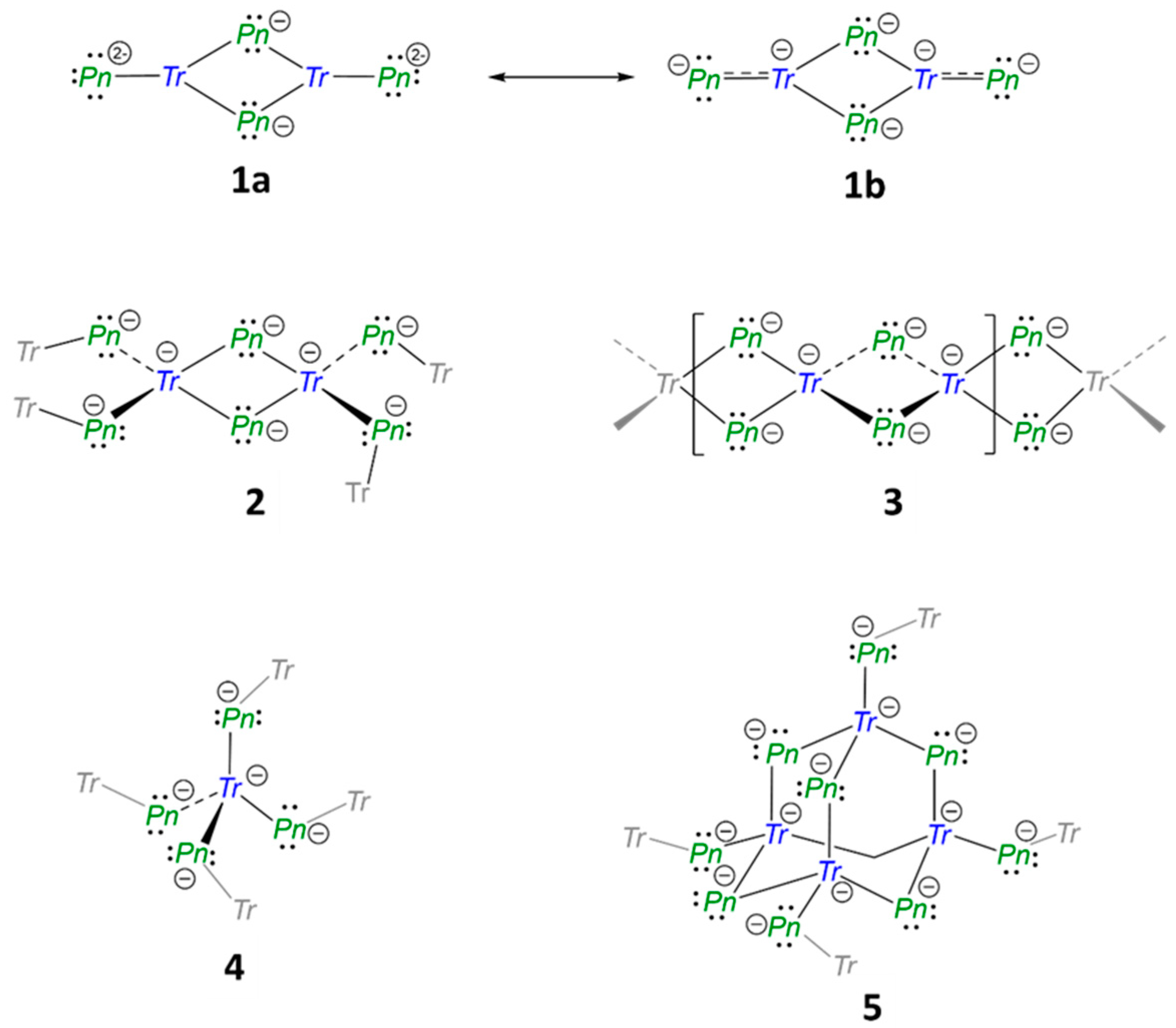
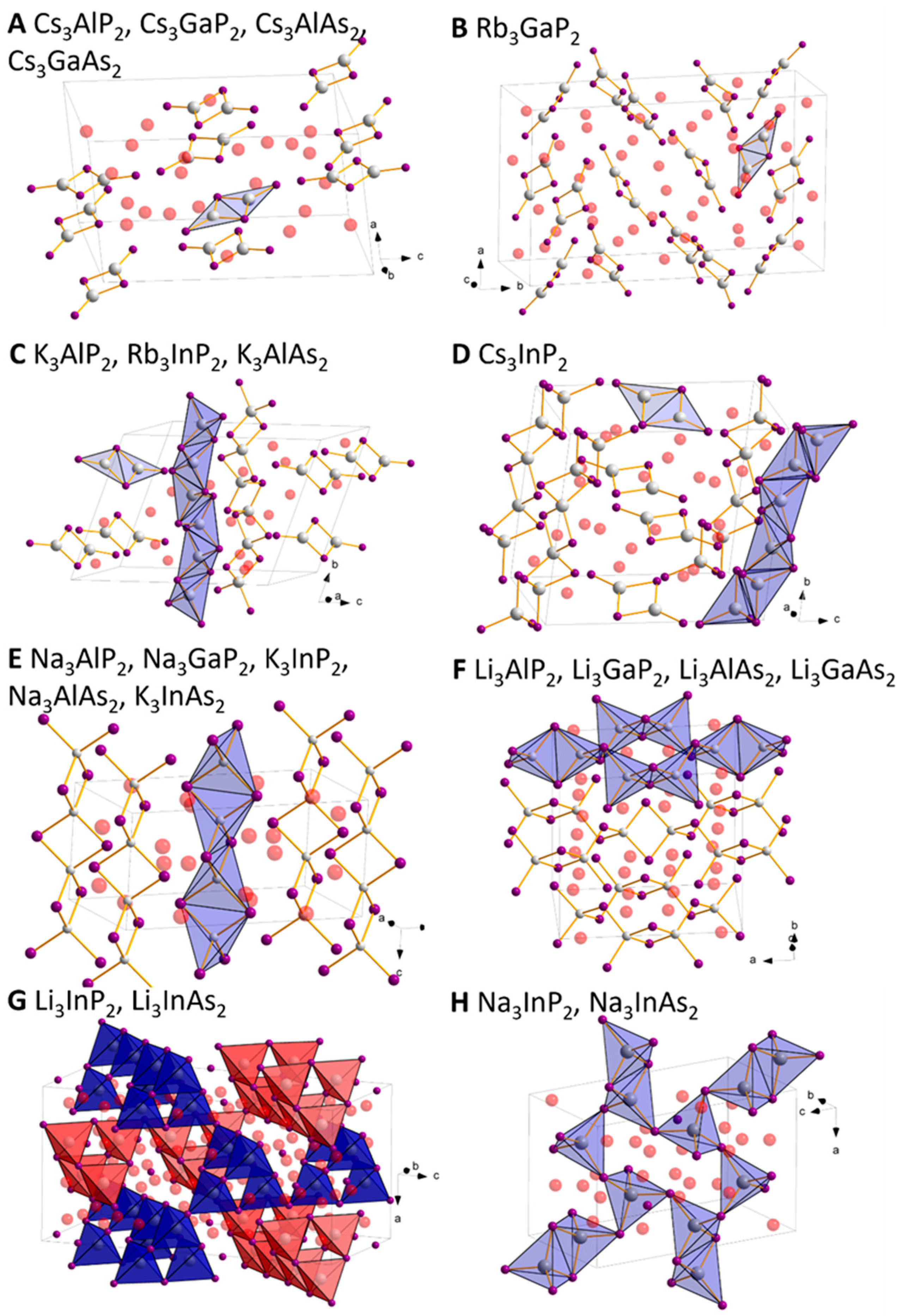
2.1. Structural Relationship of Compounds with Composition A3TrPn2 (A = Li − Cs, Tr = Al − In, Pn = P, As)
2.2. Crystal Structure Optimisation of the Known Compounds
2.3. Structure Predictions for Unknown A3TrPn2 Phosphides and Arsenides
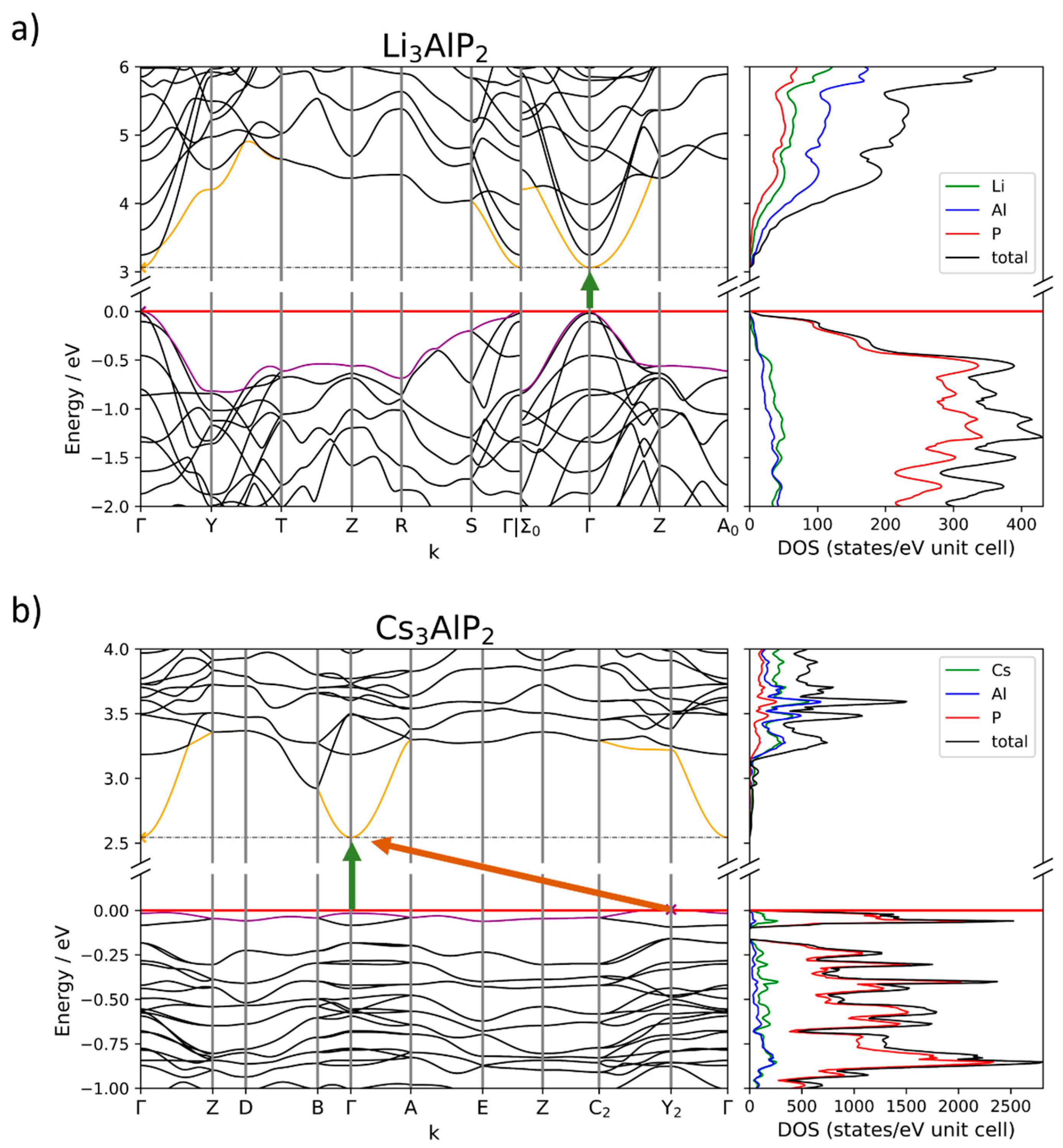
2.4. Electronic Structure Analysis
2.4.1. Size of the Band Gap
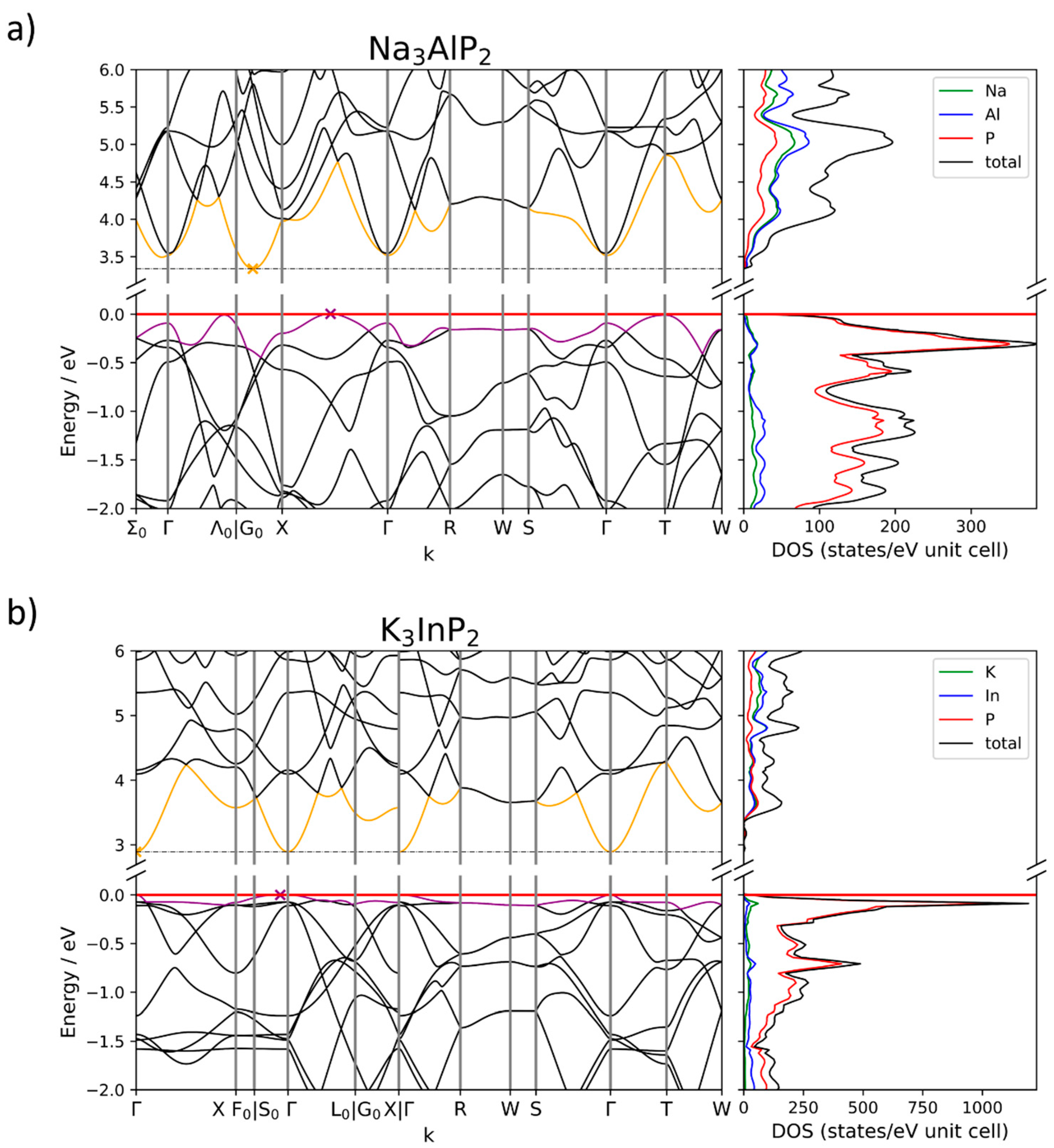
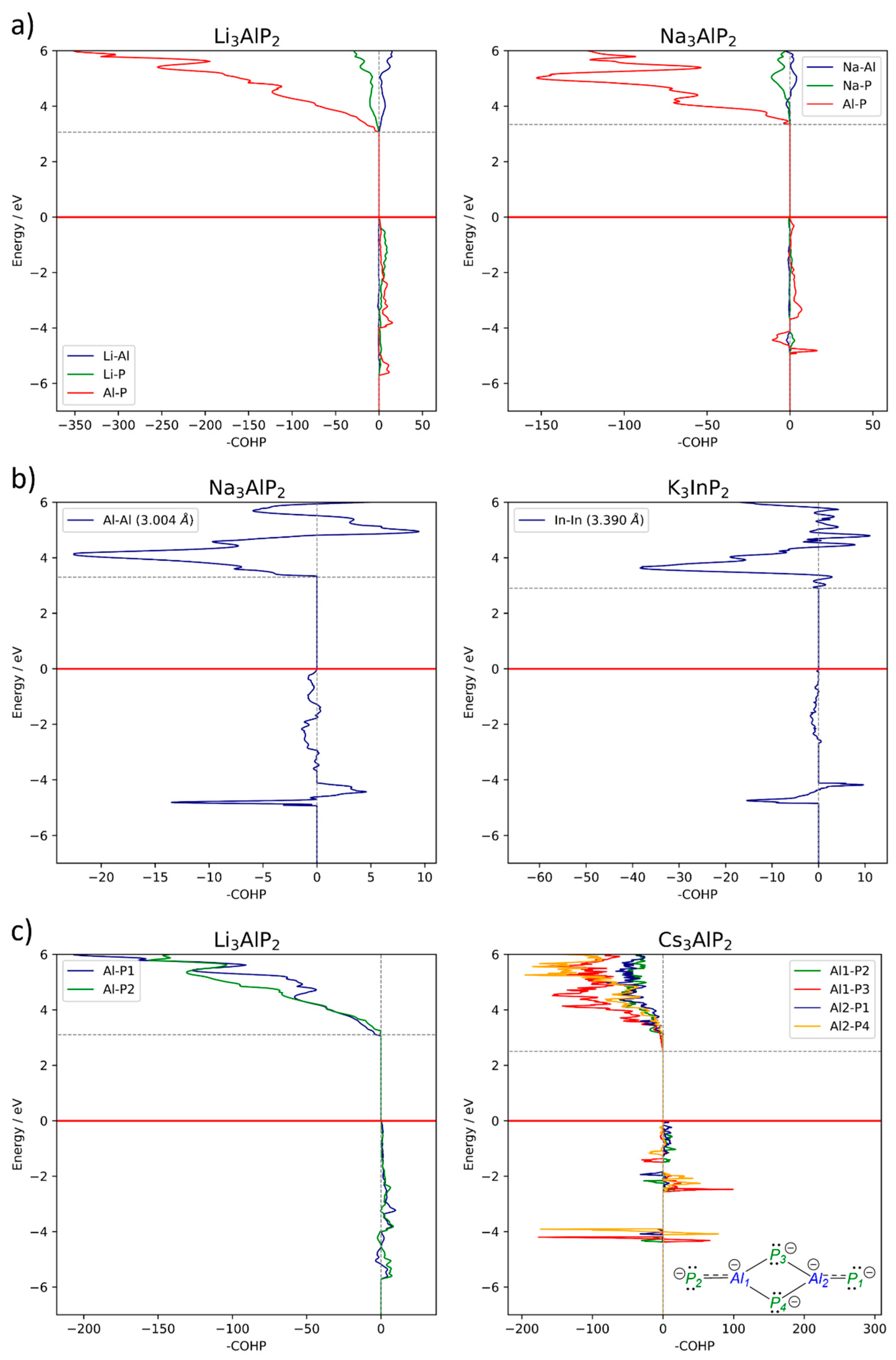
2.4.2. Band Structures and DOS
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prasanna, R.; Gold-Parker, A.; Leijtens, T.; Conings, B.; Babayigit, A.; Boyen, H.-G.; Toney, M.F.; McGehee, M.D. Band Gap Tuning via Lattice Contraction and Octahedral Tilting in Perovskite Materials for Photovoltaics. J. Am. Chem. Soc. 2017, 139, 11117–11124. [Google Scholar] [CrossRef]
- Ning, C.-Z.; Dou, L.; Yang, P. Bandgap engineering in semiconductor alloy nanomaterials with widely tunable compositions. Nat. Rev. Mater. 2017, 2, 17070. [Google Scholar] [CrossRef]
- Unger, E.L.; Kegelmann, L.; Suchan, K.; Sörell, D.; Korte, L.; Albrecht, S. Roadmap and roadblocks for the band gap tunability of metal halide perovskites. J. Mater. Chem. A 2017, 5, 11401–11409. [Google Scholar] [CrossRef]
- Johrendt, D. Structure–property relationships of iron arsenide superconductors. J. Mater. Chem. 2011, 21, 13726. [Google Scholar] [CrossRef]
- Kovnir, K.A.; Shevelkov, A.V. Semiconducting clathrates: Synthesis, structure and properties. Russ. Chem. Rev. 2004, 73, 923–938. [Google Scholar] [CrossRef]
- Pearsall, T. Ga0.47In0.53As: A ternary semiconductor for photodetector applications. IEEE J. Quantum Electron. 1980, 16, 709–720. [Google Scholar] [CrossRef]
- Smith, A.M.; Nie, S. Semiconductor nanocrystals: Structure, properties, and band gap engineering. Acc. Chem. Res. 2010, 43, 190–200. [Google Scholar] [CrossRef]
- Freundlich, A.; Guillemoles, J.-F. (Eds.) Physics, Simulation, and Photonic Engineering of Photovoltaic Devices II; SPIE OPTO: San Francisco, CA, USA, 2013. [Google Scholar]
- Kechiantz, A.; Afanasev, A. Tuning up the performance of GaAs-based solar cells by inelastic scattering on quantum dots and doping of AlyGa1−ySb type-II dots and AlxGa1−xAs spacers between dots. In Physics, Simulation, and Photonic Engineering of Photovoltaic Devices II; SPIE: Bellingham, WA, USA, 2013; Volume 8620, pp. 377–385. [Google Scholar]
- Wu, T.Y.; Pearson, G.L. Phase diagram, crystal growth, and band structure of InxGa1−xAs. J. Phys. Chem. Solids 1972, 33, 409–415. [Google Scholar] [CrossRef]
- Zeitz, S.; Antoniuk, H.; Hlukhyy, V.; Fässler, T.F. Electronic Structure Analysis of the A10Tt2P6 System (A=Li-Cs; Tt=Si, Ge, Sn) and Synthesis of the Direct Band Gap Semiconductor K10Sn2P6. Chemistry 2024, 30, e202400002. [Google Scholar] [CrossRef]
- Restle, T.M.F.; Dums, J.V.; Raudaschl-Sieber, G.; Fässler, T.F. Synthesis, Structure, Solid-State NMR Spectroscopy, and Electronic Structures of the Phosphidotrielates Li3AlP2 and Li3GaP2. Chem.-Eur. J. 2020, 26, 6812–6819. [Google Scholar] [CrossRef]
- Kuriyama, K.; Anzawa, J.; Kushida, K. Growth and band gap of the filled tetrahedral semiconductor Li3AlP2. J. Cryst. Growth 2008, 310, 2298–2300. [Google Scholar] [CrossRef]
- Restle, T.M.F.; Zeitz, S.; Stanley, P.M.; Karttunen, A.J.; Meyer, J.; Raudaschl-Sieber, G.; Klein, W.; Fässler, T.F. Direct Band Gap Semiconductors with Two- and Three-Dimensional Triel-Phosphide Frameworks (Triel=Al, Ga, In). Chemistry 2024, 30, e202304097. [Google Scholar] [CrossRef]
- Somer, Μ.; Walz, L.; Thiery, D.; von Schnering, H.G. Crystal structure of caesium di-μ-phosphido-bis- (phosphidoaluminate), Cs6(Al2Ρ4). Z. Kristallogr.-Cryst. Mater. 1990, 193, 303–304. [Google Scholar] [CrossRef]
- Somer, M.; Thiery, D.; Hartweg, M.; Walz, L.; Peters, K.; von Schnering, H.G. Crystal structure of caesium di-μ-phosphido-bis(phosphidogallate), Cs6(Ga2P4). Z. Kristallogr.-Cryst. Mater. 1990, 193, 287–288. [Google Scholar] [CrossRef]
- Somer, M.; Peters, K.; Thiery, D.; von Schnering, H.G. Crystal structure of trirubidium diphosphidogallate, Rb3GaP2. Z. Kristallogr. 1990, 192, 271–272. [Google Scholar] [CrossRef]
- Somer, M.; Thiery, D.; Hartweg, M.; Walz, L.; Popp, T.; Peters, K.; von Schnering, H.G. Crystal structure of tricaesium diarsenidoaluminate, Cs3AlAs2. Z. Kristallogr. 1990, 192, 269–270. [Google Scholar] [CrossRef]
- Somer, M.; Peters, K.; Popp, T.; von Schnering, H.G. Crystal structure of tricaesium diarsenidogallate, Cs3GaAs2. Z. Kristallogr.-Cryst. Mater. 1990, 192, 273–274. [Google Scholar] [CrossRef]
- Somer, M.; Walz, L.; Peters, Κ.; von Schnering, H.G. Crystal structure of potassium catena-di-μ- phosphidoaluminate di-μ-phosphido-bis (phosphidoaluminate), Κ12(AlP2)2(Al2P4). Z. Kristallogr.-Cryst. Mater. 1990, 193, 301–302. [Google Scholar] [CrossRef]
- Somer, M.; Carrillo-Cabrera, W.; Peters, E.M.; Peters, K.; von Schnering, H.G. Crystal structure of rubidium cα/^/2α-di-μ-phosphìdoindate di-μ-phosphi-do-bis (phosphidoindate), Rhu^ InPilz [ΙπιΡα]. Z. Kristallogr.-New Cryst. Struct. 1998, 213, 5–6. [Google Scholar] [CrossRef]
- von Schnering, H.G.; Somer, M.; Walz, L.; Peters, K.; Cordier, G.; Blase, W. Crystal structure of potassium catena-di- μ arsenidoaluminate di- μ -arsenido-bis(arsenidoaluminate), K12(AlAs2)2(Al2As4). Z. Kristallogr.-Cryst. Mater. 1990, 193, 299–300. [Google Scholar] [CrossRef]
- Blase, W.; Cordier, G.; Somer, M. Crystal structure of caesium catena-di-μ-phosphidoindate di-μ-phosphido-bis (phosphidoindate), Cs12(InP2)2(In2P4). Z. Kristallogr.-Cryst. Mater. 1991, 195, 123–124. [Google Scholar]
- Somer, M.; Carrillo-Cabrera, W.; Peters, K.; Peters, E.M.; von Schnering, H.G. Crystal structure of trisodium catena-di-μ-phosphidoaluminate, Na3AlP2. Z. Kristallogr.-Cryst. Mater. 1995, 210, 777. [Google Scholar] [CrossRef]
- Blase, W.; Cordier, G.; Somer, M. Crystal structure of tripotassium catena-di-μ-phosphido-indate, K3InP2. Z. Kristallogr.-Cryst. Mater. 1991, 195, 109–110. [Google Scholar] [CrossRef]
- Boyko, M.; Hlukhyy, V.; Fässler, T.F. K7In4As6 and K3InAs2-Two more Zintl phases showing the rich variety of In-As polyanion structures. Z. Anorg. Allg. Chem. 2023, 649, e202300164. [Google Scholar] [CrossRef]
- Cordier, G.; Ochmann, H. Na3AlAs2, eine Zintlphase mit SiS2-isosterer Anionenteilstruktur. Z. Naturforsch. B J. Chem. Sci. 1988, 43, 1538–1540. [Google Scholar]
- Restle, T.M.F.; Zeitz, S.; Meyer, J.; Klein, W.; Raudaschl-Sieber, G.; Karttunen, A.J.; Fässler, T.F. Aliovalent substitution in phosphide-based materials–Crystal structures of Na10AlTaP6 and Na3GaP2 featuring edge-sharing EP4 tetrahedra (E = Al/Ta and Ga). Z. Anorg. Allg. Chem. 2021, 647, 1804–1814. [Google Scholar] [CrossRef]
- Büssem, W.; Fischer, H.; Gruner, E. Die struktur des siliciumdisulfids. Naturwissenschaften 1935, 23, 740. [Google Scholar] [CrossRef]
- Juza, R.; Schulz, W. Herstellung und Eigenschaften der Verbindungen Li3AlP2 und Li3AlAs2. Z. Anorg. Allg. Chem. 1952, 269, 1–12. [Google Scholar] [CrossRef]
- Wegner, F.; Kamm, F.; Pielnhofer, F.; Pfitzner, A. Li3TrAs2 (Tr =Al, Ga, In)–Derivatives of the antifluorite type structure, conductivities and electronic structures. Z. Anorg. Allg. Chem. 2023, 649, e202200330. [Google Scholar] [CrossRef]
- Restle, T.M.F.; Deringer, V.L.; Meyer, J.; Raudaschl-Sieber, G.; Fässler, T.F. Supertetrahedral polyanionic network in the first lithium phosphidoindate Li3InP2-structural similarity to Li2SiP2 and Li2GeP2 and dissimilarity to Li3AlP2 and Li3GaP2. Chem. Sci. 2020, 12, 1278–1285. [Google Scholar] [CrossRef]
- Blase, W.; Cordier, G.; Somer, M. Crystal structure of trisodium tecto-diphosphidoindate, Na3InP2. Z. Kristallogr.-Cryst. Mater. 1991, 195, 119–120. [Google Scholar] [CrossRef]
- Cordier, G.; Ochmann, H. Crystal structure of trisodium tecto-diarsenidoindate, Na3InAs2. Z. Kristallogr.-Cryst. Mater. 1991, 195, 105–106. [Google Scholar] [CrossRef]
- Holleman, A.F. Lehrbuch der Anorganischen Chemie; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2019; ISBN 3110838176. [Google Scholar]
- Power, P.P. pi-Bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements. Chem. Rev. 1999, 99, 3463–3504. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J. CRYSTAL17 User’s Manual. University of Turin: Turin, Italy, 2017. Available online: https://iris.unito.it/bitstream/2318/1709158/1/crystal17.pdf (accessed on 14 July 2024).
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yang, W.; Burke, K.; Yang, Z.; Gross, E.K.U.; Scheffler, M.; Scuseria, G.E.; Henderson, T.M.; Zhang, I.Y.; Ruzsinszky, A.; et al. Understanding band gaps of solids in generalized Kohn-Sham theory. Proc. Natl. Acad. Sci. USA 2017, 114, 2801–2806. [Google Scholar] [CrossRef] [PubMed]
- Stene, R.E.; Scheibe, B.; Karttunen, A.J.; Petry, W.; Kraus, F. Lewis Acidic Behavior of MoOF4 towards the Alkali Metal Fluorides in Anhydrous Hydrogen Fluoride Solutions. Eur. J. Inorg. Chem. 2019, 2019, 3672–3682. [Google Scholar] [CrossRef]
- Scheibe, B.; Ivlev, S.I.; Karttunen, A.J.; Kraus, F. Synthesis and Characterization of the Tetrafluoridochlorates(III) A[ClF4] (A = K, Rb, Cs). Eur. J. Inorg. Chem. 2020, 2020, 1319–1324. [Google Scholar] [CrossRef]
- Sansone, G.; Maschio, L.; Usvyat, D.; Schütz, M.; Karttunen, A. Toward an Accurate Estimate of the Exfoliation Energy of Black Phosphorus: A Periodic Quantum Chemical Approach. J. Phys. Chem. Lett. 2016, 7, 131–136. [Google Scholar] [CrossRef]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef]
- Scheibe, B.; Karttunen, A.J.; Weigend, F.; Kraus, F. Photochemistry with Chlorine Trifluoride: Syntheses and Characterization of Difluorooxychloronium(V) Hexafluorido(non)metallates(V), ClOF2MF6 (M=V, Nb, Ta, Ru, Os, Ir, P, Sb). Chemistry 2021, 27, 2381–2392. [Google Scholar] [CrossRef]
- Scheibe, B.; Haiges, R.; Ivlev, S.I.; Karttunen, A.J.; Müller, U.; Christe, K.O.; Kraus, F. Difluorochloronium(III) Fluoridometallates–from Molecular Building Blocks to (Helical) Chains. Eur. J. Inorg. Chem. 2020, 2020, 4483–4496. [Google Scholar] [CrossRef]
- Cordier, G.; Ochmann, H. Crystal structure of trisodium tecto-diantimonidoindate, Na3InSb2. Z. Kristallogr.-Cryst. Mater. 1991, 195, 107–108. [Google Scholar] [CrossRef]
- Bobev, S.; Sevov, S.C. Five Ternary Zintl Phases in the Systems Alkali-Metal–Indium–Bismuth. J. Solid State Chem. 2002, 163, 436–448. [Google Scholar] [CrossRef]
- Wolf, J.; Weber, D.; von Schnering, H.-G. Rubidium-diarsasilicat(IV) Rb2SiAs2, ein Derivat der SiS2 -Struktur/Rubidium Diarsasilicate(IV) Rb2SiAs2, a Derivative of the SiS2 Structure Type. Z. Für Naturforschung B 1986, 41, 731–735. [Google Scholar] [CrossRef]
- Hurng, W.M.; Peterson, E.S.; Corbett, J.D. Synthesis and structure of the Zintl phase potassium silicon arsenide, K2SiAs2. Inorg. Chem. 1989, 28, 4177–4180. [Google Scholar] [CrossRef]
- Eisenmann, B.; Somer, M. K2SiP2, ein Phosphidopolysilikat(IV)/K2SiP2, a Phosphidopolysilicate (IV). Z. Für Naturforschung B 1984, 39, 736–738. [Google Scholar] [CrossRef]
- Eisenmann, B.; Klein, J. SiS2-isostrukturelle Anionen [SiP22−], [GeAs22−] und [SnAs22−] in Alkaliverbindungen. J. Less Common. Met. 1991, 175, 109–117. [Google Scholar] [CrossRef]
- Asbrand, M.; Eisenmann, B. Na2[SnAs2], die erste Zintl-Phase mit einem [SnAs2]-Raumnetz aus adamantan-analogen [Sn4As10]-Einheiten/Na2[SnAs2], the First Zintl Phase with a [SnAs2] Framework Based on Adamantan Analogous [Sn4As10] Units. Z. Für Naturforschung B 1993, 48, 452–456. [Google Scholar] [CrossRef]
- Per, M.C.; Cleland, D.M. Roadmap on post-DFT methods for nanoscience. Nano Futures 2020, 4, 32004. [Google Scholar] [CrossRef]
- Hasnip, P.J.; Refson, K.; Probert, M.I.J.; Yates, J.R.; Clark, S.J.; Pickard, C.J. Density functional theory in the solid state. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 20130270. [Google Scholar] [CrossRef]
- Ohse, L.; Somer, M.; Blase, W.; Cordier, G. Verbindungen mit SiS2-isosteren Anionen∞ 1 [AlX4/23-] und∞ 1 [InP4/23-]: Synthesen, Kristallstrukturen und Schwingungsspektren von Na3 [AlX2], K2Na [AlX2] und K3 [InP2](X = P, As)/Compounds with SiS2 Isoelectronic Anions∞ 1 [AlX4/23-] and∞ 1 [InP4/23-]: Synthesis, Crystal Structures and Vibrational Spectra of Na3 [AlX2], K2Na [AlX2] and K3 [InP2](X = P, As). Z. Für Nat. B 1993, 48, 1027–1034. [Google Scholar]
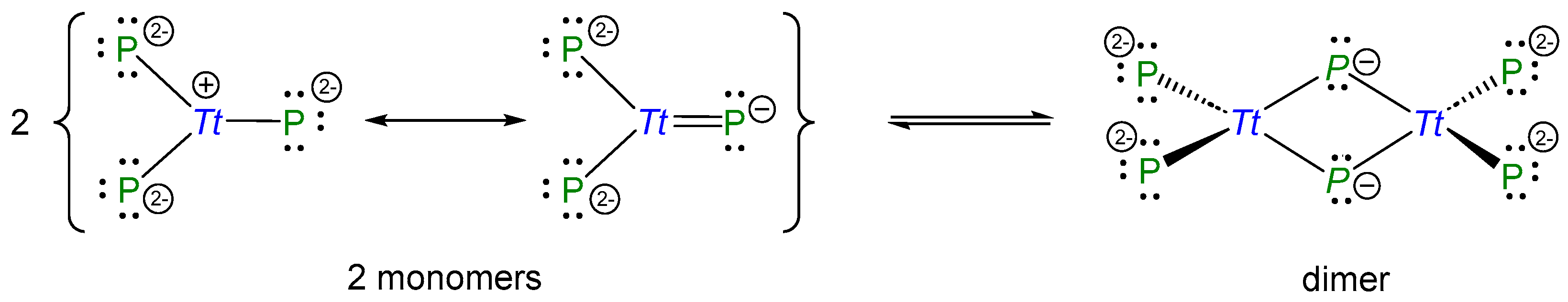
| Compound | a | b | c | α | β | γ | Space Group | No. | Crystal System | Connectivity |
|---|---|---|---|---|---|---|---|---|---|---|
| structure type F | ||||||||||
| Li3AlP2 | 11.5138 | 11.7634 | 5.8202 | Cmce | 64 | orthorhombic | 2D | |||
| 11.5388 | 11.7560 | 5.8267 | ||||||||
| 0.22 | −0.06 | 0.11 | ||||||||
| Li3GaP2 | 11.5839 | 11.7809 | 5.8129 | Cmce | 64 | orthorhombic | 2D | |||
| 11.5910 | 11.7834 | 5.8289 | ||||||||
| 0.06 | 0.02 | 0.27 | ||||||||
| Li3AlAs2 | 11.894 | 12.150 | 6.005 | Cmce | 64 | orthorhombic | 2D | |||
| 11.932 | 12.139 | 6.011 | ||||||||
| 0.32 | −0.09 | 0.11 | ||||||||
| Li3GaAs2 | 11.9626 | 12.1629 | 5.9984 | Cmce | 64 | orthorhombic | 2D | |||
| 11.9959 | 12.1610 | 6.0145 | ||||||||
| 0.28 | −0.02 | 0.27 | ||||||||
| structure type G | ||||||||||
| Li3InP2 | 12.0065 | 23.9165 | I41/acd | 142 | tetragonal | 3D | ||||
| 12.0407 | 23.9862 | |||||||||
| 0.28 | 0.29 | |||||||||
| Li3InAs2 | 12.388 | 24.6587 | I41/acd | 142 | tetragonal | 3D | ||||
| 12.409 | 24.7284 | |||||||||
| 0.17 | 0.28 | |||||||||
| structure type E | ||||||||||
| Na3AlP2 | 13.176 | 6.764 | 6.065 | Ibam | 72 | orthorhombic | 2D | |||
| 13.261 | 6.468 | 6.008 | ||||||||
| 0.64 | −4.57 | −0.94 | ||||||||
| Na3GaP2 | 13.081 | 6.728 | 6.211 | Ibam | 72 | orthorhombic | 2D | |||
| 13.304 | 6.339 | 6.123 | ||||||||
| 1.68 | −6.13 | −1.44 | ||||||||
| K3InP2 | 14.489 | 7.658 | 6.816 | Ibam | 72 | orthorhombic | 2D | |||
| 14.523 | 7.499 | 6.781 | ||||||||
| 0.23 | −2.12 | −0.52 | ||||||||
| Na3AlAs2 | 13.604 | 6.895 | 6.227 | Ibam | 72 | orthorhombic | 2D | |||
| 13.741 | 6.458 | 6.187 | ||||||||
| 1.00 | −6.77 | −0.64 | ||||||||
| K3InAs3 | 7.821 | 14.759 | 6.936 | Ibam | 72 | orthorhombic | 2D | |||
| 7.613 | 14.817 | 6.964 | ||||||||
| −2.73 | 0.39 | 0.40 | ||||||||
| Cs3InAs2 | 15.745 | 8.469 | 7.247 | Ibam | 72 | orthorhombic | 2D | |||
| structure type H | ||||||||||
| Na3InP2 | 9.401 | 7.371 | 15.358 | 92.4 | P21/c | 14 | monoclinic | 3D | ||
| 9.342 | 7.277 | 15.236 | 92.6 | |||||||
| −0.63 | −1.30 | −0.80 | 0.22 | |||||||
| Na3InAs2 | 9.677 | 7.547 | 15.731 | 92.6 | P21/c | 14 | monoclinic | 3D | ||
| 9.624 | 7.439 | 15.611 | 92.9 | |||||||
| −0.55 | −1.45 | −0.77 | 0.29 | |||||||
| Na3GaAs2 | 9.301 | 7.296 | 15.199 | 92.3 | P21/c | 14 | monoclinic | 3D | ||
| structure type C | ||||||||||
| K3AlP2 | 8.871 | 11.879 | 15.280 | 72.47 | 73.35 | 71.62 | P | 2 | triclinic | 1D + 0D |
| 8.822 | 11.767 | 15.140 | 72.94 | 73.45 | 72.40 | |||||
| −0.55 | −0.95 | −0.92 | 0.65 | 0.14 | 1.07 | |||||
| Rb3InP2 | 9.397 | 12.500 | 15.927 | 97.16 | 107.00 | 106.72 | P | 2 | triclinic | 1D + 0D |
| 9.462 | 12.556 | 15.935 | 96.87 | 107.40 | 106.18 | |||||
| 0.69 | 0.45 | 0.05 | −0.30 | 0.38 | −0.51 | |||||
| K3AlAs2 | 9.062 | 12.164 | 15.570 | 72.40 | 73.05 | 71.63 | P | 2 | triclinic | 1D + 0D |
| 8.969 | 12.070 | 15.508 | 72.69 | 73.27 | 72.16 | |||||
| −1.03 | −0.78 | −0.40 | 0.40 | 0.30 | 0.74 | |||||
| structure type D | ||||||||||
| Cs3InP2 | 9.662 | 12.884 | 15.840 | 81.1 | 81.6 | 70.7 | P | 2 | triclinic | 1D + 0D |
| 9.750 | 12.922 | 15.843 | 80.6 | 81.6 | 71.2 | |||||
| 0.90 | 0.29 | 0.02 | −0.57 | 0.01 | 0.81 | |||||
| structure type B | ||||||||||
| Rb3GaP2 | 14.634 | 24.893 | 9.163 | Pbca | 61 | orthorhombic | 0D | |||
| 14.930 | 24.905 | 9.115 | ||||||||
| 1.99 | 0.05 | −0.53 | ||||||||
| K3GaP2 | 14.496 | 23.634 | 8.740 | Pbca | 61 | orthorhombic | 0D | |||
| Rb3AlP2 | 14.880 | 24.961 | 9.140 | Pbca | 61 | orthorhombic | 0D | |||
| K3GaAs2 | 14.777 | 24.100 | 8.938 | Pbca | 61 | orthorhombic | 0D | |||
| Rb3AlAs2 | 15.175 | 25.440 | 9.343 | Pbca | 61 | orthorhombic | 0D | |||
| Rb3GaAs2 | 15.232 | 25.375 | 9.315 | Pbca | 61 | orthorhombic | 0D | |||
| structure type A | ||||||||||
| Cs3AlP2 | 11.233 | 8.641 | 18.986 | 100.056 | P21/c | 14 | monoclinic | 0D | ||
| 11.253 | 8.684 | 19.181 | 100.912 | |||||||
| 0.17 | 0.50 | 1.02 | 0.85 | |||||||
| Cs3GaP2 | 11.173 | 8.661 | 18.939 | 99.64 | P21/c | 14 | monoclinic | 0D | ||
| 11.241 | 8.672 | 19.173 | 100.77 | |||||||
| 0.60 | 0.12 | 1.22 | 1.13 | |||||||
| Cs3AlAs2 | 11.458 | 8.831 | 19.453 | 99.68 | P21/c | 14 | monoclinic | 0D | ||
| 11.427 | 8.844 | 19.578 | 100.31 | |||||||
| −0.27 | 0.14 | 0.64 | 0.63 | |||||||
| Cs3GaAs2 | 11.371 | 8.857 | 19.460 | 99.225 | P21/c | 14 | monoclinic | 0D | ||
| 11.413 | 8.836 | 19.571 | 100.180 | |||||||
| 0.37 | −0.25 | 0.57 | 0.95 | |||||||
| Rb3InAs2 | 12.074 | 8.179 | 18.868 | 101.1 | P21/c | 14 | monoclinic | 0D | ||
| Structure Type | ΔΔE (kJ/mol) | ΔΔG (kJ/mol) | Band Gap (eV) | |
|---|---|---|---|---|
| K3GaP2 | B | 0 | 0 | 2.98 (dir.) |
| C | 6.01 | 8.24 | 2.41 (dir.) | |
| E | 18.15 | 25.72 | 3.12 (p-dir.) | |
| Rb3AlP2 | B | 0 | 0 | 2.44 (dir.) |
| C | 4.32 | 6.39 | 1.85 (dir.) | |
| A | 6.21 | 5.87 | 2.37 (p-dir.) | |
| Na3GaAs2 | H | 0 | 0 | 2.03 (dir.) |
| F | 17.02 | 20.09 | 2.30 (dir.) | |
| E | 11.423 | 11.415 | 2.39 (indir.) | |
| K3GaAs2 | B | 0 | 0 | 2.79 (dir.) |
| C | 5.41 | 7.22 | 2.17 (dir.) | |
| E | 14.48 | 22.09 | 2.96 (indir.) | |
| Rb3AlAs2 | B | 0 | 0 | 2.26 (dir.) |
| C | 3.44 | 4.88 | 1.73 (dir.) | |
| A | 7.29 | 7.11 | 2.18 (dir.) | |
| Rb3GaAs2 | B | 0 | 0 | 2.23 (dir.) |
| A | 7.94 | 7.44 | 2.15 (indir.) | |
| C | 13.53 | 14.80 | 1.67 (dir.) | |
| Rb3InAs2 | C | 0 | 0.34 | 1.57 (dir.) |
| A | 1.00 | 0 | 1.86 (indir.) | |
| E | 4.19 | 11.86 | 1.96 (indir.) | |
| Cs3InAs2 | E | 0 | 0 | 2.24 (dir.) |
| D | 3.26 | 6.32 | 1.81 (dir.) | |
| A | 7.09 | 7.01 | 2.15 (dir.) | |
| E | 9.78 | 20.42 | 2.07 (indir.) |
| A3TrP2 | Li | Na | K | Rb | Cs |
| Al | F, 3.06 eV, dir. | E, 3.34 eV, indir. | C, 2.42 eV, dir. | B, 2.44 eV, dir. | A, 2.54 eV, p-dir. |
| Ga | F, 2.83 eV, dir. | E, 2.88 eV, indir. | B, 2.98 eV, dir. | B, 2.41 eV, p-dir. | A, 2.54 eV, p-dir. |
| In | G, 2.69 eV, dir. | H, 2.09 eV, dir. | E, 2.89 eV, dir. | C, 1.73 eV, dir. | D, 1.99 eV, dir. |
| A3TrAs2 | Li | Na | K | Rb | Cs |
| Al | F, 2.85 eV, dir. | E, 2.98 eV, indir. | C, 2.27 eV, dir. | B, 2.26 eV, dir. | A, 2.26 eV, p-dir. |
| Ga | F, 2.43 eV, dir. | H, 2.03 eV, dir. | B, 2.79 eV, dir. | B, 2.23 eV, dir. | A, 2.35 eV, p-dir. |
| In | G, 2.26 eV, dir. | H, 1.69 eV, dir. | E, 2.69 eV, dir. | C, 1.57eV, dir. A, 1.86 eV, indir. | B, 2.24 eV, dir. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeitz, S.; Kuznetsova, Y.; Fässler, T.F. Large Number of Direct or Pseudo-Direct Band Gap Semiconductors among A3TrPn2 Compounds with A = Li, Na, K, Rb, Cs; Tr = Al, Ga, In; Pn = P, As. Molecules 2024, 29, 4087. https://doi.org/10.3390/molecules29174087
Zeitz S, Kuznetsova Y, Fässler TF. Large Number of Direct or Pseudo-Direct Band Gap Semiconductors among A3TrPn2 Compounds with A = Li, Na, K, Rb, Cs; Tr = Al, Ga, In; Pn = P, As. Molecules. 2024; 29(17):4087. https://doi.org/10.3390/molecules29174087
Chicago/Turabian StyleZeitz, Sabine, Yulia Kuznetsova, and Thomas F. Fässler. 2024. "Large Number of Direct or Pseudo-Direct Band Gap Semiconductors among A3TrPn2 Compounds with A = Li, Na, K, Rb, Cs; Tr = Al, Ga, In; Pn = P, As" Molecules 29, no. 17: 4087. https://doi.org/10.3390/molecules29174087
APA StyleZeitz, S., Kuznetsova, Y., & Fässler, T. F. (2024). Large Number of Direct or Pseudo-Direct Band Gap Semiconductors among A3TrPn2 Compounds with A = Li, Na, K, Rb, Cs; Tr = Al, Ga, In; Pn = P, As. Molecules, 29(17), 4087. https://doi.org/10.3390/molecules29174087







