Excess Thermodynamic Properties and FTIR Studies of Binary Mixtures of Toluene with 2-Propanol or 2-Methyl-1-Propanol
Abstract
:1. Introduction
2. Results and Discussion
2.1. Density and Viscosity
| Component | T/(K) | ρ/(g·cm−3) | η/(mPas) | ||
|---|---|---|---|---|---|
| This Work | Lit. Value | This Work | Lit. Value | ||
| Toluene | 293.15 | 0.8665 | 0.86686 [19] | 0.596 | 0.598 [19] |
| 0.866859 [20] | 0.59610 [20] | ||||
| 298.15 | 0.8622 | 0.86220 [19] | 0.567 | 0.569 [19] | |
| 0.862214 [21] | 0.56703 [20] | ||||
| 0.862206 [20] | |||||
| 0.86121 [13] | |||||
| 303.15 | 0.8579 | 0.85754 [19] | 0.522 | 0.522 [22] | |
| 0.857552 [21] | 0.526 [12] | ||||
| 0.857541 [20] | |||||
| 0.85755 [22] | |||||
| 0.8578 [12] | |||||
| 308.15 | 0.8537 | 0.85285 [19] | 0.498 | 0.509 [19] | |
| 0.852858 [21] | 0.493 [22] | ||||
| 0.852861 [20] | 0.4980 [14] | ||||
| 0.85384 [13] | |||||
| 0.85272 [22] | |||||
| 313.15 | 0.8493 | 0.84816 [19] | 0.483 | 0.485 [19] | |
| 0.84836 [21] | 0.48657 [20] | ||||
| 0.848164 [20] | |||||
| 0.84802 [22] | |||||
| 2-propanol | 293.15 | 0.7860 | 0.78525 [23] | 2.414 | 2.3621 [23] |
| 0.78544 [11] | 2.3621 [11] | ||||
| 0.78535 [24] | 2.414 [24] | ||||
| 298.15 | 0.7825 | 0.78116 [13] | 2.045 | 2.035 [13] | |
| 0.78110 [24] | 2.070 [24] | ||||
| 0.7810 [25] | 2.08 [25] | ||||
| 303.15 | 0.7774 | 0.7768 [23] | 1.791 | 1.8014 [23] | |
| 0.77675 [11] | 1.7694 [11] | ||||
| 0.77712 [24] | 1.785 [24] | ||||
| 0.7767 [25] | 1.79 [25] | ||||
| 308.15 | 0.7730 | 0.77131 [13] | 1.550 | 1.535 [13] | |
| 0.77288 [24] | 1.546 [24] | ||||
| 0.7721 [25] | 1.58 [25] | ||||
| 313.15 | 0.7689 | 0.7680 [23] | 1.327 | 1.3311 [23] | |
| 0.76798 [11] | 1.3297 [11] | ||||
| 0.76879 [24] | 1.347 [24] | ||||
| 0.7678 [25] | 1.34 [25] | ||||
| 2-methyl-1-propanol | 293.15 | 0.8014 | 0.80175 [11] | 3.929 | 3.943 [28] |
| 0.80148 [26] | 4.0516 [27] | ||||
| 0.80203 [27] | |||||
| 0.80168 [28] | |||||
| 298.15 | 0.7974 | 0.79816 [27] | 3.408 | 3.4307 [27] | |
| 0.798033 [29] | 3.4023 [29] | ||||
| 0.79774 [28] | 3.332 [28] | ||||
| 303.15 | 0.7920 | 0.79399 [11] | 2.923 | 2.877 [11] | |
| 0.79360 [26] | 2.9226 [27] | ||||
| 0.79425 [27] | 2.884 [28] | ||||
| 0.79432 [28] | |||||
| 308.15 | 0.7879 | 0.79056 [14] | 2.554 | 2.5057 [14] | |
| 0.78966 [26] | 2.5053 [27] | ||||
| 0.79031 [27] | |||||
| 313.15 | 0.7832 | 0.78604 [11] | 2.187 | 2.091 [11] | |
| 0.78572 [26] | 2.1612 [27] | ||||
| 0.78631 [27] | |||||
| x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| toluene (1) + 2-propanol (2) | |||||
| 0.1020 | 0.7949 | 0.7915 | 0.7866 | 0.7825 | 0.7785 |
| 0.2001 | 0.8031 | 0.7995 | 0.7949 | 0.7908 | 0.7869 |
| 0.3004 | 0.8110 | 0.8074 | 0.8029 | 0.7988 | 0.7949 |
| 0.4030 | 0.8188 | 0.8150 | 0.8107 | 0.8066 | 0.8026 |
| 0.5051 | 0.8263 | 0.8225 | 0.8182 | 0.8141 | 0.8102 |
| 0.6029 | 0.8338 | 0.8299 | 0.8257 | 0.8216 | 0.8176 |
| 0.7052 | 0.8422 | 0.8384 | 0.8342 | 0.8301 | 0.8262 |
| 0.7998 | 0.8503 | 0.8463 | 0.8421 | 0.8380 | 0.8339 |
| 0.9005 | 0.8585 | 0.8543 | 0.8501 | 0.8460 | 0.8417 |
| toluene (1) + 2-methyl-1-propanol (2) | |||||
| 0.1000 | 0.8072 | 0.8033 | 0.7981 | 0.7942 | 0.7896 |
| 0.1969 | 0.8129 | 0.8091 | 0.8041 | 0.8002 | 0.7957 |
| 0.3008 | 0.8192 | 0.8153 | 0.8105 | 0.8065 | 0.8021 |
| 0.3922 | 0.8248 | 0.8209 | 0.8161 | 0.8121 | 0.8077 |
| 0.4947 | 0.8313 | 0.8273 | 0.8226 | 0.8186 | 0.8142 |
| 0.5952 | 0.8377 | 0.8337 | 0.8291 | 0.8251 | 0.8207 |
| 0.6936 | 0.8443 | 0.8403 | 0.8358 | 0.8318 | 0.8275 |
| 0.7941 | 0.8514 | 0.8473 | 0.8429 | 0.8388 | 0.8345 |
| 0.8965 | 0.8587 | 0.8545 | 0.8502 | 0.8461 | 0.8417 |
| x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| toluene (1) + 2-propanol (2) | |||||
| 0.1020 | 1.720 | 1.468 | 1.294 | 1.171 | 1.013 |
| 0.2001 | 1.338 | 1.144 | 1.039 | 0.939 | 0.824 |
| 0.3004 | 1.072 | 0.942 | 0.865 | 0.797 | 0.714 |
| 0.4030 | 0.882 | 0.788 | 0.732 | 0.688 | 0.624 |
| 0.5051 | 0.770 | 0.697 | 0.653 | 0.609 | 0.570 |
| 0.6029 | 0.698 | 0.637 | 0.601 | 0.557 | 0.534 |
| 0.7052 | 0.647 | 0.594 | 0.566 | 0.530 | 0.507 |
| 0.7998 | 0.619 | 0.582 | 0.546 | 0.518 | 0.495 |
| 0.9005 | 0.608 | 0.575 | 0.543 | 0.506 | 0.487 |
| toluene (1) + 2-methyl-1-propanol (2) | |||||
| 0.1000 | 2.749 | 2.392 | 2.066 | 1.861 | 1.632 |
| 0.1969 | 2.132 | 1.848 | 1.636 | 1.476 | 1.297 |
| 0.3008 | 1.626 | 1.411 | 1.297 | 1.186 | 1.024 |
| 0.3922 | 1.316 | 1.146 | 1.074 | 0.992 | 0.862 |
| 0.4947 | 1.086 | 0.969 | 0.878 | 0.816 | 0.739 |
| 0.5952 | 0.923 | 0.869 | 0.765 | 0.708 | 0.667 |
| 0.6936 | 0.813 | 0.771 | 0.704 | 0.655 | 0.615 |
| 0.7941 | 0.717 | 0.689 | 0.635 | 0.594 | 0.558 |
| 0.8965 | 0.651 | 0.631 | 0.585 | 0.561 | 0.533 |
2.2. Thermodynamic Functions of Activation
2.3. Excess Properties
2.4. Apparent and Partial Molar Volumes
2.5. Prigogine–Flory–Patterson (PFP) Theory
2.6. FTIR Spectra
3. Materials and Methods
3.1. Materials
3.2. Experimental Analysis
3.3. Spectral Analyses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alaoui, F.E.M.; Montero, E.A.; Bazile, J.-P.; Aguilar, F.; Boned, C. Liquid density of biofuel mixtures: (Dibutyl ether + 1-butanol) system at pressures up to 140 MPa and temperatures from (293.15 to 393.15) K. J. Chem. Thermodyn. 2011, 43, 1768–1774. [Google Scholar] [CrossRef]
- Hajbabaei, M.; Karavalakis, G.; Johnson, K.C.; Guthrie, J.; Mitchell, A.; Durbin, T.D. Impact of biodiesel feedstock and additives on criteria emissions from a heavy-duty engine. Fuel Process. Technol. 2014, 126, 402–414. [Google Scholar] [CrossRef]
- Karabektas, M.; Ergen, G.; Hosoz, M. The effects of using diethylether as additive on the performance and emissions of a diesel engine fuelled with CNG. Fuel 2014, 115, 855–860. [Google Scholar] [CrossRef]
- Agarwal, A.K. Biofuels (alcohols and biodiesel) applications as fuels for internal combustion engines. Prog. Energy Combust. Sci. 2007, 33, 233–271. [Google Scholar] [CrossRef]
- Luque, R.; Menendez, J.A.; Arenillas, A.; Cot, J. Microwave—Assisted pyrolysis of biomass feedstocks: The way forward. Energy Environ. Sci. 2012, 5, 5481–5488. [Google Scholar] [CrossRef]
- Higashide, W.; Li, Y.; Yang, Y.; Liao, J.C. Metabolic Engineering of Clostridium Cellulolyticum for Production of Isobutanol from Cellulose. Appl. Environ. Microbiol. 2011, 77, 2727–2733. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J.K.; Ahn, J.O.; Song, Y.H.; Shin, C.S.; Park, Y.C.; Kim, K.H. Isobutanol Production from Empty Fruit Bunches. Renew. Energy 2020, 157, 1124–1130. [Google Scholar] [CrossRef]
- Dees, C.; Askari, M.; Henley, D. Carcinogenic potential of benzene and toluene when evaluated using cyclin-dependent kinase activation and p53-DNA binding. Environ. Health Persp. 1996, 104, 1289–1292. [Google Scholar] [CrossRef]
- Verma, S.; Gahlyan, S.; Rani, M.; Maken, S. Optical and acoustic properties of binary mixtures of butanol isomers as oxygenates with cyclohexane, benzene and toluene at 308.15 K. Korean Chem. Eng. Res. 2018, 56, 663–678. [Google Scholar] [CrossRef]
- Li, X.X.; Fan, G.-C.; Wang, Y.-W.; Zhang, M.; Lu, Y.-Q. Volumetric and viscosimetric properties of the binary mixture of triethylene glycol monomethyl ether + water at T = (293.15, 303.15, 313.15, 323.15, 333.15) K under atmospheric pressure. J. Mol. Liq. 2010, 151, 62–66. [Google Scholar] [CrossRef]
- Kermanpour, F.; Niakan, H.Z. Experimental excess molar properties of binary mixtures of (3-amino-1-propanol + isobutanol, 2-propanol) at T = (293.15 to 333.15) K and modelling the excess molar volume by Prigogine-Flory-Patterson theory. J. Chem. Thermodyn. 2012, 54, 10–19. [Google Scholar] [CrossRef]
- Mahendran, G.; Palaniappan, L. Molecular interactions of aniline in toluene + iso-butanol system. Indian J. Pure Appl. Phys. 2011, 49, 803–808. [Google Scholar] [CrossRef]
- Gahlyan, S.; Verma, S.; Rani, M.; Maken, S. Viscometric and FTIR studies of molecular interactions in 2-propanol+hydrocarbons mixtures at 298.15 and 308.15 K. Korean J. Chem. Eng. 2018, 35, 1167–1173. [Google Scholar] [CrossRef]
- Verma, S.; Gahlyan, S.; Rani, M.; Maken, S. Transport Properties and Modeling of Viscosity for Binary Mixtures of Butanol Isomers + Hydrocarbons. Arab. J. Sci. Eng. 2018, 43, 6087–6097. [Google Scholar] [CrossRef]
- Ramana, C.V.V.; Kumar Kiran, A.B.V.; Kumar Satya, A.; Kumar Ashok, M.; Moodley, M.K. Dielectric and excess dielectric constants in non polar + polar binary liquid mixtures of toluene with alcohols at 303, 313 and 323 K. Thermochim. Acta 2013, 566, 130–136. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Maken, S.; Singh, K.C. Excess molar volumes of (an isomer of butanol + benzene or toluene) at the temperature 308.15 K. J. Chem. Thermodyn. 1996, 28, 1173–1177. [Google Scholar] [CrossRef]
- Swamy, G.N.; Dharmaraju, G.; Raman, K.G. Excess volumes of toluene mixtures with some alcohols at 303.15K. Can. J. Chem. 1980, 58, 229–230. [Google Scholar] [CrossRef]
- Yadav, B.L.; Maken, S.; Kalra, K.C.; Singh, K.C. Excess volumes of (an alkanol + an aromatic hydrocarbon) at the temperature 308.15K. J. Chem. Thermodyn. 1993, 25, 1345–1350. [Google Scholar] [CrossRef]
- Warminska, D.; Cichowska-Kopczynska, I. Thermodynamic study of binary mixtures of toluene with ionic liquids, 1-butyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl)imide, 1-hexyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl)imide and 1-butylpyridinium bis(trifluoromethylsulfonyl)imide. J. Mol. Liq. 2020, 304, 112754. [Google Scholar] [CrossRef]
- Bajic, D.M.; Zivkovic, E.M.; Jovanovic, J.; Serbanovic, S.P.; Kijevcanin, M.L. Experimental measurements and modelling of volumetric properties, refractive index and viscosity of binary systems of ethyl lactate with methyl ethyl ketone, toluene and n-methyl-2-pirrolidone at 288.15-323.15 K and atmospheric pressure. New UNIFAC-VISCO and ASOG-VISCO interaction parameters. Fluid Phase Equilibria 2015, 399, 50–65. [Google Scholar] [CrossRef]
- Sastry, N.V.; Thakor, R.R.; Patel, M.C. Excess molar volumes, viscosity deviations, excess isentropic compressibilities and deviations in relative permittivities of (alkyl acetates(methyl, ethyl, butyl and isoamyl) + n-hexane, + benzene, + toluene, + (o-, m-, p-) xylenes, + (chloro-, bromo-, nitro-) benzene at temperatures from 298.15 to 313.15 K. J. Mol. Liq. 2009, 144, 13–22. [Google Scholar] [CrossRef]
- Billah, M.M.; Rocky, M.M.H.; Hossen, I.; Hossain, I.; Hossain, M.N.; Akhtar, S. Densities, viscosities, and refractive indices for the binary mixtures of tri-n-butyl phosphate (TBP) with toluene and ethylbenzene between (303.15 and 323.15)K. J. Mol. Liq. 2018, 265, 611–620. [Google Scholar] [CrossRef]
- Kermanpour, F. Thermodynamic study of binary mixtures of propilophenone + 2-propanol, 2-butanol, 2-pentanol, or 2-hexanol at temperatures of 293.15 to 323.15 K: Modeling by Prigogine-Flory-Patterson theory. J. Mol. Liq. 2023, 376, 121448. [Google Scholar] [CrossRef]
- Peng, F.M.; Seng, C.E.; Teng, T.-T.; Ibrahim, M.H. Densities and viscosities of aqueous solutions of 1-propanol and 2-propanol at temperatures from 293.15 K to 333.15 K. J. Mol. Liq. 2007, 136, 71–78. [Google Scholar] [CrossRef]
- Chai, L.; Xing, G.; Wang, W.; Zhao, Z.; Zhang, J.; Cao, J. Excess properties, computational chemistry and spectroscopic analyses of 1.2-propanediamine + n-propanol/isopropanol binary mixtures. J. Mol. Liq. 2023, 382, 121896. [Google Scholar] [CrossRef]
- Nain, A.K.; Srivastava, T.; Pandey, J.D.; Gopal, S. Densities, ultrasonic speeds and excess properties of binary mixtures of methyl acrylate with 1-butanol, or 2-butanol, or 2-methyl-1-propanol, or 2-methyl-2-propanol at temperatures from 288.15 to 318.15 K. J. Mol. Liq. 2009, 149, 9–17. [Google Scholar] [CrossRef]
- Majstorovic, D.M.; Zivkovic, E.M.; Matija, L.R.; Kijevcanin, M.L. Volumetric, viscometric, spectral studies and viscosity modelling of binary mixtures of esters and alcohols (diethyl succinate, or ethyl octanoate + isobutanol, or isopentanol) at varying temperatures. J. Chem. Thermodyn. 2017, 104, 169–188. [Google Scholar] [CrossRef]
- Farhan, A.M.; Awwad, A.M. Densities, Viscosities, and Excess Molar Enthalpies of 2-Pyrrolidone + Butanol Isomers at T = (293.1, 298.15, and 303.15) K. J. Chem. Eng. Data 2009, 54, 2095–2099. [Google Scholar] [CrossRef]
- Majstorovic, D.M.; Petrovic, P.I.; Kijevcanin, M.L.; Zivkovic, E.M. Thermodynamic study of triacetin or ethyl levulinate and alcohol binary mixtures. J. Chem. Thermodyn. 2023, 180, 107004. [Google Scholar] [CrossRef]
- Wang, W.X.; Qin, X.; Ai, J.J.; Liu, X.; Liu, Y.L.; Li, X.X.; Zhang, J.B.; Wu, Z.J. Excess properties, spectral analysis and computational chemistry of (1,3-propanediol + ethylenediamine) ion-like liquids for CS2 capture. J. Mol. Liq. 2022, 363, 119830. [Google Scholar] [CrossRef]
- Emmerling, U.; Figurski, G.; Rasmussen, P. Densities and kinematic viscosities for the systems benzene + methyl formate, benzene + ethyl formate, benzene + propyl formate, and benzene + butyl formate. J. Chem. Eng. Data 1998, 43, 289–292. [Google Scholar] [CrossRef]
- Gonzales-Olmos, R.; Iglesias, M. Influence of temperature on thermodynamics of ethers + xylenes. Fluid Phase Equilibria 2008, 267, 133–139. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Shekaari, H.; Zafarani-Moattar, M.T.; Mokhtarpour, M.; Faraji, S. Volumetric and compressibility properties for aqueous solutions of choline chloride based deep eutectic solvents and Prigogine-Flory–Patterson theory to correlate of excess molar volumes at T = (293.15 to 308.15) K. J. Mol. Liq. 2019, 289, 111077. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor—Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Noda, K.; Ishida, K. Correlation and prediction of the viscosity of liquid mixtures. J. Chem. Eng. Japan 1977, 10, 478–480. [Google Scholar] [CrossRef]
- Novak, L.T. Relationship between the Intrinsic Viscosity and Eyring-NRTL Viscosity Model Parameters. Ind. Eng. Chem. Res. 2004, 43, 2602–2604. [Google Scholar] [CrossRef]
- Schrodt, J.T.; Akel, R.M. Binary liquid viscosities and their estimation from classical solution thermodynamics. J. Chem. Eng. Data 1989, 34, 8–13. [Google Scholar] [CrossRef]
- Eyring, H.; Jhon, M.S. Significant Liquid Structures; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Saleh, M.A.; Akhtar, S.; Begum, S.; Ahmed, M.S.; Begum, S.K. Density and viscosity of 1-alkanols. Phys. Chem. Liquids 2004, 42, 615–623. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Algebraic Representation of Thermodynamic Properties and the Classification of Solutions. Ing. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Prolongo, M.G.; Masegosa, R.M.; Fuentes, H.I.; Horta, A. Viscosities and excess volumes of binary mixtures. J. Phys. Chem. 1984, 88, 2163–2167. [Google Scholar] [CrossRef]
- Dubey, G.P.; Sharma, M.; Dubey, N. Study of densities, viscosities, and speeds of sound of binary liquid mixtures of butan-1-ol with n-alkanes (C6, C8, and C10) at T = (298.15, 303.15, and 308.15) K. J. Chem. Thermodyn. 2008, 40, 309–320. [Google Scholar] [CrossRef]
- Vuksanovic, J.M.; Zivkovic, E.M.; Radovic, I.R.; Djordjevic, B.D.; Serbanovic, S.P.; Kijevcanin, M.L. Experimental study and modelling of volumetric properties, viscosities and refractive indices of binary liquid mixtures benzene + PEG 200/PEG 400 and toluene + PEG200/PEG 400. Fluid Phase Equilibria 2013, 345, 28–44. [Google Scholar] [CrossRef]
- Ortega, J.; Paz-Andrade, M.I.; Rodrigues, E. Excess molar volumes of the mixtures hexan-2-ol + n-alkane at 298.15 K. J. Chem. Eng. Data 1986, 31, 336–338. [Google Scholar] [CrossRef]
- Prathibha, R.; Bhanuprakash, P.; Narasimha Rao, C.; Jyothi, N.V.V.; Sivakumar, K. Study of excess thermodynamic properties of binary systems containing cinnamaldehyde with alcohols supported by ATR-FTIR spectral studies. Chem. Data Collect. 2019, 19, 100184. [Google Scholar] [CrossRef]
- Mehra, R.; Pancholi, M. Study of molecular interactions in binary mixtures of benzene-butanol and toluene-butanol systems from acoustic and thermodynamic parameters. Indian J. Phys. 2006, 80, 253–263. [Google Scholar]
- Yang, C.; Xu, W.; Ma, P. Thermodynamic Properties of Binary Mixtures of p-Xylene with Cyclohexane, Heptane, Octane, and N-Methyl-2-pyrrolidone at Several Temperatures. J. Chem. Eng. Data 2004, 49, 1794–1801. [Google Scholar] [CrossRef]
- Mahajan, A.R.; Mirgane, S.R. Excess Molar Volumes and Viscosities for the Binary Mixtures of n-Octane, n-Decane, n-Dodecane, and n-Tetradecane with Octan-2-ol at 298.15 K. J. Thermodyn. 2013, 2013, 571918. [Google Scholar] [CrossRef]
- Hoga, H.E.; Torres, R.B. Volumetric and viscometric properties of binary mixtures of {methyl tert-butyl ether (MTBE) + alcohol} at several temperatures and p = 0.1 MPa: Experimental results and application of the ERAS model. J. Chem. Thermodyn. 2011, 43, 1104–1134. [Google Scholar] [CrossRef]
- Reed, T.M.; Taylor, T.E. Viscosities of Liquid Mixtures. J. Phys. Chem. 1959, 63, 58–67. [Google Scholar] [CrossRef]
- Palepu, R.; Oliver, J.; MacKinnon, B. Viscosities and densities of binary liquid mixtures of m-cresol with substituted anilines. Part 3. Can. J. Chem. 1985, 63, 1024–1030. [Google Scholar] [CrossRef]
- Chai, L.; Wang, Y.; Wang, X.; Wang, E.; Zhai, W.; Ma, K.; Zhang, J. Basic physicochemical properties, excess properties, and intermolecular interactions of n-propanol/isopropanol and ethylenediamine binary mixtures. J. Mol. Liq. 2023, 389, 122868. [Google Scholar] [CrossRef]
- Kinart, C.M.; Bald, A.; Kinart, W.J.; Kolasinski, A. Dimethylsulfoxide—N,N-Dimethylformamide Binary Mixtures and Their Physicochemical Properties. Phys. Chem. Liq. 1998, 36, 245–256. [Google Scholar] [CrossRef]
- Van, H.T.; Patterson, D. Volumes of mixing and the P* effect: Part I. Hexane isomers with normal and branched hexadecane. J. Solut. Chem. 1982, 11, 793–805. [Google Scholar] [CrossRef]
- Prigogine, I.; Trappeniers, N.; Mathot, V. On the Application of the Cell Method to r-mer Liquids. J. Chem. Phys. 1953, 21, 559–560. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Thermodynamics of Liquid Mixtures. J. Am. Chem. Soc. 1965, 87, 1833–1838. [Google Scholar] [CrossRef]
- Abe, A.; Flory, P.J. The Thermodynamic Properties of Mixtures of Small, Nonpolar Molecules. J. Am. Chem. Soc. 1965, 87, 1838–1846. [Google Scholar] [CrossRef]
- Ivanis, G.R.; Tasic, A.Z.; Radovic, I.R.; Djordjevic, B.D.; Serbanovic, S.P.; Kijevcanin, M.L.J. Modeling of density and calculations of derived volumetric properties for n-hexane, toluene and dichloromethane at pressures 0.1–60 MPa and temperatures 288.15–413.15 K. J. Serb. Chem. Soc. 2015, 80, 1423–1433. [Google Scholar] [CrossRef]
- Torres, R.B.; Francesconi, A.Z.; Volpe, P.L.O. Experimental study and modelling using the ERAS-Model of the excess molar volume of acetonitrile-alkanol mixtures at different temperatures and atmospheric pressure. Fluid Phase Equilibria 2003, 210, 287–306. [Google Scholar] [CrossRef]
- Heintz, A. A new Theoretical Approach for predicting Excess Properties of Alkanol/Alkane Mixtures. Ber. Bunsenges Phys. Chem. 1985, 89, 172–181. [Google Scholar] [CrossRef]
- Murakami, S.; Benson, G.C. Thermodynamic Properties of Some Isomeric Butyl Alcohol Mixtures. Bull. Chem. Soc. Jpn. 1973, 46, 74–79. [Google Scholar] [CrossRef]
- Bich, E.; Papaioannou, D.; Heintz, A.; Langer-Tusel, E.; Lichtenthaler, R. Excess enthalpy of the system propan-1-ol + MTBE + i-octane. Experimental results and ERAS model calculations. Fluid Phase Equilibria 1999, 165, 115–135. [Google Scholar] [CrossRef]
- Avram, M.; Mateescu, G.D. Spectroscopia in Infrarosu. Aplicatii in Chimia Organica; Editura Tehnică: Bucuresti, Romania, 1966. [Google Scholar]
- Satheesh, B.; Sreenu, D.; Jyostna, S. Thermodynamic and spectroscopic studies of intermolecular interactions between isoamyl alcohol and monocyclic aromatic non-ideal binary liquid mixtures. Chem. Data Collect. 2020, 28, 100448. [Google Scholar] [CrossRef]
- Losetty, V.; Chittluri, N.R.; Gardas, R.L.; Kumar, K.S. FT-IR study of excess thermodynamic properties of binary liquid mixtures of p-xylene with 1-alkanols at 303.15 K. J. Mol. Liq. 2015, 207, 171–176. [Google Scholar] [CrossRef]
- Budeanu, M.M.; Dumitrescu, V. Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures. Appl. Sci. 2022, 12, 116. [Google Scholar] [CrossRef]
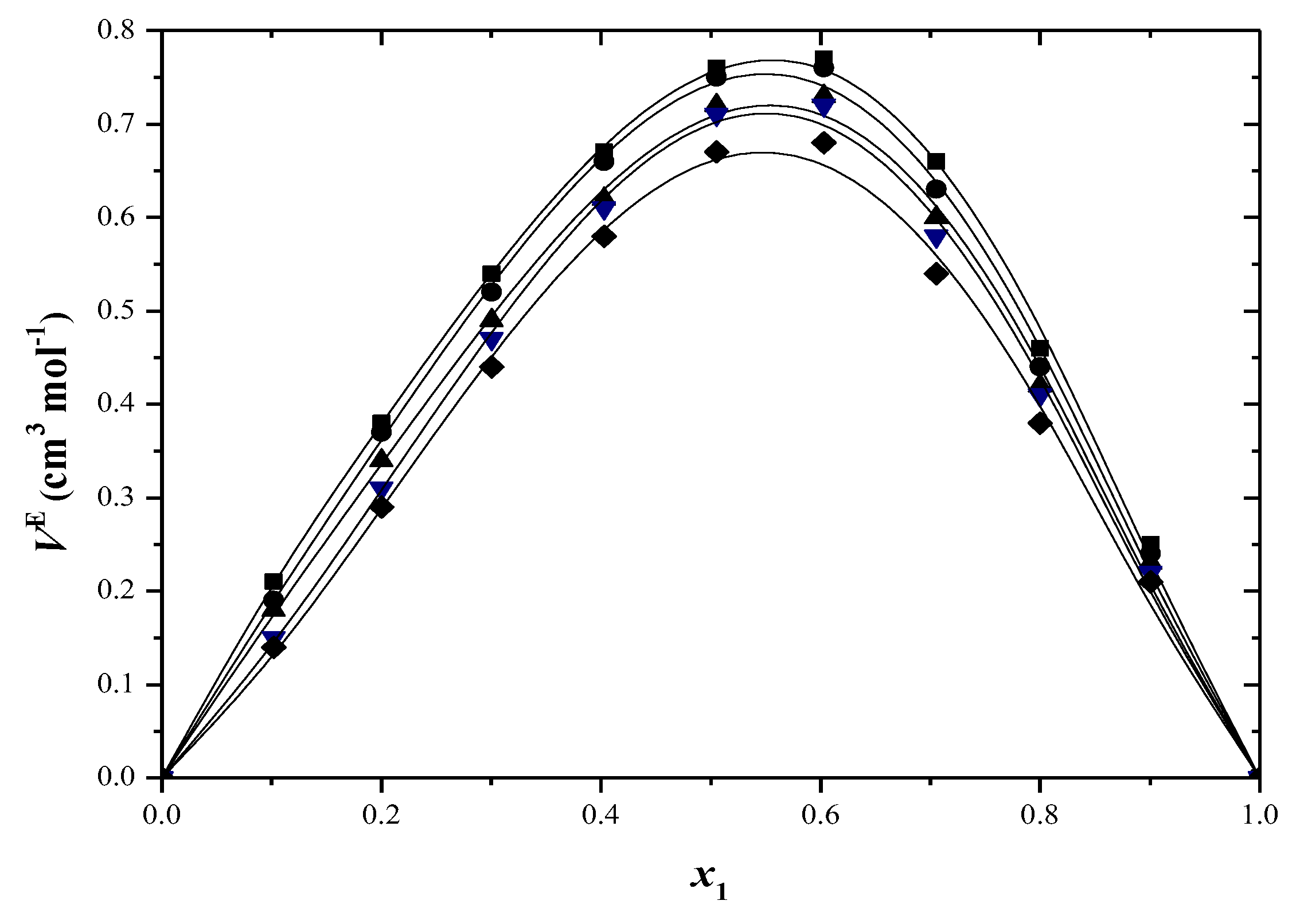

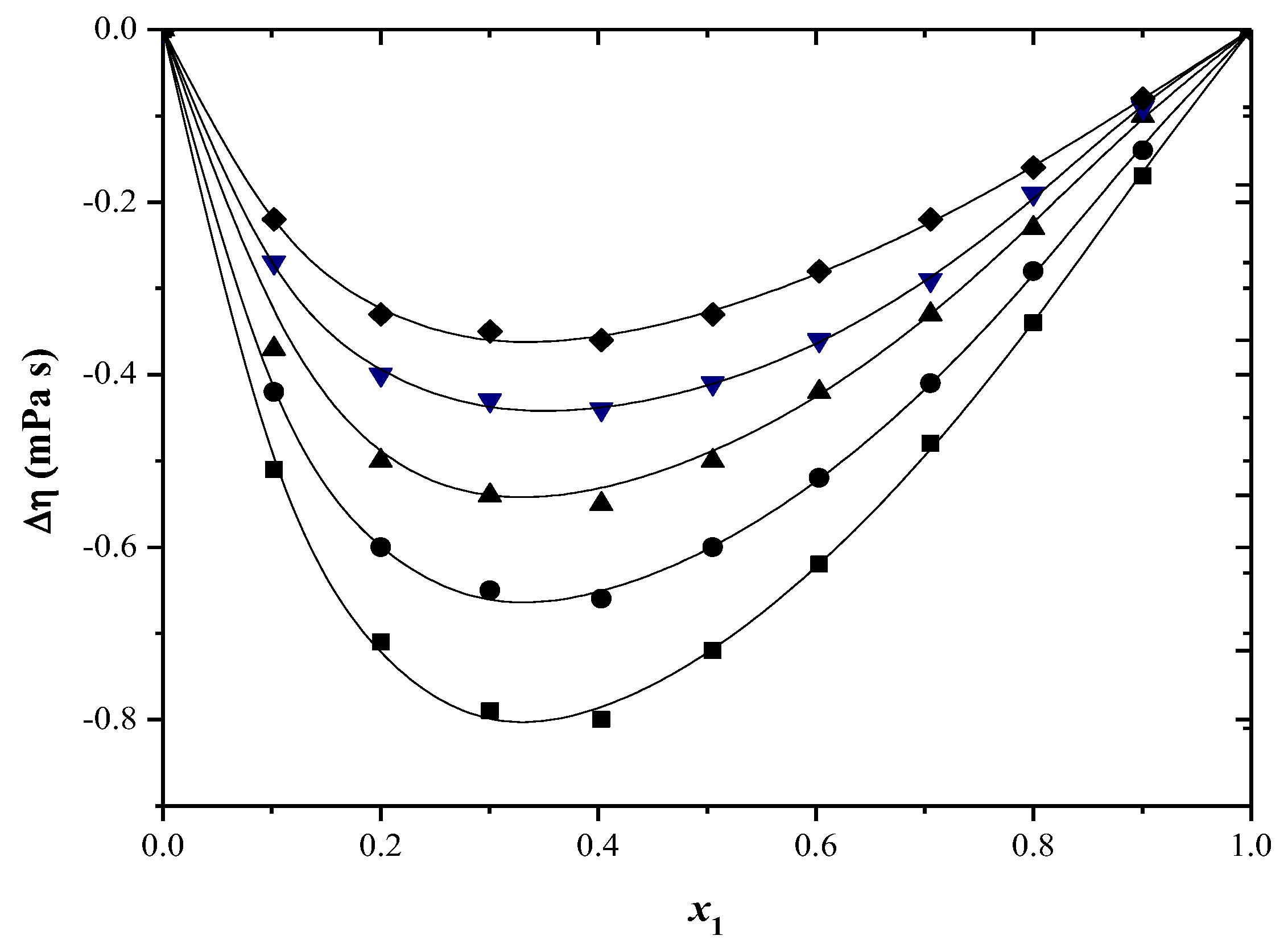
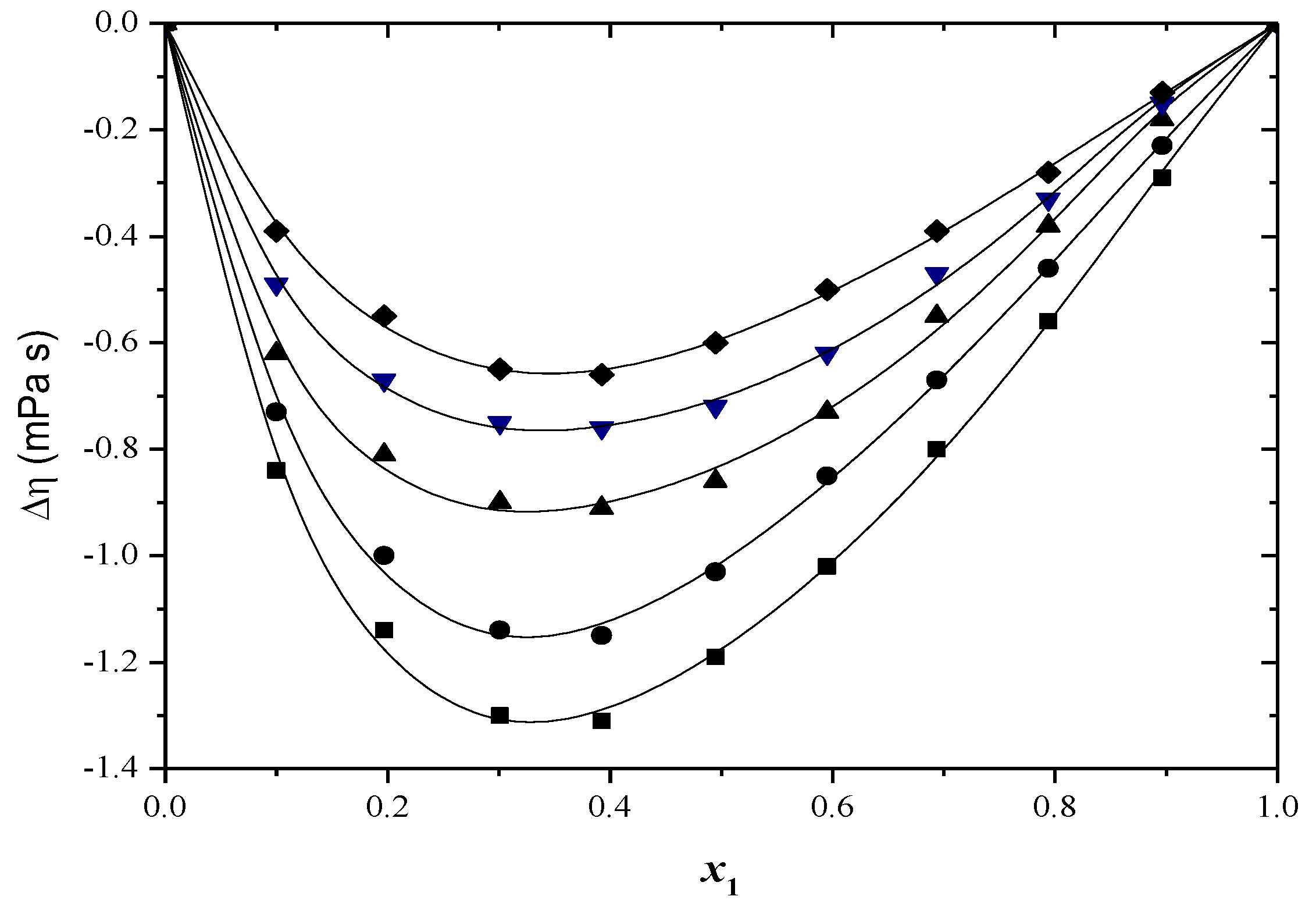
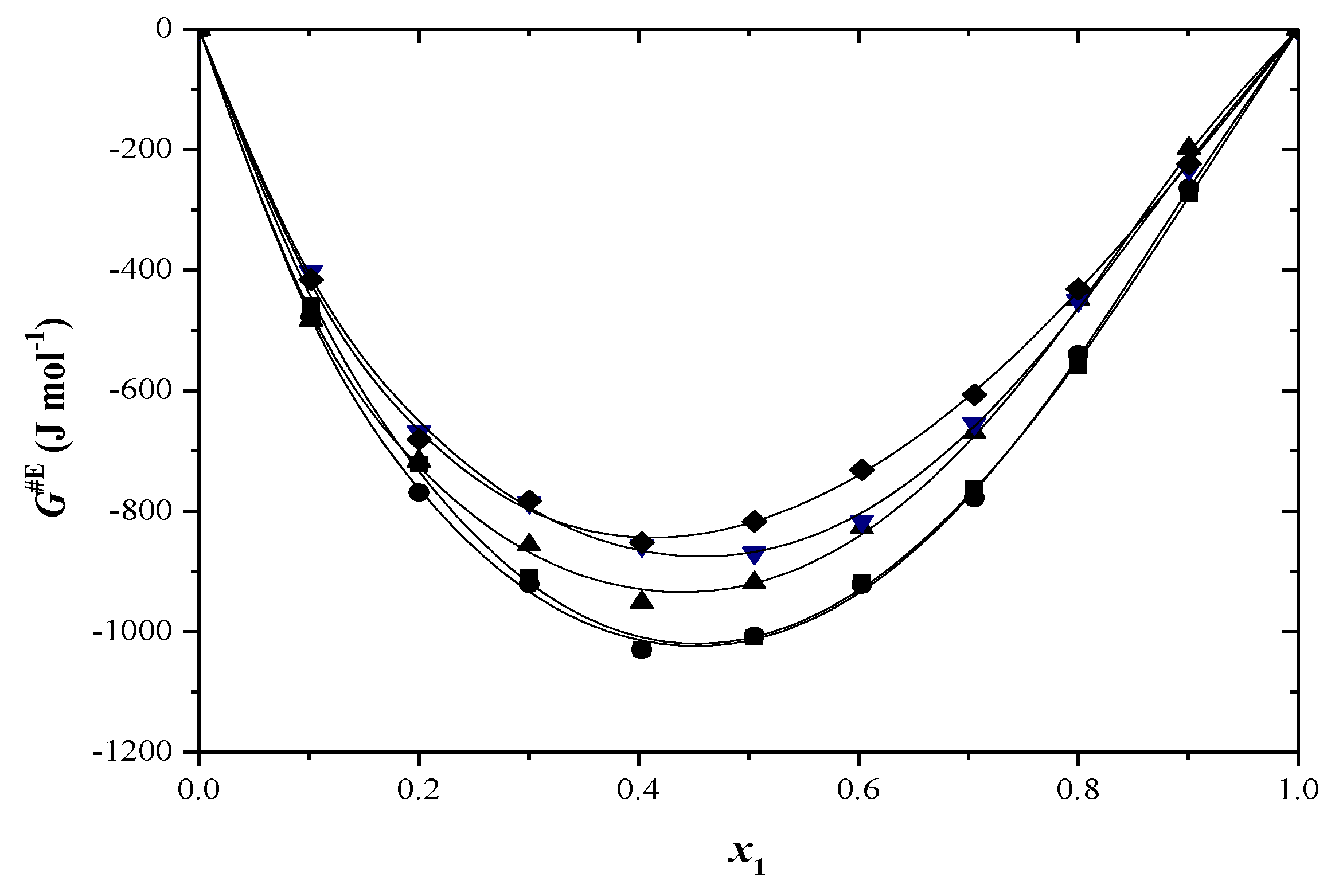
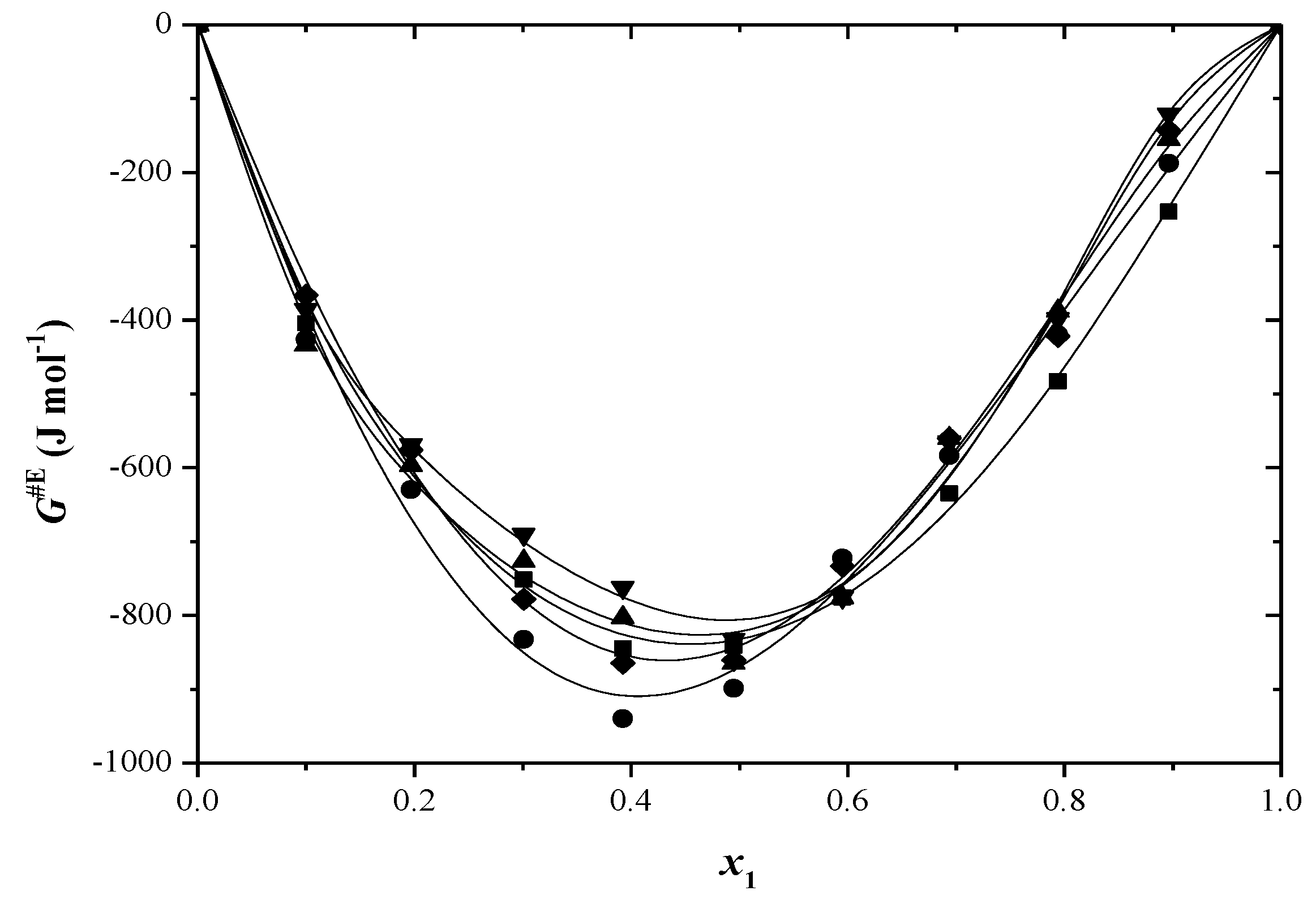
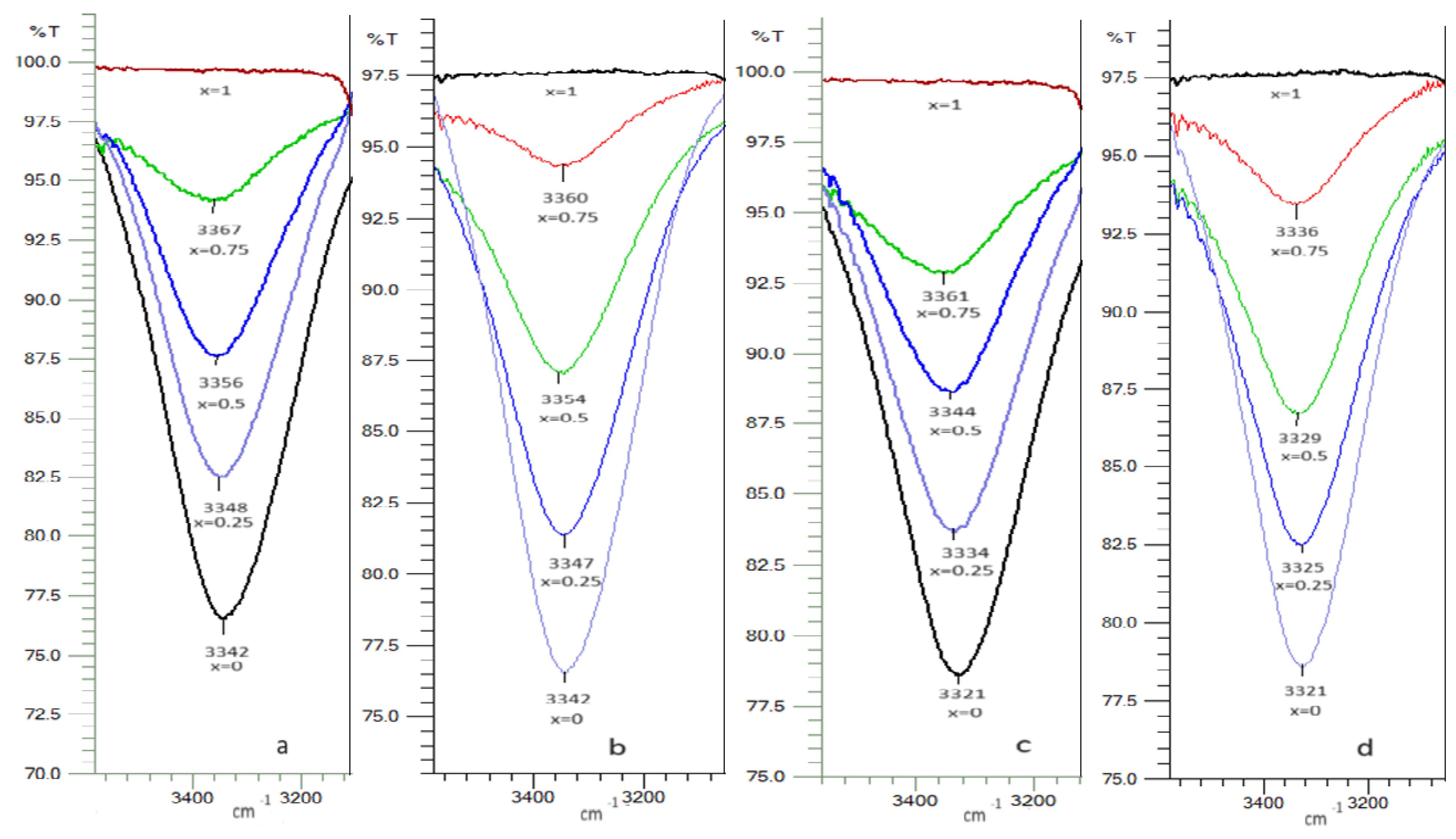
| x1 | ∆H≠ (kJ/mol) | ∆S≠ (J/mol·K) | ∆G≠ (kJ/mol) T/(K) | ||||
|---|---|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |||
| toluene (1) + 2-propanol (2) | |||||||
| 0.0000 | 21.66 | 22.88 | 14.95 | 14.84 | 14.72 | 14.61 | 14.49 |
| 0.1020 | 18.83 | 15.77 | 14.21 | 14.13 | 14.05 | 13.97 | 13.89 |
| 0.2001 | 17.03 | 11.42 | 13.68 | 13.62 | 13.57 | 13.51 | 13.45 |
| 0.3004 | 14.22 | 3.35 | 13.24 | 13.22 | 13.20 | 13.19 | 13.17 |
| 0.4030 | 11.85 | −3.40 | 12.85 | 12.87 | 12.88 | 12.90 | 12.92 |
| 0.5051 | 10.53 | −7.08 | 12.61 | 12.64 | 12.68 | 12.71 | 12.75 |
| 0.6029 | 9.51 | −9.99 | 12.44 | 12.49 | 12.54 | 12.59 | 12.64 |
| 0.7052 | 8.47 | −13.17 | 12.33 | 12.40 | 12.46 | 12.53 | 12.59 |
| 0.7998 | 7.87 | −15.13 | 12.30 | 12.38 | 12.46 | 12.53 | 12.61 |
| 0.9005 | 7.97 | −14.90 | 12.34 | 12.41 | 12.49 | 12.56 | 12.64 |
| 1.0000 | 7.69 | −15.87 | 12.35 | 12.43 | 12.50 | 12.58 | 12.66 |
| toluene (1) + 2-methyl-1-propanol (2) | |||||||
| 0.0000 | 21.41 | 16.33 | 16.62 | 16.54 | 16.46 | 16.37 | 16.29 |
| 0.1000 | 18.95 | 10.87 | 15.77 | 15.71 | 15.66 | 15.60 | 15.55 |
| 0.1969 | 17.76 | 8.81 | 15.18 | 15.13 | 15.09 | 15.05 | 15.00 |
| 0.3008 | 15.93 | 4.67 | 14.56 | 14.54 | 14.51 | 14.49 | 14.47 |
| 0.3922 | 14.33 | 0.86 | 14.07 | 14.07 | 14.06 | 14.06 | 14.06 |
| 0.4947 | 13.58 | −0.20 | 13.64 | 13.64 | 13.64 | 13.64 | 13.64 |
| 0.5952 | 12.30 | −3.47 | 13.31 | 13.33 | 13.35 | 13.37 | 13.38 |
| 0.6936 | 10.22 | −9.61 | 13.04 | 13.09 | 13.13 | 13.18 | 13.23 |
| 0.7941 | 9.18 | −12.26 | 12.77 | 12.83 | 12.90 | 12.96 | 13.02 |
| 0.8965 | 7.09 | −18.63 | 12.55 | 12.65 | 12.74 | 12.83 | 12.93 |
| 1.0000 | 7.69 | −15.87 | 12.35 | 12.43 | 12.50 | 12.58 | 12.66 |
| Component | 104·α/K−1 | kT/104·MPa−1 | V*/cm3 mol−1 | 106·p*/Jcm−3 | T*/K | ||
|---|---|---|---|---|---|---|---|
| 293.15 K | |||||||
| toluene | 9.84 | 8.715 [59] | 1.24 | 85.68 | 509.76 | 5238.74 | 0.056 |
| 2-propanol | 10.75 | 10.81 [60] | 1.26 | 60.72 | 462.29 | 4990.87 | 0.059 |
| 2-methyl- 1-propanol | 11.38 | 9.828 [11] | 1.27 | 72.74 | 548.86 | 4843.24 | 0.060 |
| 298.15 K | |||||||
| toluene | 9.92 | 9.023 [59] | 1.25 | 85.76 | 508.95 | 5254.95 | 0.057 |
| 2-propanol | 10.99 | 11.3 [61] | 1.27 | 60.59 | 465.97 | 4972.21 | 0.060 |
| 2-methyl- 1-propanol | 11.48 | 10.26 [62] | 1.28 | 72.77 | 544.26 | 4861.14 | 0.061 |
| 303.15 K | |||||||
| toluene | 10.00 | 9.349 [59] | 1.25 | 85.84 | 507.57 | 5270.52 | 0.057 |
| 2-propanol | 11.24 | 11.8 [63] | 1.28 | 60.57 | 470.36 | 4954.06 | 0.061 |
| 2-methyl- 1-propanol | 11.59 | 10.649 [11] | 1.28 | 72.93 | 543.26 | 4877.43 | 0.062 |
| 308.15 K | |||||||
| toluene | 10.08 | 9.694 [59] | 1.26 | 85.92 | 505.65 | 5287.15 | 0.058 |
| 2-propanol | 11.49 | 12.32 [51] | 1.29 | 60.51 | 474.50 | 4938.74 | 0.062 |
| 2-methyl- 1-propanol | 11.69 | 11.086 [62] | 1.29 | 72.99 | 539.80 | 4896.38 | 0.063 |
| 313.15 K | |||||||
| toluene | 10.17 | 10.06 [59] | 1.26 | 86.00 | 503.80 | 5301.47 | 0.059 |
| 2-propanol | 11.74 | 15.117 [11] | 1.29 | 60.42 | 406.97 | 4926.06 | 0.064 |
| 2-methyl-1-propanol | 11.79 | 11.541 [11] | 1.29 | 73.10 | 536.17 | 4915.81 | 0.064 |
| T/K | φ2 | θ2 | χ12·106/Jcm−3 | ψ1 | ||
|---|---|---|---|---|---|---|
| toluene (1) + 2-propanol (2) | ||||||
| 293.15 | 0.415 | 0.334 | 1.26 | 0.059 | 69.82 | 0.6088 |
| 298.15 | 0.414 | 0.333 | 1.26 | 0.060 | 67.24 | 0.6072 |
| 303.15 | 0.414 | 0.332 | 1.27 | 0.060 | 62.70 | 0.6046 |
| 308.15 | 0.413 | 0.331 | 1.28 | 0.061 | 60.44 | 0.6021 |
| 313.15 | 0.413 | 0.330 | 1.28 | 0.062 | 59.02 | 0.6379 |
| toluene (1) + 2-methyl-1-propanol (2) | ||||||
| 293.15 | 0.459 | 0.419 | 1.26 | 0.059 | 39.29 | 0.5225 |
| 298.15 | 0.459 | 0.419 | 1.27 | 0.060 | 37.25 | 0.5243 |
| 303.15 | 0.459 | 0.419 | 1.27 | 0.061 | 35.16 | 0.5237 |
| 308.15 | 0.459 | 0.419 | 1.28 | 0.061 | 32.97 | 0.5244 |
| 313.15 | 0.459 | 0.419 | 1.28 | 0.062 | 31.18 | 0.5250 |
| T/K | VEexp./ cm3 mol−1 | VEPFP/ cm3 mol−1 | VEint./ cm3 mol−1 | VEFV/ cm3 mol−1 | VEp*/ cm3 mol−1 | ADD% |
|---|---|---|---|---|---|---|
| toluene (1) + 2-propanol (2) | ||||||
| 293.15 | 0.755 | 0.768 | 0.808 | 0.009 | −0.031 | 1.7 |
| 298.15 | 0.742 | 0.755 | 0.801 | 0.012 | −0.034 | 1.7 |
| 303.15 | 0.707 | 0.719 | 0.769 | 0.016 | −0.034 | 1.7 |
| 308.15 | 0.700 | 0.712 | 0.765 | 0.021 | −0.032 | 1.7 |
| 313.15 | 0.660 | 0.673 | 0.818 | 0.026 | −0.119 | 1.9 |
| toluene (1) + 2-methyl-1-propanol (2) | ||||||
| 293.15 | 0.550 | 0.555 | 0.538 | 0.028 | 0.045 | 0.9 |
| 298.15 | 0.535 | 0.540 | 0.528 | 0.029 | 0.041 | 0.9 |
| 303.15 | 0.522 | 0.527 | 0.514 | 0.030 | 0.043 | 0.9 |
| 308.15 | 0.505 | 0.509 | 0.499 | 0.031 | 0.042 | 0.8 |
| 313.15 | 0.492 | 0.497 | 0.488 | 0.032 | 0.041 | 1.0 |
| Chemical Name | Molecular Formula | Source | CAS | Mass Fraction Purity | Water Content | Purification |
|---|---|---|---|---|---|---|
| Toluene | C7H8 | Lach:ner | 108-88-3 | ≥99.92% | ≤0.08% | None |
| 2-propanol | C3H8O | Merck | 67-63-0 | ≥99.7% | ≤0.3% | None |
| 2-methyl-1-propanol | C4H10O | Chemical Company | 78-83-1 | ≥99.7% | ≤0.3% | None |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naum, M.M.; Dumitrescu, V. Excess Thermodynamic Properties and FTIR Studies of Binary Mixtures of Toluene with 2-Propanol or 2-Methyl-1-Propanol. Molecules 2024, 29, 4706. https://doi.org/10.3390/molecules29194706
Naum MM, Dumitrescu V. Excess Thermodynamic Properties and FTIR Studies of Binary Mixtures of Toluene with 2-Propanol or 2-Methyl-1-Propanol. Molecules. 2024; 29(19):4706. https://doi.org/10.3390/molecules29194706
Chicago/Turabian StyleNaum, Maria Magdalena, and Vasile Dumitrescu. 2024. "Excess Thermodynamic Properties and FTIR Studies of Binary Mixtures of Toluene with 2-Propanol or 2-Methyl-1-Propanol" Molecules 29, no. 19: 4706. https://doi.org/10.3390/molecules29194706
APA StyleNaum, M. M., & Dumitrescu, V. (2024). Excess Thermodynamic Properties and FTIR Studies of Binary Mixtures of Toluene with 2-Propanol or 2-Methyl-1-Propanol. Molecules, 29(19), 4706. https://doi.org/10.3390/molecules29194706





