Quantum Otto Heat Engine Using Polar Molecules in Pendular States
Abstract
:1. Introduction
2. Theory
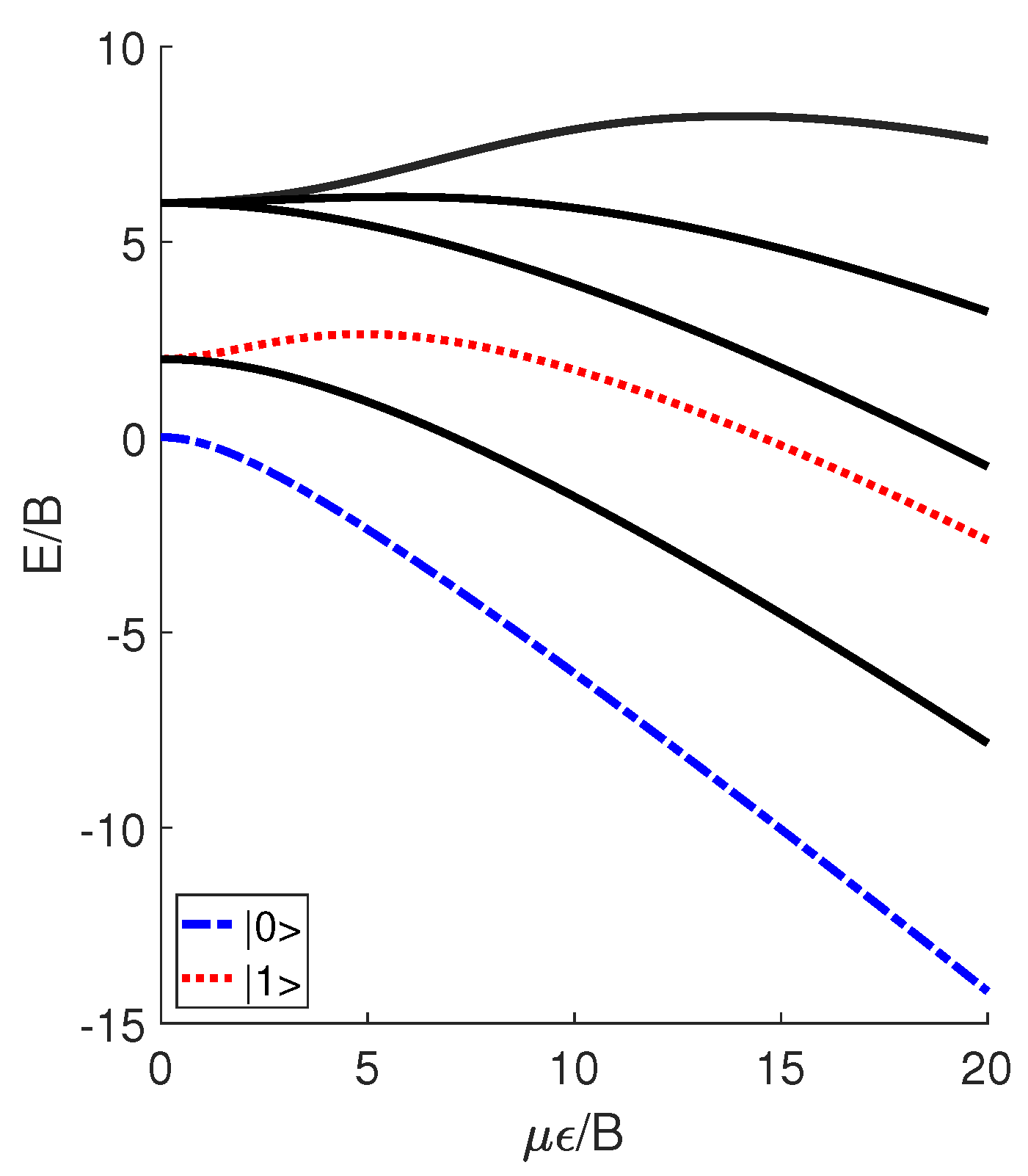
2.1. Polar Molecules in Pendular States
2.2. Quantum Otto Cycle
3. Results
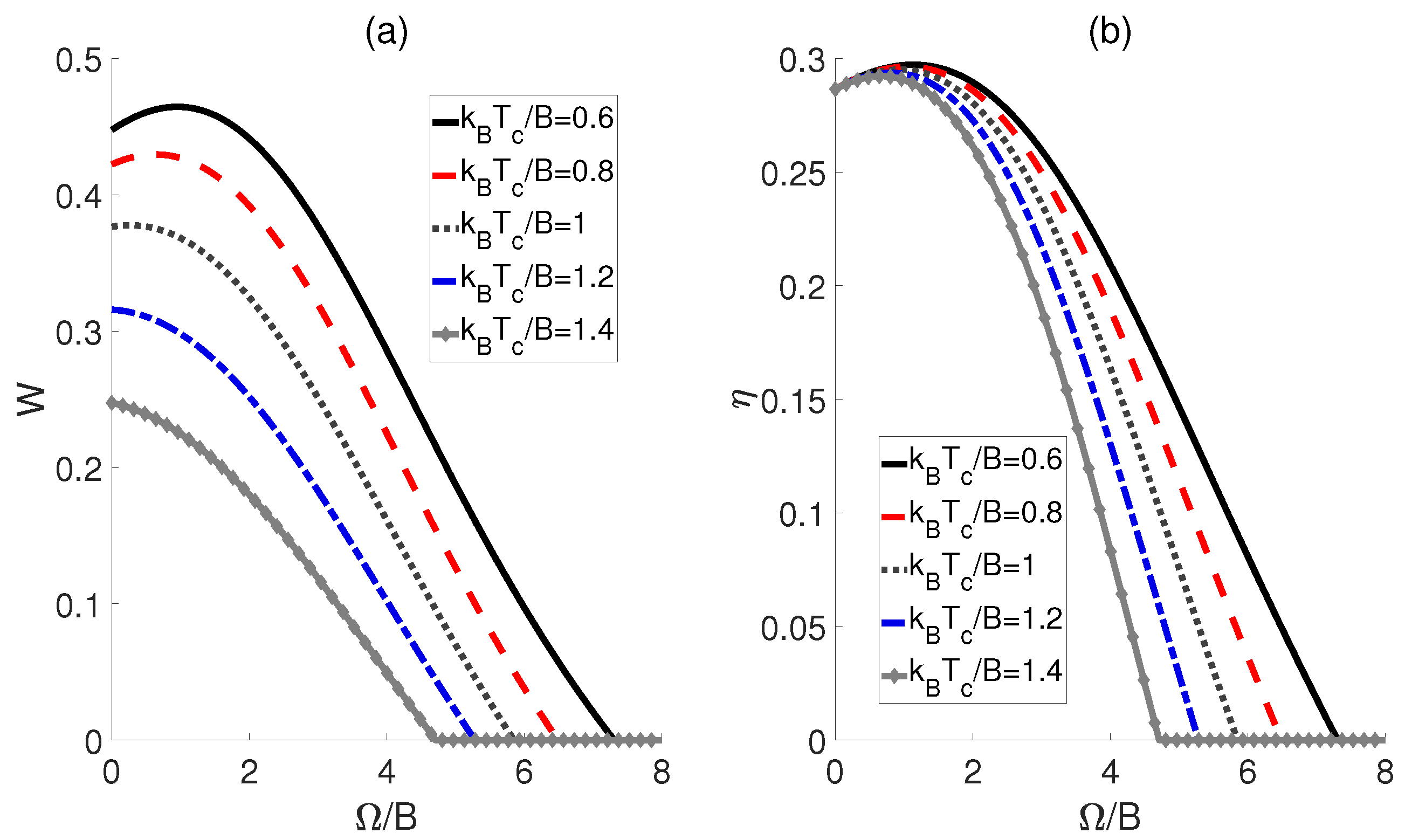
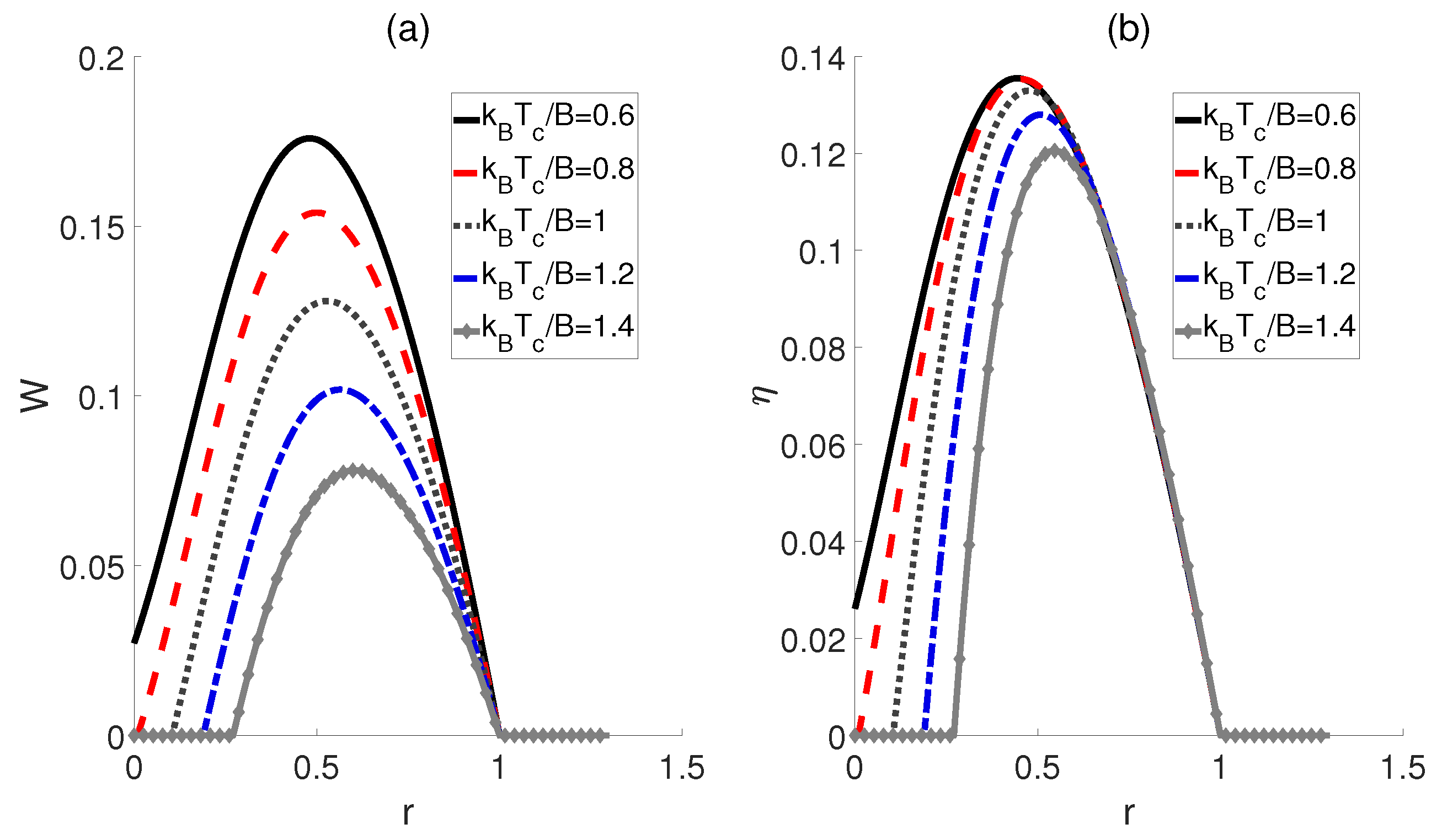
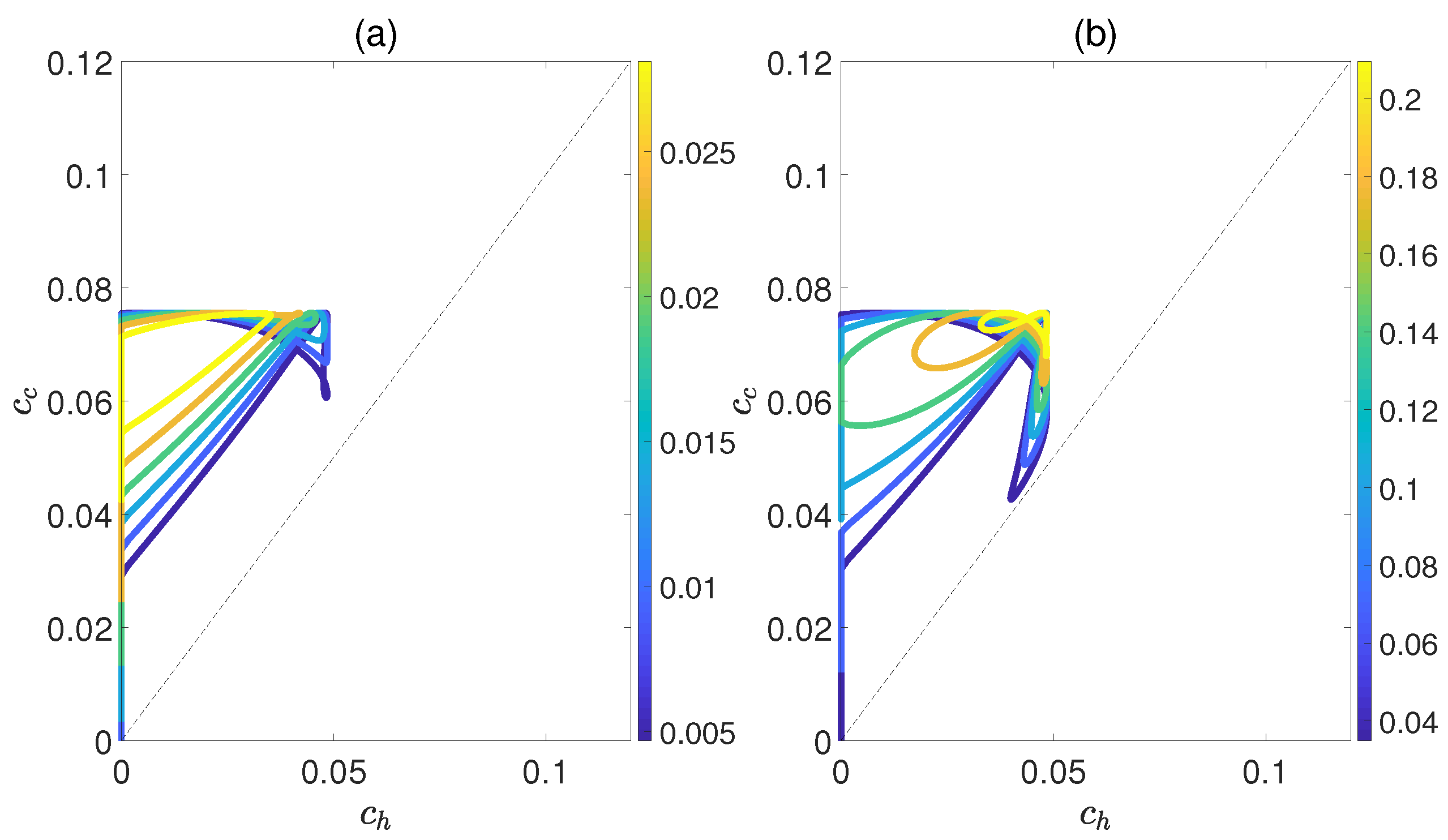
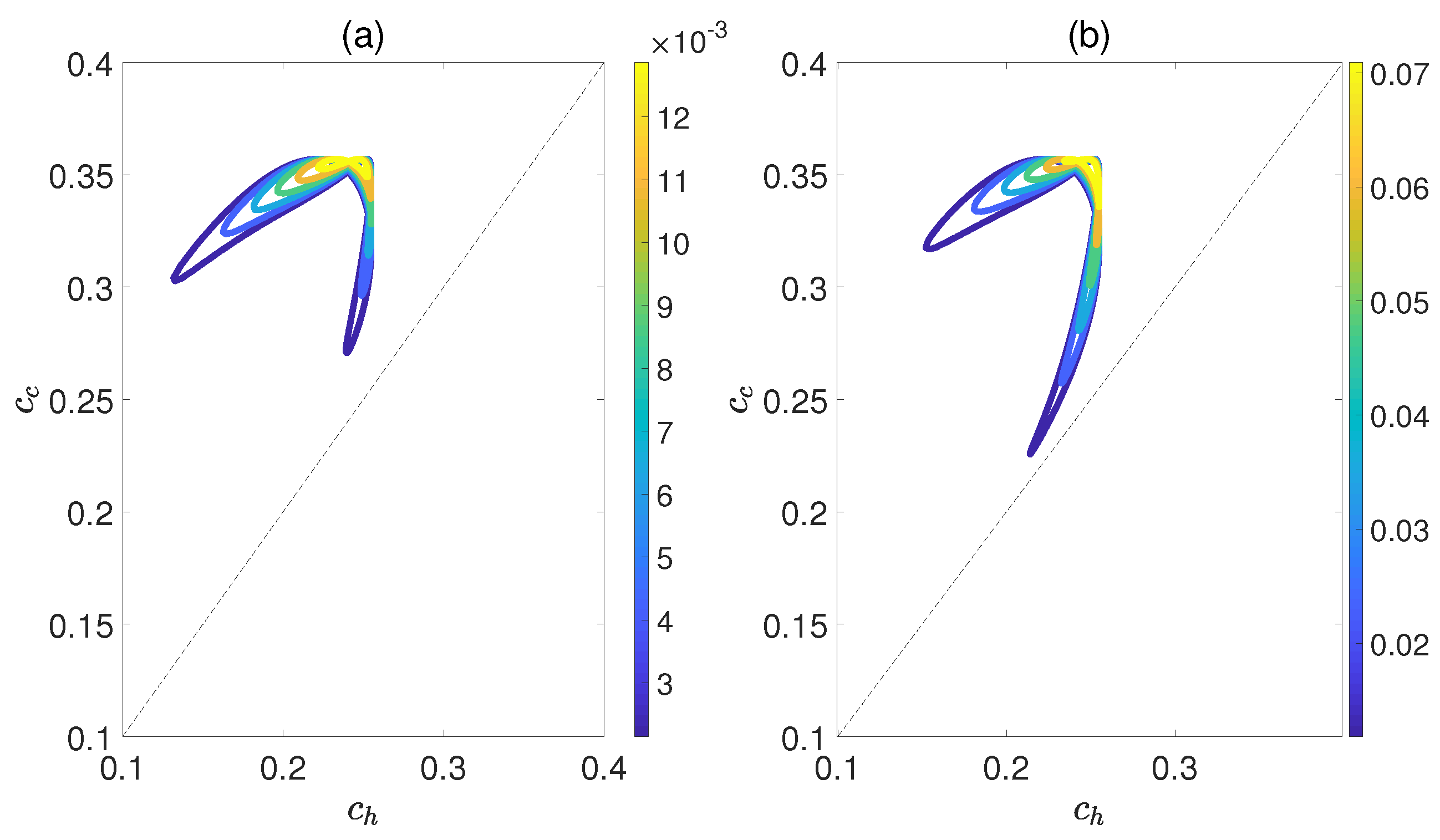
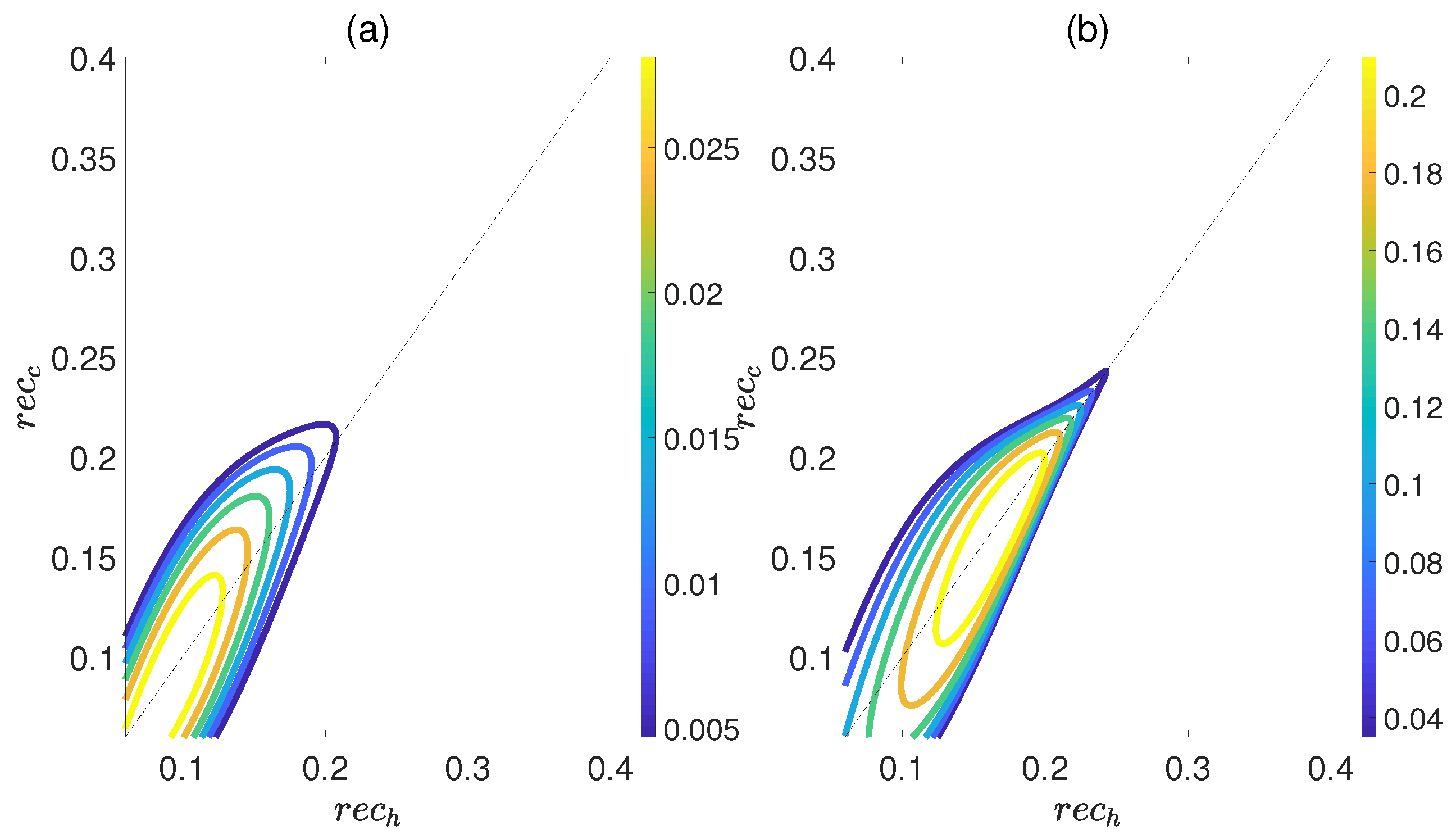
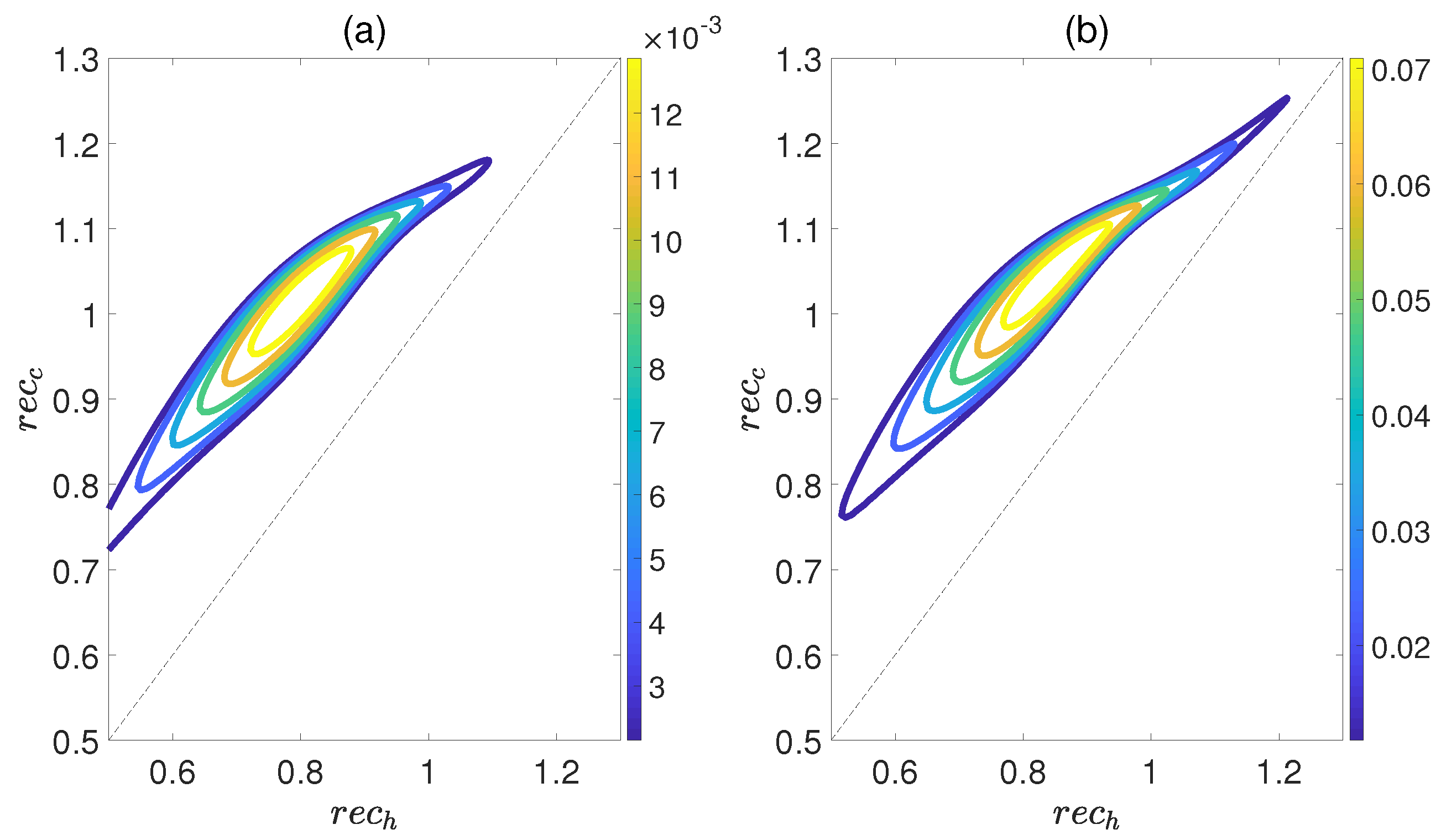
3.1. QOHE of Coupled Dipoles in Thermal Equilibrium
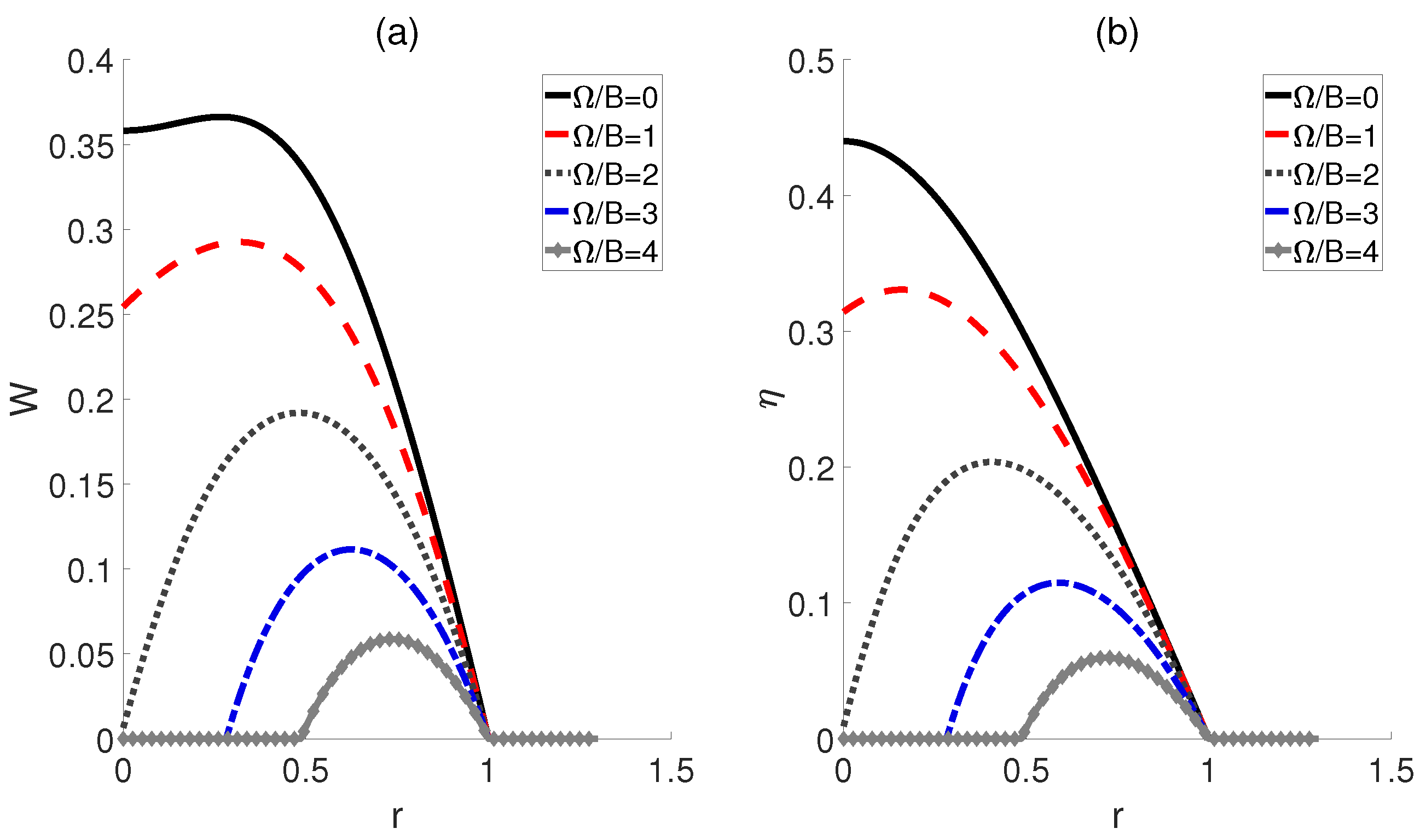
3.2. Effects of Entanglement and Coherence on QOHE
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QHEs | quantum heat engines |
| QOHE | quantum Otto heat engine |
References
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Kieu, T.D. The second law, Maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 2004, 93, 140403. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Liu, Y.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, R.; Levy, A. Quantum heat engines and refrigerators: Continuous devices. Annu. Rev. Phys. Chem. 2014, 65, 365. [Google Scholar] [CrossRef] [PubMed]
- Abd-Rabbou, M.Y.; Rahman, A.U.; Yurischev, M.A.; Haddadi, S. Comparative study of quantum Otto and Carnot engines powered by a spin working substance. Phys. Rev. E 2023, 108, 034106. [Google Scholar] [CrossRef]
- Josefsson, M.; Svilans, A.; Burke, A.M.; Hoffmann, E.A.; Fahlvik, S.; Thelander, C.; Leijnse, M.; Linke, H. A quantum-dot heat engine operating close to the thermodynamic efficiency limits. Nat. Nanotechnol. 2018, 13, 920. [Google Scholar] [CrossRef]
- Khlifi, Y.; Abaach, S.; EL Baz, M.; El Allati, A. A quantum Otto heat engine driven by three quantum dots. Phys. Scr. 2024, 99, 075967. [Google Scholar] [CrossRef]
- Zhang, J.-W.; Zhang, J.-Q.; Ding, G.-Y.; Li, J.-C.; Bu, J.-T.; Wang, B.; Yan, L.-L.; Su, S.-L.; Chen, L.; Nori, F.; et al. Dynamical control of quantum heat engines using exceptional points. Nat. Commun. 2022, 13, 6225. [Google Scholar] [CrossRef]
- Bouton, Q.; Nettersheim, J.; Burgardt, S.; Adam, D.; Lutz, E.; Widera, A. A quantum heat engine driven by atomic collisions. Nat. Commun. 2021, 12, 2063. [Google Scholar] [CrossRef]
- Macovei, M.A. Performance of the collective three-level quantum thermal engine. Phys. Rev. A 2022, 105, 043708. [Google Scholar] [CrossRef]
- Feyisa, C.G.; Jen, H.H. A photonic engine fueled by entangled two atoms. New J. Phys. 2024, 26, 033038. [Google Scholar]
- Zhang, K.; Bariani, F.; Meystre, P. Quantum optomechanical heat engine. Phys. Rev. Lett. 2014, 112, 150602. [Google Scholar] [CrossRef] [PubMed]
- Ferreri, A.; Macrŕ, V.; Wilhelm, F.K.; Nori, F.; Bruschi, D.E. Quantum field heat engine powered by phonon-photon interactions. Phys. Rev. Res. 2023, 5, 043274. [Google Scholar] [CrossRef]
- Peterson, J.P.S.; Batalhão, T.B.; Herrera, M.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Serra, R.M. Experimental characterization of a spin quantum heat engine. Phys. Rev. Lett. 2019, 123, 240601. [Google Scholar] [CrossRef] [PubMed]
- Aimet, S.; Kwon, H. Engineering a heat engine purely driven by quantum coherence. Phys. Rev. A 2023, 107, 012221. [Google Scholar] [CrossRef]
- Camati, P.A.; Santos, J.F.G.; Serra, R.M. Coherence effects in the performance of the quantum Otto heat engine. Phys. Rev. A 2019, 99, 062103. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; He, J. Thermal entanglement in two-atom cavity QED and the entangled quantum Otto engine. Phys. Rev. A 2009, 79, 041113. [Google Scholar] [CrossRef]
- Klatzow, J.; Becker, J.N.; Ledingham, P.M.; Weinzetl, C.; Kaczmarek, K.T.; Saunders, D.J.; Nunn, J.; Walmsley, I.A.; Uzdin, R.; Poem, E. Experimental demonstration of quantum effects in the operation of microscopic heat engines. Phys. Rev. Lett. 2019, 122, 110601. [Google Scholar] [CrossRef]
- Funo, K.; Lambert, N.; Karimi, B.; Pekola, J.P.; Masuyama, Y.; Nori, F. Speeding up a quantum refrigerator via counterdiabatic driving. Phys. Rev. B 2019, 100, 035407. [Google Scholar] [CrossRef]
- Denzler, T.; Lutz, E. Efficiency fluctuations of a quantum heat engine. Phys. Rev. Res. 2020, 2, 032062. [Google Scholar] [CrossRef]
- Gao, J.; Hatano, N. Maximum power of coupled-qubit Otto engines. Phys. Rev. Res. 2024, 6, 023172. [Google Scholar] [CrossRef]
- Huang, X.L.; Sun, Q.; Guo, D.Y.; Yu, Q. Quantum Otto heat engine with three-qubit XXZ model as working substance. Physica A 2018, 491, 604. [Google Scholar] [CrossRef]
- Ono, K.; Shevchenko, S.N.; Mori, T.; Moriyama, S.; Nori, F. Analog of a quantum heat engine using a single-spin qubit. Phys. Rev. Lett. 2020, 125, 166802. [Google Scholar] [CrossRef] [PubMed]
- DeMille, D. Quantum computation with trapped polar molecules. Phys. Rev. Lett. 2002, 88, 067901. [Google Scholar] [CrossRef] [PubMed]
- Yelin, S.F.; Kirby, K.; Côté, R. Schemes for robust quantum computation with polar molecules. Phys. Rev. A 2006, 74, 050301. [Google Scholar] [CrossRef]
- Yu, P.; Cheuk, L.W.; Kozyryev, I.; Doyle, J.M. A scalable quantum computing platform using symmetric-top molecules. New J. Phys. 2019, 21, 093049. [Google Scholar] [CrossRef]
- Gregory, P.D.; Blackmore, J.A.; Bromley, S.L.; Hutson, J.M.; Cornish, S.L. Robust storage qubits in ultracold polar molecules. Nat. Phys. 2021, 17, 1149. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Hu, J.-R.; Fang, Y.-Y.; Li, J.-F.; Liu, J.-M.; Huang, X.; Sun, Z. Quantum gate control of polar molecules with machine learning. J. Chem. Phys. 2024, 161, 034102. [Google Scholar] [CrossRef]
- Gorshkov, A.V.; Hazzard, K.R.A.; Rey, A.M. Kitaev honeycomb and other exotic spin models with polar molecules. Mol. Phys. 2013, 111, 1908. [Google Scholar] [CrossRef]
- Rosson, P.; Kiffner, M.; Mur-Petit, J.; Jaksch, D. Characterizing the phase diagram of finite-size dipolar Bose-Hubbard systems. Phys. Rev. A 2020, 101, 013616. [Google Scholar] [CrossRef]
- ACME Collaboration. Improved limit on the electric dipole moment of the electron. Nature 2018, 562, 355. [Google Scholar]
- Ospelkaus, S.; Ni, K.-K.; Wang, D.; de Miranda, M.H.G.; Neyenhuis, B.; Quéméner, G.; Julienne, P.S.; Bohn, J.L.; Jin, D.S.; Ye, J. Quantum-state controlled chemical reactions of ultracold potassium-rubidium molecules. Science 2010, 327, 853. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Kais, S.; Friedrich, B.; Herschbach, D. Entanglement of polar molecules in pendular states. J. Chem. Phys. 2011, 134, 124107. [Google Scholar] [CrossRef] [PubMed]
- Hughes, M.; Frye, M.D.; Sawant, R.; Bhole, G.; Jones, J.A.; Cornish, S.L.; Tarbutt, M.R.; Hutson, J.M.; Jaksch, D.; Mur-Petit, J. Robust entangling gate for polar molecules using magnetic and microwave fields. Phys. Rev. A 2020, 101, 062308. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Liu, J.-M. Creation of high-dimensional entanglement of polar molecules via optimal control fields. Phys. Rev. A 2022, 105, 023113. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Fang, Y.-Y.; Li, J.-F.; Hu, J.-R.; Liu, J.-M.; Sun, Z.; Huang, X. Entropic uncertainty relation and entanglement of molecular dipoles in an electric field. Chaos Solitons Fractals 2024, 186, 115220. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Sun, Z.; Duan, T.; Ding, Y.-K.; Huang, X.; Liu, J.-M. Entanglement generation of polar molecules via deep reinforcement learning. J. Chem. Theory Comput. 2024, 20, 1811. [Google Scholar] [CrossRef]
- Anderegg, L.; Augenbraun, B.L.; Chae, E.; Hemmerling, B.; Hutzler, N.R.; Ravi, A.; Collopy, A.; Ye, J.; Ketterle, W.; Doyle, J.M. Radio frequency magneto-optical trapping of CaF with high density. Phys. Rev. Lett. 2017, 119, 103201. [Google Scholar] [CrossRef]
- Lim, J.; Almond, J.R.; Trigatzis, M.A.; Devlin, J.A.; Fitch, N.J.; Sauer, B.E.; Tarbutt, M.R.; Hinds, E.A. Laser cooled YbF molecules for measuring the electron’s electric dipole moment. Phys. Rev. Lett. 2018, 120, 123201. [Google Scholar] [CrossRef]
- Mitra, D.; Vilas, N.B.; Hallas, C.; Anderegg, L.; Augenbraun, B.L.; Baum, L.; Miller, C.; Raval, S.; Doyle, J.M. Direct laser cooling of a symmetric top molecule. Science 2020, 369, 1366. [Google Scholar] [CrossRef]
- Wu, Y.; Burau, J.J.; Mehling, K.; Ye, J.; Ding, S. High phase-space density of laser-cooled molecules in an optical lattice. Phys. Rev. Lett. 2021, 127, 263201. [Google Scholar] [CrossRef]
- Hübner, W.; Lefkidis, G.; Dong, C.D.; Chaudhuri, D. Spin-dependent Otto quantum heat engine based on a molecular substance. Phys. Rev. B 2014, 90, 024401. [Google Scholar] [CrossRef]
- Chen, F.; Gao, Y.; Galperin, M. Molecular heat engines: Quantum coherence effects. Entropy 2017, 19, 472. [Google Scholar] [CrossRef]
- Anderegg, L.; Augenbraun, B.L.; Bao, Y.; Burchesky, S.; Cheuk, L.W.; Ketterle, W.; Doyle, J.M. Laser cooling of optically trapped molecules. Nat. Phys. 2018, 14, 890–893. [Google Scholar] [CrossRef]
- Bao, Y.C.; Yu, S.S.; Anderegg, L.; Chae, E.; Ketterle, W.; Ni, K.K.; Doyle, J.M. Dipolar spin-exchange and entanglement between molecules in an optical tweezer array. Science 2023, 382, 1138–1143. [Google Scholar] [CrossRef] [PubMed]
- Holland, C.M.; Lu, Y.K.; Cheuk, L.W. On-demand entanglement of molecules in a reconfigurable optical tweezer array. Science 2023, 382, 1143–1147. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Sun, Z.; Fang, Y.-Y.; Huang, X.-L.; Huang, X.; Li, J.-F.; Zhang, Z.-Y.; Liu, J.-M. Quantum Otto Heat Engine Using Polar Molecules in Pendular States. Molecules 2024, 29, 5617. https://doi.org/10.3390/molecules29235617
Li X, Sun Z, Fang Y-Y, Huang X-L, Huang X, Li J-F, Zhang Z-Y, Liu J-M. Quantum Otto Heat Engine Using Polar Molecules in Pendular States. Molecules. 2024; 29(23):5617. https://doi.org/10.3390/molecules29235617
Chicago/Turabian StyleLi, Xiang, Zhaoxi Sun, Yu-Yan Fang, Xiao-Li Huang, Xinning Huang, Jin-Fang Li, Zuo-Yuan Zhang, and Jin-Ming Liu. 2024. "Quantum Otto Heat Engine Using Polar Molecules in Pendular States" Molecules 29, no. 23: 5617. https://doi.org/10.3390/molecules29235617
APA StyleLi, X., Sun, Z., Fang, Y.-Y., Huang, X.-L., Huang, X., Li, J.-F., Zhang, Z.-Y., & Liu, J.-M. (2024). Quantum Otto Heat Engine Using Polar Molecules in Pendular States. Molecules, 29(23), 5617. https://doi.org/10.3390/molecules29235617





