Beyond the Harmonic Oscillator; Highlights of Selected Studies of Vibrational Potential Energy Functions
Abstract
:1. Introduction
2. Experimental and Theoretical Results
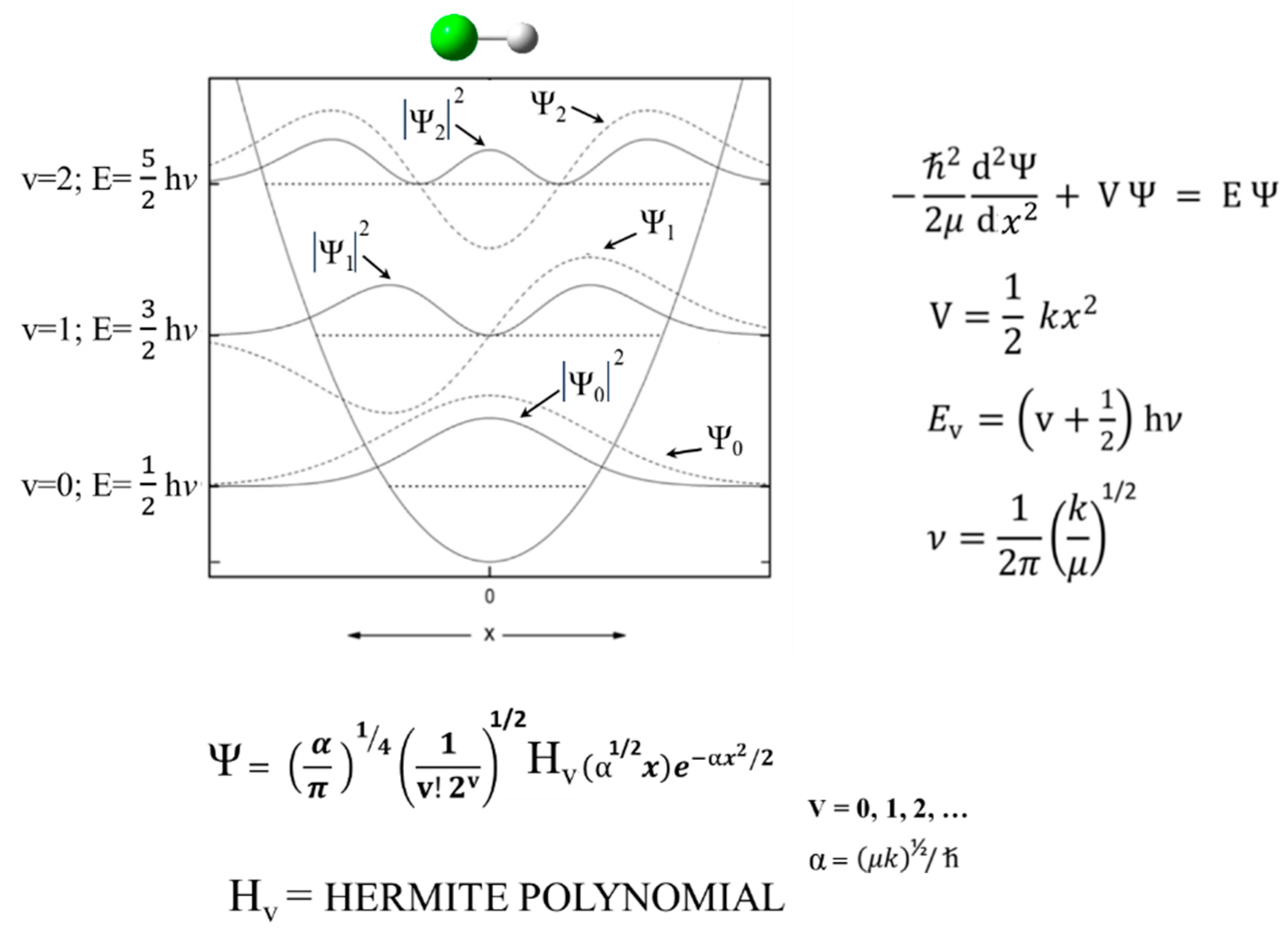
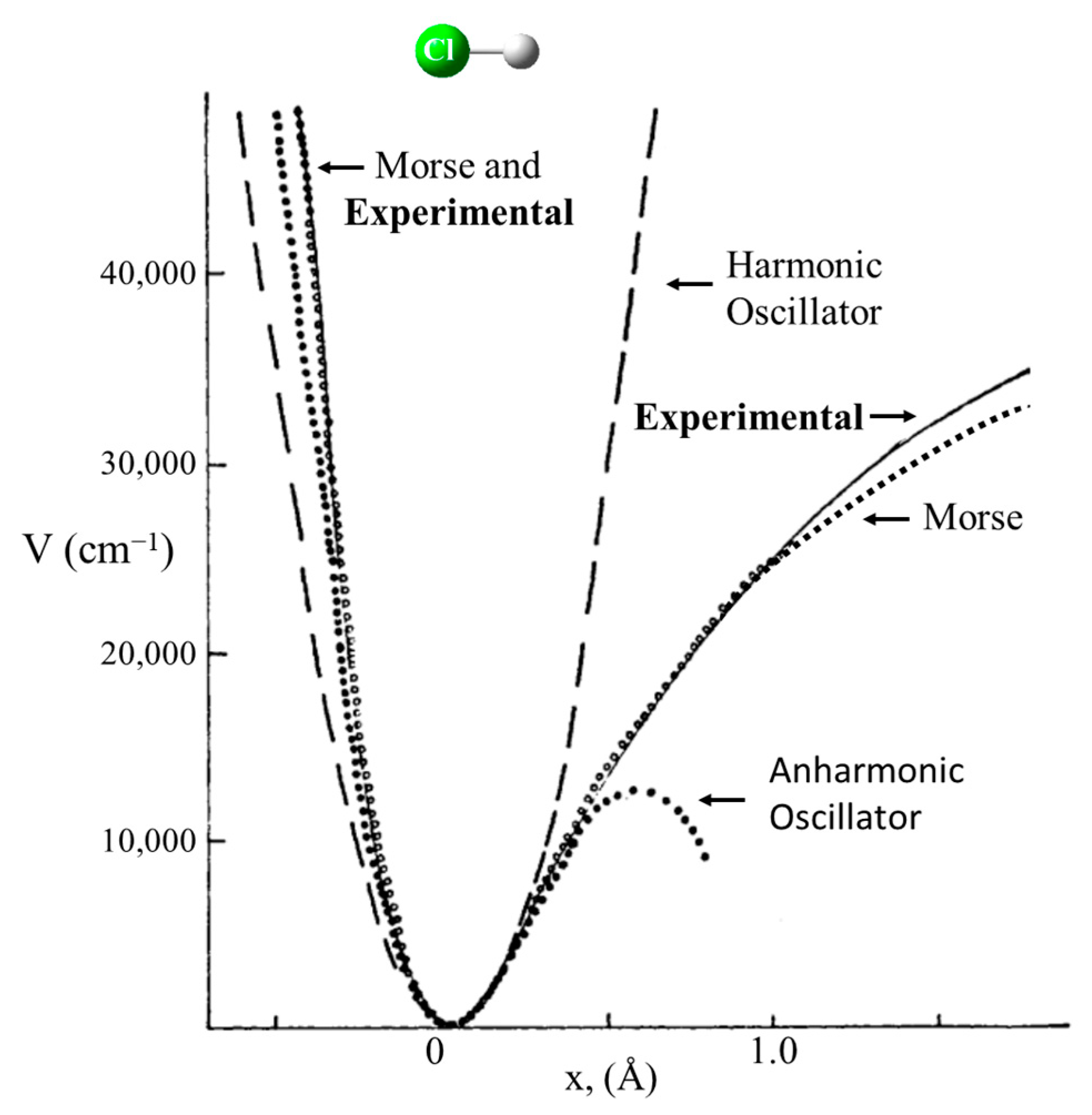
2.1. Harmonic Oscillator
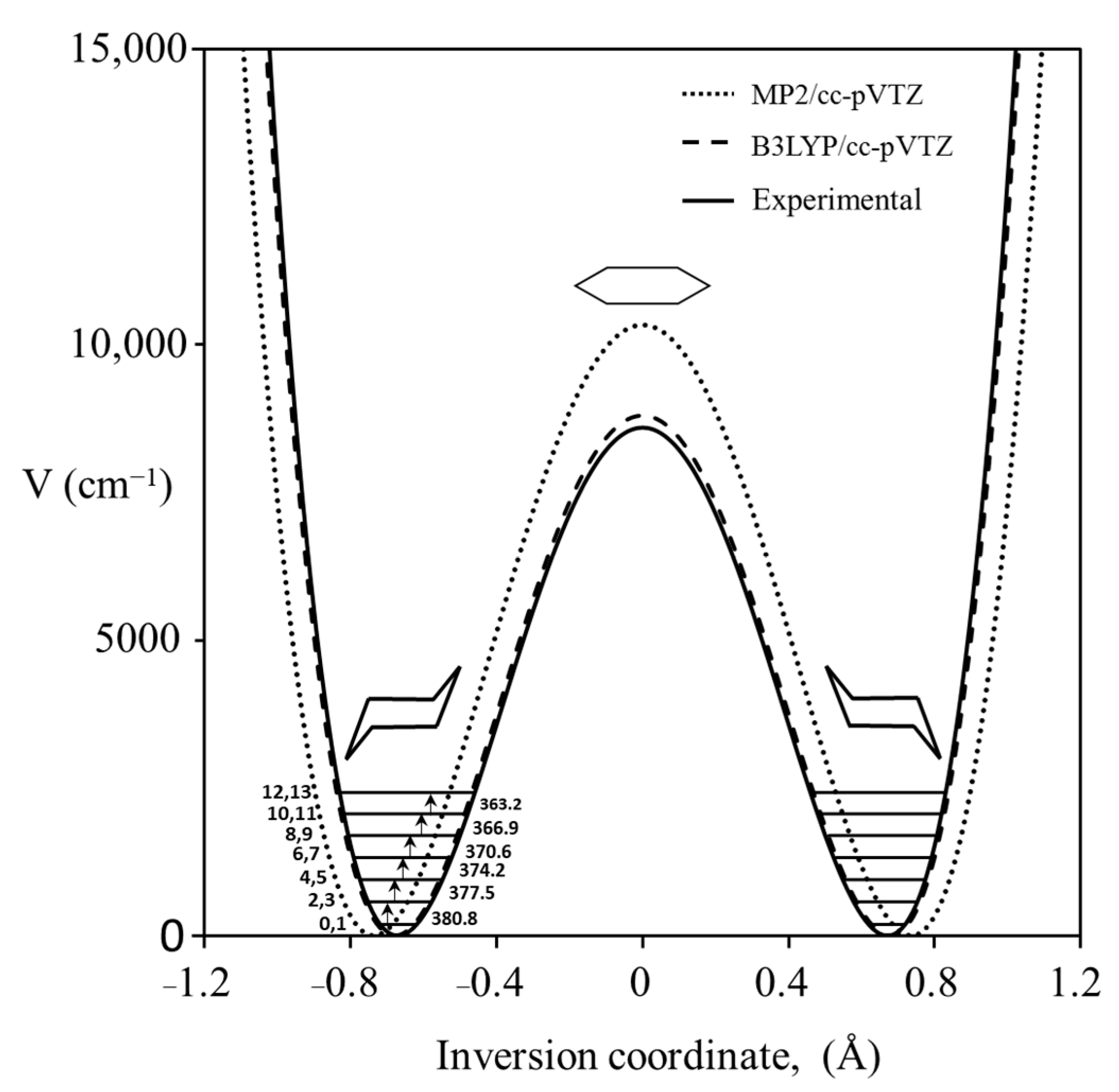
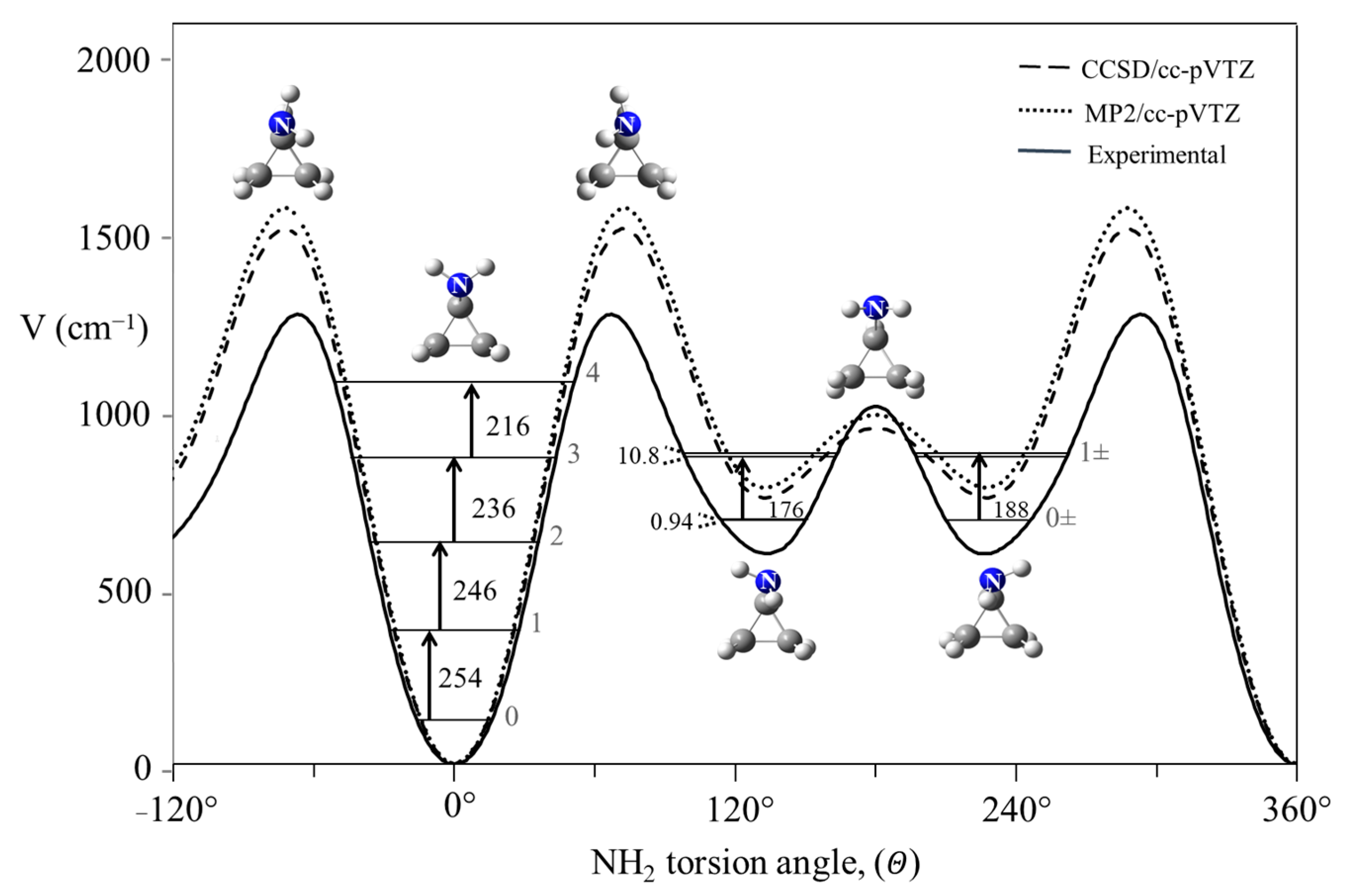
2.2. Ammonia Inversion
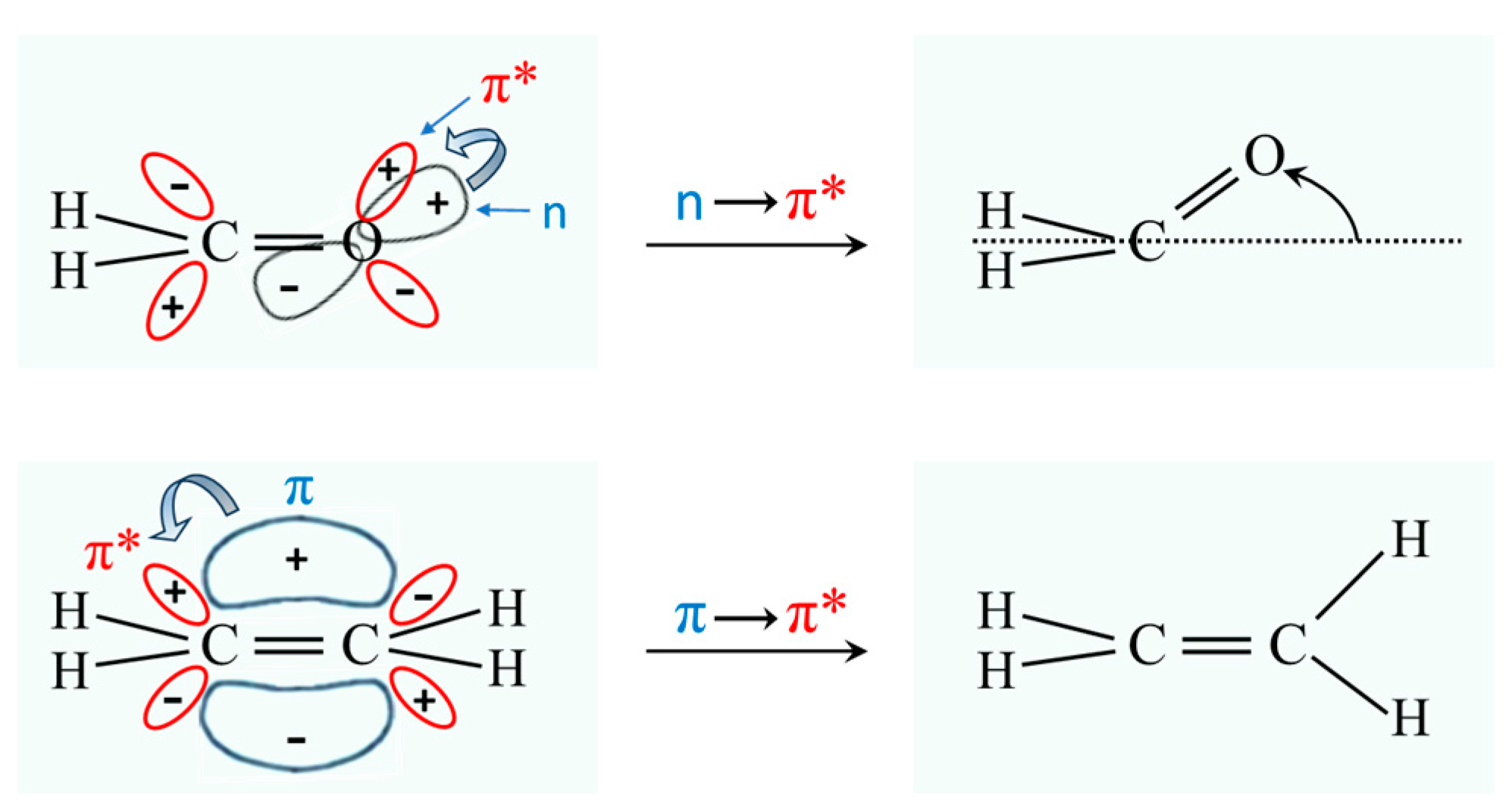
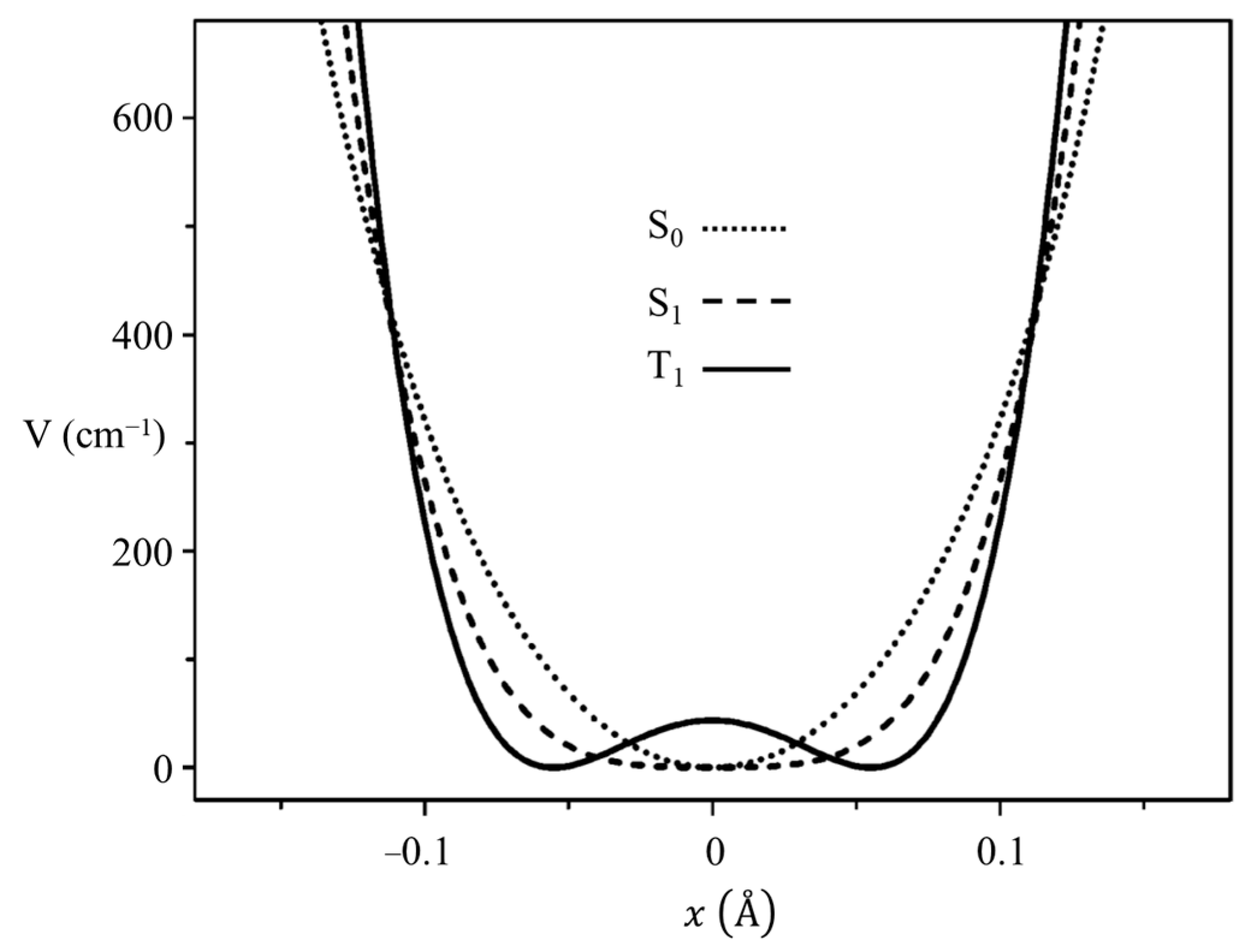
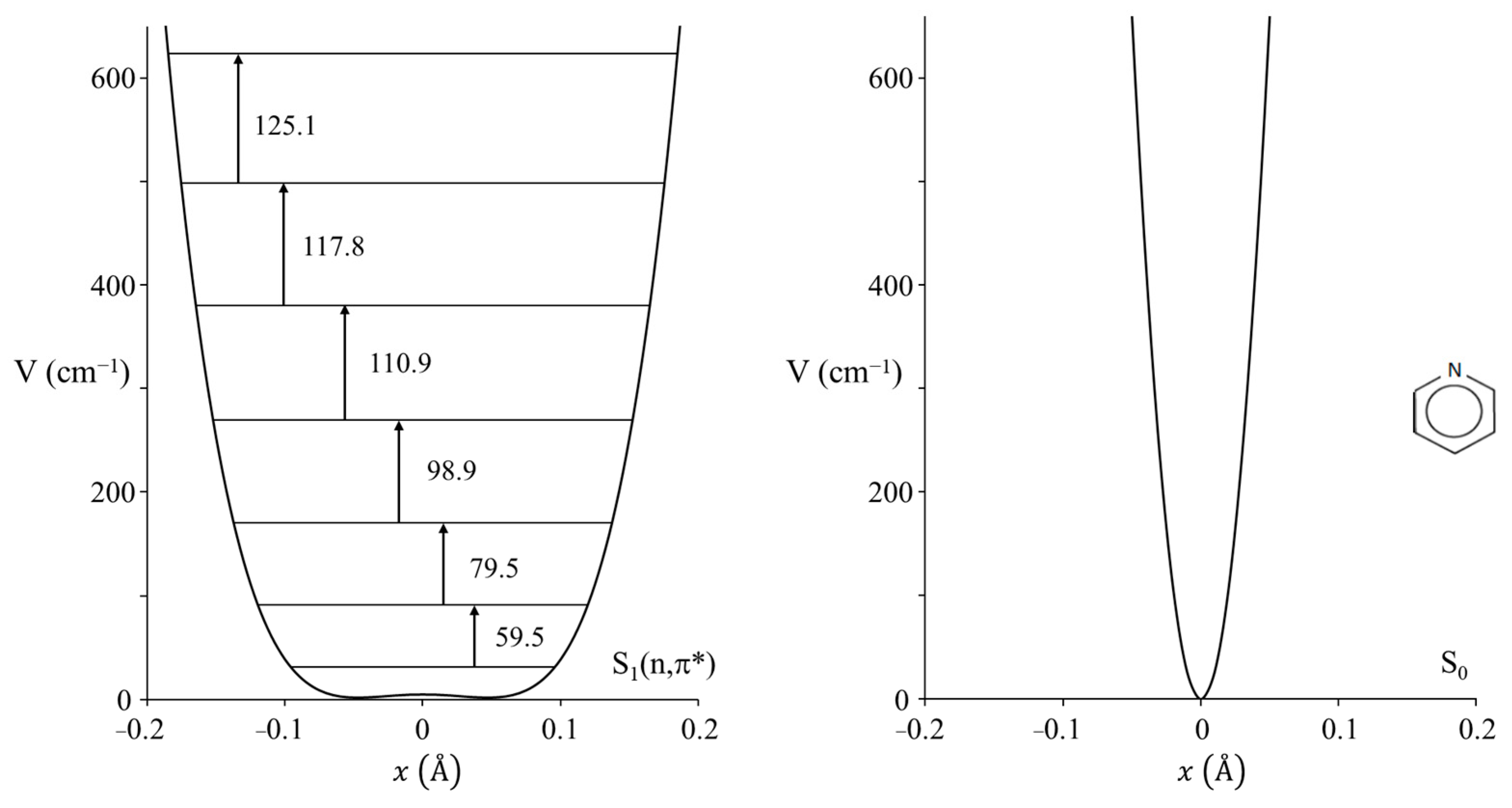
2.3. Carbonyl Inversion in the Excited State
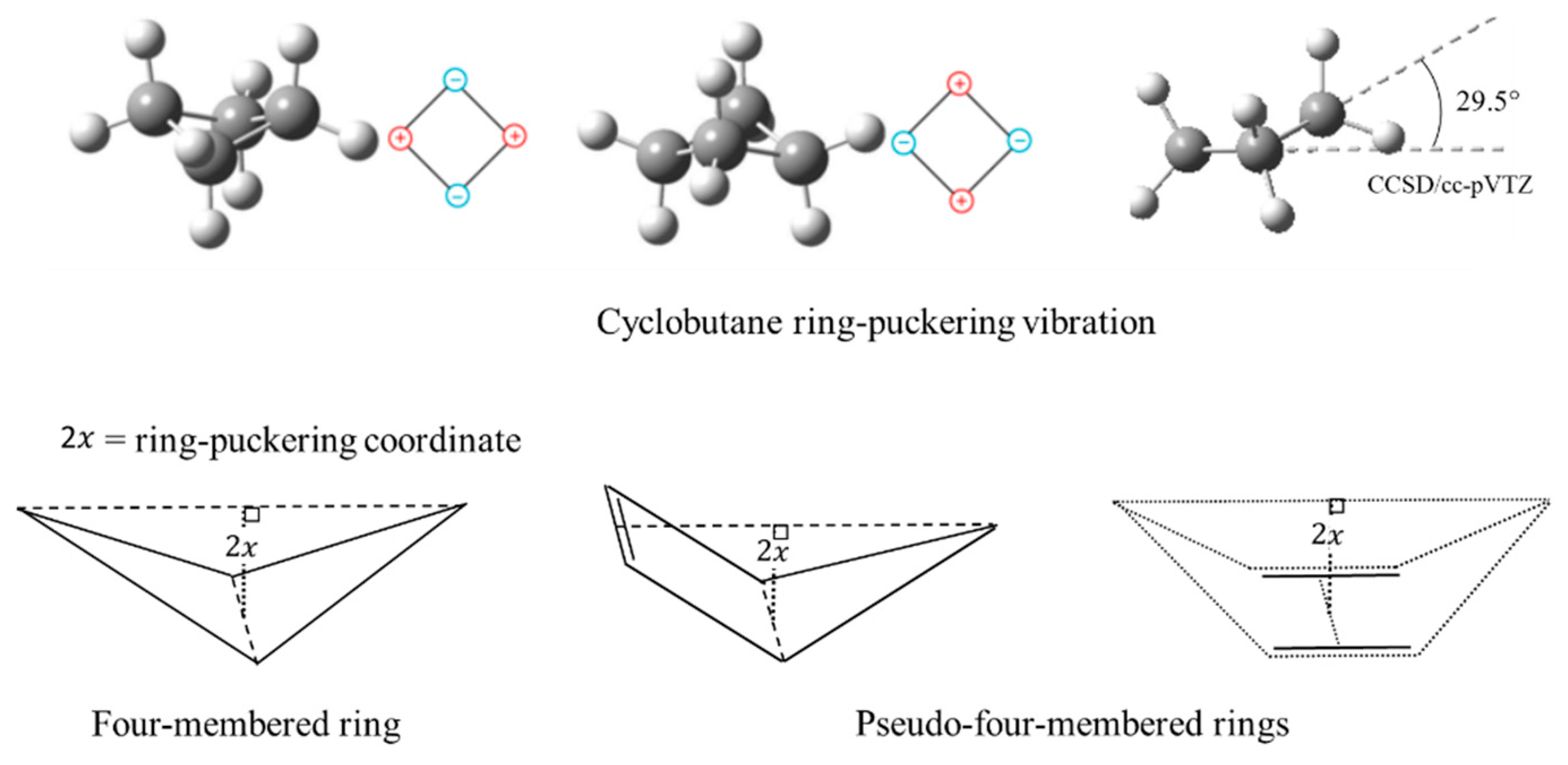
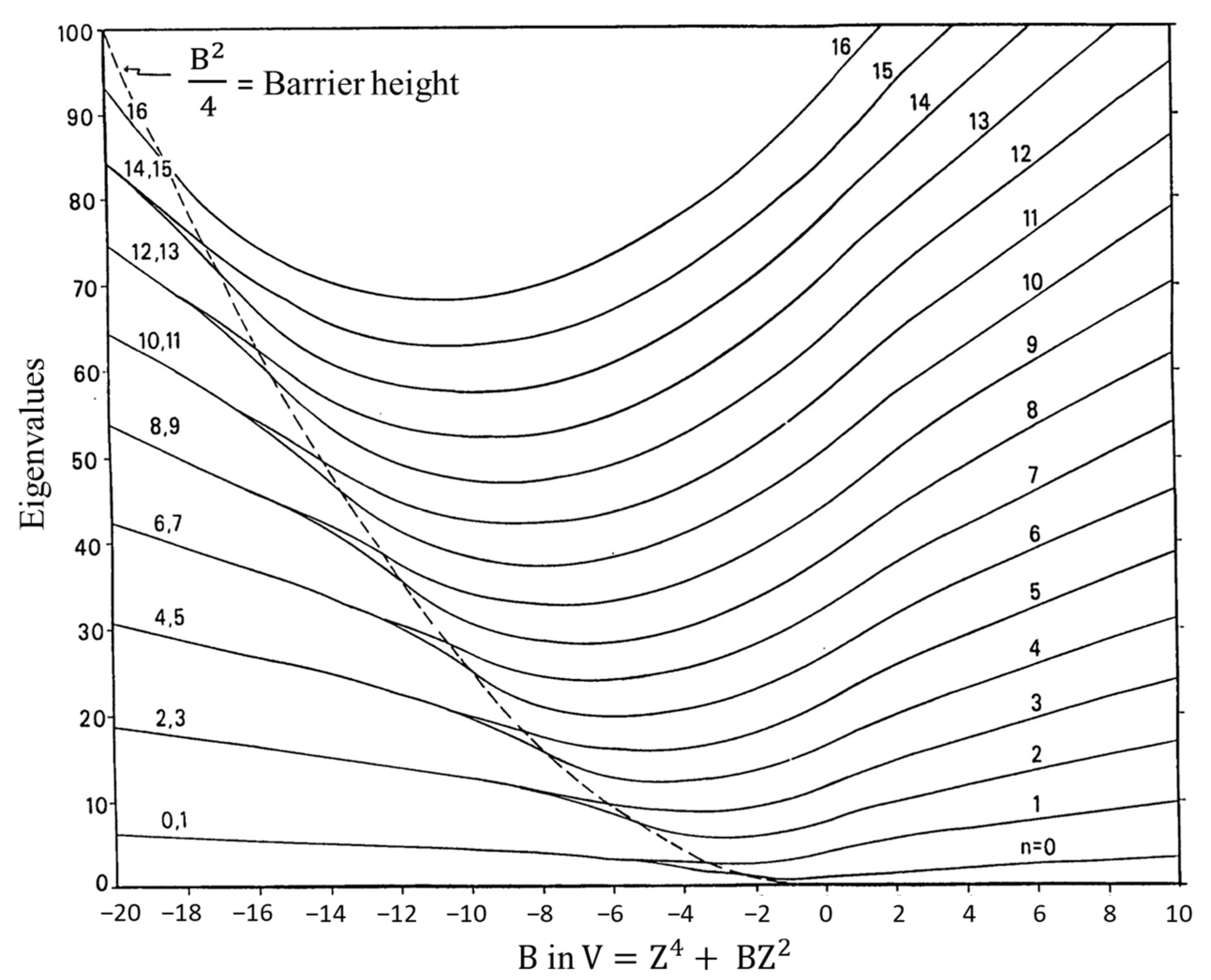
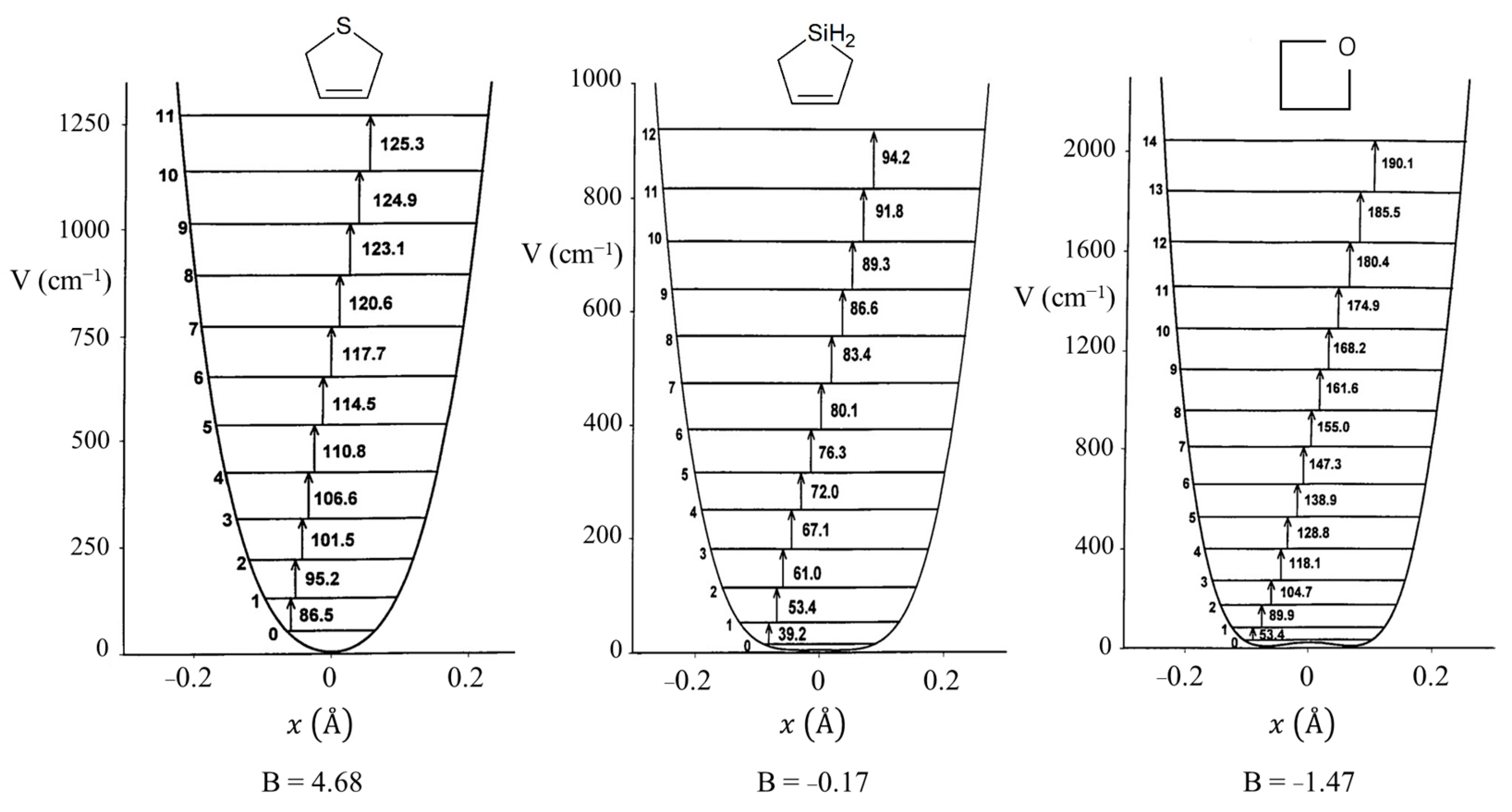
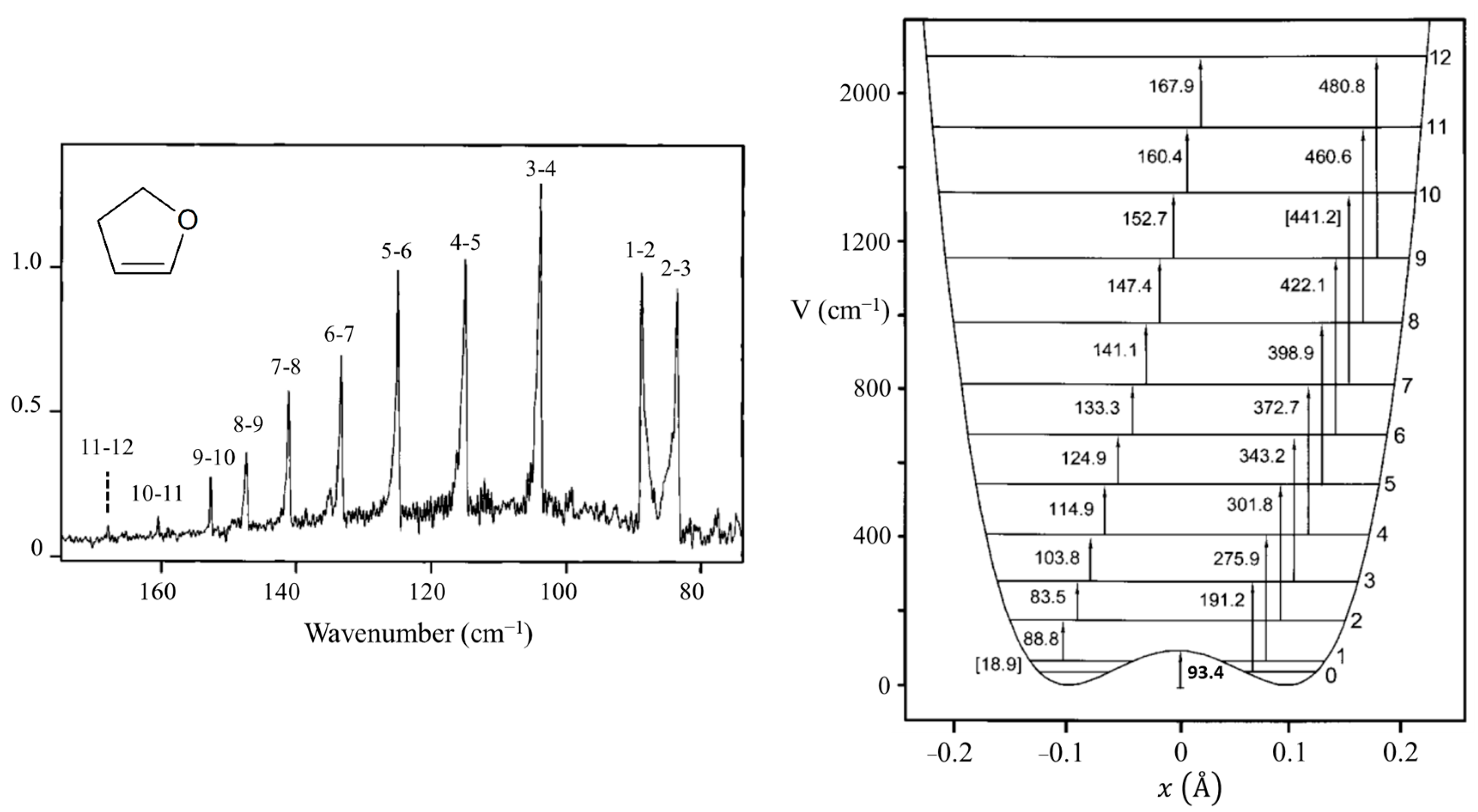
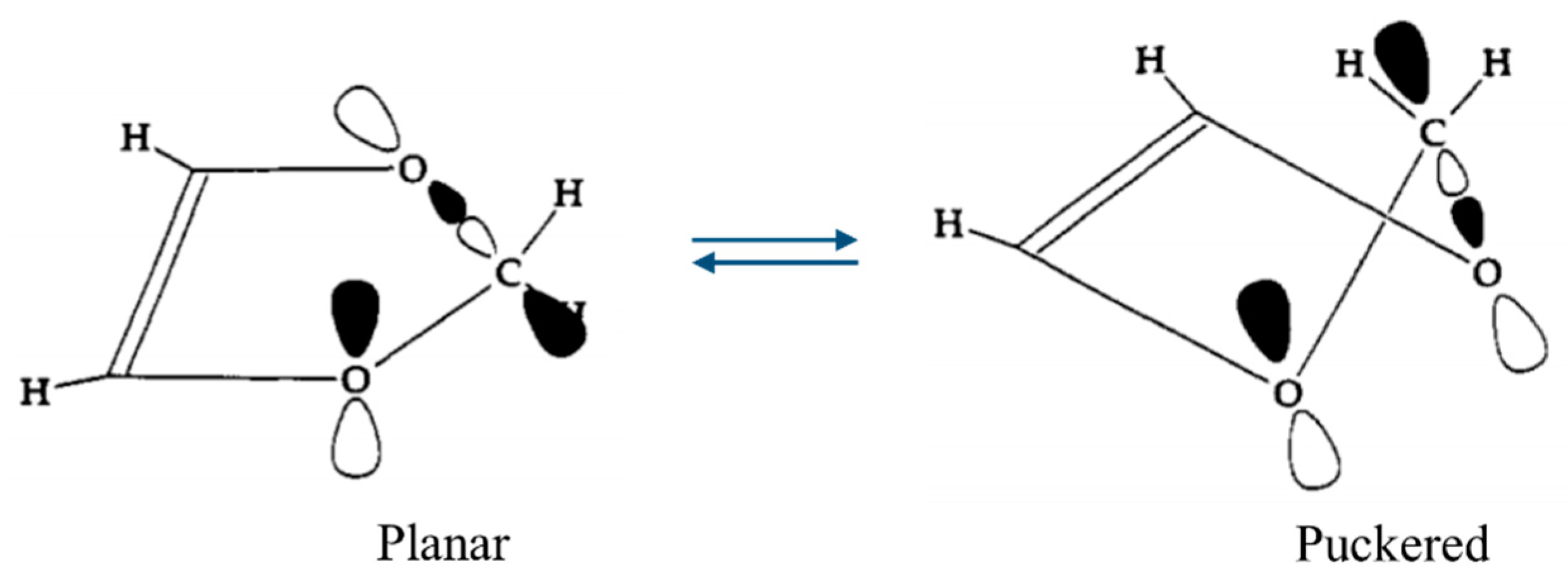
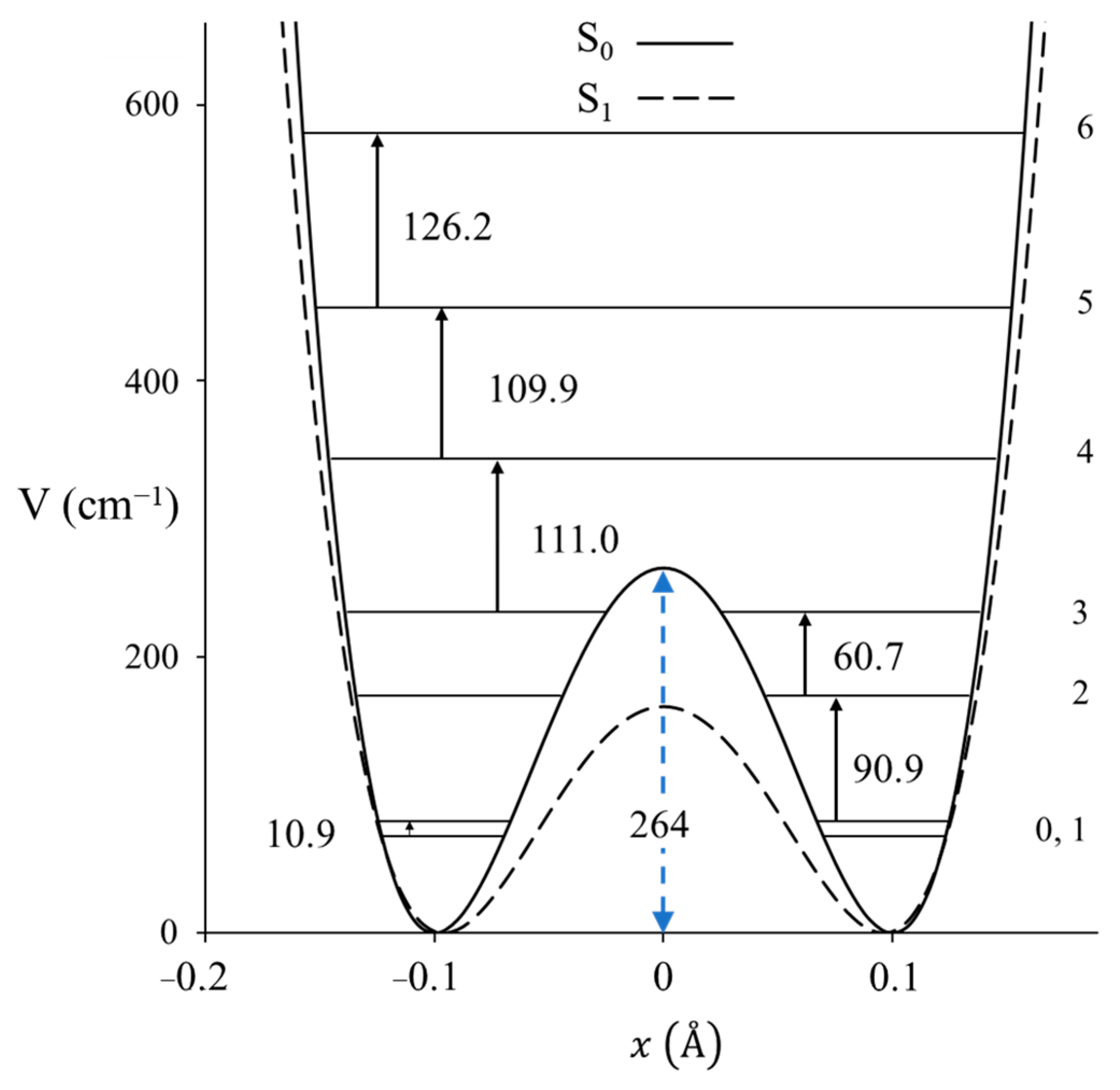
2.4. Ring Puckering
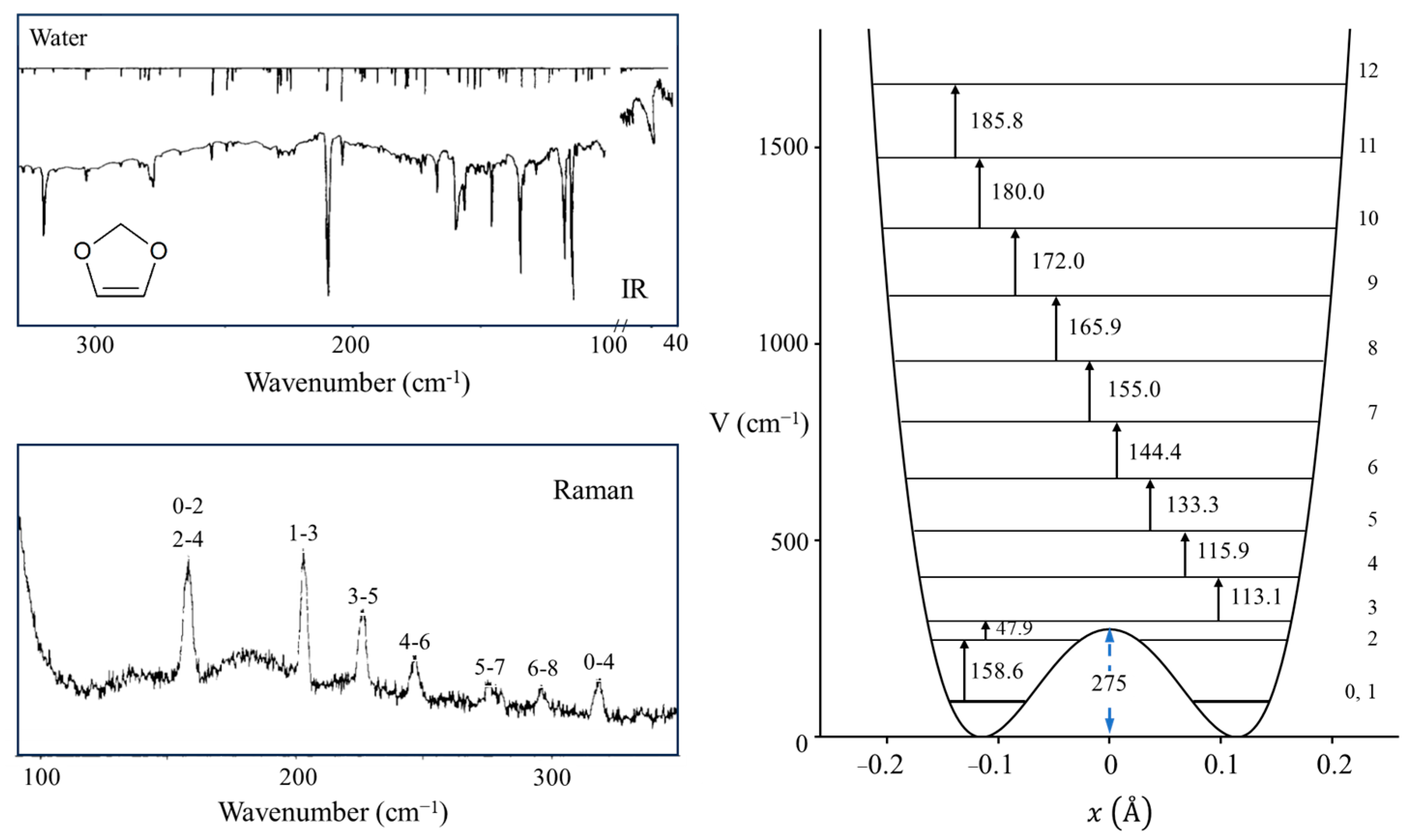
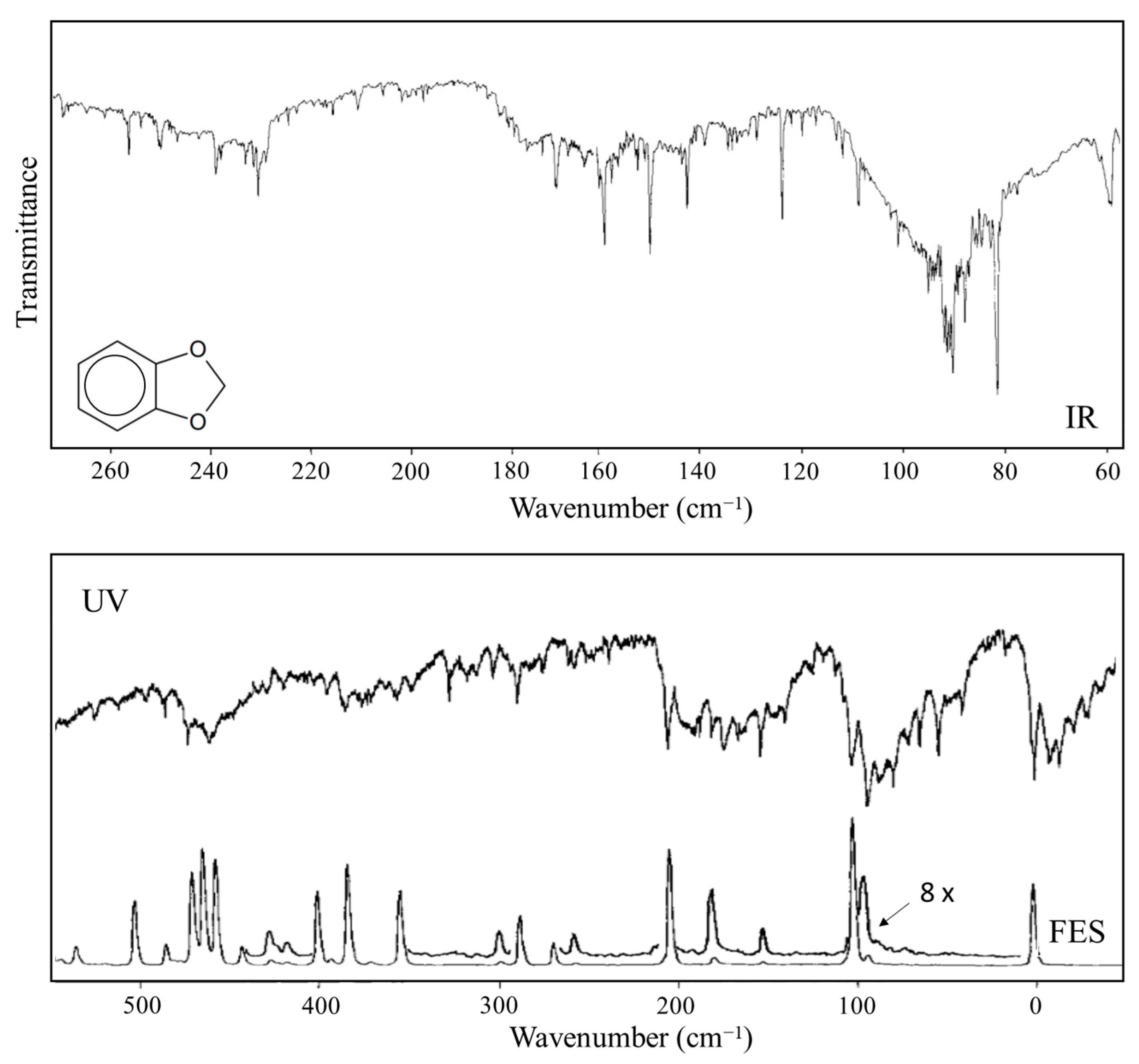
2.5. Anomeric Effect
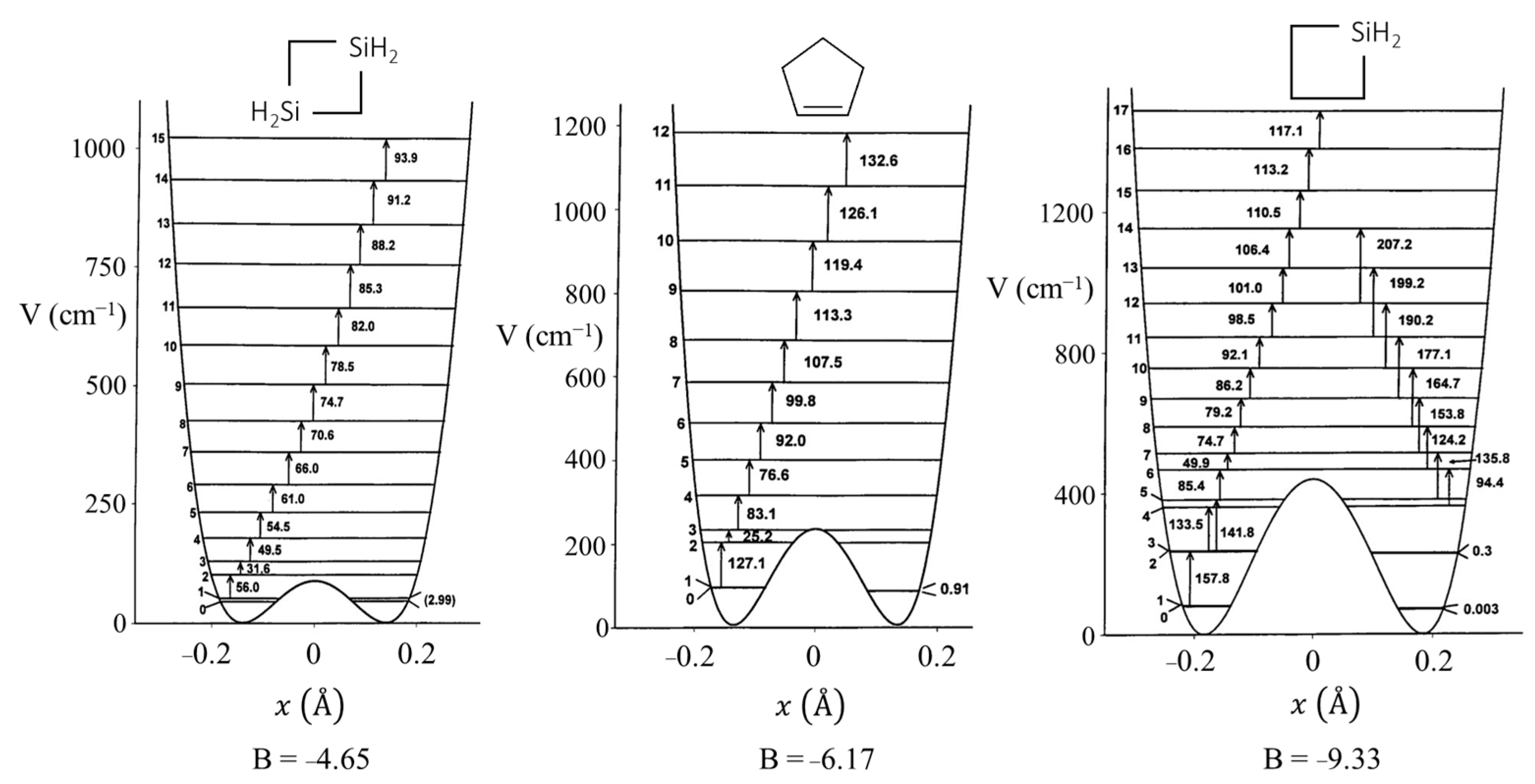
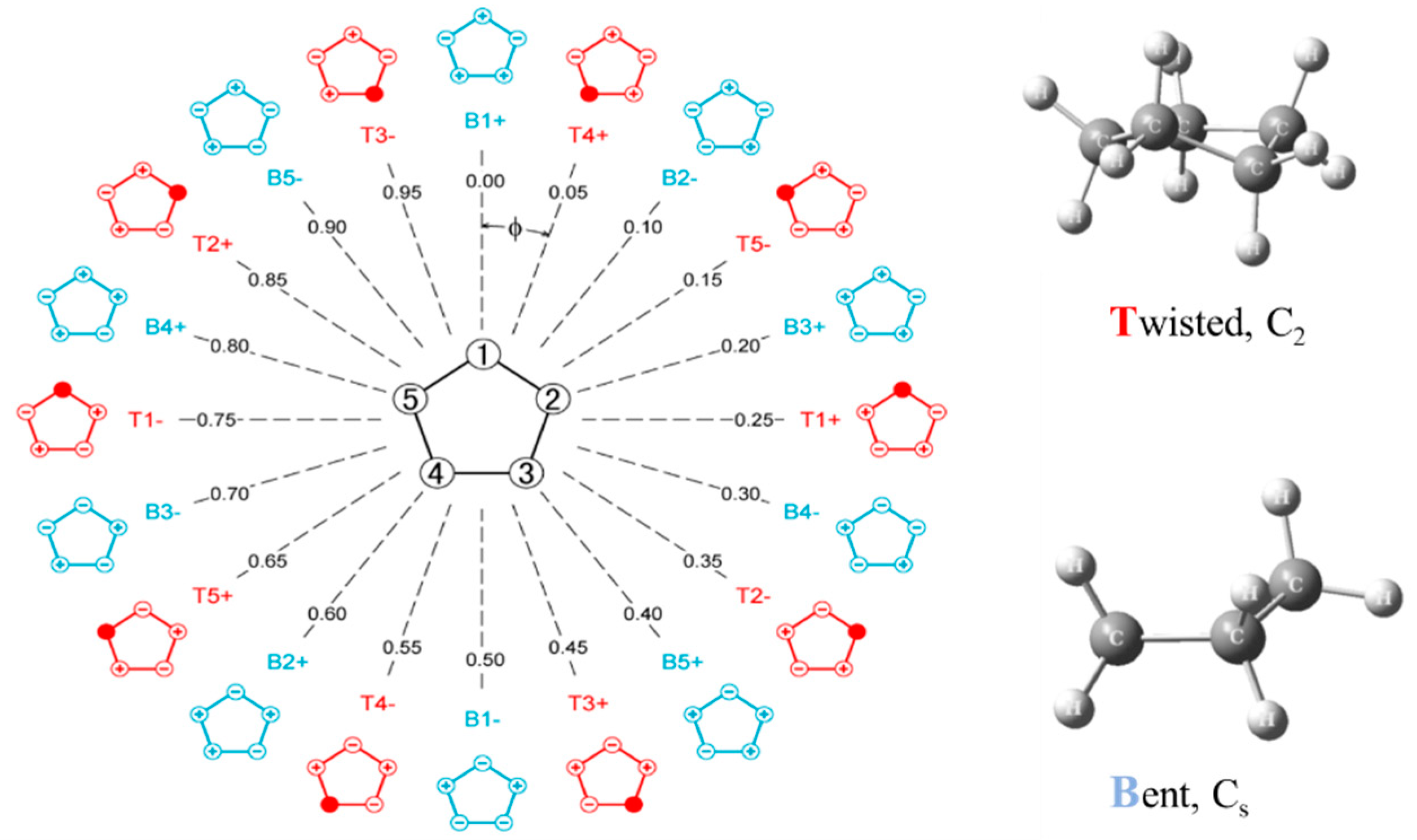
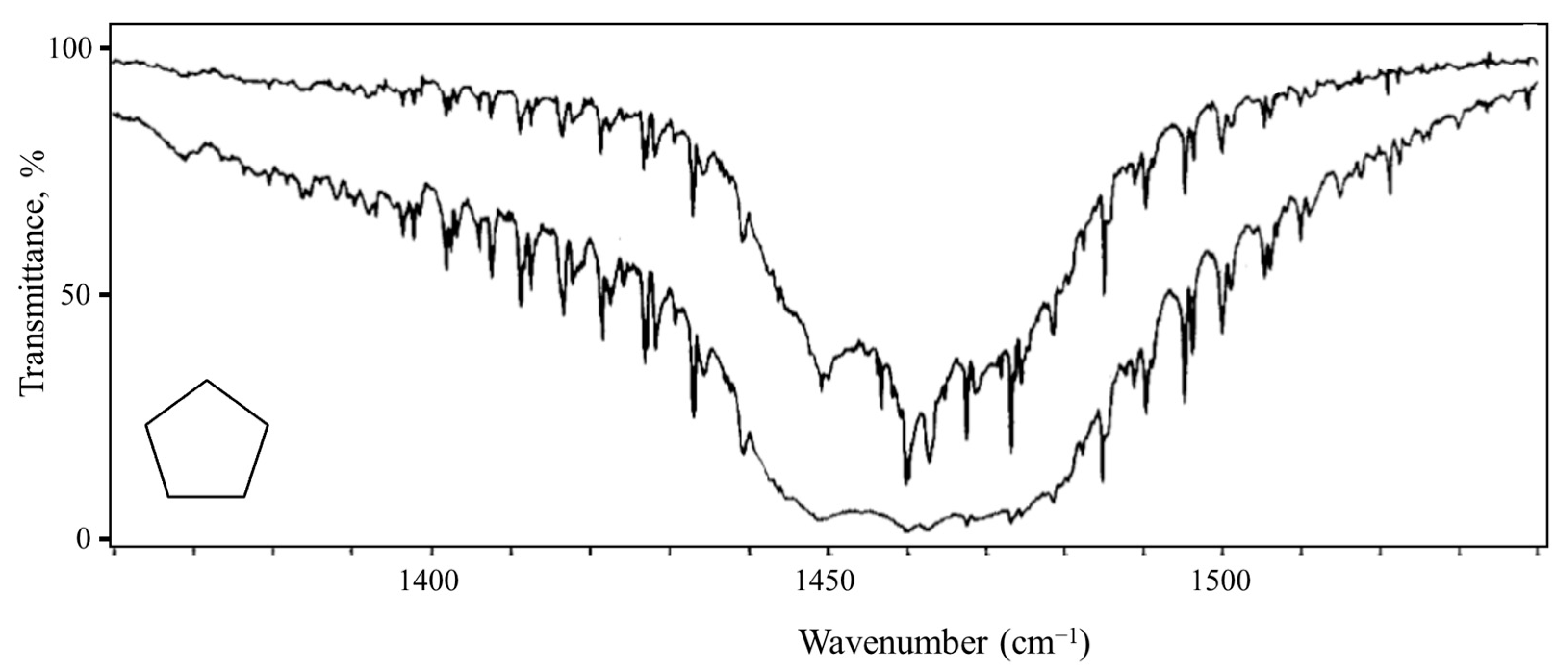
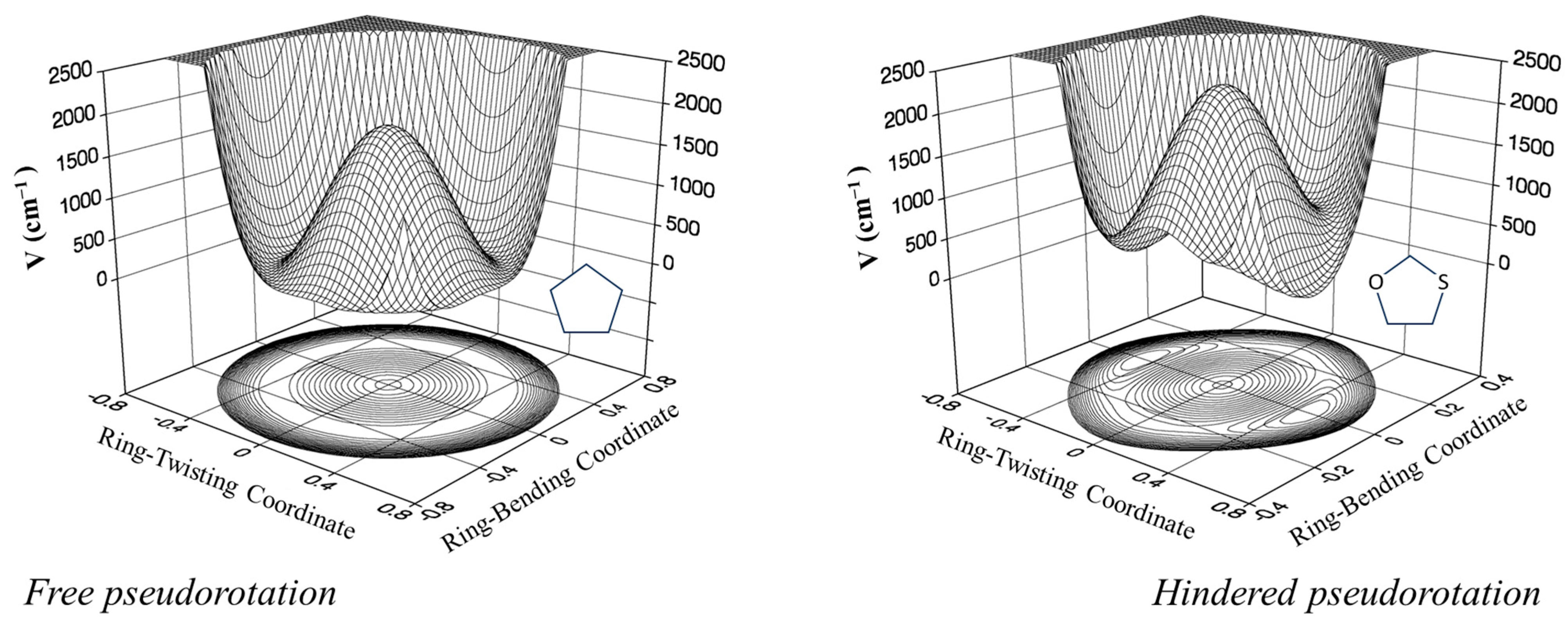
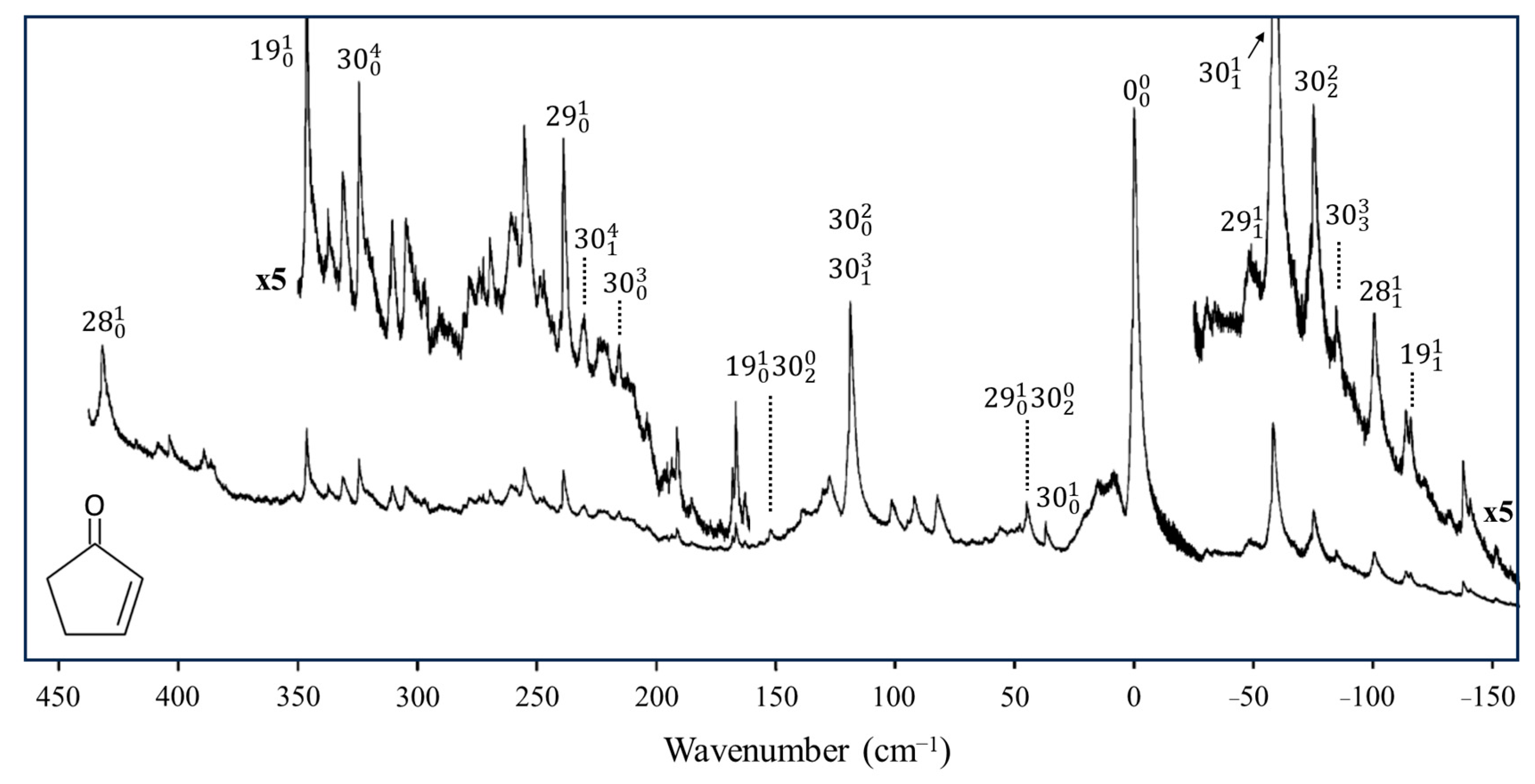
2.6. Pseudorotation
2.7. Triplet-State Ring Puckering
2.8. Cyclohexane
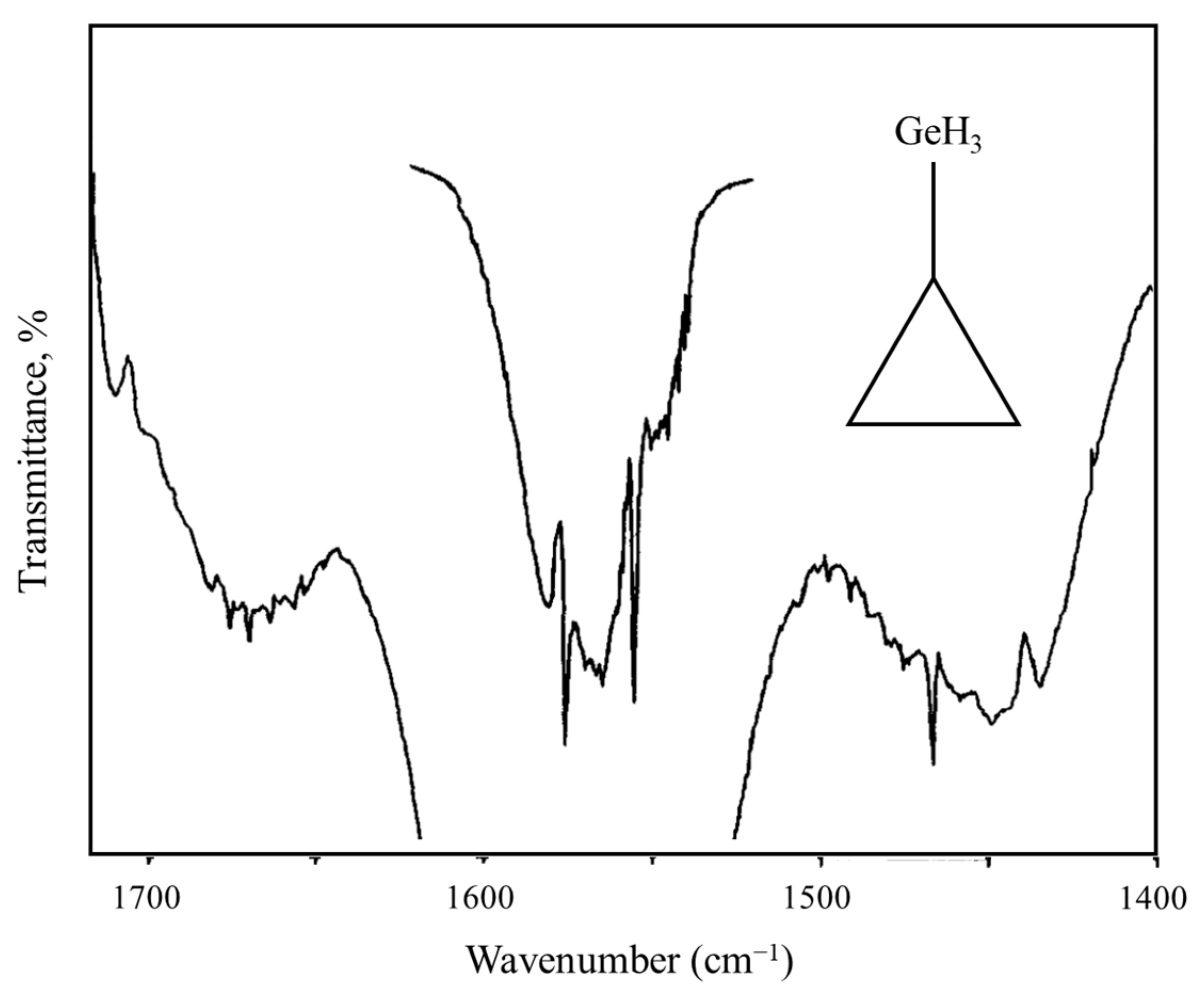
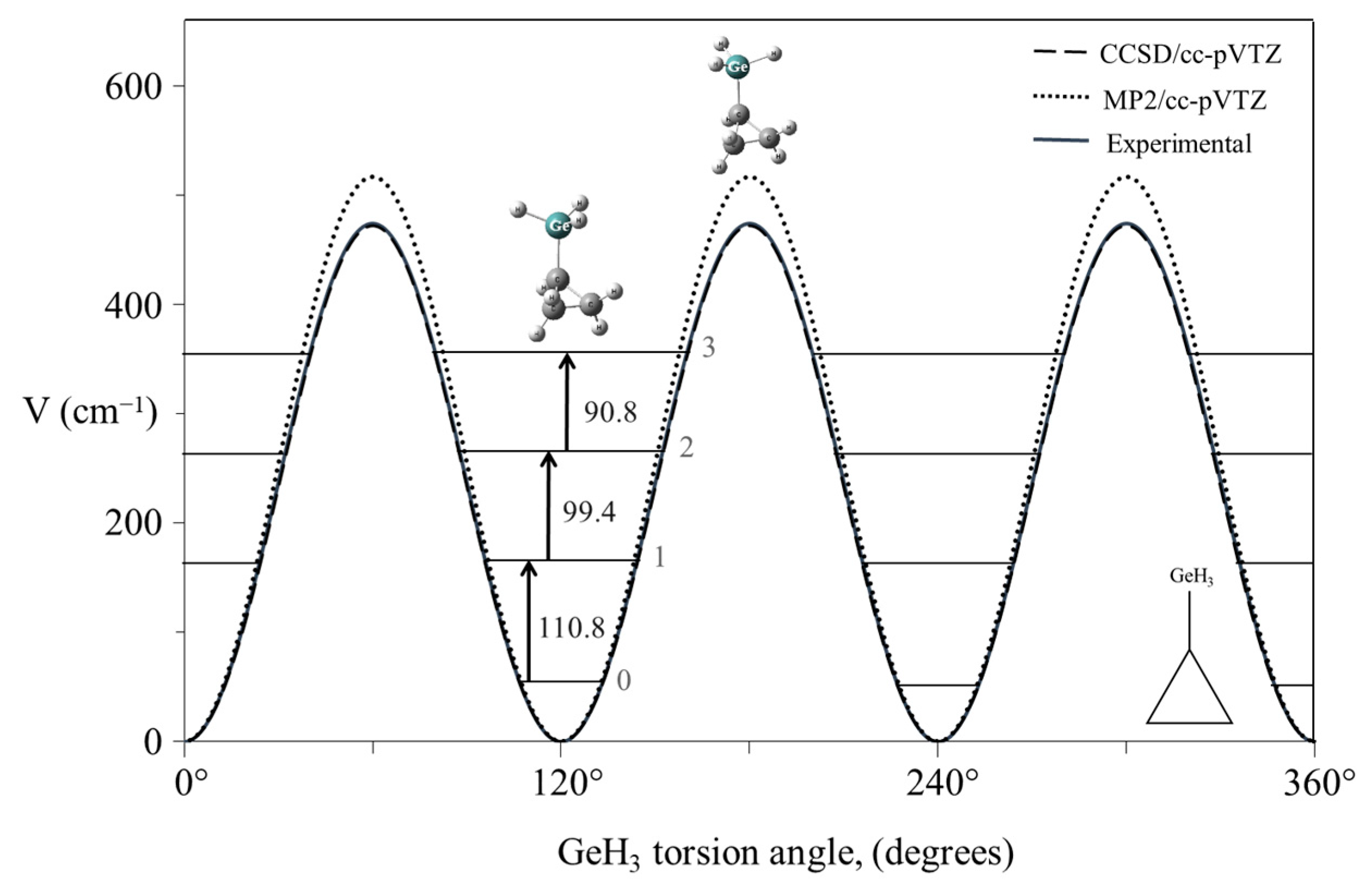
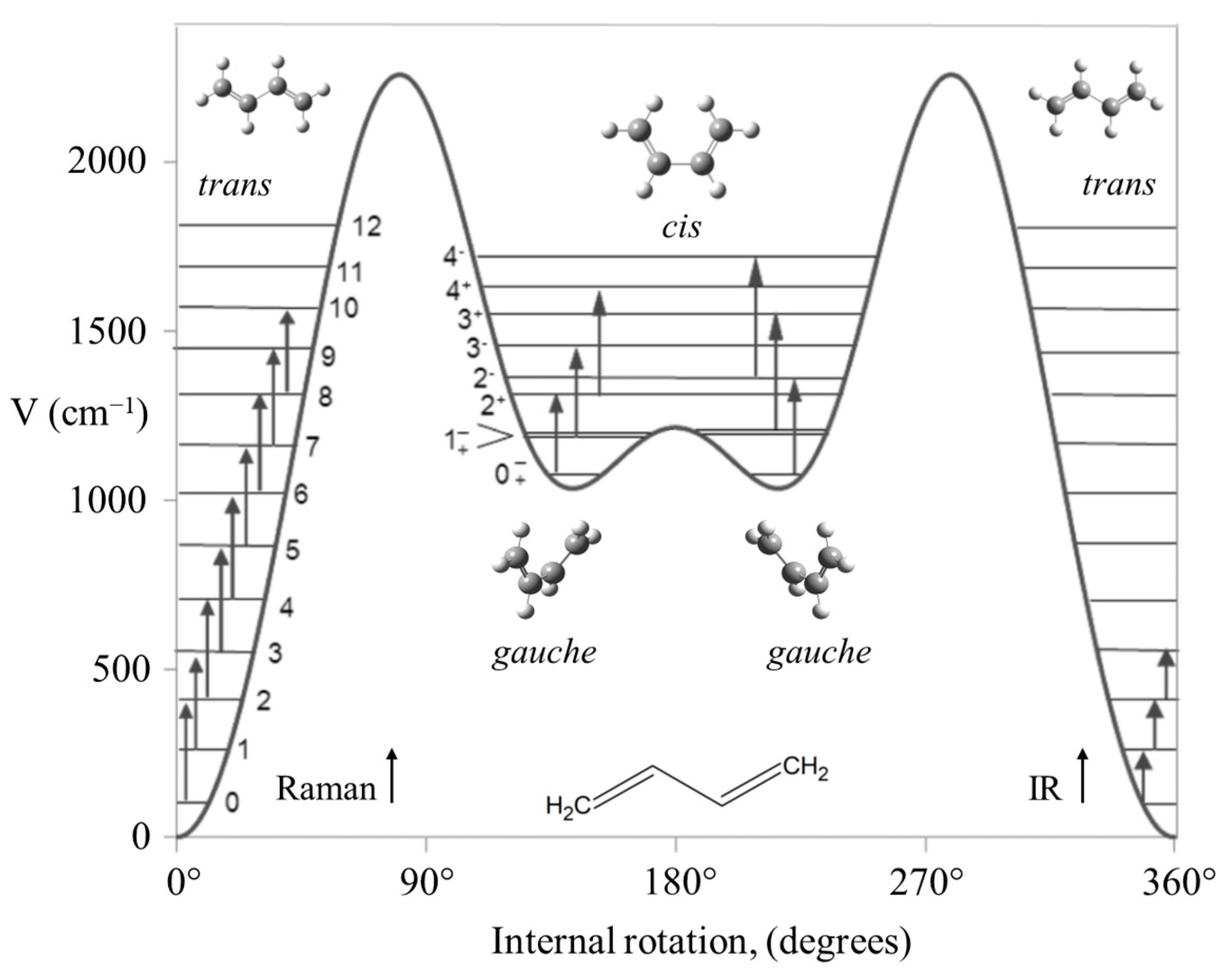
2.9. Internal Rotation
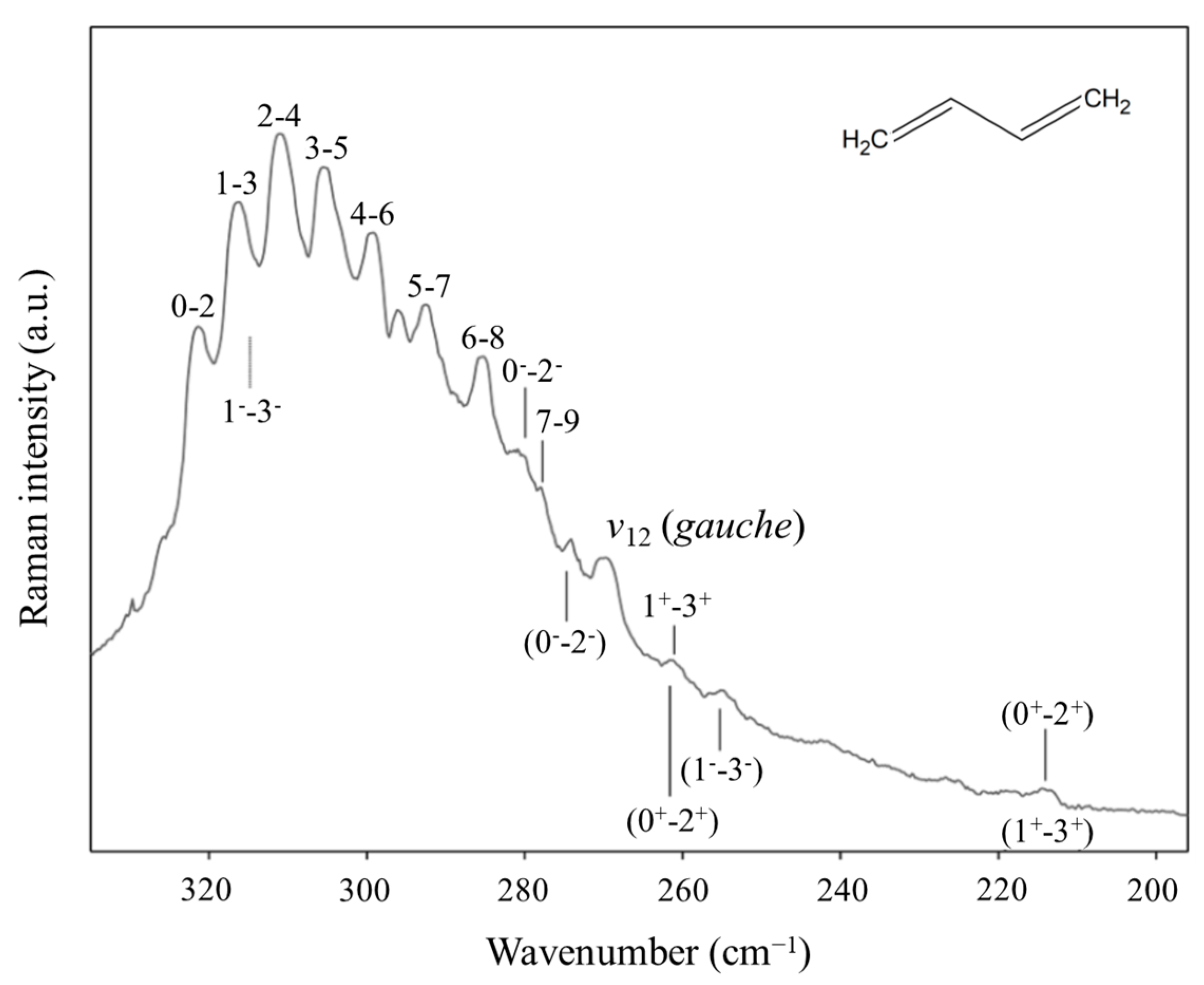
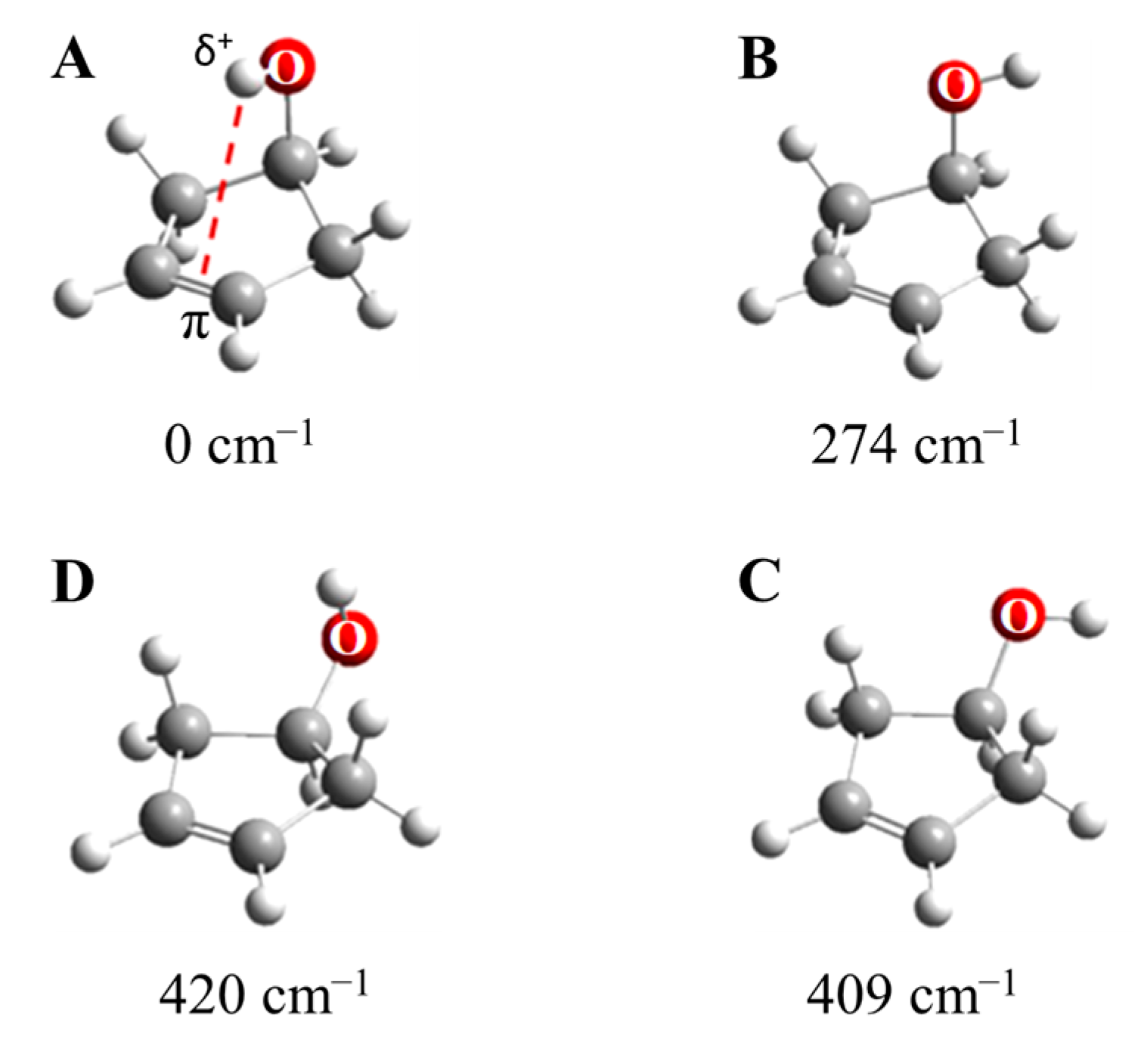
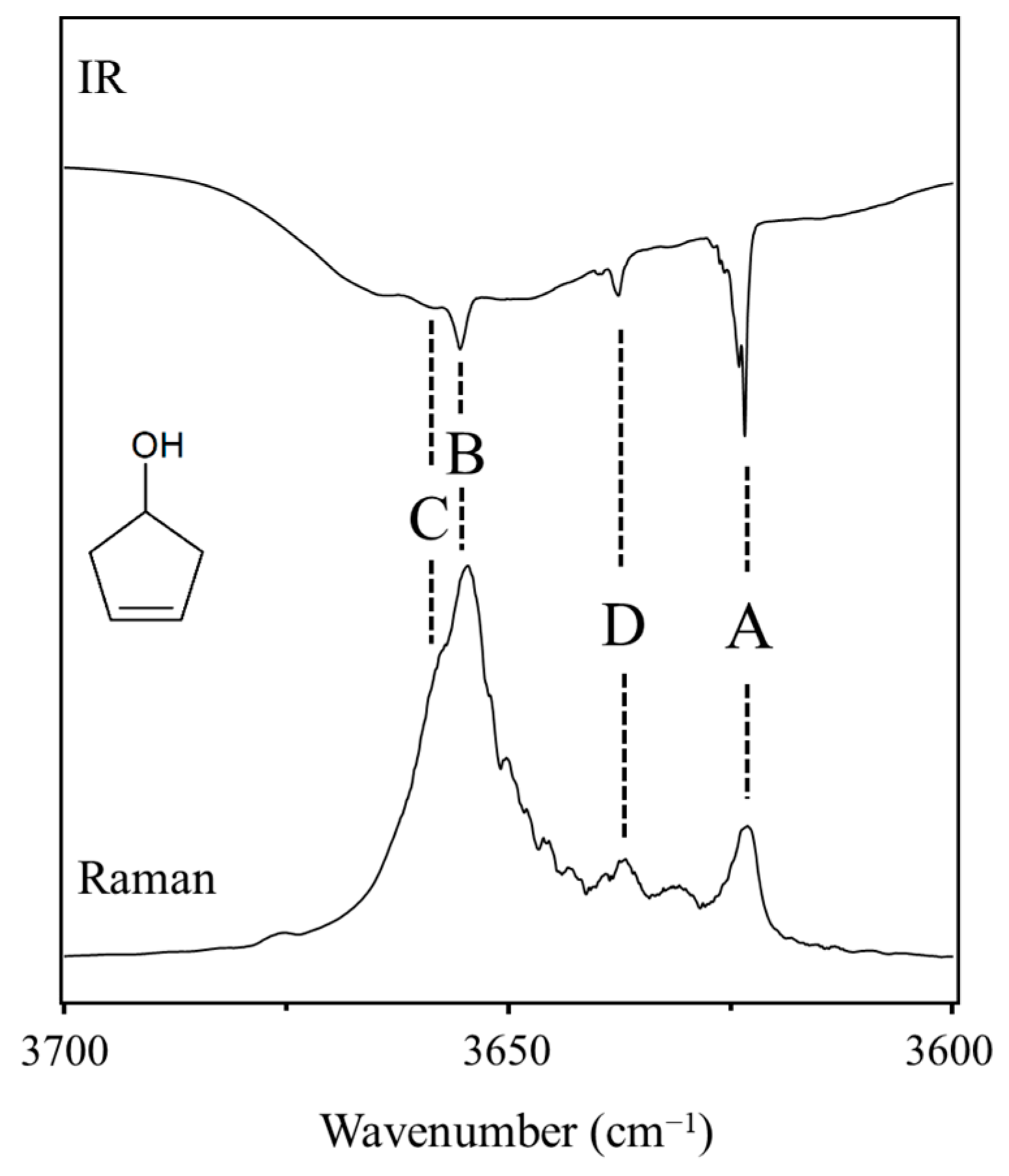
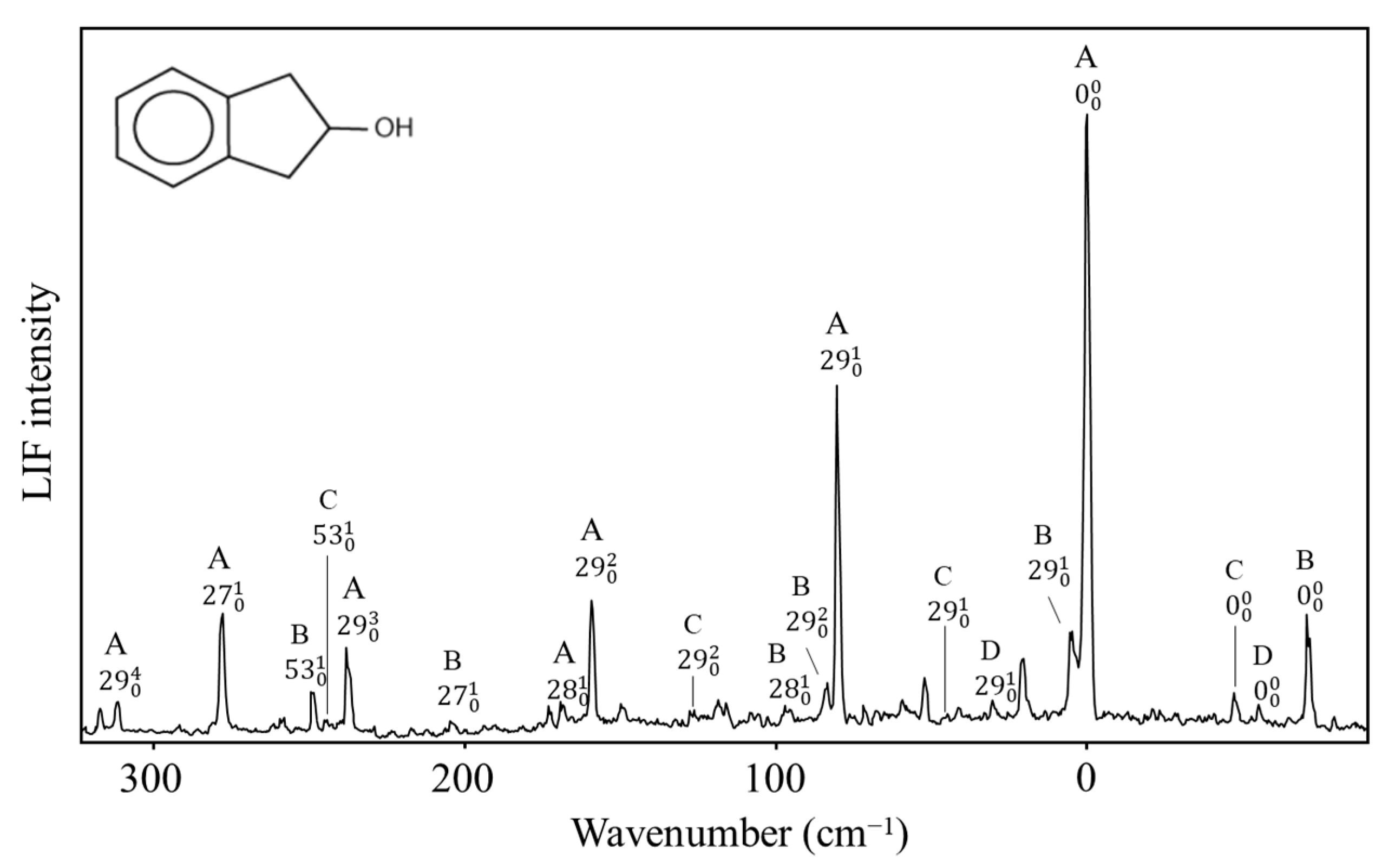
2.10. π-Type Hydrogen Bonding
2.11. Pyridine and Sir Harry Kroto
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laane, J.; Ocola, E.J.; Chun, H.J. Vibrational Potential Energy Surfaces in Ground and Electronic Excited States. In Frontiers and Advances in Molecular Spectroscopy; Laane, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 101–142. [Google Scholar] [CrossRef]
- Laane, J. Vibrational Potential Energy Surfaces in Electronic Excited States. In Frontiers of Molecular Spectroscopy; Laane, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 63–132. [Google Scholar] [CrossRef]
- Laane, J. Experimental Determination of Vibrational Potential Energy Surfaces and Molecular Structures in Electronic Excited States. J. Chem. Phys. A 2000, 104, 7715–7733. [Google Scholar] [CrossRef]
- Laane, J. Spectroscopic Determination of Ground and Excited State Vibrational Potential Energy Surfaces. Int. Rev. Phys. Chem. 1999, 18, 301–341. [Google Scholar] [CrossRef]
- Laane, J. Vibrational Potential Energy Surfaces and Conformations of Molecules in Ground and Excited Electronic States. Annu. Rev. Phys. Chem. 1994, 45, 179–211. [Google Scholar] [CrossRef]
- Laane, J. Vibrational Potential Energy Surfaces of Non-Rigid Molecules in Ground and Excited Electronic States. In Structures and Conformations of Non-Rigid Molecules; Laane, J., Dakkouri, M., Eds.; Kluwer Publishing: Amsterdam, The Netherlands, 1993; pp. 65–98. [Google Scholar] [CrossRef]
- Laane, J. Determination of Vibrational Potential Energy Surfaces from Raman and Infrared Spectra. J. Pure Appl. Chem. 1987, 59, 1307–1326. [Google Scholar] [CrossRef]
- Laane, J. One-dimensional Potential Energy Functions in Vibrational Spectroscopy. Q. Rev. Chem. Soc. 1971, 25, 533–552. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Benedict, W.S.; Player, E.L. Vibration–Rotation Bands of Ammonia: II. The Molecular Dimensions and Harmonic Frequencies of Ammonia and Deuterated Ammonia. Canad. J. Phys. 1957, 35, 1235–1241. [Google Scholar] [CrossRef]
- Coon, J.B.; Naugle, N.W.; McKenzie, R.D. The Investigation of Double-Minimum Potentials in Molecules. J. Mol. Spectrosc. 1966, 20, 107–129. [Google Scholar] [CrossRef]
- Laane, J. Eigenvalues of the Potential Function V = Z4 ± BZ2 and the Effect of Sixth Power Terms. Appl. Spectrosc. 1970, 24, 73–80. [Google Scholar] [CrossRef]
- Sagear, P.; Laane, J. Jet-Cooled Fluorescence Excitation Spectrum, Carbonyl Wagging, and Ring-Puckering Potential Energy Functions of 3-Cyclopenten-1-one in its S1(n,π*) Electronic Excited State. J. Chem. Phys. 1995, 102, 7789–7797. [Google Scholar] [CrossRef]
- Laane, J.; Zhang, J.; Chiang, W.-Y.; Sagear, P.; Cheatham, C.M. Jet-Cooled Fluorescence Excitation Spectra and Carbonyl Wagging Potential Energy Functions of Cyclic Ketones in Their Electronic Excited States. In Structure and Dynamics of Non-Rigid Systems; Smeyers, Y.G., Ed.; Kluwer Publishing: Amsterdam, The Netherlands, 1994; pp. 181–201. [Google Scholar] [CrossRef]
- Bell, R.P. The Occurrence and Properties of Molecular vibrations with V(x)=ax4. Proc. R. Soc. A 1945, 183, 328–337. [Google Scholar] [CrossRef]
- Laane, J. The Origin of the Ring-Puckering Potential Energy Function for Four-Membered Rings and Spiro Compounds. A Possibility for Pseudorotation. J. Phys. Chem. 1991, 95, 9246–9249. [Google Scholar] [CrossRef]
- Laane, J.; Lord, R.C. Far-Infrared Spectra of Ring Compounds. II. The Spectrum and Ring-puckering Potential Function of Cyclopentene. J. Chem. Phys. 1967, 47, 4941–4945. [Google Scholar] [CrossRef]
- Laane, J.; Harthcock, M.A.; Killough, P.M.; Bauman, L.E.; Cooke, J.M. Vector Representation of Large Amplitude Vibrations for the Determination of Kinetic Energy Functions. J. Mol. Spectrosc. 1982, 91, 286–299. [Google Scholar] [CrossRef]
- Harthcock, M.A.; Laane, J. Calculation of Kinetic Energy Terms for the Vibrational Hamiltonian: Application to Large Amplitude Vibrations Using One-, Two-, and Three-Dimensional Models. J. Mol. Spectrosc. 1982, 91, 300–324. [Google Scholar] [CrossRef]
- Autrey, D.; Laane, J. Far-Infrared Spectra, ab initio Calculations, and the Ring-Puckering Potential Energy Function of 2,3-Dihydrofuran. J. Phys. Chem. A 2001, 105, 6894–6899. [Google Scholar] [CrossRef]
- Ocola, E.J.; Laane, J. Ring-puckering Potential Energy Functions for Cyclobutane and Related Molecules Based on Refined Kinetic Energy Expansions and Theoretical Calculations. Chem. Phys. 2020, 532, 110647. [Google Scholar] [CrossRef]
- Cortez, E.; Verastegui, R.; Villarreal, J.R.; Laane, J. Low-Frequency Vibrational Spectra and Ring-Puckering Potential Energy Function of 1,3-Dioxole. A Convincing Demonstration of the Anomeric Effect. J. Amer. Chem. Soc. 1993, 115, 12132–12136. [Google Scholar] [CrossRef]
- Sakurai, S.; Meinander, N.; Morris, K.; Laane, J. Far-Infrared, Raman and Dispersed Fluorescence Spectra, Vibrational Potential Energy Surface, and the Anomeric Effect of 1,3-Benzodioxole. J. Amer. Chem. Soc. 1999, 121, 5056–5062. [Google Scholar] [CrossRef]
- Laane, J.; Bondoc, E.; Sakurai, S.; Morris, K.; Meinander, N.; Choo, J. Spectroscopic Determination of the Vibrational Potential Energy Surface and Conformation of 1,3-Benzodioxole in its S1(π,π*) Excited State. The Effect of the Electronic Excitation on the Anomeric Effect. J. Amer. Chem. Soc. 2000, 122, 2628–2634. [Google Scholar] [CrossRef]
- Ocola, E.J.; Laane, J. The Anomeric Effect in Five-Membered Ring Molecules. Comparison of Theoretical Computations and Experimental Spectroscopic Results. J. Phys. Chem. A 2021, 125, 327–337. [Google Scholar] [CrossRef]
- Kilpatrick, J.E.; Pitzer, K.S.; Spitzer, R. The Thermodynamics and Molecular Structure of Cyclopentane. J. Amer. Chem. Soc. 1947, 69, 2483. [Google Scholar]
- Kilpatrick, J.E.; Pitzer, K.S.; Spitzer, R. Additions and Corrections: The Thermodynamics and Molecular Structure of Cyclopentane. J. Amer. Chem. Soc. 1958, 80, 6697–6703. [Google Scholar]
- Pitzer, K.S.; Donath, W.E. Conformations and Strain Energy of Cyclopentane and its Derivatives. J. Amer. Chem. Soc. 1959, 81, 3213–3218. [Google Scholar] [CrossRef]
- Durig, J.R.; Wertz, D.W. Vibrational Spectra and Structure of Small-Ring Compounds. X. Spectroscopic Evidence for Pseudorotation in Cyclopentane. J. Chem. Phys. 1968, 49, 2118–2121. [Google Scholar] [CrossRef]
- Bauman, L.E.; Laane, J. Pseudorotation of Cyclopentane and Its Deuterated Derivatives. J. Phys. Chem. 1988, 92, 1040–1051. [Google Scholar] [CrossRef]
- Ocola, E.J.; Bauman, L.E.; Laane, J. Vibrational Spectra and Structure of Cyclopentane and its Isotopomers. J. Phys. Chem. A 2011, 115, 6531–6542. [Google Scholar] [CrossRef] [PubMed]
- Chao, T.H.; Laane, J. Vibrational Studies of Cyclopentane: Effect of 10-Fold Barrier to Pseudorotation. J. Mol. Spectrosc. 1978, 70, 357–360. [Google Scholar] [CrossRef]
- Laane, J. Far-Infrared Spectrum and the Barrier to Pseudorotation of Silacyclopentane. J. Chem. Phys. 1969, 50, 1946–1951. [Google Scholar] [CrossRef]
- Leibowitz, S.J.; Laane, J.; Verastegui, R., Jr.; Villarreal, J.R. Far-Infrared Spectra and Hindered Pseudorotation of 1,3-Oxathiolane. J. Chem. Phys. 1992, 96, 7298–7305. [Google Scholar] [CrossRef]
- Laane, J. Pseudorotation of Five-Membered Rings. In Vibrational Spectra and Structure; Durig, J.R., Ed.; Marcell Dekker, Inc.: New York, NY, USA, 1972; Volume 1, pp. 25–50. ISBN 0-8247-1149-1. [Google Scholar]
- Rosas, R.L.; Cooper, C.; Laane, J. Evaluation of Molecular Mechanics Methods for the Calculation of the Barriers to Planarity and Pseudorotation of Small Ring Molecules. J. Phys. Chem. 1990, 94, 1830–1836. [Google Scholar] [CrossRef]
- Pillsbury, N.; Choo, J.; Laane, J.; Drucker, S. Lowest n,π* Triplet State of 2-Cyclopenten-1-one: Cavity Ringdown Absorption Spectrum and Ring-Bending Potential-Energy Function. J. Phys. Chem. A 2003, 107, 10648–10654. [Google Scholar] [CrossRef]
- Choo, J.; Kim, S.; Drucker, S.; Laane, J. Density Functional Calculations, Structure, and Vibrational Frequencies of 2-Cyclopenten-1-one in its S0, S1(n,π*), T1(n,π*) and T2(π,π*) States. J. Phys. Chem. A 2003, 107, 10655–10659. [Google Scholar] [CrossRef]
- Chun, H.J.; Ocola, E.J.; Laane, J. Vapor-Phase Raman Spectra and the Barrier to Planarity of Cyclohexane. J. Phys. Chem. A 2016, 120, 7077–7680. [Google Scholar] [CrossRef]
- Lewis, J.D.; Malloy, T.B., Jr.; Chao, T.H.; Laane, J. Periodic Potential Functions for Pseudorotation and Internal Rotation. J. Mol. Struct. 1972, 12, 427–449. [Google Scholar] [CrossRef]
- Lewis, J.D.; Laane, J. Periodic Potential Energy Functions with Sine and Cosine Terms. Mol. Spectrosc. 1977, 65, 147–154. [Google Scholar] [CrossRef]
- Kelly, M.B.; Laane, J.; Dakkouri, M. Barriers to Internal Rotation of Cyclopropylsilane-d3 and Cyclopropylgermane from Combination Band Spectra. J. Mol. Spectrosc. 1989, 137, 82–86. [Google Scholar] [CrossRef]
- Ocola, E.J.; Laane, J. Internal Rotation of Methylcyclopropane and Related Molecules; Comparison of Experimental Results and Theory. J. Phys. Chem. A 2016, 120, 7269–7278. [Google Scholar] [CrossRef]
- Kalasinsky, V.F.; Powers, D.E.; Harris, W.C. Vibrational Spectra and Conformations of Cyclopropylamine. J. Phys. Chem. 1979, 83, 506–510. [Google Scholar] [CrossRef]
- Chiang, W.-Y.; Laane, J. Fluorescence Spectra and Torsional Potential Functions for trans-Stilbene in Its S0 and S1(π,π*) Electronic States. J. Chem. Phys. 1994, 101, 8755–8767. [Google Scholar] [CrossRef]
- Boopalachandran, P.; Craig, N.; Groner, P.; Laane, J. Gas-Phase Raman Spectra and the Potential Energy Function for the Internal Rotation of 1,3-Butadiene and its Isotopologues. J. Phys. Chem. A 2011, 115, 8920–8927. [Google Scholar] [CrossRef]
- Boopalachandran, P.; Craig, N.; Laane, J. Gas-Phase Raman Spectra of Hot Bands of Fundamentals and Combinations Associated with the Torsional Vibration of s-trans-1,3-Butadiene and its Deuterated Isotopologues. J. Mol. Spectrosc. 2011, 269, 236–241. [Google Scholar] [CrossRef]
- Al-Saadi, A.A.; Ocola, E.J.; Laane, J. Intramolecular π-Type Hydrogen Bonding and Conformations of 3-Cyclopenten-1-ol. 1. Theoretical Calculations. J. Phys. Chem. A 2010, 114, 7453–7456. [Google Scholar] [CrossRef]
- Ocola, E.J.; Al-Saadi, A.A.; Mlynek, C.; Hopf, H.; Laane, J. Intramolecular π-Type Hydrogen Bonding and Conformations of 3-Cyclopenten-1-ol. 2. Infrared and Raman Spectral Studies at High Temperatures. J. Phys. Chem. A 2010, 114, 7457–7461. [Google Scholar] [CrossRef] [PubMed]
- Al-Saadi, A.A.; Wagner, M.; Laane, J. Spectroscopic and Computational Studies of the Intramolecular Hydrogen Bonding of 2-Indanol. J. Phys. Chem. A 2006, 110, 12292–12297. [Google Scholar] [CrossRef] [PubMed]
- Ocola, E.J.; Laane, J. Spectroscopic and Theoretical Study of the Intramolecular π-Type Hydrogen Bonding and Conformations of 2-Cyclohexen-1-ol. J. Phys Chem. A 2016, 120, 74–80. [Google Scholar] [CrossRef]
- Ocola, E.J.; Laane, J. Theoretical Investigation of Intramolecular π-Type Hydrogen Bonding and Internal Rotation of 2-Cyclopropen-1-ol, 2-Cyclopropen-1-thiol and 2-Cyclopropen-1-amine. Mol. Phys. 2019, 17, 1404–1412. [Google Scholar] [CrossRef]
- Ocola, E.J.; Laane, J. Spectroscopic and Theoretical Study of the Intramolecular π-type Hydrogen Bonding and Conformations of 3-Cyclopentene-1-amine. J. Phys. Chem. 2020, 124, 5907–5916. [Google Scholar] [CrossRef]
- Jesson, J.P.; Kroto, H.W.; Ramsay, D.A. Quasiplanarity of Pyridine in Its First Excited Singlet State. J. Chem. Phys. 1972, 56, 6257–6258. [Google Scholar] [CrossRef]
- Boopalachandran, P.; Jaan, J. Ultraviolet Absorption Spectra of Pyridine-d0 and -d5 and their Ring-Bending Potential Energy Function in the S1(n,π*) State. Chem. Phys. Lett. 2008, 462, 178–182. [Google Scholar] [CrossRef]
- Sheu, H.-L.; Boopalachandran, P.; Kim, S.; Laane, J. Infrared, Raman, and Ultraviolet Absorption Spectra and Theoretical Calculations and Structure of 2,3,5,6-Tetrafluoropyridine in its Ground and Excited Electronic States. Chem. Phys. 2015, 456, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Boopalachandran, P.; Kim, S.; Choo, J.; Laane, J. Ultraviolet Absorption Spectra, Structure, Vibrations, and Theoretical Calculations of 2-Fluoro- and 3-Fluoropyridine in their Electronic Excited States. Chem. Phys. Lett. 2011, 514, 214–219. [Google Scholar] [CrossRef]

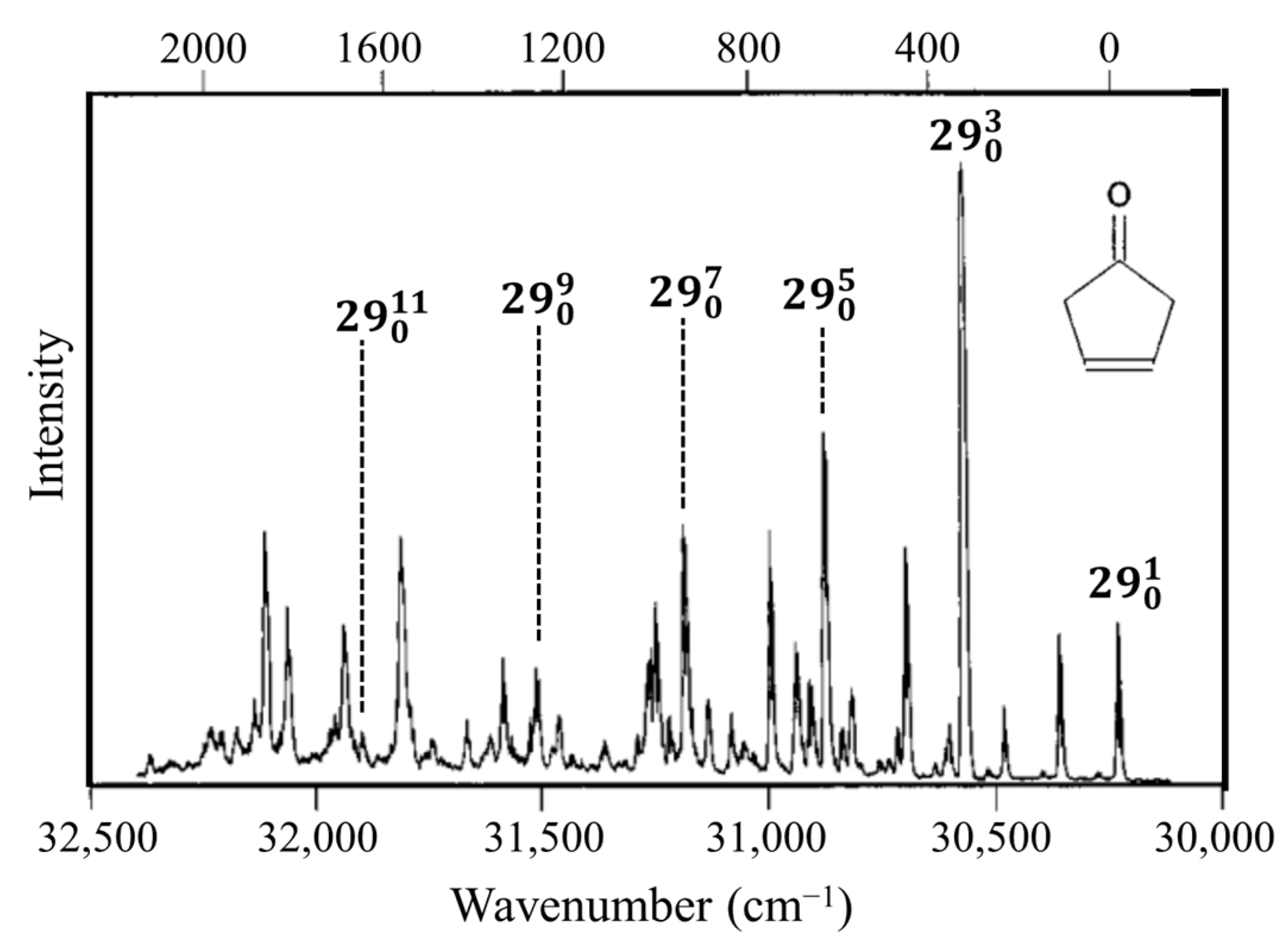
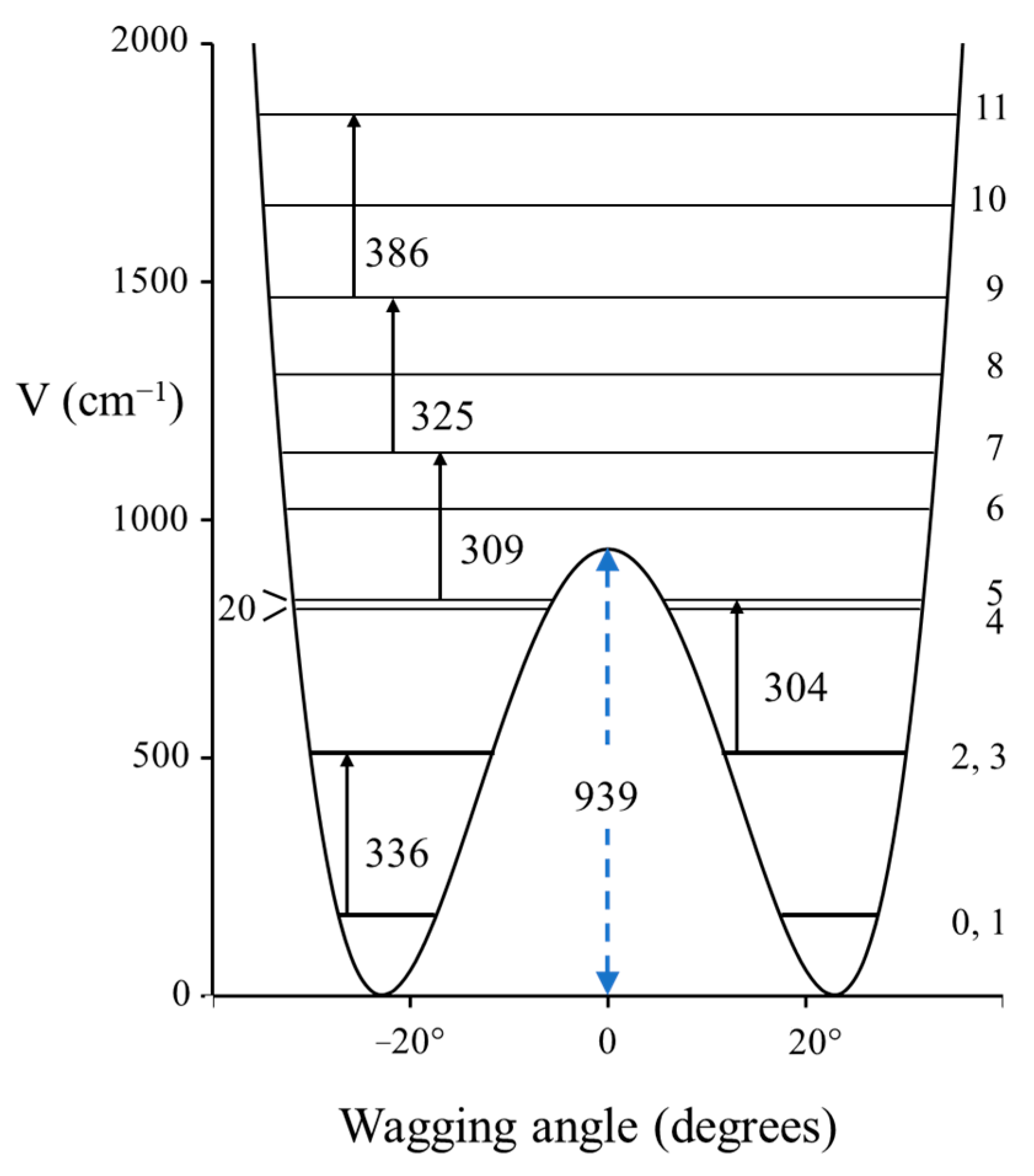





| C=O Inversion Barrier (cm−1) | |
|---|---|
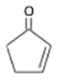 2-cyclopenten-1-one 2-cyclopenten-1-one | 0 |
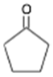 Cyclopentanone Cyclopentanone | 672 |
 Cyclobutanone Cyclobutanone | 939 |
 Cyclopentene-1-one Cyclopentene-1-one | 2149 |
| Frequency (cm−1) | Relative Intensity | ||||
|---|---|---|---|---|---|
| Transition | Observed | Calculated | ∆ | Observed | Calculated |
| vT = 0 | |||||
| 1–2 | 88.8 | 88.6 | 0.2 | 0.80 | 0.90 |
| 2–3 | 83.5 | 83.5 | 0.0 | 0.76 | 0.87 |
| 3–4 | 103.8 | 103.6 | 0.2 | (1.00) | (1.00) |
| 4–5 | 114.9 | 114.8 | 0.1 | 0.77 | 0.83 |
| 5–6 | 124.9 | 124.8 | 0.1 | 0.75 | 0.61 |
| 6–7 | 133.3 | 133.4 | −0.1 | 0.50 | 0.41 |
| 7–8 | 141.1 | 140.9 | 0.2 | 0.40 | 0.26 |
| 8–9 | 147.4 | 147.7 | −0.3 | 0.22 | 0.15 |
| 9–10 | 152.7 | 153.9 | −1.2 | 0.17 | 0.09 |
| 10–11 | 160.4 | 159.9 | 0.5 | 0.06 | 0.05 |
| 0–3 | 191.2 | 191.1 | 0.1 | 0.15 | 0.27 |
| 1–4 | 275.9 | 275.6 | 0.3 | 0.20 | 0.11 |
| 2–5 | 301.8 | 301.8 | 0.0 | 0.06 | 0.08 |
| 3–6 | 343.2 | 343.2 | 0.0 | 0.06 | 0.05 |
| 4–7 | 372.2 | 372.9 | −0.7 | 0.05 | 0.03 |
| 5–8 | 398.9 | 398.1 | 0.8 | 0.04 | 0.02 |
| 6–9 | 422.1 | 422.0 | 0.1 | 0.02 | 0.01 |
| Experimental Fit | Theoretical | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| a | CCSD/cc-pVTZ | MP2/cc-pVTZ | |||||||
| Molecule | Barrier | Barrier | Barrier | ||||||
| cm−1 | Å | Degrees | cm−1 | Å | Degrees | cm−1 | Å | Degrees | |
 C4H8 C4H8 | 510 | ±0.142 | ±29.6° | 586 | ±0.142 | ±29.5° | 821 | ±0.153 | 31.9° |
 C4H7O C4H7O | 15 | ±0.062 | ±13.4° | 0 | ±0.001 | ±0.2° | 21 | ±0.069 | 14.8° |
 C4H7S C4H7S | 273 | ±0.141 | ±26.9 | 243 | ±0.133 | ±25.5° | 412 | ±0.152 | 29.0° |
 C4H7Se C4H7Se | 378 | ±0.162 | ±30.4° | 339 | ±0.148 | ±27.8° | 512 | ±0.164 | 30.9° |
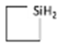 C4H7SiH2 C4H7SiH2 | 440 | ±0.163 | ±31.9° | 472 | ±0.163 | ±31.7° | 654 | ±0.176 | 34.5° |
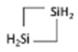 C4H7(SiH2)2 C4H7(SiH2)2 | 87 | ±0.130 | ±22.3° | 89 | ±0.130 | ±22.4° | 160 | ±0.150 | 25.8° |
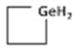 C4H7GeH2 C4H7GeH2 | --- | --- | --- | 409 | ±0.156 | ±30.1° | 567 | ±0.169 | 32.6° |
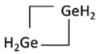 C4H7(GeH2)2 C4H7(GeH2)2 | --- | --- | --- | 1 | ±0.047 | ±7.8° | 24 | ±0.104 | 17.1° |
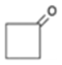 C4H4O C4H4O | 2 | ±0.043 | ±4.6° | 36 | ±0.073 | ±15.5° | 114 | ±0.097 | 20.8° |
| Molecule | Linkage | Value | a (kcal/mole) |
|---|---|---|---|
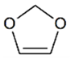 | OCO | 1.00 | 5.97 b |
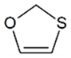 | OCS | 0.82 | 4.90 |
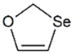 | OCSe | 0.66 | 3.94 |
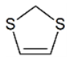 | SCS | 0.60 | 3.58 |
 | SCSe | 0.45 | 2.69 |
 | SeCSe | 0.32 | 1.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocola, E.J.; Laane, J. Beyond the Harmonic Oscillator; Highlights of Selected Studies of Vibrational Potential Energy Functions. Molecules 2025, 30, 1492. https://doi.org/10.3390/molecules30071492
Ocola EJ, Laane J. Beyond the Harmonic Oscillator; Highlights of Selected Studies of Vibrational Potential Energy Functions. Molecules. 2025; 30(7):1492. https://doi.org/10.3390/molecules30071492
Chicago/Turabian StyleOcola, Esther J., and Jaan Laane. 2025. "Beyond the Harmonic Oscillator; Highlights of Selected Studies of Vibrational Potential Energy Functions" Molecules 30, no. 7: 1492. https://doi.org/10.3390/molecules30071492
APA StyleOcola, E. J., & Laane, J. (2025). Beyond the Harmonic Oscillator; Highlights of Selected Studies of Vibrational Potential Energy Functions. Molecules, 30(7), 1492. https://doi.org/10.3390/molecules30071492







