Implementation of Machine Learning in Flat Die Extrusion of Polymers
Abstract
:1. Introduction
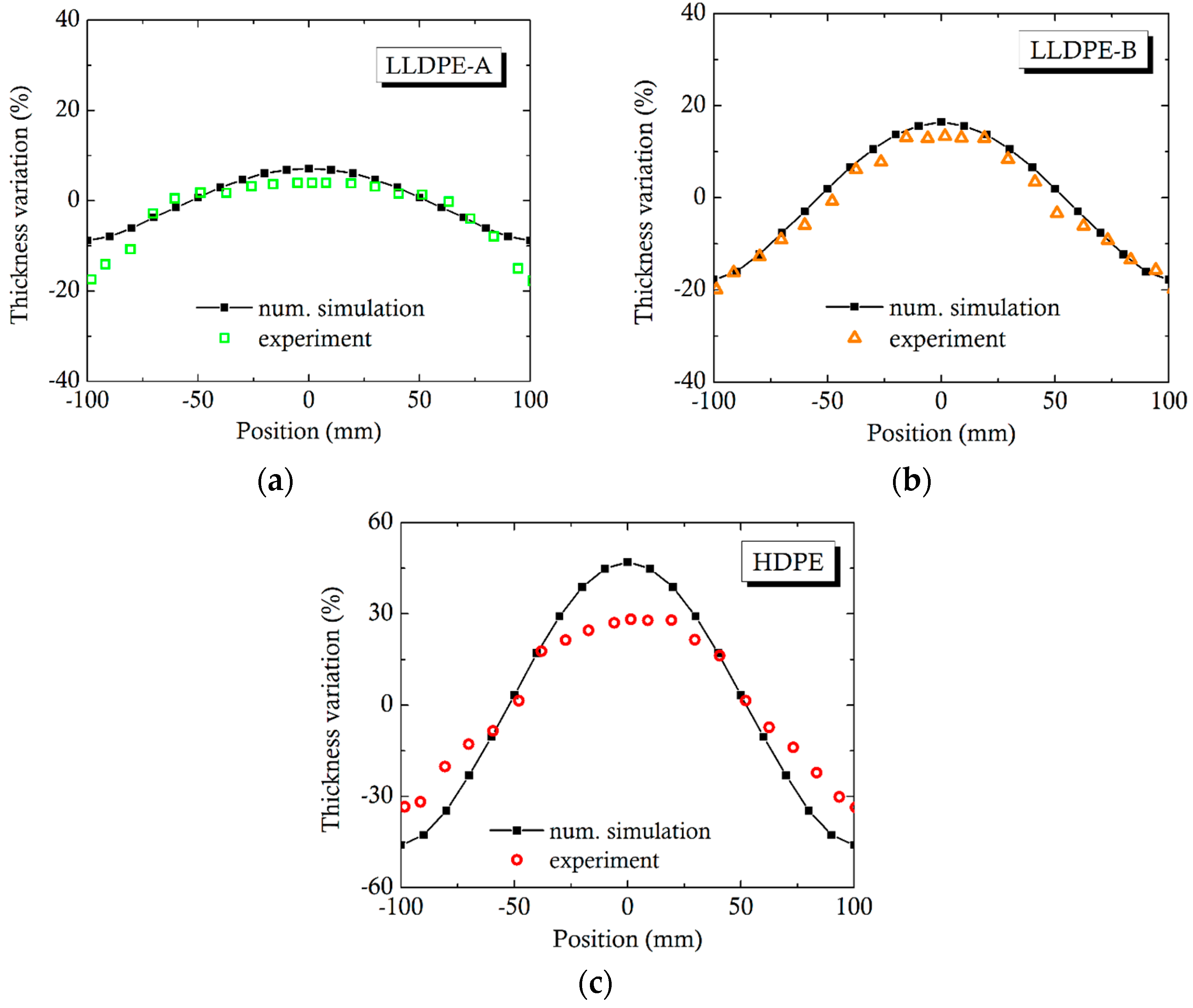
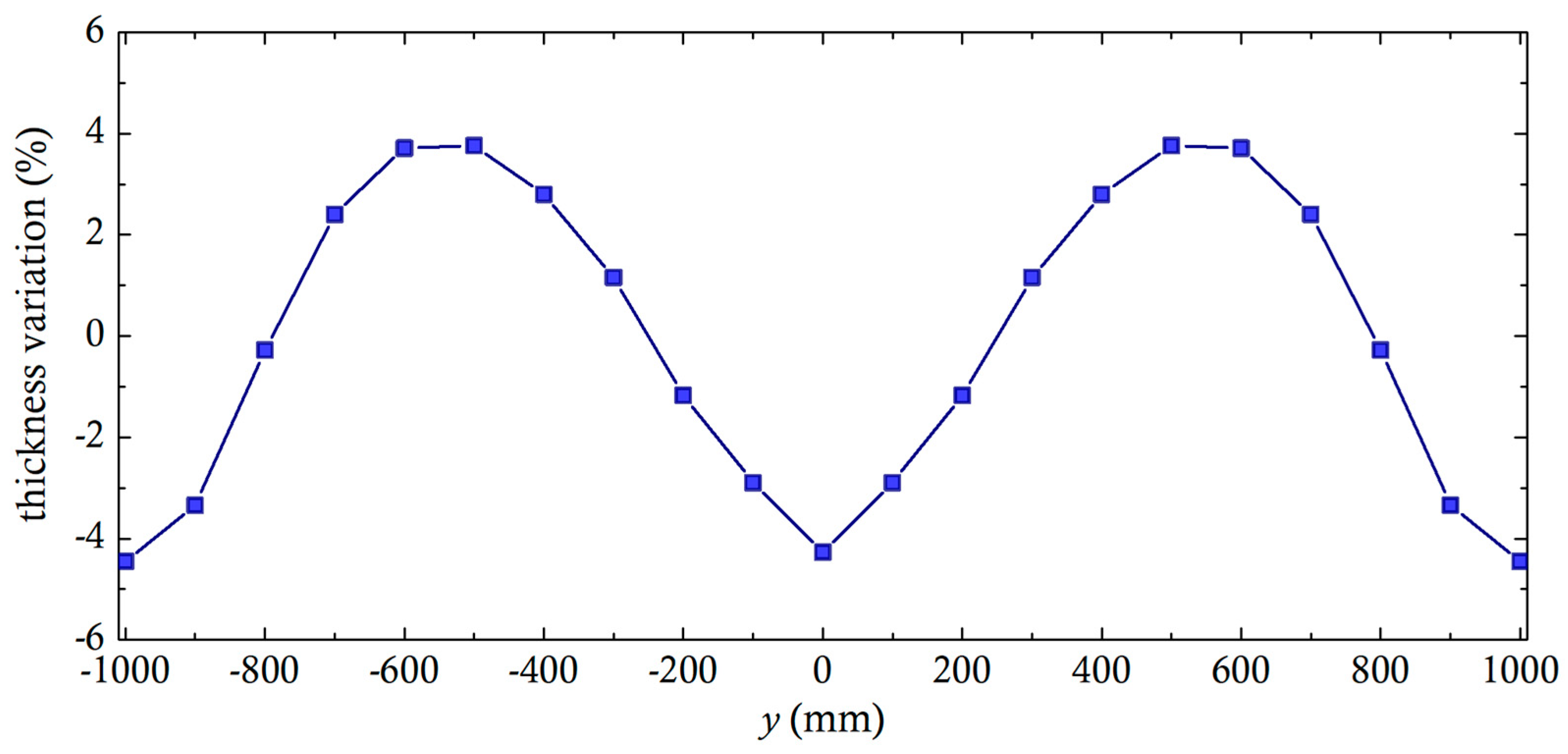
2. Results and Discussion
3. Materials and Methods
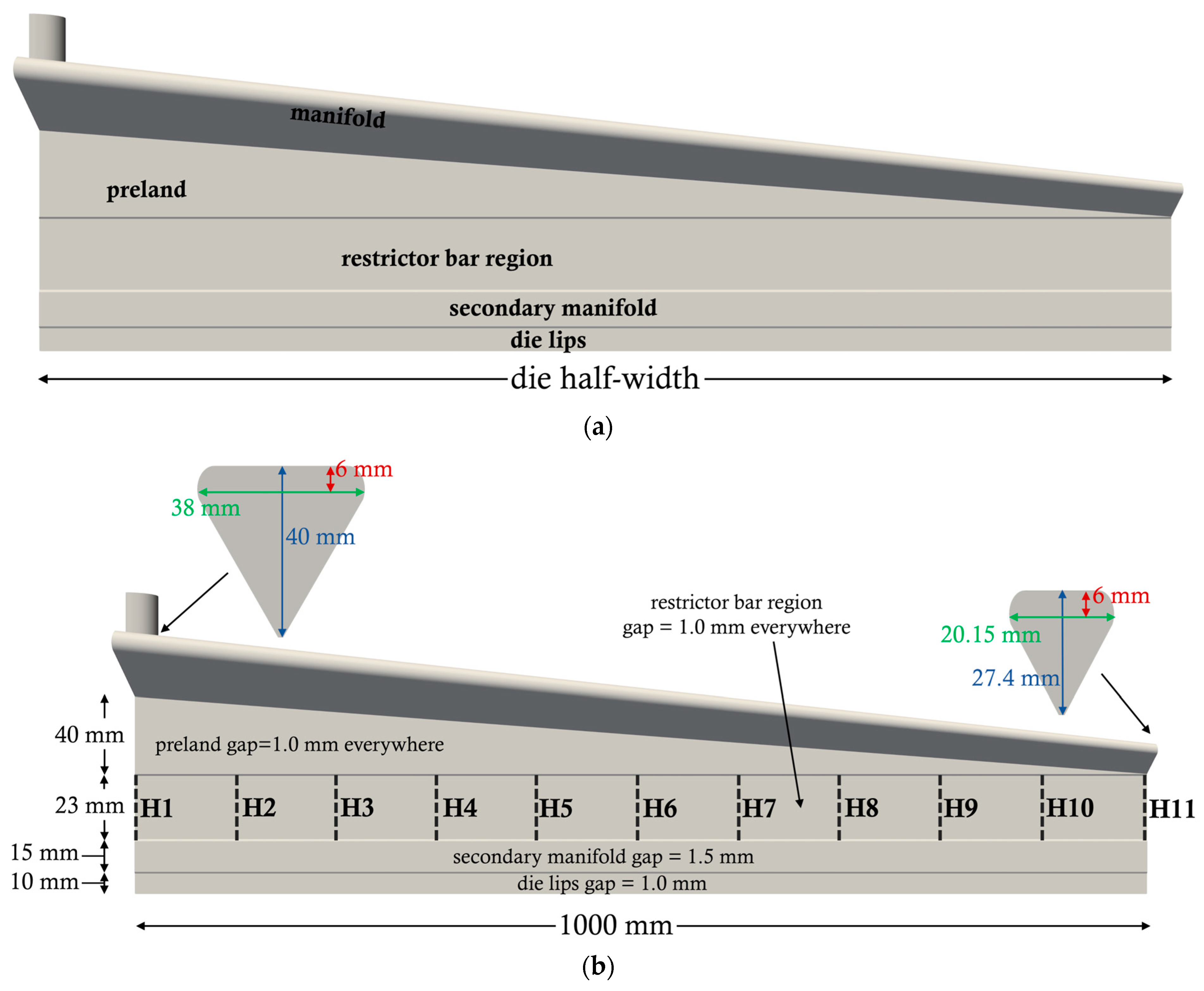
3.1. Dataset Generation for a Base Case Flat Extrusion Die
3.2. Dataset Initialization and Machine Learning Models
3.3. Algorithm Performance Evaluation
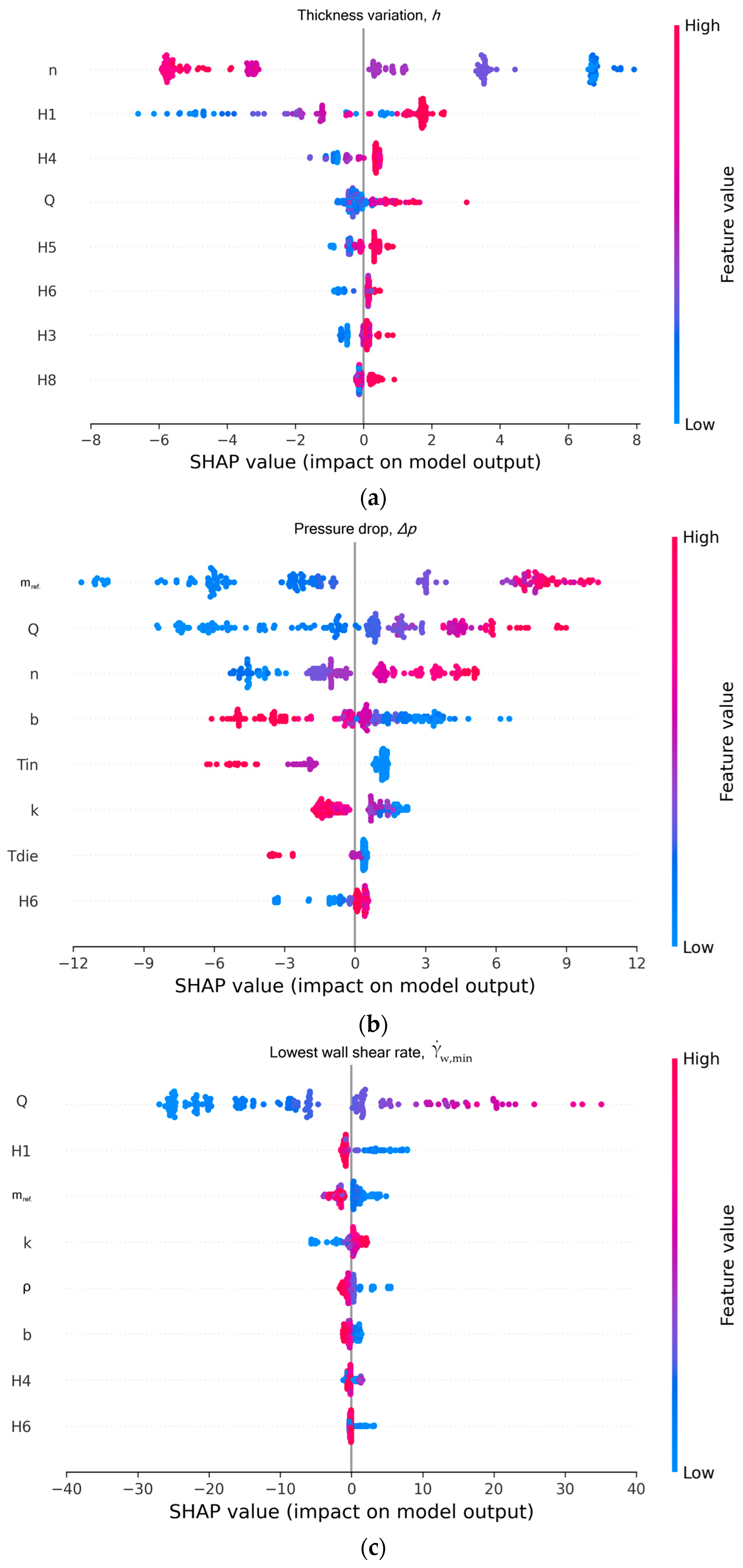
3.4. Interpretability of the Predictions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BOPP | Biaxially oriented polypropylene |
| CV | Cross validation |
| GNF | Generalized Newtonian fluid |
| HDPE | High-density polyethylene |
| LDPE | Low-density polyethylene |
| LLDPE | Linear low-density polyethylene |
| MAE | Mean absolute error |
| ML | Machine learning |
| PFAS | Per- and poly-fluorinated substances |
| PPAs | Polymer processing aids |
| RF | Random forest |
| RMSE | Root mean squared error |
| SHAP | Shapley additive explanations |
| SVR | Support vector regression |
| XGBoost | Extreme gradient boosting |
References
- Vlachopoulos, J.; Polychronopoulos, N.D.; Tanifuji, S.; Peter Müller, J. Flat Film and Sheet Dies. In Design of Extrusion Forming Tools; Carneiro, O., Nobrega, M., Eds.; Smithers Rapra: London, UK, 2012; pp. 113–140. [Google Scholar]
- ANSYS Inc. Ansys Fluent Theory Guide, Release 2022 R1; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids; Wiley: New York, NY, USA, 1987; Volume 1. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Vlachopoulos, J.; Polychronopoulos, N.D. Understanding Rheology and Technology of Polymer Extrusion; Polydynamics Inc.: Dundas, ON, Canada, 2019. [Google Scholar]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics An Advanced Introduction with OpenFOAM® and Matlab®; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Dantzig, J.A.; Tucker, C.L., III. Modeling in Materials Processing; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Smith, D.E.; Tortorelli, D.A.; Tucker, C.L., III. Optimal design for polymer extrusion. Part I: Sensitivity analysis for nonlinear steady-state systems. Comput. Methods Appl. Mech. Eng. 1998, 167, 283–302. [Google Scholar] [CrossRef]
- Smith, D.E.; Tortorelli, D.A.; Tucker, C.L., III. Optimal design for polymer extrusion. Part II: Sensitivity analysis for weakly-coupled nonlinear steady-state systems. Comput. Methods Appl. Mech. Eng. 1998, 167, 303–323. [Google Scholar] [CrossRef]
- Smith, D.E.; Wang, Q. Incorporating adjustable features in the optimal design of polymer sheet extrusion dies. J. Manuf. Sci. Eng. 2006, 128, 11–19. [Google Scholar] [CrossRef]
- Lebaal, N.; Schmidt, F.; Puissant, S. Design and optimization of three-dimensional extrusion dies, using constraint optimization algorithm. Finite Elem. Anal. Des. 2009, 45, 333–340. [Google Scholar] [CrossRef]
- Allal, A.; Lavernhe, A.; Vergnes, B.; Marin, G. Relationships between molecular structure and sharkskin defect for linear polymers. J. Non Newton. Fluid Mech. 2006, 134, 127–135. [Google Scholar] [CrossRef]
- Ghahramani, N.; Zhang, S.; Lyer, K.A.; Doufas, A.K.; Hatzikiriakos, S.G. Melt fracture and wall slip of thermoplastic vulcanizates. Polym. Eng. Sci. 2021, 61, 942–958. [Google Scholar] [CrossRef]
- Agassant, J.F.; Arda, D.R.; Combeaud, C.; Merten, A.; Münstedt, H.; Mackley, M.R.; Robert, L.; Vergnes, B. Polymer processing extrusion instabilities and methods for their elimination or minimization. Int. Polym. Process. 2006, 21, 239–255. [Google Scholar] [CrossRef]
- Denn, M.M. Extrusion instabilities and wall slip. Annu. Rev. Fluid Mech. 2001, 33, 265–287. [Google Scholar] [CrossRef]
- What’s all the Fuss About PFAS. Available online: https://www.plasticsengineering.org/2025/01/whats-all-the-fuss-about-pfas-007728/ (accessed on 7 March 2025).
- Habib, Z.; Song, M.; Ikram, S.; Zahra, Z. Overview of Per- and Polyfluoroaklyl substances (PFAS), their applications, sources, and potential impacts on human health. Pollutants 2024, 4, 136–152. [Google Scholar] [CrossRef]
- Materials Suppliers Team on PFAS-Free Solutions. Available online: https://www.ptonline.com/articles/materials-suppliers-team-on-pfas-free-solutions (accessed on 7 March 2025).
- Selig, M. UIUC Airfoil Coordinates Database. Version 2.0. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on 17 April 2025).
- Wollstadt, B.M.; Ramnath, S.; Shah, J.J.; Detwiler, D.; Menzel, S. CarHoods10k: An industry-grade data set for representation learning and design optimization in engineering applications. IEEE Trans. Evol. Comput. 2022, 26, 1221–1235. [Google Scholar] [CrossRef]
- Regenwetter, L.; Weaver, C.; Ahmed, F. FRAMED: An AutoML approach for structural performance prediction of bicycle frames. Comput. Aided. Des. 2023, 156, 103446. [Google Scholar] [CrossRef]
- Flatcad v.3.0; Polydynamics Inc.: Dundas, ON, Canada, 2025.
- Vlcek, J.; Perdikoulias, J.; Vlachopoulos, J. Chapter 10 Extrusion die flow simulation and design with FLATCAD, COEXCAD and SPIRALCAD. In Application of CAE in Extrusion and Other Continuous Processes; O’Brien, K.T., Ed.; Hanser: Munich, Germany, 1992; pp. 487–504. [Google Scholar]
- Köpplmayr, T.; Miethlinger, J. Application of the network simulation method to flat dies with inverted prelands. Int. Polym. Process. 2013, 3, 322–330. [Google Scholar] [CrossRef]
- Vlcek, J.; Mailvaganam, G.N.; Vlachopoulos, J.; Perdikoulias, J. Computer simulation and experiments of flow distribution in flat sheet dies. Polym. Eng. Sci. 1990, 10, 309–322. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Polychronopoulos, N.D. Basic concepts in polymer melt rheology and their importance in processing. In Applied Polymer Rheology; Kontopoulou, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 1–27. [Google Scholar]
- Polychronopoulos, N.D.; Moustris, K.; Karakasidis, T.; Sikora, J.; Krasinskyi, V.; Sarris, I.E.; Vlachopoulos, J. Machine learning for screw design in single-screw extrusion. Polym. Eng. Sci. 2025. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Van Le, H.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Probl. Eng. 2021, 1–15. [Google Scholar] [CrossRef]
- Bessa, R.; Barreto, G.A.; Coehlo, D.N.; de Moura, E.P.; Murta, R.H.F. On least squares support vector regression for predicting mechanical properties of steel rebars. Metals 2024, 14, 695. [Google Scholar] [CrossRef]
- Cui, Z.; Gong, G. The effect of machine learning regression algorithms and sample size on individualized behavior prediction with functional connectivity features. Neuroimage 2018, 178, 622–637. [Google Scholar] [CrossRef] [PubMed]
- Karakasidis, T.E.; Sofos, F.; Tsonos, C. The electrical conductivity of ionic liquids: Numerical and analytical machine learning approaches. Fluids 2022, 7, 321. [Google Scholar] [CrossRef]
- Benos, L.; Tsaopoulos, D.; Tagarakis, A.C.; Kateris, D.; Bochtis, D. Optimal sensor placement and multimodal fusion for human activity recognition in agricultural tasks. Appl. Sci. 2024, 14, 8520. [Google Scholar] [CrossRef]
- Sofos, F.; Stavrogiannis, C.; Exarchou-Kouveli, K.K.; Akabua, D.; Charilas, G.; Karakasidis, T.E. Current trends in fluid research in the era of Artificial Intelligence: A review. Fluids 2022, 7, 116. [Google Scholar] [CrossRef]
- Lekidis, A.; Georgakis, A.; Dalamagkas, C.; Papageorgiou, E.I. Predictive maintenance framework for fault detection in remote terminal units. Forecasting 2024, 6, 239–265. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Feng, S.; Miao, Z. Studying the thermodynamic phase stability of organic-inorganic hybrid perovskites using machine learning. Molecules 2024, 29, 2974. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.-C.; Tsai, Y.-C.; Wu, P.-Y.; Lien, Y.-H.; Chien, C.-Y.; Kuo, C.-F.; Hung, J.-F.; Chen, S.-C.; Kuo, C.-H. Predictive modeling of blood pressure during hemodialysis: A comparison of linear model, random forest, support vector regression, XGBoost, LASSO regression and ensemble method. Comput. Methods Programs Biomed. 2020, 195, 105536. [Google Scholar] [CrossRef]
- Novakovic, B.; Kashkoush, M. Modeling the matching stage of HDPE hot plate welding: A study using regression and support vector machine models. Polym. Eng. Sci. 2024, 64, 827–844. [Google Scholar] [CrossRef]
- Awad, A.; Khanna, R. Efficient Learning Machines, Theories, Concepts, and Applications for Engineers and System Designer; Apress: Berkeley, CA, USA, 2015. [Google Scholar]
- Sofos, F.; Papakonstantinou, C.G.; Valasaki, M.; Karakasidis, T.E. Fiber-reinforced polymer confined concrete: Data-driven predictions of compressive strength utilizing machine learning techniques. Appl. Sci. 2023, 13, 567. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn:machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scikit-Optimize Sequential Model-Based Optimization in Python. Available online: https://scikit-optimize.github.io/stable/ (accessed on 25 February 2025).
- Bernard, M. Integrating machine learning in geotechnical engineering: A novel approach for railway track layer design based on cone penetration test data. Infrastructures 2024, 9, 121. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, W.; Liu, X. Grid search with a weighted error function: Hyper-parameter optimization for financial time series forecasting. Appl. Soft Comput. 2024, 154, 111362. [Google Scholar] [CrossRef]
- Seifrid, M.; Lo, S.; Choi, D.G.; Tom, G.; Le, M.L.; Li, K.; Sankar, R.; Vuong, H.-T.; Wakidi, H.; Yi, A.; et al. Beyond molecular structure: Critically assessing machine learning for designing organic photovoltaic materials and devices. J. Mater. Chem. A 2024, 12, 14540. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Z.; Yang, W.; Cao, J.; Tao, S. Self-optimizing Bayesian for continuous flow synthesis process. Digit. Discov. 2024, 3, 1958. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Advanced hyperparameter optimization for improved spatial prediction of shallow landslides using extreme gradient boosting (XGBoost). Bull. Eng. Geol. Environ. 2022, 81, 201. [Google Scholar] [CrossRef]
- Rutland, H.; You, J.; Liu, H.; Bowman, K. Application of machine learning for FOS/TAC soft sensing in bio-electrochemical anaerobic digestion. Molecules 2025, 30, 1092. [Google Scholar] [CrossRef]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.A.; Hussein, H.M. Prediction of ecofriendly concrete compressive strength using gradient boosting regression tree combined with GridSearchCV hyperparameter-optimization techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef] [PubMed]
- Ethier, J.G.; Casukhela, R.K.; Latimer, J.J.; Jacobsen, M.D.; Rasin, B.; Gupta, M.K.; Baldwin, L.A.; Vaia, R.A. Predicting phase behavior of linear polymers in solution using machine learning. Macromolecules 2022, 55, 2691–2702. [Google Scholar] [CrossRef]
- Schossler, R.T.; Ojo, S.; Yu, X.B. Optimizing photodegradation rate prediction of organic contaminants: Models with fine-tuned hyperparameters and SHAP feature analysis for informed decision making. ACS ES&T Water 2023, 4, 1131–1145. [Google Scholar]
- Asiminari, G.; Benos, L.; Kateris, D.; Busato, P.; Achillas, C.; Sørensen, C.G.; Pearson, S.; Bochtis, D. Simplifying field traversing efficiency estimation using machine learning and geometric field indices. AgriEngineering 2025, 7, 75. [Google Scholar] [CrossRef]
- Rudin, C.; Chen, C.; Chen, Z.; Huang, H.; Semenova, L.; Zhong, C. Interpretable machine learning: Fundamental principles and 10 grand challenges. Statist. Surv. 2022, 16, 1–85. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning. 2020. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 15 February 2025).
- Shapley, L.S. A Value for n-Person Games. Contributions to the Theory of Games; Harold William, K., Albert William, T., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume 2, pp. 307–318. [Google Scholar]
- Štrumbelj, E.; Kononenko, I. An efficient explanation of individual classifications using game theory. J. Mach. Learn. Res. 2010, 11, 1–18. [Google Scholar]
- Ponce-Bobadilla, A.V.; Schmitt, V.; Maier, C.S.; Mensing, S.; Stodtmann, S. Practical guide to SHAP analysis: Explaining supervised machine learning model predictions in drug development. Clin. Transl. Sci. 2024, 17, e70056. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural. Inf. Proces. Syst. 2017, 30, 4766–4777. [Google Scholar]
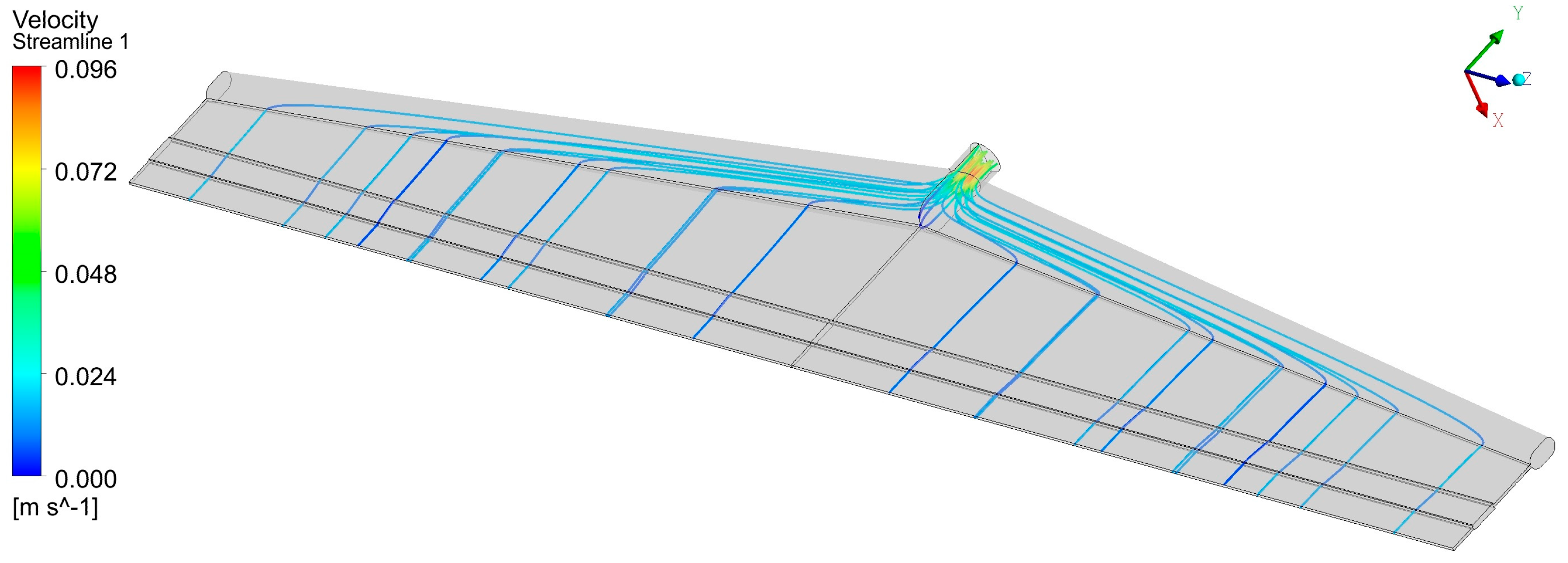
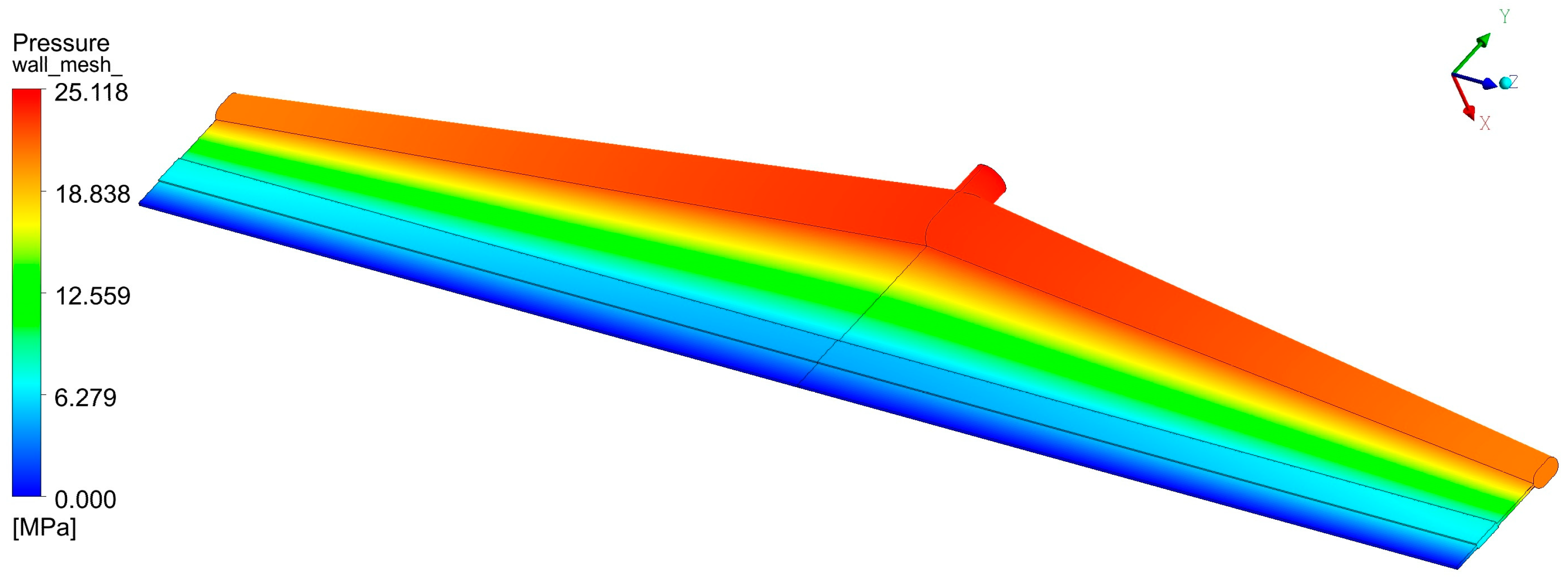
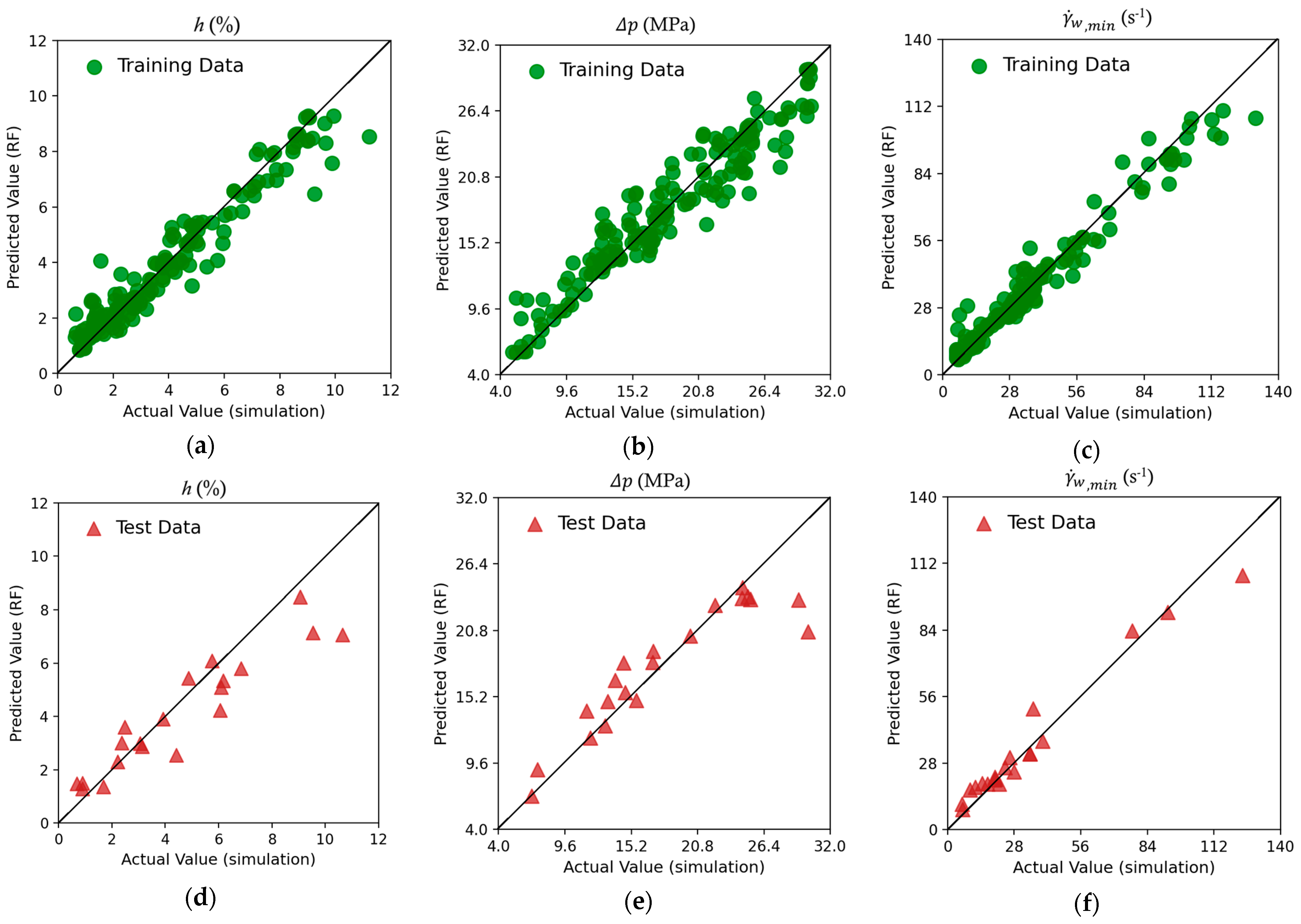


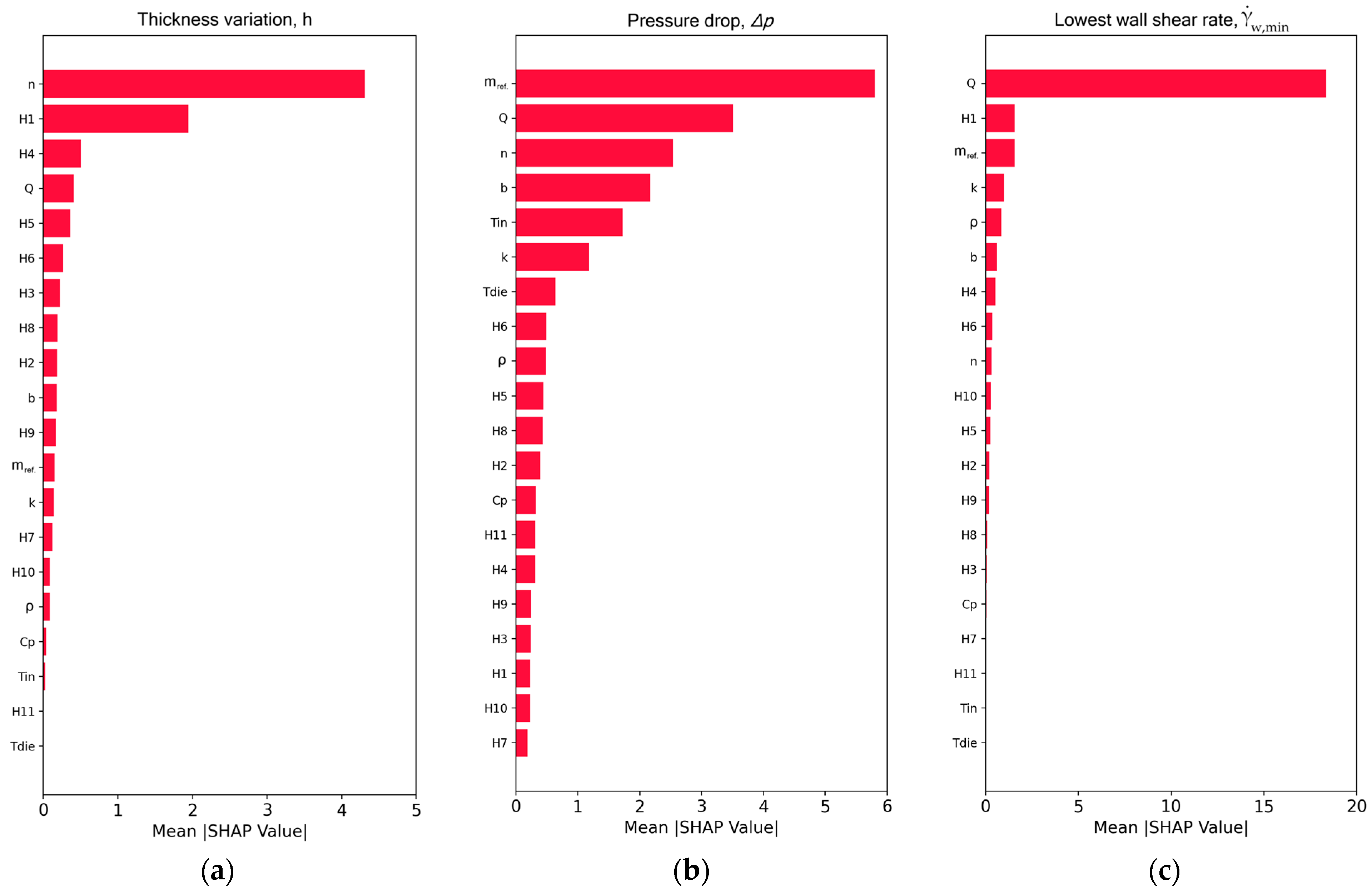
| Output (Target) | Random Forest (RF) | XGboost | Support Vector Regression (SVR) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | ||||
| Thickness variation, | 0.807 | 1.261 | 0.914 | 0.954 | 0.591 | 0.452 | 0.924 | 0.821 | 0.672 |
| Pressure drop, | 0.812 | 2.909 | 1.897 | 0.961 | 1.218 | 0.895 | 0.973 | 1.119 | 0.797 |
| Lowest wall shear rate, | 0.955 | 6.255 | 4.631 | 0.985 | 1.619 | 0.927 | 0.977 | 2.238 | 1.238 |
| Polymer | Power-Law Viscosity Model | Temperature Sensitivity, (°C−1) |
|---|---|---|
| LLDPE-A | 0.022 | |
| LLDPE-B | 0.019 | |
| HDPE | 0.02 |
| Type | Notation | Description | Min–Max Value Range |
|---|---|---|---|
| Input | H1 (mm) | - | 0.66–1.00 |
| Input | H2 (mm) | - | 0.66–1.00 |
| Input | H3 (mm) | - | 0.66–1.00 |
| Input | H4 (mm) | - | 0.68–1.00 |
| Input | H5 (mm) | Bar restrictor | 0.68–1.00 |
| Input | H6 (mm) | locations | 0.71–1.00 |
| Input | H7 (mm) | - | 0.73–1.00 |
| Input | H8 (mm) | - | 0.76–1.00 |
| Input | H9 (mm) | - | 0.84–1.00 |
| Input | H10 (mm) | - | 0.87–1.00 |
| Input | H11 (mm) | - | 0.87–1.00 |
| Input | (kg/h) | Mass flow rate | 100–2000 |
| Input | (Pa·sn) | Consistency index | 5000–35,000 |
| Input | Power-law index | 0.25–0.55 | |
| Input | (°C−1) | Temperature sensitivity | 0.015–0.05 |
| Input | (kg/m3) | Melt density | 750–1000 |
| Input | (J/kg·K) | Specific heat capacity | 1600–2300 |
| Input | (W/m·K) | Thermal conductivity | 0.15–0.25 |
| Input | (°C) | Melt entering temperature | 190–230 |
| Input | (°C) | Die walls temperature | 190–230 |
| Output | (%) | Thickness variation | 0.635–11.20 |
| Output | (MPa) | Pressure drop | 5–30.35 |
| Output | (s−1) | Lowest wall shear rate | 5.763–130.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polychronopoulos, N.D.; Sarris, I.; Vlachopoulos, J. Implementation of Machine Learning in Flat Die Extrusion of Polymers. Molecules 2025, 30, 1879. https://doi.org/10.3390/molecules30091879
Polychronopoulos ND, Sarris I, Vlachopoulos J. Implementation of Machine Learning in Flat Die Extrusion of Polymers. Molecules. 2025; 30(9):1879. https://doi.org/10.3390/molecules30091879
Chicago/Turabian StylePolychronopoulos, Nickolas D., Ioannis Sarris, and John Vlachopoulos. 2025. "Implementation of Machine Learning in Flat Die Extrusion of Polymers" Molecules 30, no. 9: 1879. https://doi.org/10.3390/molecules30091879
APA StylePolychronopoulos, N. D., Sarris, I., & Vlachopoulos, J. (2025). Implementation of Machine Learning in Flat Die Extrusion of Polymers. Molecules, 30(9), 1879. https://doi.org/10.3390/molecules30091879








