Stability of DMPC Liposomes Externally Conjugated with Branched Polyglycerol
Abstract
:1. Introduction
2. Results and Discussion
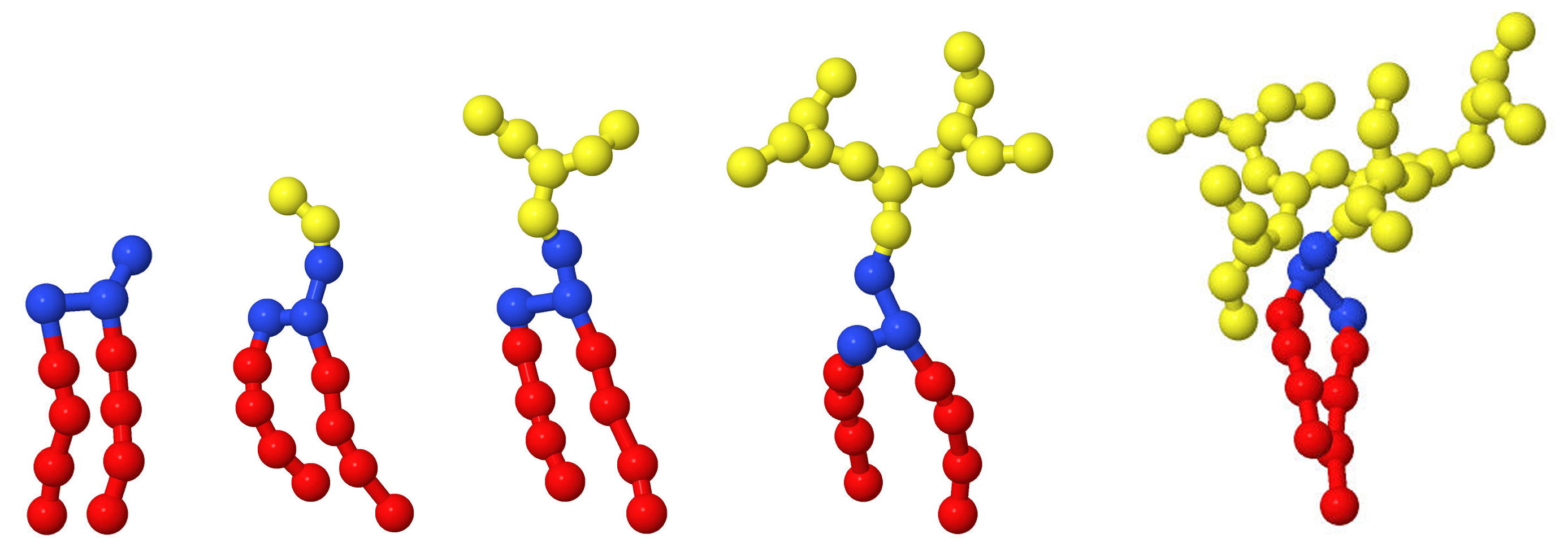
2.1. Details of Simulations
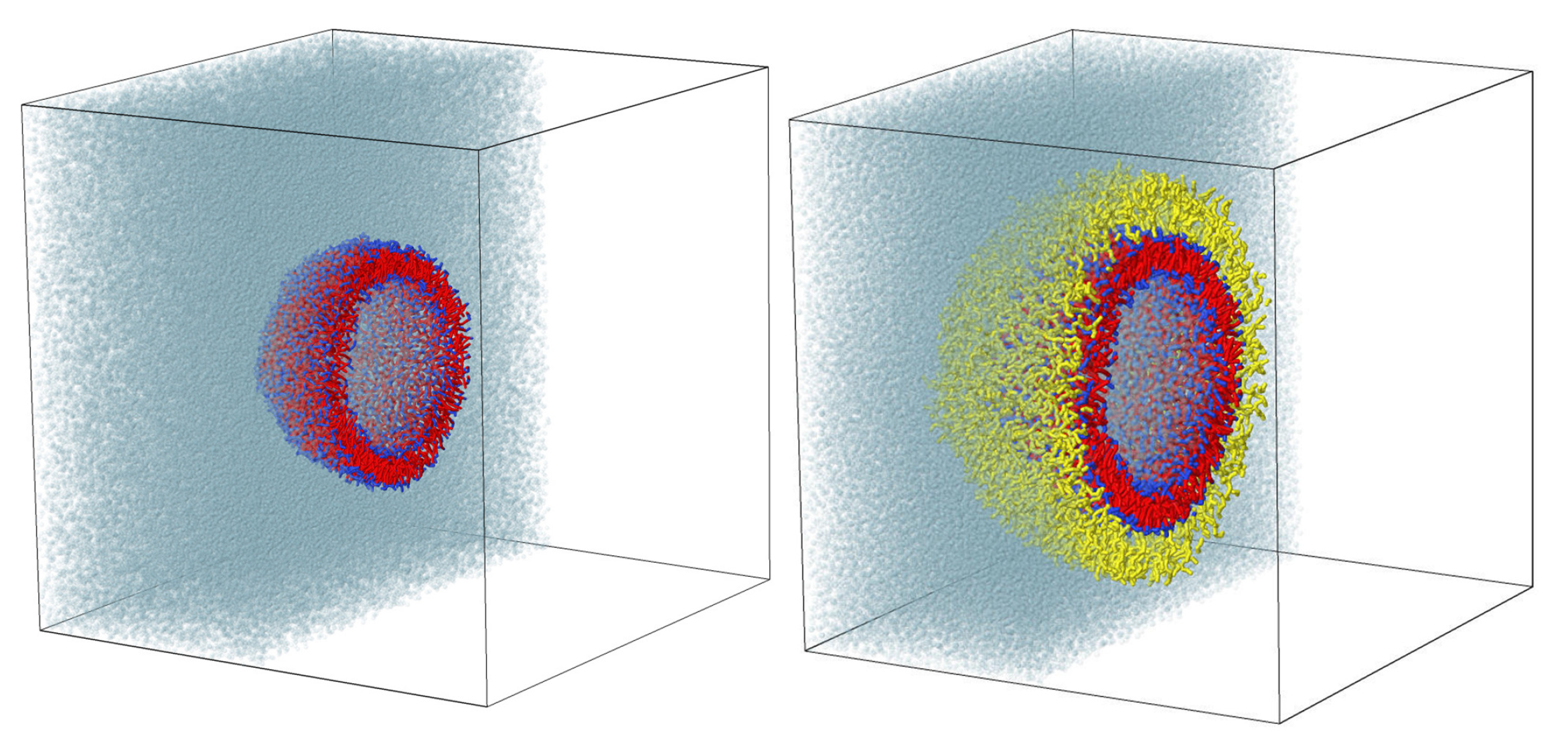
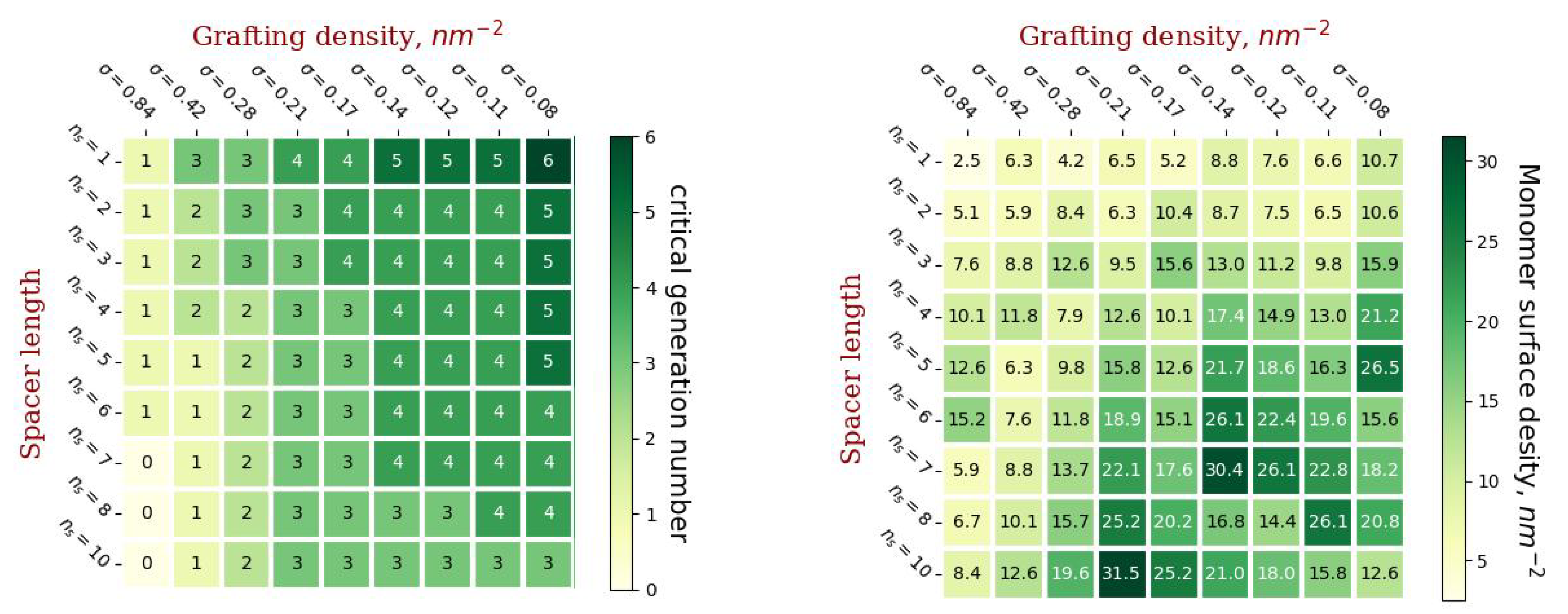
2.2. Stability of Conjugated Vesicles
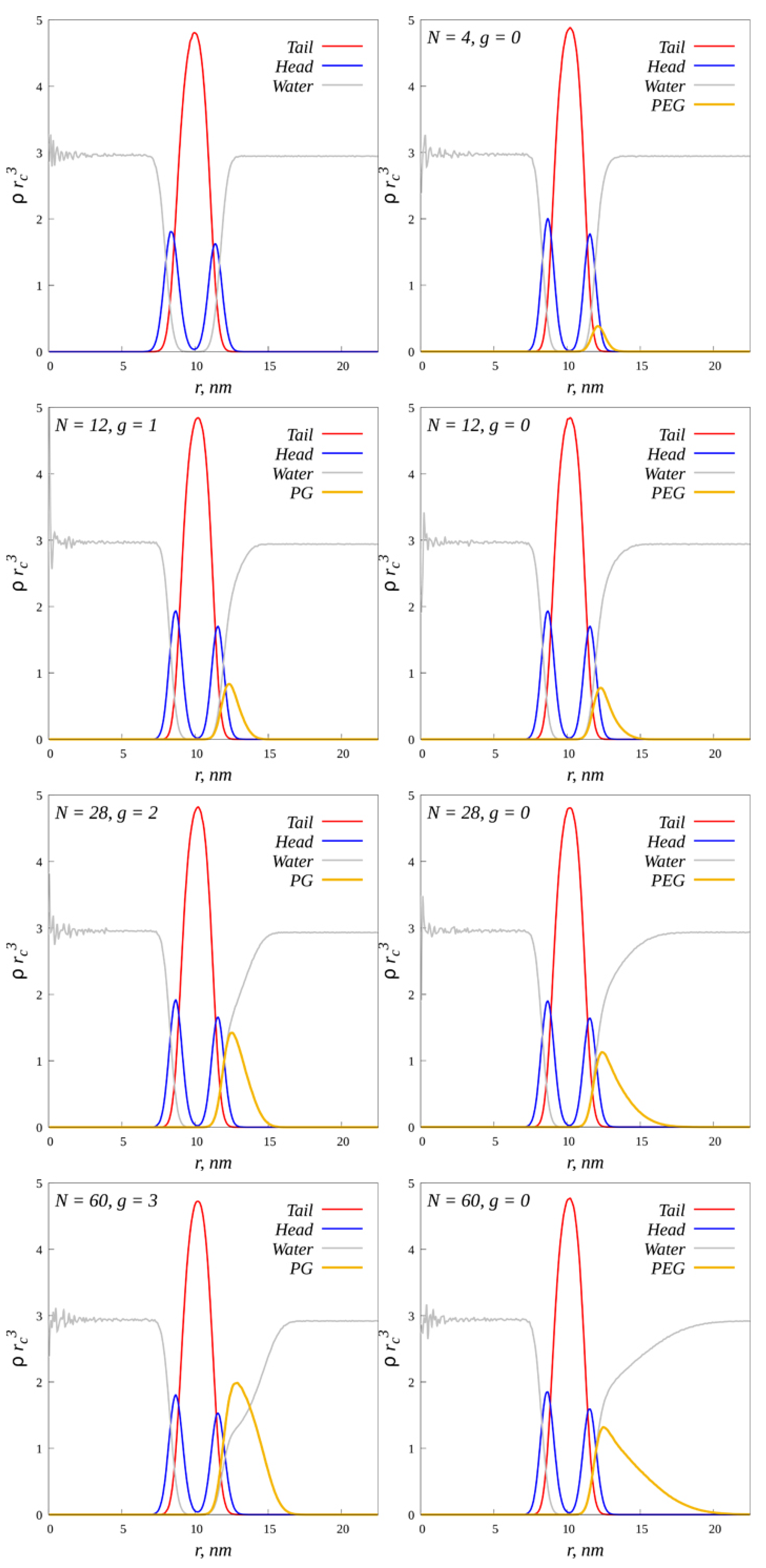
2.3. Radial Density Distribution
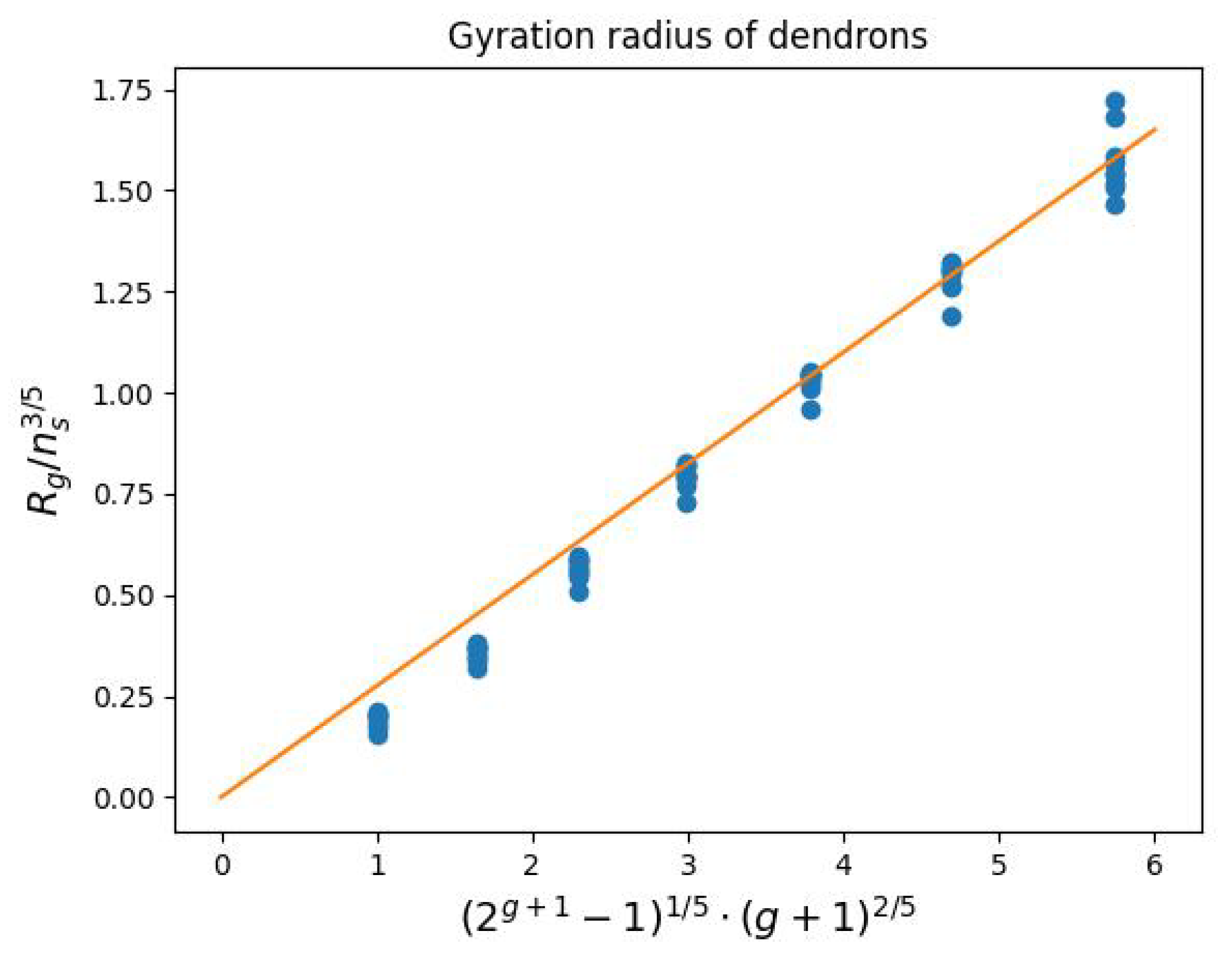
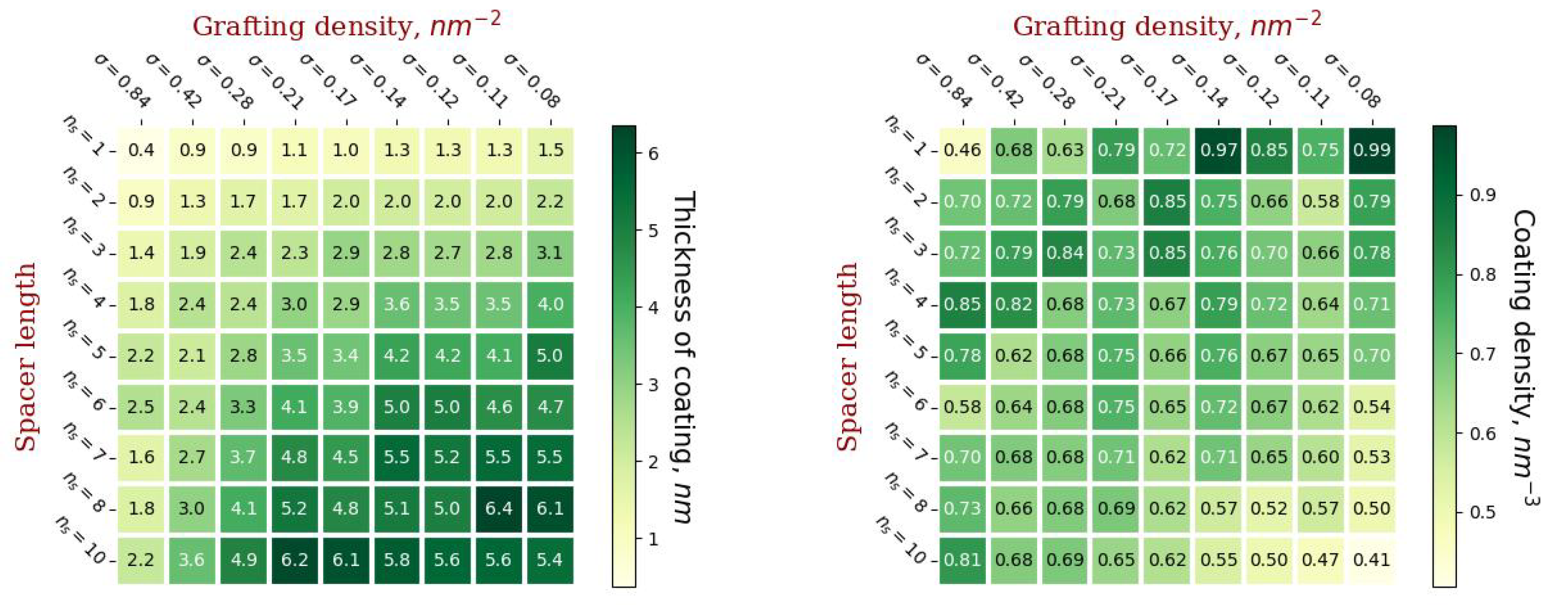
2.4. Characteristics of the External Coating
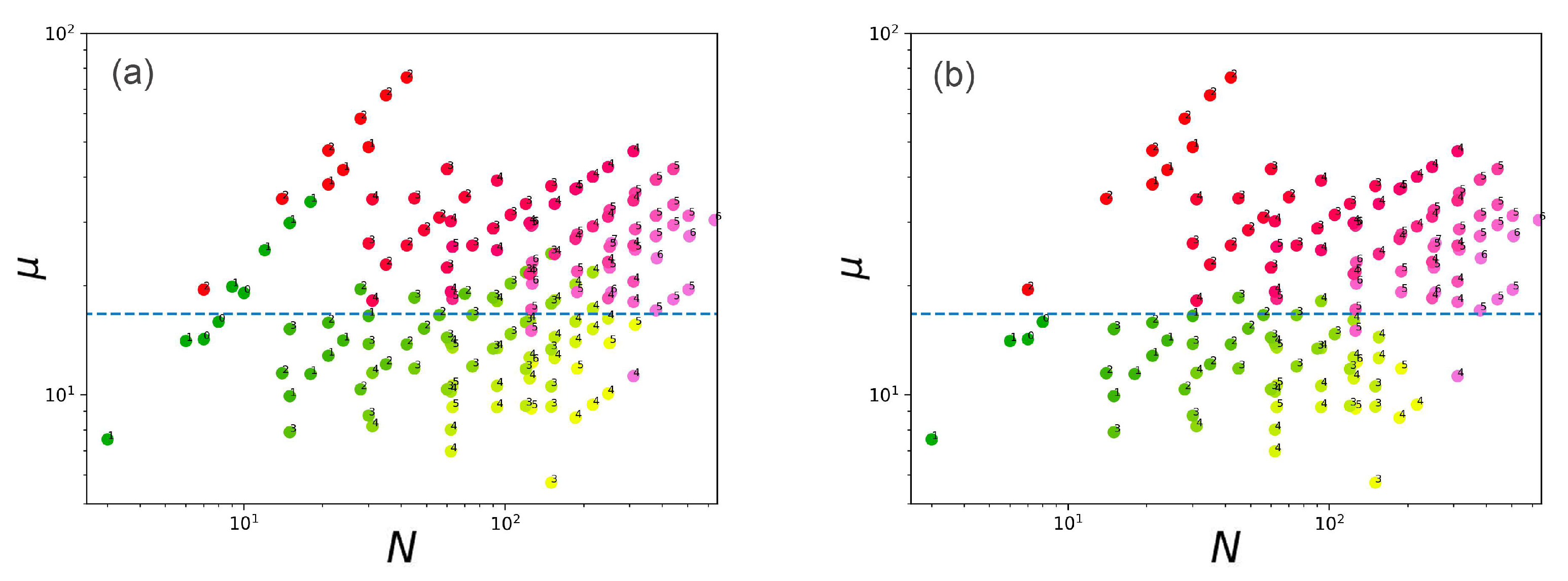
2.5. Chemical Potential as a Metric of Vesicle Stability
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DPD (method) | Dissipative particle dynamics (method) |
| DMPC | 1,2-dimyristoyl-sn-glycero-3-phosphocholine |
| PEG | Polyethylene glycol |
References
- Juliano, R.; Stamp, D. The Effect of Particle Size and Charge on the Clearance Rates of Liposomes and Liposome Encapsulated Drugs. Biochem. Biophys. Res. Commun. 1975, 63, 651–658. [Google Scholar] [CrossRef]
- Allen, T.; Cullis, P. Liposomal Drug Delivery Systems: From Concept to Clinical Applications. Adv. Drug Deliv. Rev. 2013, 65, 36–48. [Google Scholar] [CrossRef]
- Allen, T.; Hansen, C. Pharmacokinetics of Stealth versus Conventional Liposomes: Effect of Dose. Biochim. Biophys. Acta Biomembr. 1991, 1068, 133–141. [Google Scholar] [CrossRef]
- Lasic, D.; Needham, D. The “Stealth” Liposome: A Prototypical Biomaterial. Chem. Rev. 1995, 95, 2601–2628. [Google Scholar] [CrossRef]
- van Vlerken, L.; Vyas, T.; Amiji, M. Poly(ethylene Glycol)-Modified Nanocarriers for Tumor-Targeted and Intracellular Delivery. Pharm. Res. 2007, 24, 1405–1414. [Google Scholar] [CrossRef] [PubMed]
- Wilms, D.; Stiriba, S.; Frey, H. Hyperbranched Polyglycerols: From the Controlled Synthesis of Biocompatible Polyether Polyols to Multipurpose Applications. Acc. Chem. Res. 2010, 43, 129–141. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, A.M.; Wurm, F.; Huhn, E.; Nawroth, T.; Langguth, P.; Frey, H. Hyperbranched Polyglycerol-Based Lipids via Oxyanionic Polymerization: Toward Multifunctional Stealth Liposomes. Biomacromolecules 2010, 11, 568–574. [Google Scholar] [CrossRef] [PubMed]
- Kasza, G.; Kali, G.; Domján, A.; Pethő, L.; Szarka, G.; Iván, B. Synthesis of Well-Defined Phthalimide Monofunctional Hyperbranched Polyglycerols and Its Transformation to Various Conjugation Relevant Functionalities. Macromolecules 2017, 50, 3078–3088. [Google Scholar] [CrossRef]
- Wagener, K.; Worm, M.; Pektor, S.; Schinnerer, M.; Thiermann, R.; Miederer, M.; Frey, H.; Rösch, F. Comparison of Linear and Hyperbranched Polyether Lipids for Liposome Shielding by 18F-Radiolabeling and Positron Emission Tomography. Biomacromolecules 2018, 19, 2506–2516. [Google Scholar] [CrossRef] [PubMed]
- Siegers, C.; Biesalski, M.; Haag, R. Self-Assembled Monolayers of Dendritic Polyglycerol Derivatives on Gold That Resist the Adsorption of Proteins. Chem. A Eur. J. 2004, 10, 2831–2838. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.; Kainthan, R.; Zou, Y.; Chiao, M.; Kizhakkedathu, J.N. Self-Assembled Monothiol-Terminated Hyperbranched Polyglycerols on a Gold Surface: A Comparative Study on the Structure, Morphology, and Protein Adsorption Characteristics with Linear Poly(ethylene Glycol)s. Langmuir 2008, 24, 4907–4916. [Google Scholar] [CrossRef]
- Nosova, A.; Koloskova, O.; Nikonova, A.; Simonova, V.A.; Smirnov, V.; Kudlay, D.; Khaitov, M. Diversity of PEGylation methods of liposomes and their influence on RNA delivery. Med. Chem. Commun. 2019, 10, 369–377. [Google Scholar] [CrossRef] [PubMed]
- Nag, O.; Awasthi, V. Surface Engineering of Liposomes for Stealth Behavior. Pharmaceutics 2013, 5, 542–569. [Google Scholar] [CrossRef] [PubMed]
- Sou, K.; Endo, T.; Takeoka, S.; Tsuchida, E. Poly(ethylene glycol)-modification of the phospholipid vesicles by using the spontaneous incorporation of poly(ethylene glycol)-lipid into the vesicles. Bioconjug Chem. 2000, 11, 372–379. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Yamashita, K.; Itoh, Y.; Yoshino, K.; Nozawa, S.; Kasukawa, H. Comparative studies of polyethylene glycol-modified liposomes prepared using different PEG-modification methods. Biophys. Acta. 2012, 1818, 2801–2807. [Google Scholar] [CrossRef] [PubMed]
- Uster, P.; Allen, T.; Daniel, B.; Mendez, C.; Newman, M.; Zhu, G. Insertion of poly(ethylene glycol) derivatized phospholipid into pre-formed liposomes results in prolonged in vivo circulation time. FEBS Lett. 1996, 386, 243–246. [Google Scholar] [CrossRef]
- Viitala, L.; Pajari, S.; Gentile, L.; Määttä, J.; Gubitosi, M.; Deska, J.; Sammalkorpi, M.; Olsson, U.; Murtomäki, L. Shape and Phase Transitions in a PEGylated Phospholipid System. Langmuir 2019, 35, 3999–4010. [Google Scholar] [CrossRef]
- Yu, X.; Dutt, M. A multiscale approach to study molecular and interfacial characteristics of vesicles. Mol. Syst. Des. Eng. 2018, 3, 871–972. [Google Scholar] [CrossRef]
- Banerjee, A.; Tam, A.; Dutt, M. Dendronized vesicles: Formation, self-organization of dendron-grafted amphiphiles and stability. Nanoscale Adv. 2021, 3, 725–737. [Google Scholar] [CrossRef]
- Frette, V.; Tsafrir, I.; Guedeau-Boudeville, M.; Jullien, L.; Kandel, D.; Stavans, J. Coiling of Cylindrical Membrane Stacks with Anchored Polymers. Phys. Rev. Lett. 1999, 83, 2465–2468. [Google Scholar] [CrossRef]
- Tsafrir, I.; Sagi, D.; Arzi, T.; Guedeau-Boudeville, M.; Frette, V.; Kandel, D.; Stavans, J. Pearling instabilities of membrane tubes with anchored polymers. Phys. Rev. Lett. 2001, 86, 1138–1141. [Google Scholar] [CrossRef] [PubMed]
- Tsafrir, I.; Caspi, Y.; Guedeau-Boudeville, M.A.; Arzi, T.; Stavans, J. Budding and Tubulation in Highly Oblate Vesicles by Anchored Amphiphilic Molecules. Phys. Rev. Lett. 2003, 91, 138102. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.; Madden, T.; Tildesley, D. On the role of hydrodynamic interactions in block copolymer microphase separation. J. Chem. Phys. 1999, 110, 9739–9749. [Google Scholar] [CrossRef]
- Espanol, P. Hydrodynamics from dissipative particle dynamics. Phys. Rev. E. 1995, 52, 1734. [Google Scholar] [CrossRef] [PubMed]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL Europhys. Lett. 1992, 19, 155. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Groot, R.; Rabone, K.; Nakata, M.; Kaneko, M. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 2001, 81, 725–736. [Google Scholar] [CrossRef]
- Grafmüller, A.; Shillcock, J.; Lipowsky, R. The Fusion of Membranes and Vesicles: Pathway and Energy Barriers from Dissipative Particle Dynamics. Biophys. J. 2009, 96, 2658–2675. [Google Scholar] [CrossRef]
- Wu, S.; Guo, H. Dissipative particle dynamics simulation study of the bilayer-vesicle transition. China Ser. B Chem. 2008, 51, 743–750. [Google Scholar] [CrossRef]
- Maulucci, G.; Spirito, M.D.; Arcovito, G.; Boffi, F.; Castellano, A.; Briganti, G. Particle Size Distribution in DMPC Vesicles Solutions Undergoing Different Sonication Times. Biophys J. 2005, 88, 3545–3550. [Google Scholar] [CrossRef]
- Shen, Z.; Ye, H.; Kröger, M.; Li, Y. Self-assembled core–polyethylene glycol–lipid shell nanoparticles demonstrate high stability in shear flow. Phys. Chem. Chem. Phys. 2017, 19, 13294–13306. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, R.; Satarifard, V.; Grafmüller, A.; Lipowsky, R. Spherical nanovesicles transform into a multitude of nonspherical shapes. Nano Lett. 2019, 19, 7703–7711. [Google Scholar] [CrossRef] [PubMed]
- Klos, J.; Sommer, J. Properties of Dendrimers with Flexible Spacer-Chains: A Monte Carlo Study. Macromolecules 2009, 42, 4878–4886. [Google Scholar] [CrossRef]
- Zhulina, E.; Pryamitsyn, V.; Borisov, O. Structure and Conformational Transitions in Grafted Polymer Chains Layers: New Theory. Polym. Sci. USSR 1989, 31, 205–215. [Google Scholar] [CrossRef]
- Pickett, G. Classical Path Analysis of end-Grafted Dendrimers: Dendrimer Forest. Macromolecules 2001, 34, 8784–8791. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. EPL Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.; Warren, P. Dissipative Particle Dynamics: Bridging the Gap Between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Grafmüller, A.; Shillcock, J.; Lipowsky, R. Pathway of membrane fusion with two tension-dependent energy barriers. Phys. Rev. Lett. 2007, 98, 218101. [Google Scholar] [CrossRef]
- Kucerka, N.; Liu, Y.; Chu, N.; Petrache, H.; Tristram-Nagle, S.; Nagle, J. Structure of fully hydrated fluid phase dmpc and dlpc lipid bilayers using x-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys. J. 2005, 88, 2626–2637. [Google Scholar] [CrossRef]
- Orädd, G.; Lindblom, G.; Westerman, P. Lateral diffusion of cholesterol and dimyristoylphosphatidylcholine in a lipid bilayer measured by pulsed field gradient NMR spectroscopy. Biophys. J. 2002, 83, 2702–2704. [Google Scholar] [CrossRef]
- Nagle, J.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta 2000, 1469, 159–195. [Google Scholar] [CrossRef]
- Lee, H.; de Vries, A.; Marrink, S.; Pastor, R. A coarse-grained model for polyethylene oxide and polyethylene glycol: Conformation and hydrodynamics. J. Phys. Chem. B 2009, 113, 13186–13194. [Google Scholar] [CrossRef] [PubMed]




| g | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 1.571 | 1.231 | 1.020 | 0.844 | 0.693 | 0.563 | 0.453 |
| W | H | T | CM | |
|---|---|---|---|---|
| W | 25.0 | 30.0 | 75.0 | 26.3 |
| H | 30.0 | 30.0 | 35.0 | 26.3 |
| T | 75.0 | 35.0 | 10.0 | 33.7 |
| 26.3 | 26.3 | 33.7 | 25.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beketov, A.A.; Mikhailov, I.V.; Darinskii, A.A. Stability of DMPC Liposomes Externally Conjugated with Branched Polyglycerol. Int. J. Mol. Sci. 2022, 23, 9142. https://doi.org/10.3390/ijms23169142
Beketov AA, Mikhailov IV, Darinskii AA. Stability of DMPC Liposomes Externally Conjugated with Branched Polyglycerol. International Journal of Molecular Sciences. 2022; 23(16):9142. https://doi.org/10.3390/ijms23169142
Chicago/Turabian StyleBeketov, Alexander A., Ivan V. Mikhailov, and Anatoly A. Darinskii. 2022. "Stability of DMPC Liposomes Externally Conjugated with Branched Polyglycerol" International Journal of Molecular Sciences 23, no. 16: 9142. https://doi.org/10.3390/ijms23169142
APA StyleBeketov, A. A., Mikhailov, I. V., & Darinskii, A. A. (2022). Stability of DMPC Liposomes Externally Conjugated with Branched Polyglycerol. International Journal of Molecular Sciences, 23(16), 9142. https://doi.org/10.3390/ijms23169142








