Thermodynamic Origin of Negative Thermal Expansion Based on a Phase Transition-Type Mechanism in the GdF₃-TbF₃ System

Abstract

Multicomponent fluorides of rare earth elements (REEs—R) are phase transition-type negative thermal expansion (NTE-II) materials. NTE-II occurs in RF₃-R′F₃ systems formed by “mother” single-component dimorphic RF₃ (R = Pm, Sm, Eu, and Gd) with a giant NTE-II. There are two structural types of RF₃ polymorphic modifications: low-temperature β-YF₃ (β−) and high-temperature LaF₃ (t−). The change in a structural type is accompanied by a density anomaly: a volume of one formula unit (V_form) V_β− >V_t−. The empirical signs of volumetric changes ΔV/V of NTE-II materials were considered. For the GdF₃-TbF₃ model system, an “operating-temperature window ΔT” and a two-phase composition of NTE-II materials follows from the thermodynamics of chemical systems: the phase rule and the principle of continuity. A necessary and sufficient sign of NTE-II is a combination of polymorphism and the density anomaly. Isomorphism in RF₃-R′F₃ systems modifies RF₃ chemically by forming two-component t− and β− type R_1−xR’_xF₃ solid solutions (ss). Between the two monovariant curves of ss decay, a two-phase area with ΔT_trans > 0 (the “window ΔT”) forms. A two-phase composite (t−ss + β−ss) is an NTE-II material. Its constituent t−ss and β−ss phases have different V_form corresponding to the selected T. According to the lever rule on a conode, V_form is calculated from the t−ss and β−ss compositions, which vary with T along two monovariant curves of ss decay. For the GdF₃-TbF₃ system, ΔV/V = f(T), ΔV/V = f(ΔT) and the “window ΔT” = f(x) dependencies were calculated.

1. Introduction

The search for new materials with negative thermal expansion (NTE) has been conducted via trial and error for many years. Recently, there has been a noticeable change in the paradigm for creating NTE materials. Chemical modification of known “mother” materials with a giant NTE was used [1]. The method of chemically modifying “mother” substances was called “substitutions” [1]. This implies isomorphism, which can be realized in a binary (and more complex) system.

The development and application of multicomponent fluoride materials with the participation of REE trifluorides—RF₃—have been carried out since the mid-1970s [2,3,4]. No work has been performed on the search for and study of NTE materials based on REE fluorides.

The only described REE trifluoride with NTE is ScF₃ [5,6,7,8]. It belongs to the 1st type, NTE-I, which includes conventional materials with monotonous volume reduction when heated over a wide temperature (T) range [1]. Owing to its simple composition and cubic structure, a special mechanism of NTE-I was discovered for ScF₃ [5,6,7,8]. ScF₃-RF₃ systems have not been extensively studied.

The 2nd type of NTE (NTE-II) includes materials with NTE based on a phase transition-type mechanism. In such materials, a volume reduction when heating occurs during a polymorphic transformation (PolTr) [1].

RF₃-R′F₃ systems are the most suitable for studies of the common signs of NTE-II materials. They are ionic compounds with the simplest formula and high chemical stability. Their melting (T_fus) and PolTr (T_trans) temperatures ensure diffusion processes and the achievement of equilibrium.

REE trifluorides form a long homologous series of RF₃ (R = La − Lu) from extremely chemically similar compounds with a minimum difference in the atomic numbers (Z) of cations in the series (ΔZ = 1). The lanthanide compression of cations in the LnF₃ (Ln = Ce − Lu) series leads to three types of structures and two morphotropic transformations (MorphTrans).

RF₃ are polymorphic [9]. They (with the exception of volatile ScF₃) crystallize in three structural types: LaF₃ (t−) [10,11], β-YF₃ (β−) [12], and α− UO₃ (α−) [13]. There are three possible PolTrs in RF₃-R′F₃ systems: β− → t−, β− → α−, and t− → α−.

Among 17 RF₃s, four dimorphic fluorides have been discovered: PmF₃, SmF₃, EuF₃, and GdF₃ [2]. SmF₃, EuF₃, and GdF₃ were described as having a density anomaly: a high-temperature form is denser than a low-temperature form [14]. Recently, PmF₃ was attached to them [15]. The density anomaly is the main structural feature of PolTr in dimorphic RF₃s. This makes them and RF₃-R′F₃ systems, which are formed by them, sources of NTE-II materials.

In this message, a new paradigm for the design of NTE-II materials using isovalent isomorphism [1] is considered based on phase diagrams.

In [16], the principle of isovalent isomorphism in RF₃-R′F₃ systems with one (or two) components with NTE-II was used to predict two-component two-phase compositions with NTE-II in 50 (out of 105) systems. Four stages for creating two-component NTE-II materials with adjustable operational parameters were considered. For systems with the studied phase diagrams, the temperature and composition ranges in which these parameters are regulated were estimated.

The connection of empirically found features of two-component NTE-II materials with the thermodynamic rules for the design of phase diagrams of chemical systems, Gibbs’ phase rule (1879) and Kurnakov’s continuity principle [17] (1936), is established.

It is shown that NTE-II follows from the fundamental laws of thermodynamics of chemical systems. In this study, the empirical signs of NTE-II [1] in a material based on its phase diagram are substantiated for the first time on the model GdF₃-TbF₃ system [2]. One of its components, GdF₃, has a giant NTE-II.

A comparison of the rules for the phase diagram design with the thermophysical properties—coefficients of thermal expansion (CTE) of the materials formed in them—defines the universal signs of NTE-II.

The compliance of the formation of NTE-II materials with the fundamental rules of chemical thermodynamics provided a reasonable correction of their previously found empirical features.

A phase diagram of a system contains all the data for quantitative calculations of the values of the NTE-II parameters of the materials formed in this system. This report presents a scheme for calculating the parameters of an NTE-II material based on the experimental phase diagram of the selected GdF₃-TbF₃ system.

This scheme can be extended to any system with a studied phase diagram if it is equilibrium and if its components (one or both) are compounds with NTE-II.

The aims of this study are as follows: (1) a discussion of NTE-II empirical signs in one- and two-component fluoride materials on the basis of the fundamental rules for the chemical system design (the phase rule and the principle of continuity); (2) formulating the stages of the design of new fluoride NTE-II materials with adjustable parameters with isomorphic substitutions in “mother” RF₃ (R = Pm, Sm, Eu, and Gd) with PolTr (when heated); (3) consideration of the thermodynamic conditions (an “operating-temperature window ΔT” and a two-phase composite) for the NTE-II material formation in the model GdF₃-TbF₃ system; (4) and a presentation of the method for calculating the NTE-II parameters controlled by isomorphism from the phase diagram of the GdF₃-TbF₃ model system.

According to IUPAC, 17 REEs were designated R: Sc, Y, La and 14 Ln = Ce − Lu. When analyzing the periodicity of the properties of Ln compounds, it is necessary to separate La from the 4f elements Ln. If not necessary, the sum (La + Ln) was denoted by R. The inconvenience of the REE classification was noted by the IUPAC project (2015) regarding the La position.

Subscript designations of compositions in chemical formulas make it advisable to assign Z of R in the superscript position (⁵⁷Ce_0.5⁶⁴Gd_0.5F₃). Atomic weights with generally accepted superscript positions are not used in this work.

2. Results and Discussion

2.1. Signs of NTE-II Materials

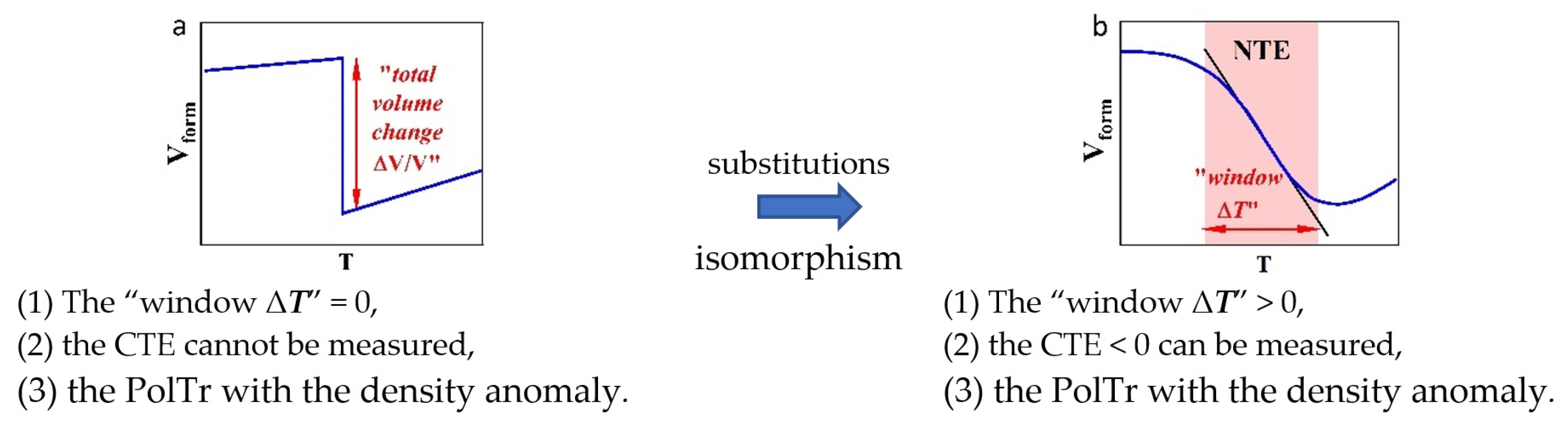
2.1.1. The Qualitative Description of the NTE-II Materials Signs

In the literature, one can find the opinion that a NTE-II material must (1) be two-phase, (2) have the “window ΔT”, and (3) have the negative CTE that can be measured within the “window ΔT”.

The thermal expansion law has the following form:

ΔV/V = α_V ΔT.

(1)

The proportionality coefficient in the linear dependence (1) represents the volumetric CTE α_V = dV/dT. It characterizes the rate of change, ΔV/V, as a function of T. NTE-II materials have negative α_V within the “window ΔT”, which can be up to 10 times greater than that of conventional materials [1]. The total volume change ΔV/V was used in the literature to compare the densities of compounds with different structures. It is recommended [1] as an intrinsic index to indicate the potential of NTE-II.

Qualitative schemes of the ΔV/V change from T for an NTE-II material according to [1] are presented in Figure 1. The diagram in Figure 1a demonstrates the PolTr occurring “at a point” (T_trans = const). At T_trans, ΔV/V jumps at ΔT = 0 (the “window ΔT” = 0) [1]. The scheme in Figure 1a from [1] corresponds to the phase rule for a single-component condensed system. The “window ΔT” is prohibited by the phase rule.

During PolTr in a single-component system, CTE cannot be measured, because ΔT at the point of the PolTr is zero. The author [1] draws a fundamental conclusion from this: “The coefficients α_V and α_L are not intrinsic for NTE-II materials. The ΔV/V is the intrinsic index of the NTE potential”.

The diagram in Figure 1a corresponds to simple “mother” substances, showing PolTr with the density anomaly of the modifications [1].

When the second component is added to a “mother” [1] simple substance, an isomorphic substitution of some of the cations occurs with the formation of ss. The term “substitutions” (Figure 4 in [1]) indicates isomorphism. The degree of freedom of a system increases by 1. The “window ΔT” > 0 appears, and the vertical line in the diagram (Figure 1a) acquires a slope (Figure 1b). In a binary system, PolTr occurs over a temperature range. If within the “window ΔT” a material has CTE < 0 that can be measured, such a material belongs to materials with NTE-II.

For a single-component dimorphic compound, ΔV/V, at the PolTr, is an intrinsic constant of a substance. The concept of the “total volume change” is applicable to it as a characteristic of PolTr.

The ΔV/V of a multicomponent material in a binary (and more complex) system generally varies with composition. Exceptions are the singular points of a phase diagram with invariant equilibria.

The “window ΔT” between two phases exists in any binary system with ss on the base of both structural modifications of components. This corresponds to the phase rule, not to the proof of the presence of NTE-II in a material. These are signs of a condensed T–x system with ss, based on its components. Many substances are polymorphic. Polymorphism is also not a sign of NTE-II.

In Figure 1, PolTr with the density anomaly is shown. The PolTr of a one-component material (Figure 1a) proceeds with the density anomaly and the “window ΔT” = 0. The PolTr of a two-component material (Figure 1b) also proceeds with the density anomaly but with the “window ΔT” > 0.

The qualitative signs of NTE-II, formulated based on empirical data, need to be tested on experimental systems with such materials. This is what the present study is dedicated to.

A necessary and sufficient condition for NTE-II is polymorphism combined with the density anomaly. Changing the structure with a decrease in ΔV/V at the PolTr (when heated) is of key importance for the emergence of NTE-II.

2.1.2. Signs of NTE-II in Ionic REE Fluorides

All RF₃, except for volatile ScF₃, are single-component condensed systems. Their PolTrs are invariant processes with T_trans = const and the “window ΔT” = 0, which are described by the scheme in Figure 1a.

The proposed [1] chemical modification of “mother” simple RF₃ with the PolTr and NTE-II by isomorphism can be obtained only in a binary (and more complex) system, forming two-component NTE-II materials. Such materials are formed in RF₃-R′F₃ systems.

The objectives of this study include the construction of the qualitative and quantitative schemes of the PolTr in these systems using the example of the GdF₃-TbF₃ system. The bank of phase diagrams of 34 studied RF₃-R′F₃ systems [2] serves as a scientific basis for this message.

Let us consider the signs of NTE-II materials in RF₃-R′F₃ systems based on empirical data from the literature.

Polymorphism is the first unconditional sign of any NTE-II material [1]. The connection with PolTr defines the type of NTE material as the 2nd type [1]. PolTr separates NTE-II from a conventional NTE (compression when heated over a wide T interval) and from normal materials (expansion when heated).

When investigating polymorphism, it is necessary to consider the peculiarities of this phenomenon. These are reflected in the discussion of polymorphism in IUPAC. It was said that its absence was most often caused by “a lack of financial resources for research”. These are state parameter changes in the areas of high pressures and low temperatures, which incur large financial costs. Under such conditions, polymorphism can remain “hidden”.

PmF₃ polymorphism is a vivid confirmation. Microquantities of PmF₃ were obtained in a nuclear reactor according to the Manhattan Project to determine its structural affiliation with the LaF₃ type [18]. The cost of the reagent was not determined. However, its high cost has contributed to the lack of knowledge concerning PmF₃.

PmF₃ polymorphism still remains “hidden” in terms of thermal analysis techniques. This occurs at low temperatures and is accompanied by a small thermal effect [15]. Only the method of structural and chemical modeling allowed the evaluation of T_trans in the model ⁶¹(Ce_0.5Gd_0.5)F₃ (“pseudo ⁶¹PmF₃”) composition [15].

Polymorphism is a necessary but insufficient feature of NTE-II. Of the eight dimorphic RF₃, only four (R = Pm, Sm, Eu, and Gd) possess a giant ΔV/V.

The second sign of NTE-II is the density anomaly at the PolTr. Under comparable conditions, the V_form (the volume of one formula unit) of a high-temperature modification is lower than that of a low-temperature modification, V_low (V_high < V_low, compression when heated).

Only β− → t− PolTr (when heated) of the three possible structural transitions yields a denser high-temperature t−modification. The volumes of dimorphic RF₃ are V_β− > V_t− (V_t− and V_β− are V_forms of t− and β− types, respectively). In single-component SmF₃, EuF₃, and GdF₃, density anomalies were noted for the first time [14].

Polymorphism and the density anomaly are determined by structural changes that occur during PolTr. Structural changes are key to understanding the NTE-II mechanism. In [1], the density anomaly as a sign of NTE-II was not discussed. This is the main structural limitation of NTE-II.

The third sign of NTE-II is a two-phase composition [1]. In a single-component RF₃ system, a two-phase area is prohibited by the phase rule. A two-phase area forms in binary systems between the two areas of homogeneity of the β-R_1−xR′_xF₃- ss and t-R_1−xR′_xF₃-ss based on RF₃ modifications.

The fourth sign of NTE-II is the “window ΔT”, according to [1]. The origin of this feature is not established [1]. The “window ΔT” defines the second fundamental parameter of an NTE-II material. Its significance in the description and use of NTE-II materials plays a dual role. First, the “window ΔT” controls ΔV/V in a particular system, which determines the use of a material. Control of ΔV/V is considered in the example of the GdF₃-TbF₃ system in this study. Secondly, the “window ΔT” “adjusts” a material to the temperature conditions of use. For one system, the value of the regulated ΔT is small. In RF₃-R′F₃ systems, the position of the “window ΔT” on the T scale can vary widely from low temperatures to melting.

The fifth sign of NTE-II is a measurable CTE. It is present only in two-component materials formed in RF₃-R′F₃ systems because their PolTrs occur over a temperature range ΔT. In a single-component RF₃, CTE cannot be measured at PolTr (ΔT = 0).

To realize NTE-II in dimorphic ionic fluorides RF₃ with R = Pm-Gd, their structural types must have features. The nature of the structural mechanism of NTE-II in RF₃ has not yet been clarified.

2.2. Two-Component NTE-II Materials with Adjustable Parameters in the GdF₃-TbF₃ System

The GdF₃-TbF₃ system was selected as a model [2] to describe the thermodynamic mechanism of the formation of NTE-II materials. Its phase diagram is shown in Figure 2. The black points represent thermal effects determined experimentally using the thermal analysis method.

2.2.1. Choosing a Model System

The first component of the GdF₃-TbF₃ model system, dimorphic GdF₃, has a giant NTE-II (ΔV/V ~ 4.3%) [14,19] at the β-GdF₃ → t-GdF₃ PolTr (when heated). The choice of GdF₃ from RF₃ (R = Pm, Sm, Eu, and Gd) is due to its stability in terms of valency reduction.

The chemical modification of GdF₃ due to isomorphism occurs when TbF₃ is added. A new state parameter, composition x (mole % of TbF₃), appears in the GdF₃-TbF₃ system. This increases the degree of freedom of the system by 1.

The PolTrs in two-component systems are a combination of peritectoid (one phase turns into two phases with an increase in T) and eutectoid (two phases turn into one phase with an increase in T) equilibria. This is accompanied by the formation of a two-phase area [20].

According to the principle of continuity [17], two-component β-Gd_1−xTb_xF₃ and t-Gd_1−xTb_xF₃ phases form the two-phase area (β + t)-Gd_1−xTb_xF₃ with the ss, which have the β− and t− structural modifications of one-component GdF₃. The properties of the β− and t− modifications change continuously when moving from the single- to two-phase area.

The GdF₃-TbF₃ system has a convenient interval of thermal effects for the thermal analysis method, as set by the difference Δ(T_fus-T_trans) of GdF₃. This made it possible to study phase diagrams that contain a high frequency of the analyzed compositions (the black dots and red circles in Figure 2) when obtaining both liquidus and solidus curves.

Curves 3 and 4 of the Gd_1−xTb_xF₃ ss decay (formation) in Figure 2 come from point 1 (the PolTr of GdF₃). The Gd_1−xTb_xF₃ ss have the same types of structures (β− and t−) that lead to the giant NTE-II in GdF₃. Anomalous volume relations remain between them: V_β−ss > V_t−ss (the compression occurs with an increase in T).

The homogeneity area of the two-phase composite (β + t)-Gd_1−xTb_xF₃ with NTE-II captures approximately 50 mol% of the TbF₃ composition axis. It is marked in Figure 2 in light green.

The Δ(T_fus − T_trans) = 1228–1070 °C interval (the GdF₃ phase transformations) from the phase diagram [2] lies in the T region of disinhibited volumetric diffusion in a solid (Tamman’s temperature is T_tamm ~ 760 °C). This ensured an equilibrium necessary for the use of materials with NTE-II.

MorphTrans (Figure 2) occurs in the GdF₃-TbF₃ system [2]. This MorphTrans is the first in the RF₃ series. It is a true MorphTrans (according to V.M. Goldschmidt, 1925) and is realized via an invariant peritectic reaction:

Liq + t-Gd_0.57Tb_0.43F₃ ↔ β-Gd_0.49Tb_0.51F₃

(point 2 in Figure 2) at T_trans = const = 1186 ± 10 °C [2]. The dotted vertical line II in Figure 2 corresponds to the point of nonvariant composition.

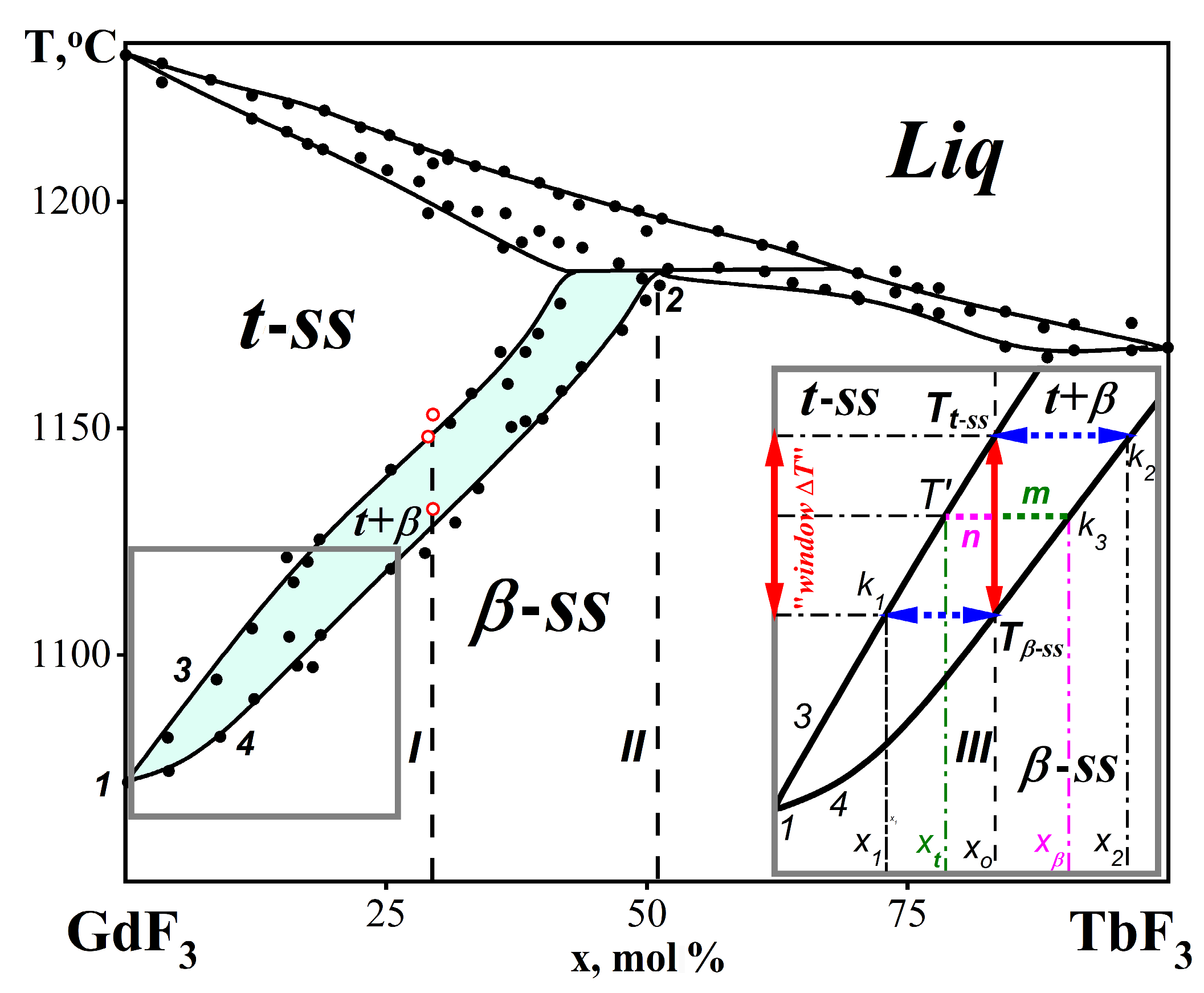
2.2.2. The Method of Calculating the Phase Composition of an NTE-II Material on the Example of the GdF₃-TbF₃ Phase Diagram

The determination of the qualitative and quantitative compositions of a two-phase (β + t)-Gd_1−xTb_xF₃ composite is shown in the insert of Figure 2. It is defined by the isothermal sections (conodes) k₁, k₂, and k₃. The β-Gd_1−xoTb_xoF₃ → t-Gd_1−xoTb_xoF₃ PolTr (when heated) of the Gd_1−xoTb_xoF₃ ss with the composition x_o begins at T_β−ss (the k₁ conode) and ends at T_t−ss (the k₂ conode).

The Single-Phase β-Gd_1−xTb_xF₃-ss Area without NTE

The figurative point, which corresponds to the gross composition, x_o, moves up (with the increase in T) along the vertical line, III, in the single-phase β−ss area to curve 4. In this area, a material is single-phase. It has a β− type structure and is a conventional material without NTE.

The Two-Phase (β + t)-Gd_1−xTb_xF₃ Area with NTE-II

At the temperature T_β−ss, the figurative point intersects with curve 4. The decay of the β-Gd_1−xTb_xF₃ phase begins with the release of the t-Gd_1−xTb_xF₃ phase. The two-phase composite (β + t)-Gd_1−xTb_xF₃ is formed. The area of the two-phase composite is limited by curves 3 and 4. This is highlighted in light green in Figure 2.

The composition (x₁) of the t-phase at the beginning of the decay is determined by the intersection of the k₁ conode (the lower horizontal dotted line) with curve 3 (insert in Figure 2).

When moving the figurative point inside the two-phase area along the vertical red arrowed line from T_β−ss to T_t−ss (insert in Figure 2), the composition of t-Gd_1−xTb_xF₃ varies from x₁ to x_o. The composition of β-Gd_1−xTb_xF₃ varies from x_o to x₂.

At T_t−ss (the left edge of the k₂ conode), the figurative point intersects curve 3, and the composition of t-Gd_1−xTb_xF₃ becomes equal to the original one (x_o). PolTr, formally similar to the β-GdF₃ → t-GdF₃ PolTr, is completed.

However, because β-Gd_1−xTb_xF₃ and t-Gd_1−xTb_xF₃ are located on the different monovariant curves 3 and 4 and are separated by the interval ΔT, the PolTr proceeds over the temperature range. The “operating-temperature window ΔT“ is formed [1]. In the insert in Figure 2, “window ΔT“ is indicated for composition x_o by the red arrow. Its value is ΔT = T_t−ss − T_β−ss.

An example of calculating the average V_form inside the “window ΔT” for the intermediate point of the PolTr at T′ (conode k₃) within the ΔT interval is shown in the insert in Figure 2. The mole fractions (m and n) of the t−ss and β−ss in the two-phase (β + t)-Gd_1−xTb_xF₃ area are shown in green and magenta, respectively. These values are calculated according to the lever rule. The concentrations of x_t and x_β of the t−ss and β−ss correspond to the extreme points of the k₃ conode.

The concentration x_o of Gd_1−xTb_xF₃ at the beginning of the PolTr at T_β−ss corresponds to V_o. It is equal to the V_form of the β−ss (V_β−) phase, which is 100%.

V_o = V_β−(x_o),

(2)

V_form of the t−ss (V_t−) and β−ss (V_β−) phases entering the two-phase composite (β + t)-Gd_1−xTb_xF₃ at T′ are calculated by (3) and (4):

V_t− = mV_t−(x_t),

(3)

V_β− = nV_β−(x_β),

(4)

V_forms V_t−(x_t) and V_β−(x_β) are calculated from the unit cell parameters of the t−ss and β−ss phases. The unit cell parameters of the t−ss and β−ss phases, in turn, are determined using Vegard’s rule from the unit cell parameters of the GdF₃ and TbF₃ components [14,19]. The unit cell parameter of TbF₃ was determined via the extrapolation of the RF₃ data [19].

Let us assume that the NTE-II composite material represents an equilibrium mechanical mixture of its constituent t−ss and β−ss phases. Then, the V_form of the two-phase compositions (V_t+β) is calculated using (5) as the sum of the volumes (V_t− + V_β−) of the t−ss and β−ss phases:

V_t+β = V_t− + V_β−

(5)

The average value of V_form of a composite is variable. It is determined by T in the interval ΔT.

The Single-Phase t-Gd_1−xTb_xF₃-ss Area without NTE

At T_t−ss, the figurative point intersects with curve 3. The decay of the β-Gd_1−xTb_xF₃ phase with the release of the t-Gd_1−xTb_xF₃ phase is completed. The figurative point falls into the t-Gd_1−xTb_xF₃ single-phase area. In this area, the material is single-phase, without NTE.

The experimental curves 3 (decay of the t−ss) and 4 (decay of the β−ss) [2] in the subsolidus region of the GdF₃-TbF₃ system (black dots and red circles in Figure 2) were approximated using second-degree polynomials (6) and (7):

T = −169.6 x² + 322.2 x + 1069.7

(6)

T = 88.4 x² + 182.6 x + 1066.5

(7)

Based on the described methodology, using Equations (6) and (7), it is possible to calculate the volume–temperature dependencies for any of the 34 RF₃-R′F systems studied experimentally [2].

Temperature is an active factor controlling ΔV/V, which is one of the parameters of NTE-II material prospects. The second factor is passive, that is, a fixed composition, x. In our case, this is the composition x_o. If ΔV/V is approximately estimated via the scope of a material application, the composition can be changed in two ways. Small changes within the two-phase area are achievable in one system. For large changes, another system is searched using the RF₃-R′F₃ array [16].

2.3. NTE-II in the GdF₃-TbF₃ System

The construction of a volume–temperature dependence is widely used in various fields of research to calculate the NTE for various purposes. ΔV/V = f(T) dependence was used [1] to determine the CTE. We present the calculation of such dependencies for Gd_1−xTb_xF₃ at several x.

2.3.1. The ΔV/V = f(T) Dependencies at the PolTr in Gd_1−xTb_xF₃

The ΔV/V = f(T) dependencies at the β− → t− PolTr in Gd_1−xTb_xF₃ for x_o = 0, 0.05, 0.1, 0.2, 0.29, 0.4 and 0.51 are shown in Figure 3.

Equation (8) is used to construct the curves:

ΔV/V = (V_(t+β) − V_t−)/V_t−

(8)

where V_(t+β) is the two-phase composite volume at T′ and V_t− is the V_form of the t− type phase at the end point of the PolTr at T_t−ss (insert in Figure 2).

ΔV/V for (β + t)-Gd_1−xTb_xF₃ changes within ΔT_trans = T_t−ss-T_β−ss (the “window ΔT”) from 0 to 4.22%. The (β + t)-Gd_1−xTb_xF₃ composites have NTE-II over the “window ΔT”. ΔV/V is decreasing with increasing T, and the CTE is negative.

Beyond the “window ΔT”, (β + t)-Gd_1−xTb_xF₃ refers to conventional materials without NTE and with the positive CTE.

The TbF₃ contents at the starting points of the β-Gd_1−xTb_xF₃ → t-Gd_1−xTb_xF₃ PolTr at T_β−ss are indicated by x_o = 0, 0.05, 0.1, 0.2, 0.29, 0.4, 0.51 numbers under the curves. The dependencies are constructed within the ΔT_trans = T_t−ss-T_β−ss (the “window ΔT”), which is highlighted in light red in the diagram in Figure 3 for x = 0.29.

The PolTr in GdF₃ and Gd_0.49Tb_0.51F₃ and NTE-II

The vapor pressure (P) for all RF₃, except ScF₃, is low. This allows us to neglect P and consider all RF₃ discussed here to be condensed systems with invariant PolTrs with T_trans = const.

For single-component GdF₃, there is the invariant PolTr of the first kind at point 1 (Figure 2). At T_trans = const, the two solid phases are in equilibrium β-GdF₃ ↔ t-GdF₃. The PolTr is accompanied by a giant volume contraction (ΔV/V ~ −4.3% [14,15,19]). The GdF₃ component has no measurable CTE at PolTr.

The ΔV/V = f(T) curve for GdF₃ (x = 0) in Figure 3 shows the absence (within the measurement error) of a slope between the β-GdF₃ and t-GdF₃ components. The shape of the curve for GdF₃ fully corresponds to the first scheme from [1] (Figure 1a) and to the phase rule.

The curve for the two-component Gd_0.49Tb_0.51F₃ ss (x = 0.51 in Figure 3) also has no slope (ΔT_trans = 0) because the PolTr of this composition represents an invariant process, a peritectic phase reaction.

The PolTr in Two-Phase (β + t)-Gd_1−xTb_xF₃ Composites and NTE-II Materials

The ΔV/V = f(T) curves for the two-phase (β + t)-Gd_1−xTb_xF₃ composites with 0.05 < x < 0.40, calculated using (2)–(8), have a slope (Figure 3), since their PolTrs represent monovariant processes and occur in the interval of ΔT_trans > 0.

The ΔV/V change within the two-phase area of the phase diagram (insert in Figure 2) consists of: (1) the changes in V_β−ss and V_t−ss with the changes in ss compositions along curves 3 and 4, (2) the differences in V_β−ss and V_t−ss of the two structural types (β−ss and t−ss) at T′ of the selected conode (k₃ in the insert, Figure 2), and (3) the quantitative ratio of the β−ss and t−ss phases (according to the lever rule) in the NTE-II composite on isothermal sections with T′ = const (the k₃ conode).

This is the thermodynamic mechanism for controlling the parameters of materials via isomorphism in any “temperature—composition” (T − x) system. It follows from the analysis of the equilibrium phase diagram of a binary system and is not related to the sign of the ΔV/V change at the PolTr and NTE-II.

Owing to its fundamental thermodynamic nature, the mechanism of formation of two-phase composites is universal for compounds of any chemical class of substances. The volume reduction at the PolTr (when heated) makes the composite an NTE-II material.

The PolTr in the Two-Phase Composite Gd_0.71Tb_0.29F₃ (Gross Composition) According to the Phase Diagram and the NTE-II Parameters

To describe an NTE-II material with the “window ΔT” formed in the GdF₃-TbF₃ system, the gross composition of Gd_0.71Tb_0.29F₃ was selected. It is obtained by averaging the compositions of the three experimental points in the phase diagram (indicated by red circles in Figure 2). It corresponds to the dashed vertical I in Figure 2.

On the curve x = 0.29 in Figure 3, three V_form values (red circles) obtained from the experimental points of the phase diagram (also red circles in Figure 2) are plotted. The concentration x = 0.29 is the average for these points.

The ΔV/V values obtained from the experimental data (red circles) of the phase diagram correlate well with the calculated ΔV/V = f(T) dependencies described by lines 3 and 4, between k₁ and k₂.

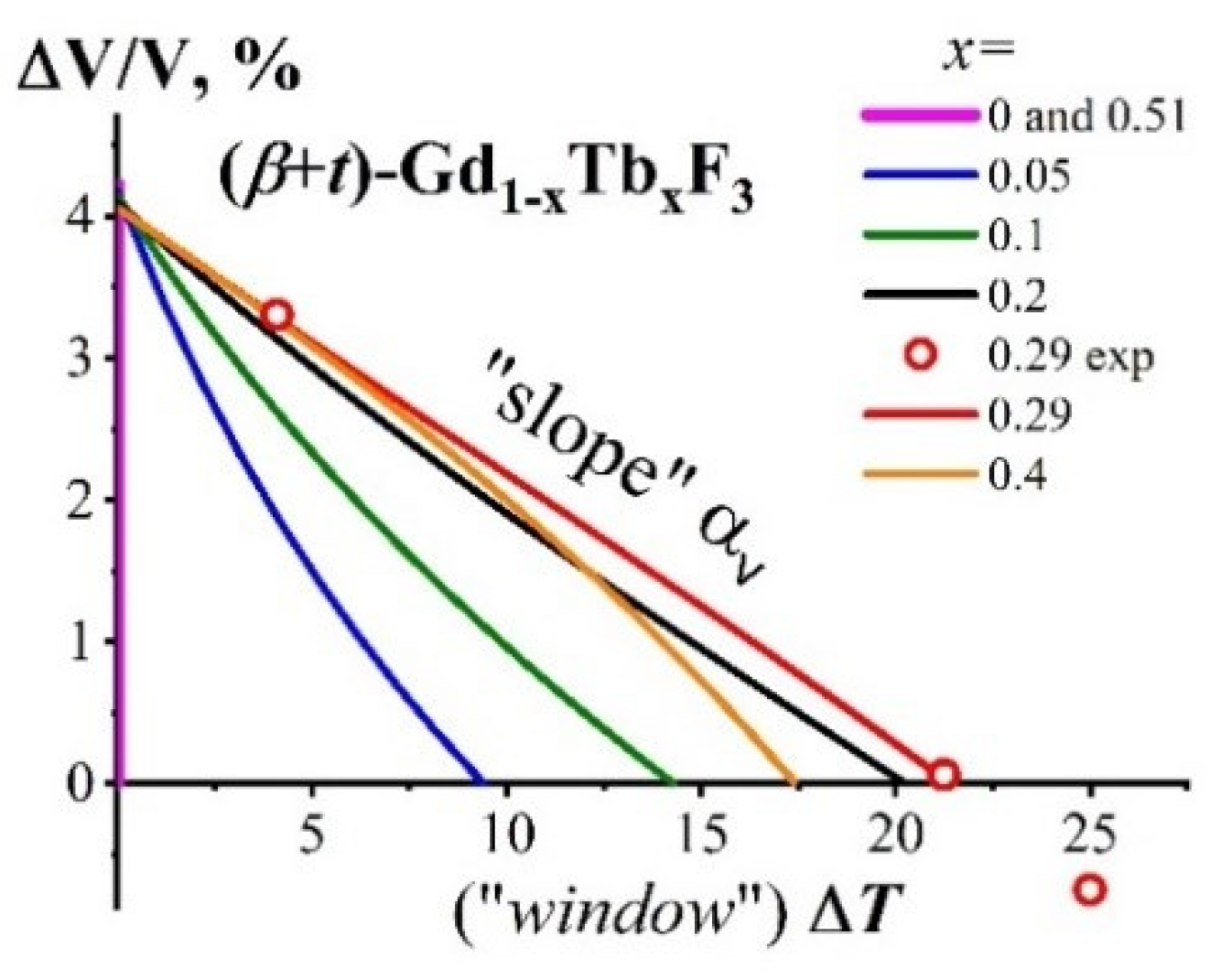
2.3.2. The ΔV/V = f(ΔT) Dependence for the (β + t)-Gd_1−xTb_xF₃ Composite

To characterize the CTE of (β + t)-Gd_1−xTb_xF₃ two-phase composites formed in the GdF₃-TbF₃ system, the dependencies of the relative volume change ΔV/V on ΔT were constructed. The ΔV/V = f(ΔT) dependencies for (β + t)-Gd_1−xTb_xF₃ (x = 0, 0.05, 0.1, 0.2. 0.29, 0.4, 0.51) are shown in Figure 4.

The ΔV/V values for the curves in Figure 4 were calculated using (2)–(8). The temperature interval ΔT is calculated using (9) for every T’ within the temperature interval of the β-Gd_1−xTb_xF₃ → t-Gd_1−xTb_xF₃ PolTr (when heated).

ΔT = T’ − T_β−ss

(9)

The three ΔV/V values obtained from the experimental data with x = 0.29 (opened red circles) are shown in Figure 4.

For x = 0 and 0.51 with invariant equilibrium, the dependencies in Figure 4 represent vertical lines (the “window ΔT” = 0). They coincide with each other and are marked in purple.

For the two-phase composite (β + t)-Gd_1−xTb_xF₃ (0 < x < 0.51), the ΔV/V = f(ΔT) dependencies are nonlinear and have different forms for different x values. The CTE of (β + t)-Gd_1−xTb_xF₃ varies within the “window ΔT”.

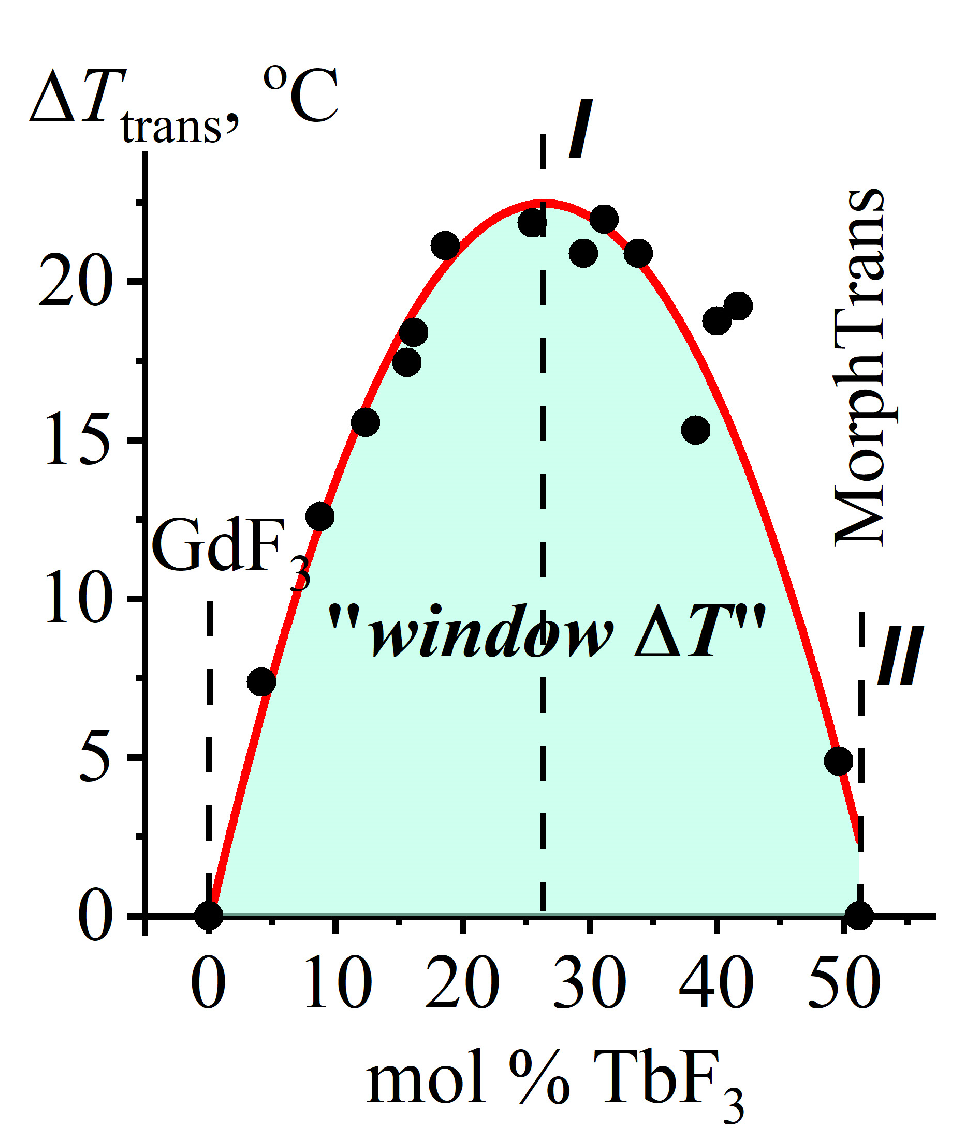
2.3.3. The Dependence of ΔT_trans (the “Window ΔT”) on a Chemical Composition for (β + t)-Gd_1−xTb_xF₃ Composites

The dependence of ΔT_trans (the “window ΔT”) on the (β + t)-Gd_1−xTb_xF₃ composition x is shown in Figure 5. It is calculated for the area between curves 3 and 4 (Figure 2). The area of the β−ss → t−ss PolTr in Gd_1−xTb_xF₃ (0 < x < 0.51) is shown in light green in Figure 2 and Figure 5.

The curve was approximated using a second-degree polynomial (10):

ΔT_trans = −325.3 x² + 171.6 x − 0.184

(10)

The approximated curve is shown in Figure 5 with a red line. It has a maximum of ΔT_trans = 22 °C at x = 0.26.

The value of ΔT (the “window ΔT“) in the GdF₃-TbF₃ system corresponds to the maximum (ΔT = 22 °C) on the curve in Figure 5. This is much higher than the reproducibility of the T measurements in RF₃-R′F₃ systems (±3 °C).

3. Materials and Methods

Two-Component NTE-II Materials in RF₃-R′F₃ and MF₂-RF₃ Systems (M = Ca, Sr, Ba; R = La − Lu)

The necessary and sufficient features (polymorphism with the density anomaly) for two-component composite NTE-II materials in the GdF₃-TbF₃ system can be applied to any RF₃-R′F₃ system.

The two-phase (t−ss + β−ss) composites are NTE-II materials with adjustable parameters. The potential for using the material is estimated using the parameter of the average volume change ΔV/V_av. The V_av at a fixed gross composition of a system is determined by the β−ss and t−ss decay (synthesis) curves and the temperature T. The regulation of ΔV/V_av is achieved by changing T within the “window ΔT”. The available ΔT values are determined using phase diagrams.

There are 50 such systems [16]. Phase diagrams of 11 types of systems with the giant NTE-II were studied: GdF₃-TbF₃, GdF₃-DyF₃, GdF₃-HoF₃, LaF₃-GdF₃, CeF₃-GdF₃, PrF₃-GdF₃, NdF₃-GdF₃, GdF₃-ErF₃, GdF₃-TmF₃, GdF₃-YbF₃, and GdF₃-LuF₃ [2].

Berthollide phases with the t− type structure formed in MF₂-RF₃ systems with M = Ca, Sr, Ba; R = Gd – Lu, Y, and NaF-RF₃ with R = Gd, Tb [2] are also composite materials with NTE-II. The temperature interval “window ΔT” of the two-phase region (t−ss + β−ss) of berthollide phases is more than 300 K.

The “window ΔT” achievable in RF₃-R′F₃ systems is comparable with the “window ΔT” of conventional NTE materials. The “window ΔT” parameter plays a decisive role in controlling the performance characteristics of NTE-II materials when they are used as thermal expansion compensators in high tech. To date, no fluoride materials (single- or multicomponent) have been tested for use in this field.

The NTE-II materials RF₃, R_1−xR′_xF₃ and berthollide phases based on RF₃ are the best superionic conductors with fluorine-ion conductivity [21,22,23,24,25,26,27,28]. They are also used as scintillators [29,30,31] and lasers [32,33] and have a low refractive index dispersion [34].

4. Conclusions

The thermodynamic mechanism for the formation of two-component, two-phase NTE-II materials with controllable properties in a binary system is described. It follows from the equilibrium phase diagram. Owing to its fundamental nature, this mechanism is universal for compounds of any chemical class of substances.

A necessary and sufficient condition for the formation of a material with NTE-II is a combination of polymorphism and density anomaly. Under comparable thermal conditions, the V_high of the high-temperature form is lower than that of the low-temperature form V_low.

The “operating temperature window ΔT” determines the range of compositions and temperatures of the existence of the two-phase composite NTE-II material in a binary system. Its dimensions are given by the monovariant decay (formation) curves of ss, with the structures giving the density anomaly at the PolTr.

The volume change at the PolTr characterizes the NTE-II potential of a material in a particular system.

Polymorphism in RF₃ (R = Pm, Sm, Eu, and Gd) occurs between the main structural types of RF₃: β-YF₃ (β-low-temperature form) and t-LaF₃ (t-high-temperature form).

RF₃ (R = Pm, Sm, Eu, and Gd) represents a new class of fluoride single-component NTE-II materials. They possess the giant NTE of the 2nd type within the “window ΔT” = 0 temperature range.

Isomorphism in RF₃-R′F₃ systems chemically modifies RF₃ to form two-component R_1−xR′_xF₃ materials. R_1−xR′_xF₃ have the giant NTE-II if one or both of their components belong to the “mother” single-component dimorphic RF₃ with R = Pm, Sm, Eu, and Gd.

R_1−xR′_xF₃ with R = Pm, Sm, Eu, and Gd expands a new class of fluoride two-component NTE-II materials. They possess the giant NTE of the 2nd type within the “window ΔT” > 0 temperature range in which the two-phase composites (β +t)-R_1−xR′_xF₃ are formed between the two monovariant decay (formation) curves of R_1−xR′_xF₃ ss. Beyond the “window ΔT” R_1−xR′_xF₃ are conventional materials without NTE.

For the GdF₃-TbF₃ model system, the schemes describing the PolTr in RF₃-R′F₃ systems are presented. The equations for calculating the formula volumes of the β-Gd_1−xTb_xF₃-ss (V_β−) and t-Gd_1−xTb_xF₃-ss (V_t−) and their percentages in the (β + t)-Gd_1−xTb_xF₃ two-phase composite at the PolTr are obtained.

For the GdF₃-TbF₃ model system, according to the experimental data, the ΔV/V = f(T), ΔV/V = f(ΔT) and the “window ΔT” = f(x) dependencies are calculated.

The scheme for calculating the specific parameters of NTE-II materials presented in this work can be applied to any RF₃-R′F₃ system.

The “window ΔT” achievable in RF₃-R′F₃ systems is comparable with the “window ΔT” of conventional NTE materials. This parameter plays a decisive role in controlling the performance characteristics of NTE-II materials when they are used as thermal expansion compensators in high-tech applications.