Addressing the Binding Mechanism of the Meprin and TRAF-C Homology Domain of the Speckle-Type POZ Protein Using Protein Engineering
Abstract
1. Introduction
2. Results and Discussion
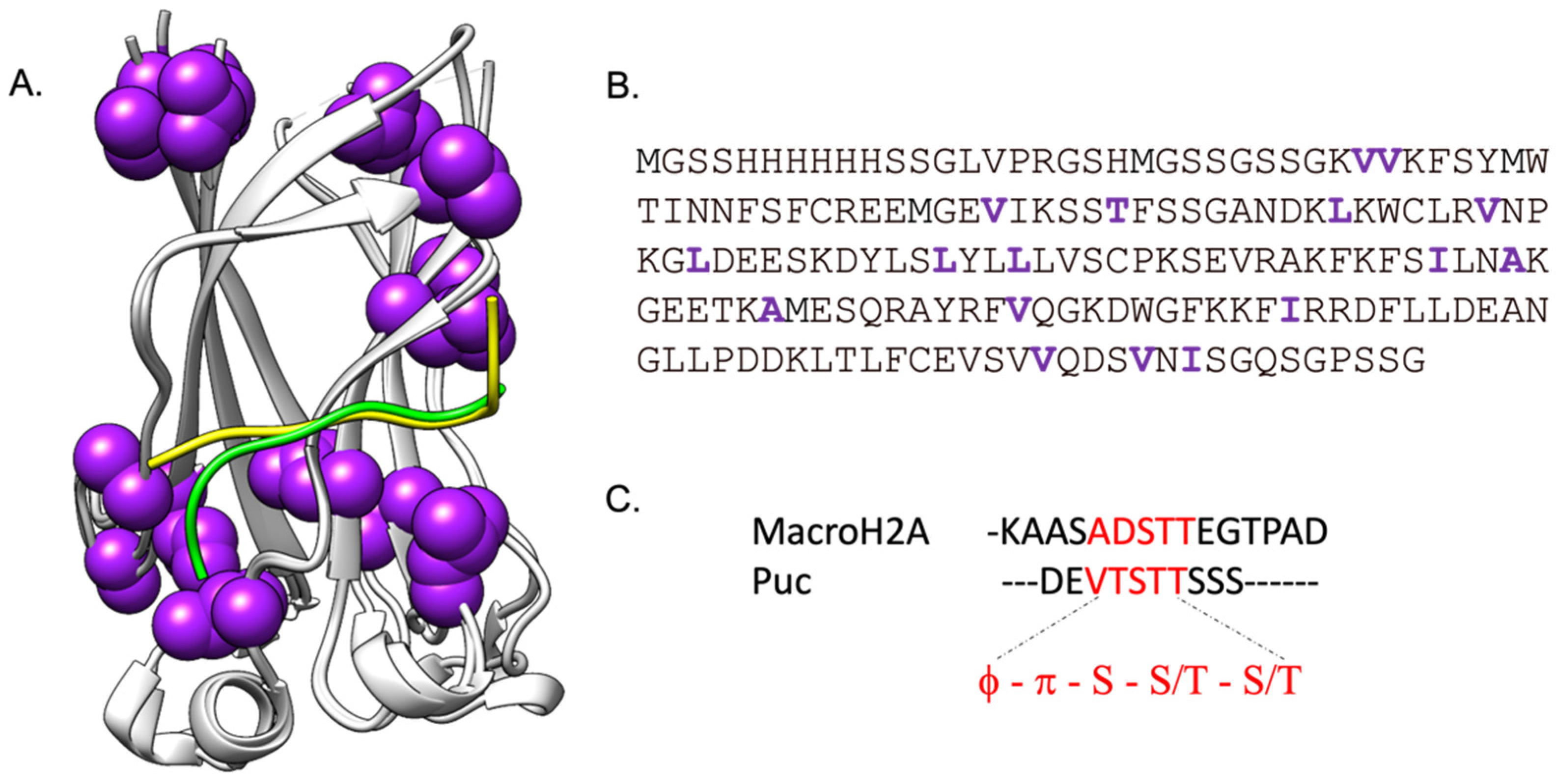
2.1. Long Range Interactions between SPOP MATH and Its Physiological Binders Govern the Binding Process
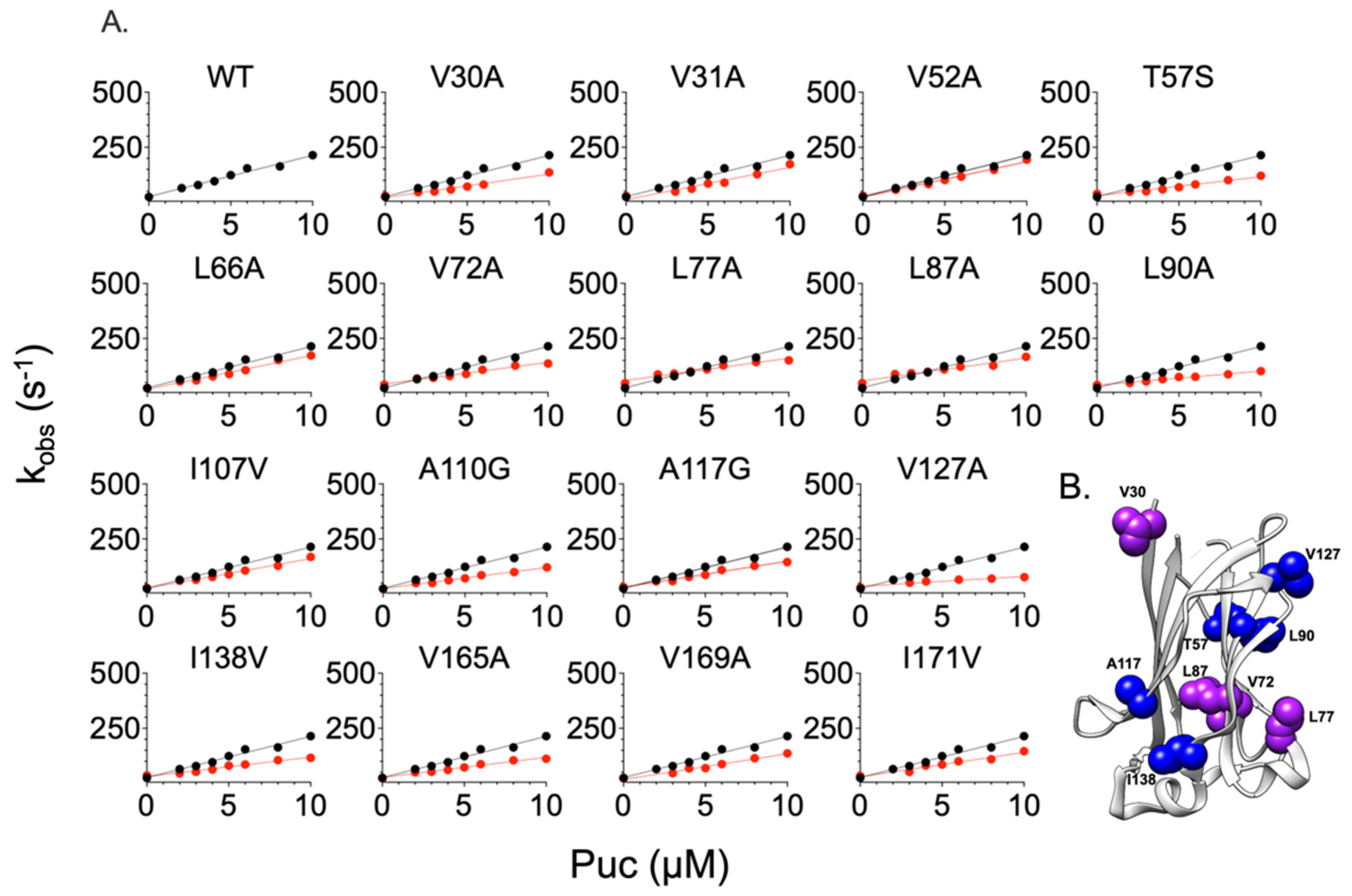
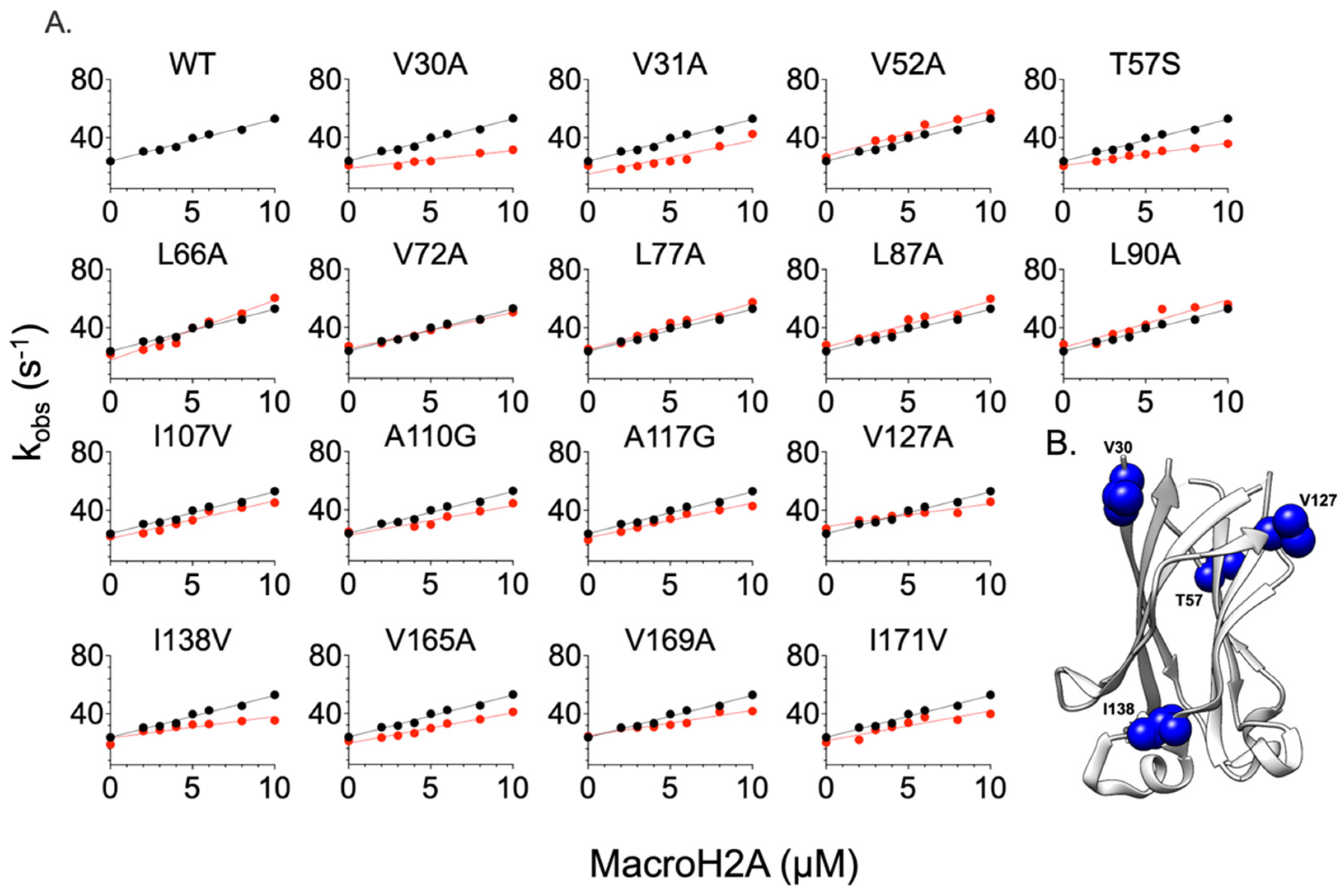
2.2. Comparing the Effect of Site-Directed Mutagenesis on the Binding of Two Different Substrates
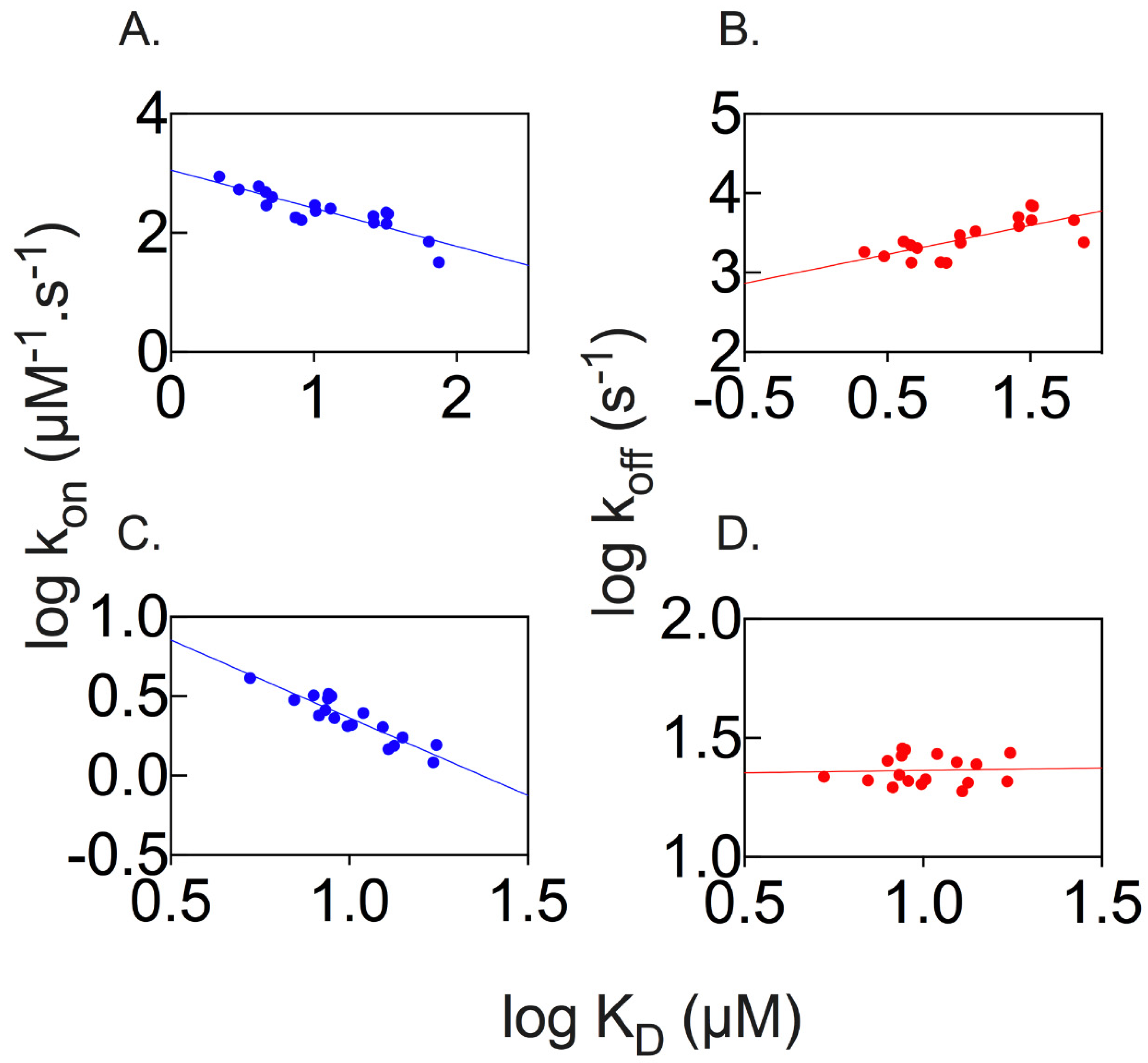
2.3. Properties of the Binding Transition States
3. Materials and Methods
3.1. Protein Expression and Purification
3.2. Stopped-Flow Binding Experiments
3.3. Stopped-Flow Displacement Experiments
3.4. Equilibrium Denaturation Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.Y.; Chen, R.H. Cullin 3 ubiquitin ligases in cancer biology: Functions and therapeutic implications. Front. Oncol. 2016, 6, 113. [Google Scholar] [CrossRef]
- Skaar, J.R.; Pagan, J.K.; Pagano, M. SCF ubiquitin ligase-targeted therapies. Nat. Rev. Drug Discov. 2014, 13, 889–903. [Google Scholar] [CrossRef]
- Hershko, A.; Ciechanover, A. The Ubiquitin System. Annu. Rev. Biochem. 1998, 67, 425–479. [Google Scholar] [CrossRef]
- Deshaies, R.J.; Joazeiro, C.A.P. RING domain E3 ubiquitin ligases. Annu. Rev. Biochem. 2009, 78, 399–434. [Google Scholar] [CrossRef]
- Komander, D.; Rape, M. The ubiquitin code. Annu. Rev. Biochem. 2012, 81, 203–229. [Google Scholar] [CrossRef]
- Komander, D. The emerging complexity of protein ubiquitination. Biochem. Soc. Trans. 2009, 37, 937–953. [Google Scholar] [CrossRef]
- Rotin, D.; Kumar, S. Physiological functions of the HECT family of ubiquitin ligases. Nat. Rev. Mol. Cell Biol. 2009, 10, 398–409. [Google Scholar] [CrossRef]
- Goldberg, A.L.; Stein, R.; Adams, J. New insights into proteasome function: From archaebacteria to drug development. Chem. Biol. 1995, 2, 503–508. [Google Scholar] [CrossRef]
- Akhouri, V.; Majumder, S.; Gaikwad, A.B. The emerging insight into E3 ligases as the potential therapeutic target for diabetic kidney disease. Life Sci. 2023, 321, 121643. [Google Scholar] [CrossRef]
- Suresh, K.; Mattern, M.; Goldberg, M.S.; Butt, T.R. The Ubiquitin Proteasome System as a Therapeutic Area in Parkinson’s Disease. NeuroMolecular Med. 2023, 25, 313–332. [Google Scholar] [CrossRef]
- Petroski, M.D.; Deshaies, R.J. Function and regulation of cullin-RING ubiquitin ligases. Nat. Rev. Mol. Cell Biol. 2005, 6, 9–20. [Google Scholar] [CrossRef]
- van Geersdaele, L.K.; Stead, M.A.; Harrison, C.M.; Carr, S.B.; Close, H.J.; Rosbrook, G.O.; Connell, S.D.; Wright, S.C. Structural basis of high-order oligomerization of the cullin-3 adaptor SPOP. Acta Crystallogr. Sect. D Biol. Crystallogr. 2013, 69, 1677–1684. [Google Scholar] [CrossRef]
- Zhuang, M.; Calabrese, M.F.; Liu, J.; Waddell, M.B.; Nourse, A.; Hammel, M.; Miller, D.J.; Walden, H.; Duda, D.M.; Seyedin, S.N.; et al. Structures of SPOP-Substrate Complexes: Insights into Molecular Architectures of BTB-Cul3 Ubiquitin Ligases. Mol. Cell 2009, 36, 39–50. [Google Scholar] [CrossRef]
- Mani, R.S. The emerging role of speckle-type POZ protein (SPOP) in cancer development. Drug Discov. Today 2014, 19, 1498–1502. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, I.; Kameoka, Y.; Hashimoto, K. MacroH2A1.2 binds the nuclear protein Spop. Biochim. Biophys. Acta-Mol. Cell Res. 2002, 1591, 63–68. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, G.; Ci, W.; Karmakar, S.; Chen, K.; Dhar, R.; Fan, Z.; Guo, Z.; Zhang, J.; Ke, Y.; Wang, L.; et al. SPOP promotes tumorigenesis by acting as a key regulatory hub in kidney cancer. Cancer Cell 2014, 25, 455–468. [Google Scholar] [CrossRef] [PubMed]
- Diop, A.; Pietrangeli, P.; Nardella, C.; Pennacchietti, V.; Pagano, L.; Toto, A.; Di Felice, M.; Di Matteo, S.; Marcocci, L.; Malagrinò, F.; et al. Biophysical characterization of the binding mechanism between the MATH domain of SPOP and its physiological partners. Int. J. Mol. Sci. 2023, 24, 10138. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R.; Sato, S. Φ-Value Analysis and the Nature of Protein-Folding Transition States. Proc. Natl. Acad. Sci. USA 2004, 101, 7976–7981. [Google Scholar] [CrossRef] [PubMed]
- Antonini, E.; Brunori, M. Hemoglobin, and myoglobin in their reactions with ligands. In Hemoglobin and Myoglobin in Their Reactions with Ligands; North-Holland: Amsterdam, The Netherlands, 1971; p. 436. Available online: https://lib.ugent.be/catalog/rug01:001650991 (accessed on 18 September 2023).
- Eaton, W.A.; Henry, E.R.; Hofrichter, J. Application of linear free energy relations to protein conformational changes: The quaternary structural change of hemoglobin. Proc. Natl. Acad. Sci. USA 1991, 88, 4472–4475. [Google Scholar] [CrossRef] [PubMed]
- Edelstein, S.J.; Changeux, J.P. Relationships between structural dynamics and functional kinetics in oligomeric membrane receptors. Biophys. J. 2010, 98, 2045–2052. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Giri, R.; Morrone, A.; Toto, A.; Brunori, M.; Gianni, S. Structure of the transition state for the binding of c-Myb and KIX highlights an unexpected order for a disordered system. Proc. Natl. Acad. Sci. USA 2013, 110, 14942–14947. [Google Scholar] [CrossRef] [PubMed]
- Haq, S.R.; Chi, C.N.; Bach, A.; Dogan, J.; Engström, Å.; Hultqvist, G.; Karlsson, O.A.; Lundström, P.; Montemiglio, L.C.; Strømgaard, K.; et al. Side-chain interactions form late and cooperatively in the binding reaction between disordered peptides and PDZ domains. J. Am. Chem. Soc. 2012, 134, 599–605. [Google Scholar] [CrossRef]
- Leffler, J.E. Parameters for the description of transition states. Science 1953, 117, 340–341. [Google Scholar] [CrossRef]
- Matouschek, A.; Fersht, A.R. Application of physical organic chemistry to engineered mutants of proteins: Hammond postulate behavior in the transition state of protein folding. Proc. Natl. Acad. Sci. USA 1993, 90, 7814–7818. [Google Scholar] [CrossRef]
- Nardella, C.; Pagano, L.; Pennacchietti, V.; Felice, M.D.; Matteo, S.D.; Diop, A.; Malagrinò, F.; Marcocci, L.; Pietrangeli, P.; Gianni, S.; et al. An intramolecular energetic network regulates ligand recognition in a SH2 domain. Protein Sci. 2023, 32, e4729. [Google Scholar] [CrossRef]
- Laursen, L.; Klichem, J.; Gianni, S.; Jemth, P. Supertertiary protein structure affects an allosteric network. Proc. Natl. Acad. Sci. USA 2020, 117, 24294–24304. [Google Scholar] [CrossRef]

| Puc | |||||
|---|---|---|---|---|---|
| MATH Variants | kon (µM−1 s−1) | koff (s−1) | KD (µM) | ∆∆G# (kcal mol−1) | ∆∆Geq (kcal mol−1) |
| WT | 19 ± 1 | 26.1 ± 0.1 | 1.4 ± 0.4 | - | - |
| V30A | 10.66 ± 0.85 | 29.29 ± 0.55 | 2.74 ± 0.1 | 0.34 ± 0.08 | 0.40 ± 0.04 |
| V31A | 14.64 ± 1.5 | 28.36 ± 0.35 | 1.94 ± 0.1 | 0.15 ± 0.10 | 0.19 ± 0.06 |
| V52A | 16.10 ± 0.68 | 29.71 ± 0.40 | 1.85 ± 0.05 | 0.10 ± 0.04 | 0.16 ± 0.03 |
| T57S | 8.60 ± 0.66 | 38.8 ± 0.5 | 4.51 ± 0.09 | 0.47 ± 0.08 | 0.69 ± 0.02 |
| L66A | 15.31 ± 0.78 | 24.63 ± 0.1 | 1.61 ± 0.05 | 0.13 ± 0.05 | 0.08 ± 0.03 |
| V72A | 9.80 ± 0.56 | 40.35 ± 0.15 | 4.12 ± 0.06 | 0.39 ± 0.06 | 0.64 ± 0.01 |
| L77A | 10.16 ± 0.65 | 46.34 ± 0.50 | 4.56 ± 0.09 | 0.37 ± 0.08 | 0.70 ± 0.02 |
| L87A | 10.41 ± 1 | 46.90 ± 0.15 | 4.51 ± 0.12 | 0.35 ± 0.12 | 0.69 ± 0.02 |
| L90A | 6.38 ± 0.43 | 38.78 ± 0.25 | 6.09 ± 0.06 | 0.64 ± 0.07 | 0.87 ± 0.01 |
| I107V | 13.46 ± 0.74 | 27.33 ± 0.35 | 2.03 ± 0.05 | 0.20 ± 0.05 | 0.22 ± 0.03 |
| A110G | 9.58 ± 0.50 | 22.90 ± 0.20 | 2.39 ± 0.06 | 0.40 ± 0.05 | 0.32 ± 0.03 |
| A117G | 11.77 ± 0.60 | 32.16 ± 0.30 | 2.73 ± 0.06 | 0.28 ± 0.05 | 0.39 ± 0.02 |
| V127A | 4.51 ± 0.30 | 29.39 ± 0.50 | 6.52 ± 0.09 | 0.85 ± 0.09 | 0.91 ± 0.01 |
| I138V | 8.74 ± 0.55 | 36.12 ± 0.40 | 4.13 ± 0.08 | 0.46 ± 0.06 | 0.64 ± 0.02 |
| V165A | 9.14 ± 0.68 | 22.74 ± 1 | 2.49 ± 0.08 | 0.43 ± 0.08 | 0.34 ± 0.05 |
| V169A | 11.70 ± 1 | 22.76 ± 1 | 1.95 ± 0.10 | 0.29 ± 0.09 | 0.19 ± 0.06 |
| I171V | 11.06 ± 1 | 33.74 ± 1 | 3.05 ± 0.12 | 0.32 ± 0.09 | 0.46 ± 0.04 |
| MacroH2A | |||||
|---|---|---|---|---|---|
| MATH Variants | kon (µM−1 s−1) | koff (s−1) | KD (µM) | ∆∆G# (kcal mol−1) | ∆∆Geq (kcal mol−1) |
| WT | 3 ± 2 | 21 ± 2.0 | 7.8 ± 0.4 | - | - |
| V30A | 1.21 ± 0.20 | 20.78 ± 1.5 | 17.17 ± 0.25 | 0.54 ± 0.20 | 0.53 ± 0.01 |
| V31A | 2.30 ± 0.30 | 20.87 ± 3.0 | 9.07 ± 0.4 | 0.16 ± 0.13 | 0.15 ± 0.03 |
| V52A | 3.06 ± 0.25 | 26.61 ± 1.5 | 8.70 ± 0.15 | −0.01 ± 0.08 | 0.13 ± 0.02 |
| T57S | 1.54 ± 0.1 | 20.54 ± 0.50 | 13.42 ± 0.09 | 0.40 ± 0.07 | 0.38 ± 0.01 |
| L66A | 4.12 ± 0.40 | 21.72 ± 2.0 | 5.30 ± 0.21 | −0.19 ± 0.10 | −0.17 ± 0.03 |
| V72A | 2.48 ± 0.15 | 27.12 ± 0.5 | 10.85 ± 0.07 | 0.11 ± 0.06 | 0.26 ± 0.01 |
| L77A | 3.20 ± 0.30 | 25.40 ± 1.5 | 7.94 ± 0.15 | −0.04 ± 0.09 | 0.07 ± 0.02 |
| L87A | 3.17 ± 0.40 | 28.24 ± 2.0 | 8.40 ± 0.20 | −0.03 ± 0.13 | 0.14 ± 0.02 |
| L90A | 3.27 ± 0.44 | 28.57 ± 2.5 | 8.66 ± 0.23 | −0.05 ± 0.13 | 0.13 ± 0.03 |
| I107V | 2.59 ± 0.25 | 22.17 ± 1.5 | 8.53 ± 0.20 | 0.09 ± 0.10 | 0.12 ± 0.02 |
| A110G | 2.02 ± 0.30 | 25.06 ± 2 | 12.41 ± 0.24 | 0.23 ± 0.15 | 0.34 ± 0.02 |
| A117G | 2.39 ± 0.20 | 19.63 ± 1 | 8.18 ± 0.15 | 0.13 ± 0.08 | 0.09 ± 0.02 |
| V127A | 1.56 ± 10 | 27.34 ± 1 | 17.53 ± 0.20 | 0.39 ± 0.13 | 0.54 ± 0.01 |
| I138V | 1.47 ± 0.30 | 18.89 ± 2 | 12.60 ± 0.30 | 0.42 ± 0.12 | 0.36 ± 0.01 |
| V165A | 2.09 ± 0.20 | 21.21 ± 1 | 11.46 ± 0.15 | 0.21 ± 0.08 | 0.22 ± 0.01 |
| V169A | 1.74 ± 0.20 | 24.53 ± 1.5 | 11.60 ± 0.10 | 0.32 ± 0.06 | 0.41 ± 0.01 |
| I171V | 2.05 ± 0.35 | 20.26 ± 3 | 9.18 ± 0.30 | 0.22 ± 0.05 | 0.20 ± 0.01 |
| MATH Variants | ∆∆GeqPuc (kcal mol−1) | ∆∆GeqMacroH2A (kcal mol−1) | ∆∆GeqPuc/∆∆GeqMacroH2A |
|---|---|---|---|
| WT | - | - | - |
| V30A | 0.40 ± 0.04 | 0.53 ± 0.01 | 0.75 ± 0.03 |
| T57S | 0.69 ± 0.02 | 0.38 ± 0.01 | 1.82 ± 2.12 |
| V72A | 0.64 ± 0.01 | 0.26 ± 0.01 | 2.42 ± 0.01 |
| L77A | 0.70 ± 0.02 | 0.07 ± 0.02 | 9.40 ± 0.01 |
| L87A | 0.69 ± 0.02 | 0.14 ± 0.02 | 4.85 ± 0.01 |
| L90A | 0.87 ± 0.01 | 0.13 ± 0.03 | 6.62 ± 0.05 |
| A117G | 0.39 ± 0.02 | 0.09 ± 0.02 | 4.18 ± 0.02 |
| V127A | 0.91 ± 0.01 | 0.54 ± 0.01 | 1.68 ± 0.01 |
| I138V | 0.64 ± 0.02 | 0.36 ± 0.01 | 1.78 ± 0.01 |
| I171V | 0.46 ± 0.04 | 0.20 ± 0.01 | 2.26 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diop, A.; Pietrangeli, P.; Pennacchietti, V.; Pagano, L.; Toto, A.; Di Felice, M.; Di Matteo, S.; Marcocci, L.; Malagrinò, F.; Gianni, S. Addressing the Binding Mechanism of the Meprin and TRAF-C Homology Domain of the Speckle-Type POZ Protein Using Protein Engineering. Int. J. Mol. Sci. 2023, 24, 17364. https://doi.org/10.3390/ijms242417364
Diop A, Pietrangeli P, Pennacchietti V, Pagano L, Toto A, Di Felice M, Di Matteo S, Marcocci L, Malagrinò F, Gianni S. Addressing the Binding Mechanism of the Meprin and TRAF-C Homology Domain of the Speckle-Type POZ Protein Using Protein Engineering. International Journal of Molecular Sciences. 2023; 24(24):17364. https://doi.org/10.3390/ijms242417364
Chicago/Turabian StyleDiop, Awa, Paola Pietrangeli, Valeria Pennacchietti, Livia Pagano, Angelo Toto, Mariana Di Felice, Sara Di Matteo, Lucia Marcocci, Francesca Malagrinò, and Stefano Gianni. 2023. "Addressing the Binding Mechanism of the Meprin and TRAF-C Homology Domain of the Speckle-Type POZ Protein Using Protein Engineering" International Journal of Molecular Sciences 24, no. 24: 17364. https://doi.org/10.3390/ijms242417364
APA StyleDiop, A., Pietrangeli, P., Pennacchietti, V., Pagano, L., Toto, A., Di Felice, M., Di Matteo, S., Marcocci, L., Malagrinò, F., & Gianni, S. (2023). Addressing the Binding Mechanism of the Meprin and TRAF-C Homology Domain of the Speckle-Type POZ Protein Using Protein Engineering. International Journal of Molecular Sciences, 24(24), 17364. https://doi.org/10.3390/ijms242417364








