The Influence of Constraints on Gelation in a Controlling/Living Copolymerization Process
Abstract
:1. Introduction
2. Results and Discussion
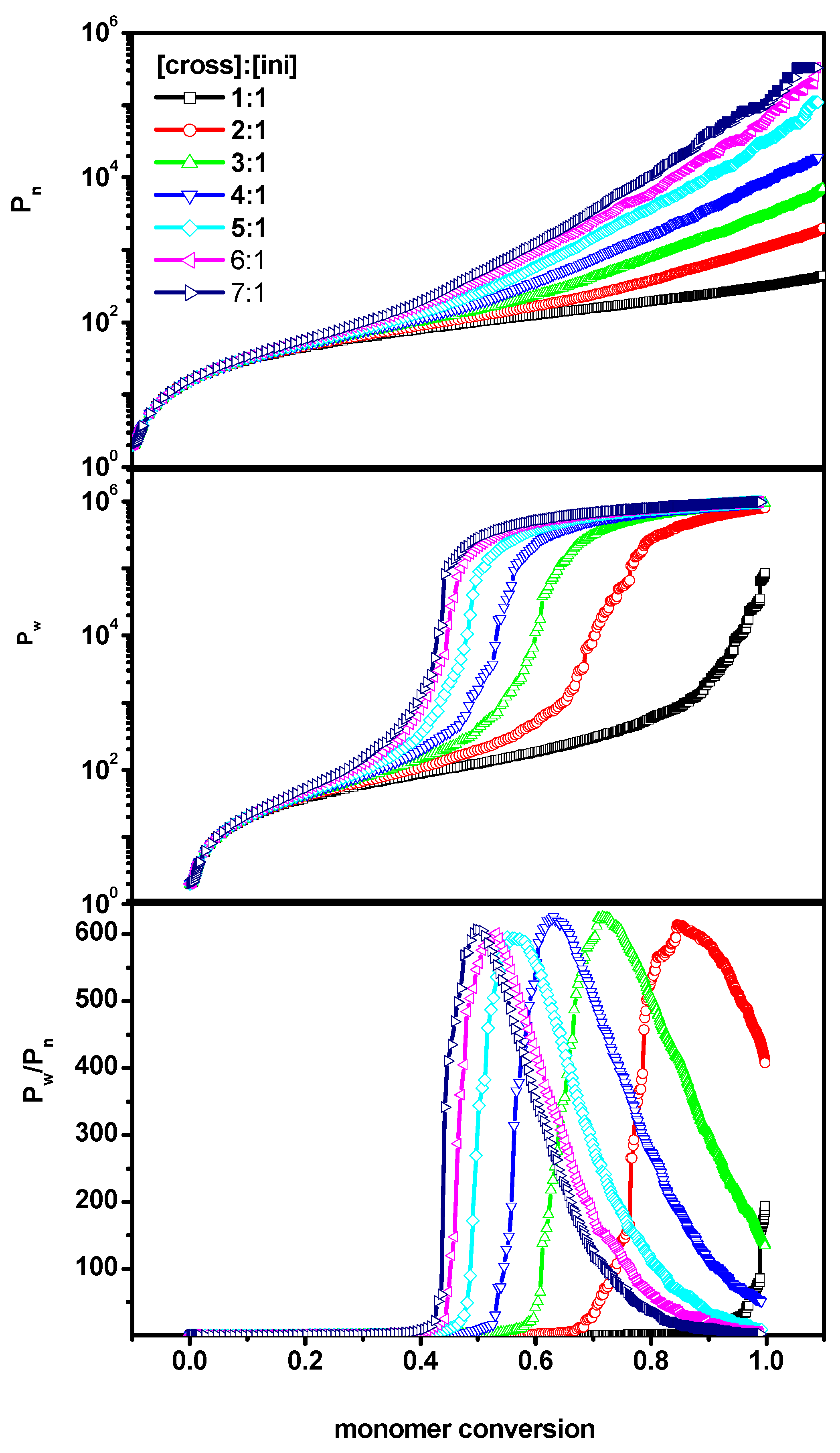
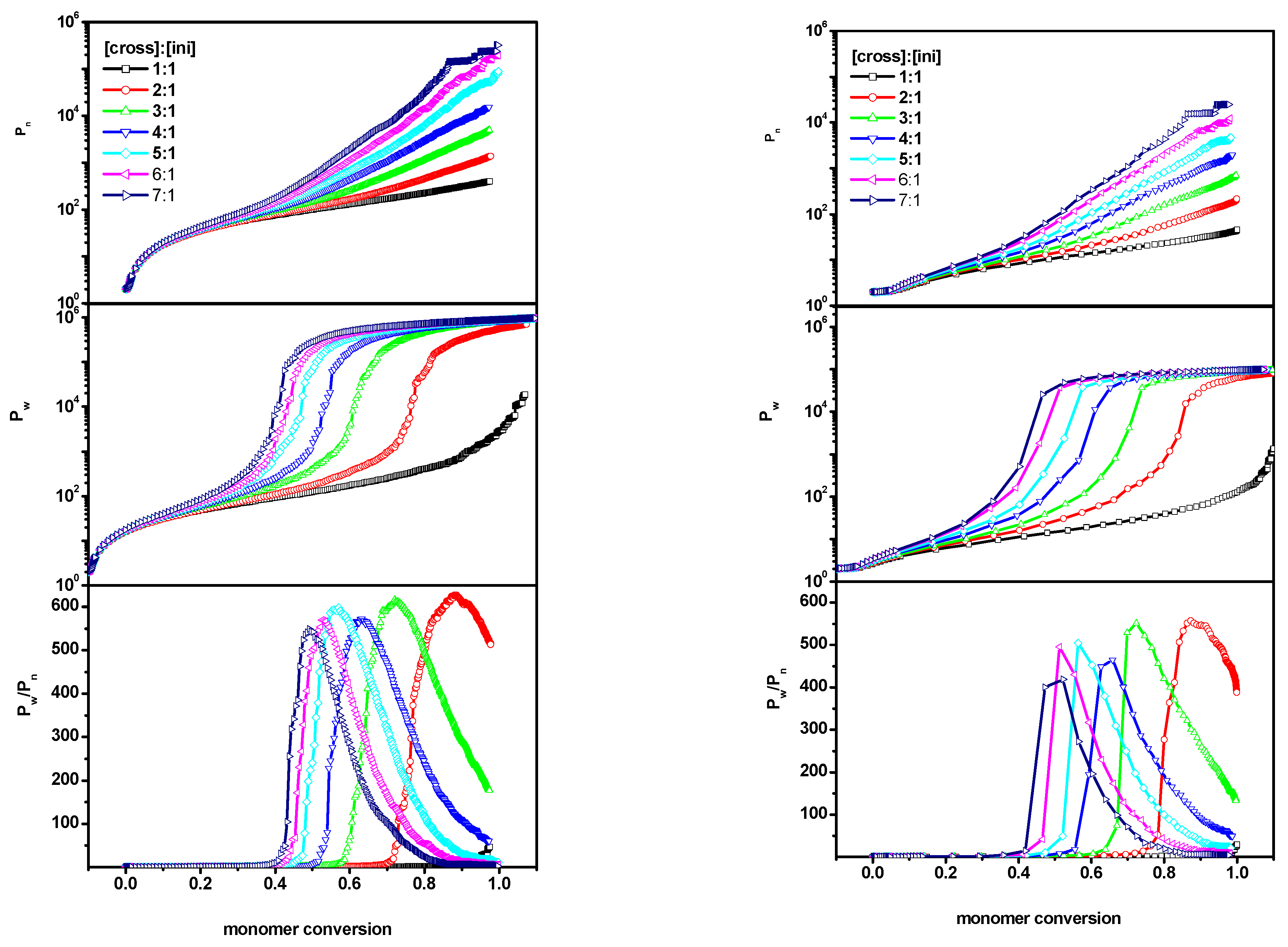
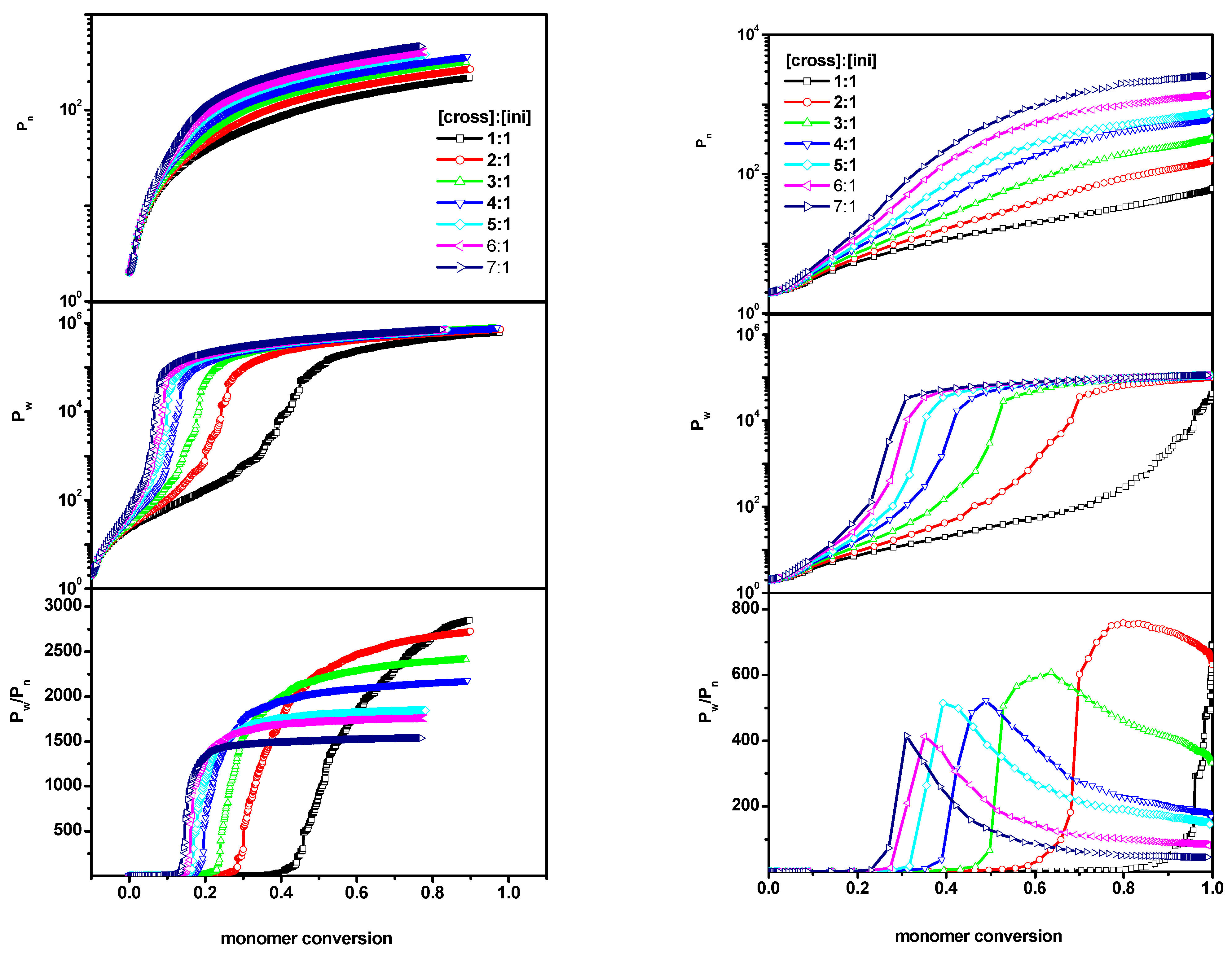
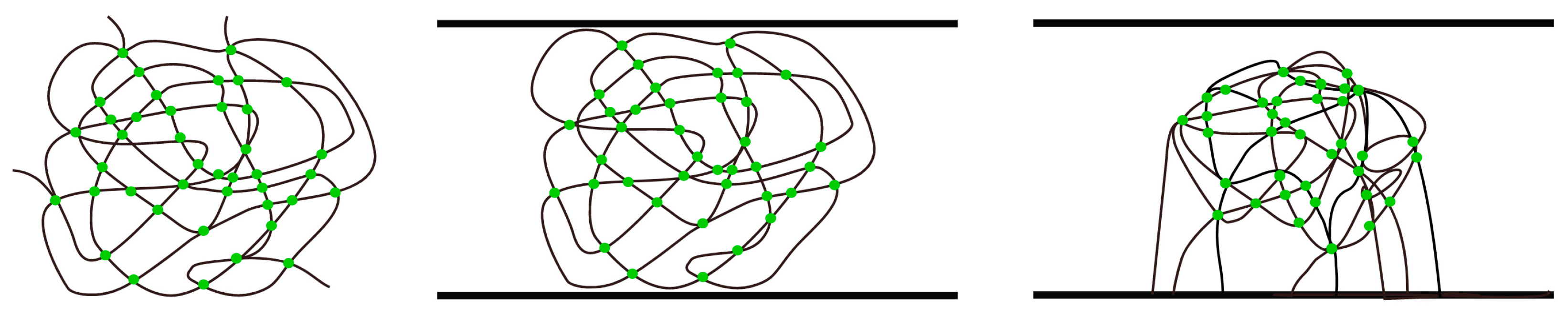
2.1. The Polymerization Process
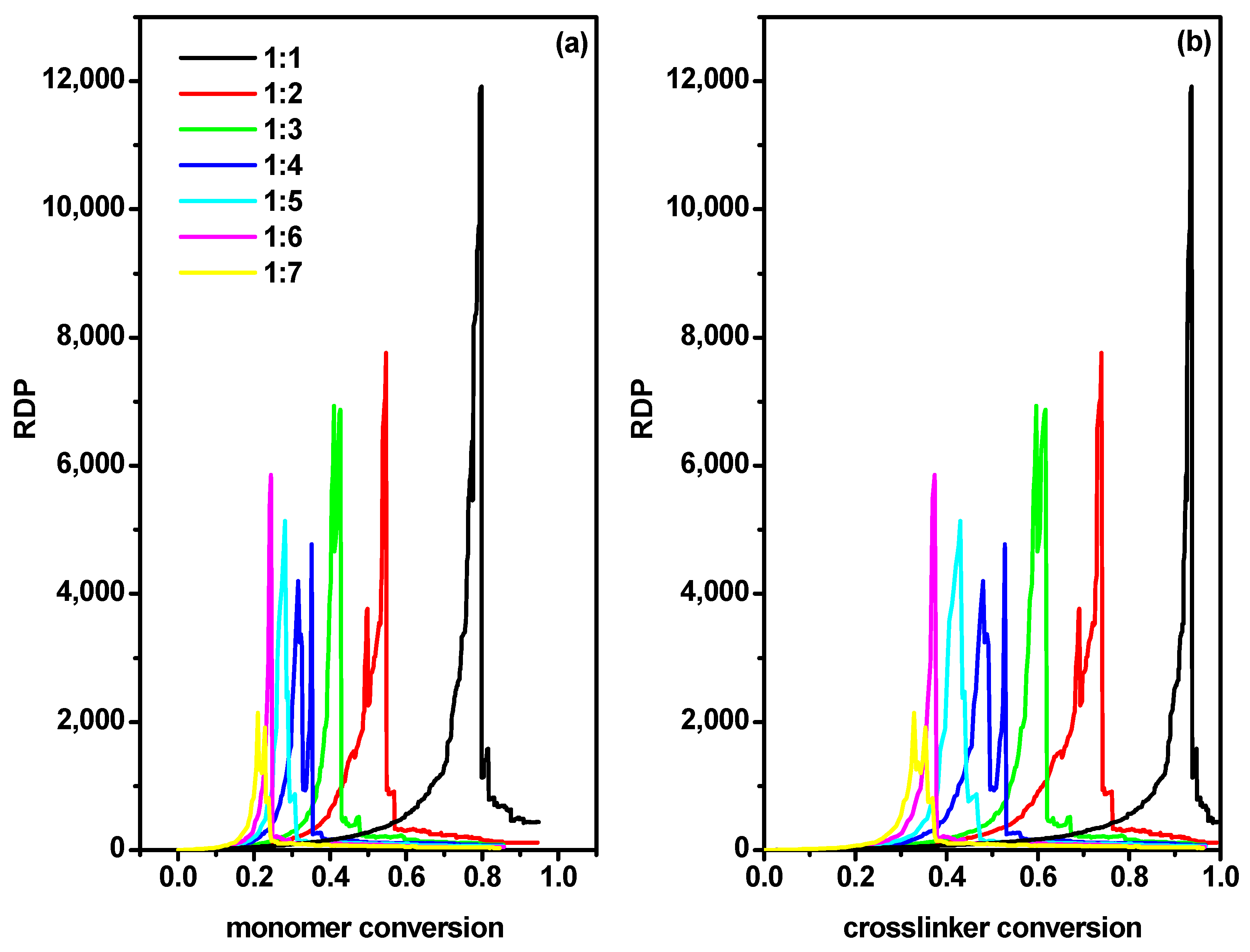
- number-average degree of polymerization of all macromolecules Pn(α) as a function of conversionwhere α is the conversion of the monomer (convM) or of the cross-linker (convX), ni represents the chain length of each polymer population (i.e., monomer is not taken into account), p(α,ni) represents the fraction of molecules of chain length ni and for each α;
- weight-average degree of polymerization Pw(α) as function of conversion
- dispersity, which is defined as .
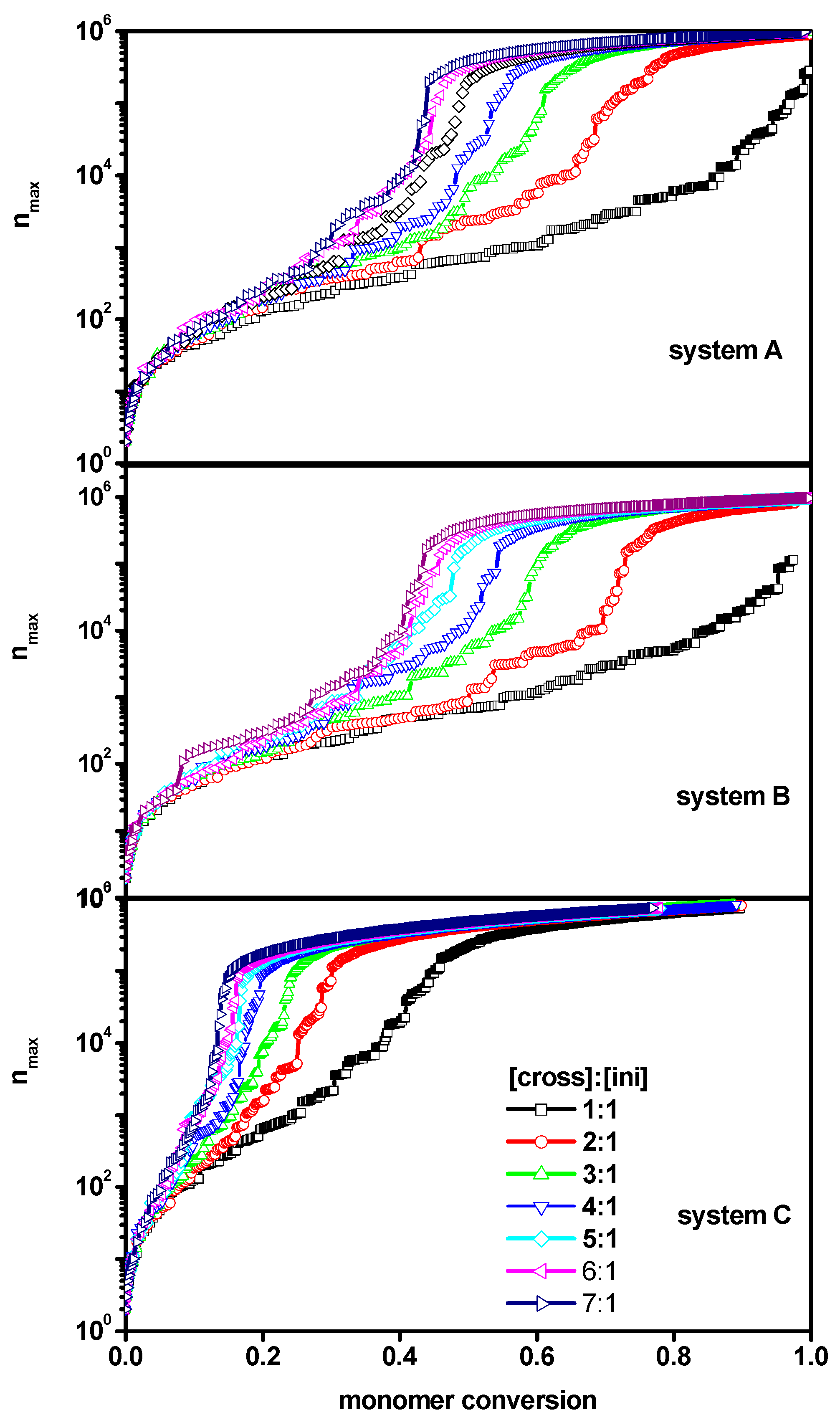
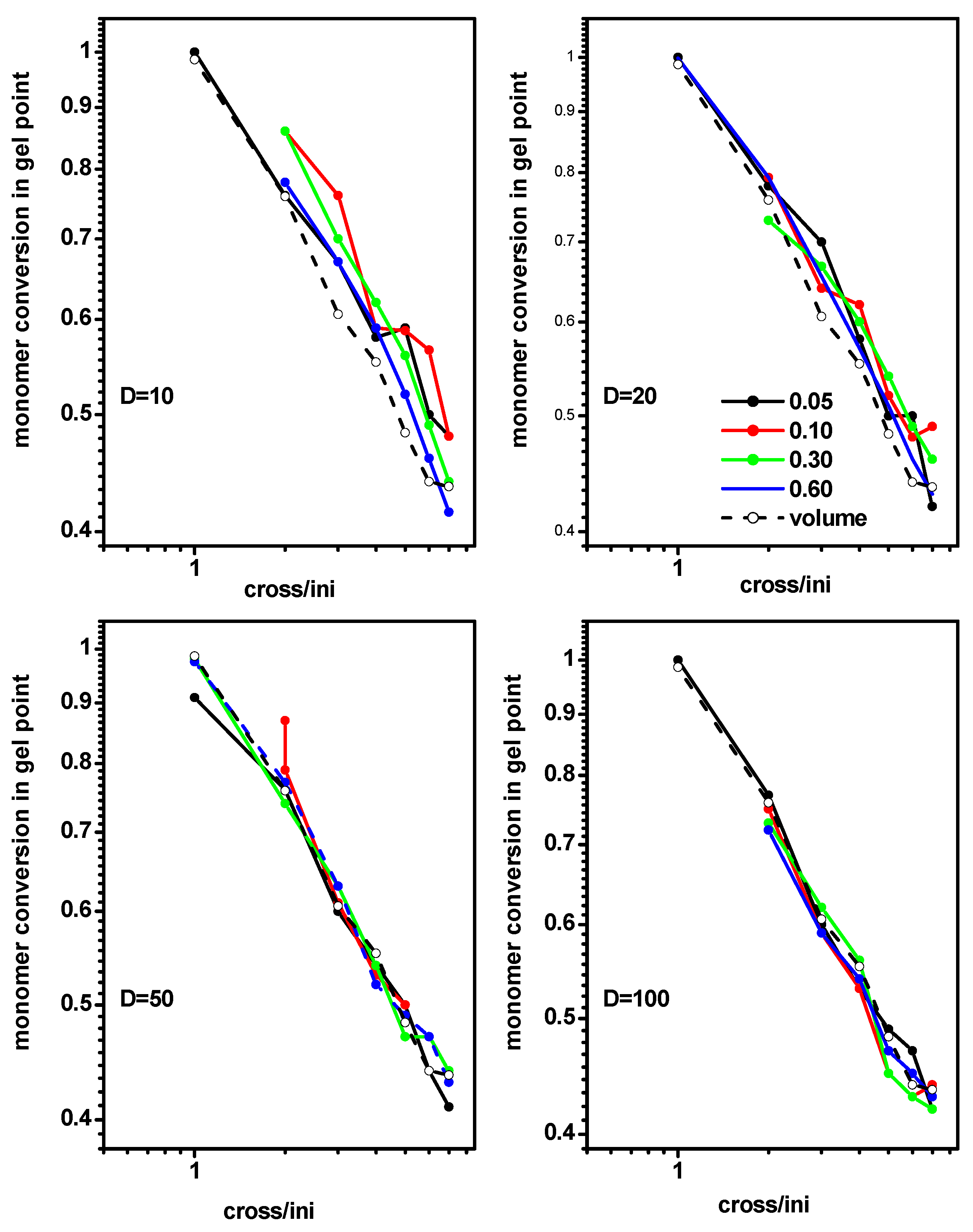
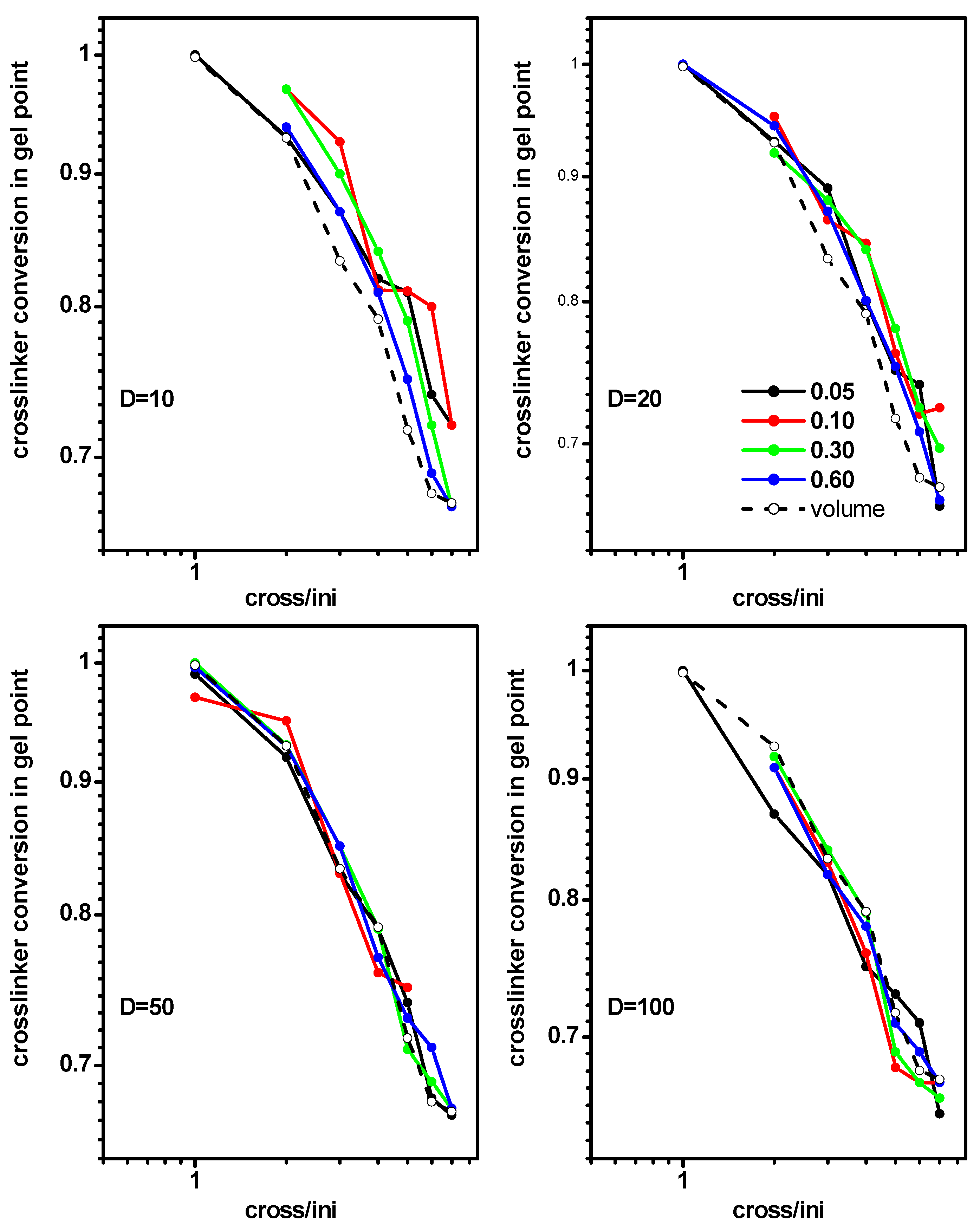
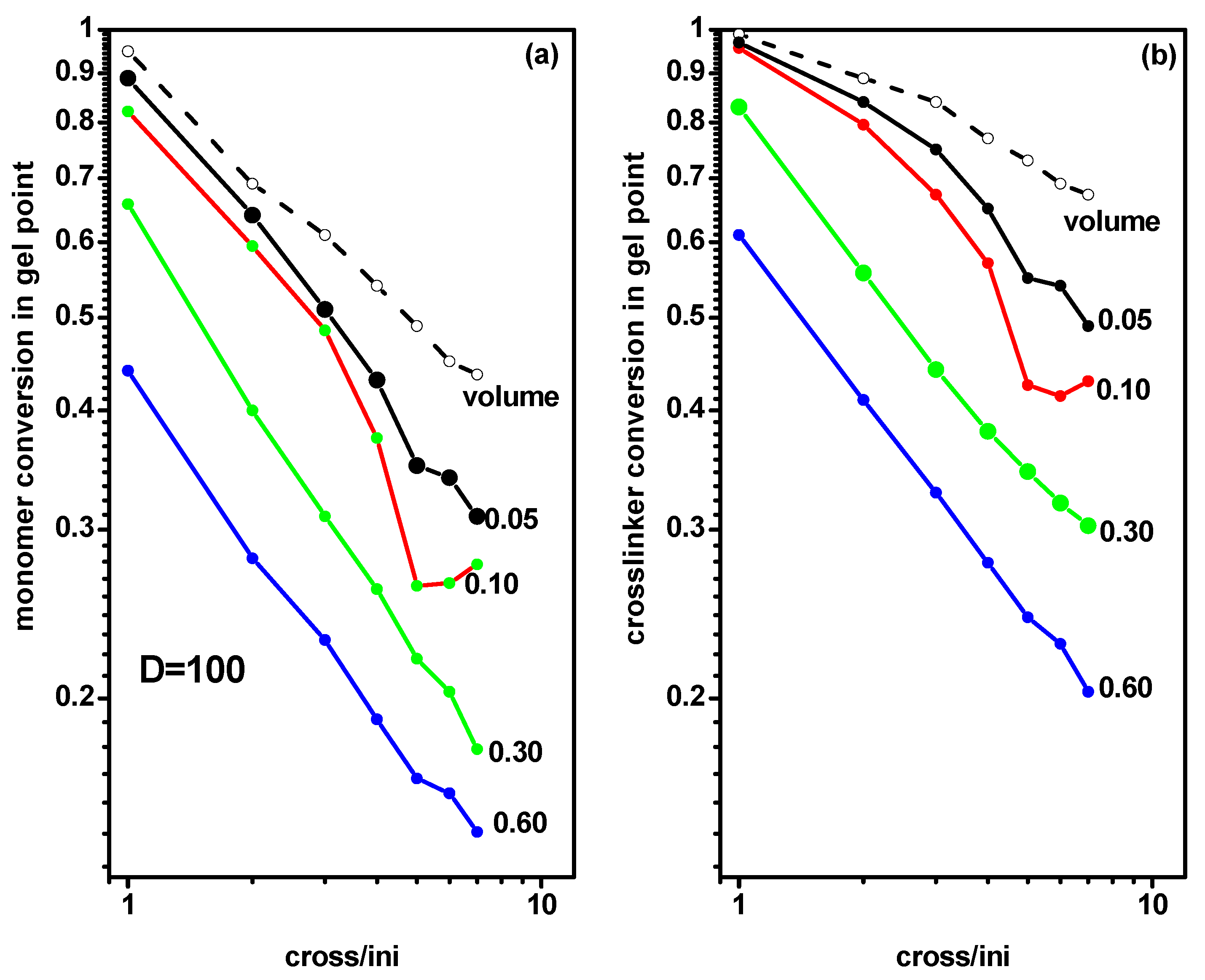
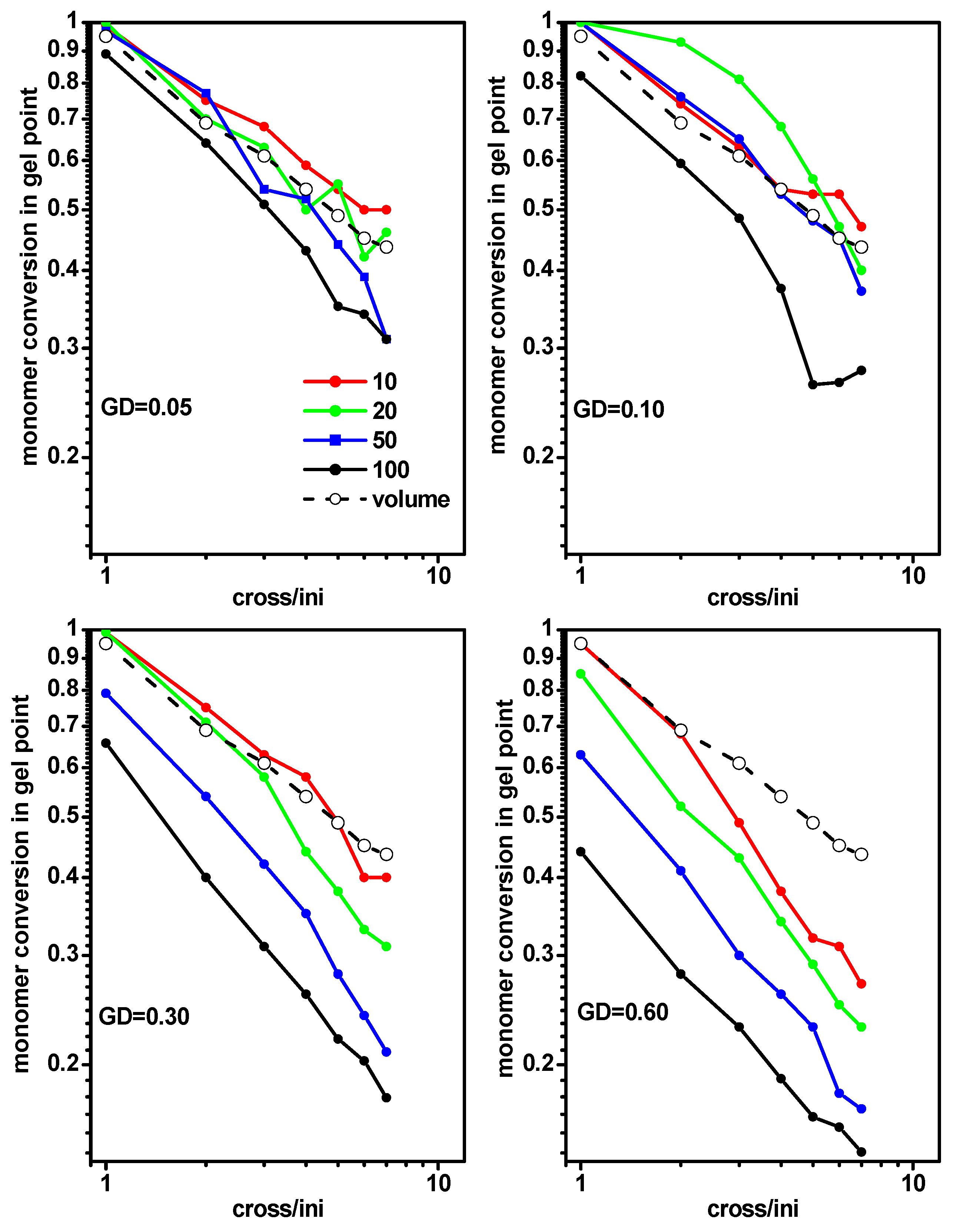
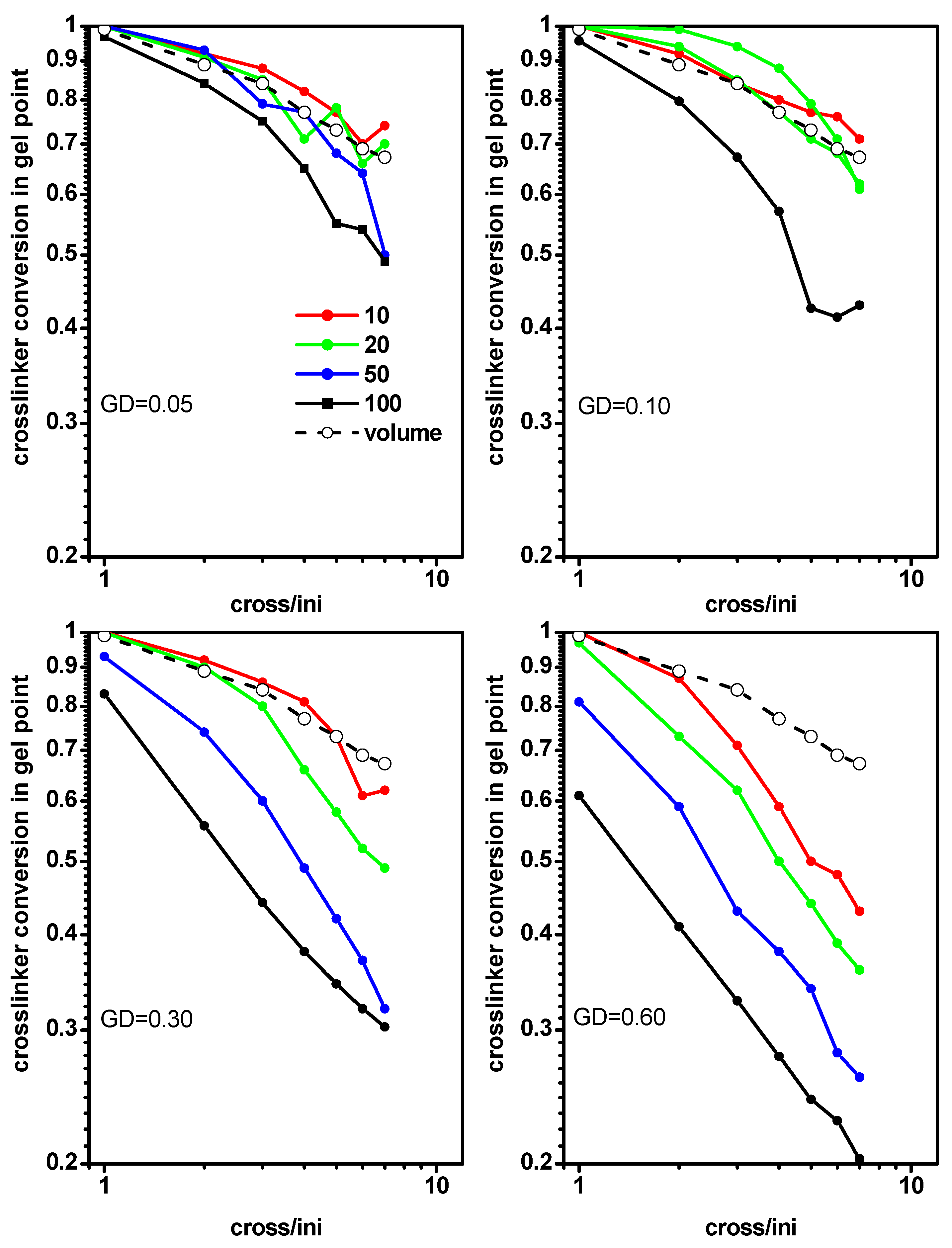
2.2. The Location of the Gel Point
3. Methods and Materials
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seo, S.E.; Hawker, C.J. The beauty of branching in polymer science. Macromolecules 2020, 53, 3257–3261. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- de Oliveira Sousa Neto, V.; Teixeira, R.N.P.; Saraiva, G.D.; do Nascimento, R.F. Polymer gels: Molecular design and practical application. In Polymer Gels. Gels Horizons: From Science to Smart Materials; Thakur, V., Thakur, M., Eds.; Springer: Singapore, 2018. [Google Scholar]
- Danielsen, S.P.O.; Beech, H.K.; Wang, S.; El-Zaatarii, B.M.; Wang, X.; Sapir, L.; Ouchi, T.; Wang, Z.; Johnson, P.N.; Hu, Y.; et al. Molecular characterization of polymer networks. Chem. Rev. 2021, 121, 5042–5092. [Google Scholar] [CrossRef]
- Gao, H.; Polanowski, P.; Matyjaszewski, K. Gelation in living copolymerization of monomer and divinyl cross linker: Comparison of ATRP experiments with Monte Carlo simulations. Macromolecules 2009, 42, 5925–5932. [Google Scholar] [CrossRef]
- Lyu, J.; Gao, Y.; Zhang, Z.; Greiser, U.; Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K.; Hongyun, T.; Wang, W. Monte Carlo simulations of Atom Transfer Radical (homo)polymerization of divinyl monomers: Applicability of Flory—Stockmayer theory. Macromolecules 2018, 51, 6673–6681. [Google Scholar] [CrossRef] [Green Version]
- Ide, N.; Fukuda, T. Nitroxide-controlled Free-Radical Copolymerization of vinyl and divinyl monomers. 2. Gelation. Macromolecules 1999, 32, 95–99. [Google Scholar] [CrossRef]
- Bannister, I.; Billingham, N.C.; Armes, S.P.; Rannard, S.P.; Findlay, P. Development of branching in living radical copolymerization of vinyl and divinyl monomers. Macromolecules 2006, 39, 7483–7492. [Google Scholar] [CrossRef]
- Yu, Q.; Zeng, F.; Zhu, S. Atom Transfer Radical Polymerization of poly(ethylene glycol) dimethacrylate. Macromolecules 2001, 34, 1612–1618. [Google Scholar] [CrossRef]
- Lyu, J.; Li, Y.; Li, Z.; Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K.; Wang, W. Modelling development in radical (co)polymerization of multivinyl monomers. Angew. Chem. Int. Ed. 2022, 62, e202212235. [Google Scholar]
- Flory, P.J. Molecular size distribution in three dimensional polymers. I. Gelation. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of molecular size distribution and gel formation in branched-chain polymers. J. Chem. Phys. 1943, 11, 45–55. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Modeling of branching and gelation in living copolymerization of monomer and divinyl cross-linker using dynamic lattice liquid model (DLL) and Flory–Stockmayer model. Polymer 2010, 51, 6084–6092. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Li, W.; Matyjaszewski, K. Effect of dilution on branching and gelation in living copolymerization ofmonomer and divinyl cross-linker: Modeling using dynamic lattice liquid model (DLL) and Flory-Stockmayer (FS) model. Polymer 2011, 52, 5092–5101. [Google Scholar] [CrossRef]
- Lang, M.; Mueller, T. Analysis of the gel point of polymer model networks by computer simulations. Macromolecules 2020, 53, 498–512. [Google Scholar] [CrossRef]
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.-J.; Li, J.-L.; Wang, R.-Y. Distinct kinetics of molecular gelation in a confined space and its relation to the structure and property of thin gel films. Phys. Chem. Chem. Phys. 2015, 17, 8258–8265. [Google Scholar] [CrossRef]
- Zhao, B.; Brittain, J.W. Polymer brushes: Surface-immobilized macromolecules. Prog. Polym. Sci. 2000, 25, 677–710. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Bockstaller, M.R.; Matyjaszewski, K. Brush-modified materials: Control of molecular architecture, assembly behavior, properties and applications. Prog. Polym. Sci. 2020, 100, 101180. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Elliot, I.G.; Kuhl, T.L.; Faller, R. Molecular simulation study of the structure of high density polymer brushes in good solvent. Macromolecules 2010, 43, 9131–9138. [Google Scholar] [CrossRef]
- Reith, D.; Milchev, A.; Virnau, P.; Binder, K. Computer simulation studies of chain dynamics in polymer brushes. Macromolecules 2012, 45, 4381–4393. [Google Scholar] [CrossRef]
- Pakula, T.; Zhulina, E.B. Computer simulations of polymers in thin layers. II. Structure of polymer melt layers consisting of end-to-end grafted chains. J. Chem. Phys. 1991, 95, 4691–4697. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers—A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of polymer brushes near the theta point—A Monte Carlo simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Pakula, T. Structure of dense polymer layers between end-grafting and end-adsorbing walls. Macromolecules 1992, 25, 754–758. [Google Scholar] [CrossRef]
- Huang, J.; Jiang, W.; Han, S. Dynamic Monte Carlo simulation on the polymer chain with one end grafted on a flat surface. Macromol. Theory Simul. 2001, 10, 339–342. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of controlled radical polymerization: Effect of chain confinement due to initiator grafting density and solvent quality in “grafting from” method. Macromolecules 2010, 43, 9567–9577. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of concurrent bulk- and surface initiated living polymerization. Macromolecules 2012, 45, 2128–2137. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Some dynamic properties of grafted polymer layers. Colloid. Surfaces A 1994, 86, 85–89. [Google Scholar] [CrossRef]
- Netz, R.R.; Schick, M. Polymer brushes: From self-consistent field theory to classical theory. Macromolecules 1998, 31, 5105–5122. [Google Scholar] [CrossRef]
- Milchev, A.; Wittmer, J.P.; Landau, D.P. Formation and equilibrium properties of living polymer brushes. J. Chem. Phys. 2000, 112, 1606–1615. [Google Scholar] [CrossRef] [Green Version]
- Binder, K. Scaling concepts for polymer brushes and their test with computer simulation. Eur. Phys. J. E 2002, 9, 293–298. [Google Scholar] [CrossRef]
- Sim, X.M.; Wang, C.-G.; Liu, X.; Goto, A. Multistimuli responsive reversible cross-linking-decross-linking of concentrated polymer brushes. ACS Appl. Mater. Interfaces 2020, 12, 28711–28719. [Google Scholar] [CrossRef]
- Hoffmann, M.; Lang, M.; Sommer, J.-U. Gelation threshold of cross-linked polymer brushes. Phys. Rev. E 2011, 83, 021803. [Google Scholar] [CrossRef]
- Singh, M.; Kang, C.; Ilg, P.; Crockett, R.; Kröger, M. Combined experimental and simulation studies of cross-linked polymer brushes under shear. Macromolecules 2018, 51, 10174–10183. [Google Scholar] [CrossRef]
- Dehghani, E.S.; Spencer, N.D.; Ramakrishna, S.N.; Benetti, E.M. Crosslinking polymer brushes with ethylene glycol-containing segments: Influence on physicochemical and antifouling properties. Langmuir 2016, 32, 10317–10327. [Google Scholar] [CrossRef]
- Huang, W.; Baker, G.L.; Bruening, M.L. Controlled synthesis of cross-linked ultrathin polymer films by using surface-initiated Atom Transfer Radical Polymerization. Angew. Chem. Int. Ed. 2001, 40, 1510–1512. [Google Scholar] [CrossRef]
- Dehghani, E.; Ramakrishna, S.; Spencer, N.; Benetti, E. Controlled crosslinking is a tool to precisely modulate the nanomechanical and anotribological properties of polymer brushes. Macromolecules 2017, 50, 2932–2941. [Google Scholar] [CrossRef]
- Pakula, T. Simulation on the completely occupied lattices. In Simulation Methods for Polymers; Kotelyanskii, M., Theodorou, D.N., Eds.; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 2004. [Google Scholar]
- Polanowski, P.; Jeszka, J.K.; Krysiak, K.; Matyjaszewski, K. Influence of intramolecular crosslinking on gelation in living copolymerization of monomer and divinyl cross-linker. Monte Carlo simulation studies. Polymer 2015, 79, 171–178. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP—Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Polymerization and structure of opposing polymer brushes. Polymers 2021, 13, 4294. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Sikorski, A. Star polymers vs. dendrimers—Studies on the synthesis based on computer simulations. Polymers 2022, 14, 2522. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Synthesis of star polymers by “core-first” one-pot method via ATRP: Monte Carlo simulations. Polymer 2014, 55, 2552–2561. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Sikorski, A. Dendrimers vs. hyperbranched polymers: Studies of the polymerization process based on Monte Carlo simulations. Comput. Methods Sci. Technol. 2022, 28, 109–117. [Google Scholar]
- Rolińska, K.; Mazurek-Budzyńska, M.; Parzuchowski, P.G.; Wołosz, D.; Balk, M.; Gorący, K.; El Fray, M.; Polanowski, P.; Sikorski, A. Polymerization of polyurethanes as shape memory polymers. Int. J. Mol. Sci. 2022, 23, 7064. [Google Scholar] [CrossRef]
- Hoshen, J.; Kopelman, R. Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm. Phys. Rev. B 1976, 14, 3438–3445. [Google Scholar] [CrossRef]
- Gao, H.; Min, K.; Matyjaszewski, K. Determination of gel point during Atom Transfer Radical Copolymerization with cross-linker. Macromolecules 2007, 40, 7763–7770. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Star polymer synthesis and gelation in ATRP copolymerization: Monte Carlo simulations. Polymer 2013, 53, 1979–1986. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of polymer conformation and dynamics in two dimensions using simulations based on the Dynamic Lattice Liquid (DLL) model. J. Chem. Phys. 2002, 117, 4022–4029. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Simulation of polymer–polymer interdiffusion using the dynamic lattice liquid model. J. Chem. Phys. 2004, 120, 6306–6311. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polanowski, P.; Sikorski, A. The Influence of Constraints on Gelation in a Controlling/Living Copolymerization Process. Int. J. Mol. Sci. 2023, 24, 2701. https://doi.org/10.3390/ijms24032701
Polanowski P, Sikorski A. The Influence of Constraints on Gelation in a Controlling/Living Copolymerization Process. International Journal of Molecular Sciences. 2023; 24(3):2701. https://doi.org/10.3390/ijms24032701
Chicago/Turabian StylePolanowski, Piotr, and Andrzej Sikorski. 2023. "The Influence of Constraints on Gelation in a Controlling/Living Copolymerization Process" International Journal of Molecular Sciences 24, no. 3: 2701. https://doi.org/10.3390/ijms24032701
APA StylePolanowski, P., & Sikorski, A. (2023). The Influence of Constraints on Gelation in a Controlling/Living Copolymerization Process. International Journal of Molecular Sciences, 24(3), 2701. https://doi.org/10.3390/ijms24032701





