Thermochemistry, Tautomerism, and Thermal Stability of 5,7-Dinitrobenzotriazoles
Abstract
1. Introduction
2. Results and Discussion
2.1. Thermal Behaviour of DBT under Atmospheric Pressure
2.2. Thermal Kinetics of DBT under Elevated Pressure
2.3. Theoretical Calculations
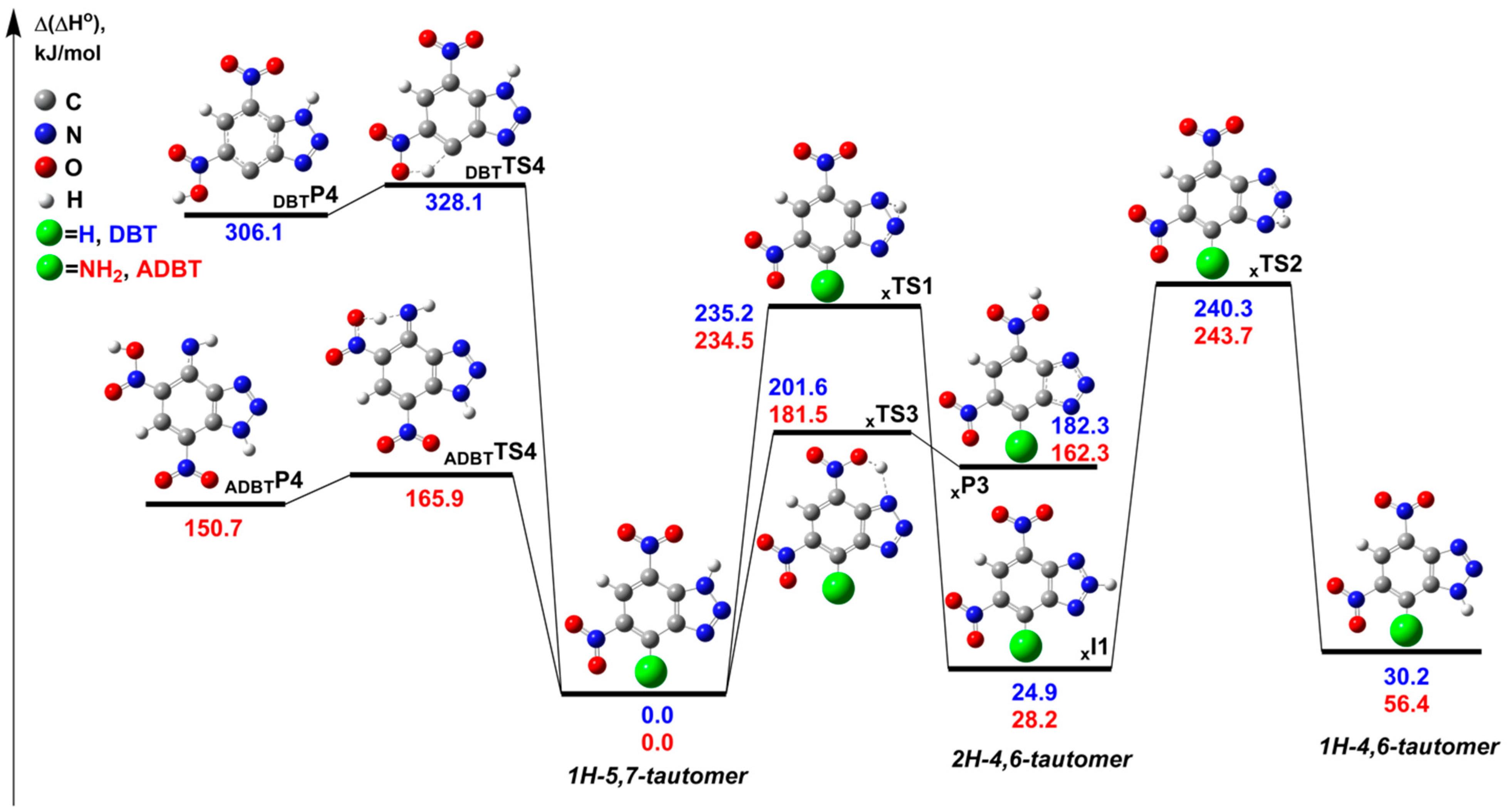
2.3.1. Mutual Interconversions of DBT and ADBT Tautomers
2.3.2. Mechanisms of the Primary Decomposition Reactions of DBT and ADBT
2.3.3. Thermochemistry of the Compounds Studied
3. Methods and Materials
3.1. Materials
3.2. Thermoanalytical Experiments
3.3. Quantum Chemical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katritzky, A.R.; Rachwal, S. Synthesis of Heterocycles Mediated by Benzotriazole. 1. Monocyclic Systems. Chem. Rev. 2010, 110, 1564–1610. [Google Scholar] [CrossRef]
- Larina, L.; Lopyrev, V. Nitroazoles: Synthesis, Structure and Applications; Springer: New York, NY, USA, 2009; p. 441. ISBN 978-0-387-98069-0. [Google Scholar]
- Briguglio, I.; Piras, S.; Corona, P.; Gavini, E.; Nieddu, M.; Boatto, G.; Carta, A. Benzotriazole: An Overview on Its Versatile Biological Behavior. Eur. J. Med. Chem. 2015, 97, 612–648. [Google Scholar] [CrossRef]
- Lv, M.; Ma, J.; Li, Q.; Xu, H. Discovery of Benzotriazole-Azo-Phenol/Aniline Derivatives as Antifungal Agents. Bioorganic Med. Chem. Lett. 2018, 28, 181–187. [Google Scholar] [CrossRef]
- Loddo, R.; Novelli, F.; Sparatore, A.; Tasso, B.; Tonelli, M.; Boido, V.; Sparatore, F.; Collu, G.; Delogu, I.; Giliberti, G.; et al. Antiviral Activity of Benzotriazole Derivatives. 5-[4-(Benzotriazol-2-Yl)Phenoxy]-2,2-Dimethylpentanoic Acids Potently and Selectively Inhibit Coxsackie Virus B5. Bioorganic Med. Chem. 2015, 23, 7024–7034. [Google Scholar] [CrossRef]
- Finšgar, M.; Milošev, I. Inhibition of Copper Corrosion by 1,2,3-Benzotriazole: A Review. Corros. Sci. 2010, 52, 2737–2749. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Wu, H.; Zhao, T.; Qian, L. 5-Methyl-1H-Benzotriazole as an Effective Corrosion Inhibitor for Ultra-Precision Chemical Mechanical Polishing of Bearing Steel. J. Electrochem. Soc. 2020, 167, 131502. [Google Scholar] [CrossRef]
- Wazzan, N.; Obot, I.B.; Fagieh, T.M. The Role of Some Triazoles on the Corrosion Inhibition of C1020 Steel and Copper in a Desalination Descaling Solution. Desalination 2022, 527, 115551. [Google Scholar] [CrossRef]
- Srinivas, D.; Ghule, V.D.; Tewari, S.P.; Muralidharan, K. Synthesis of Amino, Azido, Nitro, and Nitrogen-Rich Azole-Substituted Derivatives of 1 H -Benzotriazole for High-Energy Materials Applications. Chem. Eur. J. 2012, 18, 15031–15037. [Google Scholar] [CrossRef] [PubMed]
- Klapötke, T.M.; Pflüger, C.; Reintinger, M.W. Energetic Materials Based on 5,7-Dinitrobenzotriazole and 4,6-Dinitrobenzotriazol-3-ium 1-Oxide Derivatives. Eur. J. Inorg. Chem. 2016, 2016, 138–147. [Google Scholar] [CrossRef]
- Cai, Y.-H. Synthesis, Morphology and Theoretical Calculation of 1H-Benzotriazole Aceto-Hydrazide. JOCPR 2014, 6, 673–678. [Google Scholar]
- Nietzki, R.; Hagenbach, H. Die Reduction Des Pikramids. Berichte Dtsch. Chem. Ges. 1897, 30, 539–545. [Google Scholar] [CrossRef]
- Coburn, M.D. Nitro Derivatives of 1-Picrylbenzotriazole. J. Heterocycl. Chem. 1973, 10, 743–746. [Google Scholar] [CrossRef]
- Altmann, K.L.; Chafin, A.P.; Merwin, L.H.; Wilson, W.S.; Gilardi, R. Chemistry of Tetraazapentalenes. J. Org. Chem. 1998, 63, 3352–3356. [Google Scholar] [CrossRef]
- Graham, D.J.; McHugh, C.R.; Tackley, D. Controlled Synthesis of Electron Deficient Nitro-1H-Benzotriazoles. Heterocycles 2002, 57, 1461. [Google Scholar] [CrossRef]
- Ehlers, D.; Klapötke, T.M.; Pflüger, C. Investigations of the Vicarious C-Aminations of 5,7-Dinitrobenzotriazole and 4,6-Dinitrobenzotriazol-3-Ium-1-Oxide and Their Energetic Properties. Chem. Eur. J. 2015, 21, 16073–16082. [Google Scholar] [CrossRef] [PubMed]
- Burgess, E.M.; Carithers, R.; McCullagh, L. Photochemical Decomposition of 1H-1,2,3-Triazole Derivatives. J. Am. Chem. Soc. 1968, 90, 1923–1924. [Google Scholar] [CrossRef]
- Bégué, D.; Santos-Silva, H.; Dargelos, A.; Wentrup, C. Iminocyclohexadienylidenes: Carbenes or Diradicals? The Hetero-Wolff Rearrangement of Benzotriazoles to Cyanocyclopentadienes and 1 H-Benzo[b]Azirines. J. Phys. Chem. A 2017, 121, 5998–6003. [Google Scholar] [CrossRef] [PubMed]
- Wentrup, C.; Freiermuth, B.; Aylward, N. Pyrolysis of Benzotriazoles. 1-Acyl- and 1-Alkoxycarbonylbenzotriazoles: Hetero-Wolff Rearrangement to N-Acyl- and N-Alkoxycarbonyl-Fulvenimines and Free Radical Routes to Cyanocyclopentadienes. J. Anal. Appl. Pyrolysis 2017, 128, 187–195. [Google Scholar] [CrossRef]
- Marchais, J.; Bégué, D.; Dargelos, A.; Wentrup, C. Benzotriazoles and Triazoloquinones: Rearrangements to Carbazoles, Benzazirines, Azepinediones, and Fulvenimines. J. Org. Chem. 2021, 86, 16992–17001. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, I.N.; Kiselev, V.G.; Bastrakov, M.A.; Dalinger, I.L.; Pivkina, A.N. Thermal Stability of Energetic 6,8-Dinitrotriazolo [1,5-a]Pyridines: Interplay of Thermal Analysis and Quantitative Quantum Chemical Calculations. Thermochim. Acta 2022, 717, 179342. [Google Scholar] [CrossRef]
- Matveev, V.G.; Dubikhin, V.V.; Nazin, G.B. Radical Gas-Phase Decomposition of Nitrobenzene Derivatives. Russ. Chem. Bull. 1978, 27, 675–678. [Google Scholar] [CrossRef]
- Gonzalez, A.C.; Larson, C.W.; McMillen, D.F.; Golden, D.M. Mechanism of Decomposition of Nitroaromatics. Laser-Powered Homogeneous Pyrolysis of Substituted Nitrobenzenes. J. Phys. Chem. 1985, 89, 4809–4814. [Google Scholar] [CrossRef]
- Shao, J.; Cheng, X.; Yang, X. Density Functional Calculations of Bond Dissociation Energies for Removal of the Nitrogen Dioxide Moiety in Some Nitroaromatic Molecules. J. Mol. Struct. THEOCHEM 2005, 755, 127–130. [Google Scholar] [CrossRef]
- Wu, C.J.; Fried, L.E. Ring Closure Mediated by Intramolecular Hydrogen Transfer in the Decomposition of a Push−Pull Nitroaromatic: TATB. J. Phys. Chem. A 2000, 104, 6447–6452. [Google Scholar] [CrossRef]
- Tsyshevsky, R.; Sharia, O.; Kuklja, M. Molecular Theory of Detonation Initiation: Insight from First Principles Modeling of the Decomposition Mechanisms of Organic Nitro Energetic Materials. Molecules 2016, 21, 236. [Google Scholar] [CrossRef]
- da Silva, G.; Bozzelli, J.W. Retro-[3 + 2]-Cycloaddition Reactions in the Decomposition of Five-Membered Nitrogen-Containing Heterocycles. J. Org. Chem. 2008, 73, 1343–1353. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Zhou, P.; Yang, Y.; Liu, J.; Jin, B.; Han, K. Thermochemistry and Initial Decomposition Pathways of Triazole Energetic Materials. J. Phys. Chem. A 2020, 124, 2951–2960. [Google Scholar] [CrossRef] [PubMed]
- Minkin, V.I.; Garnovskii, A.D.; Elguero, J.; Katritzky, A.R.; Denisko, O.V. The Tautomerism of Heterocycles: Five-Membered Rings with Two or More Heteroatoms. In Advances in Heterocyclic Chemistry; Elsevier: Amsterdam, The Netherlands, 2000; Volume 76, pp. 157–323. ISBN 978-0-12-020776-3. [Google Scholar]
- Larina, L.I. Tautomerism and Structure of Azoles. In Advances in Heterocyclic Chemistry; Elsevier: Amsterdam, The Netherlands, 2018; Volume 124, pp. 233–321. ISBN 978-0-12-813760-4. [Google Scholar]
- Quesada-Moreno, M.M.; Avilés-Moreno, J.R.; López-González, J.J.; Zúñiga, F.J.; María, D.S.; Claramunt, R.M.; Reviriego, F.; Alkorta, I.; Elguero, J. The Synergy of Different Solid-State Techniques to Elucidate the Supramolecular Assembly of Two 1 H -Benzotriazole Polymorphs. Phys. Chem. Chem. Phys. 2019, 21, 19879–19889. [Google Scholar] [CrossRef] [PubMed]
- Santa María, D.; Claramunt, R.M.; Torralba, M.C.; Torres, M.R.; Alkorta, I.; Elguero, J. The Structure and Properties of 5,6-Dinitro-1H-Benzotriazole. J. Mol. Struct. 2016, 1113, 153–161. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Monogarov, K.A.; Bragin, A.A.; Fomenkov, I.V.; Pivkina, A.N. HP-DSC Study of Energetic Materials. Part I. Overview of Pressure Influence on Thermal Behavior. Thermochim. Acta 2016, 631, 1–7. [Google Scholar] [CrossRef]
- Gorn, M.V.; Monogarov, K.A.; Dalinger, I.L.; Melnikov, I.N.; Kiselev, V.G.; Muravyev, N.V. Pressure DSC for Energetic Materials. Part 2. Switching between Evaporation and Thermal Decomposition of 3,5-Dinitropyrazole. Thermochim. Acta 2020, 690, 178697. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee Recommendations for Performing Kinetic Computations on Thermal Analysis Data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Manelis, G.B.; Nazin, G.M.; Rubtsov, Y.I.; Strunin, V.A. Thermal Decomposition and Combustion of Explosives and Propellants; Taylor & Francis: London, UK, 2003; p. 376. ISBN 9780415299848. [Google Scholar]
- Shakhova, M.V.; Muravyev, N.V.; Gritsan, N.P.; Kiselev, V.G. Thermochemistry, Tautomerism, and Thermal Decomposition of 1,5-Diaminotetrazole: A High-Level Ab Initio Study. J. Phys. Chem. A 2018, 122, 3939–3949. [Google Scholar] [CrossRef] [PubMed]
- Muravyev, N.V.; Gorn, M.V.; Melnikov, I.N.; Monogarov, K.A.; Korsunskii, B.L.; Dalinger, I.L.; Pivkina, A.N.; Kiselev, V.G. Autocatalytic Decomposition of Energetic Materials: Interplay of Theory and Thermal Analysis in the Study of 5-Amino-3,4-Dinitropyrazole Thermolysis. Phys. Chem. Chem. Phys. 2022, 24, 16325–16342. [Google Scholar] [CrossRef]
- Wiik, K.; Høyvik, I.-M.; Unneberg, E.; Jensen, T.L.; Swang, O. Unimolecular Decomposition Reactions of Picric Acid and Its Methylated Derivatives─A DFT Study. J. Phys. Chem. A 2022, 126, 2645–2657. [Google Scholar] [CrossRef]
- Brill, T.B.; James, K.J. Kinetics and Mechanisms of Thermal Decomposition of Nitroaromatic Explosives. Chem. Rev. 1993, 93, 2667–2692. [Google Scholar] [CrossRef]
- Nazin, G.M.; Manelis, G.B. Thermal Decomposition of Aliphatic Nitro-Compounds. Russ. Chem. Rev. 1994, 63, 313–322. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Monogarov, K.A.; Melnikov, I.N.; Pivkina, A.N.; Kiselev, V.G. Learning to Fly: Thermochemistry of Energetic Materials by Modified Thermogravimetric Analysis and Highly Accurate Quantum Chemical Calculations. Phys. Chem. Chem. Phys. 2021, 23, 15522–15542. [Google Scholar] [CrossRef] [PubMed]
- Starosotnikov, A.M.; Bastrakov, M.A.; Knyazev, D.A.; Fedyanin, I.V.; Kachala, V.V.; Dalinger, I.L. Synthesis of N-Bridged 6,8-Dinitrotriazolo [1,5-a]Pyridines. ChemistrySelect 2019, 4, 1510–1515. [Google Scholar] [CrossRef]
- Bastrakov, M.A.; Starosotnikov, A.M.; Fedyanin, I.V.; Dalinger, I.L. Synthesis of New 2-Substituted 6,8-Dinitro [1,2,4]Triazolo [1,5-a]Pyridines. Chem. Heterocycl. Compd. 2021, 57, 95–98. [Google Scholar] [CrossRef]
- ASTM. ASTM E698-05 Standard Test Method for Arrhenius Kinetic Constants for Thermally Unstable Materials; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry. Application to a Phenolic Plastic. J. Polym. Sci. Part C Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Melnikov, I.N.; Monogarov, K.A.; Kuchurov, I.V.; Pivkina, A.N. The Power of Model-Fitting Kinetic Analysis Applied to Complex Thermal Decomposition of Explosives: Reconciling the Kinetics of Bicyclo-HMX Thermolysis in Solid State and Solution. J. Therm. Anal. Calorim. 2021, 147, 3195–3206. [Google Scholar] [CrossRef]
- Burnham, A.K.; Zhou, X.; Broadbelt, L.J. Critical Review of the Global Chemical Kinetics of Cellulose Thermal Decomposition. Energy Fuels 2015, 29, 2906–2918. [Google Scholar] [CrossRef]
- Muravyev, N.V. THINKS—Free Open-Source Thermokinetic Software; 2016. Available online: http://Thinks.Chemphys.Ru/ (accessed on 9 February 2023).
- Koga, N.; Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Muravyev, N.V.; Perez-Maqueda, L.A.; Saggese, C.; Sánchez-Jiménez, P.E. ICTAC Kinetics Committee Recommendations for Analysis of Thermal Decomposition Kinetics. Thermochim. Acta 2022, 719, 179384. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO; Version 2010.1; a Package of Ab Initio Programs; Molpro: Cardiff, UK, 2010. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Hratchian, H.P.; Schlegel, H.B. Accurate Reaction Paths Using a Hessian Based Predictor–Corrector Integrator. J. Chem. Phys. 2004, 120, 9918–9924. [Google Scholar] [CrossRef]
- Liakos, D.G.; Sparta, M.; Kesharwani, M.K.; Martin, J.M.L.; Neese, F. Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. [Google Scholar] [CrossRef]
- Kiselev, V.G.; Goldsmith, C.F. Accurate Thermochemistry of Novel Energetic Fused Tricyclic 1,2,3,4-Tetrazine Nitro Derivatives from Local Coupled Cluster Methods. J. Phys. Chem. A 2019, 123, 9818–9827. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, V.G.; Goldsmith, C.F. Accurate Prediction of Bond Dissociation Energies and Barrier Heights for High-Energy Caged Nitro and Nitroamino Compounds Using a Coupled Cluster Theory. J. Phys. Chem. A 2019, 123, 4883–4890. [Google Scholar] [CrossRef] [PubMed]
- Kossmann, S.; Neese, F. Comparison of Two Efficient Approximate Hartee–Fock Approaches. Chem. Phys. Lett. 2009, 481, 240–243. [Google Scholar] [CrossRef]
- Lee, T.J.; Taylor, P.R. A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods. Int. J. Quantum Chem. 2009, 36, 199–207. [Google Scholar] [CrossRef]
- Pechukas, P.; Light, J.C. On Detailed Balancing and Statistical Theories of Chemical Kinetics. J. Chem. Phys. 1965, 42, 3281–3291. [Google Scholar] [CrossRef]
- Pechukas, P.; Light, J.C.; Rankin, C. Statistical Theory of Chemical Kinetics: Application to Neutral-Atom—Molecule Reactions. J. Chem. Phys. 1966, 44, 794–805. [Google Scholar] [CrossRef]
- Georgievski, Y.; Miller, J.A.; Burke, M.P.; Klippenstein, S.J. Reformulation and Solution of the Master Equation for Multiple-Well Chemical Reactions. J. Phys. Chem. A. 2013, 117, 12146–12154. [Google Scholar] [CrossRef]
- Chen, X.; Goldsmith, F.C. Predictive kinetics for the thermal decomposition of RDX. Proc. Combust. Inst. 2019, 37, 3167–3173. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Karton, A.; Martin, J.M.L. Explicitly correlated W n theory: W1-F12 and W2-F12. J. Chem. Phys. 2012, 136, 124114. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Oliveira, G. de Towards standard methods for benchmark quality ab initio thermochemistry—W1 and W2 theory. J. Chem. Phys. 1999, 111, 1843–1856. [Google Scholar] [CrossRef]
- Kong, L.; Bischoff, F.A.; Valeev, E.F. Explicitly Correlated R12/F12 Methods for Electronic Structure. Chem. Rev. 2012, 112, 75–107. [Google Scholar] [CrossRef] [PubMed]
- Kesharwani, M.K.; Brauer, B.; Martin, J.M.L. Frequency and Zero-Point Vibrational Energy Scale Factors for Double-Hybrid Density Functionals (and Other Selected Methods): Can Anharmonic Force Fields Be Avoided? J. Phys. Chem. A 2015, 119, 1701–1714. [Google Scholar] [CrossRef] [PubMed]
- Karton, A.; Schreiner, P.R.; Martin, J.M.L. Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures. J. Comput. Chem. 2016, 37, 49–58. [Google Scholar] [CrossRef]
- Karton, A. A computational chemist’s guide to accurate thermochemistry for organic molecules: A computational chemist’s guide to accurate thermochemistry for organic molecules. WIREs Comput. Mol. Sci. 2016, 6, 292–310. [Google Scholar] [CrossRef]
- Allison, T. JANAF Thermochemical Tables, NIST Standard Reference Database 13; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1996.

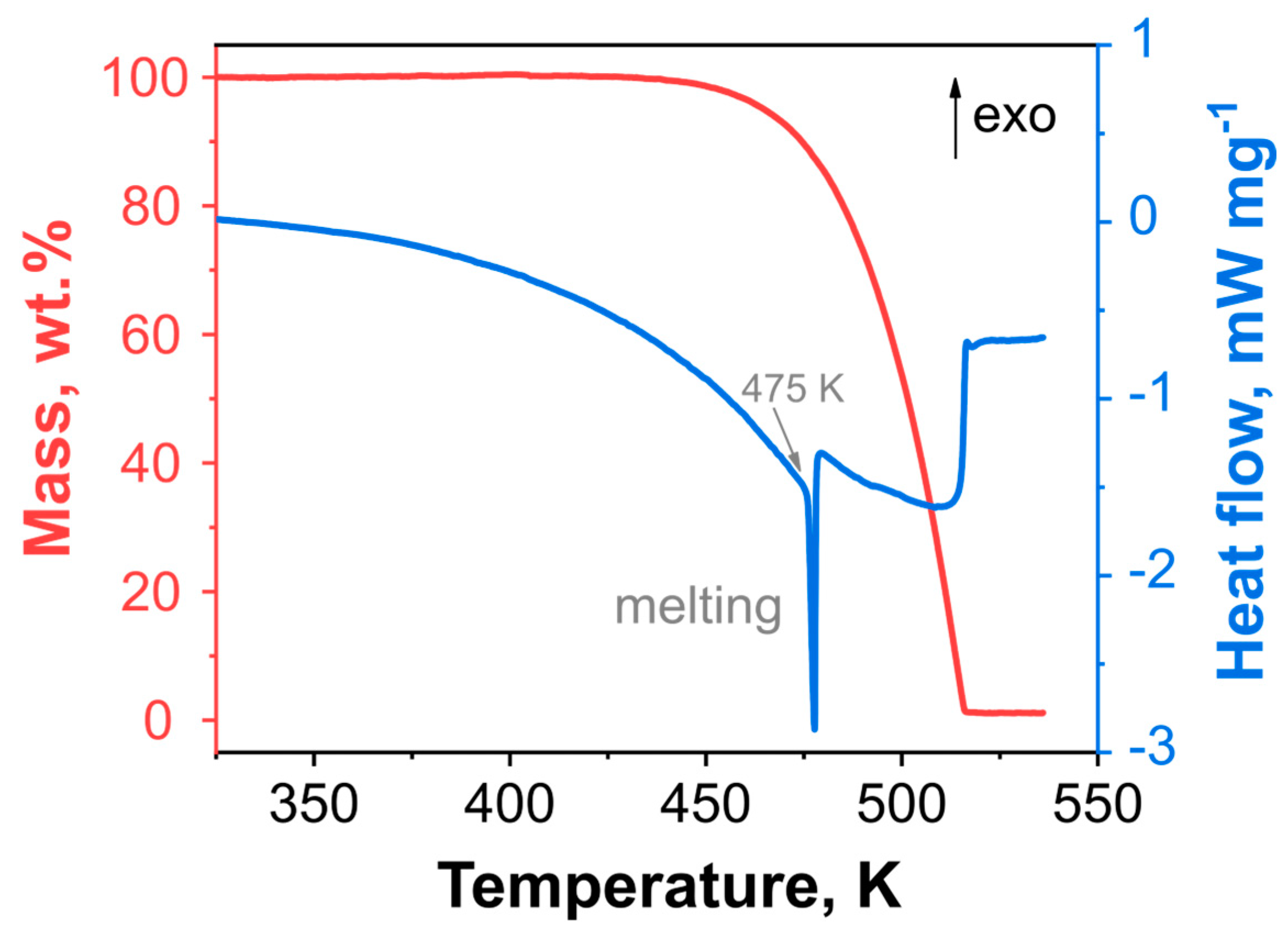
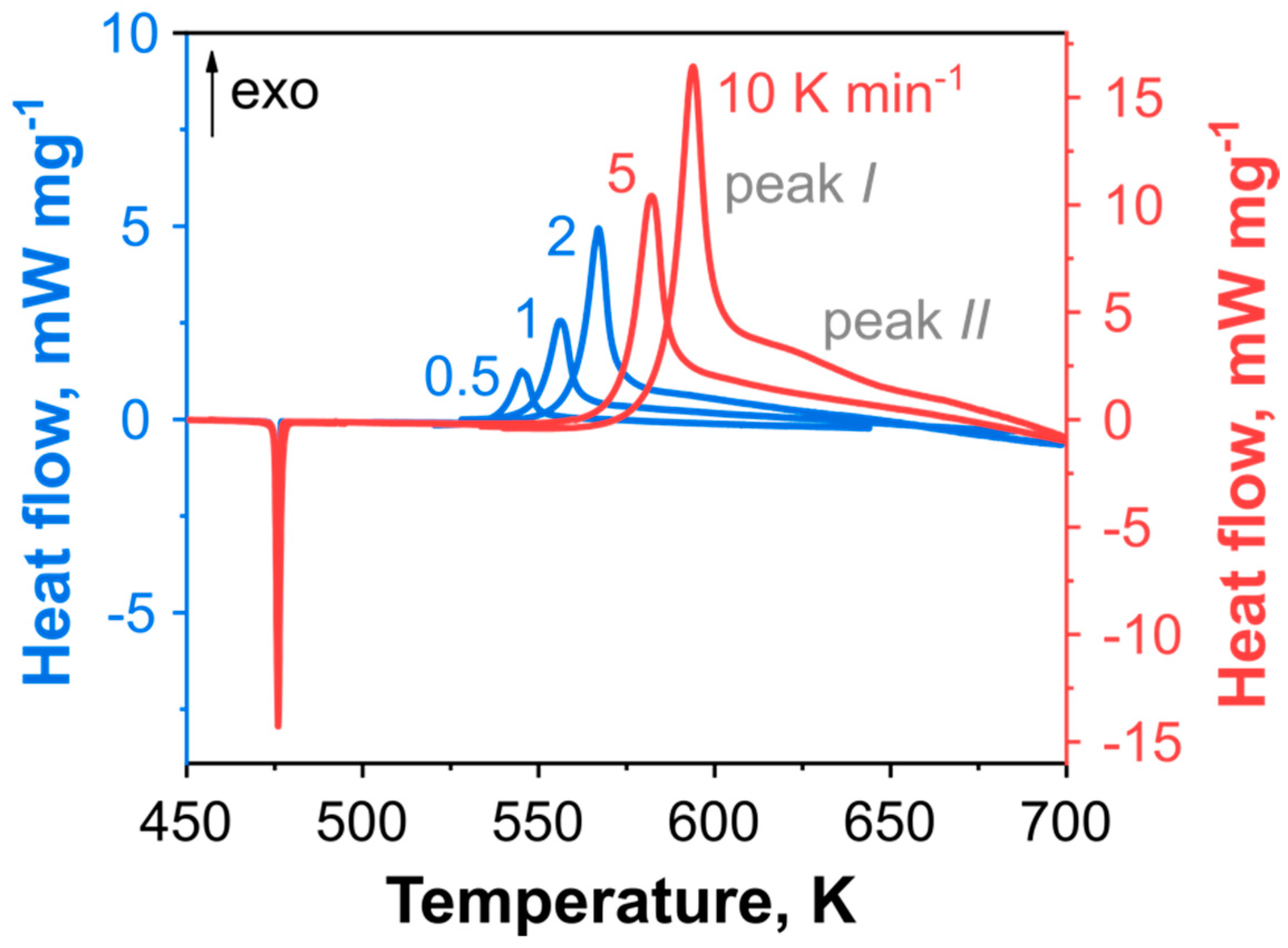
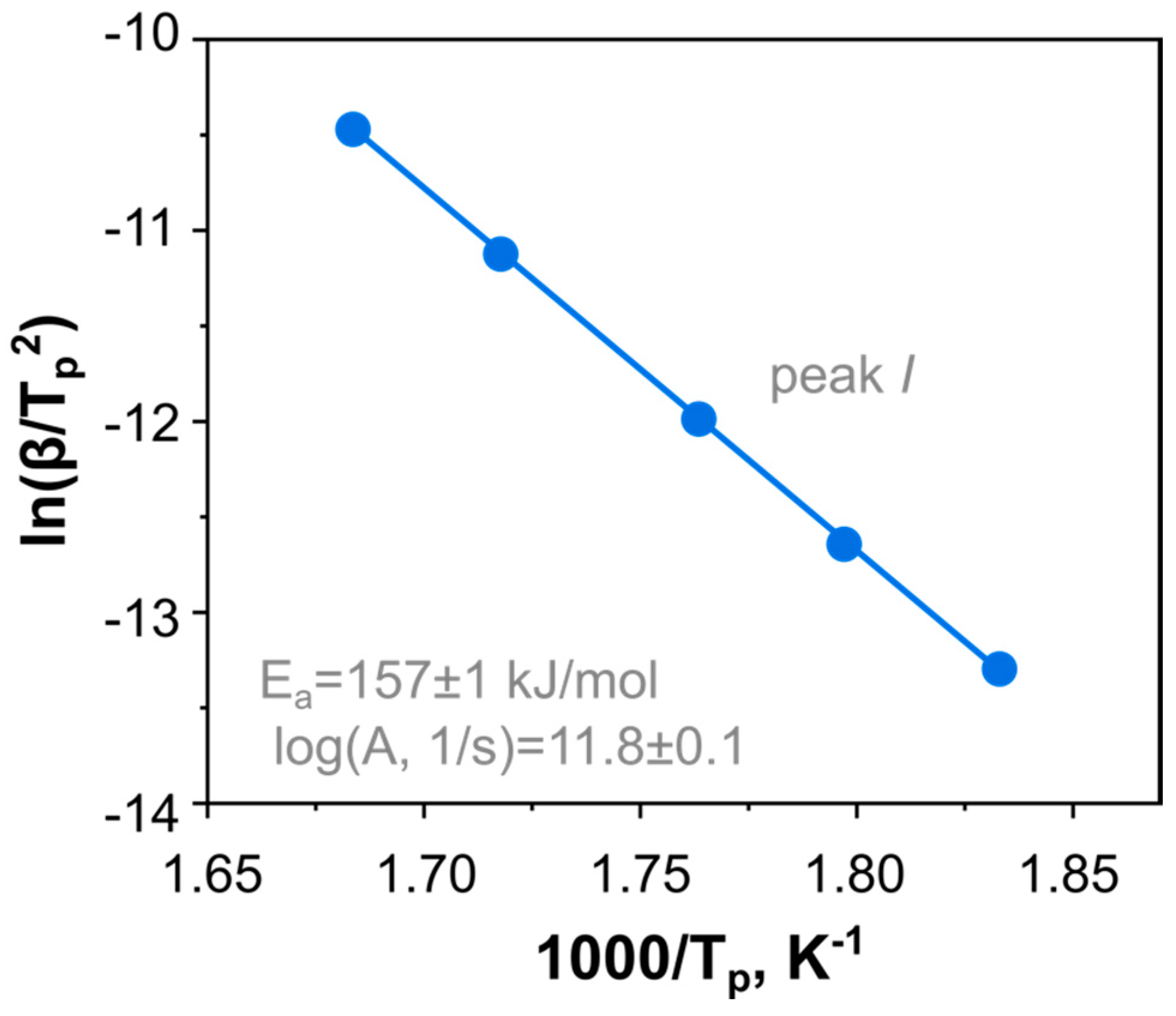

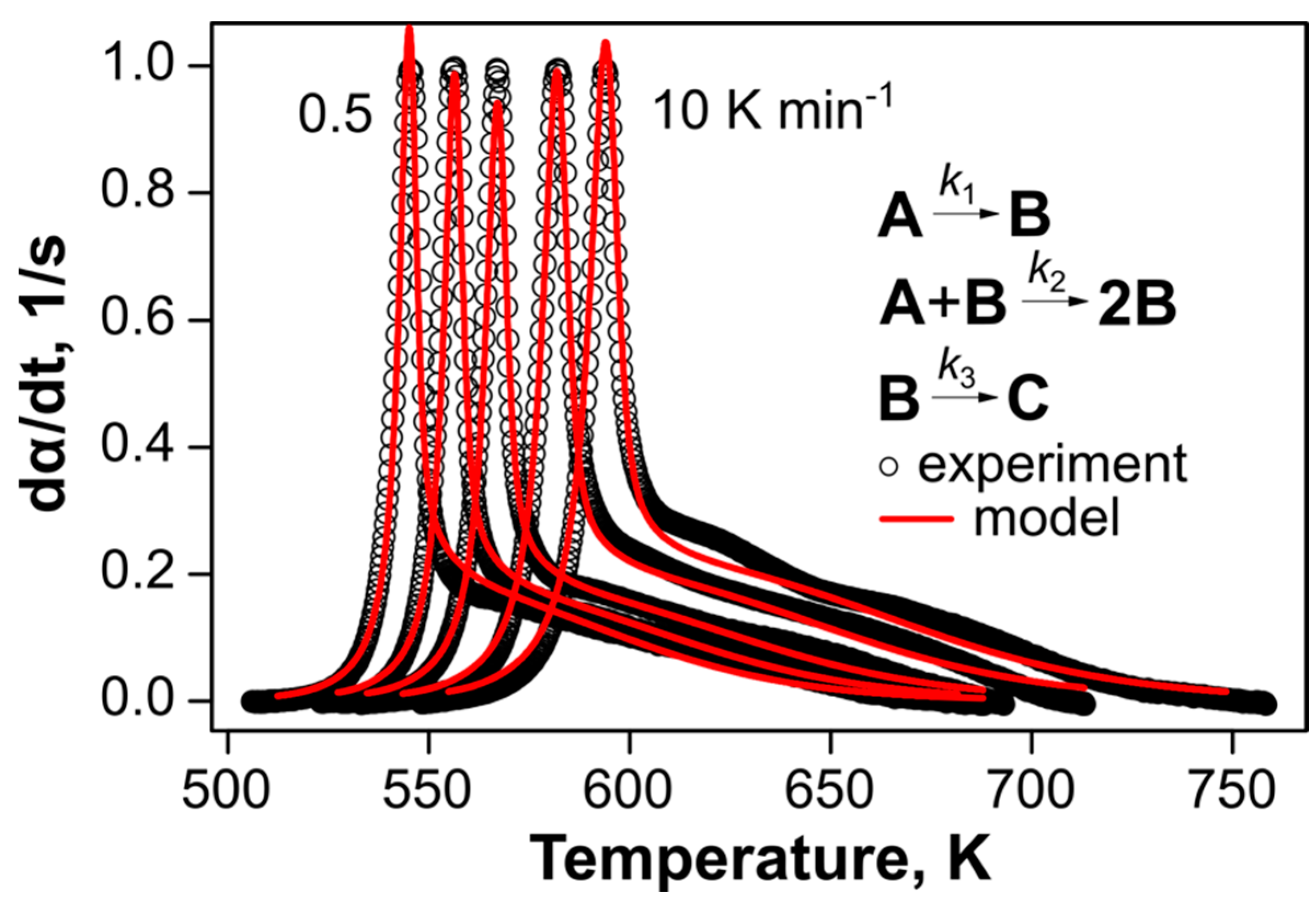



| Model Name | A | B | C | D | E |
|---|---|---|---|---|---|
| Analysis method | Kissinger | model-fitting | model-fitting | model-fitting | model-fitting |
| Kinetic model | – | ePT + ePT a | ePT → ePT | AC b → ePT | AC → ePT |
| log (A1/s−1) | 11.8 ± 0.1 | 12.61 ± 0.02 | 12.56 ± 0.02 | 18.0 ± 0.4/ 11.15 ± 0.07 | 12.82 ± 0.09/ 11.04 ± 0.07 |
| Ea1, kJ mol−1 | 157 ± 1 | 155.8 ± 0.2 | 153.7 ± 0.3 | 241.9 ± 4.8/ 141.2 ± 0.8 | 173.9 ± 0.9/ 136.5 ± 0.8 |
| n1 | – | 1.26 ± 0.03 | 0.99 ± 0.03 | 1/1 | 1/1 |
| m1 | – | 1.046 ± 0.006 | 1.95 ± 0.02 | 0/1 | 0/2 |
| q1 | – | 0.999 c | 0.9 | – | – |
| log (A2/s−1) | – | 8.6 ± 0.1 | 5.6 ± 0.2 | 9.7 ± 0.2 | 8.7 ± 0.2 |
| Ea2, kJ mol−1 | – | 126.7 ± 1.6 | 90.9 ± 2.0 | 144.4 ± 2.3 | 134.5 ± 1.8 |
| n2 | – | 3.00 ± 0.07 | 1.28 ± 0.05 | 2.50 ± 0.07 | 1.98 ± 0.05 |
| m2 | – | 0.35 ± 0.02 | −0.31 ± 0.01 | −0.25 ± 0.04 | −0.78 ± 0.06 |
| w1 d | – | 0.300 ± 0.003 | 0.284 ± 0.004 | 0.347 ± 0.005 | 0.274 ± 0.007 |
| q2 | – | 0.999 c | 0.9 | 0.999 | 0.999 |
| BICe | – | −40,489.3 | −43,590.5 | −41,524.4 | −45,643.4 |
| Reaction | ΔH°, kJ mol−1 | Ea, kJ mol−1 | log(A/s−1) |
|---|---|---|---|
| DBT→•DBTR6+•NO2 | 299.2 a | 297.6 | 18.10 |
| DBT→ DBTP7 (DBTTS7) | 267.1 | 271.2 | 13.61 |
| DBT→ DBTP8 (DBTTS8a) | 281.4 | 289.4 | 21.10 |
| ADBT→•ADBTR6+•NO2 | 318.7 a | 319.8 | 19.11 |
| ADBT→ ADBTP7 (ADBTTS7) | 276.2 | 280.3 | 13.88 |
| ADBT→ ADBTP8 (ADBTTS8a) | 286.4 | 293.3 | 20.14 |
| Species | DBT | ADBT | 3 | 4 |
|---|---|---|---|---|
| keff(650 K) a | 1 | 0.1 | 18.3 | 5.5 |
| Compound | , kJ/mol | , kJ/mol | , kJ/mol |
|---|---|---|---|
| DBT | 308.1 a | 121.8 ± 3.2 120 | 187.3 179 c |
| ADBT | 271.2 a | 150 | 129.5 128 c |
| 3 | 308.6 a 262.3 b | 124 | 184.4 191.6 d |
| 4 | 279.4 a | 150 | 129.6 138.1 d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melnikov, I.N.; Kiselev, V.G.; Dalinger, I.L.; Starosotnikov, A.M.; Muravyev, N.V.; Pivkina, A.N. Thermochemistry, Tautomerism, and Thermal Stability of 5,7-Dinitrobenzotriazoles. Int. J. Mol. Sci. 2023, 24, 5330. https://doi.org/10.3390/ijms24065330
Melnikov IN, Kiselev VG, Dalinger IL, Starosotnikov AM, Muravyev NV, Pivkina AN. Thermochemistry, Tautomerism, and Thermal Stability of 5,7-Dinitrobenzotriazoles. International Journal of Molecular Sciences. 2023; 24(6):5330. https://doi.org/10.3390/ijms24065330
Chicago/Turabian StyleMelnikov, Igor N., Vitaly G. Kiselev, Igor L. Dalinger, Alexey M. Starosotnikov, Nikita V. Muravyev, and Alla N. Pivkina. 2023. "Thermochemistry, Tautomerism, and Thermal Stability of 5,7-Dinitrobenzotriazoles" International Journal of Molecular Sciences 24, no. 6: 5330. https://doi.org/10.3390/ijms24065330
APA StyleMelnikov, I. N., Kiselev, V. G., Dalinger, I. L., Starosotnikov, A. M., Muravyev, N. V., & Pivkina, A. N. (2023). Thermochemistry, Tautomerism, and Thermal Stability of 5,7-Dinitrobenzotriazoles. International Journal of Molecular Sciences, 24(6), 5330. https://doi.org/10.3390/ijms24065330








