A Study on the Robustness and Stability of Explainable Deep Learning in an Imbalanced Setting: The Exploration of the Conformational Space of G Protein-Coupled Receptors
Abstract
1. Introduction
2. Results
3. Discussion
3.1. Performance Evaluation
3.2. Explainability of the Models
3.3. Robustness, Stability, and Consistency of the Explanations
4. Materials and Methods
4.1. Data Pre-Processing
4.2. Class Imbalance
4.3. XAI Methods
4.4. Assessment of Explanation Methods
4.5. Experimental Setup
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| (a) Active State Contributions | ||
| Residue Name | Transmembrane | Mean Contribution |
| VAL31 | H1 | 0.2092 |
| TRP32 | H1 | 0.0676 |
| VAL33 | H1 | 0.2886 |
| VAL34 | H1 | 0.5918 |
| GLY35 | H1 | 1.5021 |
| MET36 | H1 | 0.7761 |
| GLY37 | H1 | −0.3627 |
| ILE38 | H1 | −0.1454 |
| VAL39 | H1 | −1.3410 |
| MET40 | H1 | −1.7757 |
| SER41 | H1 | −1.8760 |
| LEU42 | H1 | −0.6127 |
| ILE43 | H1 | 0.1783 |
| VAL44 | H1 | 1.2615 |
| LEU45 | H1 | 0.6632 |
| ALA46 | H1 | 0.6786 |
| ILE47 | H1 | 0.1412 |
| VAL48 | H1 | 0.1233 |
| ASN51 | H1 | −0.0720 |
| LEU53 | H1 | 0.0601 |
| VAL54 | H1 | 0.0417 |
| ALA57 | H1 | −0.0615 |
| GLU62 | ICL1 | −0.0552 |
| GLN65 | ICL1 | 0.0447 |
| VAL67 | H2 | −0.0353 |
| VAL81 | H2 | −0.0325 |
| MET82 | H2 | −0.0457 |
| GLY83 | H2 | −0.0367 |
| ILE94 | H2 | 0.0436 |
| LEU95 | H2 | 0.0936 |
| MET96 | H2 | 0.0365 |
| MET98 | ECL1 | −0.0449 |
| TRP99 | ECL1 | −0.0800 |
| THR100 | ECL1 | −0.0506 |
| SER137 | ICL2 | −0.0465 |
| TYR141 | ICL2 | 0.0479 |
| GLN142 | ICL2 | 0.0565 |
| LEU145 | ICL2 | −0.0627 |
| ASN148 | H4 | 0.0412 |
| ALA150 | H4 | 0.0840 |
| VAL152 | H4 | −0.0462 |
| ILE153 | H4 | −0.0944 |
| MET156 | H4 | 0.0338 |
| VAL157 | H4 | 0.0363 |
| TRP158 | H4 | 0.0455 |
| ILE159 | H4 | 0.0378 |
| SER165 | H4 | −0.0472 |
| PHE166 | H4 | −0.0760 |
| LEU167 | H4 | −0.0764 |
| THR177 | ECL2 | 0.0340 |
| HIS178 | ECL2 | 0.0583 |
| GLN179 | ECL2 | 0.1104 |
| GLU180 | ECL2 | 0.0505 |
| ALA181 | ECL2 | 0.0358 |
| CYS184 | ECL2 | −0.0364 |
| TYR185 | ECL2 | −0.0328 |
| GLN197 | H5 | −0.0687 |
| ALA198 | H5 | −0.1220 |
| TYR199 | H5 | −0.0586 |
| ALA200 | H5 | −0.0323 |
| ILE201 | H5 | 0.0334 |
| ALA202 | H5 | 0.0485 |
| SER203 | H5 | 0.0526 |
| GLN299 | ECL3 | −0.0397 |
| ASN312 | H7 | 0.0489 |
| TYR316 | H7 | −0.0469 |
| GLY320 | H7 | 0.0312 |
| LEU339 | C-Terminus | 0.0434 |
| (b) Intermediate State Contributions | ||
| Residue Name | Transmembrane | Mean Contribution |
| VAL31 | H1 | 0.0941 |
| TRP32 | H1 | 0.0791 |
| VAL33 | H1 | 0.2116 |
| VAL34 | H1 | 0.2983 |
| GLY35 | H1 | 0.3681 |
| MET36 | H1 | −0.1076 |
| GLY37 | H1 | −0.3470 |
| ILE38 | H1 | −0.2240 |
| VAL39 | H1 | −0.5690 |
| MET40 | H1 | −0.8806 |
| SER41 | H1 | −1.0995 |
| LEU42 | H1 | −0.1839 |
| ILE43 | H1 | 0.6116 |
| VAL44 | H1 | 1.5330 |
| LEU45 | H1 | 0.6826 |
| ALA46 | H1 | 0.3322 |
| ILE47 | H1 | −0.1201 |
| VAL48 | H1 | −0.1765 |
| PHE49 | H1 | −0.1796 |
| GLY50 | H1 | −0.0685 |
| ASN51 | H1 | −0.0313 |
| VAL54 | H1 | 0.0354 |
| ILE55 | H1 | 0.0434 |
| GLN65 | ICL1 | −0.0531 |
| THR68 | H2 | 0.0325 |
| TRP99 | ECL1 | 0.0438 |
| THR100 | ECL1 | 0.0391 |
| ALA150 | H4 | 0.0866 |
| ARG151 | H4 | 0.0327 |
| LEU155 | H4 | −0.0390 |
| LEU163 | H4 | −0.0317 |
| ASN301 | ECL3 | 0.0491 |
| (c) Inactive State Contributions | ||
| Residue Name | Transmembrane | Mean Contribution |
| VAL31 | H1 | −0.0437 |
| VAL33 | H1 | −0.0845 |
| VAL34 | H1 | −0.1813 |
| GLY35 | H1 | −0.4075 |
| MET36 | H1 | −0.1317 |
| GLY37 | H1 | 0.1968 |
| ILE38 | H1 | 0.0844 |
| VAL39 | H1 | 0.3386 |
| MET40 | H1 | 0.5095 |
| SER41 | H1 | 0.5568 |
| LEU42 | H1 | 0.1875 |
| ILE43 | H1 | −0.0817 |
| VAL44 | H1 | −0.3731 |
| LEU45 | H1 | −0.2599 |
| ALA46 | H1 | −0.2053 |
Appendix B
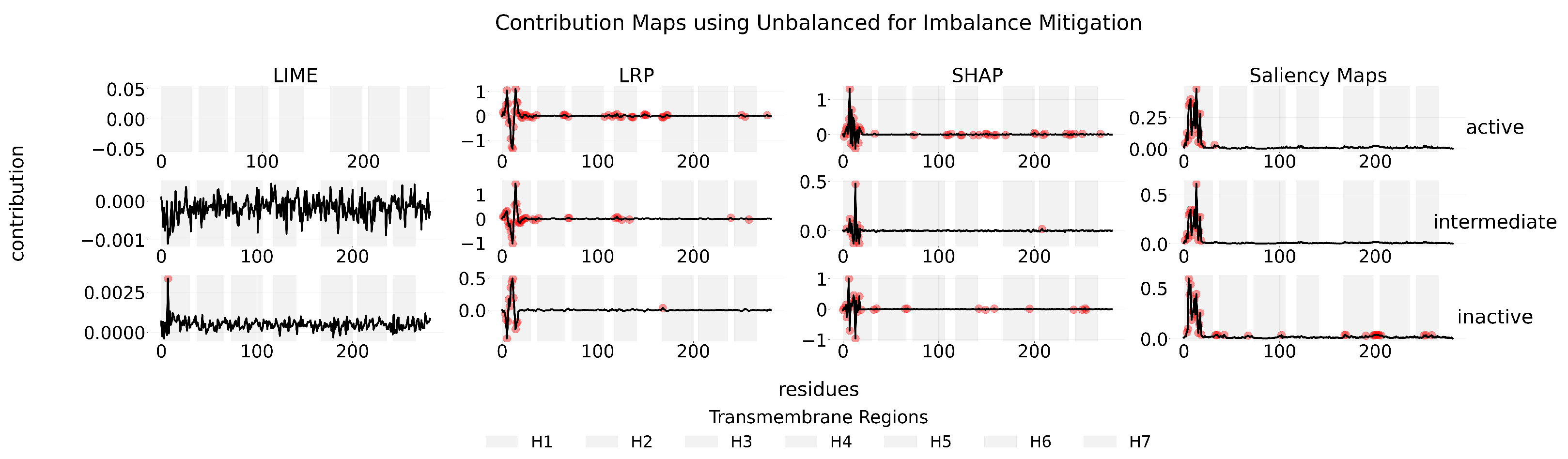
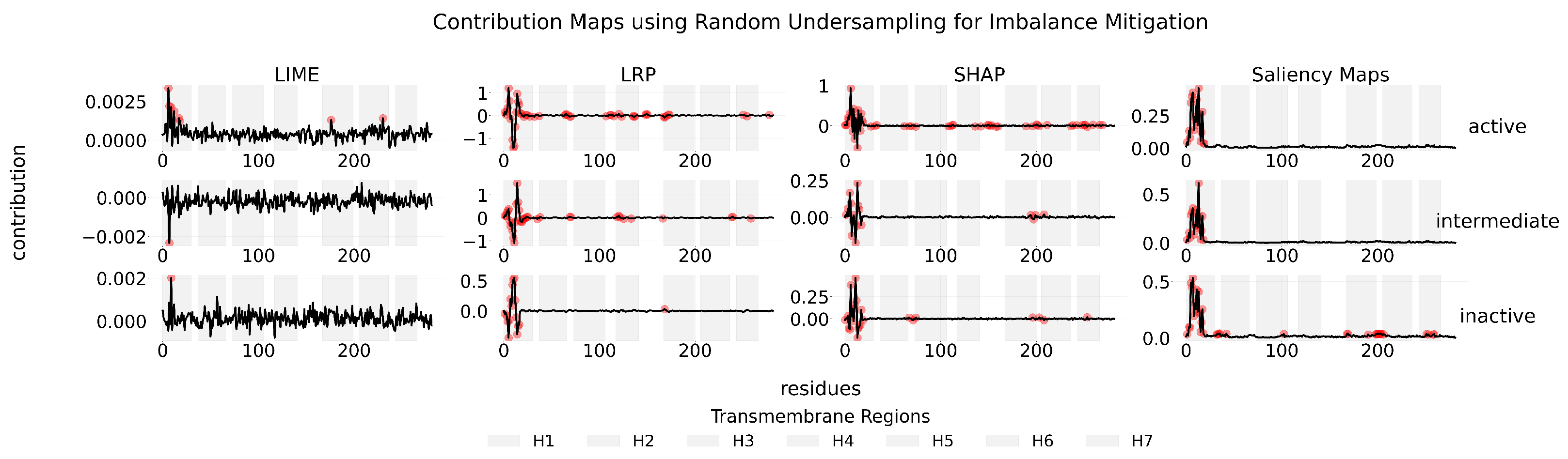
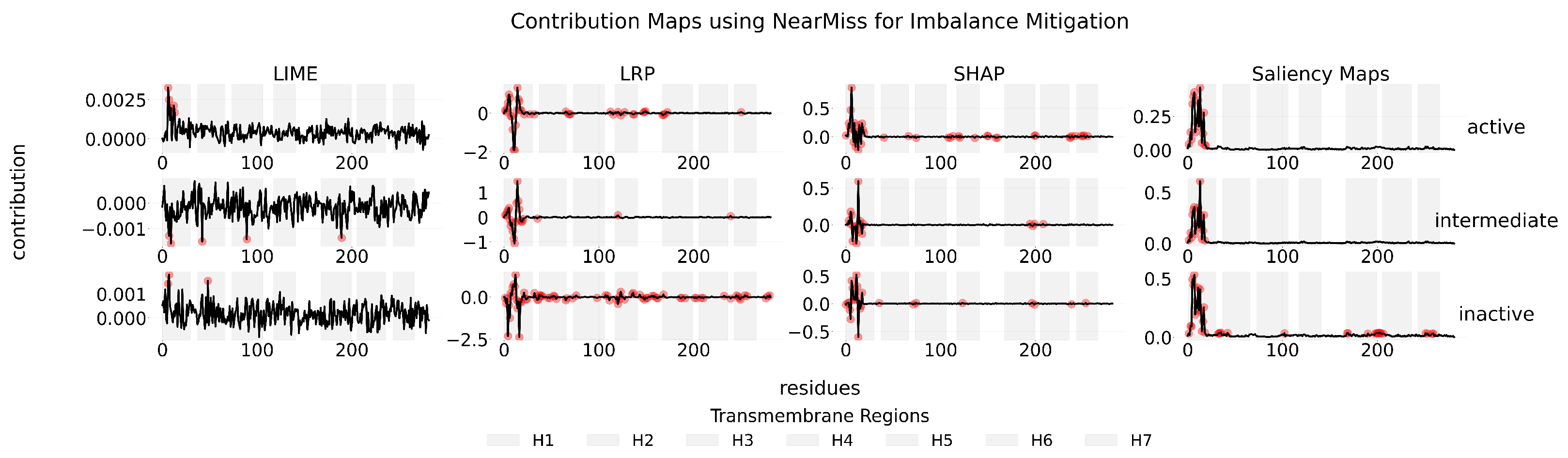
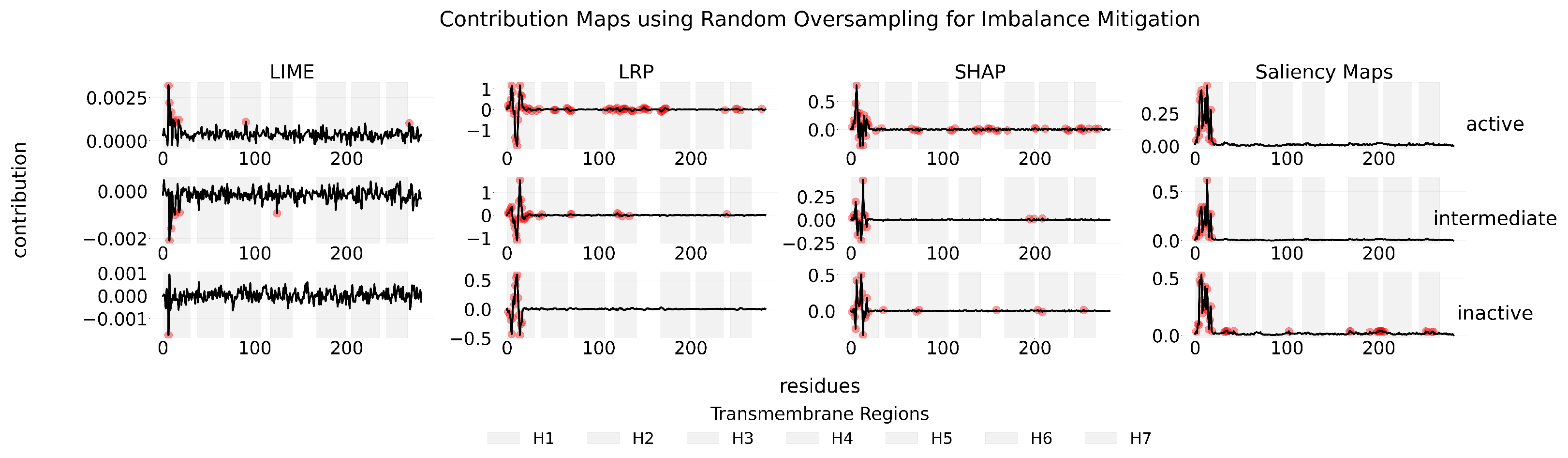

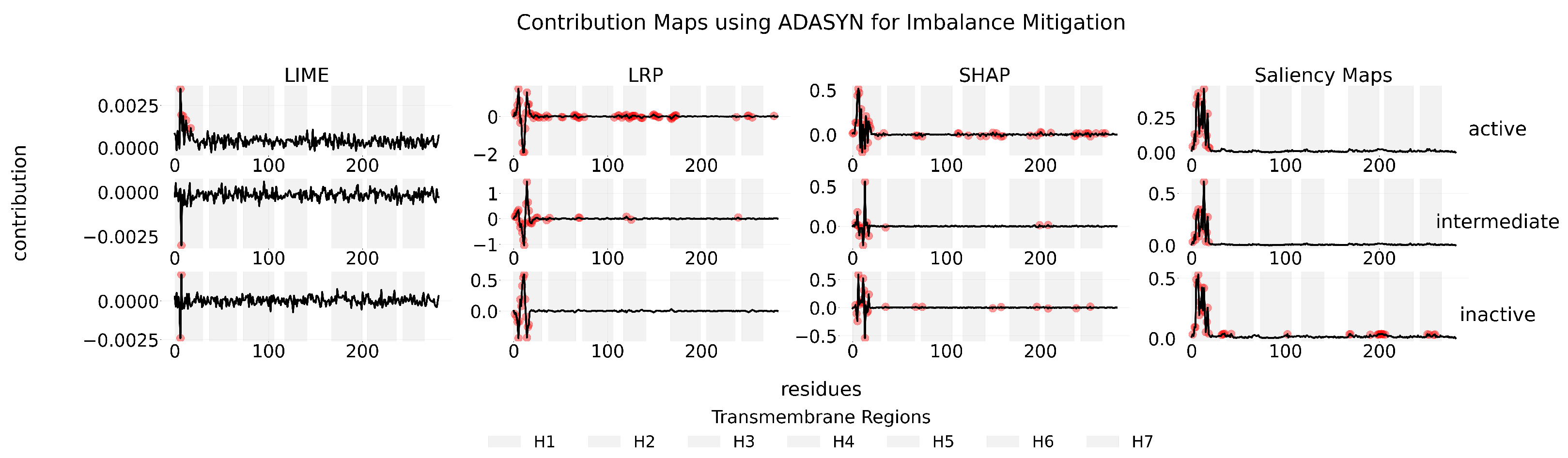
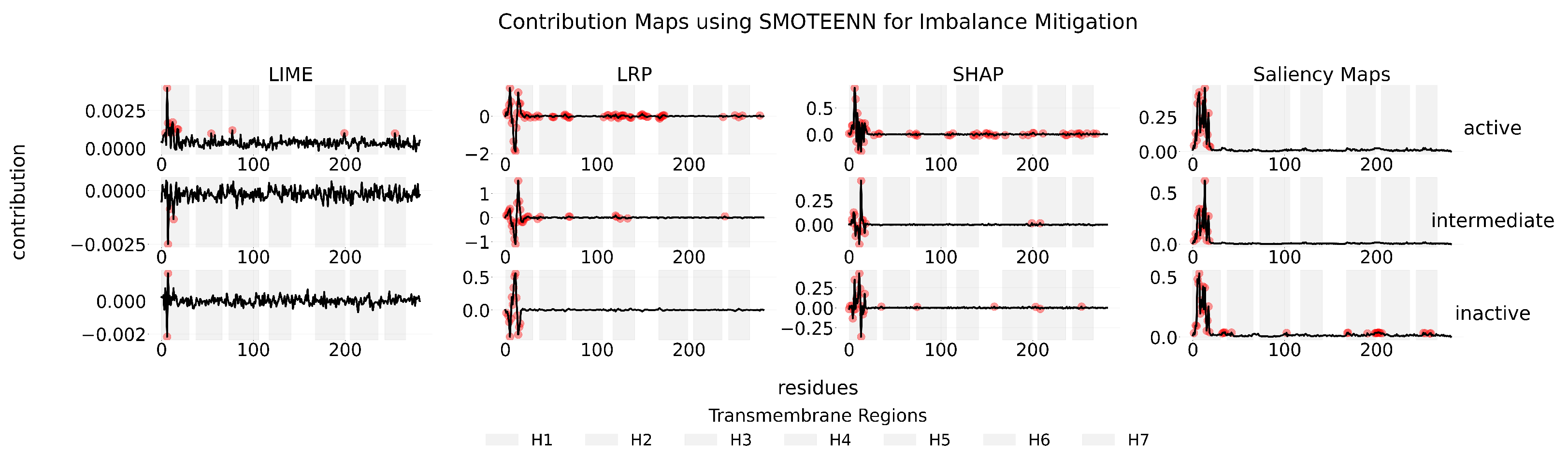

Appendix C
| Saliency Maps Common Contributions Across Imbalance Methods | |||
| State | Residue | Transmembrane | Mean Contribution |
| active | PHE49 | H1 | 0.0337 |
| intermediate | VAL31 | H1 | 0.0321 |
| intermediate | VAL33 | H1 | 0.0997 |
| intermediate | VAL34 | H1 | 0.0531 |
| intermediate | GLY35 | H1 | 0.2772 |
| intermediate | MET36 | H1 | 0.3054 |
| intermediate | GLY37 | H1 | 0.3435 |
| intermediate | ILE38 | H1 | 0.0845 |
| intermediate | VAL39 | H1 | 0.1786 |
| intermediate | MET40 | H1 | 0.1712 |
| intermediate | SER41 | H1 | 0.3422 |
| intermediate | LEU42 | H1 | 0.1551 |
| intermediate | ILE43 | H1 | 0.6180 |
| intermediate | VAL44 | H1 | 0.2698 |
| intermediate | LEU45 | H1 | 0.0372 |
| intermediate | ALA46 | H1 | 0.1233 |
| intermediate | ILE47 | H1 | 0.2716 |
| intermediate | VAL48 | H1 | 0.0317 |
| inactive | GLU62 | ICL1 | 0.0296 |
| inactive | ARG63 | ICL1 | 0.0361 |
| inactive | LEU64 | ICL1 | 0.0355 |
| inactive | GLN65 | ICL1 | 0.0393 |
| inactive | ILE72 | H2 | 0.0370 |
| inactive | TYR132 | H3 | 0.0349 |
| inactive | ALA198 | H5 | 0.0348 |
| inactive | TYR199 | H5 | 0.0360 |
| inactive | SER220 | H5 | 0.0306 |
| inactive | ARG228 | H5 | 0.0321 |
| inactive | GLN229 | H5 | 0.0344 |
| inactive | LEU230 | ICL3 | 0.0336 |
| inactive | LYS263 | ICL3 | 0.0365 |
| inactive | PHE264 | ICL3 | 0.0375 |
| inactive | CYS265 | ICL3 | 0.0363 |
| inactive | LEU266 | ICL3 | 0.0338 |
| inactive | GLU268 | H6 | 0.0322 |
| inactive | TRP313 | H7 | 0.0343 |
| inactive | GLY315 | H7 | 0.0317 |
| inactive | GLY320 | H7 | 0.0296 |
| inactive | PHE321 | H7 | 0.0323 |
| LIME Common Contributions Across Imbalance Methods | |||
| State | Residue | Transmembrane | Mean Contribution |
| active | ILE47 | H1 | 0.0014 |
| intermediate | GLY37 | H1 | −0.0021 |
| intermediate | VAL39 | H1 | −0.0012 |
| intermediate | LEU42 | H1 | −0.0009 |
| intermediate | ILE43 | H1 | −0.0009 |
| inactive | MET36 | H1 | −0.0021 |
| SHAP Common Contributions Across Imbalance Methods | |||
| State | Residue | Transmembrane | Mean Contribution |
| active | GLU30 | H1 | 0.0189 |
| active | ILE47 | H1 | 0.3491 |
| active | PHE49 | H1 | 0.0651 |
| active | ALA57 | H1 | −0.0165 |
| active | PHE104 | H3 | −0.0212 |
| active | PHE166 | H4 | −0.0197 |
| active | HIS172 | ECL2 | −0.0158 |
| active | GLN179 | ECL2 | 0.0213 |
| active | GLU188 | ECL2 | −0.0201 |
| active | CYS190 | ECL2 | −0.0184 |
| active | LEU230 | ICL3 | 0.0315 |
| active | LYS273 | H6 | 0.0180 |
| active | GLN299 | ECL3 | −0.0189 |
| active | ARG304 | ECL3 | 0.0156 |
| active | LEU310 | H7 | 0.0155 |
| active | ASN312 | H7 | 0.0144 |
| active | TRP313 | H7 | 0.0226 |
| intermediate | VAL31 | H1 | 0.0156 |
| intermediate | VAL33 | H1 | 0.0448 |
| intermediate | GLY35 | H1 | 0.1313 |
| intermediate | MET36 | H1 | 0.0838 |
| intermediate | GLY37 | H1 | −0.1190 |
| intermediate | ILE38 | H1 | −0.0173 |
| intermediate | VAL39 | H1 | 0.0416 |
| intermediate | SER41 | H1 | −0.1194 |
| intermediate | LEU42 | H1 | −0.0501 |
| intermediate | ILE43 | H1 | 0.1535 |
| intermediate | VAL44 | H1 | 0.0299 |
| intermediate | LEU45 | H1 | 0.0535 |
| intermediate | VAL48 | H1 | 0.0164 |
| intermediate | GLN229 | H5 | 0.0151 |
| intermediate | LYS270 | H6 | 0.0162 |
| inactive | VAL34 | H1 | −0.0759 |
| inactive | MET40 | H1 | 0.0963 |
| inactive | ALA46 | H1 | −0.0346 |
References
- Lundstrom, K. An overview on GPCRs and drug discovery: Structure-based drug design and structural biology on GPCRs. In G Protein-Coupled Receptors in Drug Discovery; Humana Press: Totowa, NJ, USA, 2009; pp. 51–66. [Google Scholar]
- Rosenbaum, D.M.; Rasmussen, S.G.; Kobilka, B.K. The structure and function of G-protein-coupled receptors. Nature 2009, 459, 356–363. [Google Scholar] [CrossRef] [PubMed]
- Gurevich, V.V.; Gurevich, E.V. Molecular mechanisms of GPCR signaling: A structural perspective. Int. J. Mol. Sci. 2017, 18, 2519. [Google Scholar] [CrossRef] [PubMed]
- Hilger, D.; Masureel, M.; Kobilka, B.K. Structure and dynamics of GPCR signaling complexes. Nat. Struct. Mol. Biol. 2018, 25, 4–12. [Google Scholar] [CrossRef] [PubMed]
- Maggio, R.; Fasciani, I.; Carli, M.; Petragnano, F.; Marampon, F.; Rossi, M.; Scarselli, M. Integration and spatial organization of signaling by G protein-coupled receptor homo-and heterodimers. Biomolecules 2021, 11, 1828. [Google Scholar] [CrossRef] [PubMed]
- White, M.F. Insulin signaling in health and disease. Science 2003, 302, 1710–1711. [Google Scholar] [CrossRef] [PubMed]
- Klein, M.O.; Battagello, D.S.; Cardoso, A.R.; Hauser, D.N.; Bittencourt, J.C.; Correa, R.G. Dopamine: Functions, signaling, and association with neurological diseases. Cell. Mol. Neurobiol. 2019, 39, 31–59. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zeng, L.; Zhao, S. Ligands of adrenergic receptors: A structural point of view. Biomolecules 2021, 11, 936. [Google Scholar] [CrossRef] [PubMed]
- Wachter, S.B.; Gilbert, E.M. Beta-adrenergic receptors, from their discovery and characterization through their manipulation to beneficial clinical application. Cardiology 2012, 122, 104–112. [Google Scholar] [CrossRef]
- Minneman, K.P.; Pittman, R.N.; Molinoff, P.B. Beta-adrenergic receptor subtypes: Properties, distribution, and regulation. Annu. Rev. Neurosci. 1981, 4, 419–461. [Google Scholar] [CrossRef]
- Johnson, M. Molecular mechanisms of β2-adrenergic receptor function, response, and regulation. J. Allergy Clin. Immunol. 2006, 117, 18–24. [Google Scholar] [CrossRef]
- Abosamak, N.R.; Shahin, M.H. Beta2 receptor agonists and antagonists. In StatPearls [Internet]; StatPearls Publishing: St. Petersburg, FL, USA, 2023. [Google Scholar]
- Yang, A.; Yu, G.; Wu, Y.; Wang, H. Role of β2-adrenergic receptors in chronic obstructive pulmonary disease. Life Sci. 2021, 265, 118864. [Google Scholar] [CrossRef] [PubMed]
- Ciccarelli, M.; Santulli, G.; Pascale, V.; Trimarco, B.; Iaccarino, G. Adrenergic receptors and metabolism: Role in development of cardiovascular disease. Front. Physiol. 2013, 4, 265. [Google Scholar] [CrossRef] [PubMed]
- Gether, U.; Kobilka, B.K. G protein-coupled receptors: II. Mechanism of agonist activation. J. Biol. Chem. 1998, 273, 17979–17982. [Google Scholar] [CrossRef] [PubMed]
- Latorraca, N.R.; Venkatakrishnan, A.; Dror, R.O. GPCR dynamics: Structures in motion. Chem. Rev. 2017, 117, 139–155. [Google Scholar] [CrossRef] [PubMed]
- Weis, W.I.; Kobilka, B.K. The molecular basis of G protein–coupled receptor activation. Annu. Rev. Biochem. 2018, 87, 897–919. [Google Scholar] [CrossRef] [PubMed]
- Hilger, D. The role of structural dynamics in GPCR-mediated signaling. FEBS J. 2021, 288, 2461–2489. [Google Scholar] [CrossRef] [PubMed]
- Kenakin, T. A holistic view of GPCR signaling. Nat. Biotechnol. 2010, 28, 928–929. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, C.; Zürn, A.; Bünemann, M.; Lohse, M. Conformational changes in G-protein-coupled receptors—The quest for functionally selective conformations is open. Br. J. Pharmacol. 2008, 153, S358–S366. [Google Scholar] [CrossRef]
- Wacker, D.; Stevens, R.C.; Roth, B.L. How ligands illuminate GPCR molecular pharmacology. Cell 2017, 170, 414–427. [Google Scholar] [CrossRef]
- Bermudez, M.; Nguyen, T.N.; Omieczynski, C.; Wolber, G. Strategies for the discovery of biased GPCR ligands. Drug Discov. Today 2019, 24, 1031–1037. [Google Scholar] [CrossRef]
- Wang, X.; Neale, C.; Kim, S.K.; Goddard, W.A.; Ye, L. Intermediate-state-trapped mutants pinpoint G protein-coupled receptor conformational allostery. Nat. Commun. 2023, 14, 1325. [Google Scholar] [CrossRef] [PubMed]
- Congreve, M.; de Graaf, C.; Swain, N.A.; Tate, C.G. Impact of GPCR structures on drug discovery. Cell 2020, 181, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Topiol, S. Current and future challenges in GPCR drug discovery. In Computational Methods for GPCR Drug Discovery; Humana Press: New York, NY, USA, 2018; pp. 1–21. [Google Scholar]
- García-Nafría, J.; Tate, C.G. Structure determination of GPCRs: Cryo-EM compared with X-ray crystallography. Biochem. Soc. Trans. 2021, 49, 2345–2355. [Google Scholar] [CrossRef] [PubMed]
- Topiol, S.; Sabio, M. X-ray structure breakthroughs in the GPCR transmembrane region. Biochem. Pharmacol. 2009, 78, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Leiro, R.; Scheres, S.H. Unravelling the structures of biological macromolecules by cryo-EM. Nature 2016, 537, 339. [Google Scholar] [CrossRef] [PubMed]
- Durrant, J.D.; McCammon, J.A. Molecular dynamics simulations and drug discovery. BMC Biol. 2011, 9, 71. [Google Scholar] [CrossRef]
- Velgy, N.; Hedger, G.; Biggin, P.C. GPCRs: What can we learn from molecular dynamics simulations? In Computational Methods for GPCR Drug Discovery; Humana Press: New York, NY, USA, 2018; pp. 133–158. [Google Scholar]
- Li, Z.; Su, C.; Ding, B. Molecular dynamics simulation of β-adrenoceptors and their coupled G proteins. Eur. Rev. Med. Pharmacol. Sci. 2019, 23, 6346–6351. [Google Scholar]
- Hein, P.; Rochais, F.; Hoffmann, C.; Dorsch, S.; Nikolaev, V.O.; Engelhardt, S.; Berlot, C.H.; Lohse, M.J.; Bünemann, M. Gs activation is time-limiting in initiating receptor-mediated signaling. J. Biol. Chem. 2006, 281, 33345–33351. [Google Scholar] [CrossRef] [PubMed]
- Bernetti, M.; Bertazzo, M.; Masetti, M. Data-driven molecular dynamics: A multifaceted challenge. Pharmaceuticals 2020, 13, 253. [Google Scholar] [CrossRef]
- Glazer, D.S.; Radmer, R.J.; Altman, R.B. Combining molecular dynamics and machine learning to improve protein function recognition. In Biocomputing 2008; World Scientific: Singapore, 2008; pp. 332–343. [Google Scholar]
- Feig, M.; Nawrocki, G.; Yu, I.; Wang, P.h.; Sugita, Y. Challenges and opportunities in connecting simulations with experiments via molecular dynamics of cellular environments. J. Phys. Conf. Ser. 2018, 1036, 012010. [Google Scholar] [CrossRef]
- Prašnikar, E.; Ljubič, M.; Perdih, A.; Borišek, J. Machine learning heralding a new development phase in molecular dynamics simulations. Artif. Intell. Rev. 2024, 57, 102. [Google Scholar] [CrossRef]
- Plante, A.; Shore, D.M.; Morra, G.; Khelashvili, G.; Weinstein, H. A machine learning approach for the discovery of ligand-specific functional mechanisms of GPCRs. Molecules 2019, 24, 2097. [Google Scholar] [CrossRef] [PubMed]
- Jamal, S.; Grover, A.; Grover, S. Machine learning from molecular dynamics trajectories to predict caspase-8 inhibitors against Alzheimer’s disease. Front. Pharmacol. 2019, 10, 460732. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, F.; Moroni, E.; Pandini, A.; Colombo, G. Machine learning prediction of allosteric drug activity from molecular dynamics. J. Phys. Chem. Lett. 2021, 12, 3724–3732. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, M.; Moroni, E.; Ippoliti, E.; Rinaldi, S.; Sanchez-Martin, C.; Rasola, A.; Pavarino, L.F.; Colombo, G. Machine learning of allosteric effects: The analysis of ligand-induced dynamics to predict functional effects in TRAP1. J. Phys. Chem. B 2020, 125, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Frank, M.; Drikakis, D.; Charissis, V. Machine-learning methods for computational science and engineering. Computation 2020, 8, 15. [Google Scholar] [CrossRef]
- Kaptan, S.; Vattulainen, I. Machine learning in the analysis of biomolecular simulations. Adv. Phys. X 2022, 7, 2006080. [Google Scholar] [CrossRef]
- Kohlhoff, K.J.; Shukla, D.; Lawrenz, M.; Bowman, G.R.; Konerding, D.E.; Belov, D.; Altman, R.B.; Pande, V.S. Cloud-based simulations on Google Exacycle reveal ligand modulation of GPCR activation pathways. Nat. Chem. 2014, 6, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Mondragón, M.A.; König, C.; Vellido, A. A Deep Learning-based method for uncovering GPCR ligand-induced conformational states using interpretability techniques. In Proceedings of the 9th International Work-Conference on Bioinformatics and Biomedical Engineering (IWBBIO), Maspalomas, Gran Canaria, Spain, 27–30 June 2022; pp. 275–287. [Google Scholar]
- Hill, S.J. G-protein-coupled receptors: Past, present and future. Br. J. Pharmacol. 2006, 147, S27–S37. [Google Scholar] [CrossRef]
- Tuteja, N. Signaling through G protein coupled receptors. Plant Signal. Behav. 2009, 4, 942–947. [Google Scholar] [CrossRef]
- Katritch, V.; Cherezov, V.; Stevens, R.C. Diversity and modularity of G protein-coupled receptor structures. Trends Pharmacol. Sci. 2012, 33, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Gunning, D.; Stefik, M.; Choi, J.; Miller, T.; Stumpf, S.; Yang, G.Z. XAI—Explainable artificial intelligence. Sci. Robot. 2019, 4, eaay7120. [Google Scholar] [CrossRef] [PubMed]
- Langer, M.; Oster, D.; Speith, T.; Hermanns, H.; Kästner, L.; Schmidt, E.; Sesing, A.; Baum, K. What do we want from Explainable Artificial Intelligence (XAI)?–A stakeholder perspective on XAI and a conceptual model guiding interdisciplinary XAI research. Artif. Intell. 2021, 296, 103473. [Google Scholar] [CrossRef]
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.M.; Confalonieri, R.; Guidotti, R.; Del Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable Artificial Intelligence (XAI): What we know and what is left to attain Trustworthy Artificial Intelligence. Inf. Fusion 2023, 99, 101805. [Google Scholar] [CrossRef]
- Bacciu, D.; Lisboa, P.J.; Martín, J.D.; Stoean, R.; Vellido, A. Bioinformatics and medicine in the era of deep learning. arXiv 2018, arXiv:1802.09791. [Google Scholar]
- Gallego, V.; Naveiro, R.; Roca, C.; Rios Insua, D.; Campillo, N.E. AI in drug development: A multidisciplinary perspective. Mol. Divers. 2021, 25, 1461–1479. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Rao, A.; Fernandez-Maloigne, C.; Calhoun, V.; Menegaz, G. Explainable AI (XAI) In Biomedical Signal and Image Processing: Promises and Challenges. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 1531–1535. [Google Scholar]
- Malinverno, L.; Barros, V.; Ghisoni, F.; Visonà, G.; Kern, R.; Nickel, P.J.; Ventura, B.E.; Šimić, I.; Stryeck, S.; Manni, F.; et al. A historical perspective of biomedical explainable AI research. Patterns 2023, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yeh, C.K.; Hsieh, C.Y.; Suggala, A.; Inouye, D.I.; Ravikumar, P.K. On the (in) fidelity and sensitivity of explanations. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2019; Volume 32. [Google Scholar]
- Han, H.; Liu, X. The challenges of explainable AI in biomedical data science. BMC Bioinform. 2021, 22, 443. [Google Scholar] [CrossRef]
- Saarela, M.; Geogieva, L. Robustness, stability, and fidelity of explanations for a deep skin cancer classification model. Appl. Sci. 2022, 12, 9545. [Google Scholar] [CrossRef]
- Bang, I.; Choi, H.J. Structural features of β2 adrenergic receptor: Crystal structures and beyond. Mol. Cells 2015, 38, 105–111. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Ballesteros, J.A.; Weinstein, H. Integrated methods for the construction of three-dimensional models and computational probing of structure-function relations in G protein-coupled receptors. In Methods in Neurosciences; Elsevier: Amsterdam, The Netherlands, 1995; Volume 25, pp. 366–428. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Gutiérrez-Mondragón, M.A.; König, C.; Vellido, A. Layer-Wise Relevance Analysis for Motif Recognition in the Activation Pathway of the β 2-Adrenergic GPCR Receptor. Int. J. Mol. Sci. 2023, 24, 1155. [Google Scholar] [CrossRef] [PubMed]
- Lans, I.; Dalton, J.A.; Giraldo, J. Helix 3 acts as a conformational hinge in Class A GPCR activation: An analysis of interhelical interaction energies in crystal structures. J. Struct. Biol. 2015, 192, 545–553. [Google Scholar] [CrossRef]
- Gutiérrez-Mondragón, M.A.; König, C.; Vellido, A. Recognition of Conformational States of a G Protein-Coupled Receptor from Molecular Dynamic Simulations Using Sampling Techniques. In Proceedings of the International Work-Conference on Bioinformatics and Biomedical Engineering (IWBBIO), Gran Canaria, Spain, 12–14 July 2023; pp. 3–16. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1322–1328. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lamari, M.; Azizi, N.; Hammami, N.E.; Boukhamla, A.; Cheriguene, S.; Dendani, N.; Benzebouchi, N.E. SMOTE–ENN-based data sampling and improved dynamic ensemble selection for imbalanced medical data classification. In Proceedings of the Advances on Smart and Soft Computing: Proceedings of the International Conference on Advances in Computational Intelligence (ICACI), Chongqing, China, 14–16 May 2021; pp. 37–49. [Google Scholar]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Kumar, V.; Lalotra, G.S.; Sasikala, P.; Rajput, D.S.; Kaluri, R.; Lakshmanna, K.; Shorfuzzaman, M.; Alsufyani, A.; Uddin, M. Addressing binary classification over class imbalanced clinical datasets using computationally intelligent techniques. Healthcare 2022, 10, 1293. [Google Scholar] [CrossRef]
- Japkowicz, N. Learning from imbalanced data sets: A comparison of various strategies. In AAAI Workshop on Learning from Imbalanced Data Sets; Citeseer: Princeton, NJ, USA, 2000; Volume 68, pp. 10–15. [Google Scholar]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; pp. 243–248. [Google Scholar]
- Ling, C.X.; Sheng, V.S. Cost-sensitive learning and the class imbalance problem. Encycl. Mach. Learn. 2008, 2011, 231–235. [Google Scholar]
- Fernando, K.R.M.; Tsokos, C.P. Dynamically weighted balanced loss: Class imbalanced learning and confidence calibration of deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2940–2951. [Google Scholar] [CrossRef] [PubMed]
- van der Meer, R.; Oosterlee, C.W.; Borovykh, A. Optimally weighted loss functions for solving pdes with neural networks. J. Comput. Appl. Math. 2022, 405, 113887. [Google Scholar] [CrossRef]
- Guo, X.; Yin, Y.; Dong, C.; Yang, G.; Zhou, G. On the class imbalance problem. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 4, pp. 192–201. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. Biodata Min. 2023, 16, 4. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Binder, A.; Lapuschkin, S.; Samek, W.; Müller, K.R. Layer-wise relevance propagation: An overview. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Samek, W., Montavon, G., Vedaldi, A., Hansen, L., Müller, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 193–209. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2017; Volume 30. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Zhang, Y.; Song, K.; Sun, Y.; Tan, S.; Udell, M. “Why Should You Trust My Explanation?” Understanding Uncertainty in LIME Explanations. arXiv 2019, arXiv:1904.12991. [Google Scholar]
- Kumar, I.E.; Venkatasubramanian, S.; Scheidegger, C.; Friedler, S. Problems with Shapley-value-based explanations as feature importance measures. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; Volume 119, pp. 5491–5500. [Google Scholar]
- Dombrowski, A.K.; Anders, C.J.; Müller, K.R.; Kessel, P. Towards robust explanations for deep neural networks. Pattern Recognit. 2022, 121, 108194. [Google Scholar] [CrossRef]
- Fel, T.; Vigouroux, D.; Cadène, R.; Serre, T. How good is your explanation? algorithmic stability measures to assess the quality of explanations for deep neural networks. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 720–730. [Google Scholar]
- Samek, W.; Binder, A.; Montavon, G.; Lapuschkin, S.; Müller, K.R. Evaluating the visualization of what a deep neural network has learned. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2660–2673. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Bohanec, M. Perturbation-based explanations of prediction models. In Human and Machine Learning: Visible, Explainable, Trustworthy and Transparent; Springer: Cham, Switzerland, 2018; pp. 159–175. [Google Scholar]
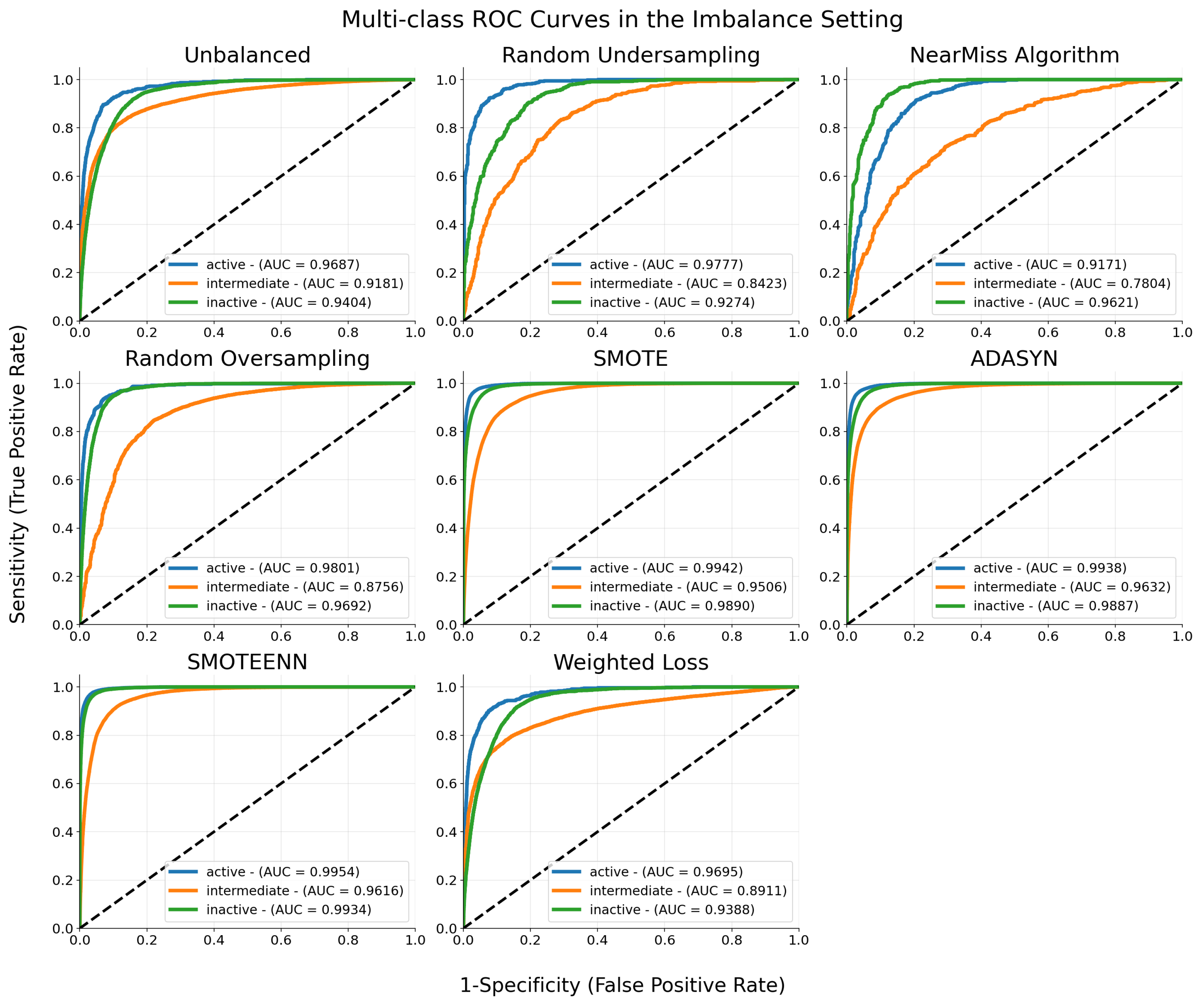
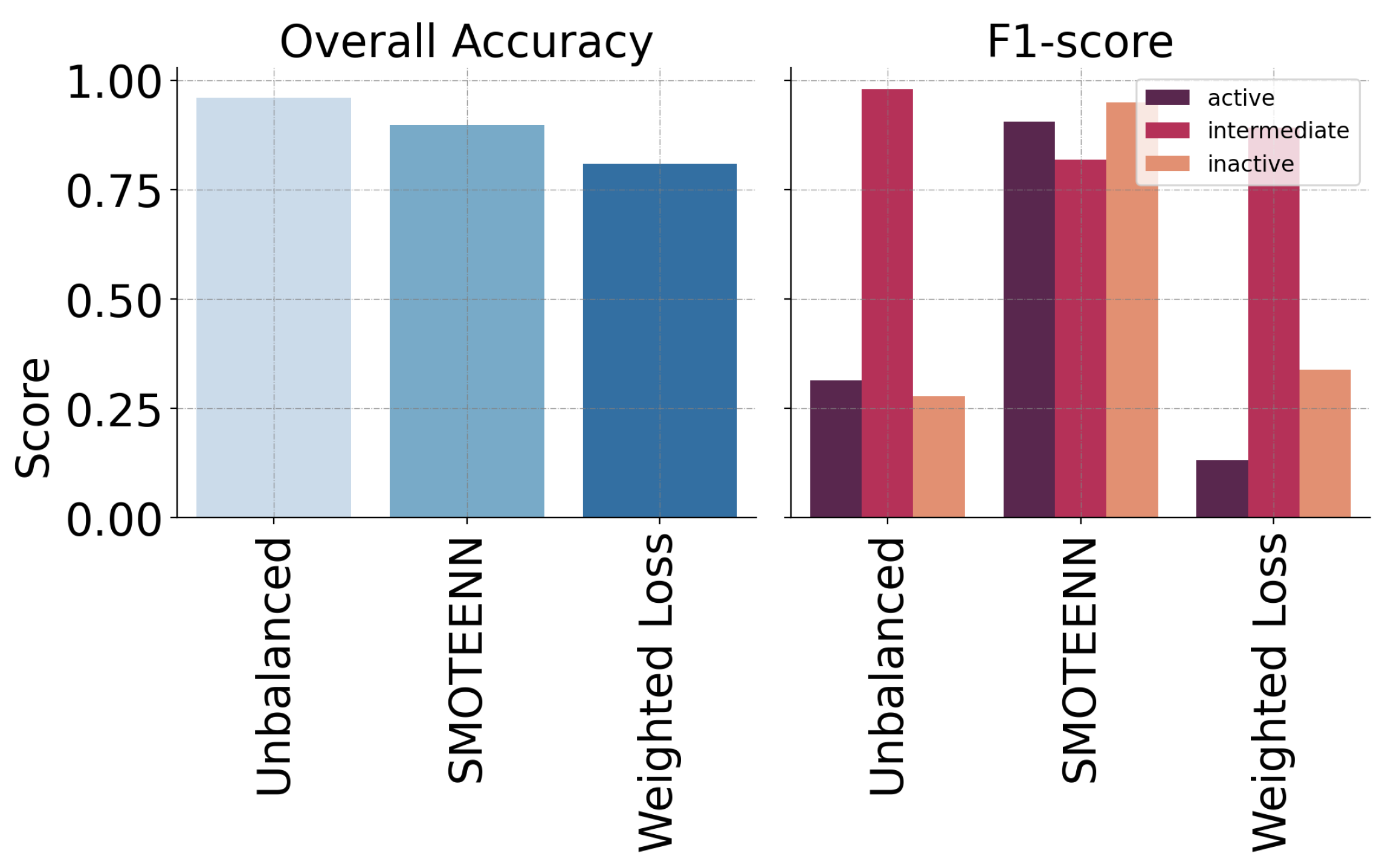




| Model | Precision | Recall | F1-Score |
|---|---|---|---|
| 1D-CNN | 0.915593 | 0.906689 | 0.908289 |
| DT | 0.710800 | 0.574343 | 0.580146 |
| RF | 0.685715 | 0.564699 | 0.484628 |
| Model | Explainable Method | Imbalance Method | Cosine Similarity |
|---|---|---|---|
| 1D-CNN | Saliency Maps | ADASYN | 0.9882 |
| 1D-CNN | Saliency Maps | SMOTEENN | 0.9884 |
| 1D-CNN | Saliency Maps | Weighted Loss | 0.9884 |
| 1D-CNN | LRP | ADASYN | 0.5306 |
| 1D-CNN | LRP | SMOTEENN | 0.0296 |
| 1D-CNN | LRP | Weighted Loss | −0.0565 |
| 1D-CNN | LIME | ADASYN | 0.0217 |
| 1D-CNN | LIME | SMOTEENN | 0.03145 |
| 1D-CNN | LIME | Weighted Loss | −0.0407 |
| 1D-CNN | SHAP | ADASYN | 0.3126 |
| 1D-CNN | SHAP | SMOTEENN | 0.2870 |
| 1D-CNN | SHAP | Weighted Loss | 0.3225 |
| DT | Feature Importance | ADASYN | 0.3605 |
| DT | Feature Importance | SMOTEEN | 0.3016 |
| RF | Feature Importance | ADASYN | 0.8704 |
| RF | Feature Importance | SMOTEEN | 0.8953 |
| Model | Explainable Method | Imbalance Method | Cosine Similarity |
|---|---|---|---|
| 1D-CNN | Saliency Maps | ADASYN | 0.9531 |
| 1D-CNN | Saliency Maps | SMOTEENN | 0.9506 |
| 1D-CNN | Saliency Maps | Weighted Loss | 0.9545 |
| 1D-CNN | LRP | ADASYN | 0.6550 |
| 1D-CNN | LRP | SMOTEENN | 0.6393 |
| 1D-CNN | LRP | Weighted Loss | 0.6649 |
| 1D-CNN | LIME | ADASYN | 0.6172 |
| 1D-CNN | LIME | SMOTEENN | 0.5908 |
| 1D-CNN | LIME | Weighted Loss | 0.5772 |
| 1D-CNN | SHAP | ADASYN | 1.0000 |
| 1D-CNN | SHAP | SMOTEENN | 1.0000 |
| 1D-CNN | SHAP | Weighted Loss | 1.0000 |
| DT | Feature Importance | ADASYN | 1.0000 |
| DT | Feature Importance | SMOTEEN | 1.0000 |
| RF | Feature Importance | ADASYN | 1.0000 |
| RF | Feature Importance | SMOTEEN | 1.0000 |
| State | Residue Name | Transmembrane | Mean Contribution |
|---|---|---|---|
| active | ASN51 | H1 | −0.0649 |
| active | LEU53 | H1 | 0.0566 |
| active | ALA57 | H1 | −0.0640 |
| active | GLU62 | ICL1 | −0.0594 |
| active | VAL67 | H2 | −0.0392 |
| active | MET82 | H2 | −0.0418 |
| active | ILE94 | H2 | 0.0419 |
| active | LEU95 | H2 | 0.0848 |
| active | MET96 | H2 | 0.0423 |
| active | MET98 | ECL1 | −0.0461 |
| active | SER137 | ICL2 | −0.0380 |
| active | TYR141 | ICL2 | 0.0388 |
| active | GLN142 | ICL2 | 0.0579 |
| active | LEU145 | ICL2 | −0.0624 |
| active | ASN148 | H4 | 0.0428 |
| active | VAL152 | H4 | −0.0462 |
| active | ILE153 | H4 | −0.0865 |
| active | MET156 | H4 | 0.0341 |
| active | VAL157 | H4 | 0.0462 |
| active | TRP158 | H4 | 0.0440 |
| active | ILE159 | H4 | 0.0389 |
| active | SER165 | H4 | −0.0547 |
| active | PHE166 | H4 | −0.0610 |
| active | LEU167 | H4 | −0.0669 |
| active | HIS178 | ECL2 | 0.0518 |
| active | GLN179 | ECL2 | 0.1001 |
| active | GLU180 | ECL2 | 0.0514 |
| active | GLN197 | H5 | −0.0591 |
| active | ALA198 | H5 | −0.1251 |
| active | TYR199 | H5 | −0.0477 |
| active | ALA200 | H5 | −0.0334 |
| active | ILE201 | H5 | 0.0375 |
| active | ALA202 | H5 | 0.0496 |
| active | SER203 | H5 | 0.0515 |
| active | GLN299 | ECL3 | −0.0319 |
| active | ASN312 | H7 | 0.0451 |
| active | TYR316 | H7 | −0.0420 |
| active | LEU339 | C-Terminus | 0.0428 |
| intermediate | VAL31 | H1 | 0.0926 |
| intermediate | TRP32 | H1 | 0.0788 |
| intermediate | VAL33 | H1 | 0.2100 |
| intermediate | VAL34 | H1 | 0.2947 |
| intermediate | GLY35 | H1 | 0.3588 |
| intermediate | MET36 | H1 | −0.1127 |
| intermediate | GLY37 | H1 | −0.3433 |
| intermediate | ILE38 | H1 | −0.2234 |
| intermediate | VAL39 | H1 | −0.5593 |
| intermediate | MET40 | H1 | −0.8689 |
| intermediate | SER41 | H1 | −1.0831 |
| intermediate | LEU42 | H1 | −0.1794 |
| intermediate | ILE43 | H1 | 0.6054 |
| intermediate | VAL44 | H1 | 1.5149 |
| intermediate | LEU45 | H1 | 0.6725 |
| intermediate | ALA46 | H1 | 0.3262 |
| intermediate | ILE47 | H1 | −0.1183 |
| intermediate | VAL48 | H1 | −0.1742 |
| intermediate | PHE49 | H1 | −0.1774 |
| intermediate | GLY50 | H1 | −0.0678 |
| intermediate | VAL54 | H1 | 0.0348 |
| intermediate | ILE55 | H1 | 0.0429 |
| intermediate | GLN65 | ICL1 | −0.0533 |
| intermediate | THR68 | H2 | 0.0326 |
| intermediate | TRP99 | ECL1 | 0.0437 |
| intermediate | THR100 | ECL1 | 0.0389 |
| intermediate | ALA150 | H4 | 0.0857 |
| intermediate | LEU155 | H4 | −0.0386 |
| intermediate | ASN301 | ECL3 | 0.0493 |
| Explainability | State | Residue | Transmembrane | Mean Contribution |
|---|---|---|---|---|
| ADASYN | intermediate | ILE43 | H1 | 0.5594 |
| ADASYN | intermediate | GLY37 | H1 | −0.1150 |
| ADASYN | intermediate | MET36 | H1 | 0.0144 |
| ADASYN | intermediate | LEU42 | H1 | −0.0936 |
| ADASYN | intermediate | ILE47 | H1 | −0.1187 |
| ADASYN | intermediate | VAL39 | H1 | −0.0259 |
| SMOTEENN | intermediate | ILE43 | H1 | 0.4544 |
| SMOTEENN | intermediate | SER41 | H1 | −0.1997 |
| SMOTEENN | intermediate | GLY37 | H1 | −0.1156 |
| SMOTEENN | intermediate | MET36 | H1 | 0.1013 |
| SMOTEENN | intermediate | LEU42 | H1 | −0.0684 |
| SMOTEENN | intermediate | VAL34 | H1 | 0.0175 |
| SMOTEENN | intermediate | ILE47 | H1 | −0.0856 |
| SMOTEENN | intermediate | VAL39 | H1 | −0.0130 |
| SMOTEENN | intermediate | VAL48 | H1 | 0.0131 |
| Weighted Loss | intermediate | ILE43 | H1 | 0.1535 |
| Weighted Loss | intermediate | SER41 | H1 | −0.1194 |
| Weighted Loss | intermediate | GLY37 | H1 | −0.1190 |
| Weighted Loss | intermediate | MET36 | H1 | 0.0838 |
| Weighted Loss | intermediate | LEU42 | H1 | −0.0501 |
| Weighted Loss | active | ILE47 | H1 | 0.3491 |
| Weighted Loss | intermediate | VAL39 | H1 | 0.0416 |
| Weighted Loss | intermediate | VAL48 | H1 | 0.0164 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Mondragón, M.A.; Vellido, A.; König, C. A Study on the Robustness and Stability of Explainable Deep Learning in an Imbalanced Setting: The Exploration of the Conformational Space of G Protein-Coupled Receptors. Int. J. Mol. Sci. 2024, 25, 6572. https://doi.org/10.3390/ijms25126572
Gutiérrez-Mondragón MA, Vellido A, König C. A Study on the Robustness and Stability of Explainable Deep Learning in an Imbalanced Setting: The Exploration of the Conformational Space of G Protein-Coupled Receptors. International Journal of Molecular Sciences. 2024; 25(12):6572. https://doi.org/10.3390/ijms25126572
Chicago/Turabian StyleGutiérrez-Mondragón, Mario A., Alfredo Vellido, and Caroline König. 2024. "A Study on the Robustness and Stability of Explainable Deep Learning in an Imbalanced Setting: The Exploration of the Conformational Space of G Protein-Coupled Receptors" International Journal of Molecular Sciences 25, no. 12: 6572. https://doi.org/10.3390/ijms25126572
APA StyleGutiérrez-Mondragón, M. A., Vellido, A., & König, C. (2024). A Study on the Robustness and Stability of Explainable Deep Learning in an Imbalanced Setting: The Exploration of the Conformational Space of G Protein-Coupled Receptors. International Journal of Molecular Sciences, 25(12), 6572. https://doi.org/10.3390/ijms25126572







