Next Article in Journal
Investigating the Effects of Diet-Induced Prediabetes on Skeletal Muscle Strength in Male Sprague Dawley Rats
Previous Article in Journal
Influence of Various Strontium Formulations (Ranelate, Citrate, and Chloride) on Bone Mineral Density, Morphology, and Microarchitecture: A Comparative Study in an Ovariectomized Female Mouse Model of Osteoporosis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 25
Issue 7
10.3390/ijms25074074
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Molecular Structure of Salicylic Acid and Its Hydrates: A Rotational Spectroscopy Study

by
Alberto Macario
1,2,
Juan Carlos López
1 and
Susana Blanco
1,*
1
Departamento de Química Física y Química Inorgánica, Facultad de Ciencias, IU CINQUIMA, Universidad de Valladolid, 47011 Valladolid, Spain
2
Département de Physique Moléculaire, IPR (Institut de Physique de Rennes), CNRS-UMP 6251, Université de Rennes, F-35000 Rennes, France
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2024, 25(7), 4074; https://doi.org/10.3390/ijms25074074
Submission received: 7 March 2024 / Revised: 1 April 2024 / Accepted: 3 April 2024 / Published: 6 April 2024
(This article belongs to the Section Physical Chemistry and Chemical Physics)
Browse Figures
Review Reports Versions Notes

Abstract

:
We present a study of salicylic acid and its hydrates, with up to four water molecules, done by employing chirped-pulse Fourier transform microwave spectroscopy. We employed the spectral data set of the parent, 13C, and 2H isotopologues to determine the molecular structure and characterize the intra- and intermolecular interactions of salicylic acid and its monohydrate. Complementary theoretical calculations were done to support the analysis of the experimental results. For the monomer, we analyzed structural properties, such as the angular-group-induced bond alternation (AGIBA) effect. In the microsolvates, we analyzed their main structural features dominated by the interaction of water with the carboxylic acid group. This work contributes to seeding information on how water molecules accumulate around this group. Moreover, we discussed the role of cooperative effects further stabilizing the observed inter- and intramolecular hydrogen bond interactions.

1. Introduction

Salicylic acid (2-hydroxybenzoic acid, SA) is a widely used compound with applications in food science and pharmacology. It is a plant hormone that plays an important role in plant defense against stress through different mechanisms, having a significant impact on photosynthesis, transpiration, the uptake and transport of ions, or plant growth [1]. SA was first identified in willow (genus Salix) bark, which has been used since ancient times to alleviate pain and reduce fevers due to its analgesic, antipyretic, and anti-inflammatory properties [2]. Furthermore, SA is the main precursor of aspirin [3]. Nowadays, SA is widely employed in dermatology as a keratolytic and bacteriostatic agent [4] or for the treatment of acne, psoriasis, and other cutaneous diseases [5]. All these biological activities related to the physical and chemical properties of SA are defined by the molecular structure of this biomolecule.
The molecular structure of SA is governed by the ortho disposition of its two functional carboxyl and hydroxyl groups. The possible intramolecular interactions in ortho isomers confer them properties different from those corresponding to meta or para derivatives [6,7]. Moreover, in benzene derivatives, the presence of functional groups that are asymmetric, with respect to the substitution axis of the phenyl ring, is associated with an alteration of the ring structure and the electronic aromatic behavior. This is due to the stabilization of one of the canonical forms of the aromatic ring over the other, a phenomenon known as the angular-group-induced bond alternation (AGIBA) effect [8,9]. The knowledge of the molecular structure of SA and of the interaction between its two groups in ortho disposition have been the subject of different investigations [10,11,12,13,14,15]. Two conformers of SA, I and II (see Figure 1), were reported to exist from a study of the jet-cooled IR-UV double-resonance spectrum [10]. By contrast, only the global minimum I form was identified from the free jet millimeter-wave absorption spectrum [11]. Both I and II conformers present planar structures with an intramolecular hydrogen bond (HB) O-H⋯O from the hydroxyl group to the carbonyl (I) or the hydroxyl (II) moieties of the carboxylic acid group. The molecular structure of SA-I has been determined by electron diffraction [12], suggesting that the intramolecular HB interaction is further stabilized by resonance-assisted hydrogen bonding (RAHB) [16]. In other studies, SA has also been employed as a model of the investigation of keto-enol tautomerism observed by excited-state intramolecular proton transfer (ESIPT) [13,14,15].
Investigation of microsolvated molecular systems is a relevant subject in chemistry and biochemistry [17,18,19]. Microwave spectroscopy techniques are exceptional tools to determine their structures, adequate for this purpose due to their inherent high resolution [20]. There are a high number of microwave studies of microsolvated organic molecules [19,21,22,23,24,25], providing models for a better understanding of the water interactions with biomolecules [26], of hydrogen bond (HB) cooperativity [27], and of the way in which solvation induces structural changes in the solute molecule [22,23,27,28]. These studies have also led to an understanding of the role of association processes and the interplay between the self-association of water and solvation. With few exceptions [22], in complexes with several H2O molecules, water prefers to link other water molecules, forming chains or cycles. When the solute has only one HB acceptor site, the structures reflect a balance between maximizing the number of water-solute interactions and the minimum-energy structures of the pure water clusters [21]. In solutes with double HB donor/acceptor character, water molecules close sequential cycles, as observed in amides [28], acids [29,30,31,32], or esters [33]. In the last years, studies of molecules forming clusters with a high number of water molecules has increased. The microsolvation of benzene derivatives is also of interest [34], since they are archetypal molecules in chemistry, and their water complexes serve as model chromophores to investigate solute-solvent interactions. Understanding these interactions in aromatic compounds is fundamentally important for studying more complex systems encountered in many natural chemical reactions [34]. In the specific case of SA, the study of its microsolvates is particularly relevant and of interest in atmospheric chemistry [35].
In a recent study [36], we observed the presence of SA as a thermal recombination product of o-anisic acid, together with methyl salicylate [37], methyl 2-methoxybenzoate [38], and their complexes with water [38,39]. Water could interact with SA in multiple ways due to the presence of several donor or acceptor groups in this molecule. As inferred from gas-phase microsolvation studies of related acids [29,31,40,41], the most favorable interaction sites correspond to the carboxyl group, with which water molecules may easily close cycles. Another aspect to consider is how microsolvation affects intramolecular interactions. A special situation is observed in the monohydrate of o-anisic acid [36], where each of the two observed conformers of the monomer forms its corresponding water cluster. One complex maintains an intramolecular interaction with a trans-COOH arrangement, and the other presents a cis carboxylic acid disposition that establishes the typical sequential ring of the carboxyl group with water.
In this work, we have taken advantage of the potential of the chirped-pulse Fourier transform microwave spectroscopy (CP-FTMW) technique, aided by supersonic jets, to study SA microsolvates with multiple water molecules. We present the gas-phase molecular structure of SA, determined through extensive isotopic species measurements. We have experimentally analyzed the structural properties of SA, such as the AGIBA effect [8,9] and the intramolecular HB interaction. We have observed and analyzed the spectra of several SA hydrates with up to four water molecules to gain information on how water molecules accumulate around an acid group, as well as information on the structures adopted by these clusters. Another aspect on which we have focused our work is the identification of pieces of evidence of cooperative effects that further stabilize HB intramolecular interactions in the complexes [42] as the number of associated interacting molecules increases.

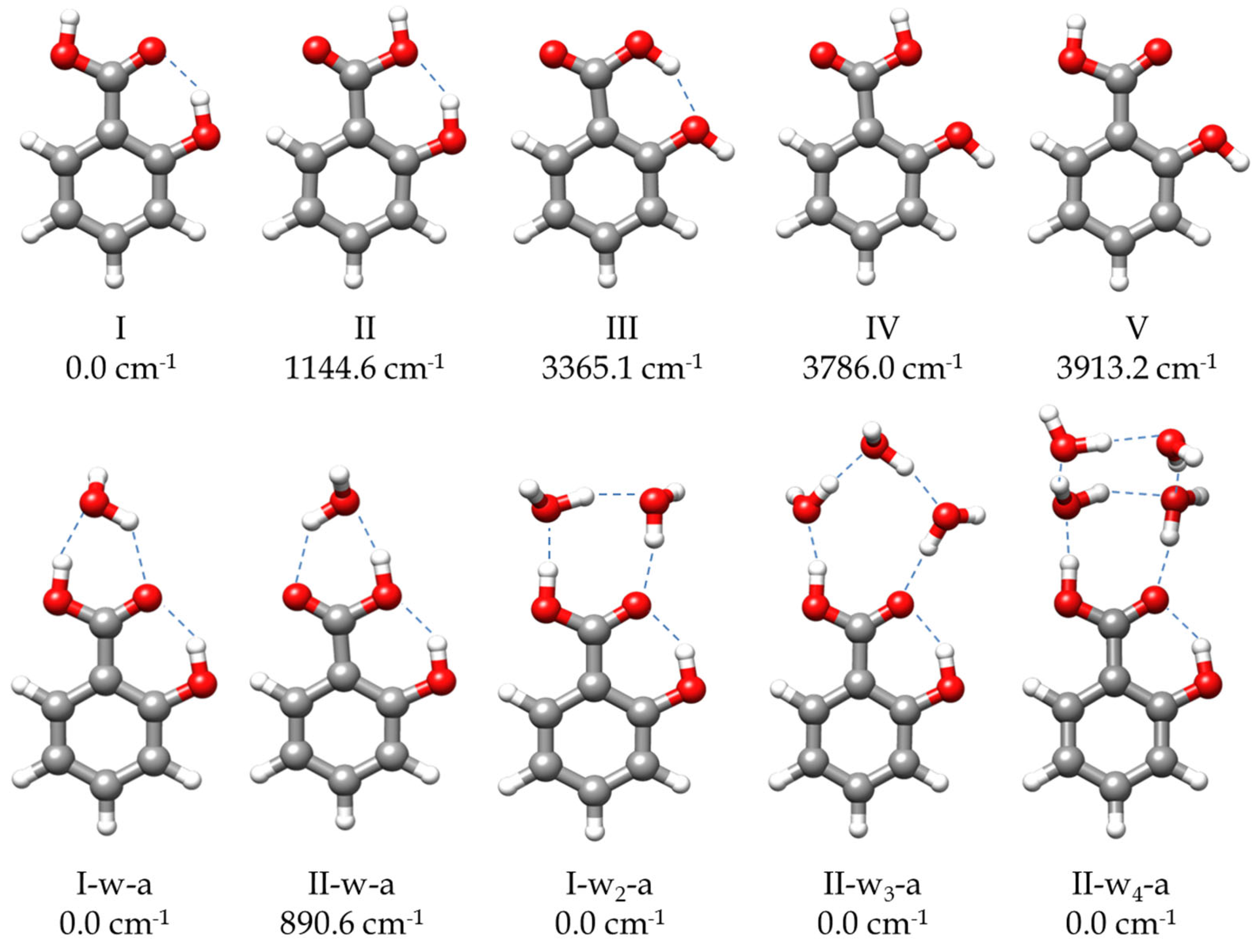
2. Results and Discussion

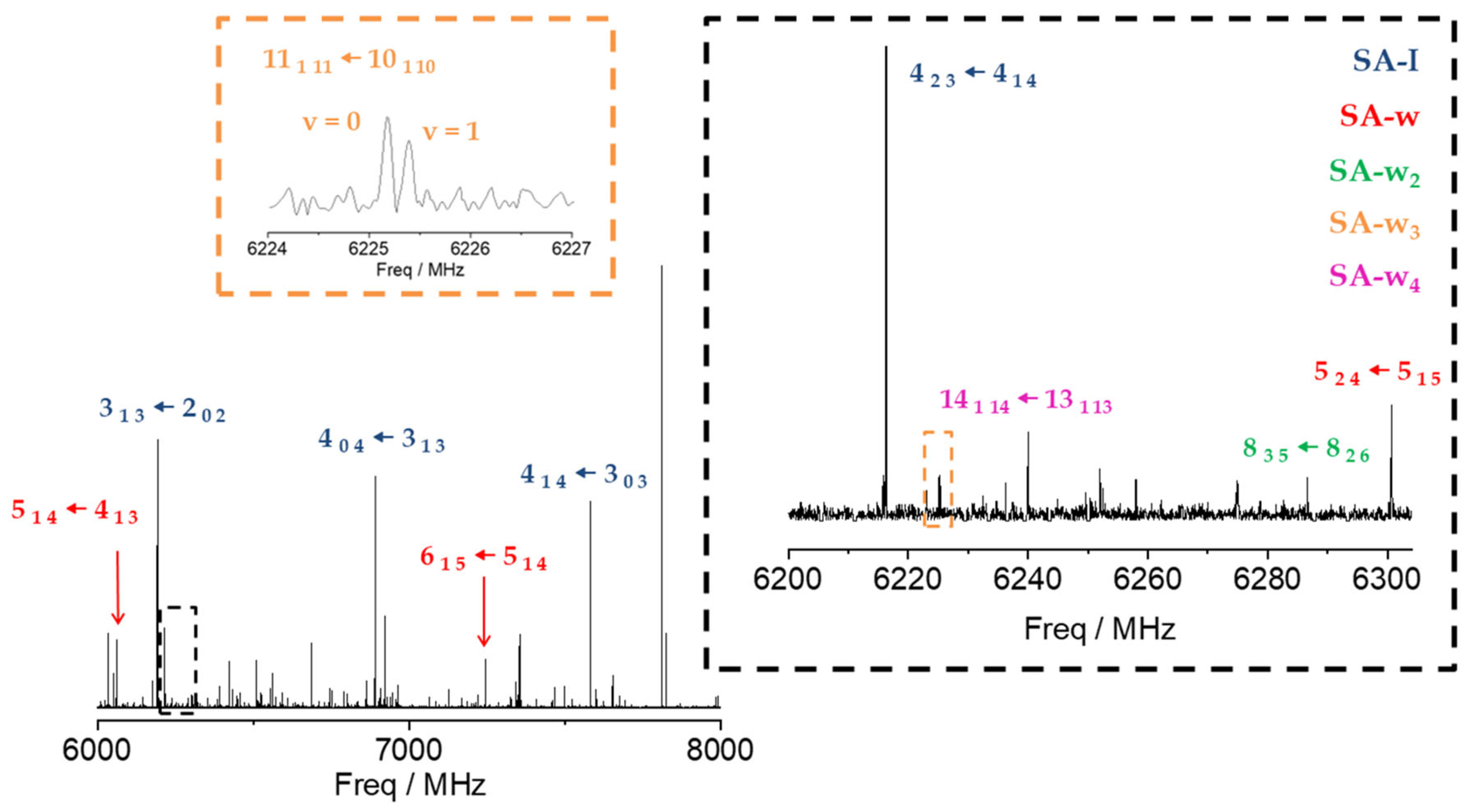
2.1. Rotational Spectrum

To address the rotational spectrum of SA (see Figure 2 and Figure S1), we used the rotational parameters determined in the millimeter-wave study [11] to predict its rotational spectrum in the 2–8 GHz microwave region. We measured a new set of 64 µb-type R- and Q–branch transitions, with J ranging from 1 to 10. The analysis of the spectrum was conducted using Watson’s semirigid rotor Hamiltonian in the A reduction and the Ir representation [43], including the transitions previously observed [11]. The resulting rotational parameters are compared with those previously obtained from millimeter-wave data [11] and with the theoretical predictions in Table 1. The high S/N ratio allowed us to identify the spectra of all the 13C isotopologues in their natural abundances, as shown in Figure S1. Moreover, when we included deuterium oxide (D2O) into the reservoir adapted to the carrier gas line, the deuterium atoms substituted the hydroxyl and carboxyl hydrogen atoms. As a result, we observed the spectra of the mono- and disubstituted deuterated species. The analyses of the spectra of the isotopologues were conducted using the same Hamiltonian used for the parent, with the quartic centrifugal distortion constants fixed to the values determined for the parent species. All the rotational parameters determined are listed in Tables S6 and S7. No other SA conformations were identified in the rotational spectrum in agreement with the calculated relative energies and the predicted values of the dipole moments (Figure 1 and Table S1).
Once the transitions observed for the monomer and its isotopologues were removed, we were able to identify the spectrum of a new species with a set of over 60 µa-type R-branch and µb-type R- and Q–branch transitions. No µc-type lines were observed. These lines were attributed to a monohydrated SA-w species (Figure 2). The analysis of this spectrum gave the set of rotational parameters listed in Table 2. A conformational search of the monohydrated clusters for the two most stable conformers of SA was performed theoretically by exploring the possible interactions of water and SA, both with a dual proton donor/proton acceptor character (Figure S3). The values of the experimental rotational constants are close to those predicted for the two lower energy conformers of the monohydrated cluster, I-w-a and II-w-a (see Figure 1 and Table 2). There are two reasons to consider conformer I-w-a as the observed species. Firstly, species I is the only one observed in the spectra for the SA monomer, so it will be the only species present in the molecular jet to form any cluster [36]. Secondly, the monohydrated cluster I-w-a is predicted to be the global minimum, being 900 cm−1 more stable than conformer II-w-a (Figure 1). This assignment was unambiguously corroborated by the measurements of monodeuterated isotopologues and the subsequent study of the monohydrate molecular structure (see below). No other monohydrated forms of SA were identified.
To explore the complexes of SA with a higher number of water molecules, conformational searches were conducted for SA-w2, SA-w3, and SA-w4 clusters using the CREST (Conformer-Rotamer Ensemble Sampling Tool) application [44] followed by B3LYP-D3/6-311++G(d,p) [45,46,47,48] structure optimizations. Some of the resulting structures are given in Figures S4–S6, and the spectroscopic parameters are given in Tables S3–S5. From the predicted energies, it can be deduced that the predicted preferred interaction sites are related to the COOH group. As examples, we have included some of the possible complexes with water molecules closing rings with the phenol group that have, in all cases, rather high energies relative to the global minima.
In the next step, we identified a weaker spectrum consisting of over 125 µa-type R-branch and µb-type R- and Q–branch transitions. These transitions were analyzed using the same Hamiltonian as before, and a set of rotational constants related to a dihydrated cluster SA-w2 was determined (Table 2). Due to its weak intensity, the deuterated species could not be identified in the spectra enriched with deuterium oxide. As with the monohydrated species, the set of rotational constants is comparable to those predicted for the I-w2-a and II-w2-a species (see Table 2). Following the same arguments considered for the monohydrated complex, the dihydrated species was identified as the predicted global minimum I-w2-a conformer.
After removing all the measured lines of the SA-w and SA-w2 complexes, there was still a dense spectrum of weaker lines. Searches for the spectra of the SA-w3 cluster led to the identification of a series of doublets attributable to one of such complexes. Most of the µa-type R-branch and µb-type R- and Q-branch transitions were split by 50–200 kHz with doublets of the same intensity (see Figure 2). This feature has been observed in similar trihydrates such as formamide-w3 [28], ethyl carbamate-w3 [49], or methyl carbamate-w3 [50], where the chain of three water molecules closes a cycle with the amide group. Considering the four most stable conformers that present this water trimer disposition with the acid group of SA, only two have rotational constants close to the experimental ones (Table 3 and Table S4). Nevertheless, the observed conformer was assigned to the global minimum I-w3-a, since the observed transitions are only in agreement with the selection rules derived from the values of the predicted dipole moment components for this conformer. A two-states Hamiltonian, in this case using Watson’s semirigid S reduction [43], including Coriolis coupling terms [51], was used to analyze the spectrum. The centrifugal distortion constants were kept equal for both states. It was possible to determine the Coriolis coupling term and the energy difference between both vibrational states. The results are summarized in Table 3.
Finally, with the remaining lines, we were able to assign another spectrum attributable to an SA-w4 cluster. The spectrum is composed of over 170 µa- and µb-type transitions. By comparing the values of the rotational constants and the observed selection rules with the theoretical values and the predicted dipole moments (Table S5), the observed species can be identified with one of the two most stable conformers. We tentatively assigned the observed species to the global minimum I-w4-a (Table S5). A summary of the results is shown in Table 4.
All the measured transitions (Tables S17–S24) and rotational determined parameters (Tables S6 and S7) for SA and its hydrated clusters are given in the Supporting Information.

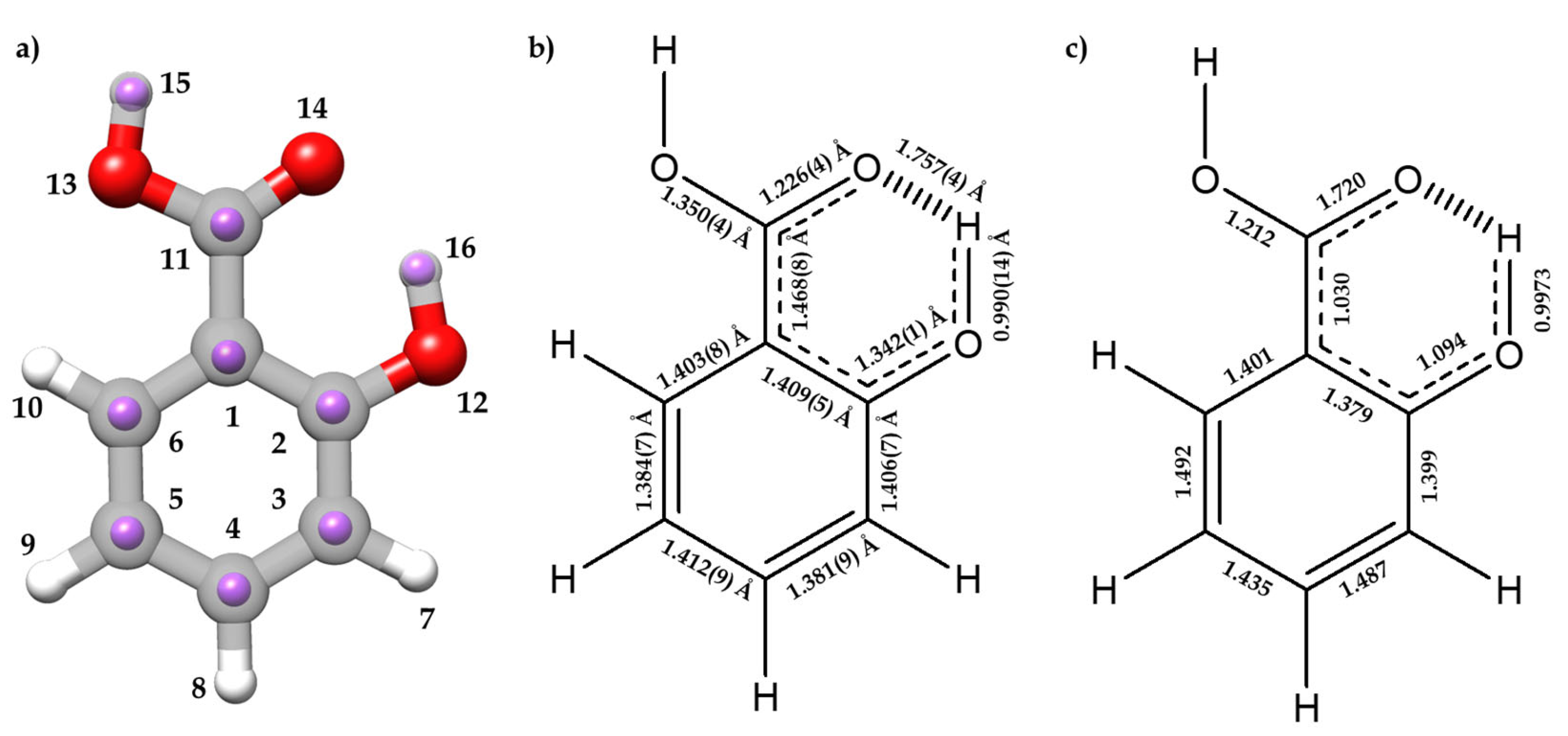
2.2. Molecular Structure

The degree of planarity of a given species is typically discussed in terms of the value of the planar moment of inertia Pcc, which represents the mass extension out of the ab inertial plane. As pointed out in the previous study [11], for an SA monomer, this value is close to zero for the parent species and remains at practically the same values for all observed isotopologues, indicating that all the substituted C atoms, as well as the hydroxyl and carboxyl hydrogen atoms, lie in the ab inertial plane. The small value of Pcc (0.12962(19) uÅ2) could be attributed to vibrational contributions [52]. Moreover, this value is smaller than that obtained for benzoic acid (0.183 uÅ2) [53] and larger than for phenol (0.015 uÅ2) [54]. These differences can be explained in terms of the intramolecular HB interaction in SA, which limits the out-of-plane vibrations of the carboxyl group in SA compared to benzoic acid, demonstrating that the presence of an intramolecular interaction somewhat decreases the flexibility of the molecule. The SA-w complex presents a slightly higher Pcc value (0.51743(24) uÅ2), attributable to the preferred orientation of water interacting with the carboxyl group that leaves the non-interacting H19 atom out of plane, and to possible intermolecular vibrational contributions. Moreover, this value is coherent with a planar skeleton structure. This structure is consistent with the Pcc values of the 2H isotopologues, except for that of the H19 atom, corroborating the conclusion of a planar skeleton structure of an SA-I-w-a complex. The dihydrated SA-I-w2-a conformer presents a value of Pcc (1.38688(57) uÅ2), consistent with two non-interacting water hydrogen atoms out of plane. The planar moment is then compatible with a planar skeleton structure, including both the water oxygen and the interacting hydrogen atoms lying in the ab inertial plane. The value of Pcc for the trihydrated complex (9.9634(11) uÅ2) reflects the contribution of water molecules lying slightly out of the ab plane, as occurs in other related complexes such as formamide–w3 [28], ethyl cabamate-w3 [49], or methyl carbamate–w3 [50]. The same behavior is observed for the SA-w4 complex with a value of Pcc (113.4455(21) uÅ2), much higher than the other values observed in this work, indicating that the configuration of this complex is nonplanar.
The complete sets of experimentally determined rotational constants for the parent species of SA and SA-w and their isotopologues were employed to determine the substitution rs [55,56] and effective r0 [57] structures. The substitution structure employs the Kraitchman method [55] to derive the absolute values of the coordinates of every isotopically substituted atom in the principal inertial axis system of the parent species. The method relies on the variation of the experimental moments of inertia upon substitution. The Costain formula [56] is usually used to estimate coordinate uncertainties. The sign of the obtained coordinates had to be resolved from a reasonable structure. Nevertheless, this method may have problems for atoms lying close to the inertial axes due to zero-point vibrational effects. On the other hand, the effective structure is determined by a least squares fit of all the experimentally determined rotational constants [57]. However, for the SA-I conformer, the effective r0 structure could not be well determined. That was also the case for planar species such as o-anisic acid [36] and anisole [58], due to the effects of vibrational contributions. Following previous works [36], the mass-dependent rm structure [59] was complementarily employed in this case. This structure introduces into the least squares fit a limited set of additional adjustable parameters that consider the mass-dependence of the vibrational contribution to determine equilibrium quality parameters [59,60]. For the SA-w monohydrated species, the rm parameters obtained for the monomer were kept fixed to determine its effective structure. Finally, for the remaining hydrated species (SA-w2, SA-w3, and SA-w4), as no isotopologues could be identified in the spectra, the equilibrium re structures were considered as a good estimation of the molecular geometries, owing to the good agreement between the predicted and the experimental rotational constants.

2.2.1. Monomer (SA-I)

The experimental rs and rm structures, the gas-phase electron diffraction ra structure [12], and the equilibrium re structure are compared in Tables S8 and S9. Figure 3a compares the rs and re structures. Overall, there is a good agreement between the different methods for all geometrical parameters, except for the C1 atom, for which the a rs coordinate results in an imaginary value, due to its proximity to the center of mass of the molecule.
It is worth analyzing the structural features associated to the O⋯H-O HB interaction between the hydroxyl and carboxyl groups, which closes a six-membered planar ring, comparing SA with phenol [54,61] and benzoic acid [12]. The rm (O12-H16) distance (0.990(14) Å) increases when compared to phenol (rs = 0.957(6) Å [54], ra = 0.958(3) Å [61]) (see Figure 3 for atom labelling). On the other hand, the rm (C2-O12) length (1.342(13) Å) decreases (rs = 1.375(5) Å [54]; ra = 1.379(2) Å [61]). Comparing the structure of the carboxyl group with that of benzoic acid [12], the following changes are observed: the C11-O13 length decreases (1.3496(42) Å vs. 1.367(8) Å), the C11=O14 distance remains unchanged (1.2258(42) Å vs. 1.225(6) Å), and the C1-C11 distance decreases (1.4682(83) Å vs. 1.484(6) Å). The distance O14⋯H16 = 1.7569(40) Å is typical of a moderate HB, and thus the enlargement of the O12-H16 distance is a natural consequence of this interaction. The alteration of the rest of the parameters relative to benzoic acid and phenol could be attributed to the effects of a resonance-assisted hydrogen bond (RAHB) [16]. From the determined bond lengths and the predicted bond orders (see Figure 3b,c), C3-C4 and C5-C6 bonds exhibit a higher double-bond character compared to their C2-C3, C4-C5, and C1-C6 neighbor bonds. Thus, the structure of the phenyl ring suggests the prevalence of one of the aromatic canonical benzene forms relative to the other, as it is schematically shown in Figure 3b,c. This prevalence is consistent with the presence of an AGIBA effect governed by the hydroxyl group [8,9]. The fact that the C1-C2 bond may not be consistent with this effect is probably due to the intramolecular hydrogen bond RAHB effects. This competition between the AGIBA and the RAHB effects, which was also observed in o-anisic acid [36], influences the structure of the phenyl ring and contributes to understanding how these effects coexist. NBO calculations support these conclusions (see Tables S10 and S11).

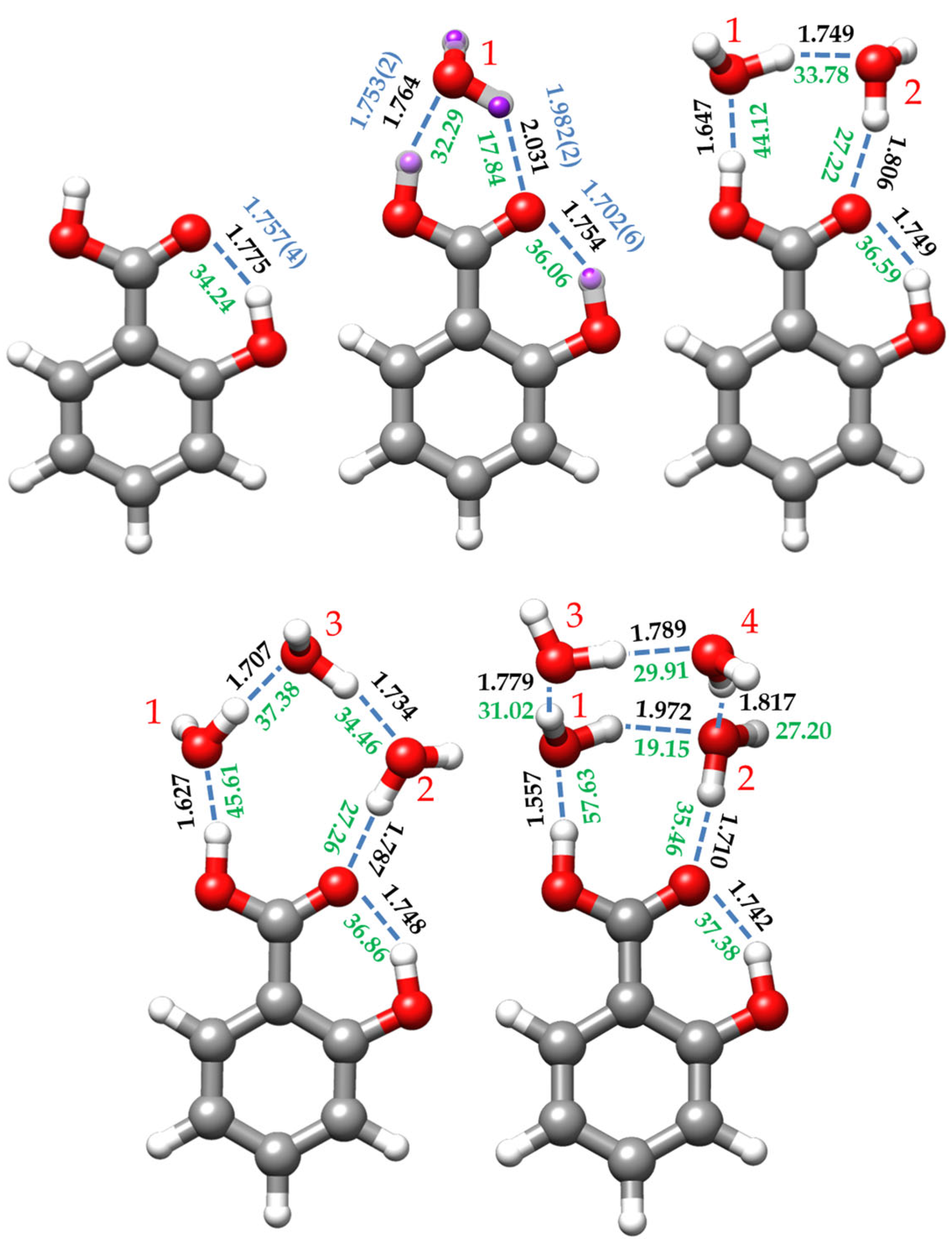
2.2.2. Monohydrated Complex (SA-w)

The rs, r0, and re geometric parameters of the monohydrated complex of SA are compared in Tables S12 and S13 and in Figure 4, where it is possible to observe a good agreement between them. The effective structure was calculated by keeping the phenyl ring rm structure of the monomer fixed in the fit to determine the intra- and intermolecular interactions. The comparison between the monomer and heterodimer re structures, together with the predicted NBO conjugative stabilization energies (Table S10), indicates that the ring structure is not substantially altered by the presence of water. In this complex water closes a six-membered sequential cycle with the carboxyl group through two O-H⋯O hydrogen bonds further stabilized by RAHB, as reflected by the structural parameters and calculated bond orders (Tables S12 and S11, respectively). This sequential cycle is also observed in the benzoic acid-water cluster [40], and in the monohydrated complexes of other benzene derivatives, such as the o-anisic acid [36] or the p-toluic acid [62], or other structures presenting a carboxylic acid such as formic acid [41], acetic acid [31], propanoic acid [29], or the di- and trifluoroacetic acids [30,32].
The dominant intermolecular interaction is the OH⋯Ow HB, reflecting the enhanced acidity of the carboxyl hydrogen atom (see Figure 4). The corresponding distance of 1.7531(24) Å (re = 1.764 Å, Table S12) is shorter than that estimated for the benzoic acid-water complex (1.80 Å) [40]. The C=O⋯Hw HB distance is 1.9819(25) Å (re = 2.031 Å), larger than that reported for the benzoic acid-water heterodimer (1.95 Å) [40]. This could be explained by considering that the carbonyl moiety also supports the intramolecular HB with the ortho hydroxy group, sharing its electron density between both HBs. This, in turn, further stabilizes the dominant intermolecular OH⋯Ow HB interaction.
The formation of the OH⋯Ow HB naturally enlarges the carboxyl O-H distance (r0 = 1.0065(13) Å) relative to that of the SA monomer (rm = 0.969(2) Å), as happens for the benzoic acid-water complex [40]. Even though the distances between C11 and both oxygen atoms could not be experimentally determined, the calculated equilibrium geometries show a shortening in the C-OH bond length and an enlargement of the C=O distance upon formation of the complex. These effects, due to RAHB, are evidenced by the changes in the calculated NBO bond orders and the delocalization energies when comparing the monomer with the monohydrated form (see Tables S10 and S11). The formation of the hydrated complex also seems to affect the geometry of the ortho alcohol group. The intramolecular HB is shorter than that observed for the monomer form, while there is an increase in the O-H bond length (see Tables S8 and S12). In other words, the interaction of water with the acid group appears to increase the strength of the intramolecular HB.
On the other hand, since the monohydrated I-w-a form presents a planar skeleton, we employed the method given by Ouyang and Howard [31] to determine the angle θ between the a principal axis of the monomer form and the intermolecular axis of the monohydrated cluster (see Supplementary Information). As a result, the calculated θ angle for I-w-a species is 7.7°, close to the observed for the water complex of benzoic acid (5°) [40]. Therefore, the intermolecular bonding axis can be considered to be nearly parallel to the a principal inertial axis of the observed monomer species.

2.2.3. Dihydrated Complex (SA-w2)

For the dihydrated SA-w2 species, the non-observation of the spectra of any monosubstituted isotopologue precludes the determination of the r0 and rs structures. However, the good agreement between the experimental and predicted rotational parameters, which is less than 1%, allows us to consider the re structure predicted for conformer I-w2-a as a reliable estimate of the molecular geometry (see Figure 4 and Table S14). In this complex, a dimer of water closes a sequential eight-membered cycle with the carboxylic acid group through a chain of three O-H⋯O HBs. The intramolecular O-H⋯O interaction between the hydroxyl and carbonyl groups is also maintained. This arrangement is similar to other cases of acid dihydrates such as formic acid [41], acetic acid [31], propanoic acid [29], or di- and trifluoroacetic acids [30,32]. In all these cases where the water dimer is closing a cycle with a molecule bearing two closely positioned proton donor and proton acceptor groups, the water molecules lie in the molecular plane or in the plane of the carboxyl group, with the non-interacting hydrogen atoms out of the plane, pointing each one in opposite directions.
In this structure, the water dimer has a distance between the interacting hydrogen and oxygen atoms closer to the equivalent length of the carboxyl group, so the interaction between them presents a natural arrangement less forced than the monohydrated conformer. The hydrogen bond angles are close to the canonical value of 180° (see Table S14). Cooperative forces are favored in homodromic cycles, reinforcing the HB interactions, leading to a shortening of the hydrogen bonds when comparing the HB distances with those of the monohydrate, as shown in Figure 4. As pointed out previously [28], the Ow1⋯Ow2 distance (2.682 Å) is shorter than that reported for water dimer (2.976 Å) [64], and even shorter than the Ow⋯Ow distance (2.78 Å) of the water tetramer [65]. All these O⋯O distances related to hydrogen bonds are listed in Table 5.

2.2.4. Trihydrated Complex (SA-w3)

The complex assigned to the I-w3-a conformer (Figure 1) shows a chain of three water molecules closing a 10-membered ring with the carboxyl group. Compared to the dihydrated complex, the presence of the third water molecule alters the planarity and the dynamics of the molecule. In terms of planarity, the oxygen atom (Ow1), which interacts with the OH-carboxyl moiety (see Figure 4), is close to the SA plane, slightly inclined backward (−4.3°, with respect to the SA ab plane), while the other water molecules lie out of plane. Thus, Ow2 is tilted over 25° and Ow3 around 10° ahead of the ab plane of the monomer (see Table S15). This is consistent with the experimentally observed Pcc value. This deviation from planarity contrasts with other acid trihydrates, such as di- and trifluoroacetic acids [30,32], which are closer to planarity. Similarly, the planar molecule of formamide forms a complex with three water molecules, presenting a Pcc value of 7.03654(6) uÅ2 [28], close to the value observed for SA-w3 (9.963(1) uÅ2, Table 3). Moreover, the most stable conformations for SA-w3 (Figure S5) closely resemble those found for the formamide-w3 complex. Regarding the dynamics of the molecule, the observation of tunneling doublets suggests an inversion of the configuration, similar to what occurs in formamide-w3 [28]. In this study, a path for the inversion of the configuration alternative to that passing by a high-energy planar molecule transition configuration was identified through successive flipping motions of the water molecules. As shown in Figure S12, a similar path is calculated for SA-w3. This periodic pseudorotation function with reasonably low barriers could explain the observed doublets associated with the dynamics created by the presence of the third water molecule.
Based on the predicted equilibrium structure (Table S15) and the NBO calculations (Tables S10 and S11), it appears that the structure of SA, particularly the CO-H and C=O acid structure and the intramolecular HB, is not significantly affected by the presence of the third water molecule. On the other hand, the cooperative effects result in a shortening of all intermolecular HB distances between water molecules and SA compared to SA-w2 and SA-w complexes, as depicted in Figure 4. Examining the distances between the oxygen atoms involved in the HBs (Table 5) reveals a shortening in the distances associated with the HBs between SA and the water molecules (O13⋯Ow1 and O14⋯Ow2), which is pronounced in the OH⋯Ow1 HB.

2.2.5. Tetrahydrated Complex (SA-w4)

In the SA-w4 complex assigned to I-w4-a (Figure 1 and Figure 4), the trend observed for the SA-w1, SA-w2, and SA-w3, where a chain of water molecules closes a cycle with the carboxyl group, breaks down. In this case, it appears as if the SA-w2 complex has captured a second water dimer. The two water molecules interacting with SA in SA-w4 have a similar arrangement as that for SA-w2. This is further corroborated after removing the contribution of the third and fourth water molecules, obtaining the same structure and planar moments as for the SA-w2. The equilibrium structure (see Table S16) also confirms that the oxygen atoms of these two water molecules interacting with the carboxyl group are in the SA plane. As mentioned, the SA-w2 has a favorable geometry for interaction with the carboxyl group. The second water dimer closes a water tetramer cycle in the most favorable arrangement. A similar disposition has been observed for the formamide-w4 complex [67]. In this case, the plane of the water tetramer is bent over 110° (see Table S16), with respect to the plane of the SA-w2 moiety.
In this cluster, as in the previous cases, cooperative effects shorten the HB distances between water and SA. In Figure 4, it can be observed that these distances progressively decrease upon the addition of new water molecules. However, in SA-w4, the water molecules do not form a sequential cycle with the carboxylic acid group. Consequentially, the HB distances between water molecules notably increase, diverging from the trend observed by the SA-w2 and SA-w3 clusters. However, the intramolecular HB is also shortened compared to the other species, indicating further stabilization of cooperativity between the four water molecules and SA. All these pieces of evidence were also corroborated by the NBO analysis (see Tables S10 and S11).

2.3. Cooperative Effects and Dissociation Energies

When discussing HB cooperativity, two aspects are usually considered. One of them involves HBs between molecules with multiple conjugated π bonds (known as RAHB or π-cooperativity) [16,42,68]. An example is the reinforcement of the O-H⋯O intramolecular HB in SA. The second aspect is related to the formation of linear or cyclic chains involving multiple molecules with double roles as HB donors and acceptors. We can consider the hydrates of SA observed in this work as good examples of σ cooperativity. A first consequence of cooperativity is the shortening of the hydrogen bonds, as described in the previous section (Figure 4). In the same way, an increase in the HB energy per bond should be analyzed.
A preliminary approach to analyzing the energies per bond involves calculating the dissociation energies. These have been obtained at MP2/6-311++G(2df,2dp) level using the counterpoise method to correct the energies for the basis set superposition error (BSSE) [69]. We selected this computational level to facilitate comparison with those obtained previously for the benzoic acid—water complex [40]. The positive value of the interaction energy obtained after BSSE correction represents the equilibrium dissociation energy De. The dissociation energies (De) are given in Table 6, together with the average energy per bond. The predicted De value in SA-w is 41.3 kJ/mol, which is close to the 41.9 kJ/mol obtained for the monohydrated cluster of benzoic acid. Hence, the presence of an ortho intramolecular HB does not seem to affect the dissociation energy. It is possible to observe that the average energy per bond increases as the number of water molecules increases along the series SA-w, SA-w2, SA-w3. However, it decreases for the SA-w4 complex consistently with the fact that this cluster is no longer formed through a single cycle as the smaller size clusters. In any case, the energy per bond in the SA-w4 cluster is higher than that calculated for the SA-w heterodimer. The reinforcement of the dissociation energy can be also interpreted as a signature of the σ cooperative effects when the number of water molecules increases in the clusters, and it is especially pronounced when the cluster consists of a cycle, as occurs for SA-w, SA-w2, and SA-w3 complexes.
To individually analyze the strength of each HB, we have performed QTAIM (Quantum Theory of Atoms in Molecules) [70,71] and NCI (Non-Covalent Interaction) [72] calculations. QTAIM analyzes the topology of the electron density to determine bond paths (BP) and bond critical points (BCP), while NCI analysis allows the visualization of the electron density regions associated with non-covalent interactions. Figures S7–S11 show the combined results of these analyses for all the identified SA species. Moreover, using the electronic density provided by the QTAIM analysis at the BCPs, the interaction energies of the HB can be estimated following the empirical equation proposed by Emamian et al. [63]. The interaction energy estimated for the intramolecular HB of SA slightly increases stepwise along the series from the monomer (34.24 kJ/mol) to the tetrahydrated complex (37.38 kJ/mol) (see Figure 4). The energy of the interaction between the carboxylic OH and the interacting water molecule (Ow1) increases its value by approximately 12 kJ/mol from the mono- to the dihydrated cluster, maintains almost the same value in the trihydrate and experiences an increment close to 12 kJ/mol when passing to the tetrahydrated complex. The high value of the energy of this bond and its increment in energy are probably due to the strong acid character of the OH carboxyl proton. The same behavior is reflected in the HB interaction between the C=O of the carboxyl moiety and its water partner (Ow2). It is worth mentioning that the intramolecular HB is dominant in SA and SA-w, while in the other clusters, the carboxyl OH–Ow1 HB is dominant.

3. Materials and Methods

3.1. Experimental Details

The rotational spectra of SA and its SA hydrates were investigated using a broadband chirped-pulse Fourier transform microwave spectrometer (CP-FTMW), as described elsewhere [73]. A commercial sample of SA (m.p. ~158 °C, b.p. ~211 °C), used without further purification, was placed in a reservoir at the heatable nozzle, where it was kept at 150 °C. A water reservoir inserted in the carrier gas line was used to increase the amount of water vapor in the expansion. Ne was used as the carrier gas, with a stagnation pressure of 2 bar and pulses of 700 µs. The gas mixture expanded supersonically into the vacuum chamber through a 0.8 mm nozzle. After a small delay, an arbitrary waveform generator created a 2–8 GHz chirped-pulse of 4 µs duration, which was then amplified to 200 W and broadcasted inside the chamber through a horn antenna, arranged perpendicular to the molecular expansion. The molecular transient emission signal was detected through a second horn antenna, preamplified, recorded with a digital oscilloscope (40 µs gate length), and Fourier-transformed into the frequency domain. For each molecular pulse, the polarization/detection steps were repeated 8 times. This operation sequence was repeated as soon as the optimum vacuum conditions were restored in the chamber, typically operating at a 5 Hz repetition rate. The accuracy of the frequency measurements is estimated to be better than 15 kHz. All the single substituted 13C isotopomers were measured in their natural abundance. To record the spectra of the deuterated isotopologues, a 1:1 mixture of water and deuterium oxide was placed in the reservoir. To measure and analyze the spectra, several available programs were used [74,75,76,77].

3.2. Theoretical Methodology

To explore the conformational landscapes of SA with two, three, and four water molecules, we employed the Conformer-Rotamer Ensemble Sampling (CREST) tool based on the xtb semiempirical extended tight-binding program package [44]. The resulting conformers were further optimized using the B3LYP hybrid density functional [45,46,47,48] with the D3 Grime’s dispersion correction term [78] and the Pople’s 6-311++G(d,p) basis set [79]. In addition to the three conformers predicted in previous work [11], for the monomer forms, we predicted two additional new stable forms, IV and V (see Figure 1 and Figure S2). The results for the hydrated complexes are compiled in Figures S3–S6 and Tables S2–S5. For all the predicted species, harmonic frequency calculations were conducted to ensure that all the calculated conformers are true minima. Natural Bond Orbital (NBO) [80], non-covalent interactions (NCI) [72], and Quantum Theory of Atoms in Molecules (QTAIM) [70,71] analyses were performed for all the experimentally observed species at the same DFT B3LYP-D3/6-311++G(d,p) level. Complementary MP2/6-311++G(2df,2pd) [81] calculations were used to estimate the dissociation energies, employing the counterpoise method to correct the basis set superposition error (BSSE) [69]. All the DFT and MP2 calculations were done using the Gaussian 16 program package [82].

4. Conclusions

In this work, we have recorded the rotational spectra of SA, its monosubstituted 13C isotopologues, several 2H species, and the SA-wn (n = 1–4) hydrates using CP-FTMW spectroscopy. The analysis of the experimental data has been complemented with computational chemistry calculations, including NBO, NCI, and QTAIM analyses, to gain a better understanding of the structural behavior of SA and its hydrates and to characterize the different inter- and intramolecular HB interactions established in these species.
The experimentally determined SA structure has allowed us to characterize the O-H⋯O intramolecular HB between the carboxylic acid and the hydroxyl functional group in ortho position. This HB forms a sequential six-membered cycle further stabilized by π cooperativity (RAHB), which reinforces the planarity and rigidity of the molecule. The AGIBA effect governed by the alcohol group is reflected in the benzene ring bond lengths. However, in proximity to the carboxylic acid or hydroxyl groups, the structure of the ring appears to be dominated by the RAHB effects.
The analysis of the spectra of the hydrated complexes revealed interesting insights into how water aggregates around an acid group. As we have already mentioned, the possible aggregates around the phenolic OH group all have high energies (see Figures S2–S5). In the complex phenol-w, the O-H group acts preferably as a proton donor. The corresponding structure is predicted to be much more stable than the form in which water behaves as the proton donor [83]. However, in the most stable forms of SA, the proton donor capacity of the phenolic OH group is employed in the intramolecular interaction, so the possible SA-water complexes with water interacting with the phenol O-H group are expected to have higher energies, as it is confirmed by the calculations.
In the mono-, di-, and trihydrated clusters, water, or its dimer or trimer, forms a chain, closing a sequential cycle with the two HB donor OH and acceptor C=O ends of the carboxyl group. In the tetrahydrated species, water molecules form a tetramer cycle, bonding to the SA carboxyl group with contacts similar to those established in the SA-w2 cluster. While the mono- and dihydrated clusters maintain the planarity of the heavy atom skeleton of the complex, the spectra of SA-w3 and SA-w4 evidence of their non-planarity, as shown by the planar moment values Pcc, further corroborated by the theoretical computations. The trihydrated cluster has two of the water molecules slightly out of the plane. In the SA-w4 complex, two of the water molecules are in the plane of SA bonded to the carboxylic acid group, keeping the form of SA-w2 species, while the other two lie above the plane of SA in an arrangement where the plane of the water molecules presents an angle of about 110° with respect to the SA-w2 plane. The cyclic structures of the hydrates of SA are comparable with those reported by Howard and coworkers on organic acid mono-, di-, and trihydrates [29,30,31,32]. However, in contrast with the non-planar heavy atom skeleton observed here for the trihydrate of SA, the trihydrates of di- and trifluoroacetic acids seems to have nearly planar heavy atom skeletons.
In the work on formamide-(H2-O)3 complexes [28], the structural relationship between the formamide-(H2O)n clusters and the pure water clusters (H2O)n+2 was pointed out. The structures determined in this work for the SA-wn complexes could be related in the same way to the structures determined or predicted for the (H2O)n+2 clusters [20,64,65,66,84]. The pieces of evidence found of the enhanced hydrogen bonding (HB), due to the cooperativity associated with the increased number of water molecules in the clusters, are remarkable. The evolution of the HB features reflected in the changes of the O··H and O⋯O distances, the BSSE corrected dissociation energies per HB, the HB strengths estimated from the QTAIM analysis, and the stabilizing delocalization energies predicted by the NBO calculations evidence the existence of σ cooperativity. The differences between the intermolecular HBs of I-w-a species and those of the monohydrated species of benzoic acid [40] indicate the strong influence of the intramolecular interaction altering the proton acceptor properties of the C=O functional group. In conclusion, the interaction with the water molecules in the clusters increases the strength of the intramolecular HB, which is the dominant interaction in complex

Supplementary Materials

The supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms25074074/s1.

Author Contributions

Conceptualization, A.M., J.C.L. and S.B.; methodology, A.M., J.C.L. and S.B.; validation, J.C.L. and S.B.; formal analysis, A.M., J.C.L. and S.B.; investigation, A.M., J.C.L. and S.B.; resources, J.C.L. and S.B.; data curation, A.M., J.C.L. and S.B.; writing—original draft preparation, A.M., J.C.L. and S.B.; writing—review and editing, A.M., J.C.L. and S.B.; supervision, J.C.L. and S.B.; project administration, J.C.L. and S.B.; funding acquisition, J.C.L. and S.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministerio de Ciencia e Innovacion (Grant PID2021-125207NB-C33) and Junta de Castilla y León (Grant INFRARED-FEDER IR2020-1-UVa02).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available in the Supplementary Material of this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hayat, S.; Ahmad, A. Salicylic Acid: A Plant Hormone; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
  2. Grosser, T.; Smyth, E.; FitzGerald, G.A. Anti-inflammatory, Antipyretic, and Analgesic Agents; Pharmacotherapy of Gout. In Goodman & Gilman’s: The Pharmacological Basis of Therapeutics, 12th ed.; Brunton, L.L., Chabner, B.A., Knollmann, B.C., Eds.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
  3. Palleros, D.R. Experimental Organic Chemistry; Wiley: New York, NY, USA, 2000. [Google Scholar]
  4. Bosund, I.; Erichsen, I.; Molin, N. The Bacteriostatic Action of Benzoic and Salicylic Acids. Physiol. Plant. 1960, 13, 800–811. [Google Scholar] [CrossRef]
  5. Madan, R.K.; Levitt, J. A review of toxicity from topical salicylic acid preparations. J. Am. Acad. Dermatol. 2014, 70, 788–792. [Google Scholar] [CrossRef] [PubMed]
  6. Jariwala, F.B.; Figus, M.; Attygalle, A.B. Ortho effect in electron ionization mass spectrometry of N-acylanilines bearing a proximal halo substituent. J. Am. Soc. Mass Spectrom. 2008, 19, 1114–1118. [Google Scholar] [CrossRef] [PubMed]
  7. Hammett, L.P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. [Google Scholar] [CrossRef]
  8. Krygowski, T.M.; Wisiorowski, M.; Howard, S.T.; Stolarczyk, L.Z. Angular-group-induced bond alternation. I. Origin of the effect from Ab Initio calculations. Tetrahedron 1997, 53, 13027–13036. [Google Scholar] [CrossRef]
  9. Howard, S.T.; Krygowski, T.M.; Ciesielski, A.; Wisiorowski, M. Angular group-induced bond alternation II. The magnitude and the nature of the effect and its application to polynuclear benzenoid systems. Tetrahedron 1998, 54, 3533–3548. [Google Scholar] [CrossRef]
  10. Yahagi, T.; Fujii, A.; Ebata, T.; Mikami, N. Infrared Spectroscopy of the OH Stretching Vibrations of Jet-Cooled Salicylic Acid and Its Dimer in S0 and S1. J. Phys. Chem. A 2001, 105, 10673–10680. [Google Scholar] [CrossRef]
  11. Evangelisti, L.; Tang, S.; Velino, B.; Caminati, W. Microwave spectrum of salicylic acid. J. Mol. Struct. 2009, 921, 285–288. [Google Scholar] [CrossRef]
  12. Aarset, K.; Page, E.M.; Rice, D.A. Molecular Structures of Benzoic Acid and 2-Hydroxybenzoic Acid, Obtained by Gas-Phase Electron Diffraction and Theoretical Calculations. J. Phys. Chem. A 2006, 110, 9014–9019. [Google Scholar] [CrossRef]
  13. Bisht, P.B.; Petek, H.; Yoshihara, K.; Nagashima, U. Excited state enol-keto tautomerization in salicylic acid: A supersonic free jet study. J. Chem. Phys. 1995, 103, 5290–5307. [Google Scholar] [CrossRef]
  14. Sobolewski, A.L.; Domcke, W. Intramolecular Hydrogen Bonding in the S1(ππ*) Excited State of Anthranilic Acid and Salicylic Acid:  TDDFT Calculation of Excited-State Geometries and Infrared Spectra. J. Phys. Chem. A 2004, 108, 10917–10922. [Google Scholar] [CrossRef]
  15. Lahmani, F.; Zehnacker-Rentien, A. Effect of Substitution on the Photoinduced Intramolecular Proton Transfer in Salicylic Acid. J. Phys. Chem. A 1997, 101, 6141–6147. [Google Scholar] [CrossRef]
  16. Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for resonance-assisted hydrogen bonding from crystal-structure correlations on the enol form of the β-diketone fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
  17. Desfrançois, C.; Carles, S.; Schermann, J.P. Weakly Bound Clusters of Biological Interest. Chem. Rev. 2000, 100, 3943–3962. [Google Scholar] [CrossRef] [PubMed]
  18. Dopfer, O.; Fujii, M. Probing Solvation Dynamics around Aromatic and Biological Molecules at the Single-Molecular Level. Chem. Rev. 2016, 116, 5432–5463. [Google Scholar] [CrossRef] [PubMed]
  19. Becucci, M.; Melandri, S. High-Resolution Spectroscopic Studies of Complexes Formed by Medium-Size Organic Molecules. Chem. Rev. 2016, 116, 5014–5037. [Google Scholar] [CrossRef] [PubMed]
  20. Pérez, C.; Muckle, M.T.; Zaleski, D.P.; Seifert, N.A.; Temelso, B.; Shields, G.C.; Kisiel, Z.; Pate, B.H. Structures of Cage, Prism, and Book Isomers of Water Hexamer from Broadband Rotational Spectroscopy. Science 2012, 336, 897–901. [Google Scholar] [CrossRef] [PubMed]
  21. Pérez, C.; Neill, J.L.; Muckle, M.T.; Zaleski, D.P.; Peña, I.; Lopez, J.C.; Alonso, J.L.; Pate, B.H. Water–Water and Water–Solute Interactions in Microsolvated Organic Complexes. Angew. Chem. Int. Ed. 2015, 54, 979–982. [Google Scholar] [CrossRef]
  22. Pérez, C.; López, J.C.; Blanco, S.; Schnell, M. Water-Induced Structural Changes in Crown Ethers from Broadband Rotational Spectroscopy. J. Phys. Chem. Lett. 2016, 7, 4053–4058. [Google Scholar] [CrossRef]
  23. López, J.C.; Pérez, C.; Blanco, S.; Shubert, V.A.; Temelso, B.; Shields, G.C.; Schnell, M. Water induces the same crown shapes as Li+ or Na+ in 15-crown-5 ether: A broadband rotational study. Phys. Chem. Chem. Phys. 2019, 21, 2875–2881. [Google Scholar] [CrossRef]
  24. Steber, A.L.; Temelso, B.; Kisiel, Z.; Schnell, M.; Pérez, C. Rotational dive into the water clusters on a simple sugar substrate. Proc. Natl. Acad. Sci. USA 2023, 120, e2214970120. [Google Scholar] [CrossRef] [PubMed]
  25. Li, W.; Pérez, C.; Steber, A.L.; Schnell, M.; Lv, D.; Wang, G.; Zeng, X.; Zhou, M. Evolution of Solute–Water Interactions in the Benzaldehyde-(H2O)1–6 Clusters by Rotational Spectroscopy. J. Am. Chem. Soc. 2023, 145, 4119–4128. [Google Scholar] [CrossRef] [PubMed]
  26. Bellissent-Funel, M.C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; van der Spoel, D.; Xu, Y.; Garcia, A.E. Water Determines the Structure and Dynamics of Proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
  27. Blanco, S.; Pinacho, P.; López, J.C. Hydrogen-Bond Cooperativity in Formamide2–Water: A Model for Water-Mediated Interactions. Angew. Chem. 2016, 128, 9477–9481. [Google Scholar] [CrossRef]
  28. Blanco, S.; Pinacho, P.; López, J.C. Structure and Dynamics in Formamide–(H2O)3: A Water Pentamer Analogue. J. Phys. Chem. Lett. 2017, 8, 6060–6066. [Google Scholar] [CrossRef] [PubMed]
  29. Ouyang, B.; Howard, B.J. High-Resolution Microwave Spectroscopic and ab initio Studies of Propanoic Acid and Its Hydrates. J. Phys. Chem. A 2008, 112, 8208–8214. [Google Scholar] [CrossRef] [PubMed]
  30. Ouyang, B.; Howard, B.J. Hydrates of trans- and gauche-Difluoroacetic Acids: A High-Resolution Microwave Spectroscopic Study. J. Phys. Chem. A 2010, 114, 4109–4117. [Google Scholar] [CrossRef] [PubMed]
  31. Ouyang, B.; Howard, B.J. The monohydrate and dihydrate of acetic acid: A high-resolution microwave spectroscopic study. Phys. Chem. Chem. Phys. 2009, 11, 366–373. [Google Scholar] [CrossRef]
  32. Ouyang, B.; Starkey, T.G.; Howard, B.J. High-Resolution Microwave Studies of Ring-Structured Complexes between Trifluoroacetic Acid and Water. J. Phys. Chem. A 2007, 111, 6165–6175. [Google Scholar] [CrossRef]
  33. Thomas, J.; Sukhorukov, O.; Jäger, W.; Xu, Y. Direct Spectroscopic Detection of the Orientation of Free OH Groups in Methyl Lactate–(Water)1,2 Clusters: Hydration of a Chiral Hydroxy Ester. Angew. Chem. Int. Ed. 2014, 53, 1156–1159. [Google Scholar] [CrossRef]
  34. Brutschy, B. The Structure of Microsolvated Benzene Derivatives and the Role of Aromatic Substituents. Chem. Rev. 2000, 100, 3891–3920. [Google Scholar] [CrossRef]
  35. Salmon, R.A.; Schiller, C.L.; Harris, G.W. Evaluation of the Salicylic Acid—Liquid Phase Scrubbing Technique to Monitor Atmospheric Hydroxyl Radicals. J. Atmospheric Chem. 2004, 48, 81–104. [Google Scholar] [CrossRef]
  36. López, J.C.; Macario, A.; Blanco, S. Conformational equilibria in o -anisic acid and its monohydrated complex: The prevalence of the trans-COOH form. Phys. Chem. Chem. Phys. 2019, 21, 6844–6850. [Google Scholar] [CrossRef] [PubMed]
  37. Melandri, S.; Giuliano, B.M.; Maris, A.; Favero, L.B.; Ottaviani, P.; Velino, B.; Caminati, W. Methylsalicylate:  A Rotational Spectroscopy Study. J. Phys. Chem. A 2007, 111, 9076–9079. [Google Scholar] [CrossRef] [PubMed]
  38. Macario, A.; López, J.C.; Blanco, S. How Solvents Change the Conformational Landscape in Molecules with Weak Intramolecular Interactions: Methyl 2-Methoxybenzoate. In Proceedings of the 76th International Symposium on Molecular Spectroscopy, Champaign and Urbana, IL, USA, 21–25 June 2021. [Google Scholar] [CrossRef]
  39. Ghosh, S.; Thomas, J.; Huang, W.; Xu, Y.; Jäger, W. Rotational Spectra of Two Hydrogen-Bonded Methyl Salicylate Monohydrates: Relative Stability and Tunneling Motions. J. Phys. Chem. Lett. 2015, 6, 3126–3131. [Google Scholar] [CrossRef]
  40. Schnitzler, E.G.; Jäger, W. The benzoic acid–water complex: A potential atmospheric nucleation precursor studied using microwave spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2014, 16, 2305–2314. [Google Scholar] [CrossRef] [PubMed]
  41. Priem, D.; Ha, T.-K.; Bauder, A. Rotational spectra and structures of three hydrogen-bonded complexes between formic acid and water. J. Chem. Phys. 2000, 113, 169–175. [Google Scholar] [CrossRef]
  42. Jeffrey, G.A. An Introduction to Hydrogen Bonding, 1st ed.; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
  43. Watson, J.K.G. Vibrational Spectra and Structure, During, J.R., Ed.; Elsevier: Amsterdam, The Netherlands, 1977; Volume 6.
  44. Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
  45. Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  46. Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  47. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
  48. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
  49. Pinacho, P.; López, J.C.; Kisiel, Z.; Blanco, S. Microsolvation of ethyl carbamate conformers: Effect of carrier gas on the formation of complexes. Phys. Chem. Chem. Phys. 2020, 22, 18351–18360. [Google Scholar] [CrossRef] [PubMed]
  50. Pinacho, P.; López, J.C.; Kisiel, Z.; Blanco, S. The effect of microsolvation on the structure, nuclear quadrupole coupling and internal rotation: The methyl carbamate⋯(H2O)1-3 complexes. J. Chem. Phys. 2024, accepted. [Google Scholar]
  51. Törring, T.; Papoušek, D.; Aliev, M.R. Molecular Vibrational and Rotational Spectra. In Studies in Physical and Theoretical Chemistry; Elsevier: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA, 1982; Volume 17. [Google Scholar]
  52. Gordy, W.; Cook, R.L. Microwave Molecular Spectra. In Techniques of Chemistry, 3rd ed.; Wiley: New York, NY, USA, 1984. [Google Scholar]
  53. Onda, M.; Asai, M.; Takise, K.; Kuwae, K.; Hayami, K.; Kuroe, A.; Mori, M.; Miyazaki, H.; Suzuki, N.; Yamaguchi, I. Microwave spectrum of benzoic acid. J. Mol. Struct. 1999, 482–483, 301–303. [Google Scholar] [CrossRef]
  54. Larsen, N.W. Microwave spectra of the six mono-13C-substituted phenols and of some monodeuterated species of phenol. Complete substitution structure and absolute dipole moment. J. Mol. Struct. 1979, 51, 175–190. [Google Scholar] [CrossRef]
  55. Kraitchman, J. Determination of Molecular Structure from Microwave Spectroscopic Data. Am. J. Phys. 1953, 21, 17–24. [Google Scholar] [CrossRef]
  56. Costain, C.C. Further comments on the accuracy of rs substitution structures. Trans. Am. Crystallogr. Assoc. 1966, 2, 157–164. [Google Scholar]
  57. Rudolph, H.D. Contribution to the systematics of r0-derived molecular structure determinations from rotational parameters. Struct. Chem. 1991, 2, 581–588. [Google Scholar] [CrossRef]
  58. Desyatnyk, O.; Pszczółkowski, L.; Thorwirth, S.; Krygowski, T.M.; Kisiel, Z. The rotational spectra, electric dipole moments and molecular structures of anisole and benzaldehyde. Phys. Chem. Chem. Phys. 2005, 7, 1708–1715. [Google Scholar] [CrossRef]
  59. Watson, J.K.G.; Roytburg, A.; Ulrich, W. Least-Squares Mass-Dependence Molecular Structures. J. Mol. Spectrosc. 1999, 196, 102–119. [Google Scholar] [CrossRef] [PubMed]
  60. Kisiel, Z. Least-squares mass-dependence molecular structures for selected weakly bound intermolecular clusters. J. Mol. Spectrosc. 2003, 218, 58–67. [Google Scholar] [CrossRef]
  61. Portalone, G.; Schultz, G.; Domenicano, A.; Hargittai, I. Molecular structure and ring distortion of phenol. An electron diffraction study. Chem. Phys. Lett. 1992, 197, 482–488. [Google Scholar] [CrossRef]
  62. Schnitzler, E.G.; Seifert, N.A.; Kusuma, I.; Jäger, W. Rotational Spectroscopy of p-Toluic Acid and Its 1:1 Complex with Water. J. Phys. Chem. A 2017, 121, 8625–8631. [Google Scholar] [CrossRef]
  63. Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef] [PubMed]
  64. Dyke, T.R.; Mack, K.M.; Muenter, J.S. The structure of water dimer from molecular beam electric resonance spectroscopy. J. Chem. Phys. 1977, 66, 498–510. [Google Scholar] [CrossRef]
  65. Cruzan, J.D.; Braly, L.B.; Liu, K.; Brown, M.G.; Loeser, J.G.; Saykally, R.J. Quantifying Hydrogen Bond Cooperativity in Water: VRT Spectroscopy of the Water Tetramer. Science 1996, 271, 59–62. [Google Scholar] [CrossRef] [PubMed]
  66. Keutsch, F.N.; Cruzan, J.D.; Saykally, R.J. The Water Trimer. Chem. Rev. 2003, 103, 2533–2578. [Google Scholar] [CrossRef] [PubMed]
  67. Blanco, S. Formamide, Water, and their Complexes: A Microwave Spectroscopy Study. In Proceedings of the 73rd International Symposium on Molecular Spectroscopy, Champaign and Urbana, IL, USA, 18–22 June 2018. [Google Scholar] [CrossRef]
  68. Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
  69. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  70. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  71. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  72. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
  73. Pinacho, P.; Blanco, S.; López, J.C. The complete conformational panorama of formanilide–water complexes: The role of water as a conformational switch. Phys. Chem. Chem. Phys. 2019, 21, 2177–2185. [Google Scholar] [CrossRef] [PubMed]
  74. Plusquellic, D.F. User Guide to JB95.exe Spectral Fitting Program v1.02.4, 1/30/01; NIST: Gaithersburg, MD, USA, 2008. Available online: https://www.nist.gov/publications/user-guide-jb95exe-spectral-fitting-program-v1024-13001 (accessed on 8 February 2024).
  75. Kisiel, Z.; Pszczółkowski, L.; Medvedev, I.R.; Winnewisser, M.; De Lucia, F.C.; Herbst, E. Rotational spectrum of trans–trans diethyl ether in the ground and three excited vibrational states. J. Mol. Spectrosc. 2005, 233, 231–243. [Google Scholar] [CrossRef]
  76. “PROSPE-Programs for ROtational SPEctroscopy”. [Online]. Available online: http://info.ifpan.edu.pl/~kisiel/prospe.htm (accessed on 6 March 2024).
  77. Pickett, H.M. The fitting and prediction of vibration-rotation spectra with spin interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
  78. Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
  79. Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
  80. Glendening, E.D.; Landis, C.; Weinhold, F. NBO 5.9: Natural Atomic Orbital and Natural Bond Orbital Analysis; Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA. 2009. Available online: https://www2.chem.wisc.edu/~nbo7/ (accessed on 1 April 2024).
  81. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
  82. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. “Gaussian 16 Rev. C.01.” Wallingford, CT, USA. 2016. Available online: https://gaussian.com/relnotes/ (accessed on 1 April 2024).
  83. Gerhards, M.; Schmitt, M.; Kleinermanns, K.; Stahl, S. The structure of phenol(H2O) obtained by microwave spectroscopy. J. Chem. Phys. 1996, 104, 967–971. [Google Scholar] [CrossRef]
  84. Vallejo, J.L.G.; Heredia, J.D.; Gordon, M.S. Bonding analysis of water clusters using quasi-atomic orbitals. Phys. Chem. Chem. Phys. 2021, 23, 18734–18743. [Google Scholar] [CrossRef]
Ijms 25 04074 g001
Figure 1. The most stable predicted forms of SA monomer and its monohydrated, dihydrated, trihydrated, and tetrahydrated complexes. The relative energies are calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Figure 1. The most stable predicted forms of SA monomer and its monohydrated, dihydrated, trihydrated, and tetrahydrated complexes. The relative energies are calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Ijms 25 04074 g001
Ijms 25 04074 g002
Figure 2. CP-FTMW, 6–8 GHz, rotational spectrum of SA and its water complexes. A selection of the most intense transitions has been pointed out for the SA-I (blue), SA-w (red), SA-w2 (green), SA-w3 (orange), and SA-w4 (purple) species to compare their relative intensities. The excerpt in black facilitates comparison between transitions of all the species observed (SA, SA-w, SA-w2, SA-w3, SA-w4). The excerpt in orange shows the doublets observed for the SA-w3 species.
Figure 2. CP-FTMW, 6–8 GHz, rotational spectrum of SA and its water complexes. A selection of the most intense transitions has been pointed out for the SA-I (blue), SA-w (red), SA-w2 (green), SA-w3 (orange), and SA-w4 (purple) species to compare their relative intensities. The excerpt in black facilitates comparison between transitions of all the species observed (SA, SA-w, SA-w2, SA-w3, SA-w4). The excerpt in orange shows the doublets observed for the SA-w3 species.
Ijms 25 04074 g002
Ijms 25 04074 g003
Figure 3. (a) The experimental rs positions of the isotopically substituted atoms (purple) for I conformer of SA with the re predicted structure at B3LYP-D3/6-311++G(d,p) level of theory. (b) and (c) are schematic representations showing the resonant form stabilized by the AGIBA effect with (b) rm bond lengths experimentally determined and (c) predicted bond orders from the NBO calculations done at B3LYP-D3/6-311++G(d,p) level of theory.
Figure 3. (a) The experimental rs positions of the isotopically substituted atoms (purple) for I conformer of SA with the re predicted structure at B3LYP-D3/6-311++G(d,p) level of theory. (b) and (c) are schematic representations showing the resonant form stabilized by the AGIBA effect with (b) rm bond lengths experimentally determined and (c) predicted bond orders from the NBO calculations done at B3LYP-D3/6-311++G(d,p) level of theory.
Ijms 25 04074 g003
Ijms 25 04074 g004
Figure 4. Predicted B3LYP-D3/6-311++G(d,p) re structures, estimated interaction energies (green, in kJ/mol), and hydrogen bond distances (black (theoretical) and blue (experimental), in Å) for the salicylic acid monomer (SA) and its complexes with one (I-w-a), two (I-w2-a), three (I-w3-a), and four (I-w4-a) water molecules. For the SA monomer, the experimental distances correspond to the mass-dependent rm (blue) structure. For the monohydrated conformer, SA-w, the re structure is compared with the experimentally determined substitution rs (purple) and effective r0 (blue) structures. The red numbers are the labelling of the water molecules. The interaction energies were estimated from the empirical equation taken from the QTAIM calculations and reference [63] (see text).
Figure 4. Predicted B3LYP-D3/6-311++G(d,p) re structures, estimated interaction energies (green, in kJ/mol), and hydrogen bond distances (black (theoretical) and blue (experimental), in Å) for the salicylic acid monomer (SA) and its complexes with one (I-w-a), two (I-w2-a), three (I-w3-a), and four (I-w4-a) water molecules. For the SA monomer, the experimental distances correspond to the mass-dependent rm (blue) structure. For the monohydrated conformer, SA-w, the re structure is compared with the experimentally determined substitution rs (purple) and effective r0 (blue) structures. The red numbers are the labelling of the water molecules. The interaction energies were estimated from the empirical equation taken from the QTAIM calculations and reference [63] (see text).
Ijms 25 04074 g004
Table 1. Experimental rotational parameters determined for SA, compared with those predicted for conformer SA-I at B3LYP-D3/6-311++G(d,p) level of theory.
Table 1. Experimental rotational parameters determined for SA, compared with those predicted for conformer SA-I at B3LYP-D3/6-311++G(d,p) level of theory.
Fitted Param. 1(MW)(MW + MMW) 2(MMW, ref. [11]) 3SA-I—Theor.
A/MHz2340.25075(42) 42340.25105(17) 2340.248(2)2336.30
B/MHz1223.76931(31)1223.76941(13)1223.79(2)1221.78
C/MHz803.89784(31)803.89788(18)803.90(1)802.24
Pcc/uÅ20.12962(19)0.12960(10)0.1270.00
ΔJ/kHz0.1091(90)0.11722(67)0.049(6)0.1897
ΔJK/kHz−0.230(28)−0.2536(26)0.130(9)−0.3939
ΔK/kHz0.134(20)0.1505(44)-0.2128
δJ/kHz−0.0303(44)−0.03392(37)-0.0843
δK/kHz0.069(14)0.0812(18)-−0.1244
N6411450-
σ/kHz6.811.123.0-
1 A, B, and C are the rotational constants. Pcc is the planar moment of inertia, derived from Pcc = (Ia + Ib − Ic)/2. ΔJ, ΔJK, ΔK, δJ, and δK are the quartic centrifugal distortion constants. N is the number of rotational transitions fitted. Σ is the rms deviations of the fit. 2 Fit of the 64 measured in this work (MW) and the 50 transitions measured in ref. [11] (MMW) transitions observed for SA-I. 3 Experimental parameters reported in reference [11]. 4 Standard error is given in parentheses in units of the last digit.
Table 2. Experimental rotational parameters obtained for the SA-w monohydrated and SA-w2 dihydrated complexes, compared with the predicted parameters of I-w-a, II-w-a, I-w2-a, and II-w2-a conformers of SA–watern (n = 1, 2) complexes calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Table 2. Experimental rotational parameters obtained for the SA-w monohydrated and SA-w2 dihydrated complexes, compared with the predicted parameters of I-w-a, II-w-a, I-w2-a, and II-w2-a conformers of SA–watern (n = 1, 2) complexes calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Fitted Param. 1SA-w I-w-aII-w-aSA-w2I-w2-aII-w2-a
A/MHz2315.34456(45) 22313.152311.931769.91699(48)1780.401759.99
B/MHz645.08107(14)648.76647.51451.04489(18)453.67450.32
C/MHz505.03872(14)507.09506.29360.15478(16)362.04359.17
Pcc/uÅ 20.51743(24)0.420.441.38688(57)0.961.17
ΔJ/kHz0.0845(37)0.0170.0160.0763(27)0.0080.007
ΔJK/kHz−0.0757(32)0.1060.104−0.0699(26)0.0640.092
ΔK/kHz-0.0660.056-0.0720.072
δJ/kHz−0.0274(15)0.0040.004−0.0333(12)0.0010.001
δK/kHz-0.0680.066-0.0490.049
µa/µb/µc/D+/+/-0.6/1.0/1.20.7/0.6/1.2+/+/-0.5/0.9/0.00.8/0.8/0.0
ΔEDFT/cm−1-0.0 3890.6-0.0 4639.9
N84--126--
σ/kHz5.4--7.7--
1 A, B, and C are the rotational constants. Pcc is the planar moment of inertia, derived from Pcc = (Ia + Ib − Ic)/2. ΔJ, ΔJK, ΔK, δJ and δK are the quartic centrifugal distortion constants. µa, µb, and µc are the components of the electric dipole moment, + or – mean the observation or not of the corresponding selection rules. ΔEDFT is the energy relative to the most stable conformer (I-w-a and I-w2-a, respectively). N is the number of rotational transitions fitted. σ is the rms deviations of the fit. 2 Standard error is given in parentheses in units of the last digit. 3 Absolute energy is −572.6949094 Eh. 4 Absolute energy is −649.1747737 Eh.
Table 3. Experimental rotational parameters obtained for the two vibrational states (ν = 0 and 1) observed for the SA-w3 species of the trihydrated complex compared with the predicted parameters of SA-I-w3-a, SA-I-w3-b, and SA-I-w3-c conformers of the SA trihydrated complex calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Table 3. Experimental rotational parameters obtained for the two vibrational states (ν = 0 and 1) observed for the SA-w3 species of the trihydrated complex compared with the predicted parameters of SA-I-w3-a, SA-I-w3-b, and SA-I-w3-c conformers of the SA trihydrated complex calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Fitted Param. 1SA-w3 (ν = 0)SA-w3 (ν = 1)I-w3-aI-w3-bI-w3-c
A/MHz1412.46036(98) 21412.42970(98)1412.101436.051421.44
B/MHz315.84360(19)315.84610(22)319.03317.16327.39
C/MHz260.77801(14)260.78823(15)263.04262.98284.18
Pcc/uÅ29.9634(11)9.9989(12)10.3311.8260.41
ΔJ/kHz0.01785(63)0.0180.0160.029
ΔJK/kHz−0.1706(86)−0.091−0.077−0.163
ΔK/kHz1.431(79)0.8460.8121.225
d1/kHz−0.00297(44)−0.001−0.002−0.001
d2/kHz0.00197(39)−0.001−0.0010.001
Fbc/MHz0.1304(52)---
ΔE01/MHz717.0(5.2)---
µa/µb/µc/D+/+/−0.6/0.6/0.60.1/0.0/0.31.5/1.3/0.1
ΔEDFT/cm−1-0.0 3130.4130.4
N160---
σ/kHz7.0---
1 A, B, and C are the rotational constants. Pcc is the planar moment of inertia, derived from Pcc = (Ia + Ib – Ic)/2. ΔJ, ΔJK, ΔK, d1, and d2 are the quartic centrifugal distortion constants. Fbc is the Coriolis coupling constant. ΔE01 is the energy difference between the two vibrational states. µa, µb, and µc are the components of the electric dipole moment, + or – mean the observation or not of the corresponding selection rules. ΔEDFT is the energy relative to the most stable I-w3-a conformer. N is the number of rotational transitions fitted. σ is the rms deviations of the fit. 2 Standard error is given in parentheses in units of the last digits. 3 Absolute energy is −725.6502119 Eh.
Table 4. Experimental rotational parameters obtained for the SA-w4 species of the tetrahydrated complex of SA compared with the predicted parameters of I-w4-a, I-w4-b, I-w4-c, and I-w4-d conformers of SA tetrahydrated complex calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Table 4. Experimental rotational parameters obtained for the SA-w4 species of the tetrahydrated complex of SA compared with the predicted parameters of I-w4-a, I-w4-b, I-w4-c, and I-w4-d conformers of SA tetrahydrated complex calculated at B3LYP-D3/6-311++G(d,p) level of theory.
Fitted Param. 1SA-w4 I-w4-aI-w4-bI-w4-cI-w4-d
A/MHz1055.8085(24) 21073.101066.291059.871093.11
B/MHz248.19262(15)250.60251.56251.90343.76
C/MHz220.88132(19)222.99224..02224.40217.21
Pcc/uÅ 2113.4455(21)110.68113.23115.48104.46
ΔJ/kHz0.191(46)0.0350.0350.0400.036
ΔJK/kHz0.094(10)−0.212−0.150−0.175−0.186
ΔK/kHz−0.239(36)1.2971.5081.3321.985
d1/kHz0.208(44)0.0010.0010.0010.001
d2/kHz−0.135(21)0.0010.0010.0010.001
HJ/Hz0.0106(20)----
µa/µb/µc/D+/+/-0.8/1.4/0.20.7/1.6/0.40.8/1.3/1.60.6/3.1/0.5
ΔEDFT/cm−1-0.0 3165.7241.2267.8
N169----
σ/kHz6.4----
1 A, B, and C are the rotational constants. Pcc is the planar moment of inertia, derived from Pcc = (Ia + Ib – Ic)/2. ΔJ, ΔJK, ΔK, d1, and d2 are the quartic centrifugal distortion constants and HJ is the sextic centrifugal distortion constant. µa, µb, and µc are the components of the electric dipole moment, + or – mean the observation or not of the corresponding selection rules. ΔEDFT is the energy relative to the most stable I-w4-a conformer. N is the number of rotational transitions fitted. σ is the rms deviations of the fit. 2 Standard error is given in parentheses in units of the last digit. 3 Absolute energy is −802.1296231 Eh.
Table 5. Predicted O⋯O distances between the oxygen atoms forming hydrogen bonds for the identified conformers of SA and its complexes SA-w (I-w-a), SA-w2 (I-w2-a), SA-w3 (I-w3-a), and SA-w4 (I-w4-a), calculated at B3LYP-D3/6-311++G(d,p) level of theory. See Figure 3 for the atom labelling and Figure 4 for the labelling of the water molecules.
Table 5. Predicted O⋯O distances between the oxygen atoms forming hydrogen bonds for the identified conformers of SA and its complexes SA-w (I-w-a), SA-w2 (I-w2-a), SA-w3 (I-w3-a), and SA-w4 (I-w4-a), calculated at B3LYP-D3/6-311++G(d,p) level of theory. See Figure 3 for the atom labelling and Figure 4 for the labelling of the water molecules.
O⋯O/ÅSAI-w-aI-w2-aI-w3-aI-w4-a
O12⋯O142.6352.6202.6172.6172.612
O13⋯Ow1-2.7102.6482.6162.576
O14⋯Ow2-2.7792.7662.7642.694
Ow1⋯Ow2--2.682-2.835
Ow1⋯Ow3---2.6912.740
Ow2⋯Ow3---2.698-
Ow3⋯Ow4----2.745
Ow2⋯Ow4----2.781
O⋯O w-dimer 12.976
O⋯O w-trimer 22.85
O⋯O w-tetramer 32.78
1 Taken from reference [64]. 2 Taken from reference [66]. 3 Taken from reference [65].
Table 6. Predicted equilibrium dissociation energies dissociation energies De and average dissociation energies per intermolecular bond (De/HB) for the identified conformers of salicylic acid—water complexes, SA-w (I-w-a), SA-w2 (I-w2-a), SA-w3 (I-w3-a), and SA-w4 (I-w4-a), calculated at MP2/6-311++G(2df,2dp) level of theory and employing the counterpoise method to correct the basis set superposition error (BSSE).
Table 6. Predicted equilibrium dissociation energies dissociation energies De and average dissociation energies per intermolecular bond (De/HB) for the identified conformers of salicylic acid—water complexes, SA-w (I-w-a), SA-w2 (I-w2-a), SA-w3 (I-w3-a), and SA-w4 (I-w4-a), calculated at MP2/6-311++G(2df,2dp) level of theory and employing the counterpoise method to correct the basis set superposition error (BSSE).
I-w-aI-w2-aI-w3-aI-w4-a
De/kJ mol−141.3488.70123.34168.87
De/HB/kJ mol−120.6729.5730.8428.14
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Macario, A.; López, J.C.; Blanco, S. Molecular Structure of Salicylic Acid and Its Hydrates: A Rotational Spectroscopy Study. Int. J. Mol. Sci. 2024, 25, 4074. https://doi.org/10.3390/ijms25074074

AMA Style

Macario A, López JC, Blanco S. Molecular Structure of Salicylic Acid and Its Hydrates: A Rotational Spectroscopy Study. International Journal of Molecular Sciences. 2024; 25(7):4074. https://doi.org/10.3390/ijms25074074

Chicago/Turabian Style

Macario, Alberto, Juan Carlos López, and Susana Blanco. 2024. "Molecular Structure of Salicylic Acid and Its Hydrates: A Rotational Spectroscopy Study" International Journal of Molecular Sciences 25, no. 7: 4074. https://doi.org/10.3390/ijms25074074

APA Style

Macario, A., López, J. C., & Blanco, S. (2024). Molecular Structure of Salicylic Acid and Its Hydrates: A Rotational Spectroscopy Study. International Journal of Molecular Sciences, 25(7), 4074. https://doi.org/10.3390/ijms25074074

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop