Population Dynamics of Wild Mongolian Gerbils: Quadratic Temperature Effects on Survival and Density-Dependent Effects on Recruitment
Abstract
1. Introduction
2. Materials and Methods
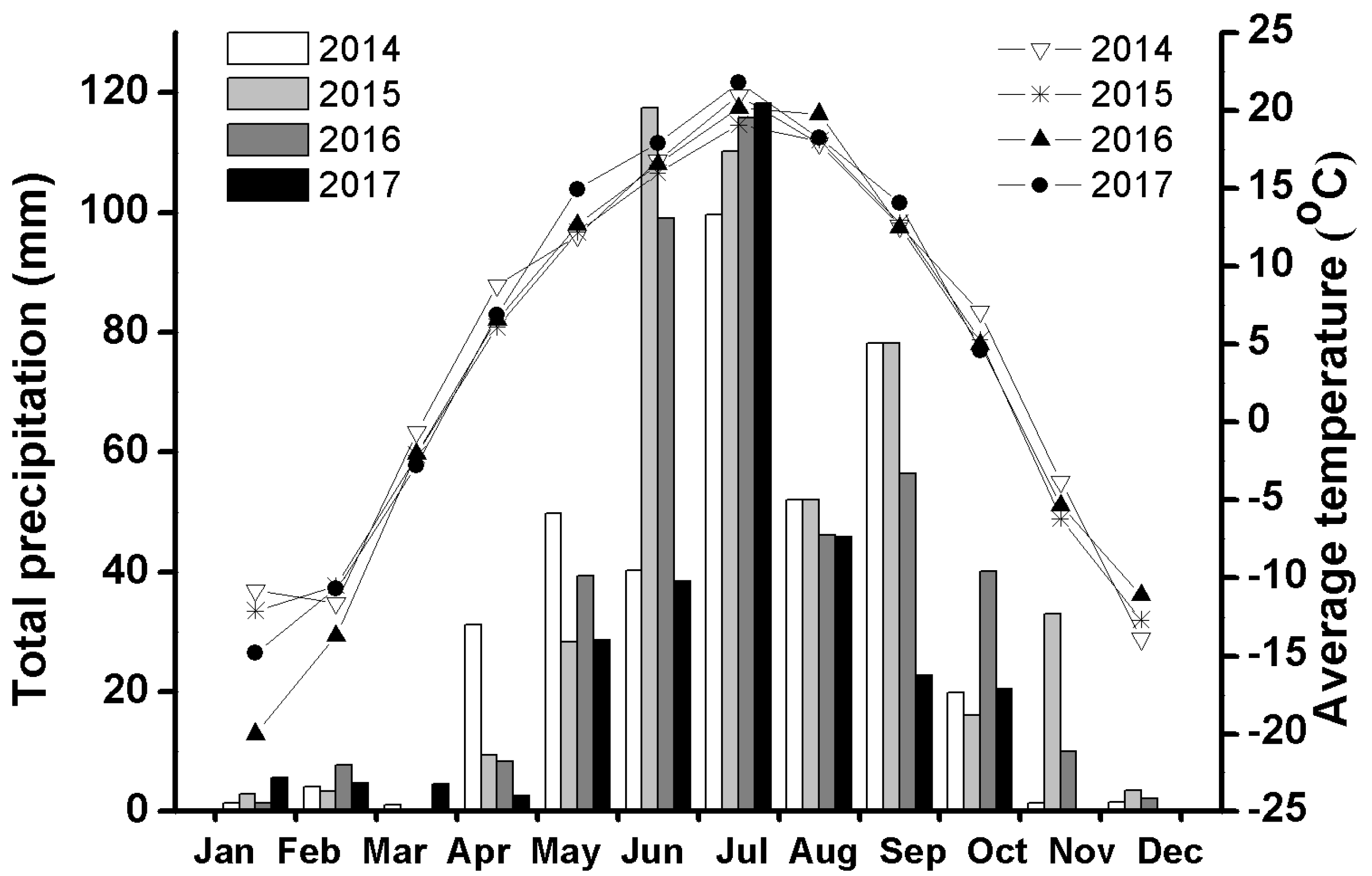
2.1. Study Area
2.2. Live Trapping and Individual Identification
2.3. Analysis of Survival and Recruitment
3. Results
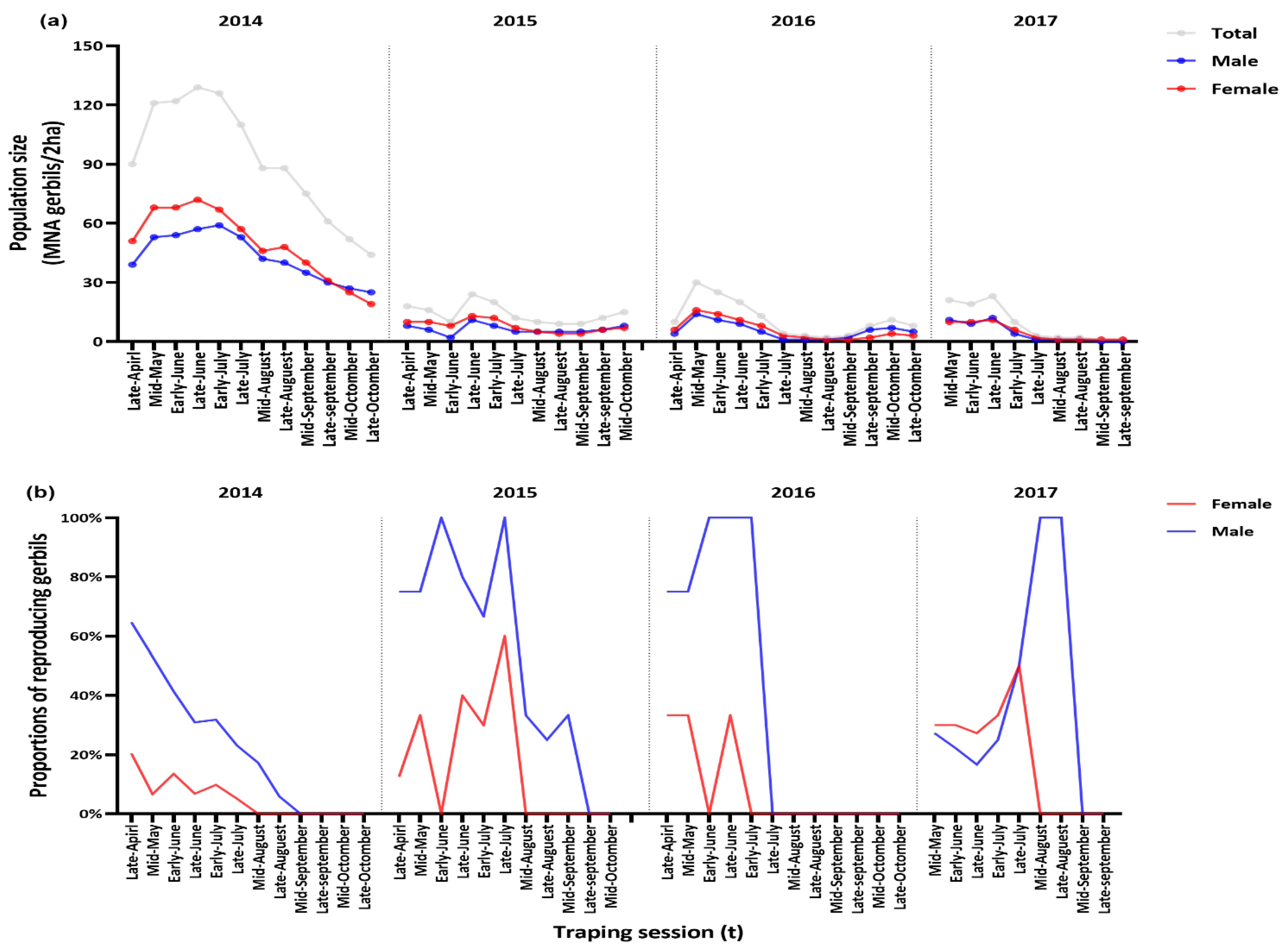
3.1. General Population Demography
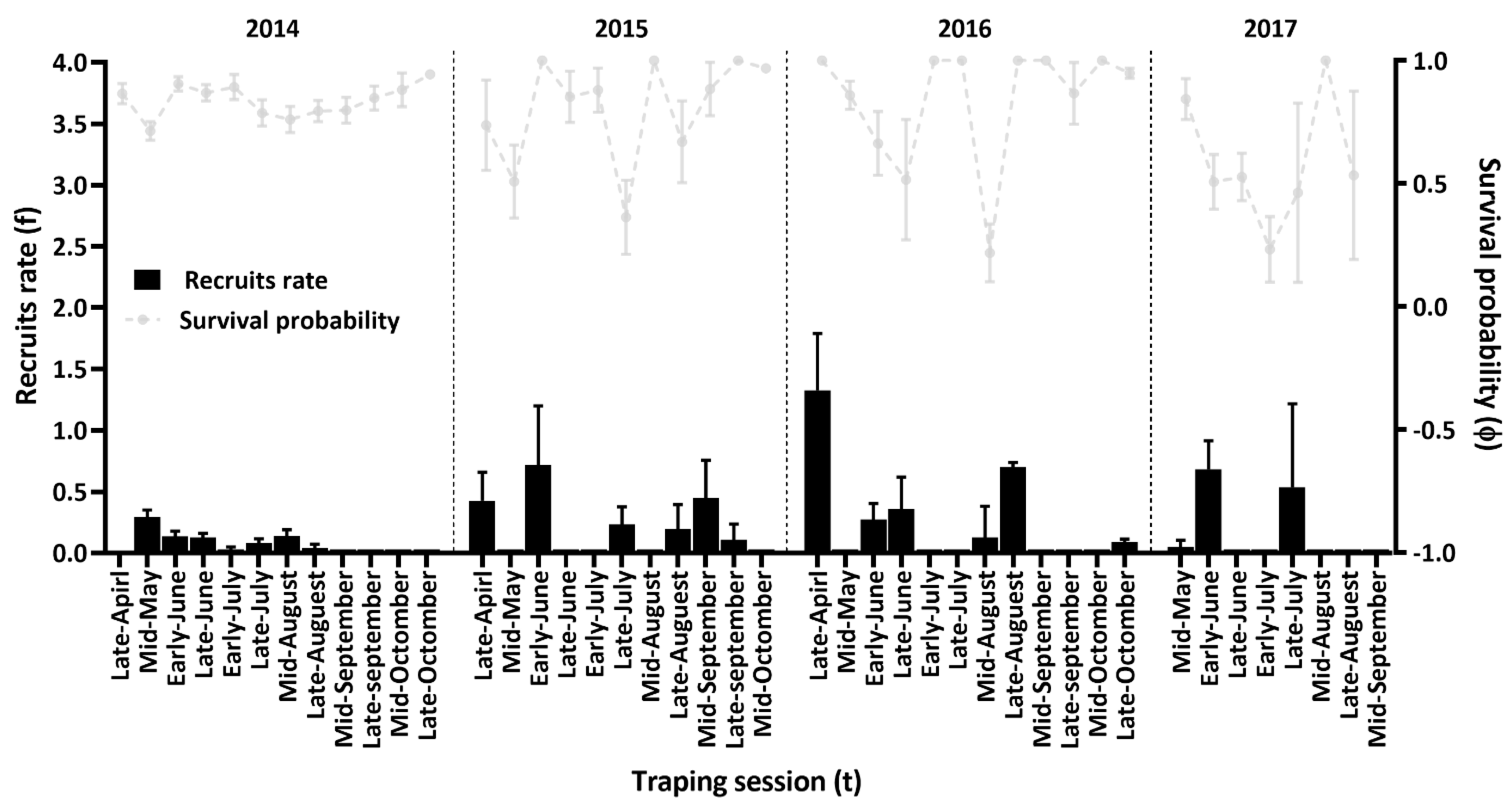
3.2. Effect of Climate and Population Density on Survival and Recruitment
3.3. Effect of Climate and Population Density on Population Growth Rate
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krebs, C.J. One hundred years of population ecology: Successes, failures and the road ahead. Integr. Zool. 2015, 10, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Andreassen, H.P.; Sundell, J.; Ecke, F.; Halle, S.; Haapakoski, M.; Henttonen, H.; Huitu, O.; Jacob, J.; Johnsen, K.; Koskela, E.; et al. Population cycles and outbreaks of small rodents: Ten essential questions we still need to solve. Oecologia 2021, 195, 1–22. [Google Scholar]
- Schwinning, S.; Sala, O.E.; Loik, M.E.; Ehleringer, J.R. Thresholds, memory, and seasonality: Understanding pulse dynamics in arid/semi-arid ecosystems. Oecologia 2004, 41, 191–193. [Google Scholar] [CrossRef] [PubMed]
- Davidson, A.D.; Detling, J.K.; Brow, J.H. Ecological roles and conservation challenges of social, burrowing, herbivorous mammals in the world’s grasslands. Front. Ecol. Environ. 2012, 10, 477–486. [Google Scholar] [CrossRef]
- Lightfoot, D.C.; Davidson, A.D.; Parker, D.G.; Hernandez, L.; Laundre, J.W. Bottom-up regulation of desert grassland and shurbland rodent communities: Implications of species-specific reproductive potentials. J. Mammal. 2012, 93, 1017–1028. [Google Scholar] [CrossRef]
- Lande, R.; Engen, S.; Saether, B.E. Stochastic Population Dynamics in Ecology and Conservation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Lima, M.; Ernest, M.S.K.; Brown, J.H.; Belgrano, A.; Stenseth, N.C. Chihuahuan desert kangaroo rats: Nonlinear effects of population dynamics, competition, and rainfall. Ecology 2008, 89, 2594–2603. [Google Scholar] [CrossRef]
- Jiang, G.; Liu, J.; Xu, L.; Yu, G.; He, H.; Zhang, Z. Climate warming increases biodiversity of small rodents by favoring rare or less abundant species in a grassland ecosystem. Integr. Zool. 2013, 8, 162–174. [Google Scholar] [CrossRef]
- Morris, W.F.; Pfister, C.A.; Tuljapurkar, S.; Haridas, C.V.; Boggs, C.L.; Boyce, M.; Bruna, E.; Church, D.R.; Coulson, T.; Doak, D.F.; et al. Longevity can buffer plant and animal populations against changing climatic variability. Ecology 2008, 89, 19–25. [Google Scholar] [CrossRef]
- Julliard, R.; Leirs, H.; Stenseth, N.C.; Yoccoz, N.G.; Prévot-Julliard, A.C.; Verhagen, R.; Verheyen, W. Survival-variation within and between functional categories of the African multi- mammate rat. J. Anim. Ecol. 1999, 68, 550–561. [Google Scholar] [CrossRef]
- Chen, I.; Hill, J.K.; Ohlemüller, R.; Roy, D.B.; Thomas, C.D. Rapid range shifts of species associated with high levels of climate warming. Science 2011, 333, 17–20. [Google Scholar] [CrossRef]
- Spooner, F.E.B.; Pearson, R.G.; Freeman, R. Rapid warming is associated with population decline among terrestrial birds and mammals globally. Glob. Chang. Biol. 2018, 24, 4521–4531. [Google Scholar] [CrossRef] [PubMed]
- Rowe, R.J.; Terry, R.C. Small mammal responses to environmental change: Integrating past and present dynamics. J. Mammal. 2014, 95, 1157–1174. [Google Scholar] [CrossRef]
- Bai, D.F.; Wan, X.R.; Li, G.L.; Wan, X.R.; Guo, Y.W.; Shi, D.Z.; Zhang, Z.B. Factors influencing range contraction of a rodent herbivore in a steppe grassland over the past decades. Ecol. Evol. 2022, 12, e8546. [Google Scholar] [CrossRef] [PubMed]
- Bruckerhoff, L.A.; Connell, R.K.; Guinnip, J.P.; Adhikari, E.; Godar, A.; Gido, K.B.; Boyle, A.W.; Hope, A.G.; Joern, A.; Welti, E. Harmony on the prairie? Grassland plant and animal community responses to variation in climate across land-use gradients. Ecology 2020, 101, 2986. [Google Scholar] [CrossRef] [PubMed]
- Bruggeman, J.E.; Licht, D.S. Drought-mediated changes in black-tailed prairie dog colonies in the Northern Great Plains. J. Mammal. 2020, 101, 1189–1204. [Google Scholar] [CrossRef]
- Milner, R.N.C.; Starrs, D.; Hayes, G.; Evans, M.C. Distribution and habitat preference of the broad-toothed rat (Mastacomys fuscus) in the Australian Capital Territory, Australia. Austral. Mammal. 2015, 37, 125–131. [Google Scholar] [CrossRef]
- Lazo-Cancino, D.; Rivera, R.; Paulsen-Cortez, K.; Gonzalez-Berrios, N.; Rodriguez-Gutierrez, R.; Rodriguez-Serrano, E. The impacts of climate change on the habitat distribution of the vulnerable Patagonian-Fueguian species Ctenomys magellanicus (Rodentia, Ctenomyidae). J. Arid. Environ. 2020, 173, 104016. [Google Scholar] [CrossRef]
- Nengovhela, A.; Baxter, R.M.; Taylor, P.J. Temporal changes in cranial size in South African vlei rats (Otomys): Evidence for the ’third universal response to warming. Afric. Zool. 2015, 50, 233–239. [Google Scholar] [CrossRef]
- Zhang, Z.; Pech, R.; Davis, S.; Shi, D.; Wan, X.; Zhong, W. Extrinsic and intrinsic factors determine the eruptive dynamics of Brandt’s voles Microtus brandtii in Inner Mongolia, China. Oikos 2003, 100, 299–310. [Google Scholar] [CrossRef]
- Jiang, G.; Zhao, T.; Liu, J.; Xu, L.; Yu, G.; He, H.; Krebs, C.J.; Zhang, Z. Effects of ENSO-linked climate and vegetation on population dynamics of sympatric rodent species in semiarid grasslands of Inner Mongolia, China. Can. J. Zool. 2011, 89, 678–691. [Google Scholar] [CrossRef]
- Brown, J.H.; Ernest, S.K.M. Rain and rodents: Complex dynamics of desert consumers. Bioscience 2002, 52, 979–987. [Google Scholar] [CrossRef]
- Kelt, D.A. Comparative ecology of desert small mammals: A selective review of the past 30 years. J. Mammal. 2011, 92, 1158–1178. [Google Scholar] [CrossRef]
- Liu, W.; Wan, X.; Zhong, W. Population dynamics of the Mongolian gerbils: Seasonal patterns and interactions among density, reproduction and climate. J. Arid. Environ. 2007, 68, 383–397. [Google Scholar] [CrossRef]
- Korpela, K.; Delgado, M.; Henttonen, H.; Korpimaki, E.; Koskela, E.; Ovaskainen, O.; Pietiäinen, H.; Sundell, J.; Gyoccoz, N.; Huitu, O. Nonlinear effects of climate on boreal rodent dynamics: Mild winters do not negate high-amplitude cycles. Glob. Chang. Biol. 2013, 19, 697–710. [Google Scholar] [CrossRef] [PubMed]
- Lima, M.; Merritt, J.F.; Bozinovic, F. Numerical fluctuations in the northern short-tailed shrew: Evidence of non-linear feedback signatures on population dynamics and demography. J. Anim. Ecol. 2002, 71, 159–172. [Google Scholar] [CrossRef]
- Letnic, M.; Story, P.; Story, G.; Field, J.; Brown, O.; Dickman, C.R. Resource pulses, switching trophic control, and the dynamics of small mammal assemblages in arid Australia. J. Mammal. 2011, 92, 1210–1222. [Google Scholar] [CrossRef]
- Shenbrot, G.; Krasnov, B.; Burdelov, S. Long-term study of population dynamics and habitat selection of rodents in the Negev Desert. J. Mammal. 2010, 91, 776–786. [Google Scholar] [CrossRef]
- Chen, L.J.; Wang, G.M.; Wan, X.R.; Liu, W. Complex and nonlinear effects of weather and density on the demography of small herbivorous mammals. Basic Appl. Ecol. 2015, 16, 172–179. [Google Scholar] [CrossRef]
- Wang, G.M.; Hobbs, N.T.; Slade, N.A.; Merritt, J.F.; Getz, L.L.; Hunter, M.; Vessey, S.H.; Witham, J.; Guillaumet, A. Comparative population dynamics of large and small mammals in the Northern Hemi-sphere: Deterministic and stochastic forces. Ecography 2013, 36, 439–446. [Google Scholar] [CrossRef]
- Lima, M.; Berryman, A.A.; Stenseth, N.C. Feedback structures of northern small rodent populations. Oikos 2006, 112, 555–564. [Google Scholar] [CrossRef]
- Reed, A.W.; Slade, N.A. Density-dependent recruitment in grassland small mammals. J. Anim. Ecol. 2008, 77, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Gaillard, J.M.; Yoccoz, N.G.; Lebreton, J.D.; Bonenfant, C.; Devillard, S.; Loison, A.; Pontier, D.; Allaine, D. Generation time: A reliable metric to measure life-history variation among mammalian populations. Am. Natural. 2005, 166, 119–123. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.E.; Reeder, D.M. Mammal Species of the World: A Taxonomic and Geographic Reference, 3rd ed.; 2 volumes; Johns Hopkins University Press: Baltimore, MD, USA, 2005. [Google Scholar]
- Liu, W.; Wang, G.M.; Wang, Y.N.; Zhong, W.Q. Population ecology of wild Mongolian gerbils Meriones unguiculatus. J. Mammal. 2009, 90, 832–840. [Google Scholar] [CrossRef]
- Ågren, G.; Zhou, Q.; Zhong, W. Ecology and social behaviour of Mongolian gerbils, Meriones unguiculatus, at Xilinhot Inner Mongolia, China. Anim. Behav. 1989, 37, 11–17. [Google Scholar] [CrossRef]
- Wang, Y.N.; Liu, W.; Wang, G.M.; Zhong, W.Q.; Wan, X.R. Genetic consequences of group living in Mongolian gerbils. J. Hered. 2011, 102, 554–561. [Google Scholar] [CrossRef][Green Version]
- Scheibler, E.; Liu, W.; Weinandy, R.; Gattermann, R. Burrow systems of the Mongolian gerbil (Meriones unguiculatus Milne-Edwards, 1867). Mammal. Biol. 2006, 71, 178–182. [Google Scholar] [CrossRef]
- Xia, W.P.; Liao, C.H.; Zhong, W.Q.; Sun, C.L.; Tian, Y. On the population dynamics and regulation of Meriones unguiculatus in agricultural region north to Yin Mountains, Inner Mongolia. Acta Their. Sin. 1982, 2, 51–71. (In Chinese) [Google Scholar]
- Wang, G.; Zhong, W. Mongolian gerbils and Daurian pikas responded differently to changes in precipitation in the Inner Mongolian grasslands. J. Arid. Environ. 2006, 66, 648–656. [Google Scholar] [CrossRef]
- Smith, R.C.; Ainley, D.; Baker, K.; Domack, E.; Emslie, S.; Fraser, B.; Kennett, J.; Leventer, A.; Mosley-Thompson, E.; Stammerjohn, S.; et al. Marine ecosystem sensitivity to climate change. Bioscience 1999, 49, 393–404. [Google Scholar] [CrossRef]
- Krebs, C.J. Ecological Methodology; Addison-Wesley: New York, NY, USA, 1999. [Google Scholar]
- Deng, K.; Liu, W.; Wang, D.H. Inter-group associations in Mongolian gerbils: Quantitative evidence from social network analysis. Integr. Zool. 2017, 12, 446–456. [Google Scholar] [CrossRef]
- Jolly, G.M. Explicit estimates from capture-recapture data with both death and immigration-stochastic model. Biometrika 1965, 52, 225–247. [Google Scholar] [CrossRef] [PubMed]
- Seber, G.A.F. A note on the multiple-recapture census. Biometrika 1965, 52, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Cormack, R.M. Estimates of survival from sighting of marked animals. Biometrika 1964, 51, 429–438. [Google Scholar] [CrossRef]
- Lebreton, J.D.; Burnham, K.P.; Clobert, J.; Anderson, D.R. Modeling survival and testing biological hypotheses using marked animals: A unified approach with case studies. Ecol. Monog. 1992, 62, 67–118. [Google Scholar] [CrossRef]
- Cooch, E.; White, G. Program MARK “A Gentle Introduction”, 6th ed. 2007. Available online: http://www.phidot.org/software/mark/docs/book/ (accessed on 5 January 2008).
- Burnham, K.P.; Anderson, D.R. Model Selection and Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- White, G.C.; Burnham, K.P. Program MARK: Survival estimation from populations of marked animals. Bird Stud. 1999, 46, 120–139. [Google Scholar] [CrossRef]
- Pradel, R. Utilization of capture-mark-recapture for the study of recruitment and population growth rate. Biometrics 1996, 52, 703–709. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.M. Mixed-Effects Models in S and S-Plus; Springer: New York, NY, USA, 2000. [Google Scholar]
- Guo, Y.Y.; Chi, Q.S.; Zhang, X.Y.; Liu, W.; Hao, S.Y.; Wang, D.H. Brown adipose tissue plays thermoregulatory role within the thermoneutral zone in Mongolian gerbils (Meriones unguiculatus). J. Therm. Biol. 2019, 81, 137–145. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Hao, S.Y.; Zhang, M.; Zhang, X.Y.; Wang, D.H. Aquaporins, evaporative water loss and thermoregulation in heat-acclimated Mongolian gerbils (Meriones unguiculatus). J. Therm. Biol. 2020, 91, 102641. [Google Scholar] [CrossRef]
- Khakisahneh, S.; Zhang, X.Y.; Nouri, Z.; Hao, S.Y.; Chi, Q.S.; Wang, D.H. Thyroid hormones mediate metabolic rate and oxidative, anti-oxidative balance at different temperatures in Mongolian gerbils (Meriones unguiculatus). Comp. Bioch. Physiol. Part C Toxicol. Pharmacol. 2019, 216, 101–109. [Google Scholar] [CrossRef]
- Schmit, C.; Hausswirth, C.; LeMeur, Y.; Duffield, R. Cognitive functioning and heat strain: Performance responses and protective strategies. Spor. Medic. 2017, 47, 1289–1302. [Google Scholar] [CrossRef]
- Yang, D.B.; Xu, Y.C.; Wang, D.H. Partial removal of brown adipose tissue enhances humoral immunity in warm-acclimated Mongolian gerbils (Meriones unguiclatus). General. Comp. Endocrinol. 2012, 175, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Khakisahneh, S.; Zhang, X.Y.; Nouri, Z.; Wang, D.H. Gut microbiota and host thermoregulation in response to ambient temperature fluctuations. mSystems 2020, 5, e00514-20. [Google Scholar] [CrossRef] [PubMed]
- Kanter, M.; Aktas, C.; Erboga, M. Heat stress decreases testicular germ cell proliferation and increases apoptosis in short term: An immunohistochemical and ultrastructural study. Toxicol. Industr. Health 2013, 29, 99–113. [Google Scholar] [CrossRef]
- Simons, M.J.P.; Reimert, I.; Van Der Vinne, V.; Hambly, C.; Vaanholt, L.M.; Speakman, J.R.; Gerkema, M.P. Ambient temperature shapes reproductive output during pregnancy and lactation in the common vole (Microtus arvalis): A test of the heat dissipation limit theory. J. Exper. Biol. 2011, 214, 38–49. [Google Scholar] [CrossRef]
- Yang, D.B.; Xu, Y.C.; Wang, D.H.; Speakman, J.R. Effects of reproduction on immuno-suppression and oxidative damage, and hence support or otherwise for their roles as mechanisms underpinning life history trade-offs, are tissue and assay dependent. J. Exp. Biol. 2013, 216, 4242–4250. [Google Scholar] [CrossRef] [PubMed]
- Craine, J.M.; Nippert, J.B.; Towne, E.G.; Tucker, S.; Kembel, S.W.; Skibbe, A.; McLauchlan, K.K. Functional consequences of climate change-induced plant species loss in a tallgrass prairie. Oecologia 2011, 165, 1109–1117. [Google Scholar] [CrossRef] [PubMed]
- Boeck, H.J.D.; Lemmens, C.M.H.M.; Gielen, B.; Bossuyt, H.; Malchair, S.; Carnol, M.; Merckx, R.; Ceulemans, R.; Nijs, I. Combined effects of climate warming and plant diversity loss on above- and below-ground grassland productivity. Environ. Exp. Botany. 2007, 60, 95–104. [Google Scholar] [CrossRef]
- Li, G.L.; Yin, B.F.; Li, J.; Wang, J.; Wei, W.H.; Bolnick, D.I.; Wan, X.; Zhu, B.; Zhang, Z.B. Host-microbiota interaction helps to explain the bottom-up effects of climate change on a small rodent species. ISME J. 2020, 14, 1795–1808. [Google Scholar] [CrossRef]
- Zhong, W.Q.; Wang, M.J.; Wan, X.R. Ecological management of Brandt’s vole in Inner Mongolia, China. In Ecologically Based Management of Rodent Pasts; Singleton, G., Hinds, L., Leirs, H., Zhang, Z.B., Eds.; Australian Centre for International Agricultural Research: Canberra, Australia, 1999; pp. 199–214. [Google Scholar]
- Zhong, W.Q.; Zhou, Q.Q.; Sun, C.L. The basic characteristics of the rodent pests on the pasture in Inner Mongolia and its ecological strategies of controlling. Acta Their.Sin. 1985, 5, 242–249. (In Chinese) [Google Scholar]
- Field, C.B.; Barros, V.R. IPCC, 2014: Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014: Impacts, Adaptation, and Vulnerability; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Eronen, J.T.; Polly, P.D.; Fred, M.; Damuth, J.; Frank, D.C.; Mosbrugger, V.; Scheidegger, C.; Stenseth, N.C.; Fortelius, M. Ecometrics: The traits that bind the past and present together. Integr. Zool. 2010, 5, 88–101. [Google Scholar] [CrossRef]

| Model | AICc | ΔAICc | AICc Weight(w) | Model Likelihood | Par | Deviance |
|---|---|---|---|---|---|---|
| Step 1: Modelling survival probability, including environmental covariates with half-monthly temporal (t)-dependent and sex-independent for recapture probabilities by the CJS models. | ||||||
| φ(quadratic_temp + Pre + MNA/ha) p(t) | 2230.407 | 0.000 | 0.983 | 1.000 | 36 | 930.785 |
| φ(temp + MNA/ha) p(t) | 2239.367 | 8.960 | 0.011 | 0.011 | 39 | 933.389 |
| φ(temp + Pre + MNA/ha) p(t) | 2240.631 | 10.220 | 0.006 | 0.006 | 40 | 932.528 |
| φ(quadratic_temp) p(t) | 2253.378 | 22.970 | 0.000 | 0.000 | 39 | 947.400 |
| φ(temp) p(t) | 2253.594 | 23.190 | 0.000 | 0.000 | 38 | 949.738 |
| φ(temp + Pre) p(t) | 2255.716 | 25.310 | 0.000 | 0.000 | 39 | 949.738 |
| φ(quadratic-Pre) p(t) | 2285.179 | 54.770 | 0.000 | 0.000 | 39 | 979.201 |
| φ(Pre) p(t) | 2295.812 | 65.400 | 0.000 | 0.000 | 38 | 991.956 |
| φ(Pre + MNA/ha) p(t) | 2297.430 | 67.020 | 0.000 | 0.000 | 39 | 991.452 |
| φ(MNA) p(t) | 2324.421 | 94.010 | 0.000 | 0.000 | 38 | 1020.565 |
| φ(.) p(t) | 2329.248 | 98.840 | 0.000 | 0.000 | 37 | 1027.510 |
| Step 2: Modelling recruitment rate (f) including environmental covariates with half-monthly temporal-dependent (t) and sex-independent for recapture probabilities by the JS modes | ||||||
| φ(quadratic_temp) p(t) f(temp+ MNA/ha) | 4333.692 | 0.000 | 0.518 | 1.000 | 43 | 1171.419 |
| φ(quadratic_temp) p(t) f(temp + prec + MNA/ha) | 4335.733 | 2.040 | 0.186 | 0.360 | 44 | 1171.322 |
| φ(temp + prec + MNA/ha) p(t) f(temp + prec+ MNA/ha) | 4337.850 | 4.160 | 0.065 | 0.125 | 43 | 1175.577 |
| φ(temp + MNA/ha) p(t) f(temp + MNA/ha) | 4338.358 | 4.670 | 0.050 | 0.097 | 42 | 1178.220 |
| φ(quadratic_temp + prec + MNA/ha) p(t) f(temp + prec+ MNA/ha) | 4338.593 | 4.900 | 0.045 | 0.086 | 46 | 1169.895 |
| φ(temp + prec) p(t) f(temp + MNA/ha) | 4338.678 | 4.990 | 0.043 | 0.083 | 43 | 1176.405 |
| φ(temp + prec+ MNA/ha) p(t) f(temp + MNA/ha) | 4338.804 | 5.110 | 0.040 | 0.078 | 44 | 1174.393 |
| φ(temp + MNA/ha) p(t) f(temp + prec + MNA/ha) | 4340.490 | 6.800 | 0.017 | 0.033 | 43 | 1178.217 |
| φ(temp + prec) p(t) f(temp + pre+ MNA/ha) | 4340.787 | 7.100 | 0.015 | 0.029 | 44 | 1176.376 |
| φ(temp + prec) p(t) f(temp + pre) | 4342.268 | 8.580 | 0.007 | 0.014 | 40 | 1186.391 |
| φ(temp + pre) p(t) f(quadratic_temp) | 4343.041 | 9.350 | 0.005 | 0.009 | 40 | 1187.163 |
| φ(quadratic_temp) p(t) f(quadratic_temp) | 4344.053 | 10.360 | 0.003 | 0.006 | 41 | 1186.047 |
| φ(temp + prec + MNA/ha) p(t) f(temp + prec) | 4344.378 | 10.690 | 0.002 | 0.005 | 41 | 1186.372 |
| φ(temp + pre + MNA/ha) p(t) f(quadratic_temp) | 4345.169 | 11.480 | 0.002 | 0.003 | 41 | 1187.163 |
| φ(quadratic_temp) p(t) f(temp + prec) | 4345.170 | 11.480 | 0.002 | 0.003 | 43 | 1182.897 |
| φ(temp + MNA/ha) p(t) f(temp + prec) | 4347.914 | 14.220 | 0.000 | 0.001 | 41 | 1189.908 |
| φ(temp + MNA/ha) p(t) f(quadratic_temp) | 4348.307 | 14.620 | 0.000 | 0.001 | 41 | 1190.301 |
| φ(.) p(t) f(.) | 4493.187 | 159.500 | 0.000 | 0.000 | 39 | 1339.435 |
| Model | AICc | ΔAICc | AICc Weight (w) | Model Likelihood | Par | Deviance |
|---|---|---|---|---|---|---|
| φ(quadratic_temp) p(t) λ(temp + MNA/ha) | 4319.623 | 0.000 | 0.412 | 1.000 | 42 | 1159.485 |
| φ(quadratic_temp) p(t) λ(quadratic_temp + pre + MNA/ha) | 4319.776 | 0.150 | 0.382 | 0.926 | 44 | 1155.365 |
| φ(quadratic_temp) p(t) λ(temp + pre + MNA/ha) | 4321.602 | 1.980 | 0.153 | 0.372 | 43 | 1159.329 |
| φ(quadratic_temp + pre + MNA/ha) p(t) λ(temp+ MNA/ha) | 4323.785 | 4.160 | 0.051 | 0.125 | 44 | 1159.374 |
| φ(quadratic_temp) p(t) λ(temp + pre) | 4332.146 | 12.520 | 0.001 | 0.002 | 39 | 1178.394 |
| φ(quadratic_temp) p(t) λ(quadratic_temp + pre) | 4333.341 | 13.720 | 0.000 | 0.001 | 40 | 1177.464 |
| φ(quadratic_temp) p(t) λ(quadratic_temp) | 4335.515 | 15.890 | 0.000 | 0.000 | 42 | 1175.378 |
| φ(.) p(t) λ(.) | 4491.065 | 171.440 | 0.000 | 0.000 | 38 | 1339.435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Deng, K. Population Dynamics of Wild Mongolian Gerbils: Quadratic Temperature Effects on Survival and Density-Dependent Effects on Recruitment. Diversity 2022, 14, 586. https://doi.org/10.3390/d14080586
Liu W, Deng K. Population Dynamics of Wild Mongolian Gerbils: Quadratic Temperature Effects on Survival and Density-Dependent Effects on Recruitment. Diversity. 2022; 14(8):586. https://doi.org/10.3390/d14080586
Chicago/Turabian StyleLiu, Wei, and Ke Deng. 2022. "Population Dynamics of Wild Mongolian Gerbils: Quadratic Temperature Effects on Survival and Density-Dependent Effects on Recruitment" Diversity 14, no. 8: 586. https://doi.org/10.3390/d14080586
APA StyleLiu, W., & Deng, K. (2022). Population Dynamics of Wild Mongolian Gerbils: Quadratic Temperature Effects on Survival and Density-Dependent Effects on Recruitment. Diversity, 14(8), 586. https://doi.org/10.3390/d14080586






