Detection of Participation and Training Task Difficulty Applied to the Multi-Sensor Systems of Rehabilitation Robots
Abstract
:1. Introduction
2. LLR-II Rehabilitation Robot
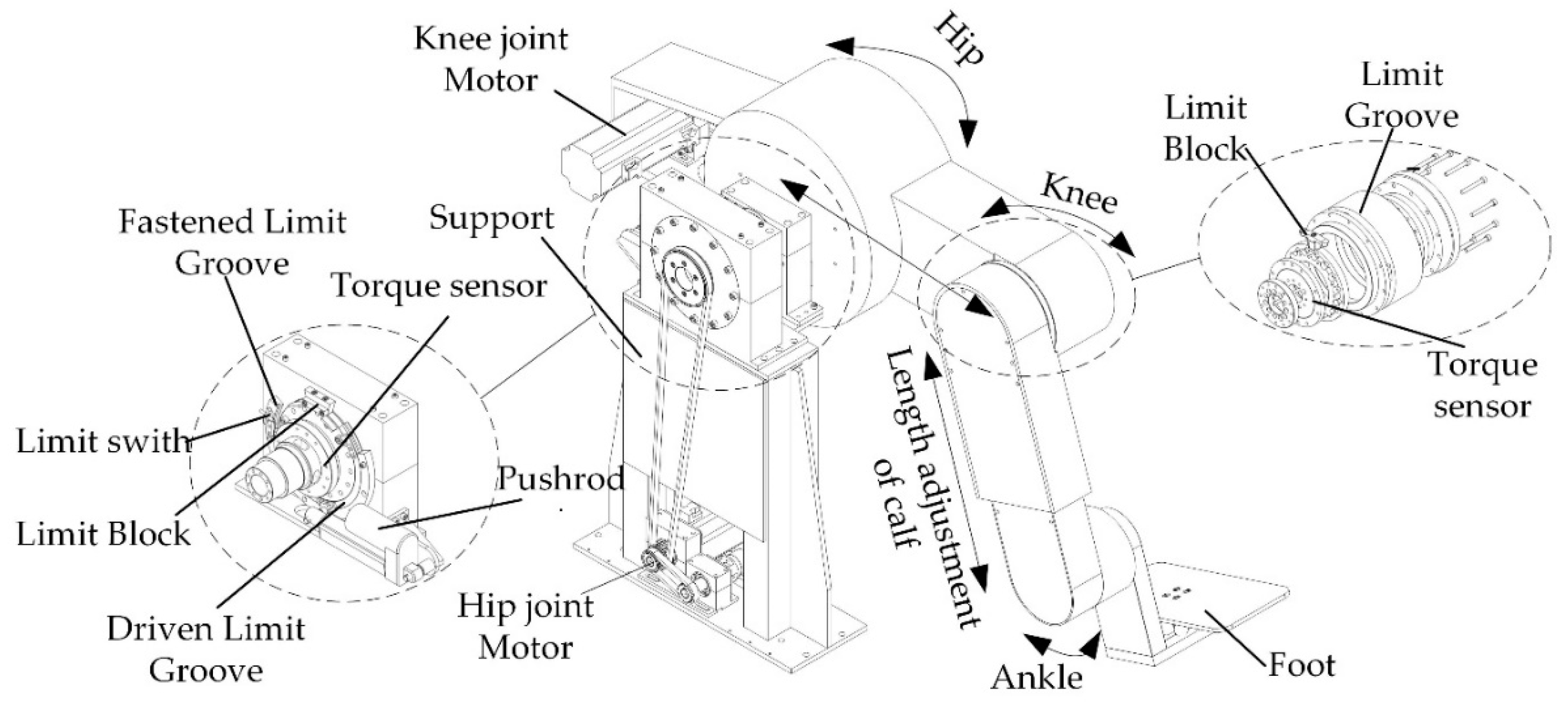
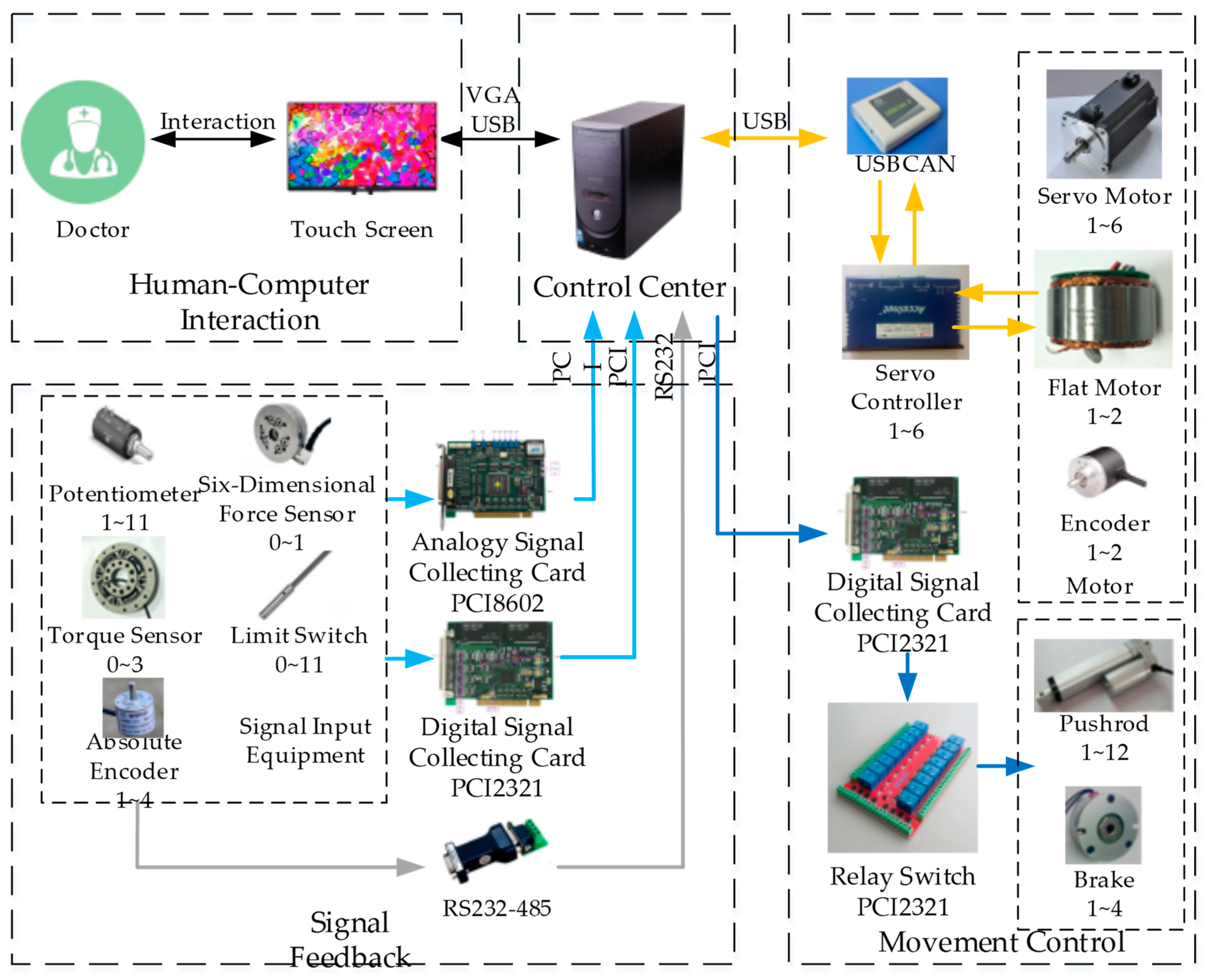
2.1. Structural Design of LLR-II
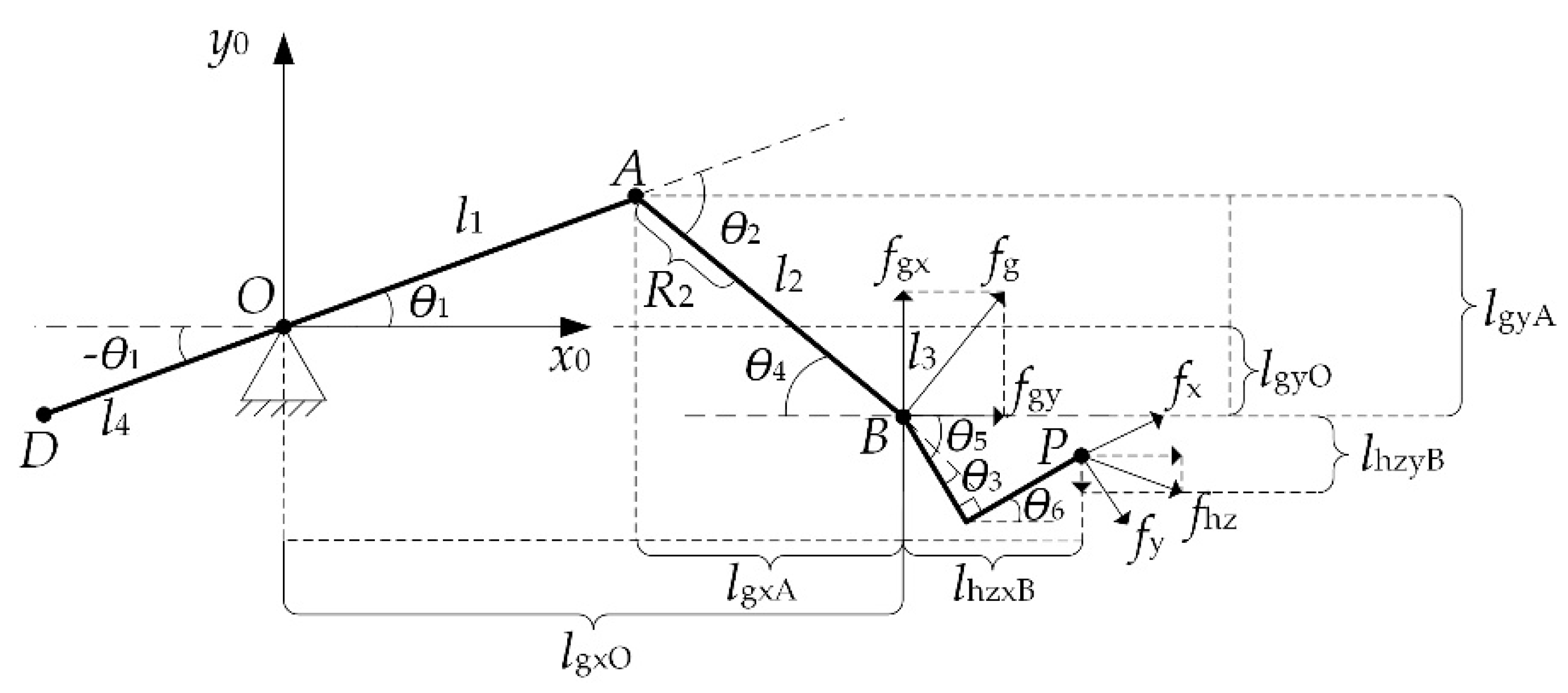
2.2. Man–Machine Interaction Mechanics Model of LLR-II
3. Participation Detection of LLR-II
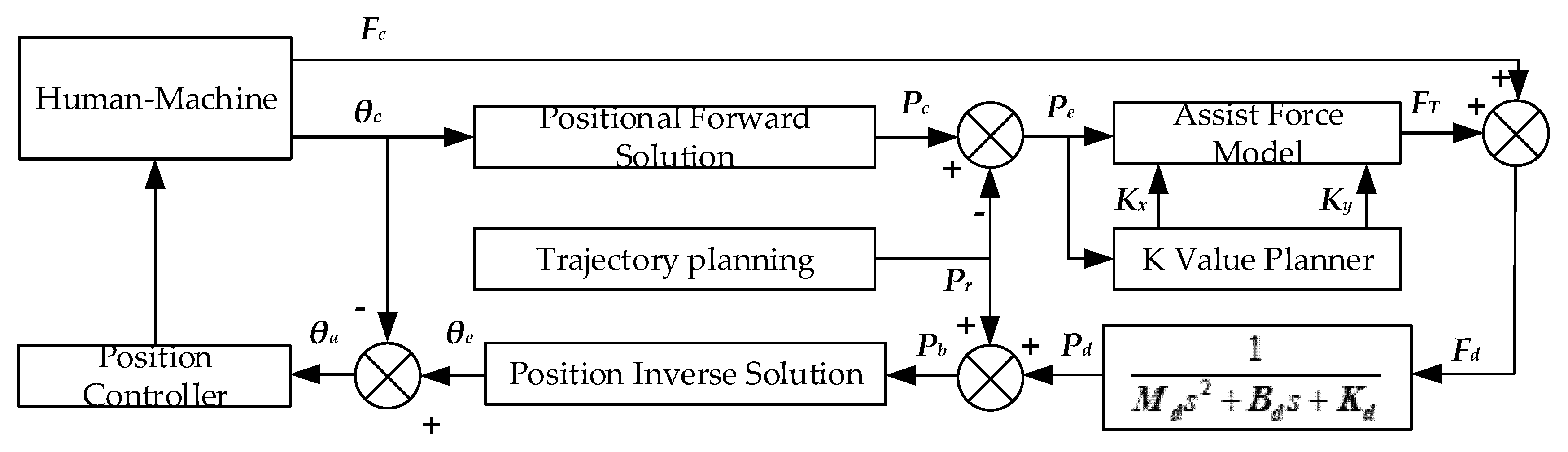
3.1. Assist Force Training Control
3.2. Patient Participation and Training Task Difficulty Prediction Model
4. Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dong, Q.; Guo, Q.; Luo, B.; Xu, Y. Expert consensus on post-stroke cognitive management. Chin. J. Stroke 2017, 12, 519–531. [Google Scholar]
- Feigin, V.L.; Forouzanfar, M.H.; Krishnamurthi, R.; Mensah, G.A.; Connor, M.; Bennett, D.A.; Moran, A.E.; Sacco, R.L.; Anderson, L.; Truelsen, T. Global and regional burden of stroke during 1990–2010: Findings from the Global Burden of Disease Study 2010. Lancet 2014, 383, 245–255. [Google Scholar] [CrossRef]
- Xiang, S.D.; Meng, Q.L.; Yu, H.L.; Meng, Q.Y. Research status of compliant exoskeleton rehabilitation manipulator. Chin. J. Rehabil. Med. 2018, 33, 461–465. [Google Scholar]
- Xie, S. Advanced Robotics for Medical Rehabilitation. Springer Tracts Adv. Robot. 2016, 108, 1–357. [Google Scholar]
- Hou, Z.G.; Zhao, X.G.; Cheng, L.; Wang, Q.N.; Wang, W.Q. Recent advances in rehabilitation robots and intelligent assistance systems. Acta Autom. Sin. 2016, 42, 1765–1779. [Google Scholar]
- Losey, D.; McDonald, C.; Battaglia, E.; O"Malley, M.K. A review of intent detection, arbitration, and communication aspects of shared control for physical human-robot interaction. Appl. Mech. Rev. 2018, 70, 1. [Google Scholar] [CrossRef]
- Tao, H.B.; Yu, Y.; Zhang, Q.; Sun, H.Y. A control system based on MCU for wearable power assist legs. In Proceedings of the IEEE International Conference on Robotics & Biomimetics, Karon Beach, Phuket, Thailand, 7–11 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2193–2198. [Google Scholar]
- Victor, G.; Svetlana, G.; Bram, V.; Dirk, L.; Carlos, R.G. Multi-Axis force sensor for human-robot interaction sensing in a rehabilitation robotic device. Sensors 2017, 17, 1294. [Google Scholar]
- Hwang, B.; Jeon, D. Estimation of the user’s muscular torque for an over-ground gait rehabilitation robot using torque and insole pressure sensors. Int. J. Control Autom. 2018, 16, 275–283. [Google Scholar] [CrossRef]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Alin, A.S. Variable stiffness actuators: Review on design and components. IEEE/ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Bongsu, K.; Aurelien, R.; Deshpande, A.D. Impedance control based on a position sensor in a rehabilitation robot. In Proceedings of the ASME 2014 Dynamic Systems and Control Conference, San Antonio, TX, USA, 22–24 October 2014; pp. 1–7. [Google Scholar]
- Kim, B.; Deshpande, A.D. Controls for the shoulder mechanism of an upper-body exoskeleton for promoting scapulohumeral rhythm. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Singapore, 11–14 August 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Novak, D.; Riener, R. A survey of sensor fusion methods in wearable robotics. Robot. Auton. Syst. 2015, 73, 155–170. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Chung, W.Y. Detection of driver braking intention using EEG signals during simulated driving. Sensors 2019, 19, 2863. [Google Scholar] [CrossRef] [PubMed]
- Washabaugh, E.P.; Guo, J.; Chang, C.K.; Remy, C.D. A portable passive rehabilitation robot for upper-extremity functional resistance training. IEEE Trans. Biomed. Eng. 2019, 66, 496–508. [Google Scholar] [CrossRef] [PubMed]
- Magdalena, Z.; Malgorzata, S.; Celina, P. Use of the surface electromyography for a quantitative trend validation of estimated muscle forces. Biocybern. Biomed. Eng. 2018, 38, 243–250. [Google Scholar]
- Tang, Z.C.; Shouqian, S.; Sanyuan, Z.; Chen, Y.; Li, C.; Chen, S. A Brain-Machine Interface Based on ERD/ERS for an Upper-Limb Exoskeleton Control. Sensors 2016, 16, 2050. [Google Scholar] [CrossRef]
- Yepes, J.C.; Portela, M.A.; Saldarriaga, Á.J.; Pérez, V.Z.; Betancur, M.J. Myoelectric control algorithm for robot-assisted therapy: A hardware-in-the-loop simulation study. Biomed. Eng. Online 2019, 18, 3. [Google Scholar] [CrossRef]
- Farina, D.; Jiang, N.; Rehbaum, H.; Holobar, A.; Graimann, B.; Dietl, H. The extraction of neural information from the surface emg for the control of upper-limb prostheses: Emerging avenues and challenges. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 797–809. [Google Scholar] [CrossRef]
- Ison, M.; Vujaklija, I.; Whitsell, B.; Farina, D.; Artemiadis, P. High-density electromyography and motor skill learning for robust long-term control of a 7-dof robot arm. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 424–433. [Google Scholar] [CrossRef]
- Engemann, D.A.; Gramfort, A. Automated model selection in covariance estimation and spatial whitening of MEG and EEG signals. NeuroImage 2015, 108, 328–342. [Google Scholar] [CrossRef]
- Fougner, A.; Scheme, E.; Chan, A.D.C.; Englehart, K.; Stavdahl, J. Resolving the limb position effect in myoelectric pattern recognition. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 644–651. [Google Scholar] [CrossRef]
- Peng, L.; Hou, Z.G.; Chen, Y.X.; Wang, W.Q.; Tong, L.N.; Li, P.F. Combined use of sEMG and accelerometer in hand motion classification considering forearm rotation. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 4227–4230. [Google Scholar]
- Lo, A.C.; Guarino, P.D.; Richards, L.G.; Jodie, K.H.; George, F.W.; Daniel, G.F.; Robert, J.R.; Todd, H.W.; Hermano, I.K.; Bruce, T.V.; et al. Robot-assisted therapy for long-term upper-limb impairment after stroke. N. Engl. J. Med. 2010, 362, 1772–1783. [Google Scholar] [CrossRef]
- Reinkensmeyer, D.J.; Wolbrecht, E.; Bobrow, J. A computational model of human-robot load sharing during robotassisted arm movement training after stroke. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 4019–4023. [Google Scholar]
- Qian, Z.Q.; Lv, D.Y.; Lv, Y. Modeling and quantification of impact of psychological factors on rehabilitation of stroke patients. IEEE J. Biomed. Health Inform. 2019, 23, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Yatsenko, D.; Mcdonnall, D.; Guillory, K.S. Simultaneous, proportional, multi-axis prosthesis control using multichannel surface EMG. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 6133–6136. [Google Scholar]
- Lenzi, T.; De Rossi, S.M.M.; Vitiello, N.; Carrozza, M.C. Intention-based EMG control for powered exoskeletons. IEEE Trans. Biomed. Eng. 2012, 59, 2180–2190. [Google Scholar] [CrossRef] [PubMed]
- Duschau-Wicke, A.; Zitzewitz, J.V.; Caprez, A.; Lunenburger, L.; Riener, R. Path control: A method for patient-cooperative robot-aided gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Krebs, H.I.; Palazzolo, J.J.; Dipietro, L.; Ferraro, M.; Krol, J.; Rannekleiv, K. Rehabilitation robotics: Performance-based progressive robot-assisted therapy. Auton. Robot. 2003, 15, 7–20. [Google Scholar] [CrossRef]
- Cai, L.L.; Fong, A.J.; Liang, Y.Q.; Burdick, J.; Edgerton, V.R. Assist-as-needed training paradigms for robotic rehabilitation of spinal cord injuries. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 3504–3511. [Google Scholar] [Green Version]
- Wolbrecht, E.T.; Chan, V.; Reinkensmeyer, D.J.; Bobrow, J.E. Optimizing compliant, model-based robotic assistance to promote neurorehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 286–297. [Google Scholar] [CrossRef]
- Pehlivan, A.U.; Losey, D.P.; Ormalley, M.K. Minimal assist-as-needed controller for upper limb robotic rehabilitation. IEEE Trans. Robot. 2016, 32, 113–124. [Google Scholar] [CrossRef]
- Kleinsmith, A.; Bianchi-Berthouze, N. Affective body expression perception and recognition: A survey. IEEE Trans. Affect. Comput. 2013, 4, 15–33. [Google Scholar] [CrossRef]
- Khosrowabadi, R.; Quek, C.; Ang, K.K.; Wahab, A. ERNN: A biologically inspired feedforward neural network to discriminate emotion from EEG signal. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 609–620. [Google Scholar] [CrossRef]
- Xu, G.; Gao, X.; Pan, L.; Chen, s.; Wang, Q.; Zhu, B. Anxiety detection and training task adaptation in robot-assisted active stroke rehabilitation. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Ozkul, F.; Palaska, Y.; Masazade, E.; Erol-Barkana, D. Exploring dynamic difficulty adjustment mechanism for rehabilitation tasks using physiological measures and subjective ratings. IET Signal Process. 2019, 13, 378–386. [Google Scholar] [CrossRef]
- Fundaro, C.; Maestri, R.; Ferriero, G.; Chimento, P.; Taveggia, G.; Casale, R. Self-selected speed gait training in parkinson’s disease: Robot-assisted gait training with virtual reality versus gait training on the ground. Eur. J. Phys. Rehabil. Med. 2019, 55, 456–462. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.F.; Wang, H.B.; Yan, H.; Wang, X.; Jin, Z.; Vladareanu, L. Research on safety and compliance of a new lower limb rehabilitation robot. J. Healthc. Eng. 2017, 2017, 1523068. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Wang, H.; Vladareanu, L.; Wang, X.C.; Jin, Z.N.; Vladareanu, L. New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors. Sensors 2019, 19, 3439. [Google Scholar] [CrossRef]
- Wang, H.B.; Feng, Y.F.; Yu, H.N.; Wang, Z.H.; Vladareanuv, V.; Du, Y.X. Mechanical design and trajectory planning of a lower limb rehabilitation robot with a variable workspace. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zhuang, J.X.; Jiang, H.Y.; Liu, L.L.; Wang, F.F.; Tang, L.; Zhu, Y. Parameters optimization of rice development stage model based on individual advantages genetic algorithm. Sci. Agric. Sin. 2013, 46, 2220–2231. [Google Scholar]
- Gou, X.; Peng, C.; Zhang, S.; Yan, J.; Duan, S.; Wang, L. A novel feature extraction approach using window function capturing and QPSO-SVM for enhancing electronic nose performance. Sensors 2015, 15, 15198–15217. [Google Scholar]
- Zhao, Y.T.; Shan, Z.Y.; Chang, Y.; Chen, Y.; Hao, X.C. Soft sensor modeling for cement fineness based on least squares support vector machine and mutual information. Chin. J. Sci. Instrum. 2017, 38, 487–496. [Google Scholar]



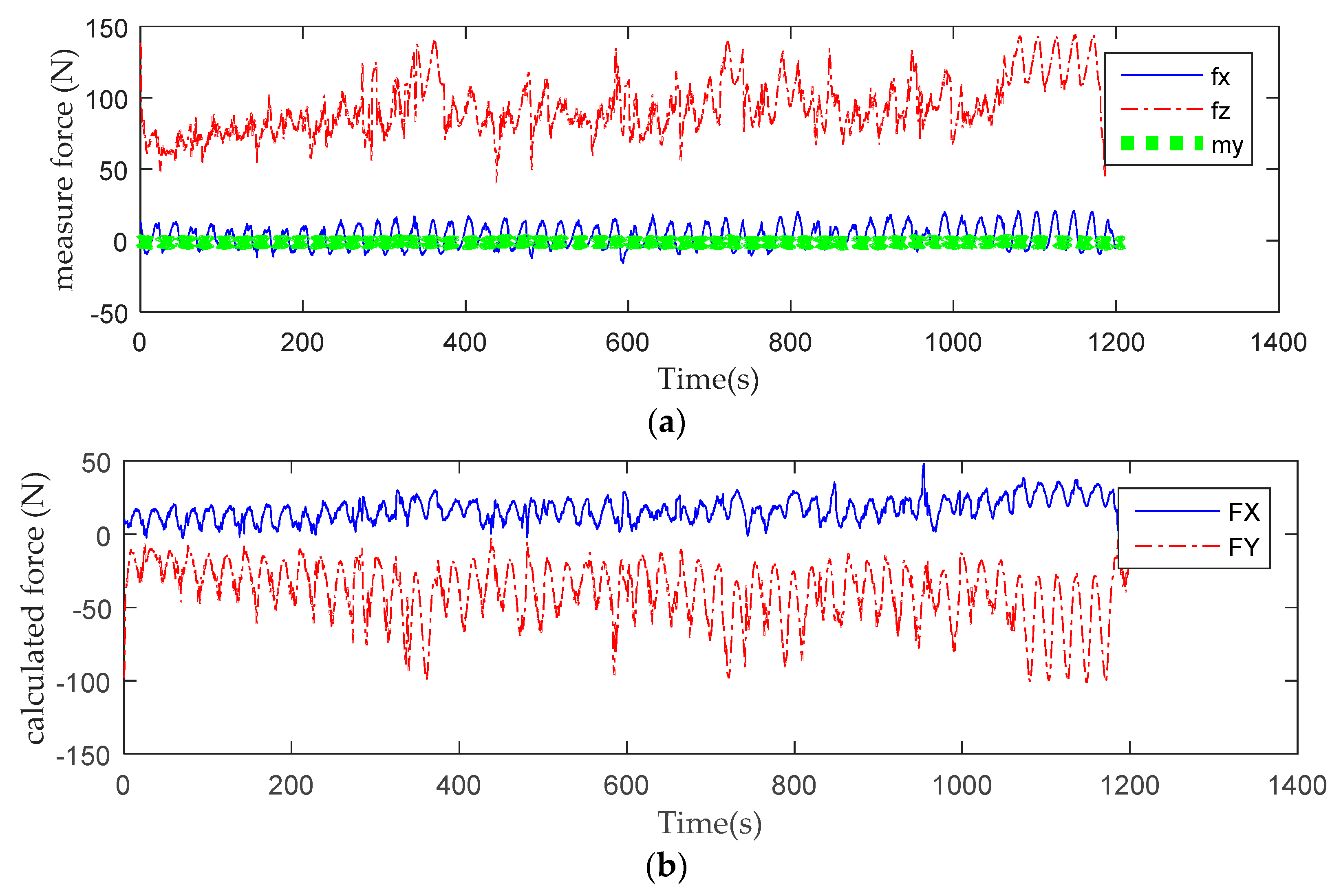
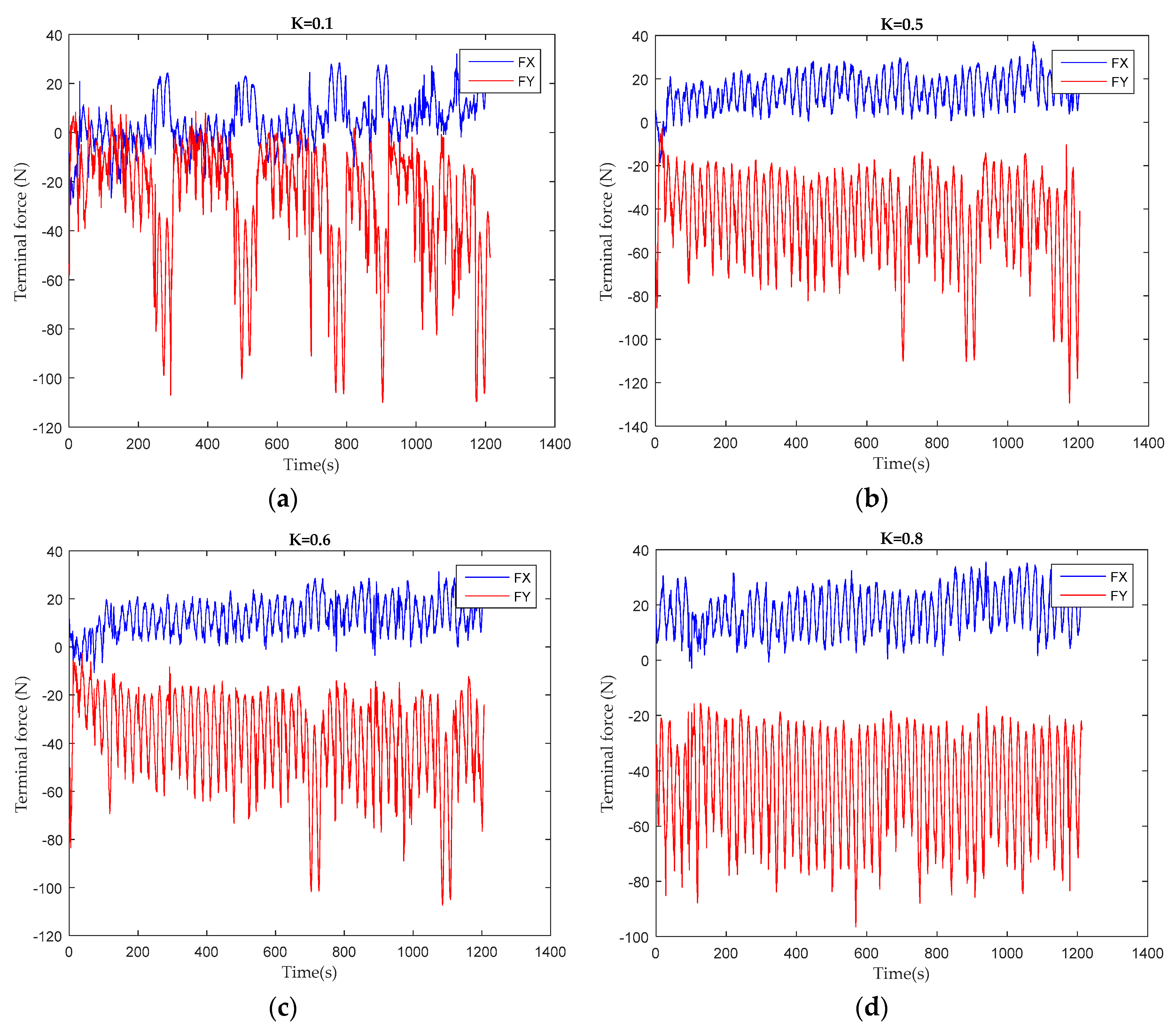
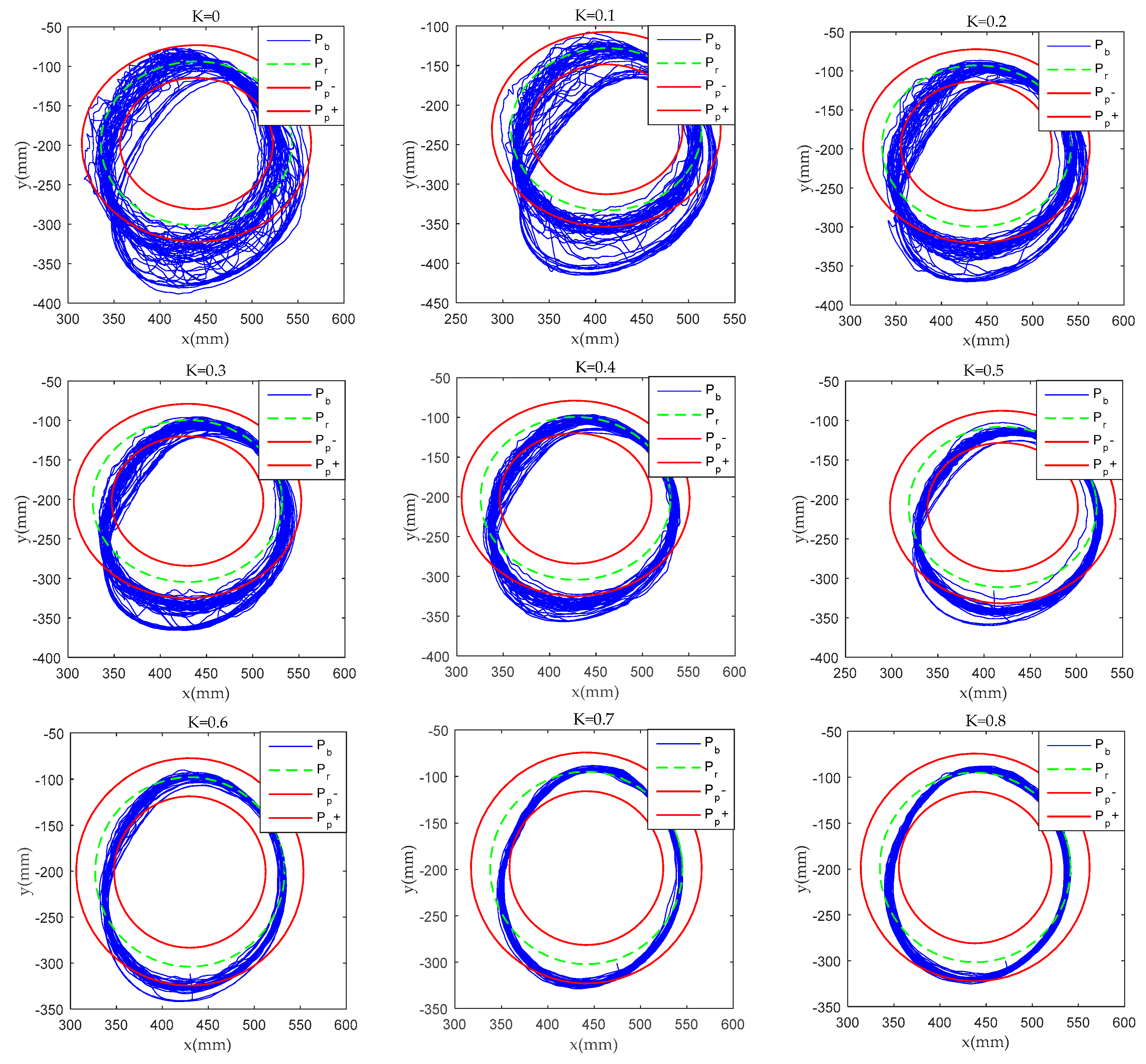
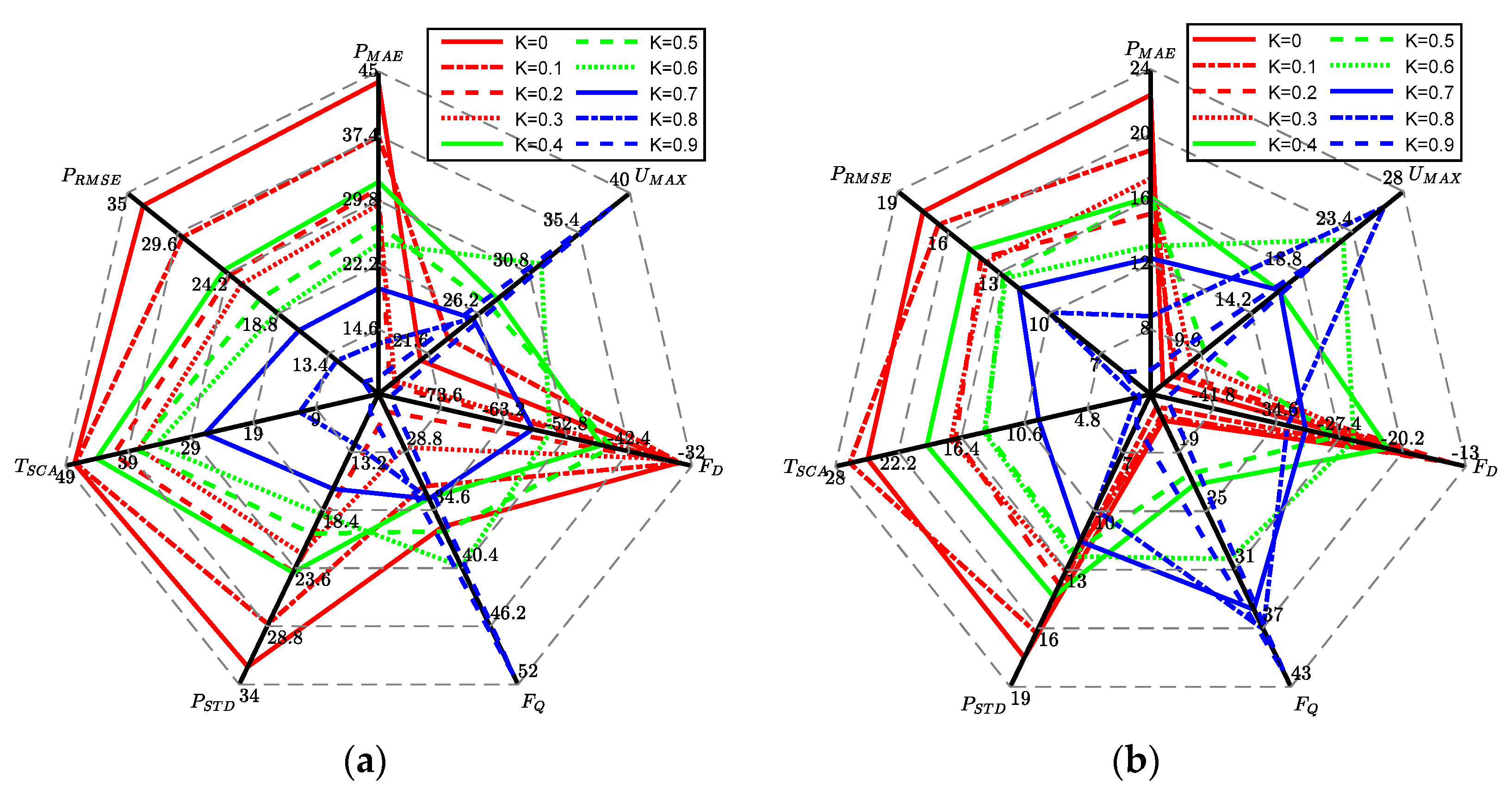

| Type | Description |
|---|---|
| PRMSE | Mean square error of position |
| PSTD | Position standard deviation |
| TSCA | The proportion of time outside the safe passage |
| FQ | Inter-quartile range of terminal force |
| UMAX | Maximum value in frequency domain of terminal force |
| fMAX | Peak frequency in frequency domain of terminal force |
| FD | Component at frequency 0 in frequency domain of terminal force |
| FVAR | Variance of terminal force |
| POR | Offset range of position |
| UhMAX | Maximum value in frequency domain of volunteer motivation |
| fhMAX | Peak frequency in frequency domain of volunteer motivation |
| PMAE | Mean absolute error of position |
| Comparison | PRMSE | PSTD | TSCA | |||
| P | F | P | F | P | F | |
| Difficult/Medium | 3.19 × 10−4 | 1.09 × 10−11 | 1.5 × 10−4 | 3.76 × 10−10 | 1.44 × 10−3 | 5.9 × 10−4 |
| Difficult /Easy | 2.74 × 10−7 | 3.2 × 10−14 | 4.26 × 10−8 | 1.08 × 10−12 | 2.06 × 10−11 | 1.9 × 10−4 |
| Medium/ Easy | 8.08 × 10−9 | 0.1 | 1.26 × 10−8 | 0.112 | 6.13 × 10−10 | 0.634 |
| Comparison | FQ | UMAX | fMAX | |||
| P | F | P | F | P | F | |
| Difficult/Medium | 0.844 | 0.0904 | 0.136 | 0.07 | 0.39 | 0.382 |
| Difficult /Easy | 9.97 × 10−3 | 0.01 | 6.37 × 10−4 | 0.028 | 0.028 | 0.007 |
| Medium/ Easy | 4.7 × 10−3 | 0.339 | 0.0147 | 0.65 | 0.154 | 0.066 |
| Comparison | FD | FVAR | POR | |||
| P | F | P | F | P | F | |
| Difficult/Medium | 0.735 | 2 × 10−5 | 0.255 | 0.001 | 7.59 × 10−6 | 0.0035 |
| Difficult /Easy | 0.033 | 0.221 | 0.961 | 0.072 | 3.07 × 10−13 | 5.66 × 10−11 |
| Medium/ Easy | 0.0013 | 0.002 | 0.193 | 0.212 | 2.922 × 10−8 | 1.78 × 10−5 |
| Comparison | UhMAX | fhMAX | PMAE | |||
| P | F | P | F | P | F | |
| Difficult/Medium | 0.0013 | 0.009 | 0.001 | 0.6789 | 0.0005 | 5.38 × 10−12 |
| Difficult /Easy | 0.1478 | 0.003 | 0.072 | 0.5531 | 3.19 × 10−7 | 4.29 × 10−13 |
| Medium/ Easy | 0.5216 | 6.06 × 10−7 | 0.929 | 0.8565 | 2.32 × 10−9 | 0.339 |
| MSE | MAE | STD | |
|---|---|---|---|
| Matching degree | 0.0428 | 0.1822 | 0.1006 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Wang, H.; Vladareanu, L.; Lin, M.; Vladareanu, V.; Li, Y. Detection of Participation and Training Task Difficulty Applied to the Multi-Sensor Systems of Rehabilitation Robots. Sensors 2019, 19, 4681. https://doi.org/10.3390/s19214681
Yan H, Wang H, Vladareanu L, Lin M, Vladareanu V, Li Y. Detection of Participation and Training Task Difficulty Applied to the Multi-Sensor Systems of Rehabilitation Robots. Sensors. 2019; 19(21):4681. https://doi.org/10.3390/s19214681
Chicago/Turabian StyleYan, Hao, Hongbo Wang, Luige Vladareanu, Musong Lin, Victor Vladareanu, and Yungui Li. 2019. "Detection of Participation and Training Task Difficulty Applied to the Multi-Sensor Systems of Rehabilitation Robots" Sensors 19, no. 21: 4681. https://doi.org/10.3390/s19214681
APA StyleYan, H., Wang, H., Vladareanu, L., Lin, M., Vladareanu, V., & Li, Y. (2019). Detection of Participation and Training Task Difficulty Applied to the Multi-Sensor Systems of Rehabilitation Robots. Sensors, 19(21), 4681. https://doi.org/10.3390/s19214681







