Design of a Planar Sensor Based on Split-Ring Resonators for Non-Invasive Permittivity Measurement
Abstract
:1. Introduction
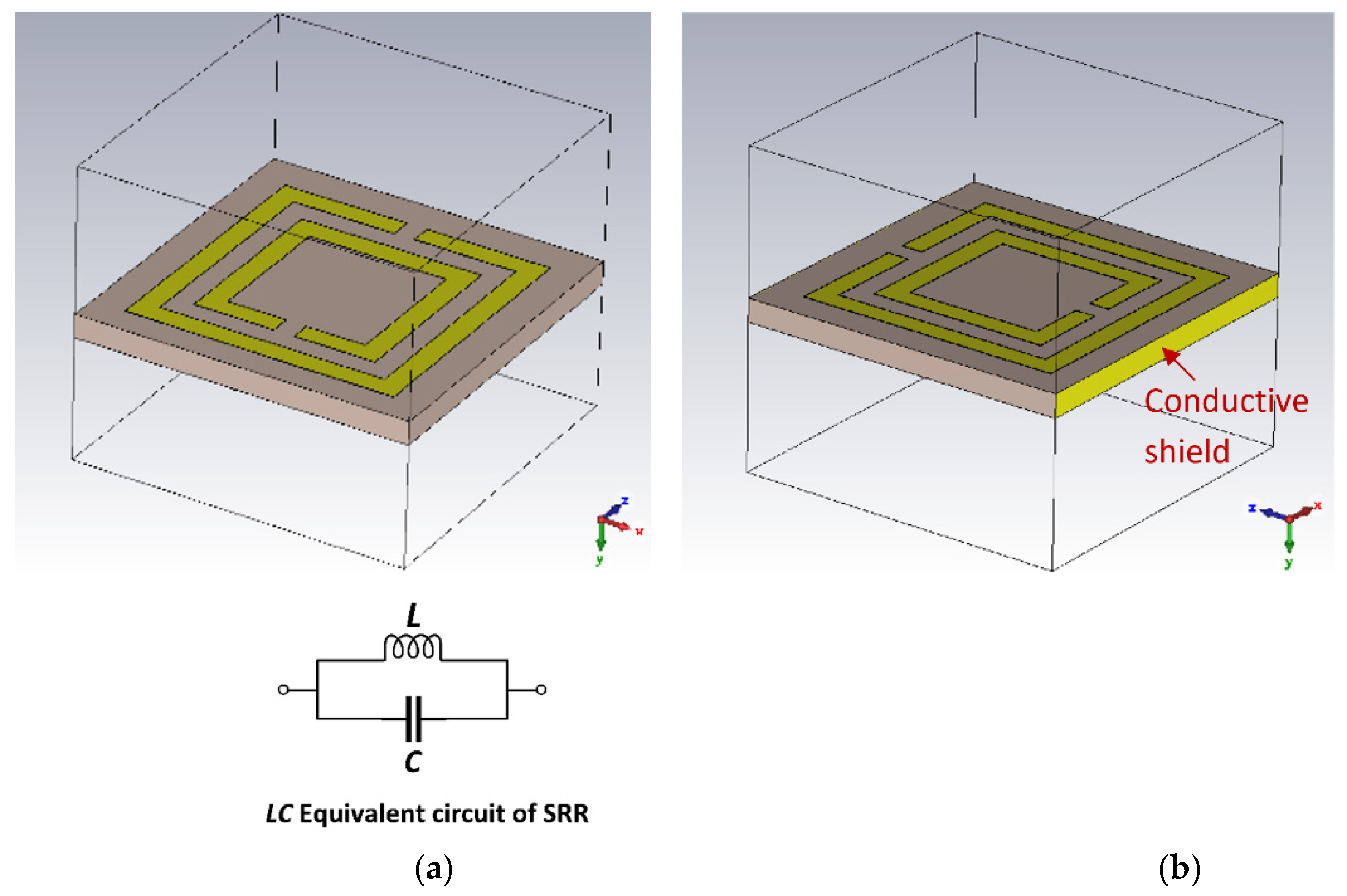
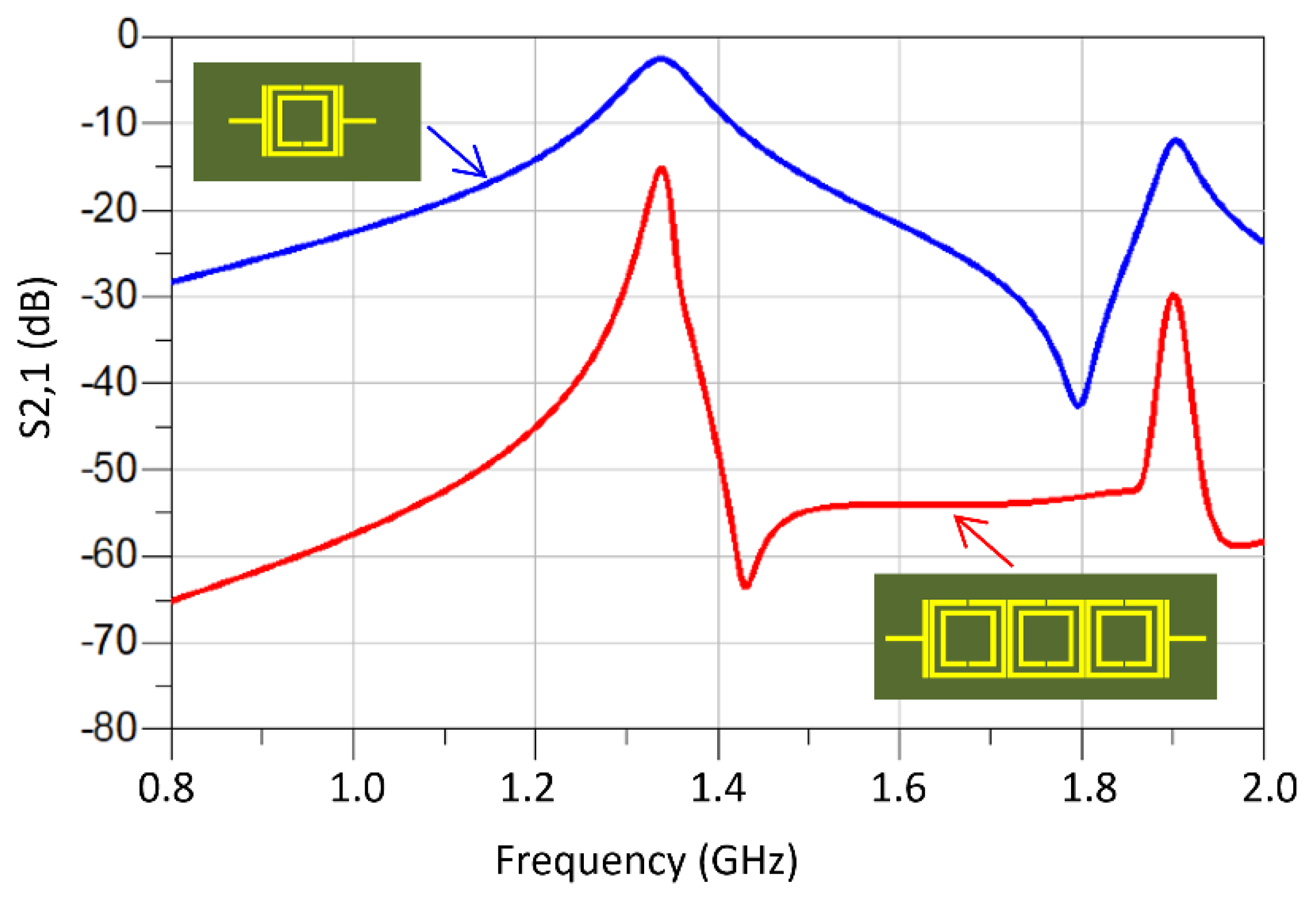
2. Complementary Split-Ring Resonator (SRR)
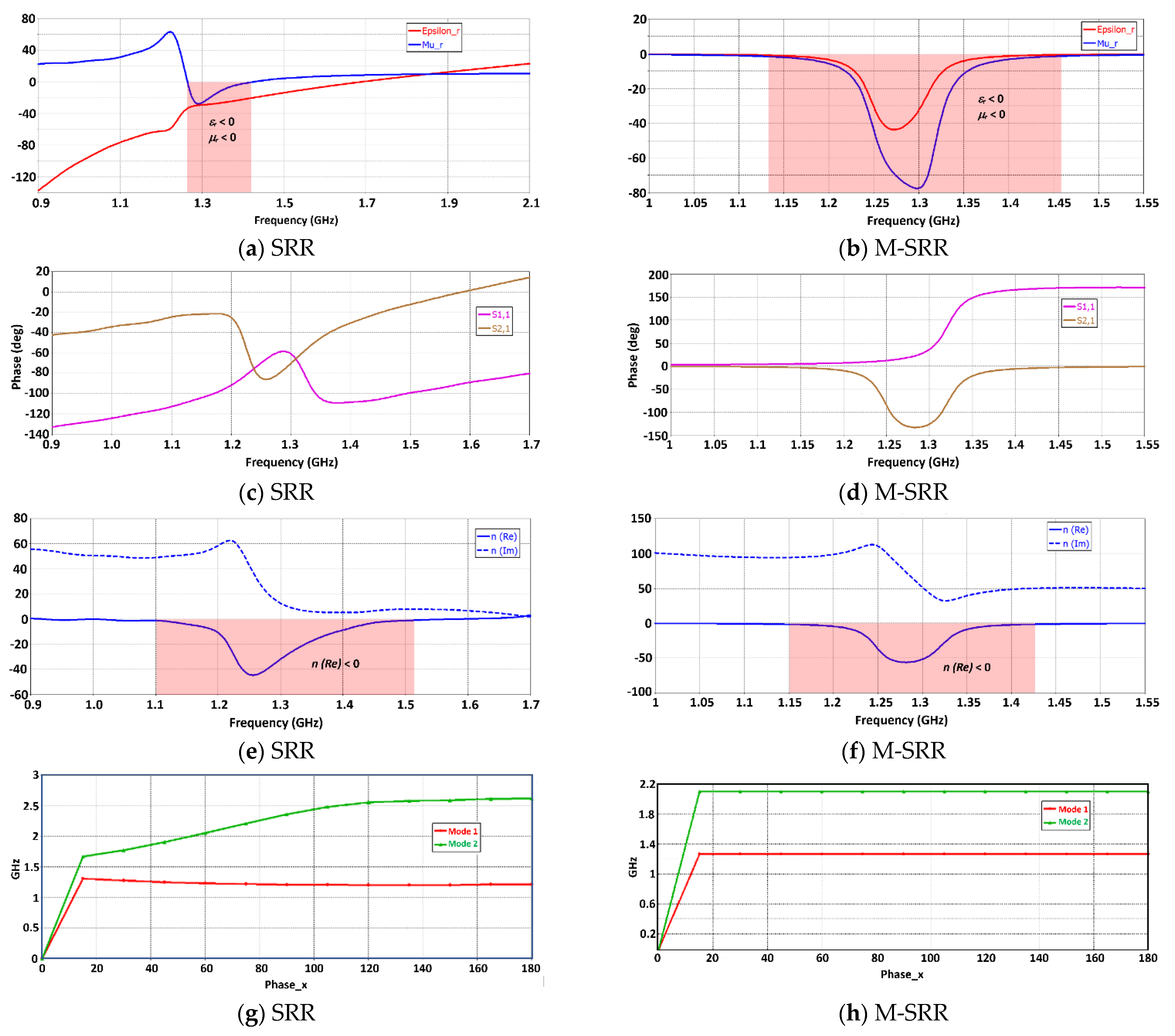
3. Theoretical Analysis of a Split-Ring Resonator Unit-Cell
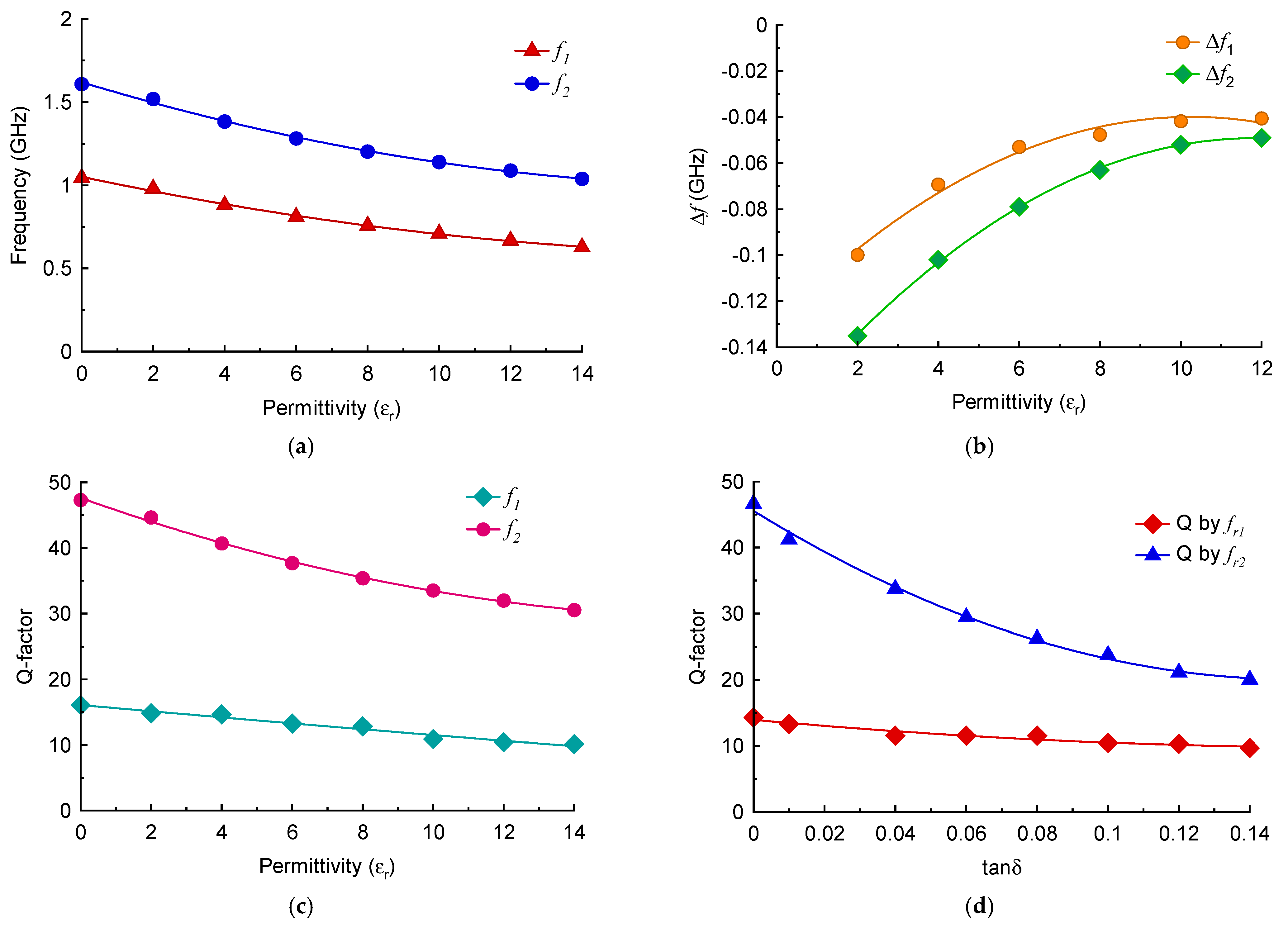
3.1. Sensitivity Analysis of the Unit-Cell M-SRR Sensor
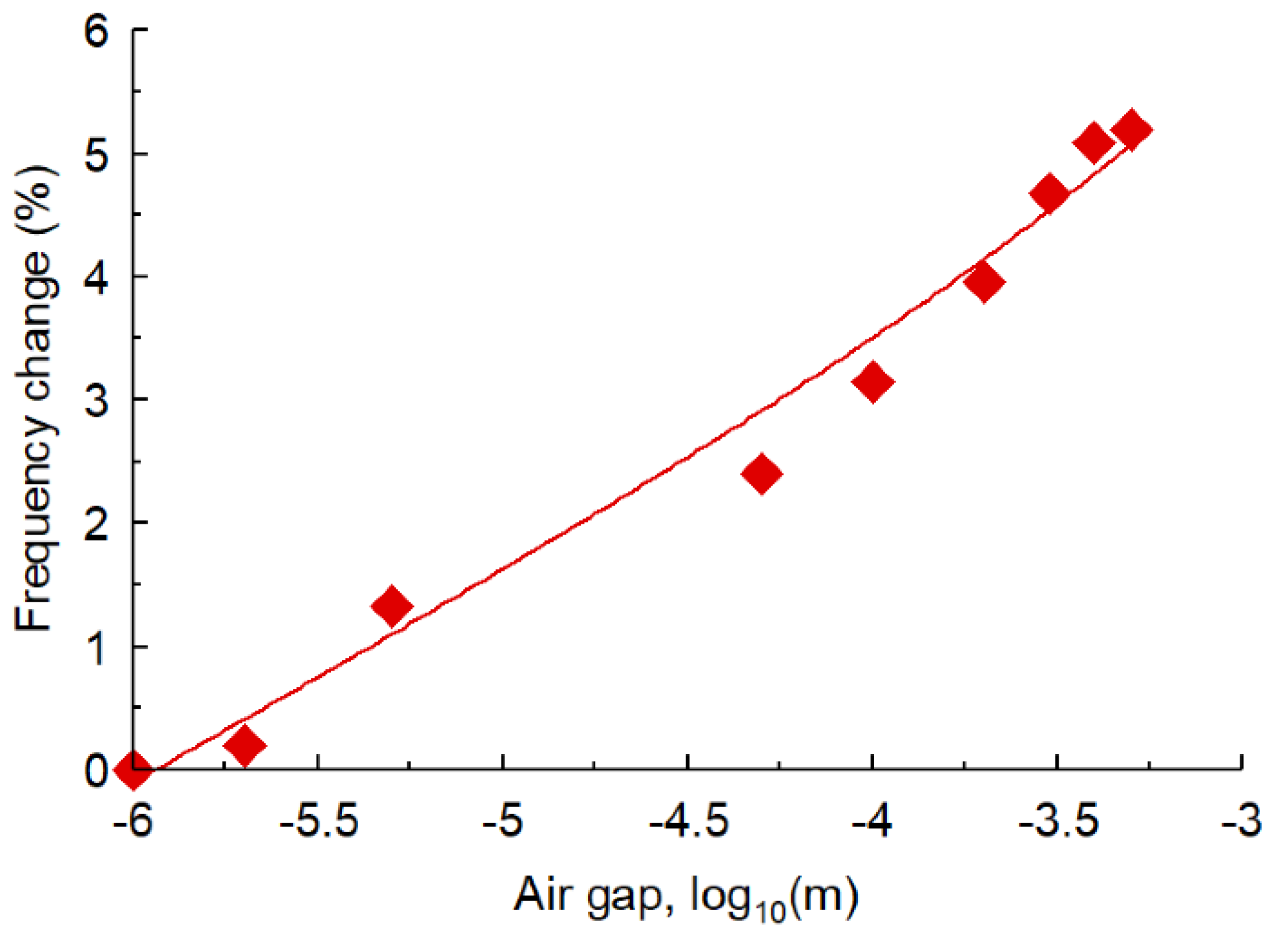
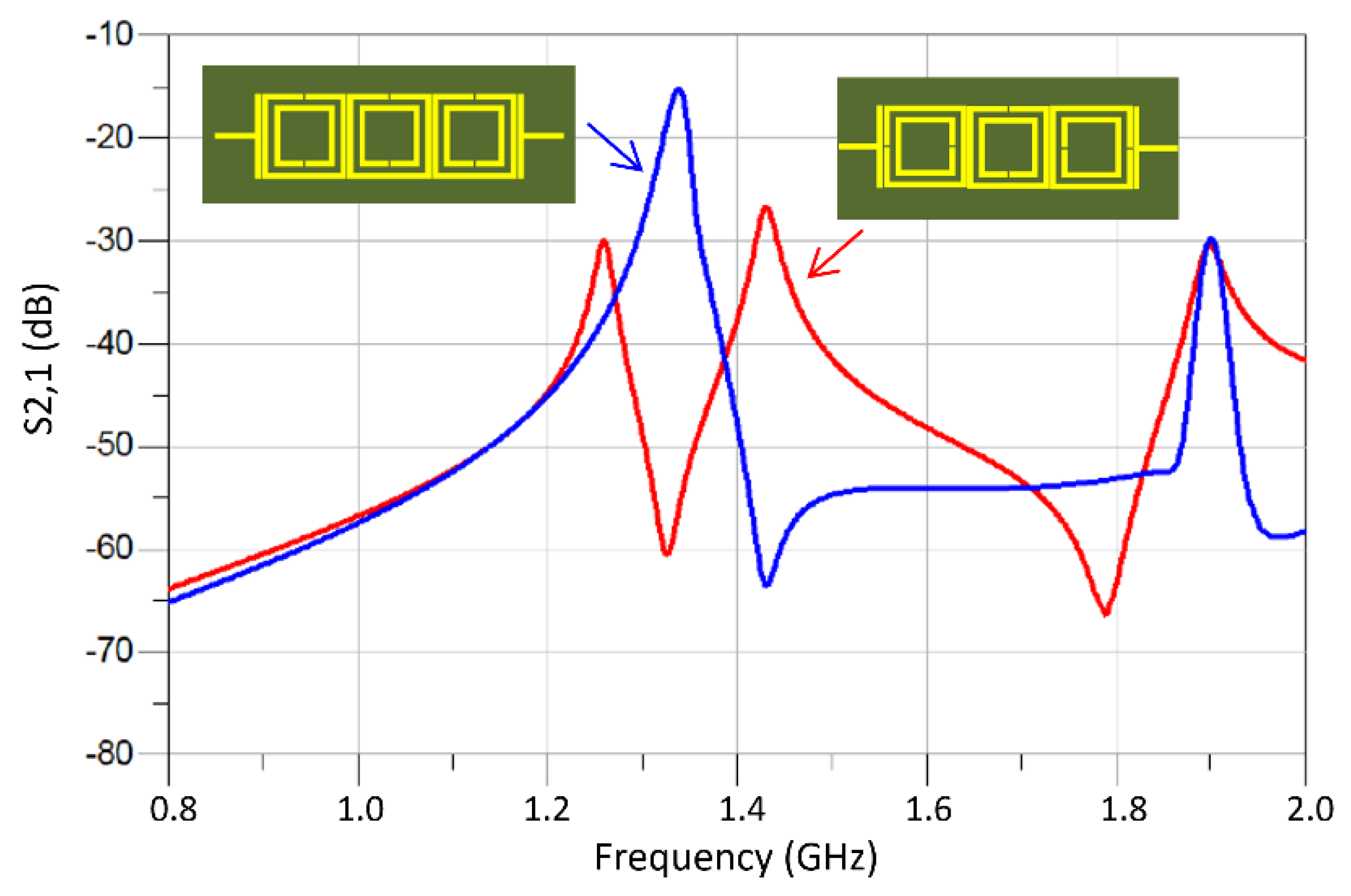
3.2. Enhancing the Sensitivity of the M-SRR Sensor
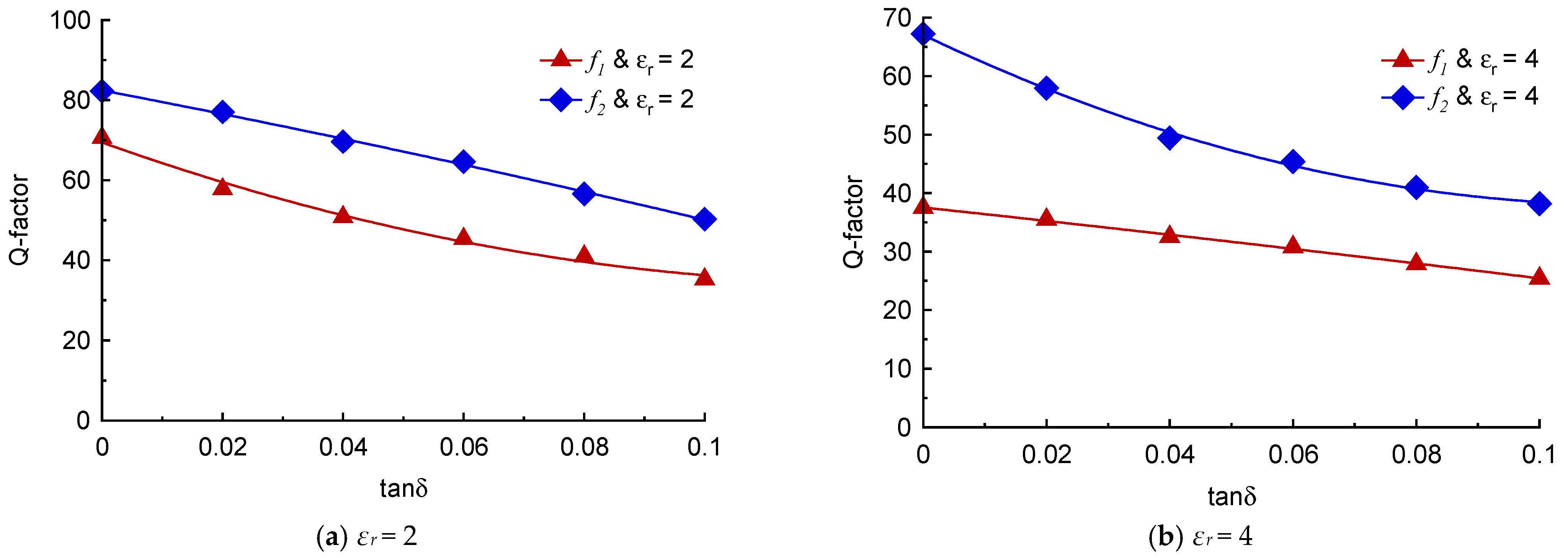
3.3. Sensitivity Analysis of the TC-SRR Sensor
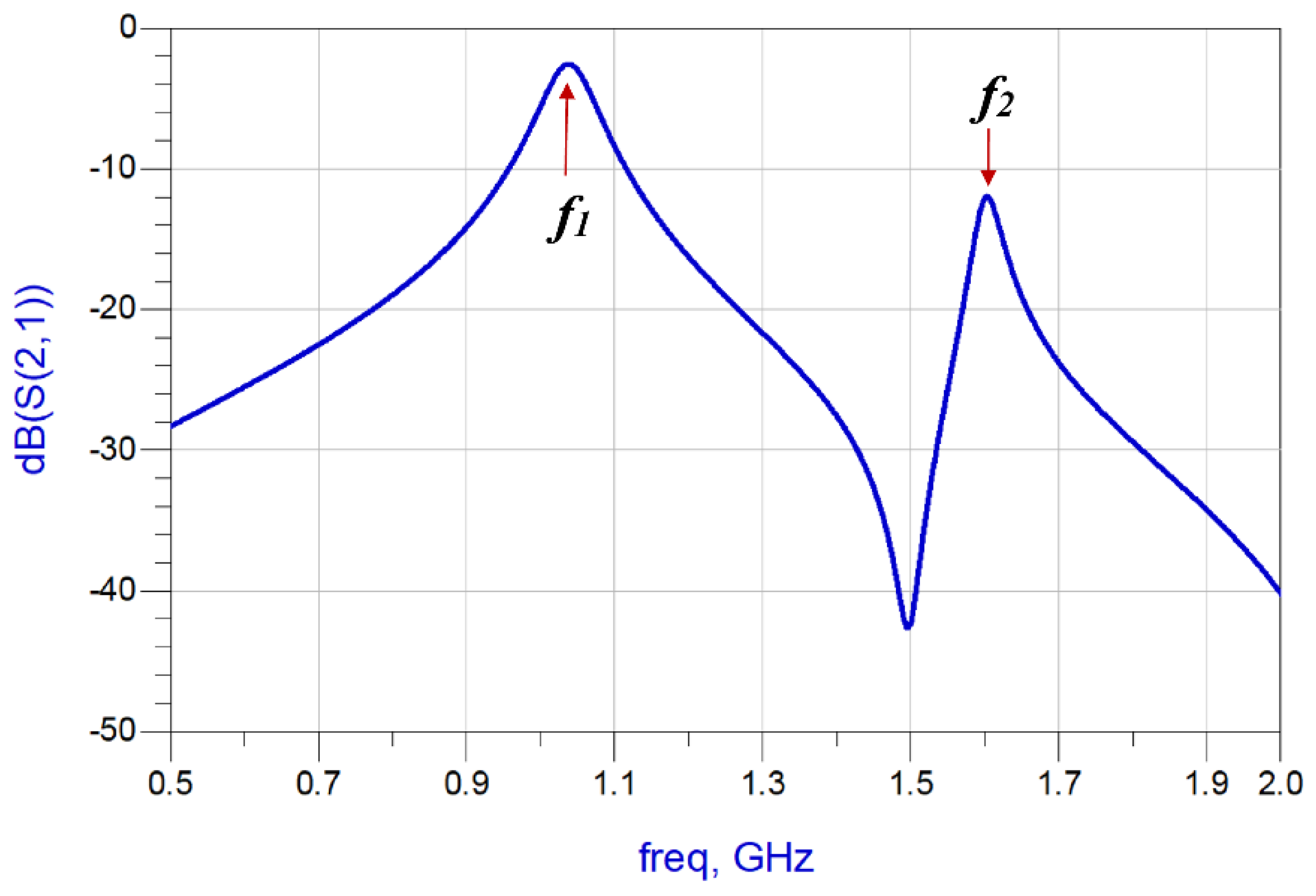
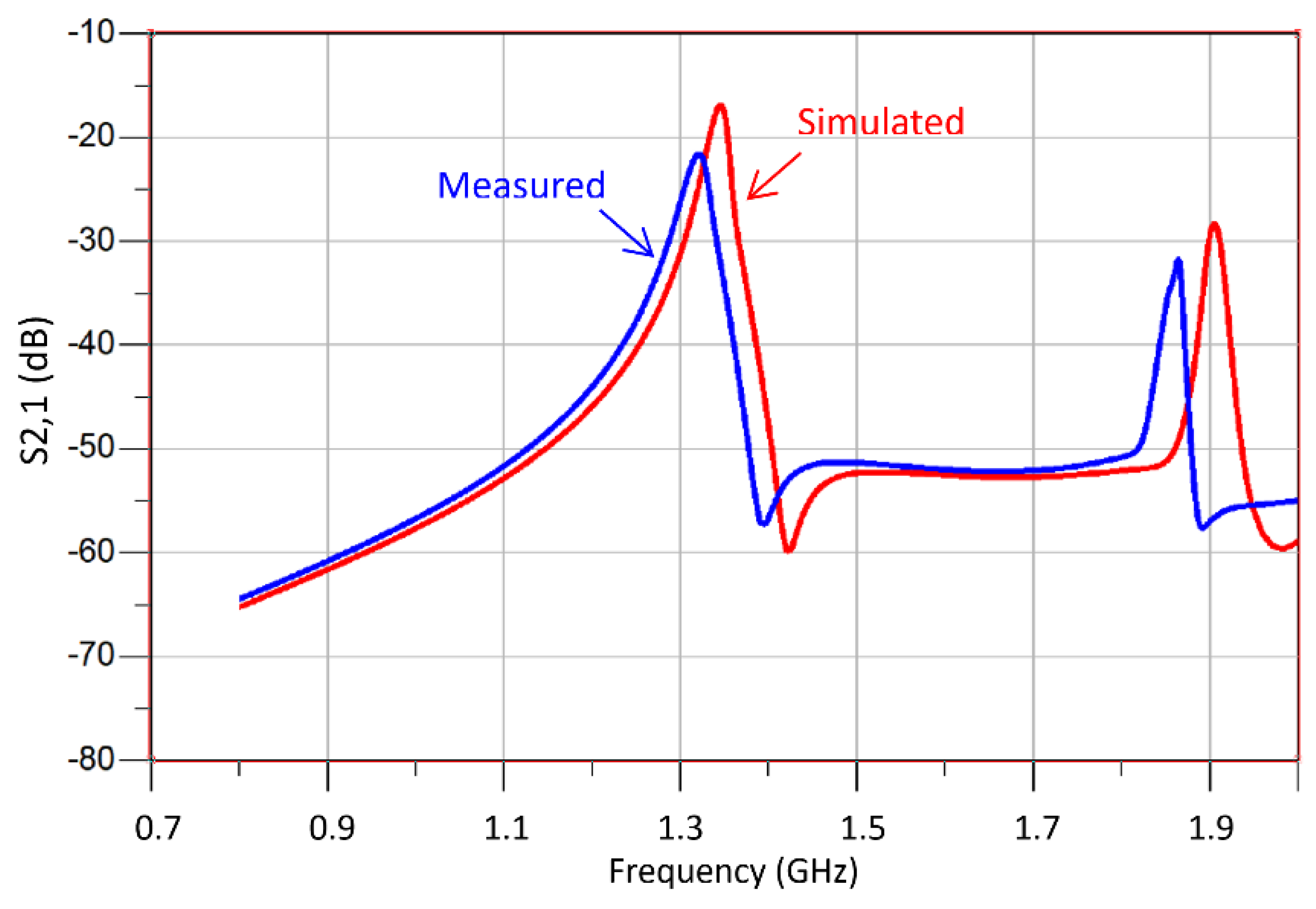
4. Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Celik, N.; Gagarin, R.; Huang, G.C.; Iskander, M.F.; Berg, B.W. Microwave stethoscope: Development and benchmarking of a vital signs sensor using computer-controlled phantoms and human studies. IEEE Trans. Biomed. Eng. 2014, 61, 2341–2349. [Google Scholar] [CrossRef]
- Shaji, M.; Akhtar, M.J. Microwave coplanar sensor system for detecting contamination in food products. In Proceedings of the IEEE MTT-S International Microwave and RF Conference, New Delhi, India, 14–16 December 2013; pp. 1–4. [Google Scholar]
- Kulkarni, S.; Joshi, M.S. Design and analysis of shielded vertically stacked ring resonator as complex permittivity sensor for petroleum oils. IEEE Trans. Microw. Theory Tech. 2015, 63, 2411–2417. [Google Scholar] [CrossRef]
- Bahar, A.A.M.; Zakaria, Z.; Ruslan, E.; Isa, A.A.M.; Alahnomi, R.A. Circular microfluidic substrate integrated waveguide resonator sensor for materials characterization. ARPN J. Eng. Appl. Sci. 2016, 11, 3217–3221. [Google Scholar]
- Silavwe, E.; Somjit, N.; Robertson, I.D. A microfluidic-integrated SIW lab-on-substrate sensor for microliter liquid characterization. IEEE Sens. J. 2016, 16, 7628–7635. [Google Scholar] [CrossRef]
- Baena, J.D.; Bonache, J.; Martin, F.; Marque’s, R.; Falcone, F.; Lopetegi, T.; Laso, M.A.G.; Garcia-Garcia, J.; Gil, I.; Flores, M.; et al. Equivalent circuit models for split ring resonators and complementary split ring resonators coupled to planar transmission lines. IEEE Trans. Microw. Theory Tech. 2005, 53, 1451–1461. [Google Scholar] [CrossRef]
- Nogueira, J.K.A.; Oliveira, J.G.D.; Paiva, S.B.; Neto, V.P.S.; D’Assunção, A.G. A compact C-SRR-based sensor for characterization of the complex permittivity of dielectric materials. Electronics 2022, 11, 1787. [Google Scholar] [CrossRef]
- Durán-Sindreu, M.; Naqui, J.; Bonache, J.; Martín, F. Split rings for metamaterial and microwave circuit design: A review of recent developments. Int. J. RF Microw. Comput. Aided Eng. 2012, 22, 439–458. [Google Scholar] [CrossRef]
- Bonache, J.; Gil, I.; García-García, J.; Martín, F. New microstrip filters based on complementary split rings resonators. IEEE Trans. Microw. Theory Tech. 2006, 54, 265–271. [Google Scholar] [CrossRef]
- Al-Behadili, A.A.; Mocanu, I.A.; Codreanu, N.; Pantazica, M. Modified split ring resonators sensor for accurate complex permittivity measurements of solid dielectrics. Sensors 2020, 20, 6855. [Google Scholar] [CrossRef]
- Veselago, V.G. The Electrodynamics of Substances with Simultaneously Negative Values of ε and µ. Sov. Phys. Uspekhi 1967, 10, 509–514. [Google Scholar] [CrossRef]
- Pendry, J.B. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Caloz, C.; Itoh, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; Wiley-IEEE Press: New York, NY, USA, November 2005. [Google Scholar]
- Kiani, S.; Rezaei, P.; Navaei, M.; Abrishamian, M.S. Microwave sensor for detection of solid material permittivity in single/multilayer samples with high quality factor. IEEE Sens. J. 2018, 18, 9971–9977. [Google Scholar] [CrossRef]
- Lee, C.-S.; Yang, C.-L. Complementary split-ring resonators for measuring dielectric constants and loss tangents. IEEE Microw. Wireless Compon. Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
- Yang, C.-L.; Lee, C.-S.; Chen, K.-W.; Chen, K.-Z. Noncontact measurement of complex permittivity and thickness by using planar resonators. IEEE Trans. Microw. Theory Tech. 2016, 64, 247–257. [Google Scholar] [CrossRef]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Mata-Contreras, J.; Martín, F. Transmission lines loaded with pairs of stepped impedance resonators: Modeling and application to differential permittivity measurements. IEEE Trans. Microw. Theory Tech. 2016, 64, 3864–3877. [Google Scholar] [CrossRef] [Green Version]
- Puentes, M.; Weiß, C.; Schüßler, M.; Jakoby, R. Sensor array based on split ring resonators for analysis of organic tissues. In Proceedings of the IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Alam, S.; Zakaria, Z.; Surjati, I.; Shairi, N.A.; Alaydrus, M.; Firmansyah, T. Dual-band independent permittivity sensor using single-port with a pair of U-shaped structures for solid material detection. IEEE Sens. J. 2022, 22, 16111–16119. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. A microwave and microfluidic planar resonator for efficient and accurate complex permittivity characterization of aqueous solutions. IEEE Trans. Microw. Theory Tech. 2013, 61, 972–978. [Google Scholar] [CrossRef] [Green Version]
- Abduljabar, A.A.; Rowe, D.J.; Porch, A.; Barrow, D.A. Novel microwave microfluidic sensor using a microstrip split-ring resonator. IEEE Trans. Microw. Theory Tech. 2014, 62, 679–688. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-sensitivity metamaterial-inspired sensor for microfluidic dielectric characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef] [Green Version]
- Llamas-Garro, I.; Brito-Brito, Z.; Mira, F.; de Melo, M.T.; Kim, J.-M. Microwave Spoof Surface Plasmon Sensor for Dielectric Material Characterization. IEEE Sens. Lett. 2022, 6, 3501104. [Google Scholar] [CrossRef]
- Su, L.; Muñoz-Enano, J.; Vélez, P.; Casacuberta, P.; Gil, M.; Martín, F. Phase-variation microwave sensor for permittivity measurements based on a high-impedance half-wavelength transmission line. IEEE Sens. J. 2021, 21, 10647–10656. [Google Scholar] [CrossRef]
- Hong, J.-S.; Lancaster, M.J. (Eds.) Microstrip Filters for RF/Microwave Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- RT/duroid® 5870 Laminates. Available online: https://www.rogerscorp.com/advanced-electronics-solutions/rt-duroid-laminates/rt-duroid-5870-laminates (accessed on 26 May 2023).
- RT/duroid® 5880 Laminates. Available online: https://www.rogerscorp.com/advanced-electronics-solutions/rt-duroid-laminates/rt-duroid-5880-laminates (accessed on 26 May 2023).
- PTFE. Available online: https://www.directplastics.co.uk/pdf/datasheets/ptfe-data-sheet.pdf (accessed on 26 May 2023).
- Alumina Substrates. Available online: https://www.maruwa-g.com/e/products/ceramic/000256.html (accessed on 26 May 2023).
- RO3003G2™ Laminates. Available online: https://www.rogerscorp.com/advanced-electronics-solutions/ro3000-series-laminates/ro3003g2-laminates (accessed on 26 May 2023).
- RO3006™ Laminates. Available online: https://www.rogerscorp.com/advanced-electronics-solutions/ro3000-series-laminates/ro3006-laminates (accessed on 26 May 2023).
- Buragohain, A.; Mostako, A.T.T.; Das, G.S. Low-cost CSRR based sensor for determination of dielectric constant of liquid samples. IEEE Sens. J. 2021, 21, 27450–27457. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D.; Yu, S.; Wang, C.; Yang, X.; Wang, Y. A dual-band resonator sensor for low permittivity characterization. IEEE Trans. Instrum. Meas. 2022, 71, 8006511. [Google Scholar] [CrossRef]
- Chavoshi, M.; Martinic, M.; Nauwelaers, B.; Markovic, T.; Schreurs, D. Design of uncoupled and cascaded array of resonant microwave sensors for dielectric characterization of liquids. IEEE Trans. Microw. Theory Tech. 2023, 71, 1687–1695. [Google Scholar] [CrossRef]
- Pourafzal, A.; Roi-Taravella, T.; Cheffena, M.; Yayilgan, S.Y. A low-cost and accurate microwave sensor system for permittivity characterization. IEEE Sens. J. 2023, 23, 1234–1248. [Google Scholar] [CrossRef]

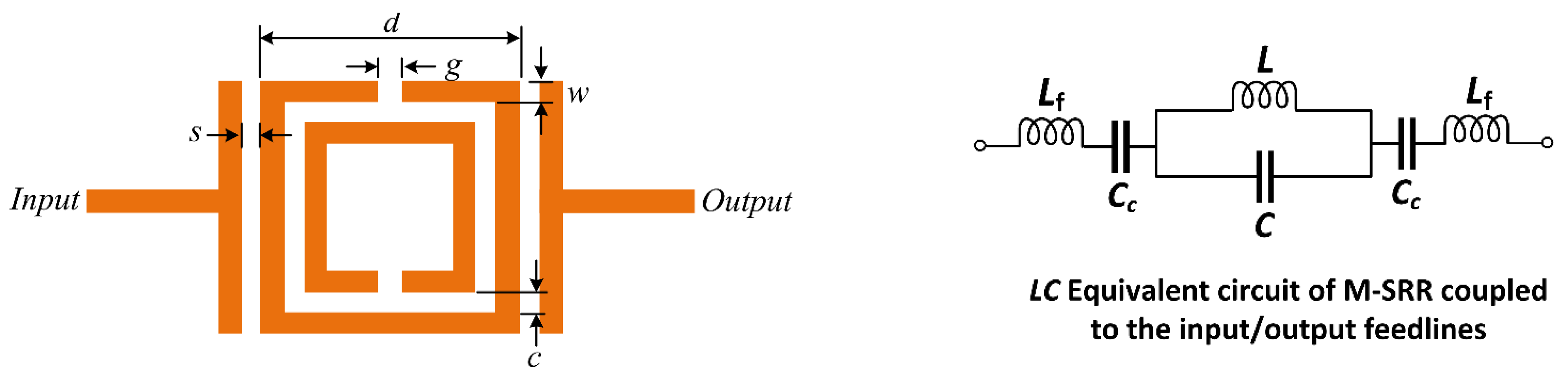


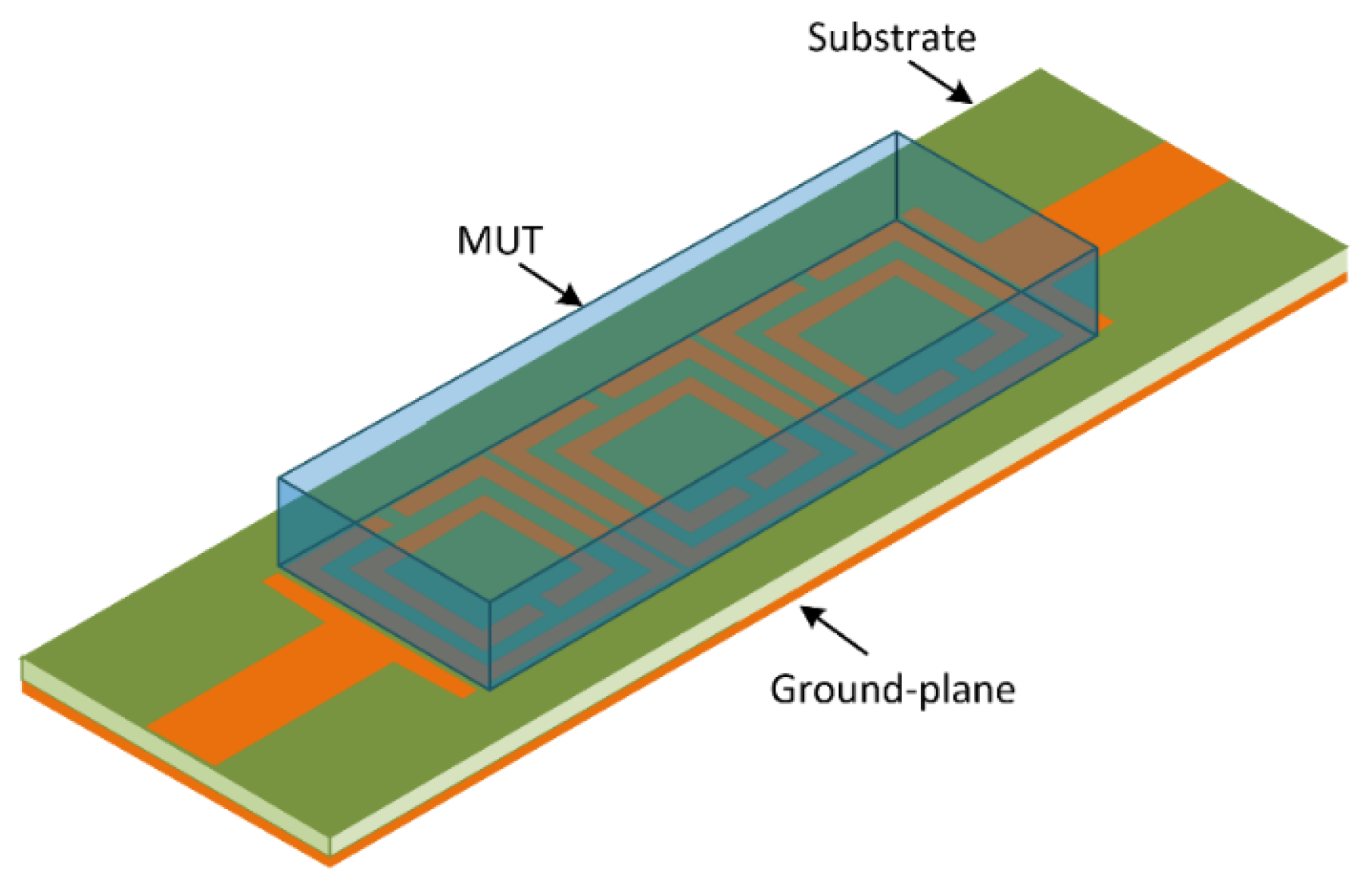
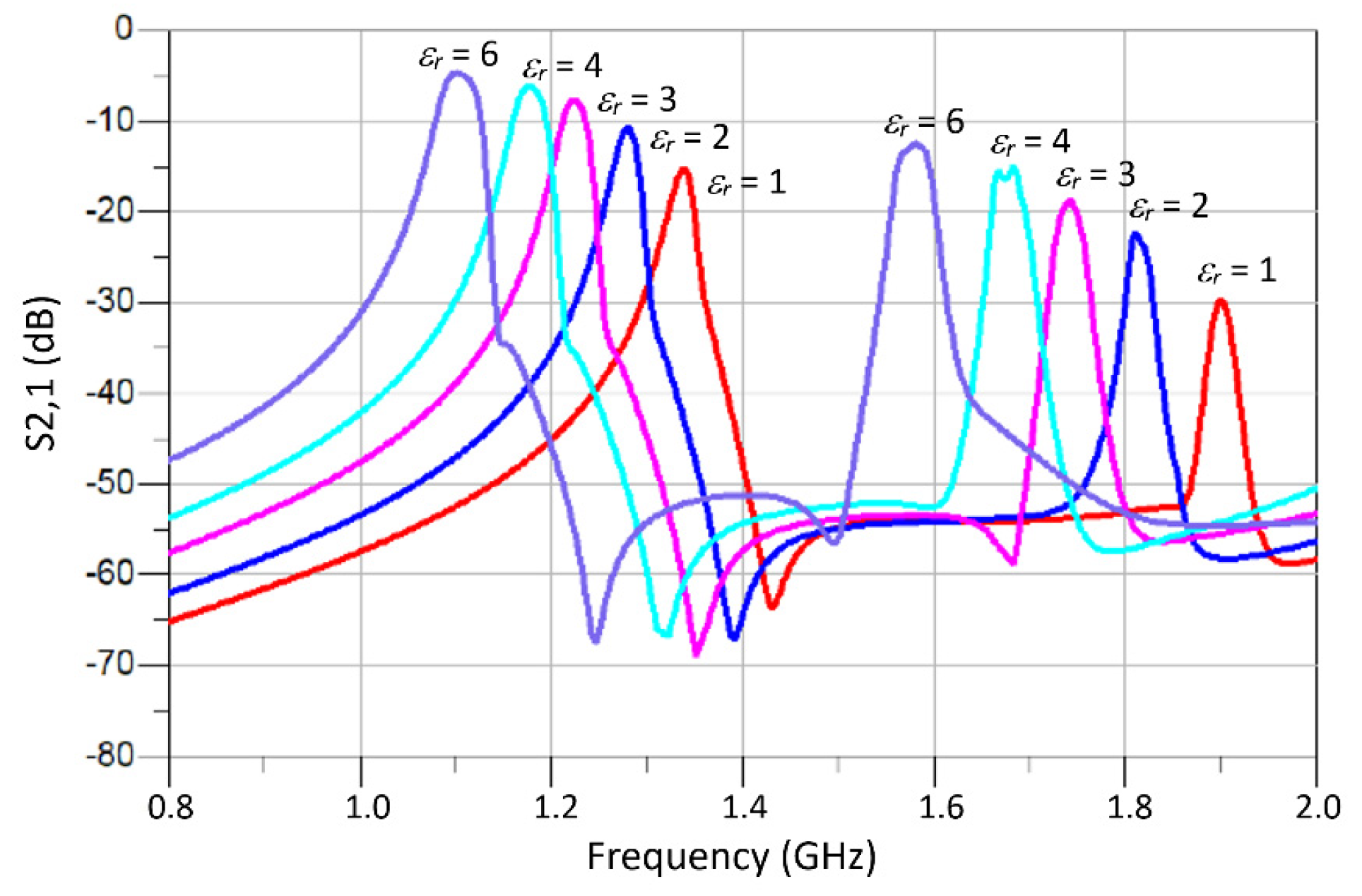
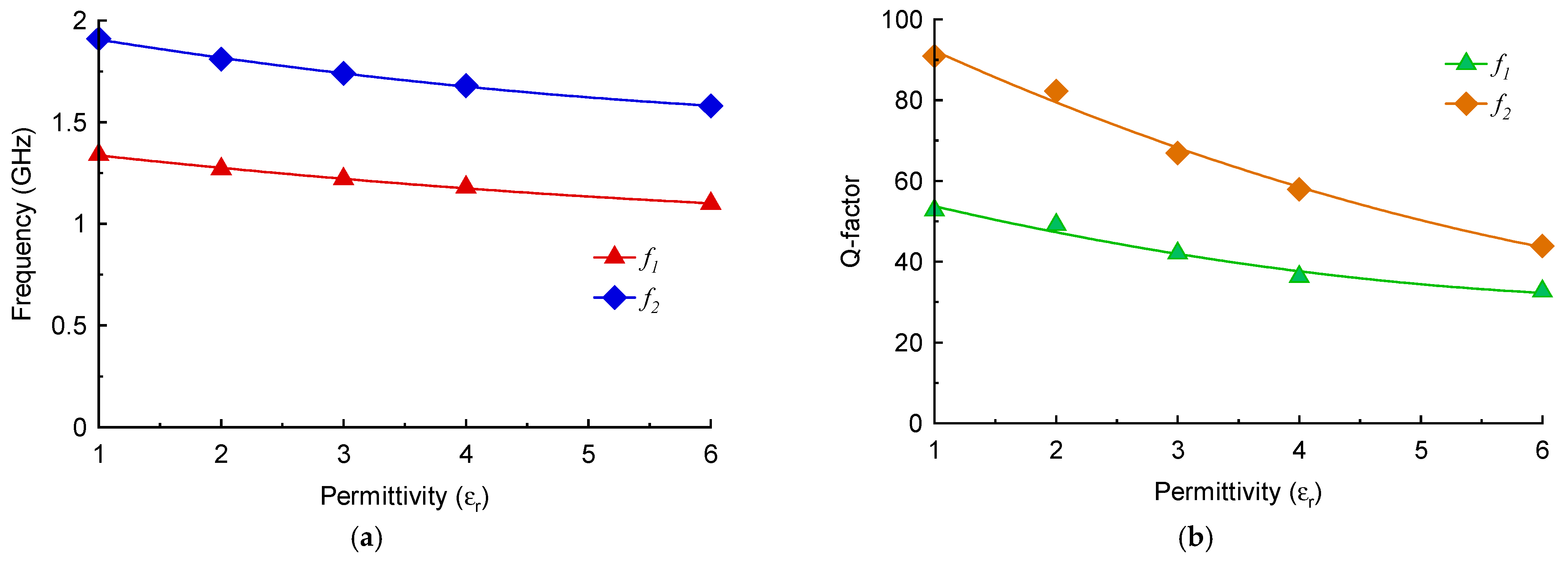
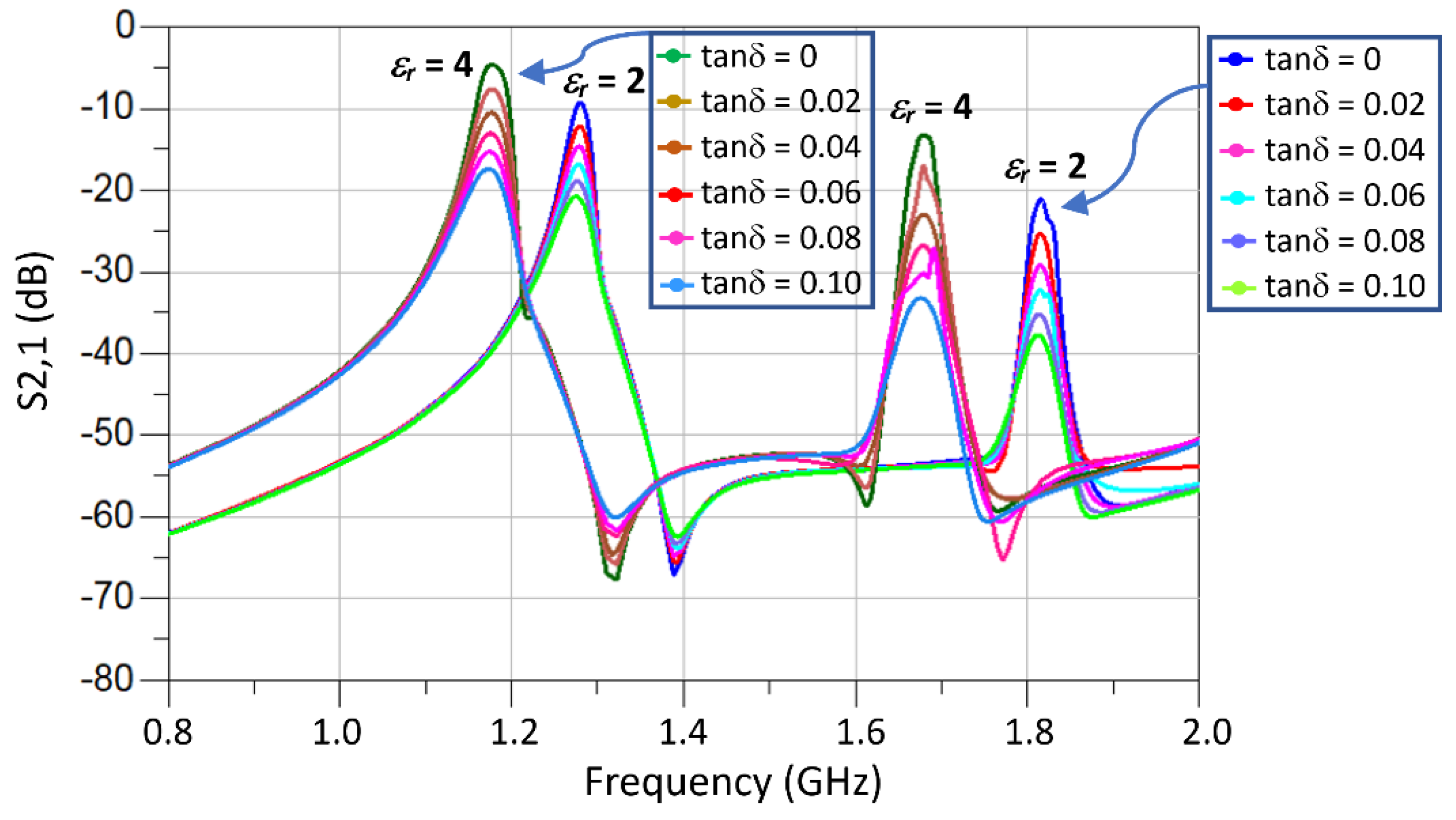

| Parameters | Value (mm) |
|---|---|
| d | 21.3 |
| W | 1.5 |
| g | 0.5 |
| c | 1.5 |
| s | 0.2 |
| Ref. | MUT | Permittivity (Real Part) | ||
|---|---|---|---|---|
| Measured | Published | Error (%) | ||
| [26] | Rogers RT/duroid 5870 | 2.30 | 2.33 | 1.29 |
| [27] | Rogers RT/duroid 5880 | 2.17 | 2.2 | 1.36 |
| [28] | PTFE | 2.08 | 2.1 | 0.95 |
| [29] | Alumina | 9.78 | 9.9 | 1.21 |
| [30] | Rogers RO3003 | 2.96 | 3 | 1.33 |
| [31] | Rogers PR3006 | 6.07 | 6.15 | 1.3 |
| Ref. | MUT | Freq. (GHz) | Size | Error in Measurement (%) |
|---|---|---|---|---|
| [10] | Split-ring resonator | 1.152 | 0.7 × 0.16 | 3.91 |
| [32] | Split-ring resonator | 1.2 | 0.48 × 0.16 | 2.91 |
| [33] | Complementary square spiralresonator | 2 & 5.41 | 0.45 × 0.54 | 5.0 |
| [34] | Cascaded sensor array | 4.84, 5.63, 6.97, 8.4 | 0.28 × 0.14 | 5.7 |
| [35] | Split-ring | 2.56 | 0.51 × 0.34 | 4.36 |
| This work | Tri-composite split-ring resonator | 1.32 | 0.32 × 0.12 | 1.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alibakhshikenari, M.; Virdee, B.S.; Elwi, T.A.; Lubangakene, I.D.; Jayanthi, R.K.R.; Al-Behadili, A.A.; Hassain, Z.A.A.; Ali, S.M.; Pau, G.; Livreri, P.; et al. Design of a Planar Sensor Based on Split-Ring Resonators for Non-Invasive Permittivity Measurement. Sensors 2023, 23, 5306. https://doi.org/10.3390/s23115306
Alibakhshikenari M, Virdee BS, Elwi TA, Lubangakene ID, Jayanthi RKR, Al-Behadili AA, Hassain ZAA, Ali SM, Pau G, Livreri P, et al. Design of a Planar Sensor Based on Split-Ring Resonators for Non-Invasive Permittivity Measurement. Sensors. 2023; 23(11):5306. https://doi.org/10.3390/s23115306
Chicago/Turabian StyleAlibakhshikenari, Mohammad, Bal S. Virdee, Taha A. Elwi, Innocent D. Lubangakene, Renu K. R. Jayanthi, Amer Abbood Al-Behadili, Zaid A. Abdul Hassain, Syed Mansoor Ali, Giovanni Pau, Patrizia Livreri, and et al. 2023. "Design of a Planar Sensor Based on Split-Ring Resonators for Non-Invasive Permittivity Measurement" Sensors 23, no. 11: 5306. https://doi.org/10.3390/s23115306
APA StyleAlibakhshikenari, M., Virdee, B. S., Elwi, T. A., Lubangakene, I. D., Jayanthi, R. K. R., Al-Behadili, A. A., Hassain, Z. A. A., Ali, S. M., Pau, G., Livreri, P., & Aïssa, S. (2023). Design of a Planar Sensor Based on Split-Ring Resonators for Non-Invasive Permittivity Measurement. Sensors, 23(11), 5306. https://doi.org/10.3390/s23115306










