Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods
Abstract
:1. Introduction
- Developing a novel method for unsupervised drone swarm characterization and detection using RF signals and machine-learning algorithms with no a priori knowledge and no labeled data.
- We propose an efficient way to assess the number of drones in a swarm and the risk that comes from automated UAVs beforehand.
- An evaluation of the proposed approach on common datasets published in the literature.
- A comparison of the performance using various features, such as WST and CWT, and different dimension reduction methods.
2. Background and Related Work
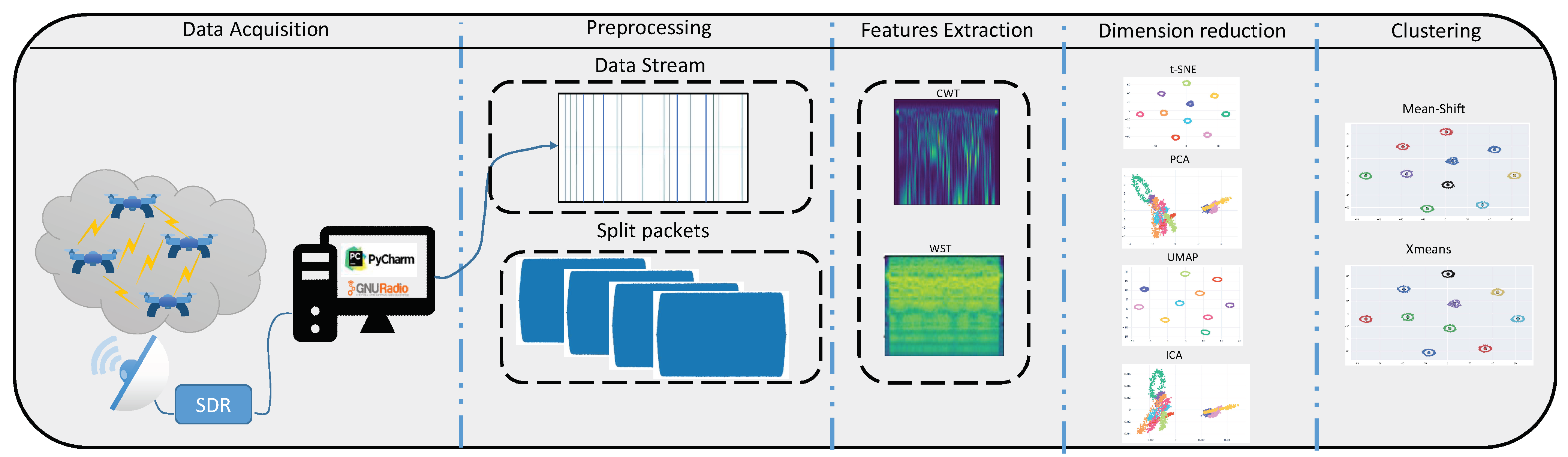
3. Proposed Approach
3.1. Datasets
3.1.1. Self-Built Dataset
3.1.2. Common Dataset
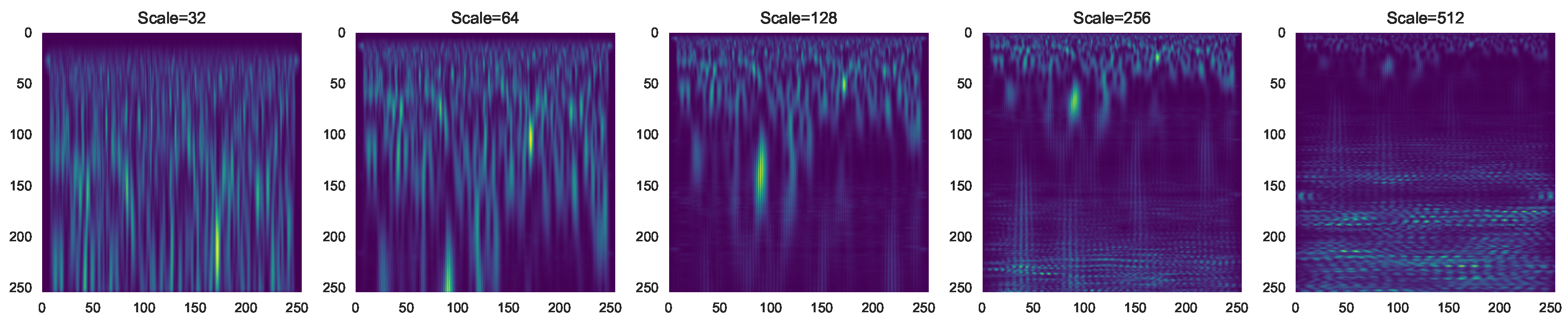
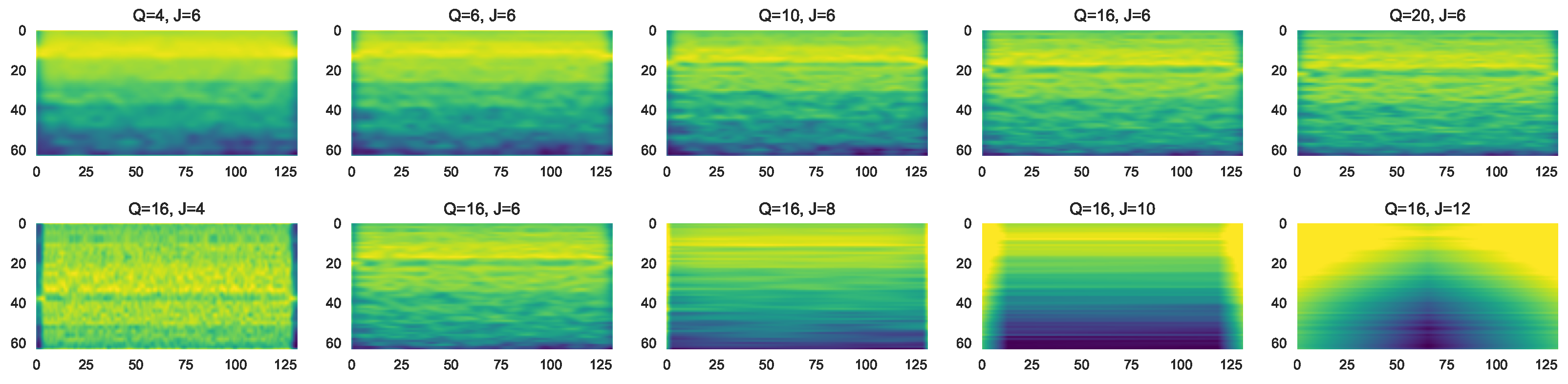
3.2. Feature Extraction
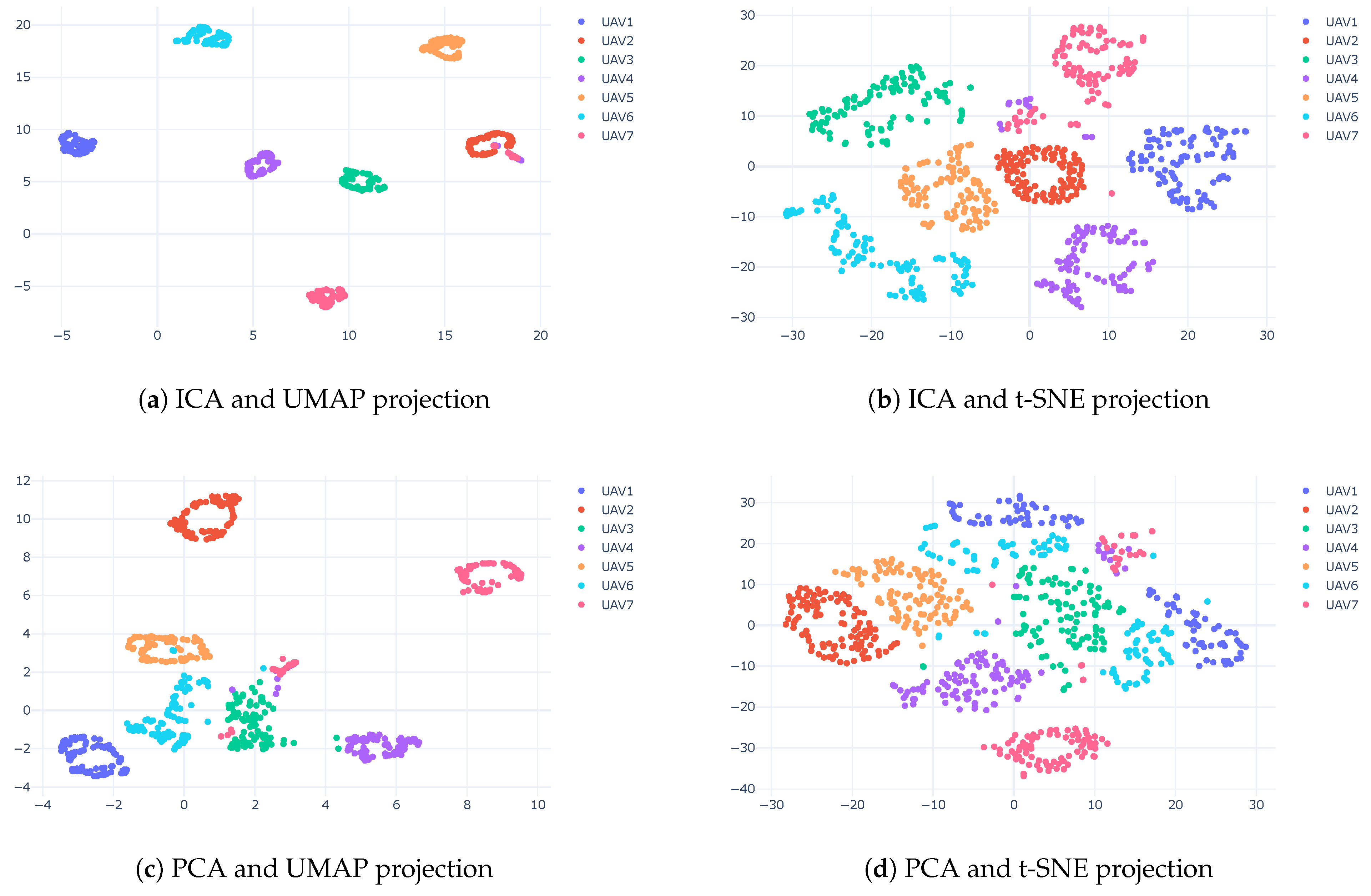
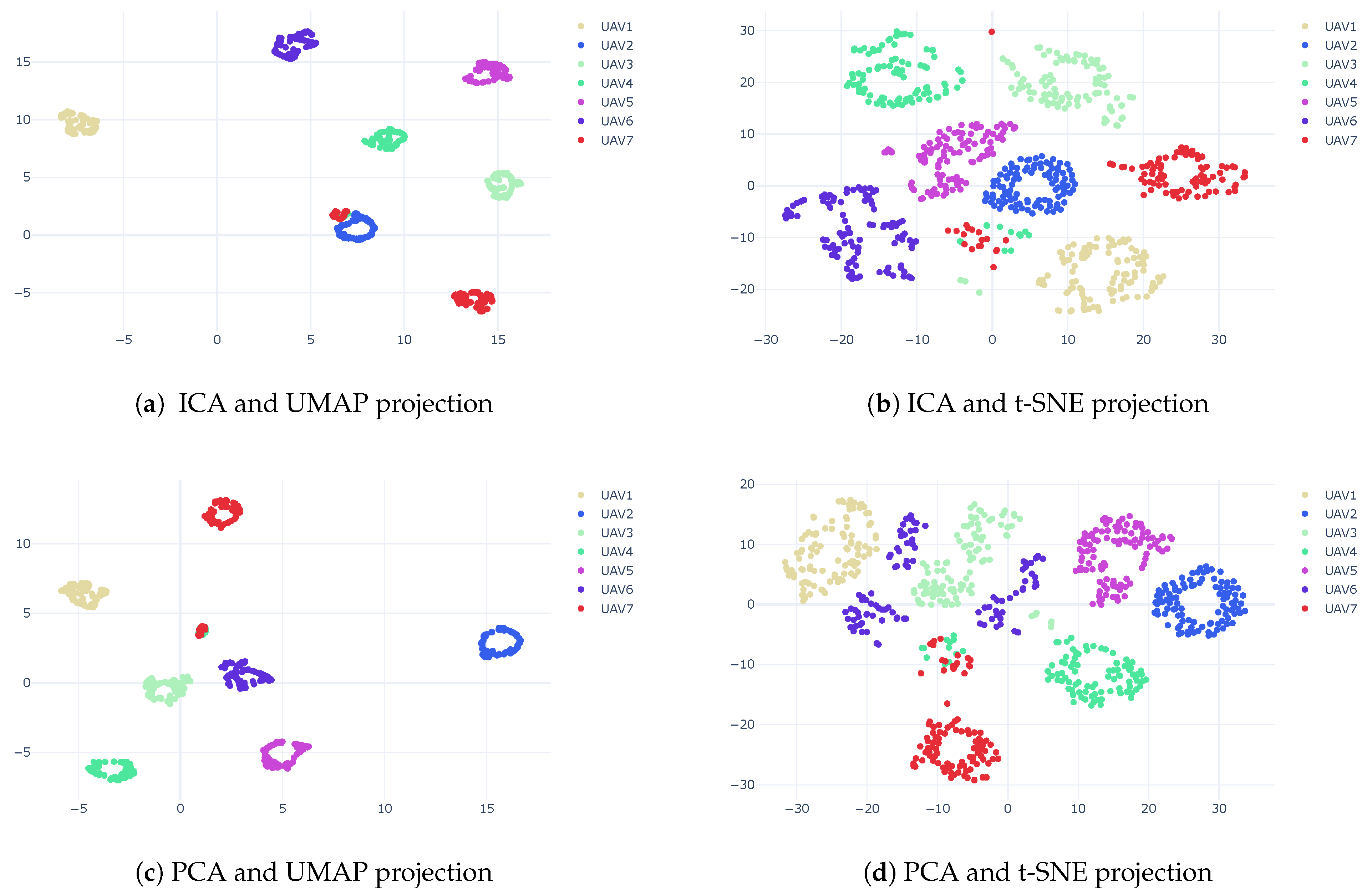
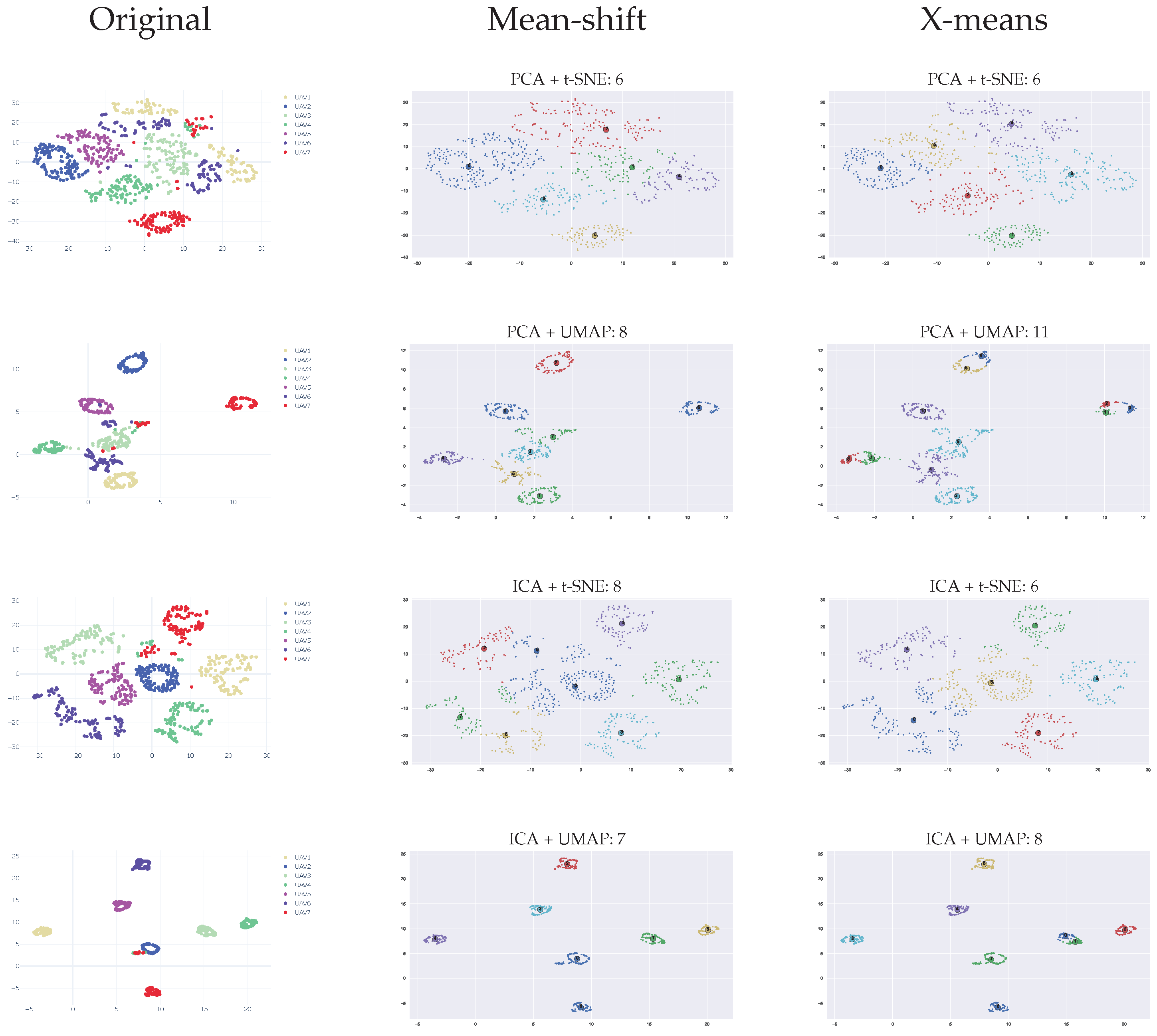
3.3. Dimension Reduction
3.4. Clustering
4. Experimental Results
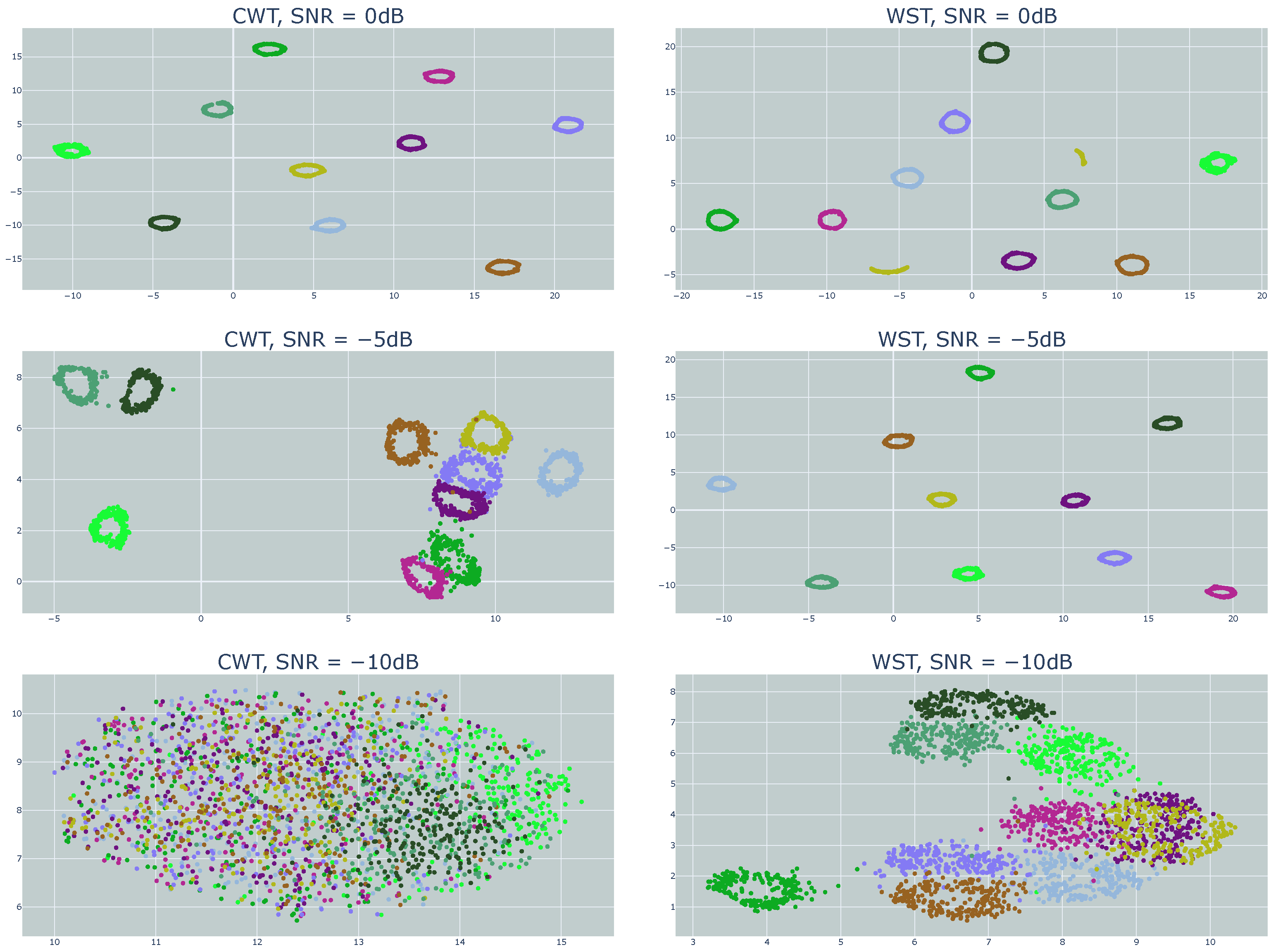
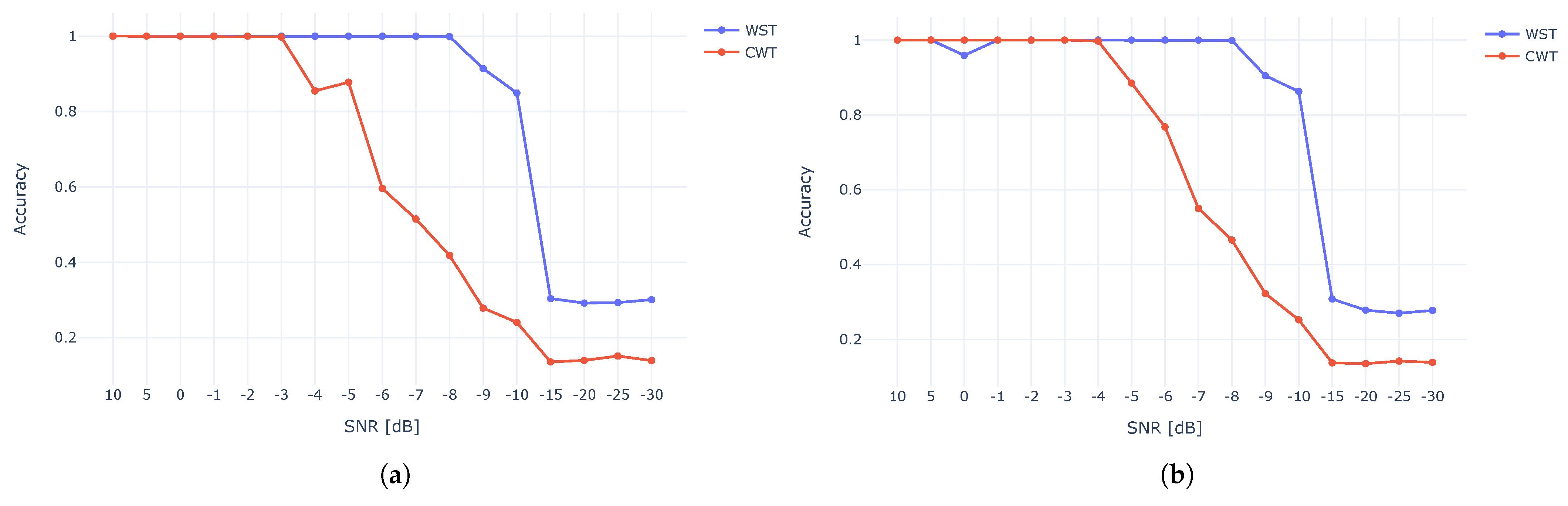
4.1. Various RF Sources (VRF Dataset)
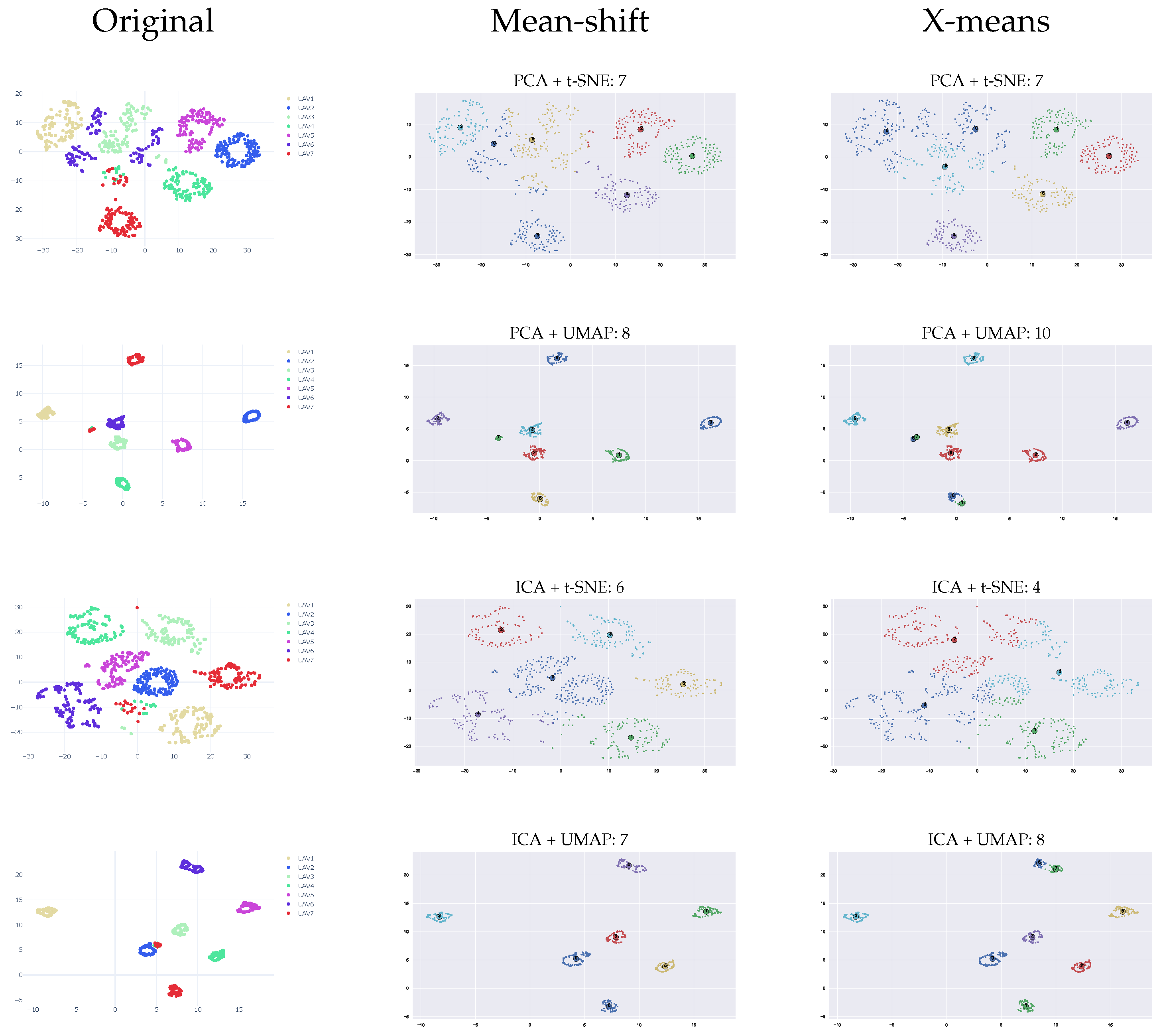
4.1.1. Clustering Accuracy Criteria (CAC)
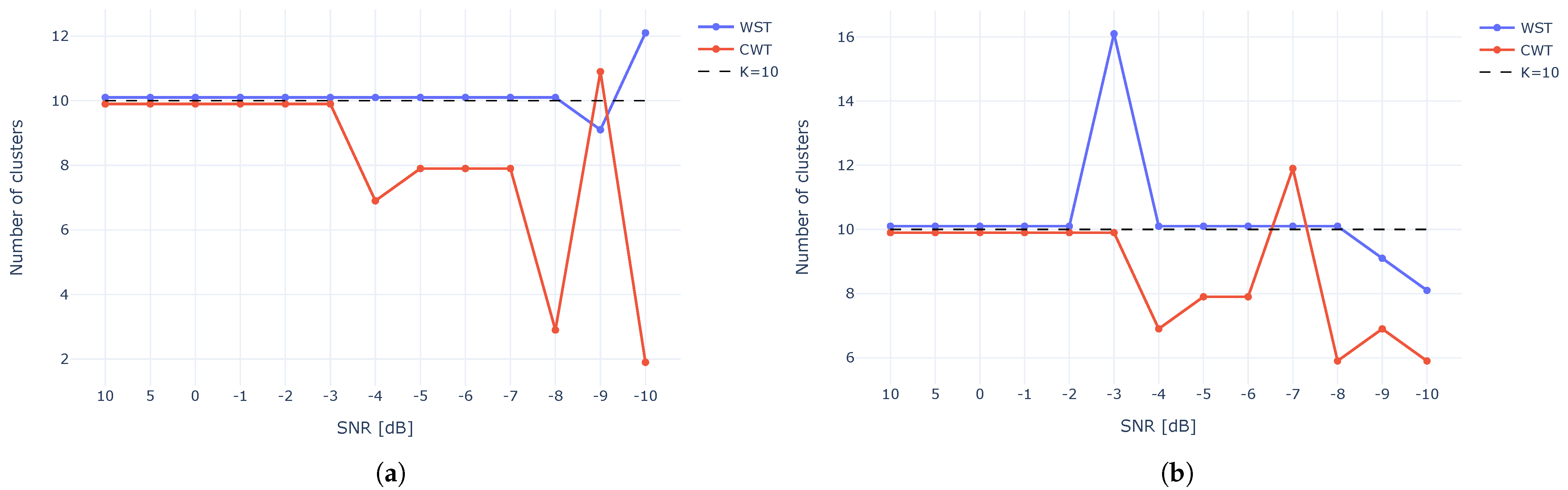
4.1.2. Estimating the of Number of Clusters
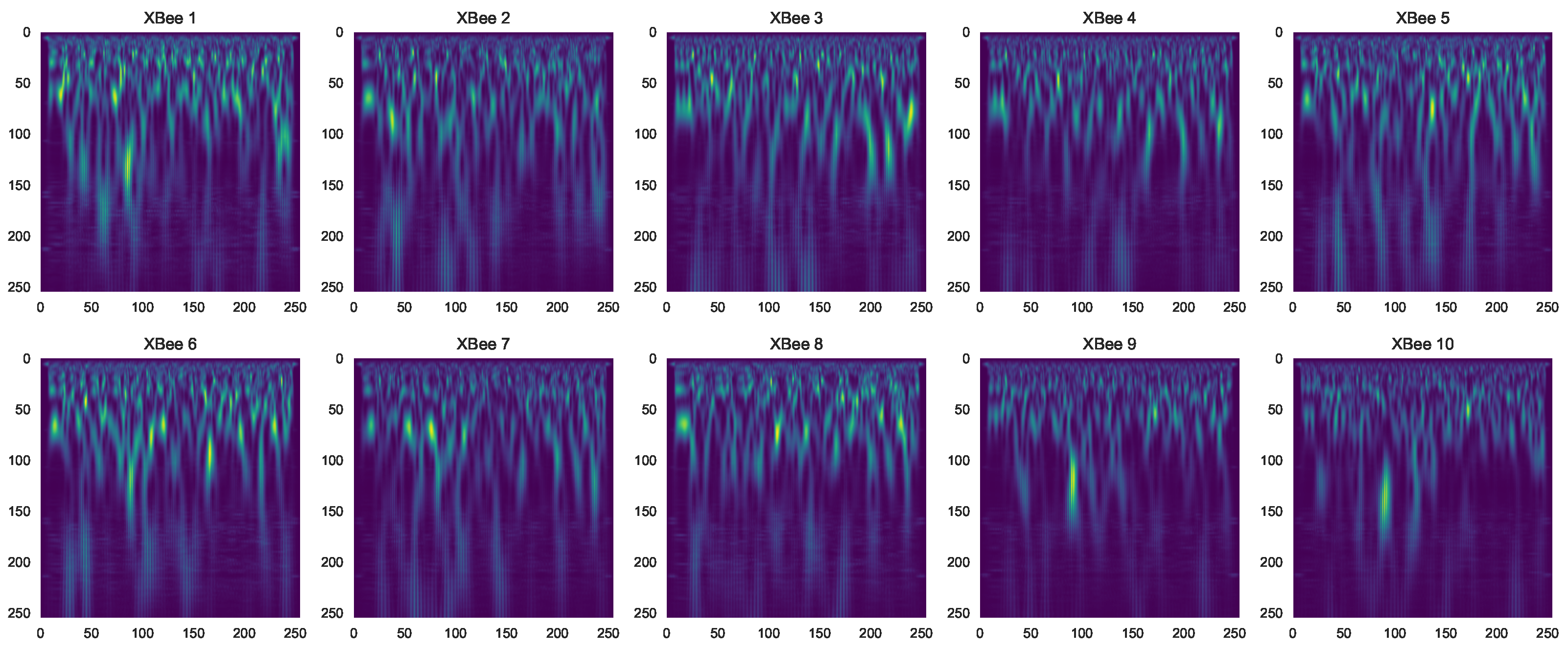
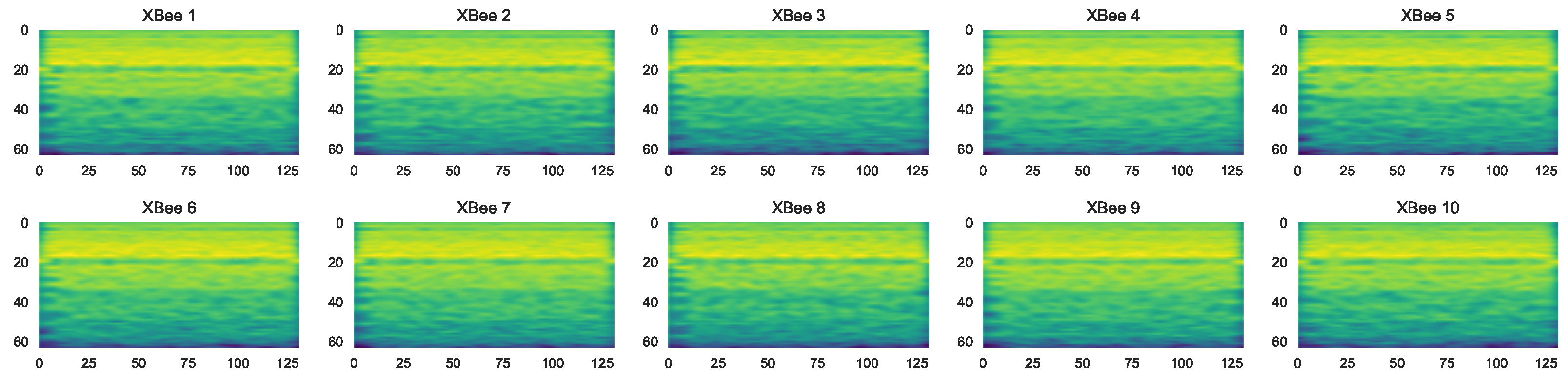
4.2. XBee Dataset
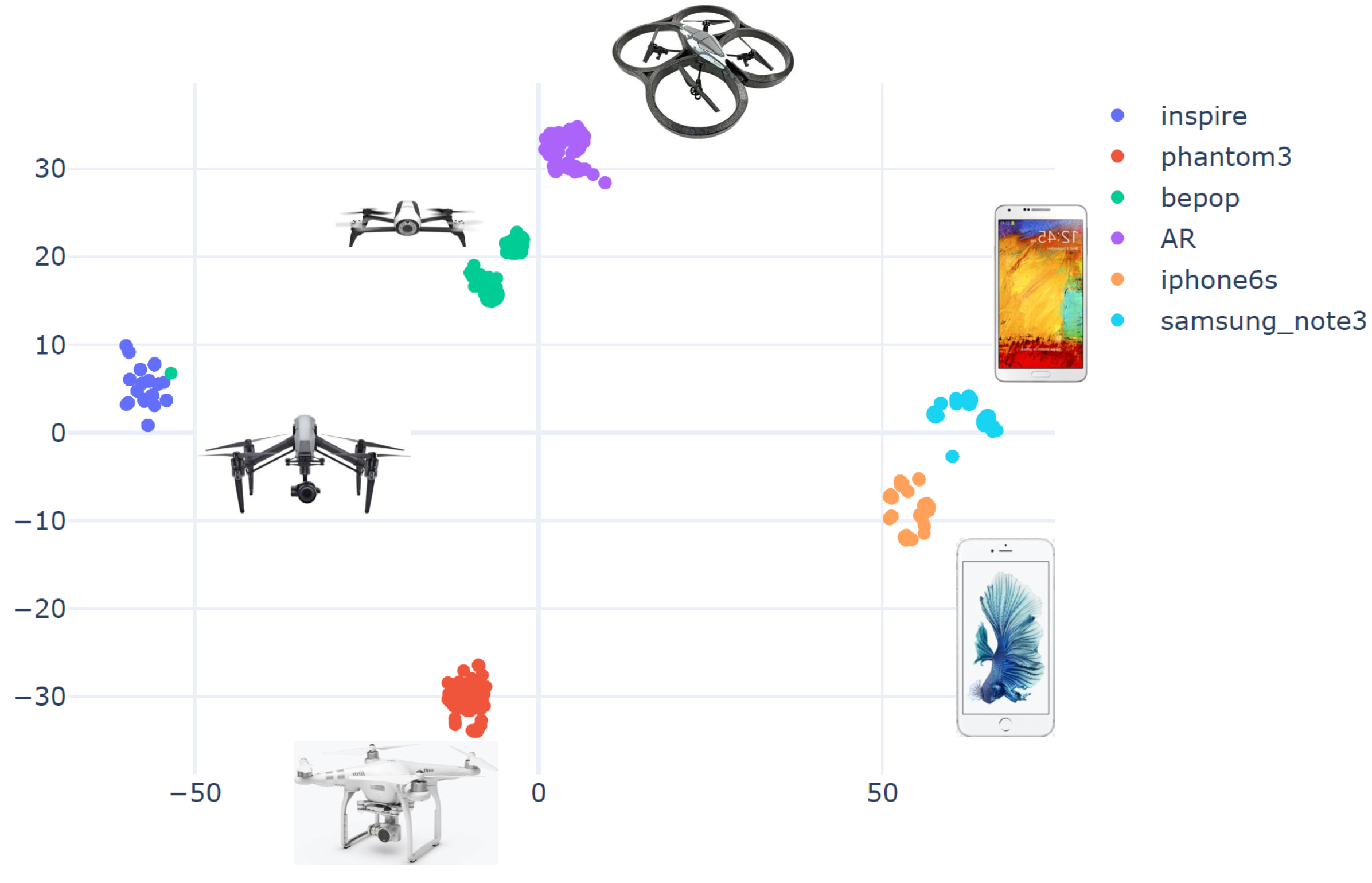
4.3. Matrice Dataset
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Ali, M. A bean optimization-based cooperation method for target searching by swarm uavs in unknown environments. IEEE Access 2020, 8, 43850–43862. [Google Scholar] [CrossRef]
- Lee, K.B.; Kim, Y.J.; Hong, Y.D. Real-time swarm search method for real-world quadcopter drones. Appl. Sci. 2018, 8, 1169. [Google Scholar] [CrossRef]
- Chen, E.; Chen, J.; Mohamed, A.W.; Wang, B.; Wang, Z.; Chen, Y. Swarm intelligence application to UAV aided IoT data acquisition deployment optimization. IEEE Access 2020, 8, 175660–175668. [Google Scholar] [CrossRef]
- Islam, A.; Shin, S.Y. Bus: A blockchain-enabled data acquisition scheme with the assistance of uav swarm in internet of things. IEEE Access 2019, 7, 103231–103249. [Google Scholar] [CrossRef]
- Tosato, P.; Facinelli, D.; Prada, M.; Gemma, L.; Rossi, M.; Brunelli, D. An autonomous swarm of drones for industrial gas sensing applications. In Proceedings of the 2019 IEEE 20th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Washington, DC, USA, 10–12 June 2019; pp. 1–6. [Google Scholar]
- Qu, C.; Boubin, J.; Gafurov, D.; Zhou, J.; Aloysius, N.; Nguyen, H.; Calyam, P. UAV Swarms in Smart Agriculture: Experiences and Opportunities. In Proceedings of the 2022 IEEE 18th International Conference on e-Science (e-Science), Salt Lake City, UT, USA, 11–14 October 2022. [Google Scholar]
- Alkouz, B.; Bouguettaya, A.; Mistry, S. Swarm-based Drone-as-a-Service (SDaaS) for Delivery. In Proceedings of the 2020 IEEE International Conference on Web Services (ICWS), Beijing, China, 19–23 October 2020; pp. 441–448. [Google Scholar] [CrossRef]
- Homayounnejad, M. Autonomous Weapon Systems, Drone Swarming and the Explosive Remnants of War. TLI Think 2017. [Google Scholar] [CrossRef]
- O’Malley, J. The no drone zone. Eng. Technol. 2019, 14, 34–38. [Google Scholar] [CrossRef]
- Singha, S.; Aydin, B. Automated Drone Detection Using YOLOv4. Drones 2021, 5, 95. [Google Scholar] [CrossRef]
- Rozantsev, A.; Lepetit, V.; Fua, P. Detecting flying objects using a single moving camera. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 879–892. [Google Scholar] [CrossRef]
- Aker, C.; Kalkan, S. Using deep networks for drone detection. In Proceedings of the 2017 14th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Lecce, Italy, 29 August–1 September 2017; pp. 1–6. [Google Scholar]
- Peng, J.; Zheng, C.; Lv, P.; Cui, T.; Cheng, Y.; Lingyu, S. Using Images Rendered by PBRT to Train Faster R-CNN for UAV Detection; Václav Skala-UNION Agency, 2018. [Google Scholar] [CrossRef]
- Unlu, E.; Zenou, E.; Riviere, N. Using shape descriptors for UAV detection. Electron. Imaging 2018, 2018, 1–5. [Google Scholar] [CrossRef]
- Fu, R.; Al-Absi, M.A.; Kim, K.H.; Lee, Y.S.; Al-Absi, A.A.; Lee, H.J. Deep Learning-Based Drone Classification Using Radar Cross Section Signatures at mmWave Frequencies. IEEE Access 2021, 9, 161431–161444. [Google Scholar] [CrossRef]
- Jahangir, M.; Baker, C. Persistence surveillance of difficult to detect micro-drones with L-band 3-D holographic radarTM. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar]
- Torvik, B.; Olsen, K.E.; Griffiths, H. Classification of birds and UAVs based on radar polarimetry. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1305–1309. [Google Scholar] [CrossRef]
- Fuhrmann, L.; Biallawons, O.; Klare, J.; Panhuber, R.; Klenke, R.; Ender, J. Micro-Doppler analysis and classification of UAVs at Ka band. In Proceedings of the 2017 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017; pp. 1–9. [Google Scholar]
- Mendis, G.J.; Randeny, T.; Wei, J.; Madanayake, A. Deep learning based doppler radar for micro UAS detection and classification. In Proceedings of the MILCOM 2016–2016 IEEE Military Communications Conference, Baltimore, MD, USA, 1–3 November 2016; pp. 924–929. [Google Scholar]
- Molchanov, P.; Harmanny, R.I.; de Wit, J.J.; Egiazarian, K.; Astola, J. Classification of small UAVs and birds by micro-Doppler signatures. Int. J. Microw. Wirel. Technol. 2014, 6, 435–444. [Google Scholar] [CrossRef]
- Al-Emadi, S.; Al-Ali, A.; Al-Ali, A. Audio-based drone detection and identification using deep learning techniques with dataset enhancement through generative adversarial networks. Sensors 2021, 21, 4953. [Google Scholar] [CrossRef] [PubMed]
- Warden, P. Speech commands: A dataset for limited-vocabulary speech recognition. arXiv Prepr. 2018, arXiv:1804.03209. [Google Scholar]
- Kim, J.; Park, C.; Ahn, J.; Ko, Y.; Park, J.; Gallagher, J.C. Real-time UAV sound detection and analysis system. In Proceedings of the 2017 IEEE Sensors Applications Symposium (SAS), Glassboro, NJ, USA, 13–15 March 2017; pp. 1–5. [Google Scholar]
- Seo, Y.; Jang, B.; Im, S. Drone detection using convolutional neural networks with acoustic STFT features. In Proceedings of the 2018 15th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Auckland, New Zealand, 27–30 November 2018; pp. 1–6. [Google Scholar]
- Uddin, Z.; Qamar, A.; Alharbi, A.G.; Orakzai, F.A.; Ahmad, A. Detection of Multiple Drones in a Time-Varying Scenario Using Acoustic Signals. Sustainability 2022, 14, 4041. [Google Scholar] [CrossRef]
- Medaiyese, O.O.; Ezuma, M.; Lauf, A.P.; Guvenc, I. Wavelet transform analytics for RF-based UAV detection and identification system using machine learning. Pervasive Mob. Comput. 2022, 82, 101569. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, M.; Zhao, C.; Huang, L.; Du, X.; Zhao, Y. Detection of LSSUAV using hash fingerprint based SVDD. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–26 May 2017; pp. 1–5. [Google Scholar]
- Nguyen, P.; Ravindranatha, M.; Nguyen, A.; Han, R.; Vu, T. Investigating cost-effective RF-based detection of drones. In Proceedings of the 2nd Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use, Singapore, 26 June 2016; pp. 17–22. [Google Scholar]
- Nguyen, P.; Truong, H.; Ravindranathan, M.; Nguyen, A.; Han, R.; Vu, T. Matthan: Drone presence detection by identifying physical signatures in the drone’s rf communication. In Proceedings of the 15th Annual International Conference on Mobile Systems, Applications, and Services, Niagara Falls, NY, USA, 19–23 June 2017; pp. 211–224. [Google Scholar]
- Ezuma, M.; Erden, F.; Anjinappa, C.K.; Ozdemir, O.; Guvenc, I. Micro-UAV detection and classification from RF fingerprints using machine learning techniques. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–13. [Google Scholar]
- Soltani, N.; Reus-Muns, G.; Salehi, B.; Dy, J.; Ioannidis, S.; Chowdhury, K. RF fingerprinting unmanned aerial vehicles with non-standard transmitter waveforms. IEEE Trans. Veh. Technol. 2020, 69, 15518–15531. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Vo, N.T.; Nguyen, V.T.T. Wireless Communications for Data Security: Efficiency Assessment of Cybersecurity Industry—A Promising Application for UAVs. Drones 2022, 6, 363. [Google Scholar] [CrossRef]
- Brik, V.; Banerjee, S.; Gruteser, M.; Oh, S. Wireless device identification with radiometric signatures. In Proceedings of the 14th ACM International Conference on Mobile Computing and Networking, San Francisco, CA, USA; 2008; pp. 116–127. [Google Scholar]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Nepusz, T.; Eiben, A.E.; Vicsek, T. Optimized flocking of autonomous drones in confined environments. Sci. Robot. 2018, 3, eaat3536. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, F.; Ou, D.; Huang, X.l. UAV Swarm Networks: Models, Protocols, and Systems; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Blossom, E. GNU radio: Tools for exploring the radio frequency spectrum. Linux J. 2004, 2004, 4. [Google Scholar]
- Allahham, M.S.; Al-Sa’d, M.F.; Al-Ali, A.; Mohamed, A.; Khattab, T.; Erbad, A. DroneRF dataset: A dataset of drones for RF-based detection, classification and identification. Data Brief 2019, 26, 104313. [Google Scholar] [CrossRef] [PubMed]
- Ezuma, M.; Erden, F.; Anjinappa, C.K.; Ozdemir, O.; Guvenc, I. Drone remote controller RF signal dataset. IEEE Dataport 2020. [Google Scholar] [CrossRef]
- Uzundurukan, E.; Dalveren, Y.; Kara, A. A database for the radio frequency fingerprinting of Bluetooth devices. Data 2020, 5, 55. [Google Scholar] [CrossRef]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Andreux, M.; Angles, T.; Exarchakis, G.; Leonarduzzi, R.; Rochette, G.; Thiry, L.; Zarka, J.; Mallat, S.; Andén, J.; Belilovsky, E.; et al. Kymatio: Scattering Transforms in Python. J. Mach. Learn. Res. 2020, 21, 1–6. [Google Scholar]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Mallat, S. Group invariant scattering. Commun. Pure Appl. Math. 2012, 65, 1331–1398. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv Prepr. 2018, arXiv:1802.03426. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Novikov, A.V. PyClustering: Data mining library. J. Open Source Softw. 2019, 4, 1230. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Chen, W.; Hu, X.; Chen, W.; Hong, Y.; Yang, M. Airborne LiDAR remote sensing for individual tree forest inventory using trunk detection-aided mean shift clustering techniques. Remote. Sens. 2018, 10, 1078. [Google Scholar] [CrossRef] [Green Version]
- Pelleg, D.; Moore, A.W. X-means: Extending k-means with efficient estimation of the number of clusters. In Proceedings of the ICML, Stanford, CA, USA, 29 June–2 July 2000; Volume 1, pp. 727–734. [Google Scholar]
- MacQueen, J. Classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics Probability; University of California: Los Angeles, LA, USA, 1967; pp. 281–297. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashush, N.; Greenberg, S.; Manor, E.; Ben-Shimol, Y. Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods. Sensors 2023, 23, 1589. https://doi.org/10.3390/s23031589
Ashush N, Greenberg S, Manor E, Ben-Shimol Y. Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods. Sensors. 2023; 23(3):1589. https://doi.org/10.3390/s23031589
Chicago/Turabian StyleAshush, Nerya, Shlomo Greenberg, Erez Manor, and Yehuda Ben-Shimol. 2023. "Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods" Sensors 23, no. 3: 1589. https://doi.org/10.3390/s23031589
APA StyleAshush, N., Greenberg, S., Manor, E., & Ben-Shimol, Y. (2023). Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods. Sensors, 23(3), 1589. https://doi.org/10.3390/s23031589





