The Study of the Acoustic Characteristics of Chitosan Acetate Film Using a Radial Electric Field Excited Resonator
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model of a Free Radial Electric Field Excited Circular Piezoresonator
2.2. Numerical Model of a Radial Electric Field Excited Circular Piezoresonator Loaded with a Viscoelastic Film, Which Has a Finite Thickness and a Finite Electrical Conductivity
2.3. Features of the Finite Element Resonator Model Containing a Thin Film
2.4. Creation of a Disk Resonator with a Radial Exciting Field from BPZT Piezoceramics
2.5. Measurement of Resonator Characteristics. Taking into Account the Influence of Temperature
2.6. Creation of a Chitosan Acetate Film on the Resonator Surface
2.7. Measurement of the Characteristics of a Resonator Loaded with a Chitosan Acetate Film in an Ammonia Atmosphere
3. Results
3.1. Measurement Results for a Free Resonator. Determination of Temperature Dependencies of Material Constants of BPZT Piezoceramics
3.2. Measurement Results for a Resonator Loaded with a Chitosan Acetate Film. Determination of the Mechanical Characteristics and Conductivity of the Film at Different Concentrations of Ammonia
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ohring, M. Materials Science of Thin Films: Deposition and Structure, 2nd ed.; Academic Press: San Diego, CA, USA, 2002; ISBN 9780125249751. [Google Scholar]
- Venables, J.A. Introduction to Surface and Thin Film Processes, 1st ed.; Cambridge University Press: Cambridge, UK, 2000; ISBN 978-0-521-78500-6. [Google Scholar] [CrossRef]
- Krutov, B.N.; Mansfel’d, G.D.; Freik, A.D. Determination of Acoustic Parameters of Thin Layers and Films from Electrical Characteristics of a Compound Resonator. Acoust. Phys. 1994, 40, 562–566. [Google Scholar]
- Kuznetsova, I.E.; Zaitsev, B.D.; Shikhabudinov, A.M. Elastic and viscous properties of nanocomposite films based on low-density polyethylene. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2010, 57, 2099–2102. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsova, I.; Zaitsev, B.; Shikhabudinov, A.; Tsivileva, O.; Pankratov, A.; Verona, E. Acoustoelectronic Acousto—Electronic Gas Sensor Based on Mushroom Mycelial Extracts. Sens. Actuators B Chem. 2017, 243, 525–531. [Google Scholar] [CrossRef]
- Kuznetsova, I.; Zaitsev, B.; Krasnopolskaya, L.; Teplykh, A.; Semyonov, A.; Avtonomova, A.; Ziangirova, M.; Smirnov, A.; Kolesov, V. Influence of humidity on the acoustic properties of mushroom mycelium films used as sensitive layers for acoustic humidity sensors. Sensors 2020, 20, 2711. [Google Scholar] [CrossRef]
- Teplykh, A.; Zaitsev, B.; Borodina, I.; Semyonov, A.; Ziangirova, M.; Almyasheva, N.; Golyshkin, A.; Krasnopolskaya, L.; Kuznetsova, I. The study of the mechanical properties of thin films using piezoceramic acoustic resonators. ITM Web Conf. 2019, 30, 07002. [Google Scholar] [CrossRef]
- Zaitsev, B.D.; Teplykh, A.A.; Fedorov, F.S.; Grebenko, A.K.; Nasibulin, A.G.; Semyonov, A.P.; Borodina, I.A. Evaluation of Elastic Properties and Conductivity of Chitosan Acetate Films in Ammonia and Water Vapors Using Acoustic Resonators. Sensors 2020, 20, 2236. [Google Scholar] [CrossRef] [PubMed]
- Zaitsev, B.; Fedorov, F.; Semyonov, A.; Teplykh, A.; Borodina, I.; Nasibulin, A. Gas Sensor Based on the Piezoelectric Resonator with Lateral Electric Field and Films of Chitosan Salts. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; pp. 607–610. [Google Scholar] [CrossRef]
- Knapp, M.; Lomonosov, A.M.; Warkentin, P.; Jager, P.M.; Ruile, W.; Kirschner, H.-P.; Honal, M.; Bleyl, I.; Mayer, A.P.; Reindl, L.M. Accurate Characterization of SiO2 Thin Films Using Surface Acoustic Waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2015, 62, 736–743. [Google Scholar] [CrossRef] [PubMed]
- Zaitsev, B.; Teplykh, A.; Shikhabudinov, A.; Borodina, I.; Kisin, V.; Sinev, I. The influence of the conducting film on the characteristics of the lateral electric field excited piezoelectric resonator. Ultrasonics 2018, 84, 96–100. [Google Scholar] [CrossRef]
- Zaitsev, B.; Semyonov, A.; Teplykh, A.; Borodina, I. The effect of the conductivity of a film located near a piezoelectric resonator with a lateral electric field based on the PZT ceramics on its characteristics. Ultrasonics 2019, 94, 169–173. [Google Scholar] [CrossRef]
- Hu, Y.; French, L., Jr.; Radecsky, K.; Pereira da Cunha, M.; Millard, P.; Vetelino, J. A lateral field excited liquid acoustic wave sensor. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2004, 51, 1373–1379. [Google Scholar] [CrossRef]
- Zaitsev, B.; Shikhabudinov, A.; Teplykh, A.; Kuznetsova, I. Liquid sensor based on a piezoelectric lateral electric field-excited resonator. Ultrasonics 2016, 68, 179–183. [Google Scholar] [CrossRef] [PubMed]
- McCann, D.; McCann, J.; Parks, J.; Frankel, D.; Pereira da Cunha, M.; Vetelino, J. A lateral-field-excited LiTaO3 high frequency bulk acoustic wave sensor. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 779–787. [Google Scholar] [CrossRef]
- Vetelino, J. A lateral field excited acoustic wave sensor platform. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 2269–2272. [Google Scholar] [CrossRef]
- de Castilla, H.; Bélanger, P.; Zednik, R.J. Generalized Dynamic Analytical Model of Piezoelectric Materials for Characterization Using Electrical Impedance Spectroscopy. Materials 2019, 12, 2502. [Google Scholar] [CrossRef] [PubMed]
- Borodina, I.; Zaitsev, B.; Teplykh, A. The effect of the conductivity of a thin film located near the acoustic delay line on the characteristics of the propagating SH0 wave. Ultrasonics 2019, 91, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Tohmyoh, H.; Imaizumi, T.; Saka, M. Acoustic resonant spectroscopy for characterization of thin polymer films. Rev. Sci. Instrum. 2006, 77, 104901. [Google Scholar] [CrossRef]
- Bavencoffe, M.; Tembhurnikar, N.; Negulescu, B.; Wolfman, J.; Feuillard, G. Modelling and experimental measurements of the mechanical response of piezoelectric structures from millimetre to micrometer. Adv. Appl. Ceram. 2018, 117, 285–290. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Tailor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000; ISBN 0-7506-5049-4. [Google Scholar]
- Teplykh, A.; Zaitsev, B.; Semyonov, A.; Borodina, I. The Radial Electric Field Excited Circular Disk Piezoceramic Acoustic Resonator and Its Properties. Sensors 2021, 21, 608. [Google Scholar] [CrossRef]
- Kumar, R.; Tiwari, R.; Kumar, R. Significance of memory-dependent derivative approach for the analysis of thermoelastic damping in micromechanical resonators. Mech. Time-Depend. Mater. 2020, 26, 101–118. [Google Scholar] [CrossRef]
- Bruno, B.P.; Fahmy, A.R.; Stürmer, M.; Wallrabe, U.; Wapler, M.C. Properties of piezoceramic materials in high electric field actuator applications. Smart. Mater. Struct. 2019, 28, 015029. [Google Scholar] [CrossRef]
- Teplykh, A.; Zaitsev, B.; Semyonov, A.; Borodina, I. Determination of the Acoustic Properties of a Phenolic Resin Film Using a Radial Electric Field Excited Piezoceramic Resonator. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Kumar, P.; Leong, J. Finite Element Modeling and Simulations of Piezoelectric Actuators Responses with Uncertainty Quantification. Computation 2018, 6, 60. [Google Scholar] [CrossRef]
- Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Available online: https://gmsh.info (accessed on 27 December 2022).
- Jaffe, B.; Cook, W.R., Jr.; Jaffe, H. Piezoelectric Ceramics; Academic Press: London, UK, 1971. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput Optim Appl. 2010, 51, 259–277. [Google Scholar] [CrossRef]
- Pérez, N.; Buiochi, F.; Andrade, M.A.B.; Adamowski, J.C. Numerical Characterization of Piezoceramics Using Resonance Curves. Materials 2016, 9, 71. [Google Scholar] [CrossRef] [PubMed]
- Pérez, N.; Andrade, M.A.; Buiochi, F.; Adamowski, J.C. Identification of Elastic, Dielectric, and Piezoelectric Constants in Piezoceramic Disks. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2010, 57, 2772–2783. [Google Scholar] [CrossRef] [PubMed]
- Pugachev, S.I. (Ed.) Piezoceramic Transducers. Measurement Methods and Calculation of Parameters. Reference Book; Sudostroenie: Leningrad, Russia, 1984; 256p. (In Russian) [Google Scholar]

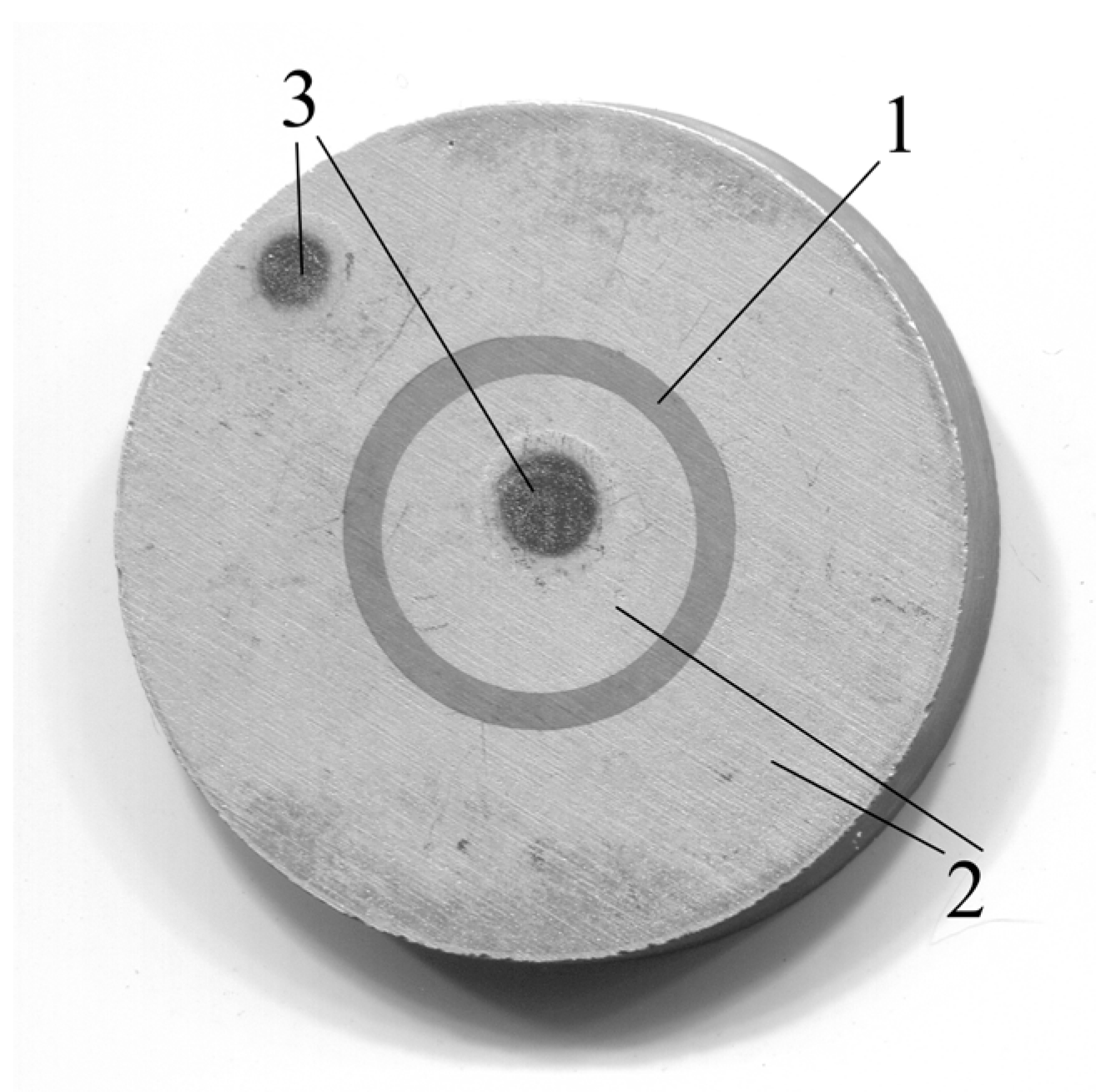


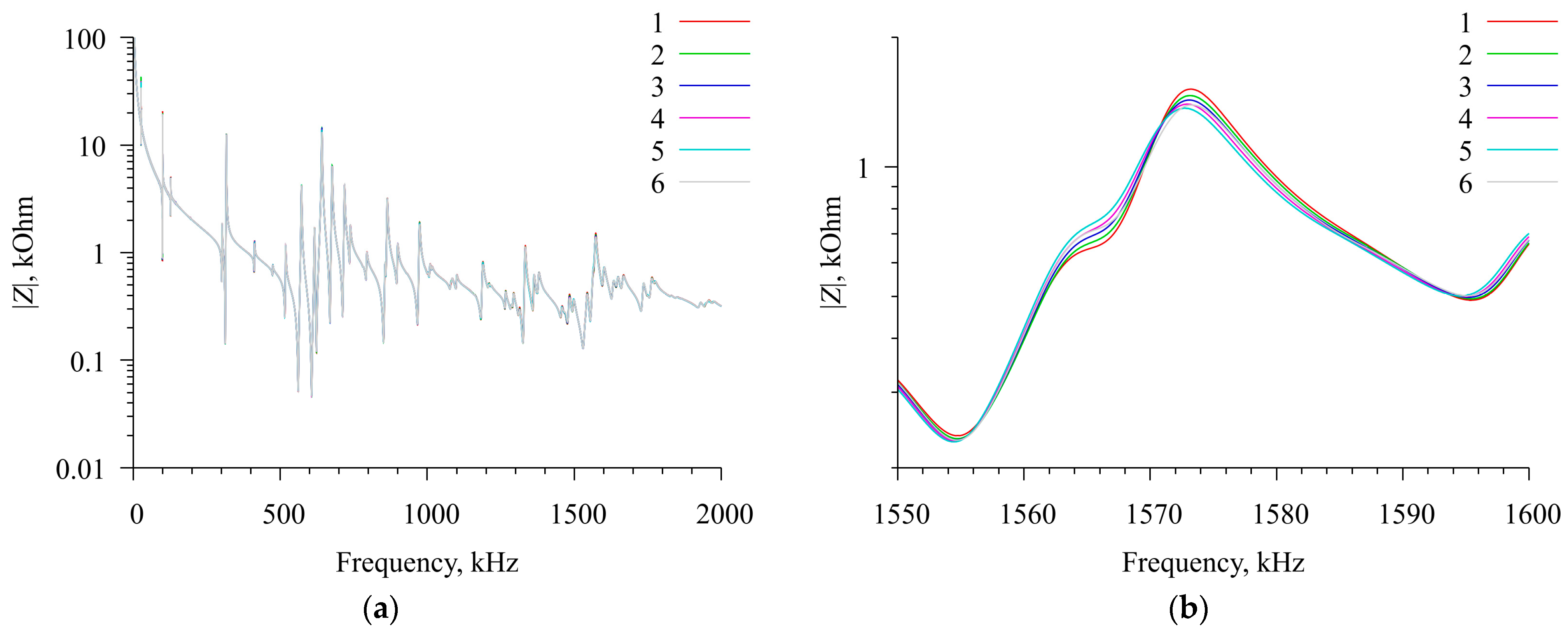


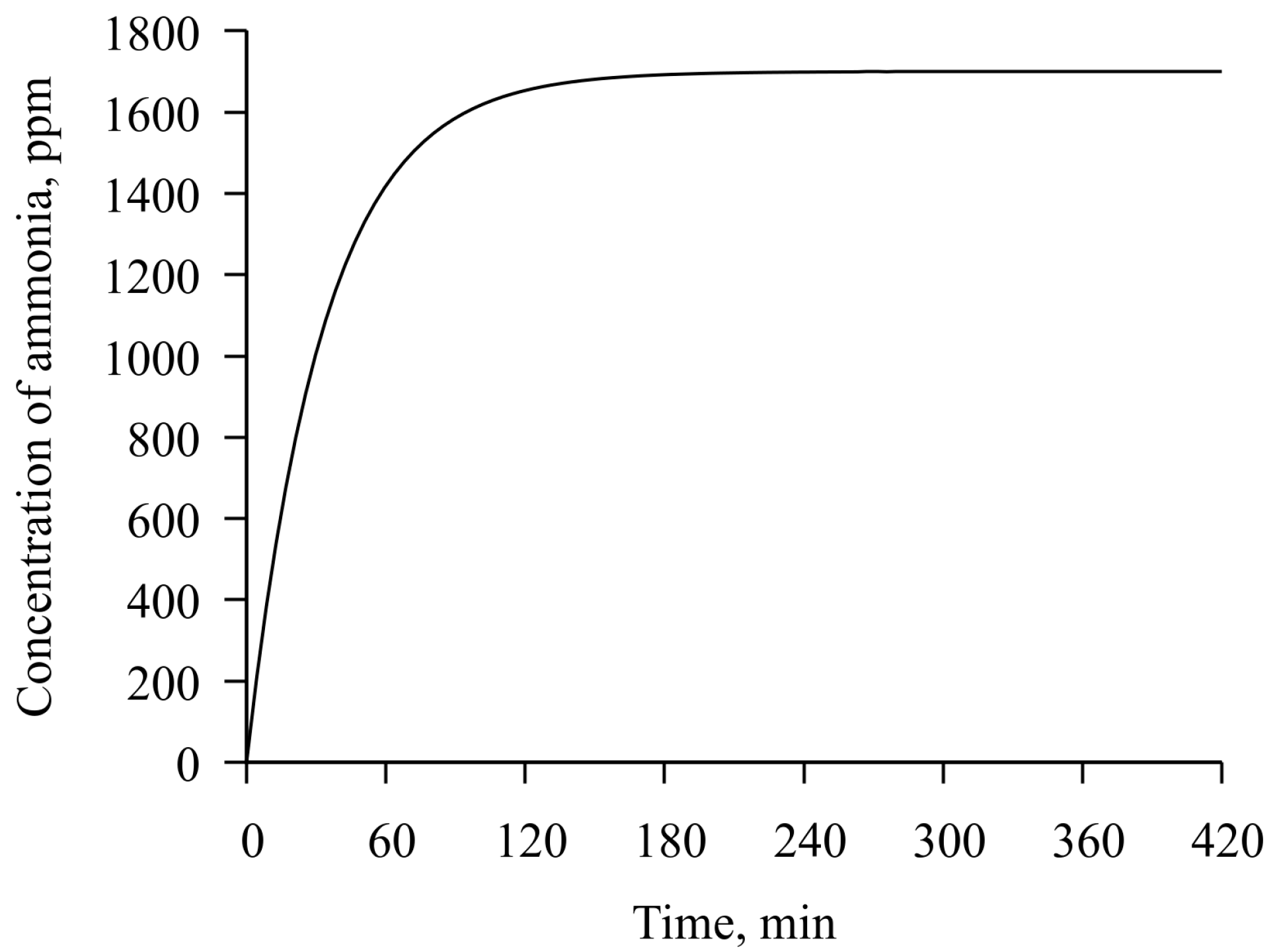
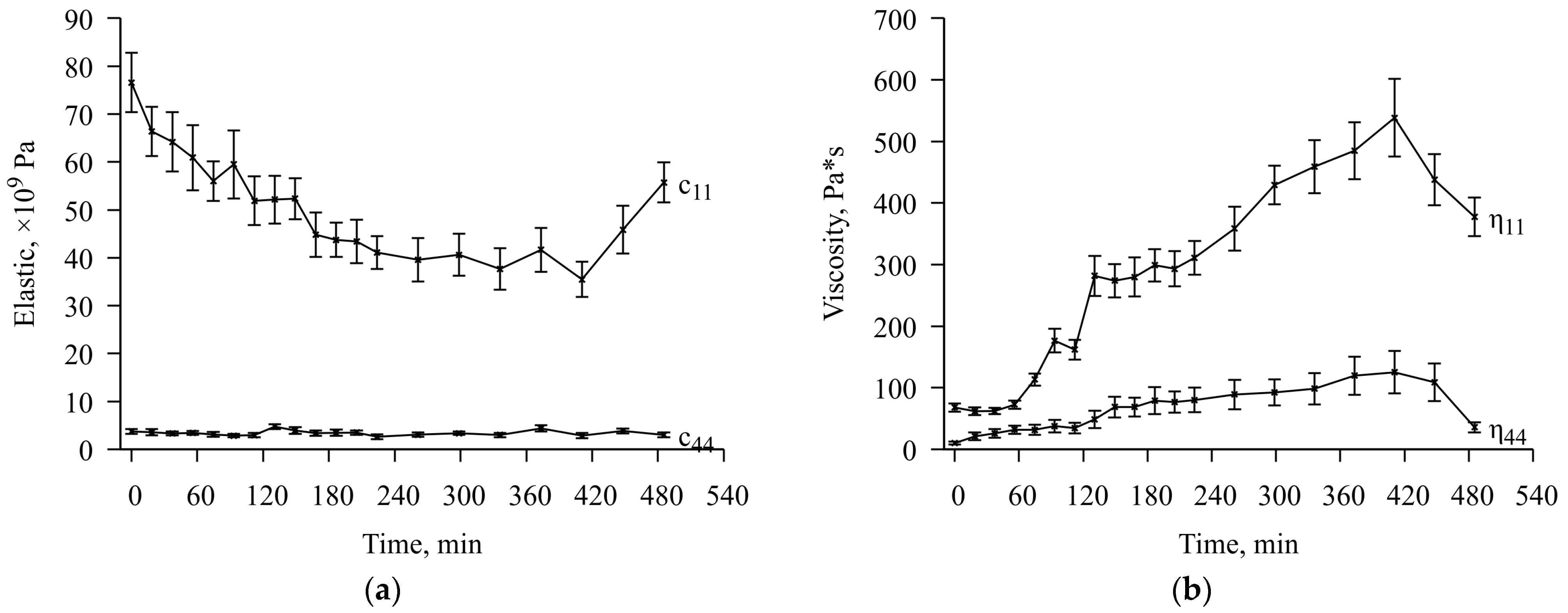

| Property | Value |
|---|---|
| Diameter (mm) | 21.89 |
| Thickness (μm) | 1930 |
| Mass (g) | 5.287 |
| Density (kg/m3) | 7347 |
| Radius e1 | 4.05 |
| Radius e2 | 5.04 |
| Constant | Reference Value [33] | Value at t = 35 °C | Change on Δt = 1 °C |
|---|---|---|---|
| c11 × 1010 Pa | 15.1 | 15.505 | 4.953 × 10−4 |
| c12 × 1010 Pa | 7.9 | 9.172 | −7.651 × 10−4 |
| c13 × 1010 Pa | 8.0 | 8.711 | 3.450 × 10−3 |
| c33 × 1010 Pa | 13.6 | 13.867 | 1.653 × 10−4 |
| c44 × 1010 Pa | 2.9 | 2.775 | −1.461 × 10−3 |
| e15, C/m2 | 15.4 | 15.470 | 2.918 × 10−3 |
| e31, C/m2 | −7.9 | −6.427 | 4.665 × 10−3 |
| e33, C/m2 | 17.7 | 17.188 | −4.885 × 10−3 |
| ε11/ε0 | 1610 | 1439.3 | 8.758 × 10−2 |
| ε33/ε0 | 1280 | 1220.0 | 9.334 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teplykh, A.; Zaitsev, B.; Semyonov, A.; Borodina, I. The Study of the Acoustic Characteristics of Chitosan Acetate Film Using a Radial Electric Field Excited Resonator. Sensors 2023, 23, 1808. https://doi.org/10.3390/s23041808
Teplykh A, Zaitsev B, Semyonov A, Borodina I. The Study of the Acoustic Characteristics of Chitosan Acetate Film Using a Radial Electric Field Excited Resonator. Sensors. 2023; 23(4):1808. https://doi.org/10.3390/s23041808
Chicago/Turabian StyleTeplykh, Andrey, Boris Zaitsev, Alexander Semyonov, and Irina Borodina. 2023. "The Study of the Acoustic Characteristics of Chitosan Acetate Film Using a Radial Electric Field Excited Resonator" Sensors 23, no. 4: 1808. https://doi.org/10.3390/s23041808
APA StyleTeplykh, A., Zaitsev, B., Semyonov, A., & Borodina, I. (2023). The Study of the Acoustic Characteristics of Chitosan Acetate Film Using a Radial Electric Field Excited Resonator. Sensors, 23(4), 1808. https://doi.org/10.3390/s23041808






