Automatic Assessments of Parkinsonian Gait with Wearable Sensors for Human Assistive Systems
Abstract
:1. Introduction
2. Methods
2.1. Participants and Protocols
2.2. The Configuration of System
2.3. Wearable System
2.4. Feature Calculation
2.5. Nonlinear Model
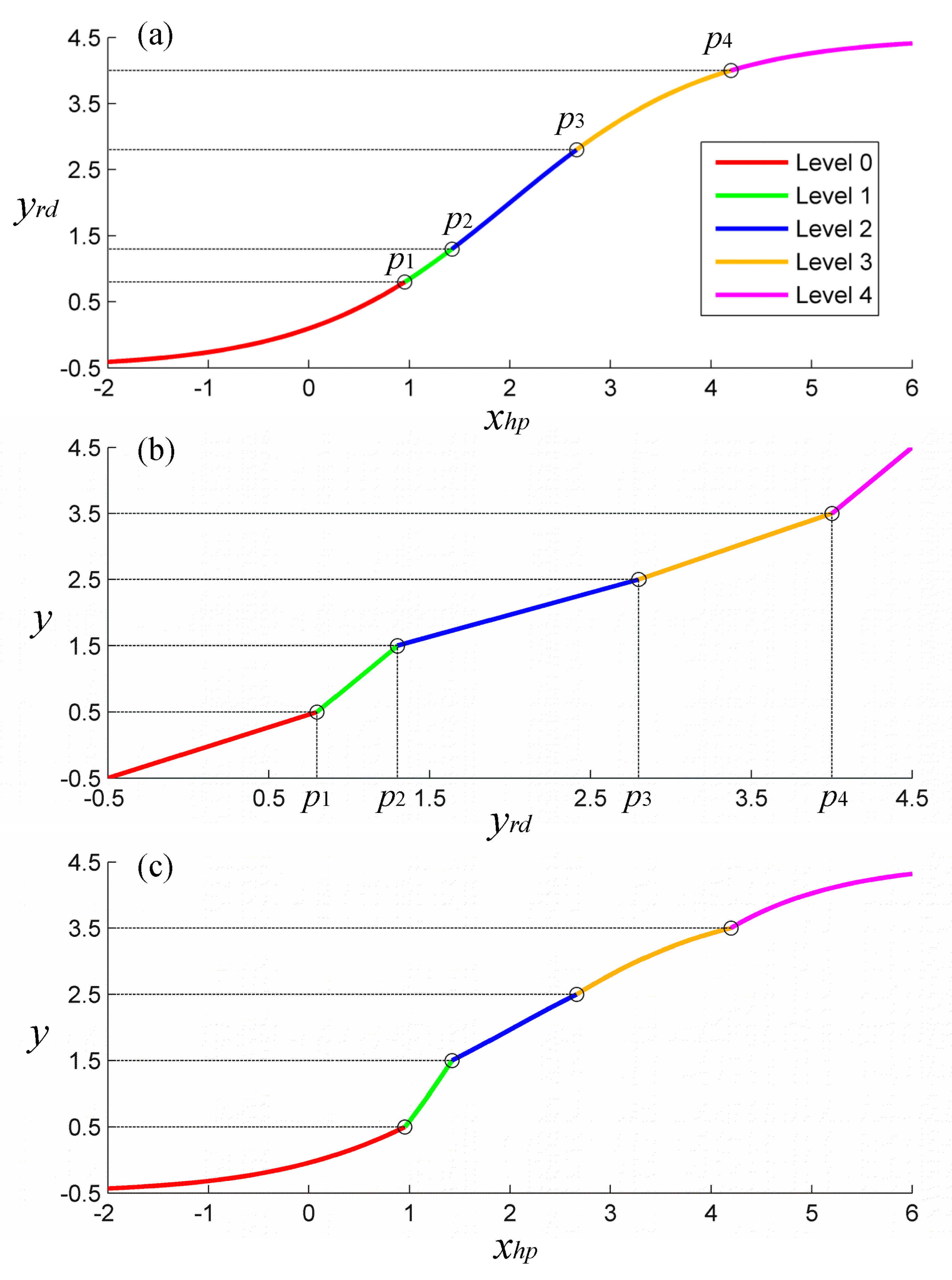
2.5.1. Structure
2.5.2. Training and Validation
2.6. Traditional Models for Comparisons
2.7. Statistical Analysis
3. Results
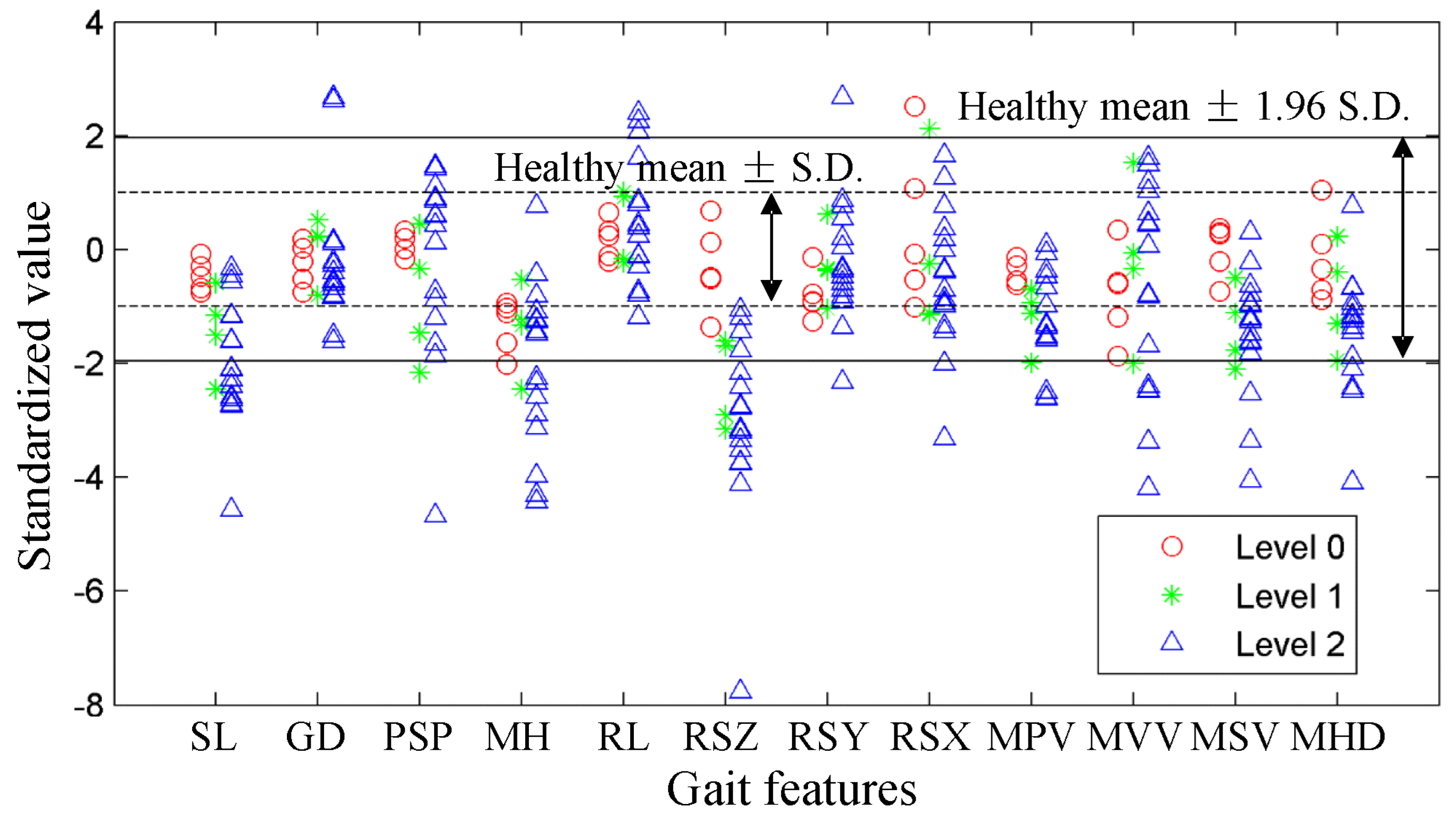
3.1. Gait Features Distributions
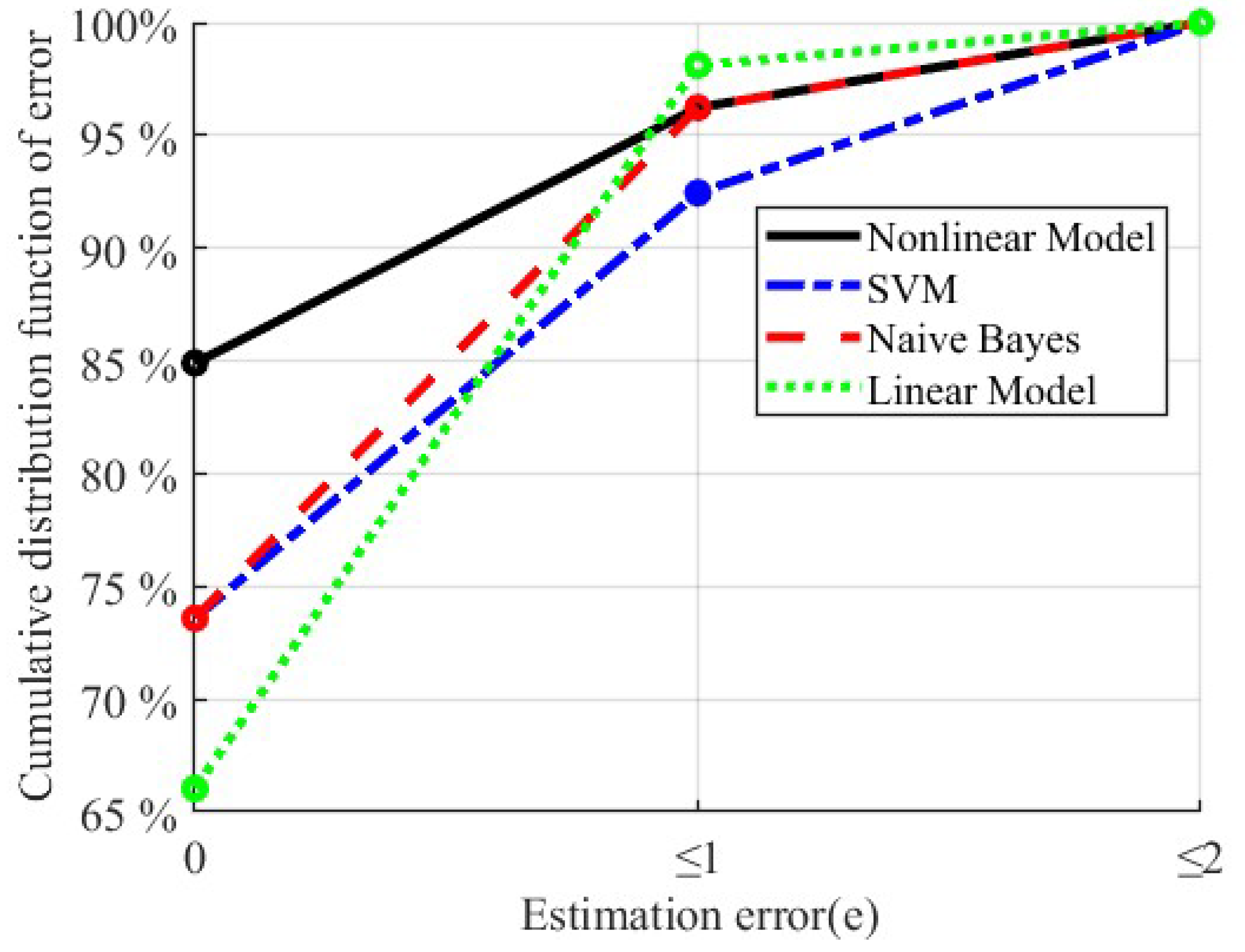
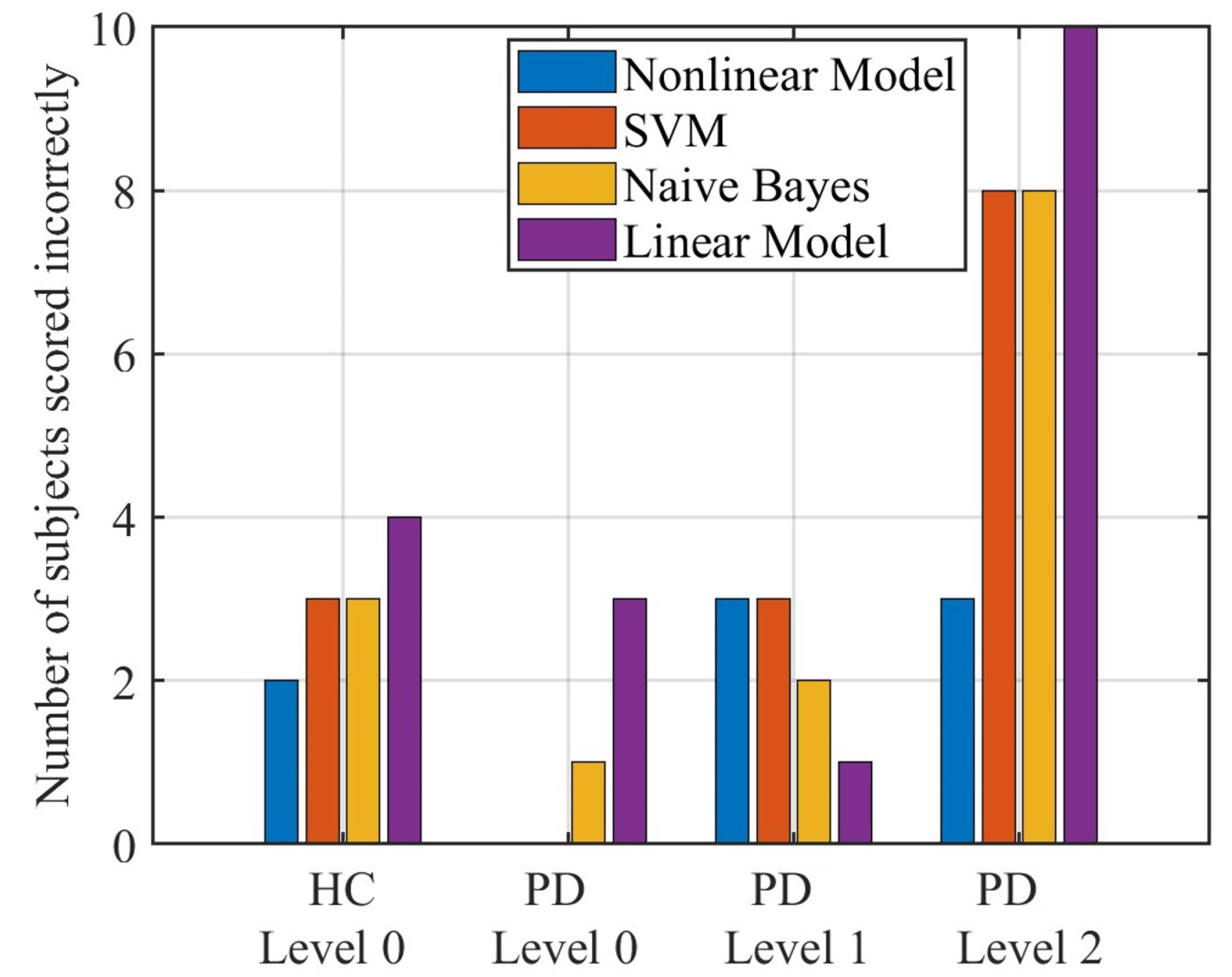
3.2. Results of Gait Task Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Alwardat, M.; Etoom, M.; Al Dajah, S.; Schirinzi, T.; Di Lazzaro, G.; Sinibaldi Salimei, P.; Biagio Mercuri, N.; Pisani, A. Effectiveness of robot-assisted gait training on motor impairments in people with Parkinson’s disease: A systematic review and meta-analysis. Int. J. Rehabil. Res. 2018, 41, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Picelli, A.; Melotti, C.; Origano, F.; Waldner, A.; Fiaschi, A.; Santilli, V.; Smania, N. Robot-assisted gait training in patients with Parkinson disease: A randomized controlled trial. Neurorehabilit. Neural Repair 2012, 26, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Fahn, S. Unified Parkinson’s disease rating scale. Recent Development in Parkinson’s Disease; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Post, B.; Merkus, M.P.; De Bie, R.M.; De Haan, R.J.; Speelman, J.D. Unified Parkinson’s disease rating scale motor examination: Are ratings of nurses, residents in neurology, and movement disorders specialists interchangeable? Mov. Disord. Off. J. Mov. Disord. Soc. 2005, 20, 1577–1584. [Google Scholar] [CrossRef] [PubMed]
- Parisi, F.; Ferrari, G.; Giuberti, M.; Contin, L.; Cimolin, V.; Azzaro, C.; Albani, G.; Mauro, A. Inertial BSN-based characterization and automatic UPDRS evaluation of the gait task of Parkinsonians. IEEE Trans. Affect. Comput. 2016, 7, 258–271. [Google Scholar] [CrossRef]
- Bouça-Machado, R.; Jalles, C.; Guerreiro, D.; Pona-Ferreira, F.; Branco, D.; Guerreiro, T.; Matias, R.; Ferreira, J.J. Gait kinematic parameters in Parkinson’s disease: A systematic review. J. Park. Dis. 2020, 10, 843–853. [Google Scholar] [CrossRef]
- Serrao, M.; Chini, G.; Caramanico, G.; Bartolo, M.; Castiglia, S.F.; Ranavolo, A.; Conte, C.; Venditto, T.; Coppola, G.; Di Lorenzo, C.; et al. Prediction of responsiveness of gait variables to rehabilitation training in Parkinson’s disease. Front. Neurol. 2019, 10, 826. [Google Scholar] [CrossRef]
- Kour, N.; Sunanda; Arora, S. Computer-vision based diagnosis of Parkinson’s disease via gait: A survey. IEEE Access 2019, 7, 156620–156645. [Google Scholar] [CrossRef]
- Mughal, H.; Javed, A.R.; Rizwan, M.; Almadhor, A.S.; Kryvinska, N. Parkinson’s disease management via wearable sensors: A systematic review. IEEE Access 2022, 10, 35219–35237. [Google Scholar] [CrossRef]
- Lu, R.; Xu, Y.; Li, X.; Fan, Y.; Zeng, W.; Tan, Y.; Ren, K.; Chen, W.; Cao, X. Evaluation of wearable sensor devices in Parkinson’s disease: A review of current status and future prospects. Park. Dis. 2020, 2020. [Google Scholar] [CrossRef]
- Zijlstra, A.; Zijlstra, W. Trunk-acceleration based assessment of gait parameters in older persons: A comparison of reliability and validity of four inverted pendulum based estimations. Gait Post. 2013, 38, 940–944. [Google Scholar] [CrossRef]
- Chang, H.C.; Hsu, Y.L.; Yang, S.C.; Lin, J.C.; Wu, Z.H. A wearable inertial measurement system with complementary filter for gait analysis of patients with stroke or Parkinson’s disease. IEEE Access 2016, 4, 8442–8453. [Google Scholar] [CrossRef]
- Rodríguez-Molinero, A.; Samà, A.; Pérez-López, C.; Rodríguez-Martín, D.; Alcaine, S.; Mestre, B.; Quispe, P.; Giuliani, B.; Vainstein, G.; Browne, P.; et al. Analysis of correlation between an accelerometer-based algorithm for detecting parkinsonian gait and UPDRS subscales. Front. Neurol. 2017, 8, 431. [Google Scholar] [CrossRef]
- Oğul, B.B.; Özdemir, S. A Pairwise Deep Ranking Model for Relative Assessment of Parkinson’s Disease Patients From Gait Signals. IEEE Access 2021, 10, 6676–6683. [Google Scholar] [CrossRef]
- Caramia, C.; Torricelli, D.; Schmid, M.; Munoz-Gonzalez, A.; Gonzalez-Vargas, J.; Grandas, F.; Pons, J.L. IMU-based classification of Parkinson’s disease from gait: A sensitivity analysis on sensor location and feature selection. IEEE J. Biomed. Health Inform. 2018, 22, 1765–1774. [Google Scholar] [CrossRef]
- Klucken, J.; Barth, J.; Kugler, P.; Schlachetzki, J.; Henze, T.; Marxreiter, F.; Kohl, Z.; Steidl, R.; Hornegger, J.; Eskofier, B.; et al. Unbiased and mobile gait analysis detects motor impairment in Parkinson’s disease. PLoS ONE 2013, 8, e56956. [Google Scholar] [CrossRef]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.; Dehollain, C.; Blanc, Y.; Burkhard, P.R.; Aminian, K. Gait assessment in Parkinson’s disease: Toward an ambulatory system for long-term monitoring. IEEE Trans. Biomed. Eng. 2004, 51, 1434–1443. [Google Scholar] [CrossRef]
- Patel, S.; Lorincz, K.; Hughes, R.; Huggins, N.; Growdon, J.; Standaert, D.; Akay, M.; Dy, J.; Welsh, M.; Bonato, P. Monitoring motor fluctuations in patients with Parkinson’s disease using wearable sensors. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 864–873. [Google Scholar] [CrossRef]
- Giuberti, M.; Ferrari, G.; Contin, L.; Cimolin, V.; Azzaro, C.; Albani, G.; Mauro, A. Automatic UPDRS evaluation in the sit-to-stand task of Parkinsonians: Kinematic analysis and comparative outlook on the leg agility task. IEEE J. Biomed. Health Inform. 2015, 19, 803–814. [Google Scholar] [CrossRef]
- Jeon, H.; Lee, W.; Park, H.; Lee, H.J.; Kim, S.K.; Kim, H.B.; Jeon, B.; Park, K.S. High-accuracy automatic classification of Parkinsonian tremor severity using machine learning method. Physiol. Measur. 2017, 38, 1980. [Google Scholar] [CrossRef]
- Giuberti, M.; Ferrari, G.; Contin, L.; Cimolin, V.; Azzaro, C.; Albani, G.; Mauro, A. Assigning UPDRS scores in the leg agility task of Parkinsonians: Can it be done through BSN-based kinematic variables? IEEE Internet Things J. 2015, 2, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Heldman, D.A.; Filipkowski, D.E.; Riley, D.E.; Whitney, C.M.; Walter, B.L.; Gunzler, S.A.; Giuffrida, J.P.; Mera, T.O. Automated motion sensor quantification of gait and lower extremity bradykinesia. In Proceedings of the Annual Conference of the IEEE Engineering in Medicine and Bilogy Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 1956–1959. [Google Scholar]
- Liu, X.; Zhou, B.; Zhang, B.; Liu, T. A Potential-Real-Time Thigh Orientation Prediction Method Based on Two Shanks-Mounted IMUs and Its Clinical Application. IEEE Trans. Autom. Sci. Eng. 2022, 1–10. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y.; Li, Q.; Liu, T.; Yi, J. IMU-based gait normalcy index calculation for clinical evaluation of impaired gait. IEEE J. Biomed. Health Inform. 2020, 25, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Sun, Y.; Li, Q.; Liu, T.; Yi, J. Two shank-mounted IMUs-based gait analysis and classification for neurological disease patients. IEEE Robot. Autom. Lett. 2020, 5, 1970–1976. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y.; Li, Q.; Liu, T. Estimation of step length and gait asymmetry using wearable inertial sensors. IEEE Sens. J. 2018, 18, 3844–3851. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemesbow, S. Goodness of fit tests for the multiple logistic regression model. Commun. Stat. Theory Methods 1980, 9, 1043–1069. [Google Scholar] [CrossRef]
- Mannini, A.; Trojaniello, D.; Cereatti, A.; Sabatini, A.M. A machine learning framework for gait classification using inertial sensors: Application to elderly, post-stroke and Huntington’s disease patients. Sensors 2016, 16, 134. [Google Scholar] [CrossRef]
- Rehman, R.Z.U.; Del Din, S.; Guan, Y.; Yarnall, A.J.; Shi, J.Q.; Rochester, L. Selecting clinically relevant gait characteristics for classification of early Parkinson’s disease: A comprehensive machine learning approach. Sci. Rep. 2019, 9, 17269. [Google Scholar] [CrossRef]
- Chen, S.; Lach, J.; Lo, B.; Yang, G.Z. Toward pervasive gait analysis with wearable sensors: A systematic review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef]



| Subjects | UPDRS | Height/m | Weight/kg | Age/Years | Number of Subjects |
|---|---|---|---|---|---|
| 0 | 5 | ||||
| Subjects with | 1 | 1.64 ± 1.07 | 62 ± 8 | 69 ± 8 | 4 |
| Parkinson | 2 | 16 | |||
| Young Healthy subjects | 0 | 1.67 ± 1.24 | 62 ± 11 | 32 ± 5 | 19 |
| Old Healthy subjects | 0 | 1.58 ± 3.13 | 56 ± 6 | 69 ± 7 | 9 |
| Gait Parameter | Definition | RMSE (Validated in [24]) |
|---|---|---|
| Stride length (SL) | The height-normalized linear displacement between two adjacent ankle landing points. | 2.3 m |
| Gait cycle duration (GD) | The duration between two adjacent HS events. | 14 ms |
| Percentage swing phase (PSP) | The duration between adjacent TO event and HS event divided by GD. | no validated |
| Max ankle height (MH) | The maximum value of height-normalized ankle displacement in V-axis direction during the gait cycle. | 1.0 cm |
| Range of lateral displacement (RL) | The range of height-normalized displacement along the L-axis direction during the gait cycle. | no validated |
| Range of shank Z-axis rotation (RSZ) | The range of the integration of IMU Z-axis angular velocity during the gait cycle. | no validated |
| Range of shank Y-axis rotation (RSY) | The range of the integration of IMU Y-axis angular velocity during the gait cycle. | no validated |
| Range of shank X-axis rotation (RSX) | The range of the integration of IMU X-axis angular velocity during the gait cycle. | no validated |
| Max ankle progressive velocity (MPV) | The maximum value of height-normalized ankle velocity in P-axis direction during the gait cycle. | 3.0 cm/s |
| Max ankle vertical velocity (MVV) | The maximum value of height-normalized ankle velocity in V-axis direction during the gait cycle. | no validated |
| Max shank Z-axis angular velocity (MSV) | The maximum value of IMU z-axis angular velocity during the swing phase. | no validated |
| Ankle displacement at MH (MHD) | The height-normalized ankle displacement in P-axis direction when MH occurs. | 1.9 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Liu, X.; Zhang, N.; Zhang, X.; Zhang, B.; Wang, S.; Liu, T.; Yi, J. Automatic Assessments of Parkinsonian Gait with Wearable Sensors for Human Assistive Systems. Sensors 2023, 23, 2104. https://doi.org/10.3390/s23042104
Han Y, Liu X, Zhang N, Zhang X, Zhang B, Wang S, Liu T, Yi J. Automatic Assessments of Parkinsonian Gait with Wearable Sensors for Human Assistive Systems. Sensors. 2023; 23(4):2104. https://doi.org/10.3390/s23042104
Chicago/Turabian StyleHan, Yi, Xiangzhi Liu, Ning Zhang, Xiufeng Zhang, Bin Zhang, Shuoyu Wang, Tao Liu, and Jingang Yi. 2023. "Automatic Assessments of Parkinsonian Gait with Wearable Sensors for Human Assistive Systems" Sensors 23, no. 4: 2104. https://doi.org/10.3390/s23042104
APA StyleHan, Y., Liu, X., Zhang, N., Zhang, X., Zhang, B., Wang, S., Liu, T., & Yi, J. (2023). Automatic Assessments of Parkinsonian Gait with Wearable Sensors for Human Assistive Systems. Sensors, 23(4), 2104. https://doi.org/10.3390/s23042104







