Reconfigurable Fault-Tolerant Control for Spacecraft Formation Flying Based on Iterative Learning Algorithms
Abstract
:1. Introduction
- (1)
- Motivated by sliding mode methodology, a new ILO was designed for robust thruster bias fault reconstruction for spacecraft formation flying systems, subject to space perturbations. In addition, compared with the existing ILOs, a new ILO stability analysis methodology was provided in detail.
- (2)
- Based on two iterative learning algorithms, a new LOF2TC approach was explored for accurate spacecraft formation configuration maintenance in presence of space perturbations and possible uncertainties.
- (3)
- It is worth noting that iterative learning algorithms were not developed for spacecraft formation control systems. Therefore, the proposed ILO-based robust thruster fault reconstruction and LOF2TC approach provide an extension for spacecraft application.
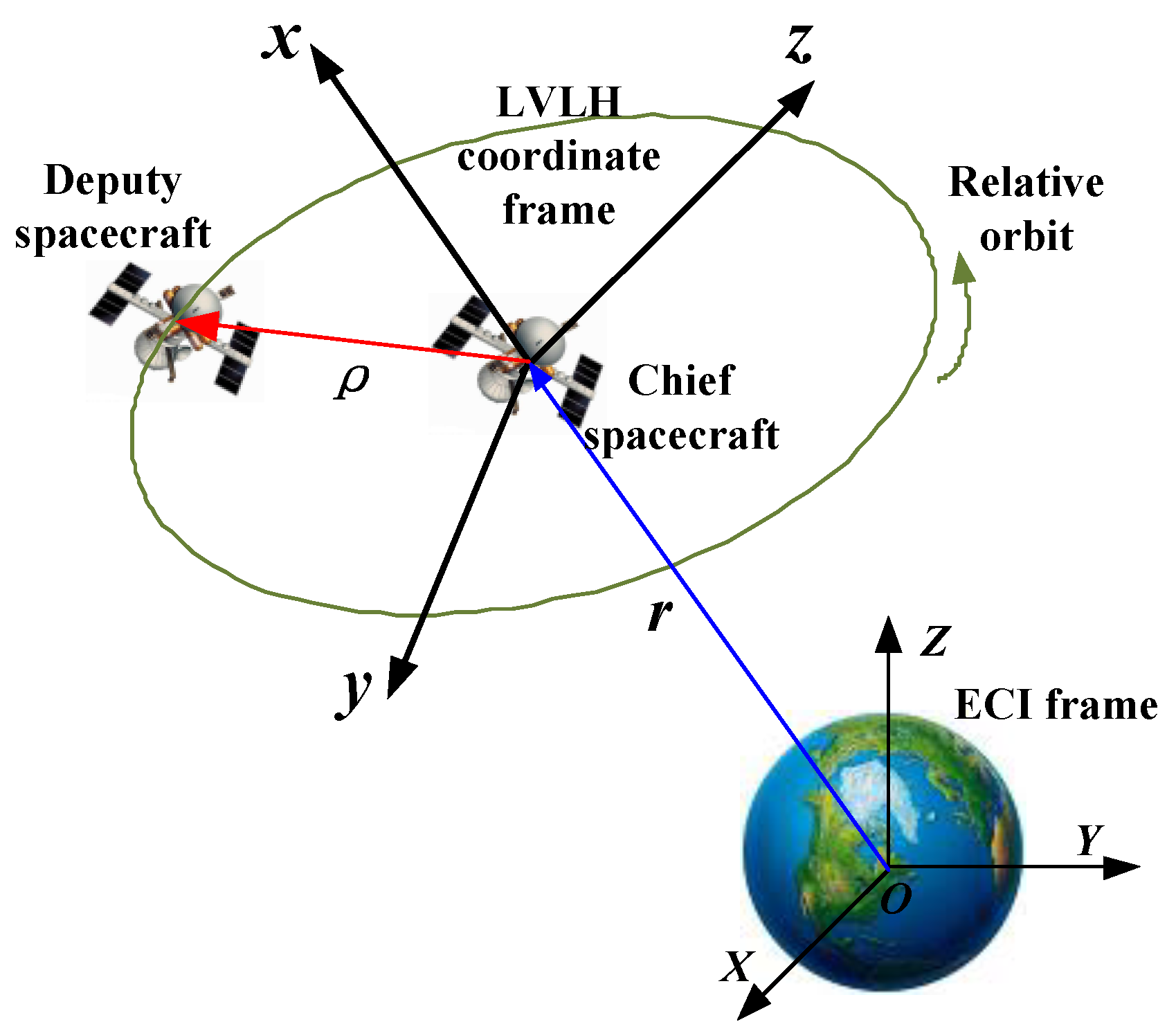
2. Problem Formulation
3. Iterative Learning Observer-Based Thruster Fault Reconstruction Approach
3.1. Design of the Iterative Learning Observer
3.2. Stability Analysis of the Iterative Learning Observer
- (1)
- Select appropriate positive scalars and , then compute and .
- (2)
- Select a small positive scalar , then compute through solving (10).
- (3)
- Choose a sufficiently small positive scalar , then matrices , , and can be obtained readily by using the Matlab/LMI toolbox to solve inequalities (8) and (27).
- (4)
- Compute the gain matrix by using the matrices obtained in step (3).
- (5)
- Choose the appropriate learning interval and establish the learning observer in the form of (5) according to the above gain matrices and parameters.
4. Learning Output–Feedback Fault-Tolerant Tracking Control for Spacecraft Formation Configuration Maintenance
4.1. Design of the Learning Output–Feedback Fault-Tolerant Controller
4.2. Stability Analysis of the Learning Output–Feedback Fault-Tolerant Controller
- (1)
- Select appropriate positive scalars , , and , then compute parameters and .
- (2)
- Select appropriate matrix , then matrices and can be obtained readily by solving (34) and (35).
- (3)
- Choose small positive scalars and , then compute and through solving (36) and (37).
- (4)
- Choose the appropriate learning interval and design the controller in the form of (30) according to the above gain matrices and parameters.
5. Simulation Studies
- The abrupt constant fault in the x-axis thruster:
- Fault-free condition in the y-axis thruster:
- The time-varying fault in the z-axis thruster:
5.1. ILO-Based Thruster Fault Reconstruction
5.2. LOF2TC-Based Formation Configuration Maintenance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Wu, B.; Chung, E.K.P. Satellite Formation Flying; Springer: Singapore, 2017. [Google Scholar]
- Mathavaraj, S.; Padhi, R. Satellite Formation Flying; Springer: New Delhi, India, 2021. [Google Scholar]
- Alfriend, K.T.; Vadali, S.R.; Gurfil, P.; How, J.P.; Breger, L.S. Spacecraft Formation Flying: Dynamics, Control and Navigation; Elsevier Science & Technology: London, UK, 2009. [Google Scholar]
- Scharf, D.P.; Hadaegh, F.Y.; Ploen, S.R. A survey of spacecraft formation flying guidance and control. Part II: Control. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 4, pp. 2976–2985. [Google Scholar]
- Liu, Q.P.; Zhang, S.J. A survey on formation control of small satellites. Proc. IEEE 2018, 106, 440–457. [Google Scholar] [CrossRef]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-based fault diagnosis for aerospace systems: A survey. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1329–1360. [Google Scholar] [CrossRef] [Green Version]
- Yin, S.; Xiao, B.; Ding, S.X.; Zhou, D.H. A review on recent development of spacecraft attitude fault tolerant control system. IEEE Trans. Ind. Electron. 2016, 63, 3311–3320. [Google Scholar] [CrossRef]
- Barua, A.; Khorasani, K. Hierarchical fault diagnosis and fuzzy rule-based reasoning for satellites formation flight. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2435–2456. [Google Scholar] [CrossRef]
- Lian, X.B.; Liu, J.F.; Yuan, L.H.; Cui, N.G. Mixed fault diagnosis scheme for satellite formation. Aircr. Eng. Aerosp. Technol. 2018, 90, 427–434. [Google Scholar] [CrossRef]
- Nemati, F.; Hamami, S.M.S.; Zemouche, A. A nonlinear observer-based approach to fault detection, isolation and estimation for satellite formation flight application. Automatica 2019, 107, 474–482. [Google Scholar] [CrossRef]
- Azizi, S.M.; Khorasani, K. Cooperative state and fault estimation of formation flight of satellites in deep space subject to unreliable information. IFAC Pap. 2019, 52, 206–213. [Google Scholar] [CrossRef]
- Godard, G.; Kumar, K.D. Fault tolerant reconfigurable satellite formations using adaptive variable structure techniques. J. Guid. Control Dyn. 2010, 33, 969–984. [Google Scholar] [CrossRef]
- Cao, L.; Chen, X.Q.; Misra, A.K. Minimum sliding mode error feedback control for fault tolerant reconfigurable satellite formations with J2 perturbations. Acta Astronaut. 2014, 96, 201–216. [Google Scholar] [CrossRef]
- Lee, D.; Kumar, K.D.; Sinha, M. Fault detection and recovery of spacecraft formation flying using nonlinear observer and reconfigurable controller. Acta Astronaut. 2014, 97, 58–72. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Yang, H.; Jiang, B. Decentralised fault-tolerant control of tethered spacecraft formation: An interconnected system approach. IET Control Theory Appl. 2017, 11, 3047–3055. [Google Scholar] [CrossRef]
- Li, P.; Liu, Z.; He, C.; Liu, Q.; Liu, X. Distributed adaptive fault-tolerant control for spacecraft formation with communication delays. IEEE Access 2020, 8, 118653–118663. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, H.; Stojanovic, V.; He, S.; Shi, K.; Luan, X.; Liu, F.; Sun, C. Synchronous fault detection observer for 2-d markov jump systems. IEEE Trans. Cybern. 2021, 1–12. [Google Scholar] [CrossRef]
- Tao, H.F.; LI, X.H.; Paszke, W.; Stojanovic, V.; Yang, H.Z. Robust PD-type iterative learning control for discrete systems with multiple time-delays subjected to polytopic uncertainty and restricted frequency-domain. Multidimens. Syst. Signal Processing 2021, 32, 671–692. [Google Scholar] [CrossRef]
- Jia, Q.X.; Chen, W.; Zhang, Y.C.; Li, H.Y. Fault reconstruction and fault-tolerant control via learning observers in takagi–sugeno fuzzy descriptor systems with time delays. IEEE Trans. Ind. Electron. 2015, 62, 3885–3895. [Google Scholar] [CrossRef]
- Hu, Q.L.; Niu, G.L.; Wang, C.L. Spacecraft attitude fault-tolerant control based on iterative learning observer and control allocation. Aerosp. Sci. Technol. 2018, 75, 245–253. [Google Scholar] [CrossRef]
- Zhang, C.X.; Wang, J.H.; Zhang, D.X.; Shao, X.W. Learning observer based and event-triggered control to spacecraft against actuator faults. Aerosp. Sci. Technol. 2018, 78, 522–530. [Google Scholar] [CrossRef]
- Jia, Q.X.; Li, H.Y.; Chen, X.Q.; Zhang, Y.C. Observer-based reaction wheel fault reconstruction for spacecraft attitude control systems. Aircr. Eng. Aerosp. Technol. 2019, 91, 1268–1277. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.L.; Ma, G.F.; Yang, Y.S. Fault-tolerant attitude stabilization incorporating closed-loop control allocation under actuator failure. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1989–2000. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Chen, J.L.; Zhu, Z.H. Adaptive learning observer for spacecraft attitude control with actuator fault. Aerosp. Sci. Technol. 2021, 108, 106389. [Google Scholar] [CrossRef]
- Jia, Q.X.; Chen, W.; Zhang, Y.C.; Li, H.Y. Fault reconstruction for continuous-time systems via learning observers. Asian J. Control 2016, 18, 549–561. [Google Scholar] [CrossRef]
- Yang, X.B.; Cao, X.B. A new approach to autonomous rendezvous for spacecraft with limited impulsive thrust: Based on switching control strategy. Aerosp. Sci. Technol. 2015, 43, 454–462. [Google Scholar] [CrossRef]
- Peng, Z.H.; Wang, D.; Zhang, H.W. Cooperative tracking and estimation of linear multi-agent systems with a dynamic leader via iterative learning. Int. J. Control 2014, 87, 1163–1171. [Google Scholar] [CrossRef]
- Liu, M.; Shi, P. Sensor fault estimation and tolerant control for Itô stochastic systems with a descriptor sliding mode approach. Automatica 2013, 49, 1242–1250. [Google Scholar] [CrossRef]
- Garcia, G.; Bernussou, J. Pole assignment for uncertain systems in a specified disk by state feedback. IEEE Trans. Autom. Control 1995, 40, 184–190. [Google Scholar] [CrossRef]
- Yang, X.B.; Gao, H.J. Robust reliable control for autonomous spacecraft rendezvous with limited-thrust. Aerosp. Sci. Technol. 2013, 24, 161–168. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, Y.; Jia, Q.; Li, H.; Cheng, Y. Reconfigurable Fault-Tolerant Control for Spacecraft Formation Flying Based on Iterative Learning Algorithms. Appl. Sci. 2022, 12, 2485. https://doi.org/10.3390/app12052485
Gui Y, Jia Q, Li H, Cheng Y. Reconfigurable Fault-Tolerant Control for Spacecraft Formation Flying Based on Iterative Learning Algorithms. Applied Sciences. 2022; 12(5):2485. https://doi.org/10.3390/app12052485
Chicago/Turabian StyleGui, Yule, Qingxian Jia, Huayi Li, and Yuehua Cheng. 2022. "Reconfigurable Fault-Tolerant Control for Spacecraft Formation Flying Based on Iterative Learning Algorithms" Applied Sciences 12, no. 5: 2485. https://doi.org/10.3390/app12052485
APA StyleGui, Y., Jia, Q., Li, H., & Cheng, Y. (2022). Reconfigurable Fault-Tolerant Control for Spacecraft Formation Flying Based on Iterative Learning Algorithms. Applied Sciences, 12(5), 2485. https://doi.org/10.3390/app12052485





