Using Energy Storage-Based Grid Forming Inverters for Operational Reserve in Hybrid Diesel Microgrids
Abstract
:1. Introduction
2. Simulation Modeling
2.1. Microgrid Model
2.2. Diesel Generator Model
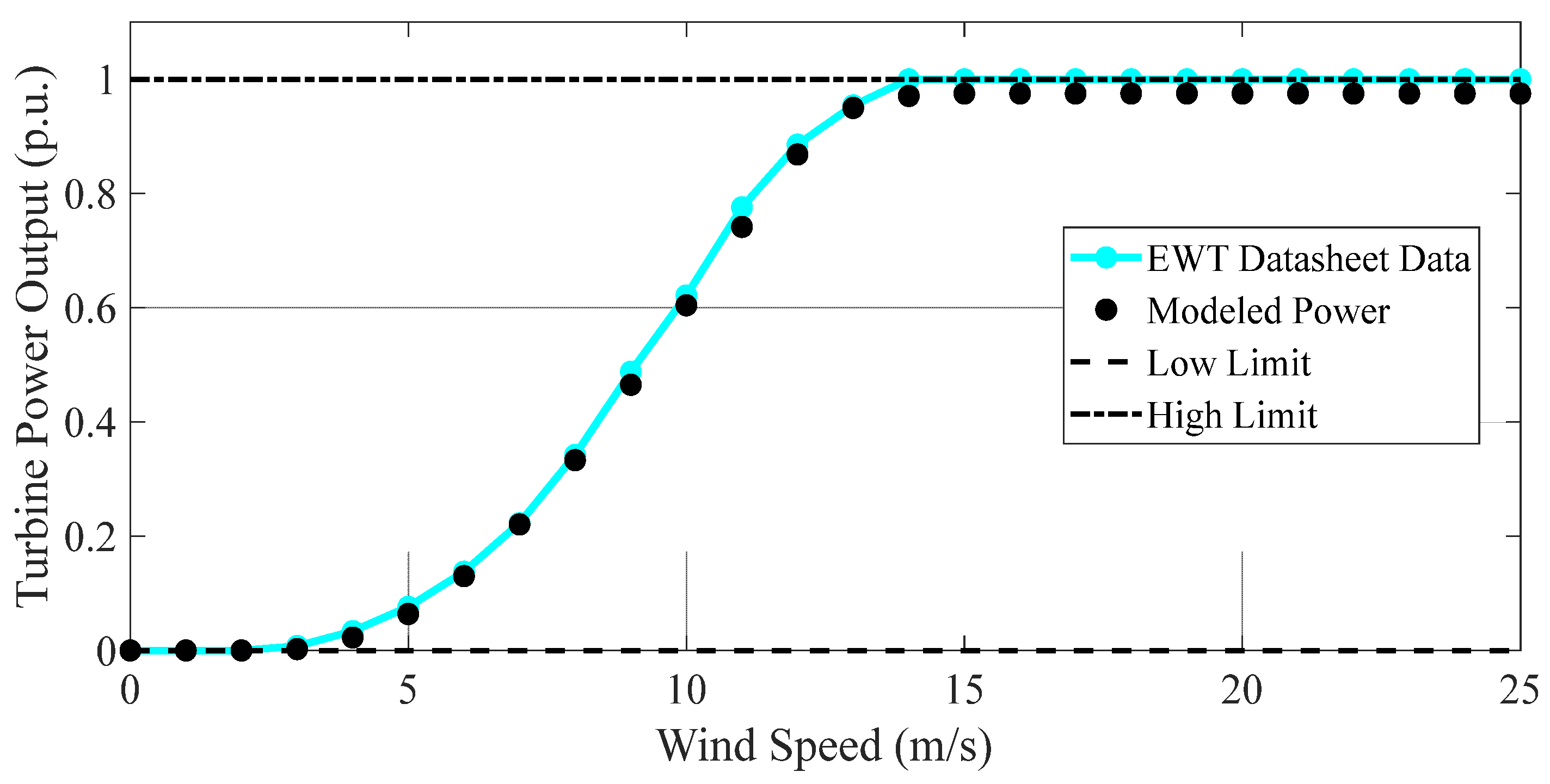
2.3. Wind Turbine Model
2.4. Grid-Forming Inverter Model
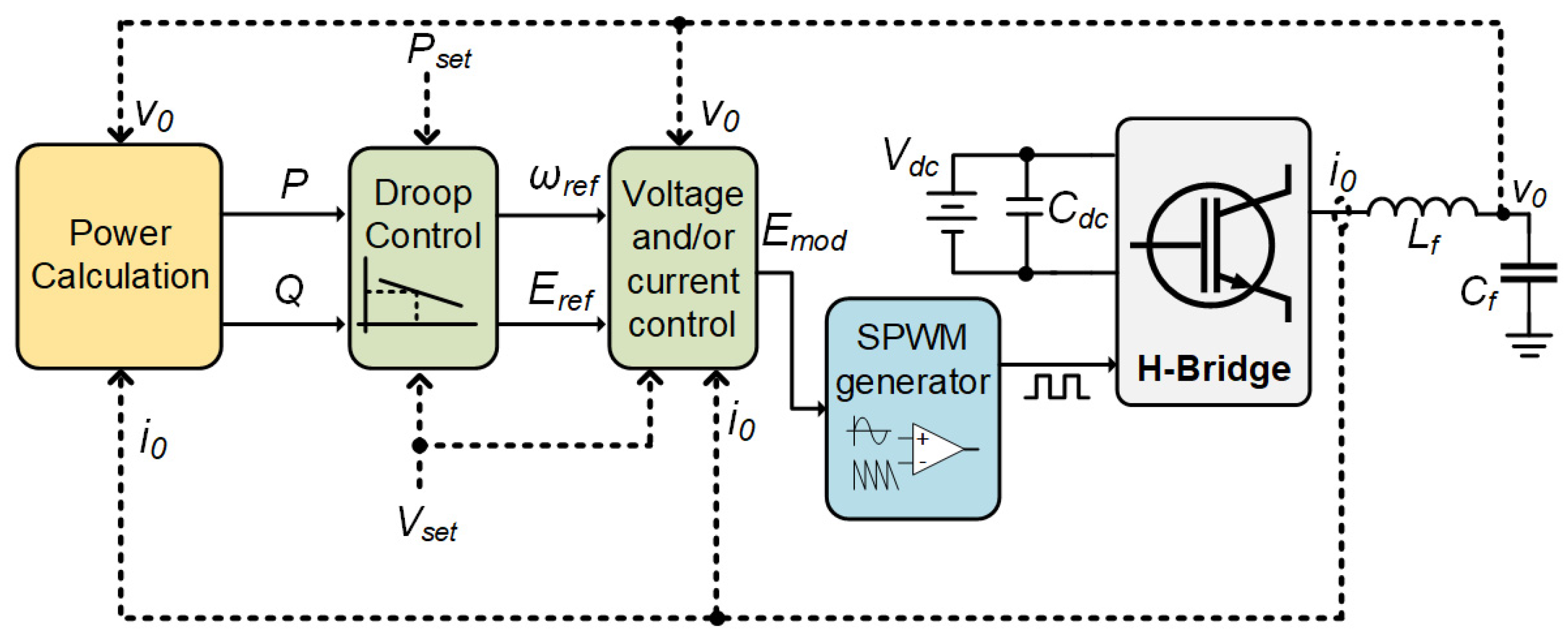
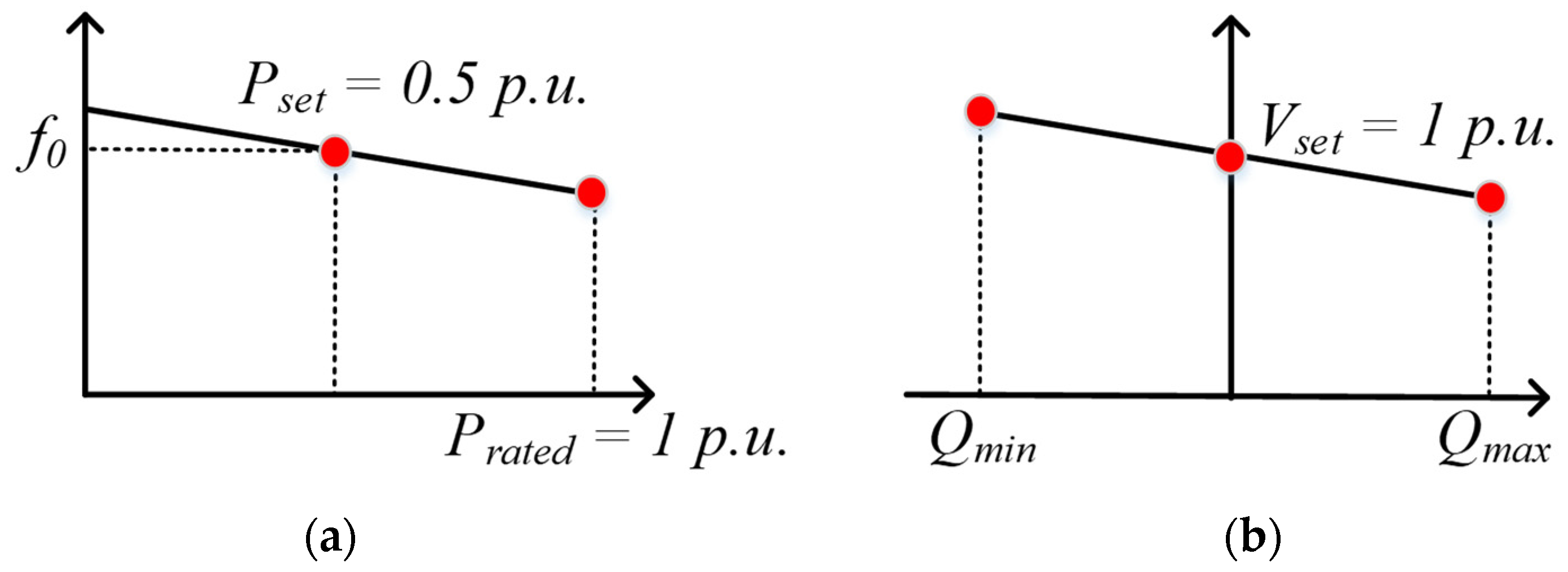
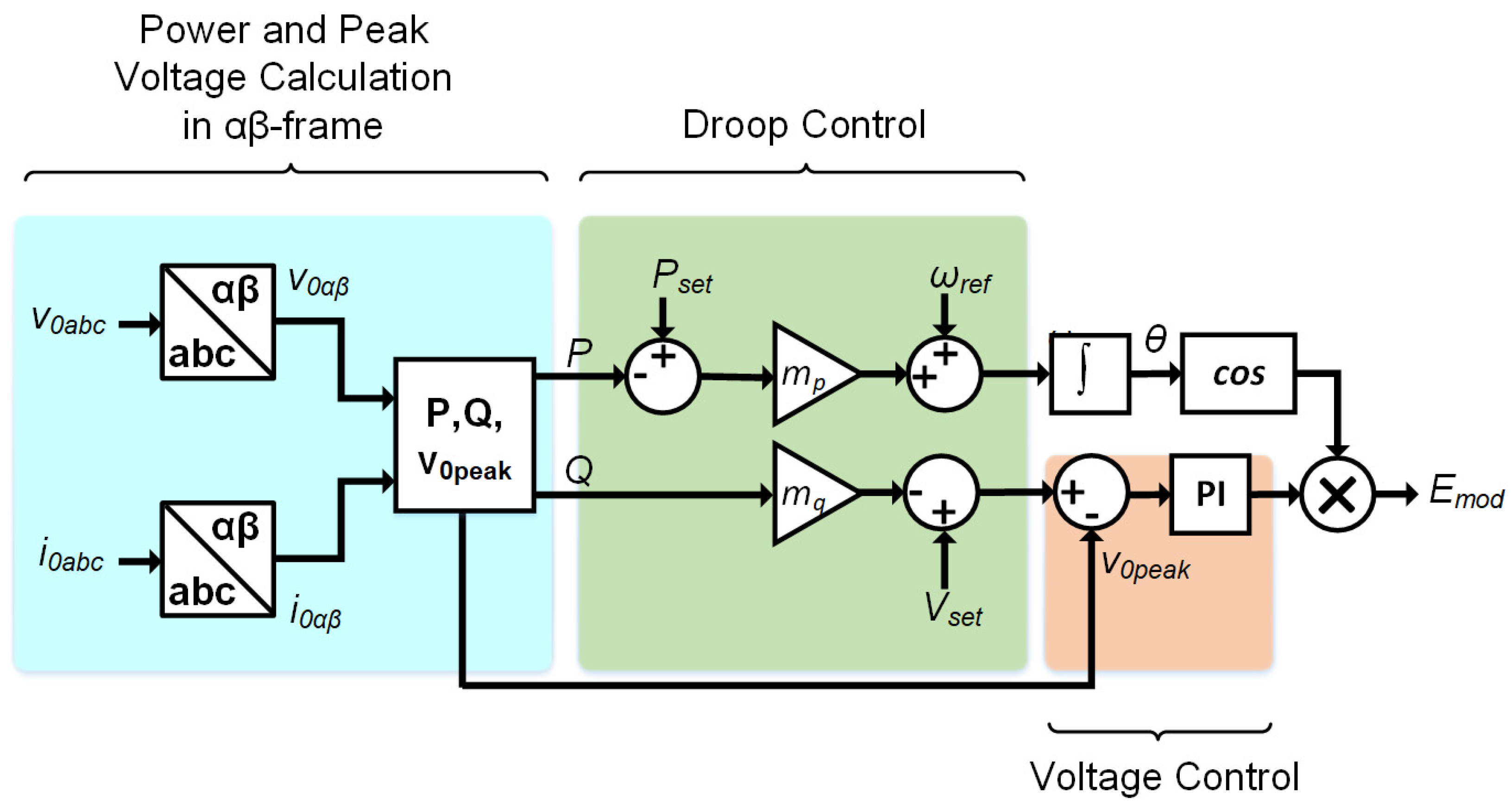
2.4.1. CERTS-Based Grid Forming Inverter Droop Control
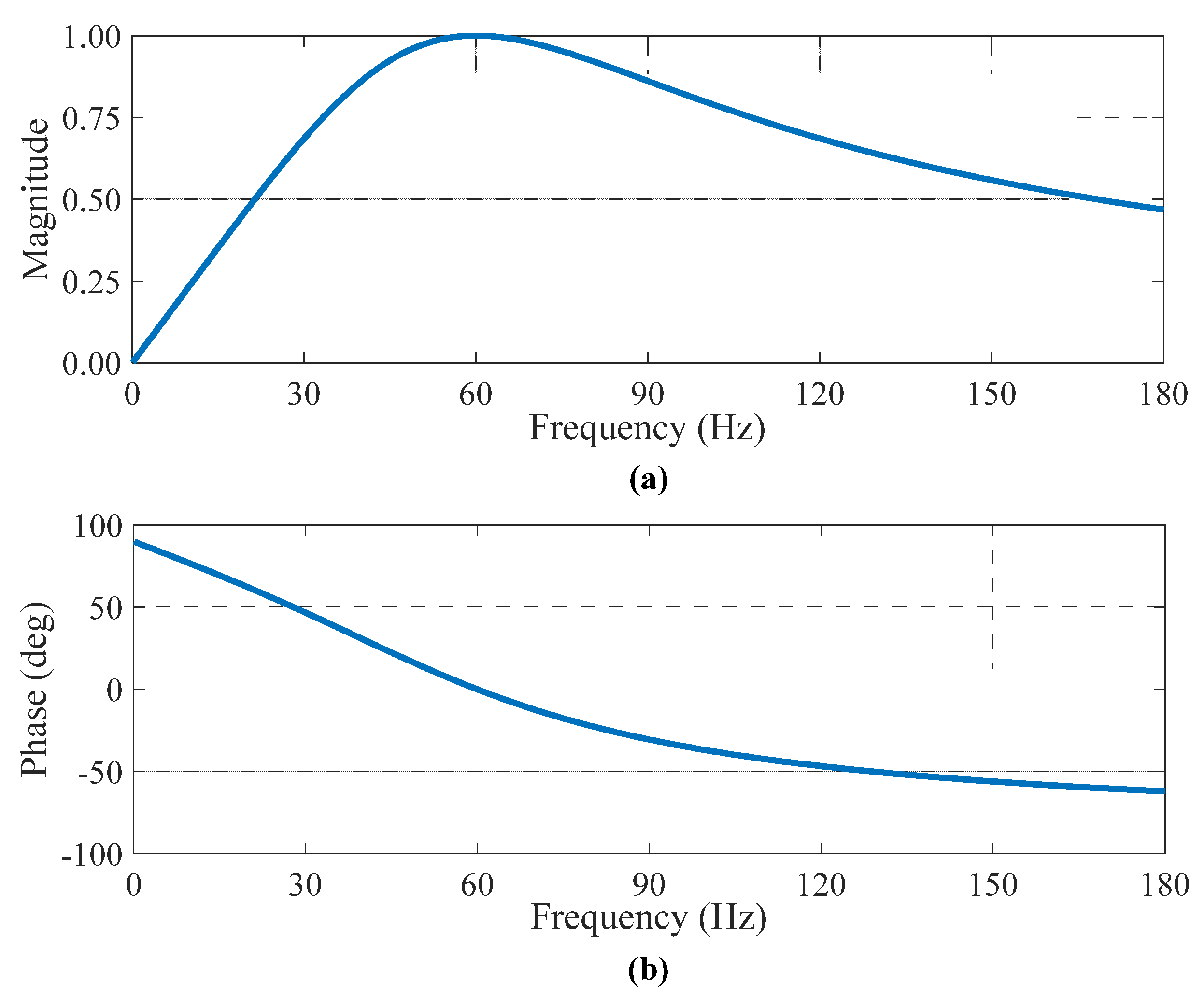
2.4.2. DQ-Based Grid-Forming Inverter Model
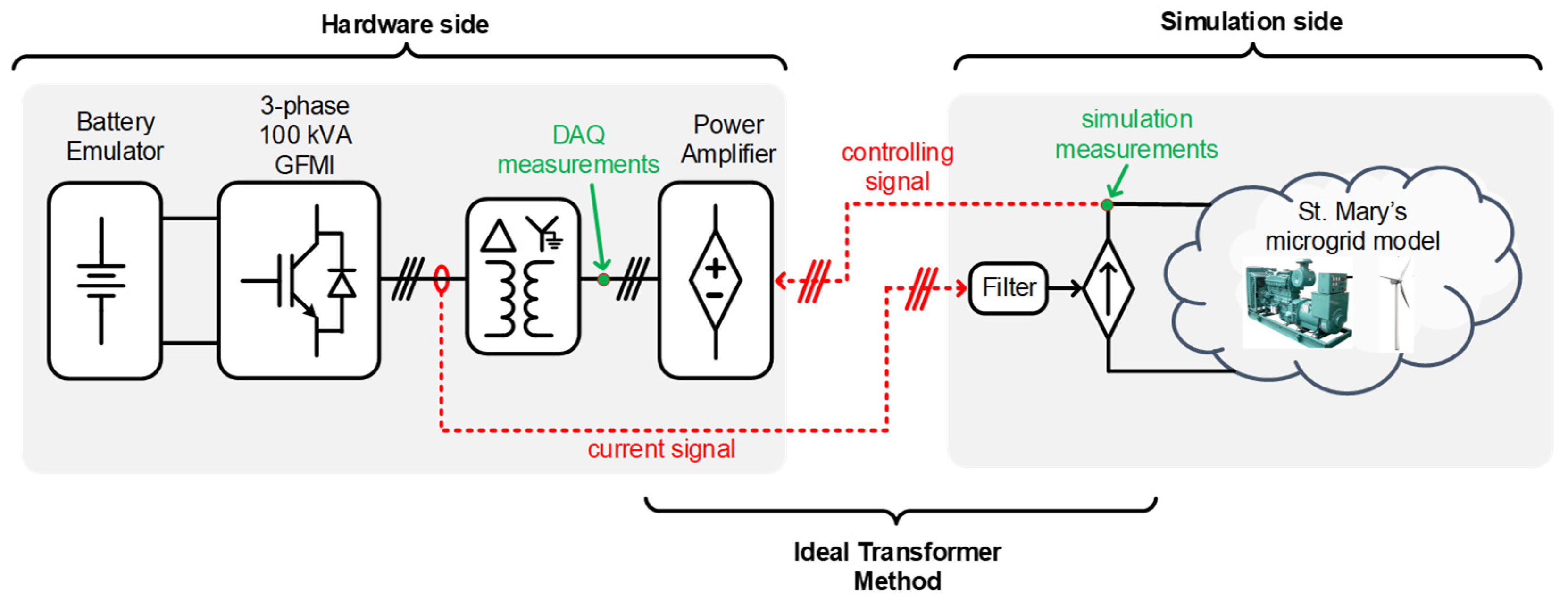
3. Power Hardware-in-the-Loop Setup
- (1)
- The Virtual Generator Mode (VGM), in which the GFMI interacts with the grid emulating a synchronous generator by presenting a low impedance voltage source to the grid. While on VGM, the GFMI can be operated in either: PQ power flow control, where the converter operates with set-points for active and reactive power; or Vf control, where the converter operates with fixed voltage and frequency set-points allowing islanding. Either of these two control modes can be selected while the GFMI is running.
- (2)
- The Current Source Inverter Mode (CSI), in which the GFMI presents a high-impedance current source to the grid and allowing only PQ control mode. Since no inertia is emulated, this operation mode is suitable for grid-tied support functions where sub-cycle response to power commands is required. It is important to point out that changing between VGM and CSI modes is not allowed while the GFMI is running.
4. Results and Discussion
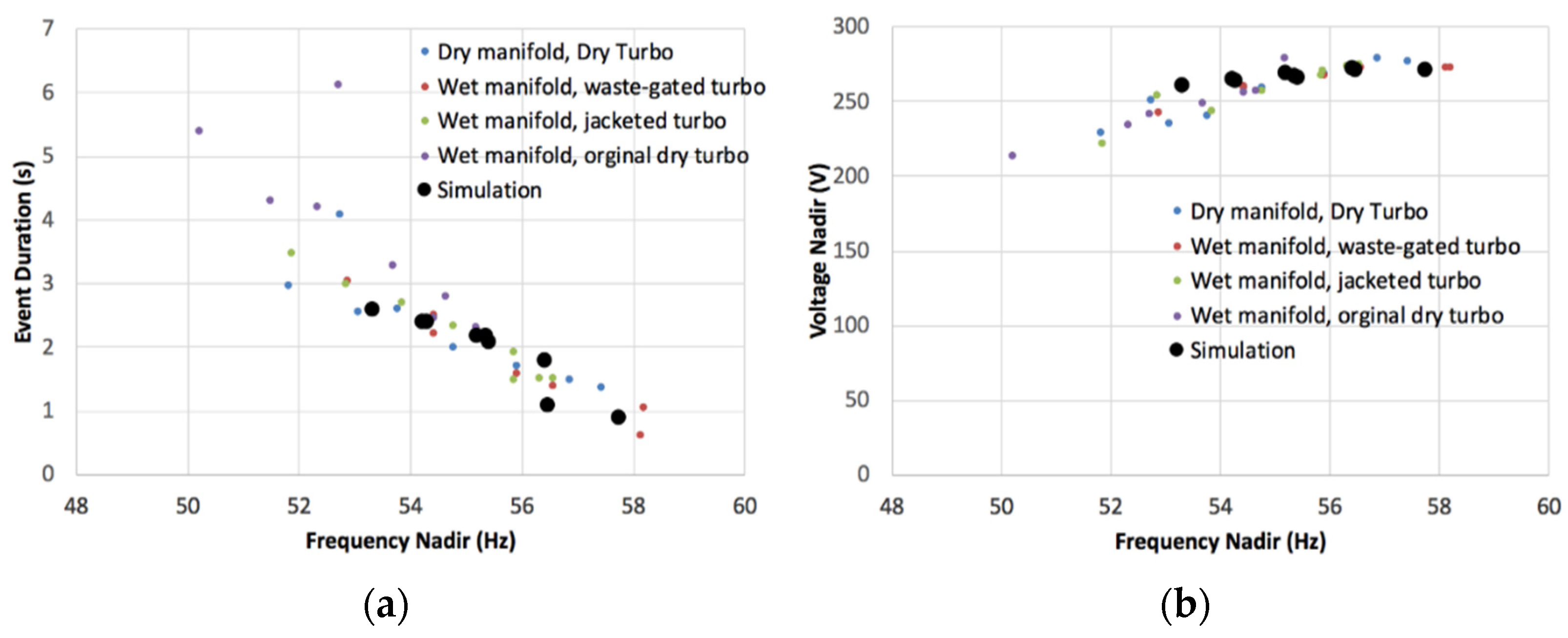
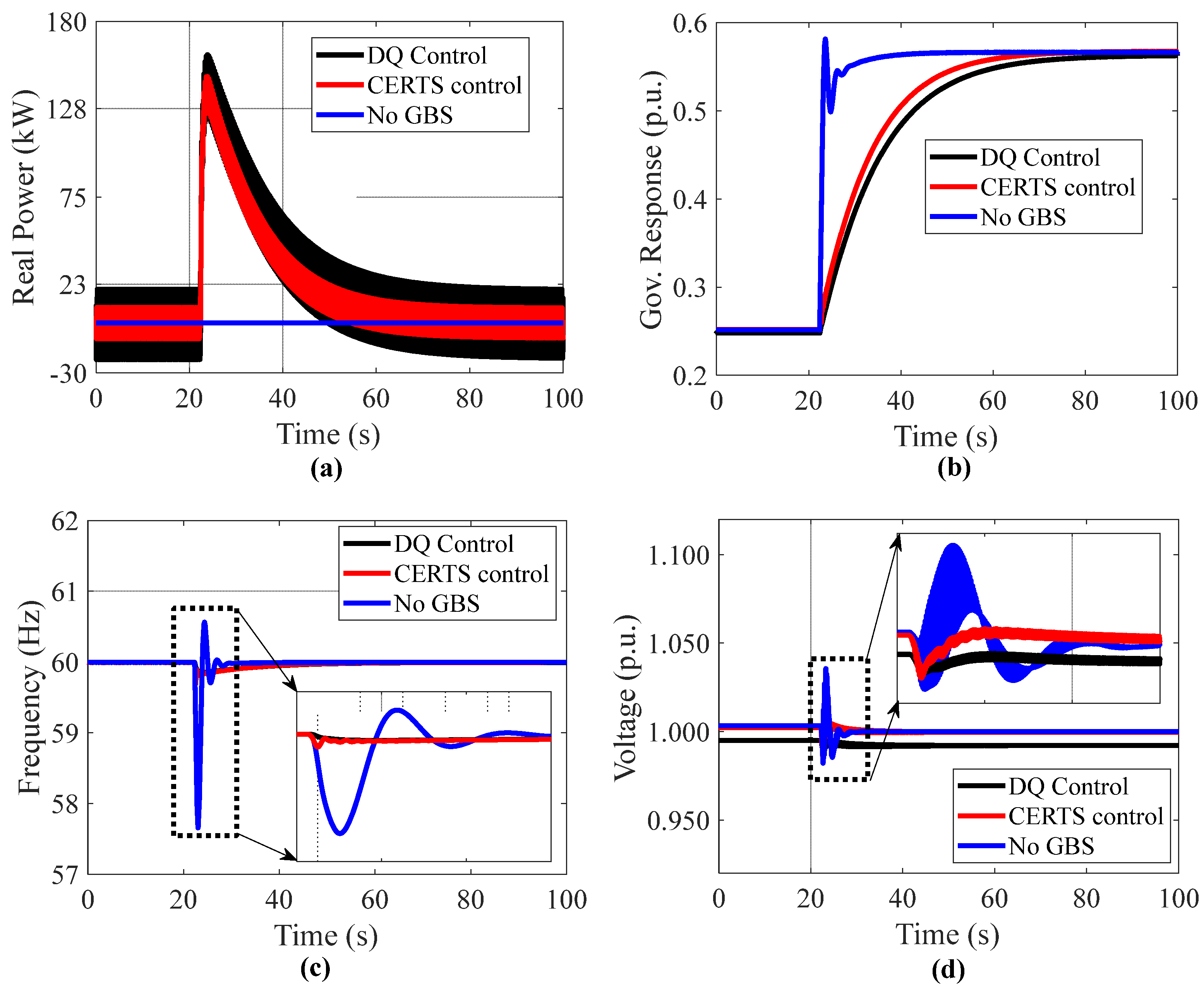
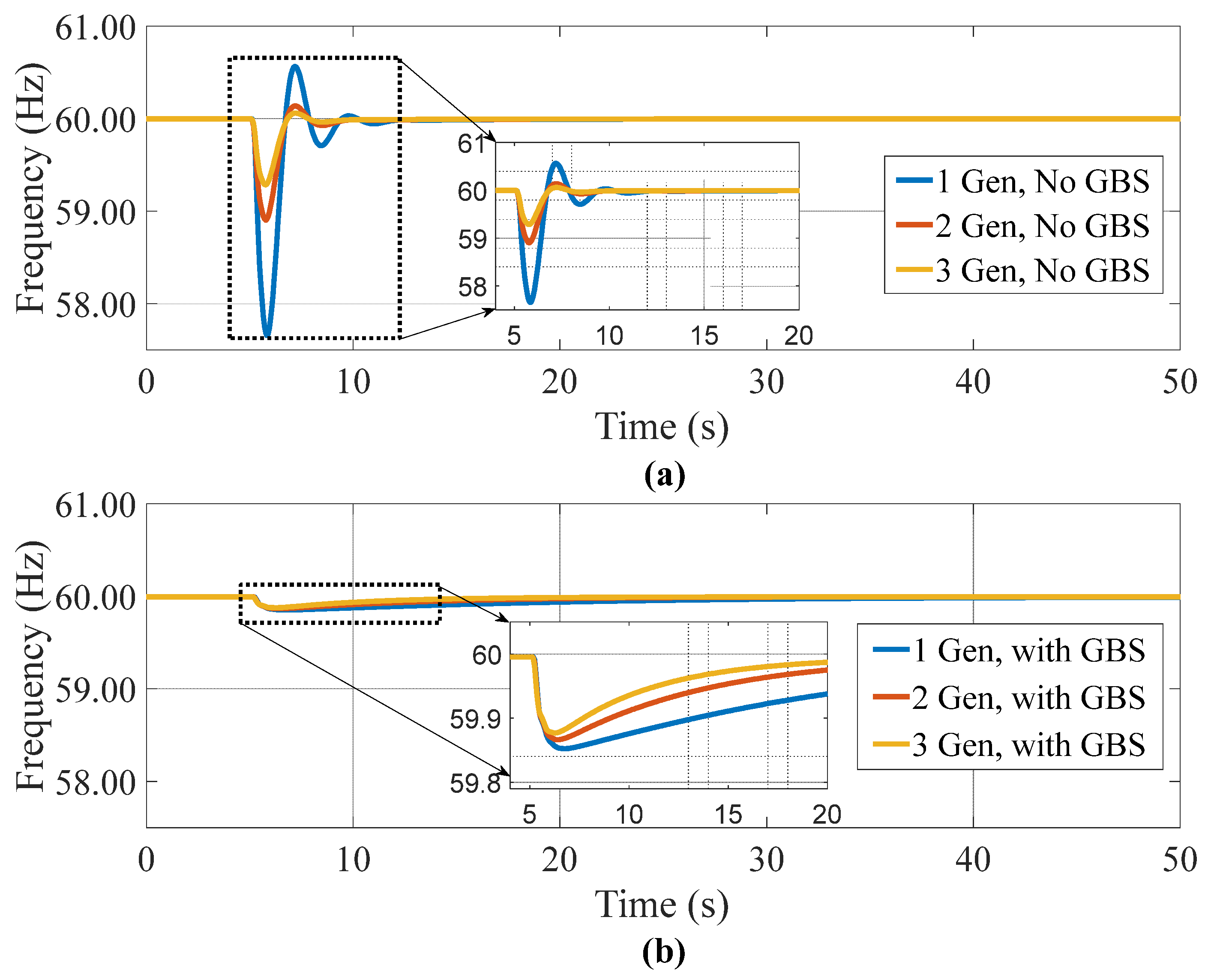
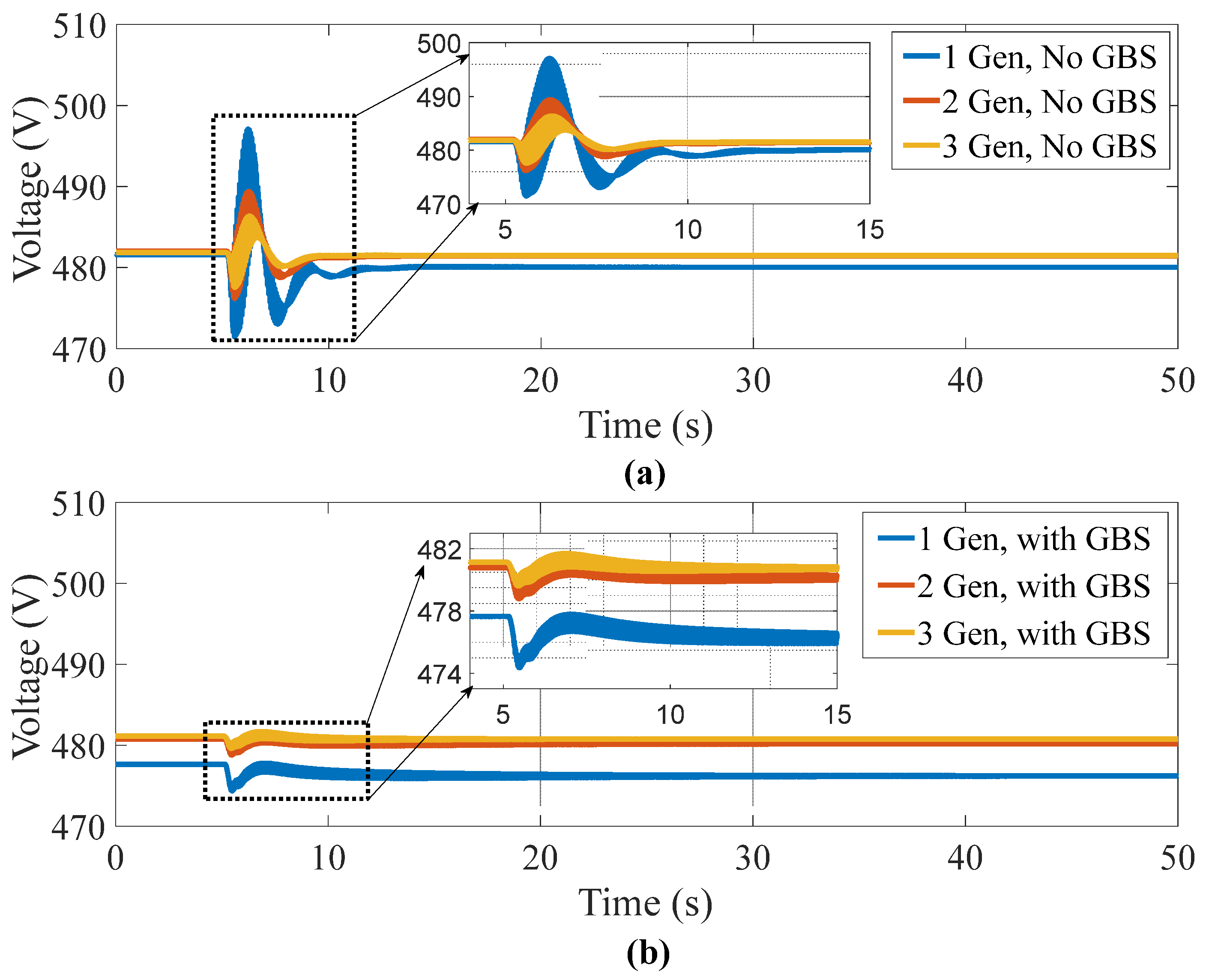
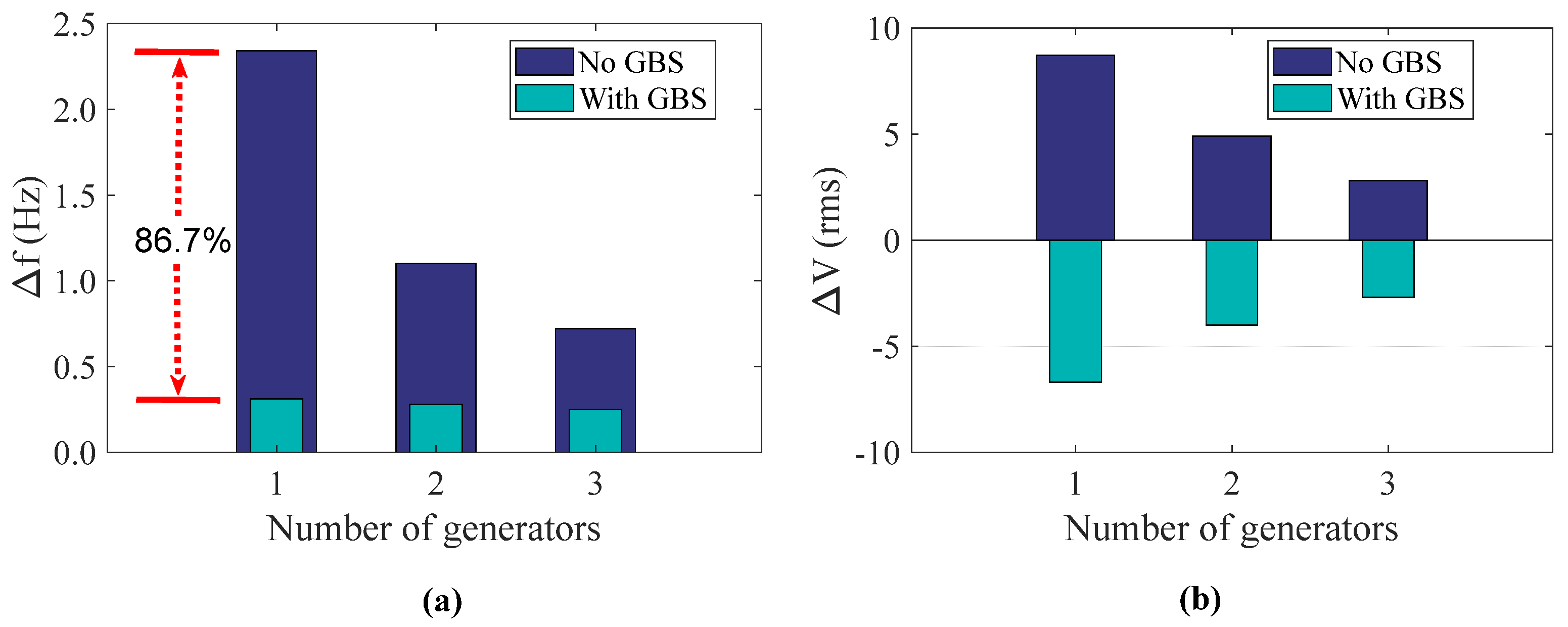
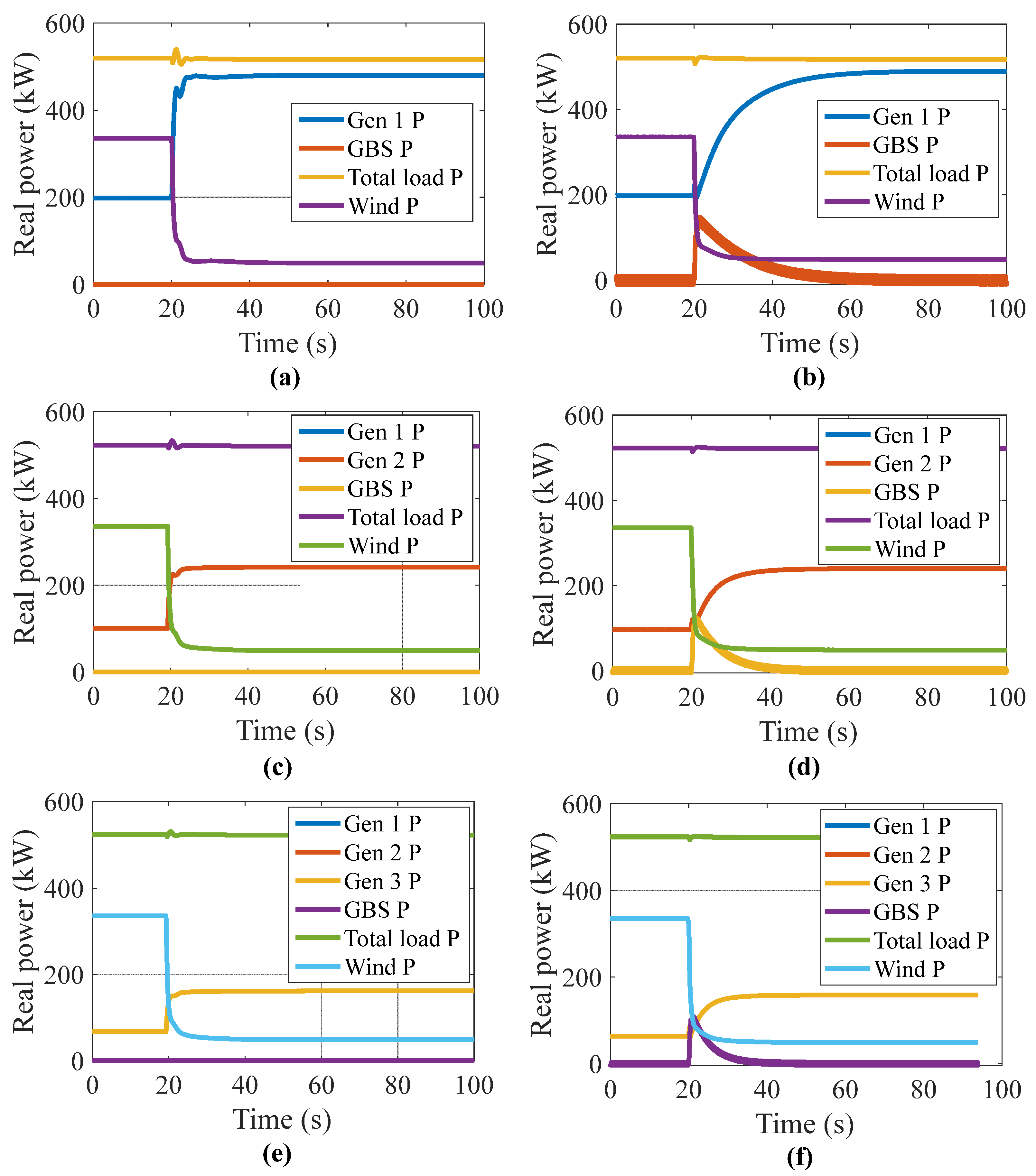
4.1. Simulation Results of Each Grid-Forming Inverter Control Scheme
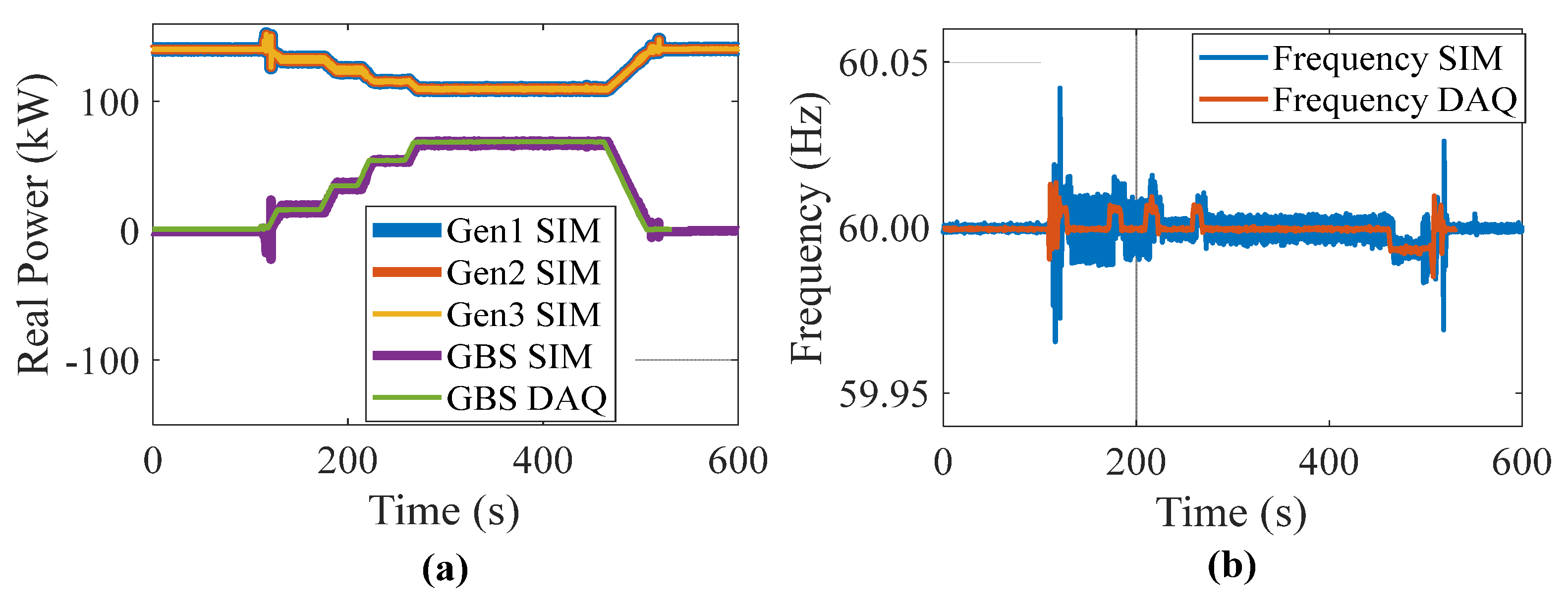
4.2. Power Hardware-in-the-Loop Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holdmann, G.P.; Wies, R.W.; Vandermeer, J.B. Renewable Energy Integration in Alaska’s Remote Islanded Microgrids: Economic Drivers, Technical Strategies, Technological Niche Development, and Policy Implications. Proc. IEEE 2019, 107, 1820–1837. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of Grid-Forming and Grid-Following Inverters for Dynamic Simulation of Large-Scale Distribution Systems. IEEE Trans. Power Deliv. 2021, 36, 2035–2045. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Piagi, P. Microgrid: A Conceptual Solution. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004. [Google Scholar]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Milano, F.; Dorfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the 20th Power Systems Computation Conference, PSCC 2018, Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Hernandez-Alvidrez, J.; Gurule, N.S.; Darbali-Zamora, R.; Reno, M.J.; Flicker, J.D. Modeling a Grid-Forming Inverter Dynamics under Ground Fault Scenarios Using Experimental Data from Commercially Available Equipment. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1517–1523. [Google Scholar]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Nexans. Bare Overhead Conductors: AAC, ACSR, ACSR II. 2003. Available online: http://www.docdatabase.net/more-bare-overhead-conductors-nexans-usa-1275046.html (accessed on 7 September 2020).
- Sybille, G.; Brunelle, P.; Giroux, P.; Casoria, S.; Gagnon, R.; Kamwa, I.; Roussel, R.; Chamagne, R.; Dessaint, L.; Lehuy, H. SimPowerSystems for Use with Simulink; Mathworks: Natick, MA, USA, 2003. [Google Scholar]
- Sybille, G.; Zabaiou, T. Emergency Diesel-Generator and Asynchronous Motor. 2018. Available online: https://www.mathworks.com/help/physmod/sps/examples/emergency-diesel-generator-and-asynchronous-motor.html (accessed on 1 February 2022).
- Yeager, K.; Willis, J.R. Modeling of emergency diesel generators in an 800 megawatt nuclear power plant. IEEE Trans. Energy Convers. 1993, 8, 433–441. [Google Scholar] [CrossRef]
- Zabaiou, T.; Dessaint, L.A.; Brunelle, P. Development of a new library of IEEE excitation systems and its validation with PSS/E. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Woodward Inc. EGCP-2 Genset Controller. Available online: http://www.woodward.com/egcp2.aspx (accessed on 1 February 2022).
- Gagnon, R.; Brochu, J. Wind Farm—Synchronous Generator and Full Scale Converter (Type 4) Detailed Model. 2016. Available online: https://www.mathworks.com/help/physmod/sps/examples/wind-farm-synchronous-generator-and-full-scale-converter-type-4-detailed-model.html (accessed on 1 February 2022).
- Hernandez-Alvidrez, J.; Summers, A.; Reno, M.J.; Flicker, J.; Pragallapati, N. Simulation of Grid-Forming Inverters Dynamic Models using a Power Hardware in the Loop Testbed. In Proceedings of the 46th IEEE Photovoltaic Specialists Conference, Chicago, IL, USA, 16–24 June 2019. [Google Scholar]
- Kundur, P. Power System Stability and Control; Tata McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Bevrani, H.; François, B.; Ise, T. Microgrid Dynamics and Control; Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Bidram, A.; Nasirian, V.; Davoudi, A.; Lewis, F.L. Cooperative Synchronization in Distributed Microgrid Control, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Vinayagam, A.; Swarna, K.S.V.; Khoo, S.Y.; Oo, A.T.; Stojcevski, A. PV Based Microgrid with Grid-Support Grid-Forming Inverter Control-(Simulation and Analysis). Smart Grid Renew. Energy 2017, 8, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Du, W.; Schneider, K.P.; Tuffner, F.K.; Chen, Z.; Lasseter, R.H. Modeling of Grid-Forming Inverters for Transient Stability Simulations of an all Inverter-based Distribution System. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 18–21 February 2019; pp. 1–5. [Google Scholar]
- Yao, W.; Chen, M.; Matas, J.; Guerrero, J.M.; Qian, Z.M. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing. IEEE Trans. Ind. Electron. 2011, 58, 576–588. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; IEEE Press: Piscataway, NJ, USA; John Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Du, W.; Lasseter, R.H.; Khalsa, A.S. Survivability of autonomous microgrid during overload events. IEEE Trans. Smart Grid 2019, 10, 3515–3524. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Summers, A.; Hernandez-Alvidrez, J.; Darbali-Zamora, R.; Reno, M.J.; Johnson, J.; Gurule, N.S. Comparison of Ideal Transformer Method and Damping Impedance Method for PV Power-Hardware-In-The-Loop Experiments. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Chicago, IL, USA, 19–21 June 2019; pp. 2989–2996. [Google Scholar]
- Hernandez-Alvidrez, J.; Gurule, N.S.; Reno, M.J.; Flicker, J.D.; Summers, A.; Ellis, A. Method to Interface Grid-Forming Inverters into Power Hardware in the Loop Setups. In Proceedings of the 47th IEEE Photovoltaic Specialists Conference, Calgary, AB, Canada, 15 June–21 August 2020. [Google Scholar]
- ABB. PCS100 ESS Grid Connect Interface for Energy Storage Systems User Manual, 1st ed.; Available online: https://cdn2.hubspot.net/hubfs/1828458/Website%20downloads/Brochures/Battery/Product%20Brochure%20-%20ABB%20PCS%20-%20Spirit%20Energy%20.pdf (accessed on 1 February 2022).
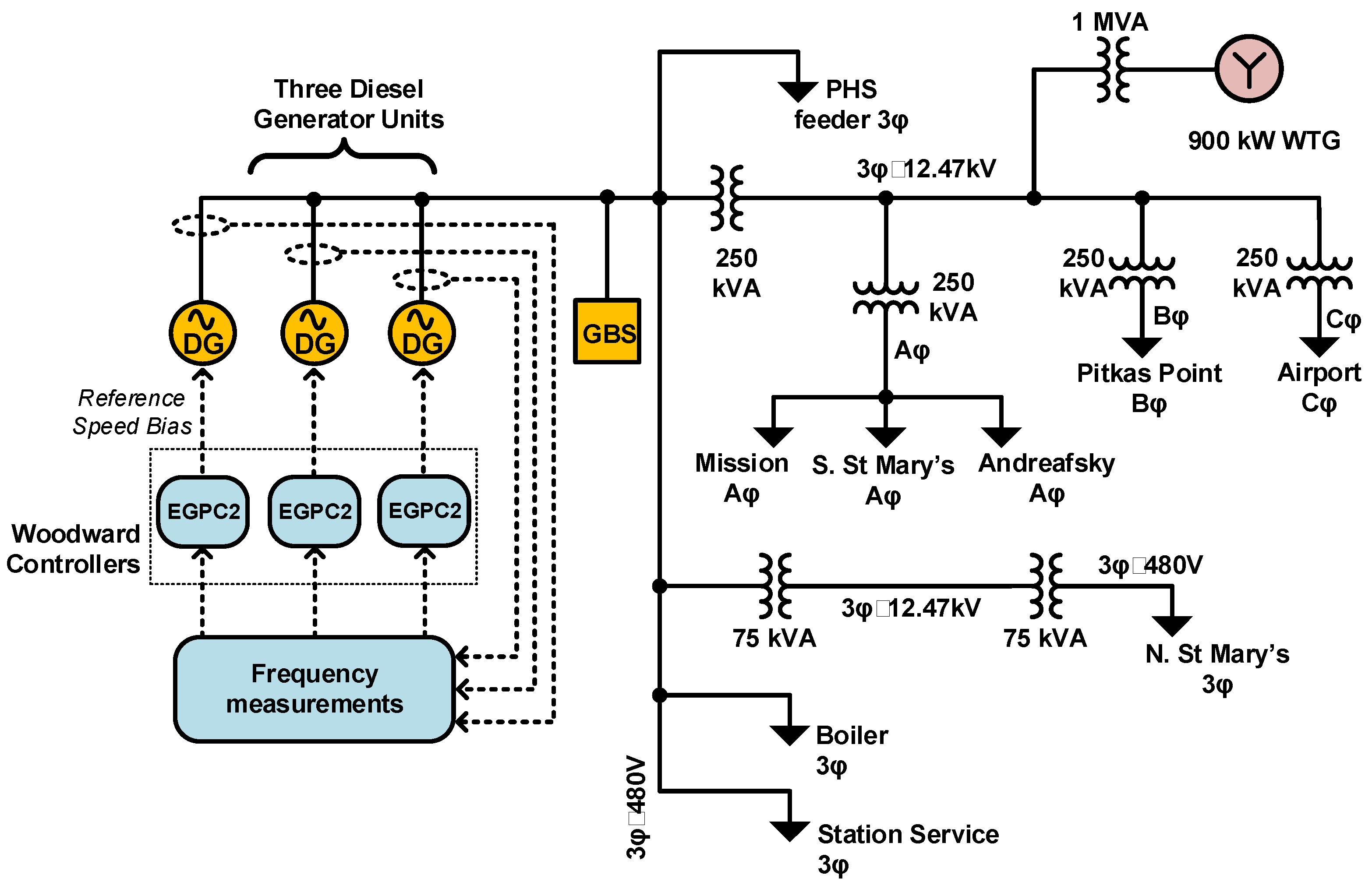




| Load ID | Type of Load | Value of Load (kW) |
|---|---|---|
| Station Service | 3 φ | 6 |
| Public Health Service | 3 φ | 19 |
| N. St. Mary’s | 3 φ | 207 |
| Boiler | 3 φ | 100 |
| Mission | A φ | 5 |
| S. St Mary’s | A φ | 15 |
| Andreafsky | A φ | 72 |
| Pitkas Point | B φ | 36 |
| Airport | C φ | 60 |
| Total | – | 520 |
| Line Segment | Distance (km) |
|---|---|
| North St. Mary’s to Power House | 0.10 |
| Public Health Service to Power House | 0.25 |
| Mission Load to Power House | 1.00 |
| South St. Mary’s Load to to Power House | 1.30 |
| Andreafsky Load to Power House | 1.70 |
| Wind Turbine Interconnect to Power House | 5.00 |
| Wind Turbine Interconnect Turbine | 0.60 |
| Pitkas Load to Wind Turbine Interconnect | 3.20 |
| Airport Load Wind Turbine Interconnect | 3.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez-Alvidrez, J.; Darbali-Zamora, R.; Flicker, J.D.; Shirazi, M.; VanderMeer, J.; Thomson, W. Using Energy Storage-Based Grid Forming Inverters for Operational Reserve in Hybrid Diesel Microgrids. Energies 2022, 15, 2456. https://doi.org/10.3390/en15072456
Hernandez-Alvidrez J, Darbali-Zamora R, Flicker JD, Shirazi M, VanderMeer J, Thomson W. Using Energy Storage-Based Grid Forming Inverters for Operational Reserve in Hybrid Diesel Microgrids. Energies. 2022; 15(7):2456. https://doi.org/10.3390/en15072456
Chicago/Turabian StyleHernandez-Alvidrez, Javier, Rachid Darbali-Zamora, Jack D. Flicker, Mariko Shirazi, Jeremy VanderMeer, and William Thomson. 2022. "Using Energy Storage-Based Grid Forming Inverters for Operational Reserve in Hybrid Diesel Microgrids" Energies 15, no. 7: 2456. https://doi.org/10.3390/en15072456






