Green Total-Factor Energy Efficiency of Construction Industry and Its Driving Factors: Spatial-Temporal Heterogeneity of Yangtze River Economic Belt in China
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Study Area
3.2. Methods
3.2.1. The Super-EBM Model Based on Undesirable Output
3.2.2. Moran Index
3.3. Construction of the Indicator System
- (1)
- Energy input: The measurement of energy efficiency is the main objective of this paper. Energy input is the core input element of the whole index system. There are abundant types of energy consumption and a diversity of energy structures in the construction industry of each province. Energy consumption in the construction industry is mainly composed of 12 kinds of energy, such as coal, oil, natural gas, electric power, etc. If all kinds of energy were incorporated into the index system directly, it would not only be cumbersome but also the statistical caliber would be inconsistent. To unify and facilitate calculation, the total amount of the twelve types of energy consumption in the regional energy balance table is converted into standard coal according to the energy conversion coefficient of “10,000 t of standard coal,” and takes the calculated total energy consumption as an energy input.
- (2)
- Labor input: The labor force is the main body of energy utilization in the construction industry. Only when energy is combined with labor force elements, can it really play its role. Generally speaking, labor hours are the best indicator to measure labor input, but considering that data on labor hours cannot be obtained directly, this paper selects “the number of employees in the construction industry” as the indicator to measure labor input.
- (3)
- Capital input: According to the production function in economics, capital is the basic factor of production. When measuring the capital input, the perpetual inventory method (PIM) [30] is often used to estimate the capital stock in research. However, in view of the depreciation rate of fixed assets in the construction industry is not available, it is not feasible to directly estimate the capital stock of the construction industry as a capital input. Therefore, this paper directly adopts “investment in fixed assets of the construction industry” to measure capital input of the construction industry and uses the deflator method to convert it into actual investment in fixed assets of the construction industry, with 2003 as the base period.
- (4)
- Economic output: The gross output of the construction industry, that is, the total value created by construction enterprises, can best reflect the total output level of the construction industry. On this account, this paper selects “total output of the construction industry” as the economic output. Similarly, to eliminate the influence of price factors, the current total output of the construction industry is transformed into the actual total output of construction in the region using GDP deflators with 2003 as the base period.
- (5)
- Carbon dioxide emissions: At present, the development of the construction industry depends on the support of fossil fuel, but the utilization of fossil fuel will inevitably emit a large amount of direct and indirect emissions. Among them, carbon dioxide, as a typical representative of environmental pollutants, is the main control and emission reduction object in the energy utilization of the construction industry advocated by most scholars. It should be noted that because the relevant statistical yearbook has not yet given the direct data of carbon emissions from the construction industry, this paper estimates the energy carbon emissions by multiplying the physical quantities of various energy consumption in the regional energy balance tables in the China Energy Statistical Yearbook by the reference coefficients of each energy converted into standard coal in the General Principles for Comprehensive Energy Consumption Calculation, and then multiplied by the respective carbon emission coefficient, published in the IPCC (2006) document internationally.
3.4. Data Source
3.5. Driving Factors on CIGTFEE
- (1)
- Economic growth (EG): Previous studies have shown the relationship between energy consumption and economic growth is highly related to the actual social development in the study area [31,32]. EG is often accompanied by the agglomeration of talent, capital, and technology, and these factors are crucial to the development of the construction industry. However, the effects of EG on the ecosystem might be considerably more harmful. Thus, it is essential to investigate the correlation between EG and CIGTFEE. EG was measured by the per capita GDP of each province and city, and at the same time, in order to eliminate the influence of collinearity, the natural logarithm of this index was taken. Therefore, the nexus between EG and CIGTFEE is uncertain.
- (2)
- Technological progress (TP): As a dominant contributor, TP is conductive to reducing energy consumption intensity [25,33]. Relevant research shows that TP improves the quality of energy inputs, significantly reduces the associated cost, frees up resources, and maximizes output [34]. Moreover, TP can upgrade the traditional high-energy equipment and improve the production efficiency of enterprises, and then promote the rational utilization of energy in the construction industry and reduce the energy consumption intensity, thus promoting the green transformation and growth of regional industries.TP is expressed by the ratio of regional R&D expenditure to GDP, and it is expected that TP promotes CIGTFEE.
- (3)
- Urbanization level (UL): The level of urbanization is closely related to the energy efficiency of the building sector, and there are two contrasting views on the relationship between the two. One thing, urbanization is accompanied by population migration from rural to urban areas, stimulating housing demand and promoting the continuous expansion of the construction industry, which increases building energy consumption and emits a lot of carbon dioxide [27]. For another, the increasing level of urbanization may have facilitated the inflow of high-quality educational resources and skills, raising labor value, facilitating the development of energy-saving technology, and enhancing energy efficiency [29]. Therefore, the relationship between UL and CIGTFEE is uncertain. Here, UL is expressed by the ratio of the resident population in urban areas to the total population.
- (4)
- Energy structure (ES): The optimization and adjusting of ES are conducive to slowing down energy consumption growth and are crucial to green construction development. Compared with traditional fossil fuels such as coal and oil, an increase in the proportion of electricity consumed could significantly enhance labor and energy efficiency [29]. The clean energy represented by electricity has higher energy conversion efficiency and lower carbon dioxide emissions. By increasing the ratio of electric energy consumption in the construction sector, it is possible to upgrade the ES and promote emission reduction in the construction sector. Therefore, ES can be expressed by the ratio of electric energy consumption to the total energy consumption in the construction industry and is expected to promote CIGTFEE.
- (5)
- Human capital (HC): Scientific production skills, advanced production equipment, and well environmental consciousness are better mastered by high-quality employees, who can provide the necessary intellectual support for reducing energy consumption and promoting the green transformation of enterprises [35]. Therefore, this paper substitutes HC with the per capita years of education of the labor force in a region, and it is expected that HC promotes CIGTFEE.
- (6)
- Technology and equipment level (TL): The increase in the ratio of technical equipment indicates an increase in investment in fixed capital [29]. This value is a measure of the level of technological development of the construction industry in terms of the value of fixed assets and equipment per person employed in the construction industry. The higher the technical equipment ratio in the construction industry, the higher the level of technology, and vice versa, the lower [36]. Therefore, it is expected that TL will promote CIGTFEE.
4. Results and Discussion
4.1. Regional Differences
4.2. Spatial Correlations
4.2.1. Global Spatial Correlations
4.2.2. Spatial Distribution Evolution Characteristics
- (1)
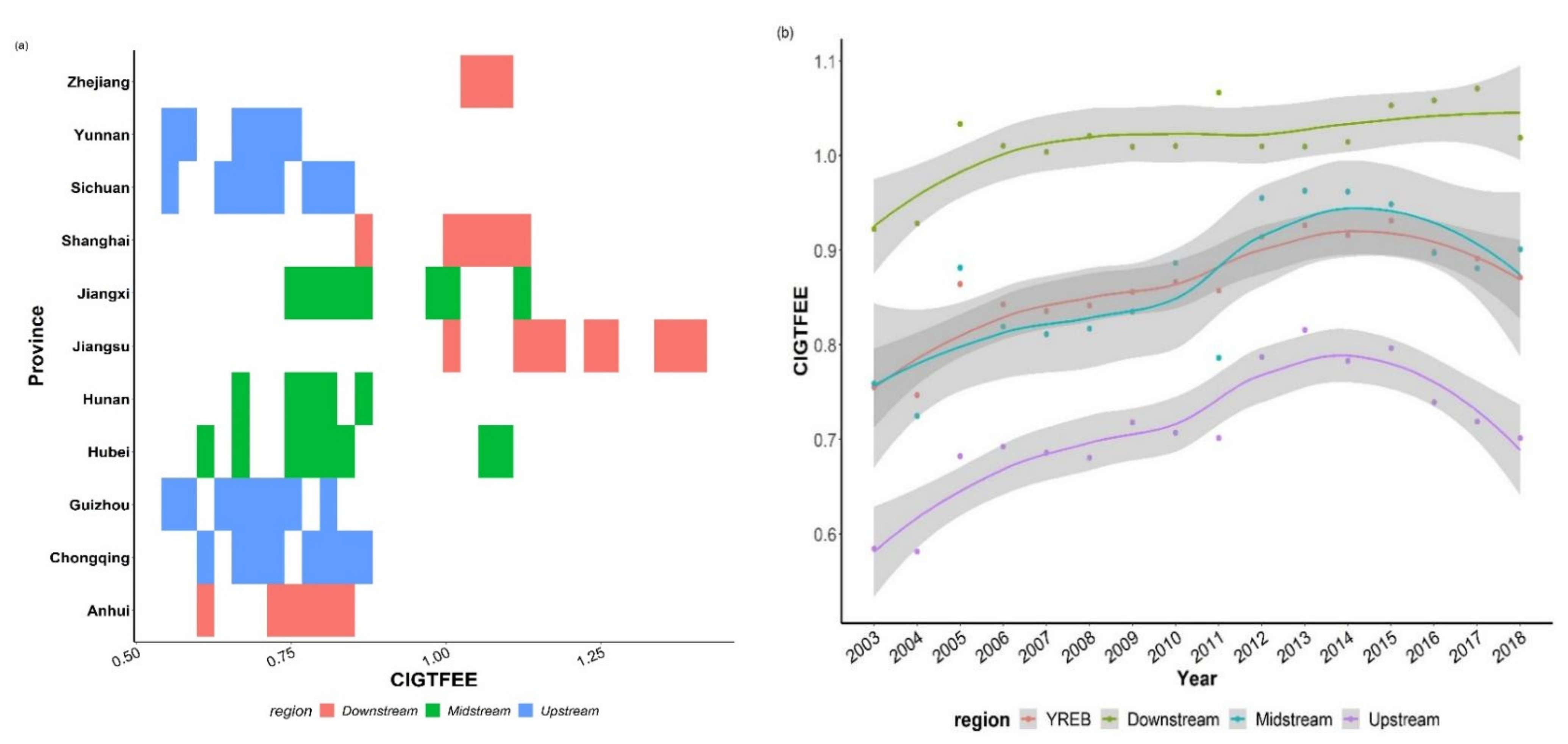
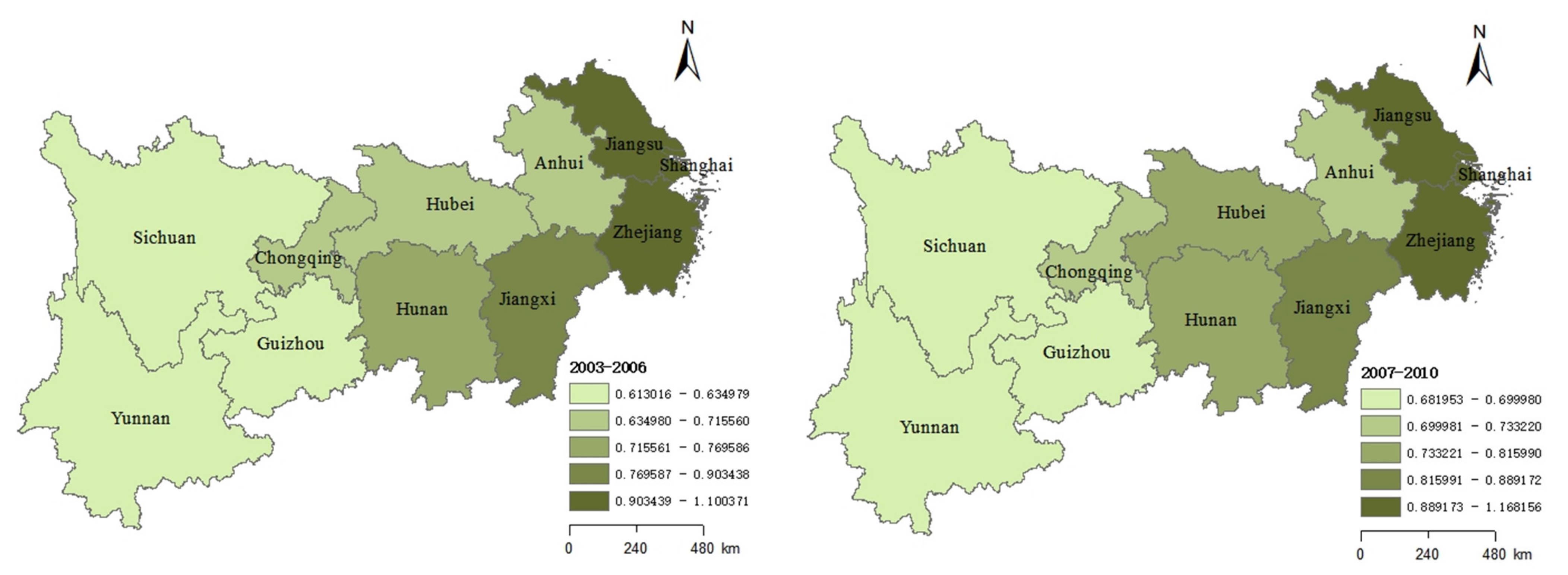
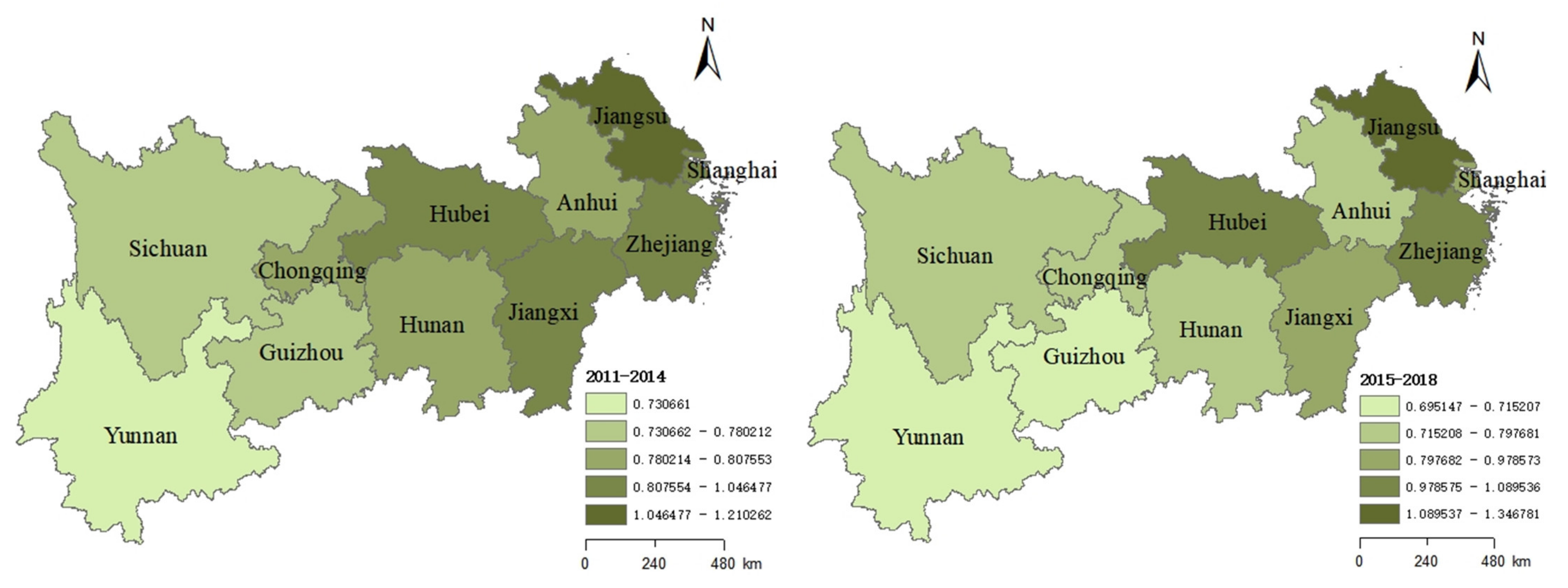
- As shown in Figure 4, the spatial distribution of CIGTFEE in YREB generally presents a ladder-shaped change trend, with the regional average CIGTFEE from high to low levels was as follows: Downstream, Midstream, and Upstream. This is directly tied to the variations in resource endowment and economic development between provinces. It can be seen that the provinces in the downstream and upstream regions show obvious polarization.
- (2)
- During four periods, Jiangsu, Zhejiang were ranked in the highest efficiency range. Although the CIGTFEE in Shanghai showed a downward trend, it still placed high on the list.
- (3)
- In contrast, Sichuan, Guizhou and Yunnan, which located in the economically and technologically underdeveloped upstream, always in a state of inefficiency. Compared with other upstream provinces, Chongqing’s CIGTFEE placed high during four periods. Therefore, in the upstream region, Chongqing should play a good role in leading the way, strengthen the cooperation between the upper, middle and lower reaches, and narrow the gap.
- (4)
- CIGTFEE has to some extent been enhanced in Hubei. Moreover, CIGTFEE has declined to a certain extent in Hunan and Jiangxi.but Jiangxi still ranked first in the midstream.
4.3. Analysis of Driving Factors
4.3.1. Spatial Correlation Test on Residual Terms
4.3.2. Analysis on Driving Factors of the CIGTFEE in YREB
5. Conclusions and Policy Implication
5.1. Conclusions
- (1)
- During the sample period, only Jiangsu, Zhejiang, and Shanghai’s CIGTFEE are in a state of effective, while other provinces fail to achieve the effective state, and there is room for improvement.
- (2)
- In terms of temporal evolution, the CIGTFEE during the research periods revealed an overall growing tendency. The CIGTFEE in the YREB’s upstream, midstream, and downstream followed different trajectories. Prior to 2006, the CIGTFEE in the downstream grew dramatically, then stayed rather steady. In the midstream, they had an “M” shape with “two peaks and one valley”. The inverted “U” curve was the trend of the upstream.
- (3)
- Global Moran’s I testify the significant spatial correlations between provincial CIGTFEEs. The distribution of CIGTFEE in YREB generally exhibits a ladder-shaped change trend, with the regional average CIGTFEE from high to low levels was as follows: Downstream, Midstream and Upstream. Overall, the provinces in the downstream are clearly polarized with those in the upstream.
- (4)
- The results of spatial econometric model demonstrated that the CIGTFEE is significantly promoted by EG, ES and HC, suppressed by UL, yet the impact of TP and TL is not significant.
5.2. Policy Implication
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, T.; Chen, W.; Zhou, K.; Ren, M. Regional energy efficiency evaluation in China: A super efficiency slack-based measure model with undesirable outputs. J. Clean. Prod. 2018, 198, 859–866. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, L.; Zhu, Z. The environmental-adjusted energy efficiency of China’s construction industry: A three-stage undesirable SBM-DEA model. Environ. Sci. Pollut. Res. 2021, 28, 58442–58455. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Qi, X.; Zhou, X.; Li, W. Total-factor energy efficiency of coal consumption: An empirical analysis of China’s energy intensive industries. J. Clean. Prod. 2018, 172, 2618–2624. [Google Scholar] [CrossRef]
- Wilson, B.; Trieu, L.H.; Bowen, B. Energy efficiency trends in Australia. Energy Policy 1994, 22, 287–295. [Google Scholar] [CrossRef]
- Hu, J.-L.; Wang, S.-C. Total-factor energy efficiency of regions in China. Energy Policy 2006, 34, 3206–3217. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Ma, D.; Xiong, H.; Zhang, F.; Gao, L.; Zhao, N.; Yang, G.; Yang, Q. China’s industrial green total-factor energy efficiency and its influencing factors: A spatial econometric analysis. Environ. Sci. Pollut. Res. Int. 2022, 29, 18559–18577. [Google Scholar] [CrossRef]
- Ouyang, X.; Chen, J.; Du, K. Energy efficiency performance of the industrial sector: From the perspective of technological gap in different regions in China. Energy 2021, 214, 118865. [Google Scholar] [CrossRef]
- Wang, N.; Zhu, Y.; Yang, T. The impact of transportation infrastructure and industrial agglomeration on energy efficiency: Evidence from China’s industrial sectors. J. Clean. Prod. 2020, 244, 118708. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, D.; Du, T.; Zhang, A.; Zhou, Y. Total-factor energy efficiency in China’s agricultural sector: Trends, disparities and potentials. Energies 2018, 11, 853. [Google Scholar] [CrossRef]
- Jiang, M.; Hu, X.; Chunga, J.; Lin, Z.; Fei, R. Does the popularization of agricultural mechanization improve energy-environment performance in China’s agricultural sector? J. Clean. Prod. 2020, 276, 124210. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Xia, B.; Skitmore, M. Impact of environment regulation on the efficiency of regional construction industry: A 3-stage Data Envelopment Analysis (DEA). J. Clean. Prod. 2018, 200, 770–780. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Xie, Y. Level and drivers of China’s construction industry energy efficiency under carbon dioxide emissions. Discret. Dyn. Nat. Soc. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Xiang, P.; Li, Z.; Hu, M. Research on energy efficiency of chinese provincial construction industry from 2006 to 2015 based on Super-SBM model. In ICCREM 2019: Innovative Construction Project Management and Construction Industrialization; American Society of Civil Engineers: Reston, VA, USA, 2019. [Google Scholar]
- Tone, K.; Tsutsui, M. An epsilon-based measure of efficiency in DEA—A third pole of technical efficiency. Eur. J. Oper. Res. 2010, 207, 1554–1563. [Google Scholar] [CrossRef]
- Yang, L.; Wang, K.-L.; Geng, J.-C. China’s regional ecological energy efficiency and energy saving and pollution abatement potentials: An empirical analysis using epsilon-based measure model. J. Clean. Prod. 2018, 194, 300–308. [Google Scholar] [CrossRef]
- Tang, D.; Li, Z.; Bethel, B.J. Relevance analysis of sustainable development of China’s Yangtze River Economic Belt based on spatial structure. Int. J. Environ. Res. Public Health 2019, 16, 3076. [Google Scholar] [CrossRef]
- Xue, X.; Wu, H.; Zhang, X.; Dai, J.; Su, C. Measuring energy consumption efficiency of the construction industry: The case of China. J. Clean. Prod. 2015, 107, 509–515. [Google Scholar] [CrossRef]
- Li, W.; Sun, W.; Li, G.; Cui, P.; Wu, W.; Jin, B. Temporal and spatial heterogeneity of carbon intensity in China’s construction industry. Resour. Conserv. Recycl. 2017, 126, 162–173. [Google Scholar] [CrossRef]
- Wang, L.; Song, X.; Song, X. Research on the measurement and spatial-temporal difference analysis of energy efficiency in China’s construction industry based on a game cross-efficiency model. J. Clean. Prod. 2021, 278, 123918. [Google Scholar] [CrossRef]
- Xu, Q.; Dong, Y.-X.; Yang, R.; Zhang, H.-O.; Wang, C.-J.; Du, Z.-W. Temporal and spatial differences in carbon emissions in the Pearl River Delta based on multi-resolution emission inventory modeling. J. Clean. Prod. 2019, 214, 615–622. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Zhang, W.; Lin, X. Study on the Impact of energy poverty on energy efficiency of construction industry: Mediating role of energy consumption structure. Front. Energy Res. 2021, 9, 760895. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Z.; Li, X.; Feng, W.; Li, J. Assessing the effects of technological progress on energy efficiency in the construction industry: A case of China. J. Clean. Prod. 2019, 238, 117908. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Pu, S.; Skitmore, M.; Philbin, S.P.; Ballesteros-Perez, P. Environmental regulation and green productivity of the construction industry in China. Proc. Inst. Civ. Eng.-Eng. Sustain. 2021, 174, 58–68. [Google Scholar] [CrossRef]
- Lin, B.; Liu, H. China’s building energy efficiency and urbanization. Energy Build. 2015, 86, 356–365. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Exploring the driving forces of energy-related CO2 emissions in China’s construction industry by utilizing production-theoretical decomposition analysis. J. Clean. Prod. 2018, 202, 710–719. [Google Scholar] [CrossRef]
- Liang, X.; Lin, S.; Bi, X.; Lu, E.; Li, Z. Chinese construction industry energy efficiency analysis with undesirable carbon emissions and construction waste outputs. Environ. Sci. Pollut. Res. 2021, 28, 15838–15852. [Google Scholar] [CrossRef]
- Goldsmith, R.D. A Perpetual Inventory of National Wealth. Natl. Bur. Econ. Res. 1951, 14, 5–61. [Google Scholar]
- Sener, S.; Karakas, A.T. The effect of economic growth on energy efficiency: Evidence from high, upper-middle and lower-middle income countries. Procedia Comput. Sci. 2019, 158, 523–532. [Google Scholar] [CrossRef]
- He, Y.; Lin, B. Investigating environmental kuznets curve from an energy intensity perspective: Empirical evidence from China. J. Clean. Prod. 2019, 234, 1013–1022. [Google Scholar] [CrossRef]
- Ma, C.; Stern, D.I. China’s changing energy intensity trend: A decomposition analysis. Energy Econ. 2008, 30, 1037–1053. [Google Scholar] [CrossRef]
- Adom, P.K.; Agradi, M.; Vezzulli, A. Energy efficiency-economic growth nexus: What is the role of income inequality? J. Clean. Prod. 2021, 310, 127382. [Google Scholar] [CrossRef]
- Akram, V.; Jangam, B.P.; Rath, B.N. Examining the linkage between human capital and energy consumption: Cross-country evidence. OPEC Energy Rev. 2020, 44, 3–26. [Google Scholar] [CrossRef]
- Liu, L. Research on the Evolution of Energy Consumption Intensity in China’s Construction Industry Master; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Acemoglu, D.; Aghion, P.; Bursztyn, L.; Hemous, D. The environment anddirected technical change. Am. Econ. Rev. 2012, 102, 131–166. [Google Scholar] [CrossRef]
- Wang, X.; Lou, X.; Yang, Q. Inter-provincial difference in energy efficiency of construction industry and its influencing factors in China. China Popul. Resour. Environ. 2012, 22, 56–61. [Google Scholar]


| Input/Output | Variable | Meaning (Units) |
|---|---|---|
| Inputs | Energy input | Comprehensive energy consumption of the construction industry (1000 t) |
| Labor input | The number of employees of industrial enterprises in the region (1000 people) | |
| Capital input | The actual net construction fixed assets in the region with 2000 as the base period (CNY 100 million yuan) | |
| Desirable output | Economic output | The actual total output of construction in the region with 2003 as the base period (CNY 100 million yuan) |
| Undesirable output | Carbon dioxide emissions | The carbon dioxide emissions of construction in the region (10,000 t) |
| 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | 1.029 | 1.027 | 1.052 | 1.069 | 1.072 | 1.110 | 1.097 | 1.103 | 1.097 | 1.045 | 1.024 | 1.015 | 1.033 | 1.015 | 1.004 | 0.862 | 1.041 |
| Jiangsu | 1.009 | 1.015 | 1.244 | 1.133 | 1.156 | 1.186 | 1.162 | 1.169 | 1.340 | 1.164 | 1.174 | 1.163 | 1.276 | 1.337 | 1.398 | 1.377 | 1.206 |
| Zhejiang | 1.045 | 1.053 | 1.075 | 1.067 | 1.051 | 1.055 | 1.050 | 1.032 | 1.075 | 1.034 | 1.034 | 1.043 | 1.051 | 1.099 | 1.106 | 1.102 | 1.061 |
| Anhui | 0.607 | 0.619 | 0.762 | 0.772 | 0.737 | 0.732 | 0.728 | 0.736 | 0.754 | 0.795 | 0.807 | 0.837 | 0.852 | 0.784 | 0.776 | 0.734 | 0.752 |
| Jiangxi | 0.787 | 0.820 | 1.128 | 0.878 | 0.840 | 0.834 | 0.876 | 1.008 | 0.763 | 1.018 | 1.014 | 1.000 | 0.980 | 0.847 | 0.809 | 0.857 | 0.904 |
| Hubei | 0.623 | 0.675 | 0.763 | 0.802 | 0.799 | 0.803 | 0.821 | 0.841 | 0.775 | 1.053 | 1.070 | 1.074 | 1.057 | 1.057 | 1.070 | 1.087 | 0.898 |
| Hunan | 0.867 | 0.679 | 0.754 | 0.778 | 0.795 | 0.814 | 0.809 | 0.811 | 0.821 | 0.794 | 0.804 | 0.812 | 0.809 | 0.787 | 0.765 | 0.759 | 0.791 |
| Chongqing | 0.664 | 0.599 | 0.734 | 0.705 | 0.695 | 0.704 | 0.736 | 0.731 | 0.715 | 0.796 | 0.855 | 0.844 | 0.832 | 0.805 | 0.767 | 0.787 | 0.748 |
| Sichuan | 0.562 | 0.558 | 0.653 | 0.696 | 0.694 | 0.705 | 0.729 | 0.673 | 0.665 | 0.790 | 0.835 | 0.803 | 0.806 | 0.772 | 0.725 | 0.690 | 0.710 |
| Guizhou | 0.566 | 0.592 | 0.679 | 0.703 | 0.695 | 0.661 | 0.703 | 0.715 | 0.740 | 0.821 | 0.810 | 0.750 | 0.806 | 0.701 | 0.703 | 0.651 | 0.706 |
| Yunnan | 0.546 | 0.577 | 0.664 | 0.666 | 0.660 | 0.654 | 0.705 | 0.709 | 0.686 | 0.741 | 0.761 | 0.734 | 0.743 | 0.679 | 0.681 | 0.678 | 0.680 |
| Periods | 2003–2006 | 2007–2010 | 2011–2014 | 2015–2018 |
|---|---|---|---|---|
| Moran’s I | 0.642 | 0.618 | 0.449 | 0.309 |
| p-value | 0.005 | 0.005 | 0.013 | 0.032 |
| Z-value | 3.523 | 3.580 | 2.767 | 2.241 |
| Variables | Non-Fixed Effects Model | Space Fixed Effects Model | Time Fixed Effects Model | Two-Way Fixed Effects Model |
|---|---|---|---|---|
| EG | 0.194 *** (3.220) | 0.094 (0.994) | 1.273 *** (13.849) | 0.127 (0.709) |
| TP | 0.007 (0.240) | −0.048 ** (−2.111) | −0.001 (−0.043) | −0.0027 (−0.078) |
| UL | 0.532 *** (2.598) | 0.655 * (1.836) | −1.472 *** (−7.199) | 1.286 *** (3.534) |
| ES | 0.108 (1.003) | −0.009 (−0.129) | 0.475 *** (5.808) | 0.170 ** (2.372) |
| HC | −0.017 (−0.628) | −0.015 (−0.683) | 0.081 *** (3.909) | 0.020 (0.747) |
| TL | −0.026 (−0.977) | 0.006 (0.322) | 0.017 (0.882) | −0.005 (−0.264) |
| R-squared | 0.511 | 0.334 | 0.758 | 0.178 |
| DW | 1.529 | 1.822 | 2.072 | 1.885 |
| LM-lag | 9.080 *** | 4.707 ** | 2.844 * | 1.052 |
| Robust LM-lag | 14.660 *** | 8.979 *** | 20.186 *** | 5.067 ** |
| LM-err | 4.106 ** | 7.195 *** | 2.340 * | 0.355 |
| Robust LM-err | 9.686 *** | 11.467 *** | 19.682 *** | 4.369 ** |
| Variables | SAR | SEM |
|---|---|---|
| EG | 1.263 *** (14.013) | 1.273 *** (13.592) |
| TP | −0.006 (−0.311) | 0.023 (1.237) |
| UL | −1.490 *** (−7.430) | −1.585 *** (−7.424) |
| ES | 0.459 *** (5.727) | 0.470 *** (5.676) |
| HC | 0.078 *** (3.826) | 0.091 *** (4.563) |
| TL | 0.018 (0.997) | 0.0010 (0.516) |
| W*dep. var | 0.101 * (1.537) | |
| Spat. aut. | −0.269 *** (−2.609) | |
| R-squared | 0.781 | 0.774 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Zhao, N.; Zhang, F.; Xiao, Y.; Guo, Z.; Liu, C. Green Total-Factor Energy Efficiency of Construction Industry and Its Driving Factors: Spatial-Temporal Heterogeneity of Yangtze River Economic Belt in China. Int. J. Environ. Res. Public Health 2022, 19, 9972. https://doi.org/10.3390/ijerph19169972
Ma D, Zhao N, Zhang F, Xiao Y, Guo Z, Liu C. Green Total-Factor Energy Efficiency of Construction Industry and Its Driving Factors: Spatial-Temporal Heterogeneity of Yangtze River Economic Belt in China. International Journal of Environmental Research and Public Health. 2022; 19(16):9972. https://doi.org/10.3390/ijerph19169972
Chicago/Turabian StyleMa, Dalai, Na Zhao, Fengtai Zhang, Yaping Xiao, Zuman Guo, and Chunlan Liu. 2022. "Green Total-Factor Energy Efficiency of Construction Industry and Its Driving Factors: Spatial-Temporal Heterogeneity of Yangtze River Economic Belt in China" International Journal of Environmental Research and Public Health 19, no. 16: 9972. https://doi.org/10.3390/ijerph19169972
APA StyleMa, D., Zhao, N., Zhang, F., Xiao, Y., Guo, Z., & Liu, C. (2022). Green Total-Factor Energy Efficiency of Construction Industry and Its Driving Factors: Spatial-Temporal Heterogeneity of Yangtze River Economic Belt in China. International Journal of Environmental Research and Public Health, 19(16), 9972. https://doi.org/10.3390/ijerph19169972








