Numerical Solution for Fuzzy Time-Fractional Cancer Tumor Model with a Time-Dependent Net Killing Rate of Cancer Cells
Abstract
:Simple Summary
Abstract
1. Introduction
2. Time-Fractional Cancer Tumor Models in Fuzzy Environment
3. Explicit Finite Difference Scheme for Solving Fuzzy Cancer Tumor Models
4. Stability Analysis
- (1)
- ,
- (2)
- (3)
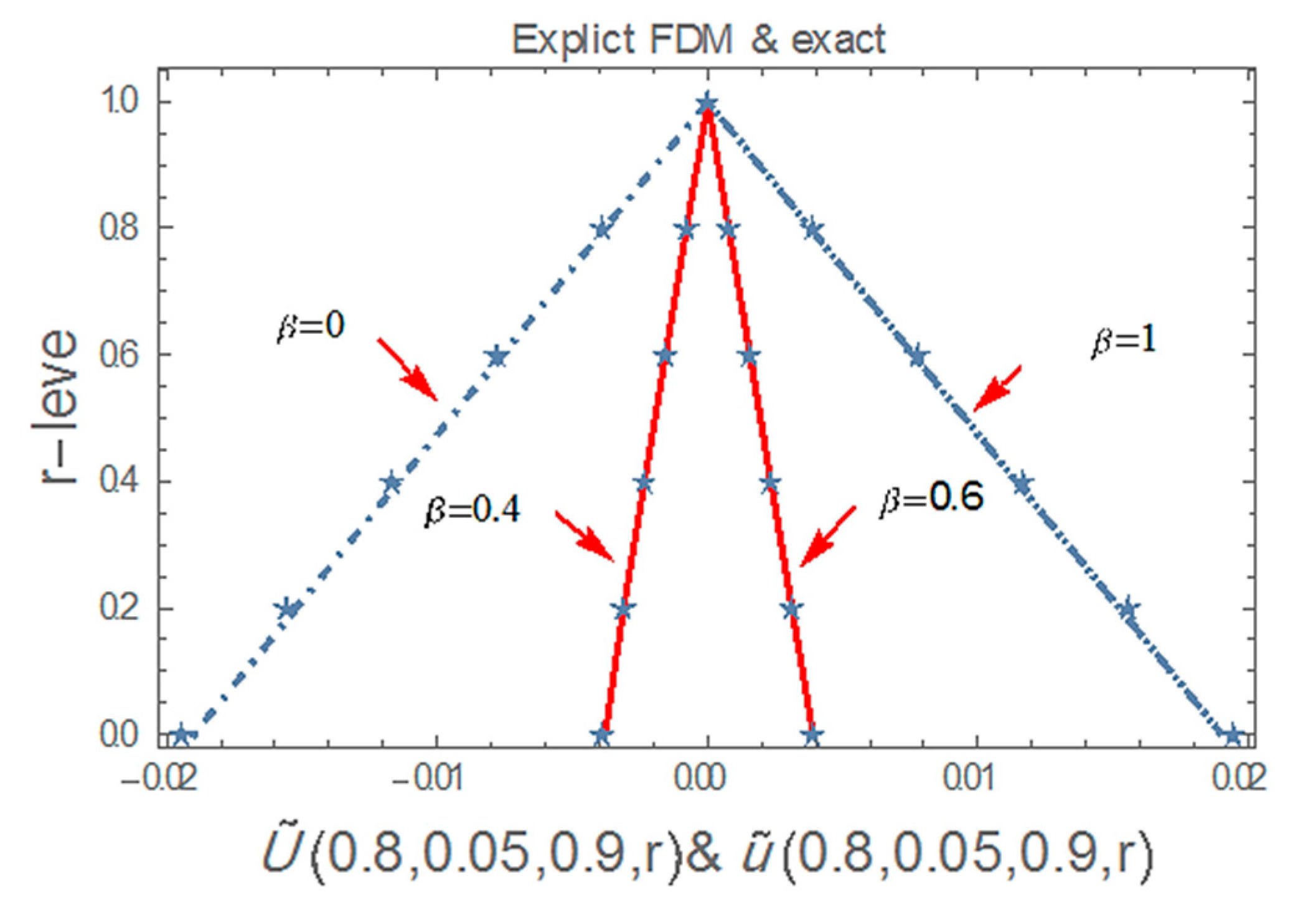
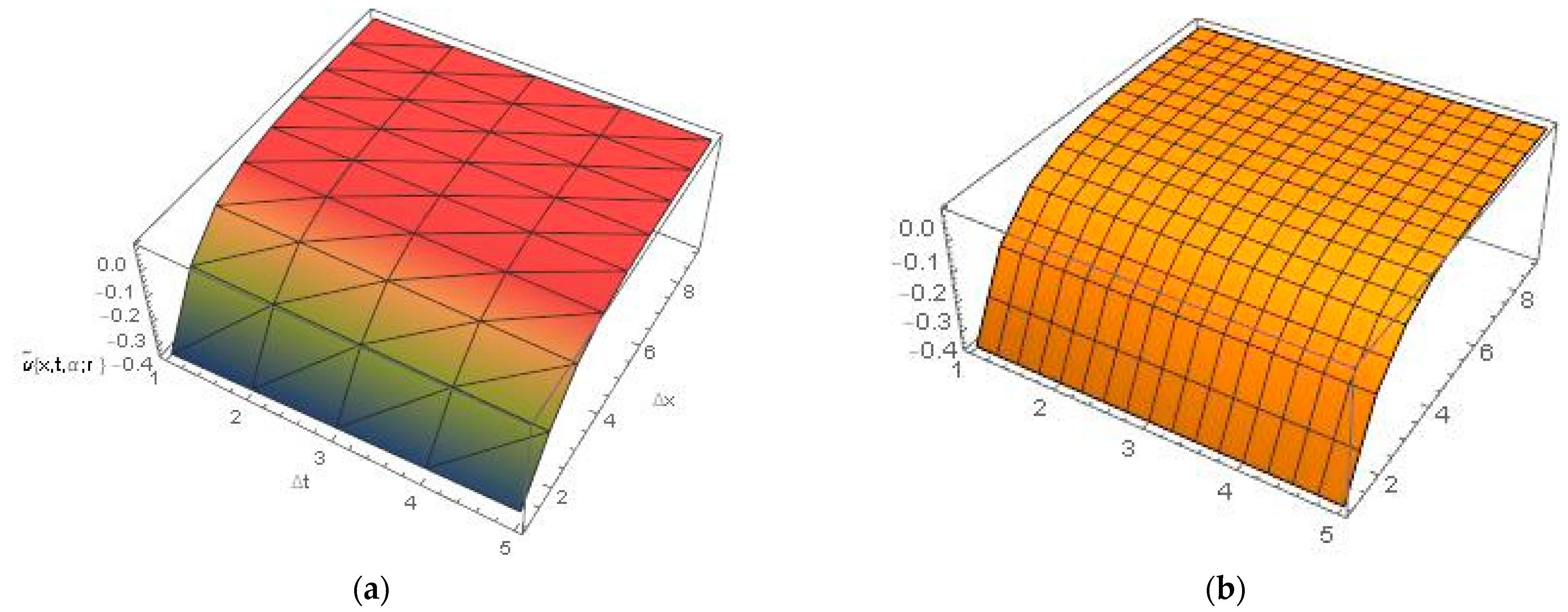
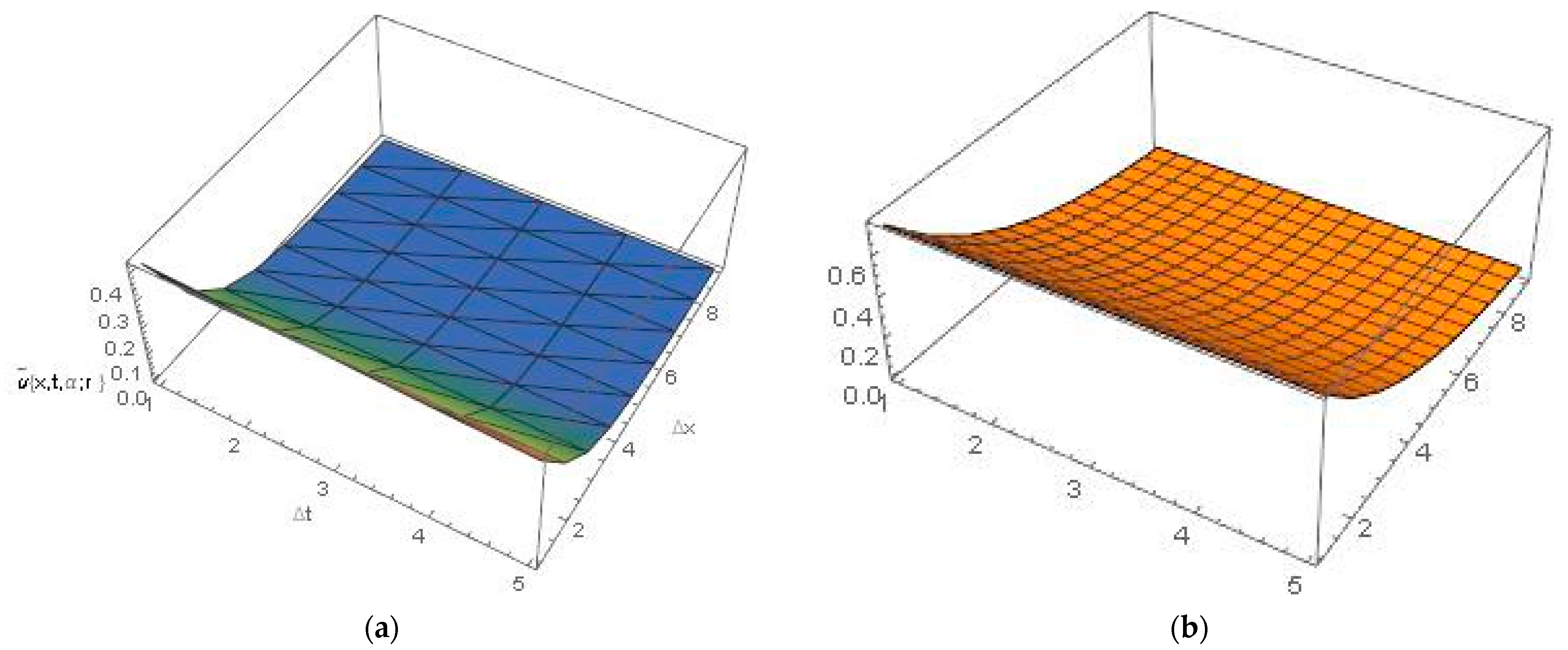
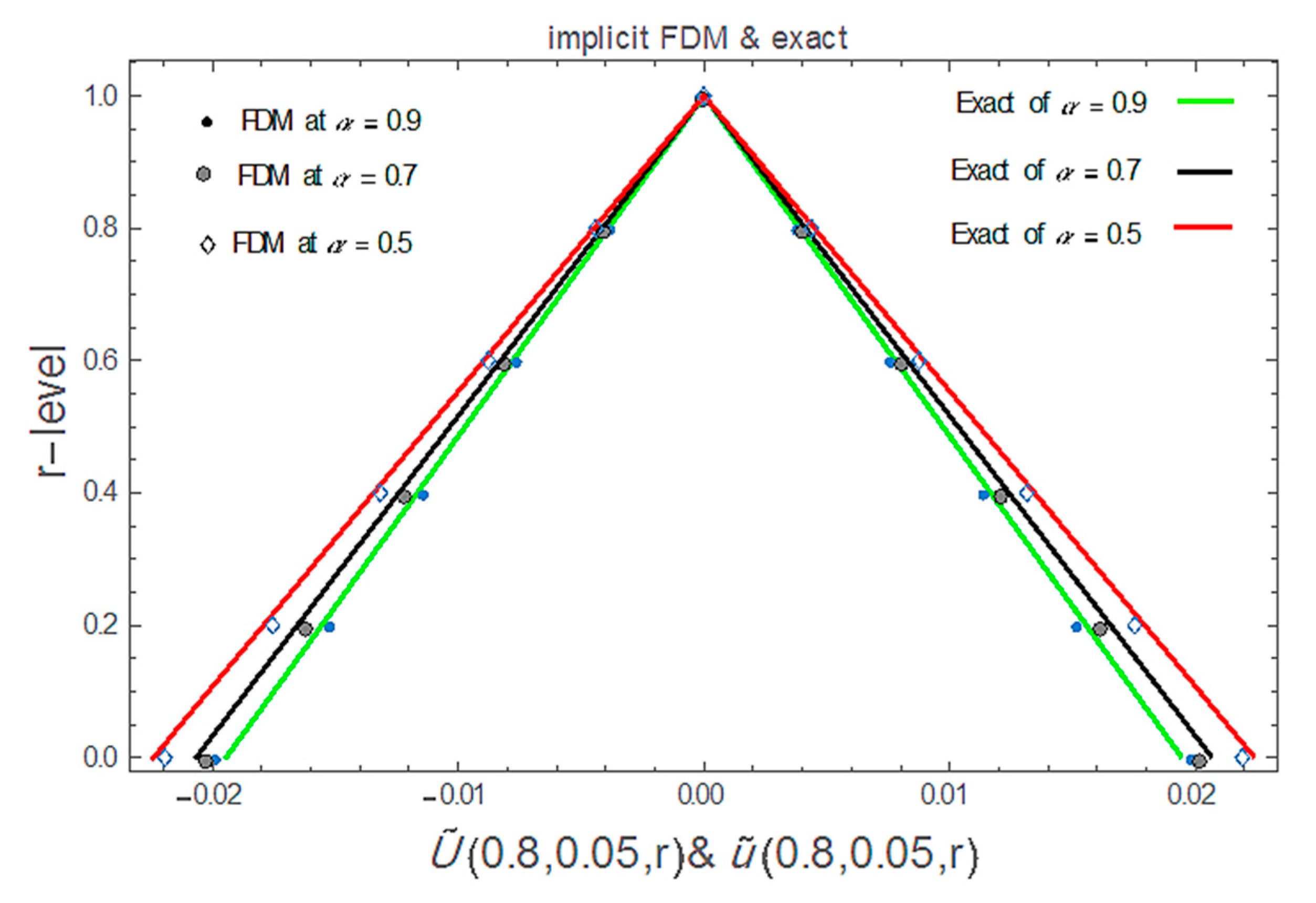
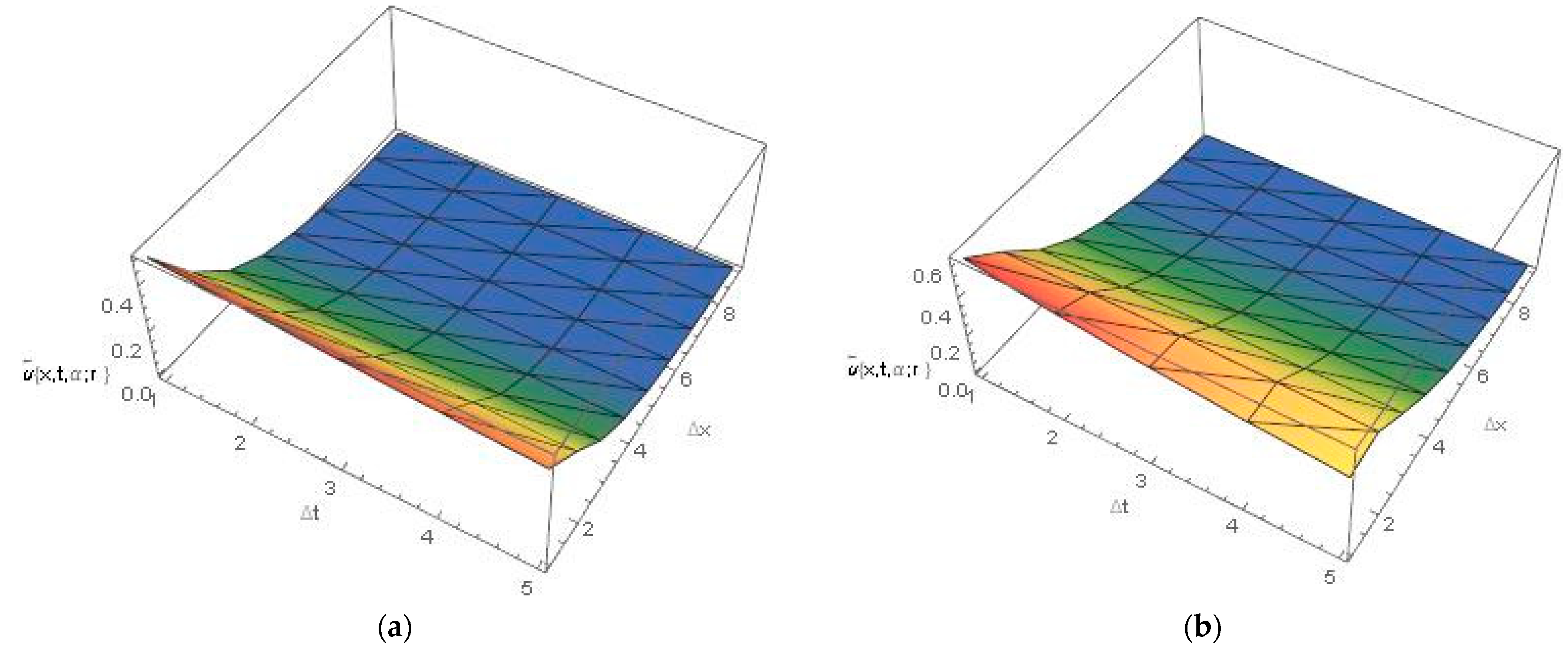
5. Numerical Experiment and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laajala, T.D.; Corander, J.; Saarinen, N.M.; Mäkelä, K.; Savolainen, S.; Suominen, M.I.; Alhoniemi, E.; Mäkelä, S.; Poutanen, M.; Aittokallio, T. Improved Statistical Modeling of Tumor Growth and Treatment Effect in Preclinical Animal Studies with Highly Heterogeneous Responses In VivoImproved Modeling of Heterogeneous Tumor Growth Experiments. Clin. Cancer Res. 2012, 18, 4385–4396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Hınçal, E.; Baleanu, D. Residual power series algorithm for fractional cancer tumor models. Alex. Eng. J. 2020, 59, 1405–1412. [Google Scholar] [CrossRef]
- Burgess, P.K.; Kulesa, P.M.; Murray, J.D.; Alvord, E.C., Jr. The interaction of growth rates and diffusion coefficients in a three-dimensional mathematical model of gliomas. J. Neuropathol. Exp. Neurol. 1997, 56, 704–713. [Google Scholar] [CrossRef]
- Moyo, S.; Leach, P. Symmetry methods applied to a mathematical model of a tumour of the brain. Proc. Inst. Math. NAS Ukr. 2004, 50, 204–210. [Google Scholar]
- Obembe, A.; Al-Yousef, H.Y.; Hossain, M.E.; Abu-Khamsin, S.A. Fractional derivatives and their applications in reservoir engineering problems: A review. J. Pet. Sci. Eng. 2017, 157, 312–327. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Saeedi, H.; Moghadam, M.M.; Mollahasani, N.; Chuev, G. A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1154–1163. [Google Scholar] [CrossRef]
- Conejero, J.A.; Franceschi, J.; Picó-Marco, E. Fractional vs. Ordinary Control Systems: What Does the Fractional Derivative Provide? Mathematics 2022, 10, 2719. [Google Scholar] [CrossRef]
- Iomin, A. Superdiffusion of cancer on a comb structure. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2005; Volume 7, p. 005. [Google Scholar]
- Nemati, K.; Matinfar, M. An Implicit Method For Fuzzy Parabolic partial differential Equations. J. Nonlinear Sci. Appl. 2008, 1, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Faran, B.; Saleem, K.; Yasir, N.; Imran, M. Design Model of Fuzzy Logic Medical Diagnosis Control System. Int. J. Comput. Sci. Eng. 2011, 3, 2093–2108. [Google Scholar]
- Muhamediyeva, D.T. Approaches To The Numerical Solving Of Fuzzy Differential Equations. Int. J. Res. Eng. Technol. 2014, 3, 335–342. [Google Scholar]
- Huang, L.L.; Baleanu, D.; Mo, Z.W.; Wu, G.C. Fractional discrete-time diffusion equation with uncertainty: Applications of fuzzy discrete fractional calculus. Phys. A Stat. Mech. Its Appl. 2018, 508, 166–175. [Google Scholar] [CrossRef]
- Abaid, U.; Rehman, M.; Ahmad, J.; Hassan, A.; Awrejcewicz, J.; Pawlowski, W.; Karamti, H.; Alharbi, F.M. The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease. Symmetry 2022, 14, 1694. [Google Scholar]
- Kumar, S.; Chauhan, R.P.; Abdel-Aty, A.H.; Abdelwahab, S.F. A study on fractional tumour–immune–vitamins model for intervention of vitamins. Results Phys. 2022, 33, 104963. [Google Scholar] [CrossRef]
- Xu, C.; Farman, M.; Akgül, A.; Nisar, K.S.; Ahmad, A. Modeling and analysis fractal order cancer model with effects of chemotherapy. Chaos Solitons Fractals 2022, 161, 112325. [Google Scholar] [CrossRef]
- Alghamdi, N.A.; Youssef, H.M. The biothermal analysis of a human eye subjected to exponentially decaying laser radiation under the dual phase-lag heat conduction law. Case Stud. Therm. Eng. 2021, 25, 100863. [Google Scholar] [CrossRef]
- Alghamdi, N.A.; Youssef, H.M. The Thermal Behavior Analysis of a Human Eye Subjected to Laser Radiation Under the Non-Fourier Law of Heat Conduction. J. Heat Transfer. Apr. 2021, 143, 041201. [Google Scholar] [CrossRef]
- Youssef, H.M.; Alghamdi, N.; Ezzat, M.A.; El-Bary, A.A.; Shawky, A.M. A proposed modified SEIQR epidemic model to analyze the COVID-19 spreading in Saudi Arabia. Alex. Eng. J. 2022, 61, 2456–2470. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M.; Alhazmi, S. Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma. Symmetry 2023, 15, 361. [Google Scholar] [CrossRef]
- Alaroud, M.; Tahat, N.; Ababneh, O.; Agarwal, P. Certain Computational Method for Constructing Approximate Analytic Solution for Non-linear Time-Fractional Physical Problem. Appl. Math. Sci. Eng. 2023, in press.
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation of the Stress-Strain Problem in Capillary-Porous Materials with Fractal Structure. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 1, pp. 1–4. [Google Scholar]
- Rahman, M.U.; Althobaiti, A.; Riaz, M.B.; Al-Duais, F.S. A Theoretical and Numerical Study on Fractional Order Biological Models with Caputo Fabrizio Derivative. Fractal Fract. 2022, 6, 446. [Google Scholar] [CrossRef]
- Sweilam, N.H.; AL-Mekhlafi, S.M.; Hassan, S.M.; Alsenaideh, N.R.; Radwan, A.E. New Coronavirus (2019-nCov) Mathematical Model Using Piecewise Hybrid Fractional Order Derivatives; Numerical Treatments. Mathematics 2022, 10, 4579. [Google Scholar] [CrossRef]
- Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S.E. Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative. Fractal Fract. 2023, 7, 47. [Google Scholar] [CrossRef]
- Almutairi, M.; Zureigat, H.; Izani Ismail, A.; Fareed Jameel, A. Fuzzy numerical solution via finite difference scheme of wave equation in double parametrical fuzzy number form. Mathematics 2021, 9, 667. [Google Scholar] [CrossRef]
- Keshavarz, M.; Qahremani, E.; Allahviranloo, T. Solving a fuzzy fractional diffusion model for cancer tumor by using fuzzy transforms. Fuzzy Sets Syst. 2022, 443, 198–220. [Google Scholar] [CrossRef]
- Bodjanova, S. Median alpha-levels of a fuzzy number. Fuzzy Sets Syst. 2006, 157, 879–891. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Towards fuzzy differential calculus part 3: Differentiation. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a generalized theory of uncertainty (GTU) an outline. Inf. Sci. 2005, 172, 1–40. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Salahshour, S.; Abbasbandy, S. Explicit solutions of fractional differential equations with uncertainty. Soft Comput. 2012, 16, 297–302. [Google Scholar] [CrossRef]
- Fard, O.S. An iterative scheme for the solution of generalized system of linear fuzzy differential equations. World Appl. Sci. J. 2009, 7, 1597–1604. [Google Scholar]
- Zureigat, H.; Ismail, A.; Sathasiva, S. A compact Crank–Nicholson scheme for the numerical solution of fuzzy time fractional diffusion equations. Neural Comput. Appl. 2020, 32, 6405–6412. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Ding, H.F.; Zhang, Y.X. Notes on Implicit finite difference approximation for time fractional diffusion equations. Comput. Math. Appl. 2011, 61, 2924–2928. [Google Scholar] [CrossRef] [Green Version]
- Matoog, R.T.; Salas, A.H.; Alharbey, R.A.; El-Tantawy, S.A. Rational solutions to the cylindrical nonlinear Schrödinger equation: Rogue waves, breathers, and Jacobi breathers solutions. J. Ocean. Eng. Sci. 2022, 13, 19. [Google Scholar] [CrossRef]
- Hou, E.; Hussain, A.; Rehman, A.; Baleanu, D.; Nadeem, S.; Matoog, R.T.; Khan, I.; Sherif, E.S.M. Entropy generation and induced magnetic field in pseudoplastic nanofluid flow near a stagnant point. Sci. Rep. 2021, 11, 23736. [Google Scholar] [CrossRef]
- Trikha, P.; Mahmoud, E.E.; Jahanzaib, L.S.; Matoog, R.T.; Abdel-Aty, M. Fractional order biological snap oscillator: Analysis and control. Chaos Solitons Fractals 2021, 145, 110763. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Matoog, R.T. Chaos control and Penta-compound combination anti-synchronization on a novel fractional chaotic system with analysis and application. Results Phys. 2021, 24, 104130. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Matoog, R.T.; El-Tantawy, S.A. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys. Fluids 2022, 34, 103105. [Google Scholar] [CrossRef]
| r | |||||||
|---|---|---|---|---|---|---|---|
| Lower solution when | .4 | 0 | |||||
| 0.2 | |||||||
| 0.4 | |||||||
| 0.6 | |||||||
| 0.8 | |||||||
| 0 | 0 | 1 | 0 | 0 | |||
| Upper solution when | 0 | 0 | |||||
| 0.2 | 0.2 | ||||||
| 0.4 | 0.4 | ||||||
| 0.6 | 0.6 | ||||||
| 0.8 | 0.8 | ||||||
| 1 | 0 | 0 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S. Numerical Solution for Fuzzy Time-Fractional Cancer Tumor Model with a Time-Dependent Net Killing Rate of Cancer Cells. Int. J. Environ. Res. Public Health 2023, 20, 3766. https://doi.org/10.3390/ijerph20043766
Zureigat H, Al-Smadi M, Al-Khateeb A, Al-Omari S, Alhazmi S. Numerical Solution for Fuzzy Time-Fractional Cancer Tumor Model with a Time-Dependent Net Killing Rate of Cancer Cells. International Journal of Environmental Research and Public Health. 2023; 20(4):3766. https://doi.org/10.3390/ijerph20043766
Chicago/Turabian StyleZureigat, Hamzeh, Mohammed Al-Smadi, Areen Al-Khateeb, Shrideh Al-Omari, and Sharifah Alhazmi. 2023. "Numerical Solution for Fuzzy Time-Fractional Cancer Tumor Model with a Time-Dependent Net Killing Rate of Cancer Cells" International Journal of Environmental Research and Public Health 20, no. 4: 3766. https://doi.org/10.3390/ijerph20043766





