Comparison between Measured and Predicted Resting Metabolic Rate Equations in Cross-Training Practitioners
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
2.3. Anthropometry and Body Composition
2.4. Measurement of Resting Metabolic Rate via Indirect Calorimetry
2.5. Predictive Equations for Calculating Resting Metabolic Rate
2.6. Statistical Analysis
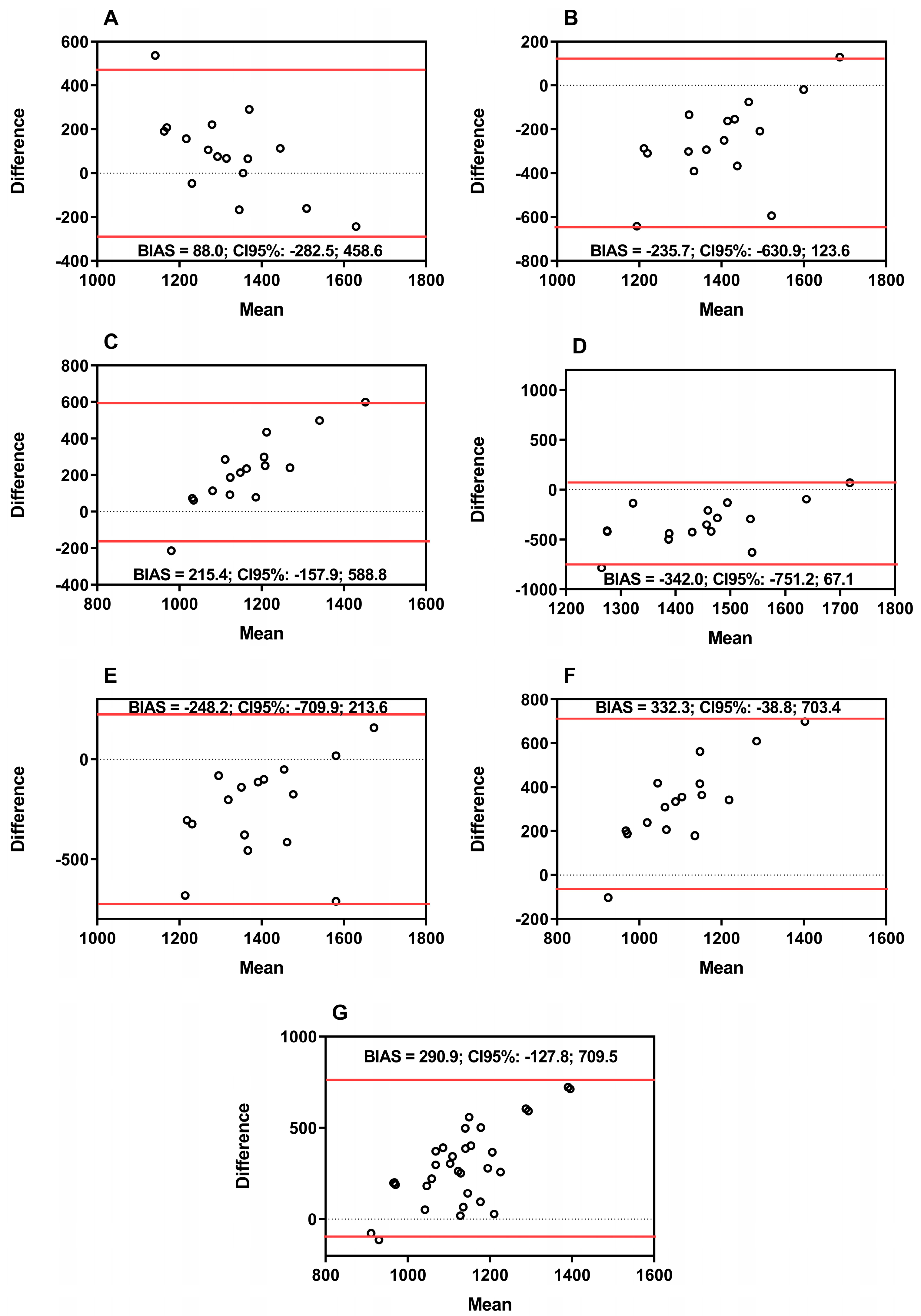
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martínez-Gómez, R.; Valenzuela, P.L.; Alejo, L.B.; Gil-Cabrera, J.; Montalvo-Pérez, A.; Talavera, E.; Lucia, A.; Moral-González, S.; Barranco-Gil, D. Physiological predictors of competition performance in CrossFit athletes. Int. J. Environ. Res. Public Health 2020, 17, 3699. [Google Scholar] [CrossRef] [PubMed]
- Tibana, R.A.; Almeida, L.M.D.; Prestes, J. Crossfit® risks or benefits? What we know so far? Rev. Bras. Ciência Mov. 2015, 23, 182–185. [Google Scholar]
- Meyer, J.; Morrison, J.; Zuniga, J. The benefits and risks of CrossFit: A systematic review. Workplace Health Saf. 2017, 65, 612–618. [Google Scholar] [CrossRef]
- Dominski, F.H.; Tibana, R.A.; Andrade, A. “Functional Fitness Training”, CrossFit, HIMT, or HIFT: What Is the Preferable Terminology? Front. Sports Act. Living 2022, 4, 882195. [Google Scholar] [CrossRef] [PubMed]
- Tibana, R.A.; De Sousa, N.M.F.; Cunha, G.V.; Prestes, J.; Fett, C.; Gabbett, T.J.; Voltarelli, F.A. Validity of session rating perceived exertion method for quantifying internal training load during high-intensity functional training. Sports 2018, 6, 68. [Google Scholar] [CrossRef]
- Cadegiani, F.A.; Kater, C.E.; Gazola, M. Clinical and biochemical characteristics of high-intensity functional training (HIFT) and overtraining syndrome: Findings from the EROS study (The EROS-HIFT). J. Sports Sci. 2019, 37, 1296–1307. [Google Scholar] [CrossRef]
- Jacob, N.; Novaes, J.S.; Behm, D.G.; Vieira, J.G.; Dias, M.R.; Vianna, J.M. Characterization of hormonal, metabolic, and inflammatory responses in CrossFit® training: A systematic review. Front. Physiol. 2020, 11, 1001. [Google Scholar] [CrossRef]
- Schofield, K.L.; Thorpe, H.; Sims, S.T. Resting metabolic rate prediction equations and the validity to assess energy deficiency in the athlete population. Exp. Physiol. 2019, 104, 469–475. [Google Scholar] [CrossRef]
- Marques, D.C.S.; Coelho, A.A.; de Oliveira, F.M.; de Souza, M.G.; Ferrari, A.; Mariano, I.R.; Branco, B.H.M. Resting metabolic rate: A comparison between different measurement methods used in men university students. Sport Sci. Health 2021, 17, 449–457. [Google Scholar] [CrossRef]
- Sordi, A.F.; Mariano, I.R.; Silva, B.F.; Branco, B.H.M. Resting metabolic rate in bodybuilding: Differences between indirect calorimetry and predictive equations. Clin. Nutr. ESPEN 2022, 51, 239–245. [Google Scholar] [CrossRef]
- Achamrah, N.; Delsoglio, M.; de Waele, E.; Berger, M.M.; Pichard, C. Indirect calorimetry: The 6 main issues. Clin. Nutr. 2020, 40, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Y.; Ding, Z.; Cao, G.; Hu, F.; Sun, Y.; Ma, Z.; Zhou, D.; Su, B. Relative validity of an indirect calorimetry device for measuring resting energy expenditure and respiratory quotient. Asia Pac. J. Clin. Nutr. 2018, 27, 72–77. [Google Scholar] [PubMed]
- Cunningham, J.J. Body composition as a determinant of energy expenditure: A synthetic review and a proposed general prediction equation. Am. J. Clin. Nutr. 1991, 54, 963–969. [Google Scholar] [CrossRef] [PubMed]
- Redondo, R.B. Resting energy expenditure: Assessment methods and applications. Nutr. Hosp. 2015, 31, 245–253. [Google Scholar]
- Jajim, A.R.; Camic, C.L.; Kisiolek, J.; Luedke, J.; Erickson, J.; Jones, M.T.; Oliver, J.M. Accuracy of Resting Metabolic Rate Prediction Equations in Athletes. J. Strength Cond. Red. 2018, 32, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Carlsohn, A.; Scharhad-Rosenberger, F.; Cassel, M.; Mayer, F. Resting metabolic rate in elite rowers and canoeists: Difference between indirect calorimetry and prediction. Ann. Nutr. Metab. 2011, 58, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Tinsley, G.M.; Graybeal, A.J.; Moore, M.L. Resting metabolic rate in muscular physique athletes: Validity of existing methods and development of new prediction equations. Appl. Physiol. Nutr. Metab. 2018, 44, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Purcell, S.A.; Johnson-Stoklossa, C.; Tibaes, J.R.B.; Frankish, A.; Elliott, S.A.; Padwal, R.; Prado, C.M. Accuracy and reliability of a portable indirect calorimeter compared to whole-body indirect calorimetry for measuring resting energy expenditure. Clin. Nutr. ESPEN 2020, 39, 67–73. [Google Scholar] [CrossRef]
- Flack, K.D.; Siders, W.A.; Johnson, L.; Roemmich, J.N. Cross-validation of resting metabolic rate prediction equations. J. Acad. Nutr. Diet. 2016, 116, 1413–1422. [Google Scholar] [CrossRef]
- Balci, A.; Badem, E.A.; Yılmaz, A.E.; Devrim-Lanpir, A.; Akınoğlu, B.; Kocahan, T.; Hasanoğlu, A.; Hill, L.; Rosemann, T.; Knechtle, B. Current predictive resting metabolic rate equations Are Not sufficient to determine proper resting energy expenditure in Olympic young adult national team athletes. Front. Physiol. 2021, 12, 625370. [Google Scholar] [CrossRef]
- Butcher, S.J.; Neyedly, T.J.; Horvey, K.J.; Benko, C.R. Do physiological measures predict selected CrossFit® benchmark performance? J. Sports Med. 2015, 6, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Vandarakis, D.; Salacinski, A.J.; Broeder, C.E. A comparison of COSMED metabolic systems for the determination of resting metabolic rate. Res. Sports Med. 2012, 21, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Branco, B.H.M.; Bernuci, M.P.; Marques, D.C.; Carvalho, I.Z.; Barrero, C.A.L.; De Oliveira, F.M.; Ladeia, G.F.; Júnior, N.N. Proposal of a normative table for body fat percentages of Brazilian young adults through bioimpedanciometry. J. Exerc. Rehabil. 2018, 14, 974–979. [Google Scholar] [CrossRef] [PubMed]
- Heyward, V.H. Evaluation of Body Composition, 2nd ed.; Human Kinetics: Champaign, IL, USA, 2004; pp. 1–268. [Google Scholar]
- Lohman, T.G.; Roche, A.F.; Martorell, R. Anthropometric Standardization Reference Manual, 1st ed.; Human Kinetics Books: Champaign, IL, USA, 1988; pp. 1–184. [Google Scholar]
- Campbell, B.; Zito, G.; Colquhoun, R.; Martinez, N.; St Louis, C.; Johnson, M.; Buchanan, L.; Lehn, M.; Smith, Y.; Cloer, B.; et al. Interand intra-day test-retest reliability of the Cosmed Fitmate ProTM indirect calorimeter for resting metabolic rate. J. Int. Soc. Sports Nutr. 2014, 11, P46. [Google Scholar] [CrossRef]
- Harris, J.A.; Benedict, F.G. A Biometric Study of Human Basal Metabolism. Proc. Natl. Acad. Sci. USA 1918, 4, 370–373. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, A.; Bertini, I.; Candeloro, N.; Piccinelli, R. A new predictive equation to calculate resting metabolic rate in athletes. J. Sports Med. Phys. Fitness 1999, 39, 213–219. [Google Scholar] [PubMed]
- Johnstone, A.M.; Rance, K.A.; Murison, S.D.; Duncan, J.S.; Speakman, J.R. Additional anthropometric measures may improve the predictability of basal metabolic rate in adult subjects. Eur. J. Clin. Nutr. 2006, 60, 1437–1444. [Google Scholar] [CrossRef]
- In Body 570 Training Manual. Available online: https://inbodycanada.ca/wp-content/uploads/2020/04/InBody-570-Training-Manual.pdf (accessed on 28 July 2022).
- Jeukendrup, A.; Gleeson, M. Sport Nutrition, 3rd ed.; Manole: Sao Paulo, Brazil, 2021; pp. 1–576. [Google Scholar]
- Giavarina, D. Understanding bland altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Academic Press: Cambridge, UK, 2013; pp. 1–567. [Google Scholar]
- Fink, J.; Schoenfeld, B.J.; Nakazato, K. The role of hormones in muscle hypertrophy. Phys. Sportsmed. 2018, 46, 129–134. [Google Scholar] [CrossRef]
- Alizadeh, S.; Machel Rayner, M.; Behm, D.G. Push-ups vs. Bench press differences in repetitions and muscle activation between sexes. J. Sport Sci. Med. 2020, 19, 289–297. [Google Scholar]
- Bassett, A.J.; Ahlmen, A.; Rosendorf, J.M.; Romeo, A.A.; Erickson, B.J.; Bishop, M.E. The Biology of Sex an Sport. JBJS Rev. 2020, 8, e0140. [Google Scholar] [CrossRef] [PubMed]
- Mangine, G.T.; Stratton, M.T.; Almeda, C.G.; Roberts, M.D.; Esmat, T.A.; VanDusseldorp, T.A.; Feito, Y. Physiological differences between advanced CrossFit athletes, recreational CrossFit participants, and physically-active adults. PLoS ONE 2020, 15, e0223548. [Google Scholar] [CrossRef] [PubMed]
- Aragon, A.A.; Schoenfeld, B.J.; Wildman, R.; Kleiner, S.; VanDusseldorp, T.; Taylor, L.; Earnest, C.P.; Arciero, P.J.; Wilborn, C.; Kalman, D.S.; et al. International society of sports nutrition position stand: Diets and body composition. J. Int. Soc. Sports Nutr. 2017, 14, 16. [Google Scholar] [CrossRef] [PubMed]
- Fukagawa, N.K.; Bandini, L.G.; Young, J.B. Effect of age on body composition and resting metabolic rate. Am. J. Physiol. Endocrinol. Metab. 1980, 259, E233–E238. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.; Manore, M.M. Predicted and measured resting metabolic rate of men and women endurance athletes. J. Am. Diet. Assoc. 1996, 96, 30–34. [Google Scholar] [CrossRef] [PubMed]
- Ten Haaf, T.; Weijs, P.J. Resting energy expenditure prediction in recreational athletes of 18-35 years: Confirmation of Cunningham equation and an improved weight-based alternative. PLoS ONE 2014, 9, e108460. [Google Scholar] [CrossRef] [PubMed]
- Delsoglio, M.; Achamrah, N.; Berger, M.M.; Pichard, C. Indirect calorimetry in clinical practice. J. Clin. Med. 2019, 8, 1387. [Google Scholar] [CrossRef] [PubMed]
- Witkowski, K.; Superson, M.; Piepiora, P. Body composition and motor potential of judo athletes in selected weight categories. Arch. Budo 2021, 17, 161–175. [Google Scholar]
- Loucks, A.B.; Kiens, B.; Wright, H.H. Energy availability in athletes. J. Sports Sci. 2011, 29 (Suppl. 1), S7–S15. [Google Scholar] [CrossRef]
- Mountjoy, M.; Sundgot-Borgen, J.; Burke, L.; Carter, S.; Constantini, N.; Lebrun, C.; Meyer, N.; Sherman, R.; Steffen, K.; Budgett, R.; et al. The IOC consensus statement: Beyond the women athlete triad—Relative energy deficiency in sport (RED-S). Br. J. Sports Med. 2014, 48, 491–497. [Google Scholar] [CrossRef]

| Reference | Equation |
|---|---|
| Harris and Benedict (1918) [27] | Men RMR (kcal/d) = 66.47 + 13.75 × BM + 5 × Height − 6.76 × Age Women RMR (kcal/d) = 655.7 + 9.56 × BM + 1.85 × Height − 4.68 × Age |
| Cunningham (1991) [13] | RMR (kcal/d) = 500 + 22 × FFM |
| De Lorenzo (1999) [28] | RMR (kcal/d) = −857 + 9 × BM + 11.7 × Height |
| Tinsley (a) (2018) [17] | RMR (kcal/d) = 24.8 × BM + 10 |
| Tinsley (b) (2018) [17] | RMR (kcal/d) = 25.9 × FFM + 284 |
| Johnstone (2016) [29] | RMR (kJ/d) = 90.2 × FFM + 31.6 × FM − 122 × Age + 1613 |
| BIA InBody 570® [30] | RMR (kcal/d) = 21.6 × LM + 370 |
| Variables | NW (n = 17) | NM (n = 15) | AW (n = 17) | AM (n = 16) |
|---|---|---|---|---|
| Age (years old) | 29.5 ± 5.4 | 29.7 ± 6.0 | 30.0 ± 5.5 | 28.5 ± 5.3 |
| Height (cm) | 164.5 ± 5.4 | 180.4 ± 5.4 # | 164.1 ± 7.2 | 175.2 ± 5.8 * |
| Body mass (kg) | 61.1 ± 5.6 | 88.5 ± 10.9 # | 63.6 ± 8.8 | 85.8 ± 13.1 * |
| Lean mass (kg) | 43.2 ± 3.9 | 68.3 ± 6.5 # | 47.3 ± 6.9 | 68.4 ± 9.0 * |
| Fat mass (kg) | 15.1 ± 4.2 | 15.8 ± 6.8 | 13.3 ± 3.2 | 13.3 ± 5.3 |
| Skeletal muscle mass (kg) | 25.4 ± 2.52 | 41.5 ± 3.9 # | 28.0 ± 4.4 | 41.8 ± 5.9 * |
| Body fat percentage (%) | 24.6 ± 5.3 | 17.6 ± 5.9 # | 21.0 ± 3.8 | 15.7 ± 5.5 * |
| RMR (kcal) | 1275 ± 209.5 | 2147 ± 320.0 # | 1530 ± 375.8 | 2069 ± 469.9 * |
| Variables | NW (n = 17) | NM (n = 15) | AW (n = 17) | AM (n = 16) | X2 | p-Value |
|---|---|---|---|---|---|---|
| Energy supplements | 10 (58.8%) | 9 (60.0%) | 11 (64.7%) | 12 (75.0%) | 1.14 | 0.7 |
| Vitamin supplements | 6 (35.3%) | 3 (20.0%) | 6 (35.3%) | 7 (43.8%) | 2.01 | 0.5 |
| Anabolic steroids | 1 (5.9%) | 1 (6.7%) | 4 (23.5%) | 3 (18.8%) | 3.21 | 0.3 |
| Groups | NW (n = 17) | NM (n = 15) | AW (n = 17) | AM (n = 16) |
|---|---|---|---|---|
| BIA | 1362.5 (91.2) | 1935.3 (150.0) # | 1455.0 (160.6) | 1936.0 (208.9) * |
| IC | 1274.6 (209.5) | 2147.3 (319.9) # | 1529.6 (375.7) | 2069.4 (469.8) * |
| Harris–Benedict | 1533.4 (111.7) | 1984.4 (152.0) # | 1426.2 (84.1) | 1929.4 (217.7) * |
| Cunningham | 1059.0 (55.6) | 1414.9 (87.7) # | 1117.8 (98.4) | 1421.1 (130.9) * |
| De Lorenzo | 1618.0 (103.0) | 2049.9 (141.5) # | 1636.0 (157.6) | 1965.3 (171.0) * |
| Tinsley (a) | 1525.7 (140.9) | 2205.2 (271.1) # | 1587.5 (220.5) | 2138.1 (327.2) * |
| Tinsley (b) | 942.1 (65.4) | 2205.9 (271.1) # | 1011.3 (115.9) | 1368.4 (154.1) * |
| Johnstone | 962.0 (65.78) | 1314.0 (105.1) # | 1004.0 (95.87) | 1305.0 (158.7) * |
| Groups | CW (n = 34) | CM (n = 31) |
|---|---|---|
| IC | 1568.5 (1513.7–1623.3) | 1868.8 (1826.8–1910.8) |
| BIA | 1577.1 (1523.1–1632.1) | 1722.7 (1681.3–1764.1) # |
| Harris–Benedict | 1654.6 (1600.6–1708.7) | 1742.3 (1700.8–1783.7) # |
| Cunningham | 1195.1 (1141.0–1249.1) * | 1283.0 (1241.6–1324.4) # |
| De Lorenzo | 1833.7 (1779.6–1887.7) * | 1780.6 (1739.2–1822.0) # |
| Tinsley (a) | 1759.8 (1705.7–1813.8) * | 1934.7 (1893.3–1976.1) |
| Tinsley (b) | 1065.8 (1011.7–1119.8) * | 1240.4 (1199.0–1281.8) # |
| Johnstone | 1072.4 (051.8–1171.4) * | 1195.6 (1119.8–1202.7) # |
| Groups | CW (n = 34) | CM (n = 31) |
|---|---|---|
| IC | 1649.8 (1598.5–1710.2) | 1805.6 (1763.5–1847.6) |
| BIA | 1651.3 (1591.5–1711.1) | 1668.1 (1626.6–1709.6) # |
| Harris–Benedict | 1724.2 (1664.5–1784.0) | 1683.0 (1641.5–1724.4) # |
| Cunningham | 1244.1 (1184.4–1303.9) * | 1247.0 (1205.6–1288.5) # |
| De Lorenzo | 1918.0 (1858.2–1977.8) * | 1720.6 (1679.1–1762.0) # |
| Tinsley (a) | 1838.7 (1778.9–1898.4) * | 1864.0 (1822.5–1905.5) |
| Tinsley (b) | 1107.9 (1048.1–1167.7) * | 1206.2 (1164.8–1247.7) # |
| Johnstone | 1111.6 (1051.8–1171.4) * | 1161.2 (1119.8–1202.7) # |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sordi, A.F.; Silva, B.F.; Silva, B.G.d.; Marques, D.C.d.S.; Ramos, I.M.; Camilo, M.L.A.; Mota, J.; Valdés-Badilla, P.; Peres, S.B.; Branco, B.H.M. Comparison between Measured and Predicted Resting Metabolic Rate Equations in Cross-Training Practitioners. Int. J. Environ. Res. Public Health 2024, 21, 891. https://doi.org/10.3390/ijerph21070891
Sordi AF, Silva BF, Silva BGd, Marques DCdS, Ramos IM, Camilo MLA, Mota J, Valdés-Badilla P, Peres SB, Branco BHM. Comparison between Measured and Predicted Resting Metabolic Rate Equations in Cross-Training Practitioners. International Journal of Environmental Research and Public Health. 2024; 21(7):891. https://doi.org/10.3390/ijerph21070891
Chicago/Turabian StyleSordi, Ana Flávia, Bruno Ferrari Silva, Breno Gabriel da Silva, Déborah Cristina de Souza Marques, Isabela Mariano Ramos, Maria Luiza Amaro Camilo, Jorge Mota, Pablo Valdés-Badilla, Sidney Barnabé Peres, and Braulio Henrique Magnani Branco. 2024. "Comparison between Measured and Predicted Resting Metabolic Rate Equations in Cross-Training Practitioners" International Journal of Environmental Research and Public Health 21, no. 7: 891. https://doi.org/10.3390/ijerph21070891
APA StyleSordi, A. F., Silva, B. F., Silva, B. G. d., Marques, D. C. d. S., Ramos, I. M., Camilo, M. L. A., Mota, J., Valdés-Badilla, P., Peres, S. B., & Branco, B. H. M. (2024). Comparison between Measured and Predicted Resting Metabolic Rate Equations in Cross-Training Practitioners. International Journal of Environmental Research and Public Health, 21(7), 891. https://doi.org/10.3390/ijerph21070891







