Improved Analytical Solution for Air–Boosted Vacuum Consolidation of Saturated Soil Using Eigenfunction Expansion Method

Abstract

Soft foundation consolidation engineering applications and experimental studies have proven the effectiveness of the air–boosted vacuum preloading method (AVP). The sand well consolidation theory, a typical axisymmetric consolidation, is adapted to analyze the whole consolidation process of the saturated soil by air–boosted vacuum preloading. The present analytical solution for air–boosted vacuum consolidation of the saturated soil is more suitable for application in a deep soft foundation. With the solving method, the general solution through separation of variables is used, which is mathematically used for the homogeneous partial differential equations. However, the partial differential equations for solving the consolidation of the AVP method are nonhomogeneous. Therefore, the eigenfunction expansion method for nonhomogeneous equations is proposed and validated in this study. Results showed that the improved analytical solution by the eigenfunction expansion method is more consistent with the numerical solution than that of the previous method using the general solution by separation of variables, which leads to a lower error ratio of less than 2%. The improved analytical solution can be used to predict the consolidation of deep foundations by air–boosted vacuum preloading effectively.

1. Introduction

Soft soil foundations often pose problems to civil engineers [1]. Limitations arising from self–weight and surcharge load consolidation promoted several other means of soil consolidation such as vacuum preloading, which was the most popular due to its lower cost, environmental friendliness, and rapid pace of construction [2]. However, the clogging effect problem and the increasing depth of the soil foundation require the introduction of additional technologies to broaden the scope of application of vacuum preloading. Therefore, a proposed idea was to inject the air between prefabricated vertical drains (PVDs) combined with vacuum preloading [3,4,5,6,7,8], which is called air–boosted vacuum preloading. As shown in Figure 1, additional booster pipes are set up between the PVDs in the vacuum preloading system to inject the high–pressure gas into the soil so that the increased pressure between the soil and the PVDs promotes the directional flow of free water to PVDs and generates more fissures, thereby improving the consolidation behavior of the soil.

The AVP method has been successfully applied in many projects of soft ground treatment [4,5,6,9,10,11,12,13], and it has proven that the AVP method can effectively accelerate the consolidation of soft soil [14,15,16]. What is more, both the analysis of microstructure characteristics of the dredged soil [17] and the clogging effect study [18] have demonstrated that the reinforcement effect of the AVP method is superior to that of the conventional vacuum preloading method. However, there are many influential factors on the consolidation of the air–boosted vacuum preloading method in practical engineering, and the determination of that depends much more on experience, such as the pressurized value, positions, duration, etc. Therefore, different laboratory experiments [19,20,21] were designed to explore the appropriate value of the influential factors. For example, Anda et al. [20] pointed out that the best pressurizing time for the use of an air booster is the time when the soil had been consolidated to a degree of consolidation of 60%.

In addition to the experimental methods, theoretical analyses could be reliable to study the influential factors on the effect of the air–boosted vacuum preloading method as well. The consolidation theory of the VP method is simplified as an axisymmetric problem belonging to the symmetry problem, known as the sand well theory. According to the working mechanism of the AVP method, the consolidation theory of the AVP method can be also based on the sand well theory. Existing studies [22,23] have addressed that the effects of boosted air have a boosting effect [24] and a puncturing effect, as shown in Figure 2.

The existing consolidation theories [25,26,27,28,29] for soft clays improved by the AVP method are based on the sand well theory considering one of the effects of the boosted air. Hu et al. [25] only considered the puncturing effect of boosted air, belonging to the condition as shown in Figure 2b. With the injection of the boosted air, a highly permeable layer was formed with the monolayer soil taking on a multilayer form, and then, the sand well theory of the layered foundation was used to study the influential factors on the AVP method. Correspondingly, Shen et al. [26,28] simplified the boosted air as an even load applied at the boundary as shown in Figure 2a, and they adopted the analytical solution of one–dimensional drainage radial consolidation of the monolayer and double–layer soil foundation based on assumptions similar to those proposed by Barron [30] and Hansbo [31]. The consolidation theory proposed by Hu et al. over–amplified the puncturing effect but ignored the boosting effect. As the AVP method is proposed for the deep soft foundation, the injected air is mainly performed as the elastic–plastic expansion, i.e., the boosting effect. Thus, the consolidation theory proposed by Shen et al. needs further study.

This study intends to improve the analytical estimation of the settlement of the AVP soft foundation by solving the nonhomogeneous consolidation equations through the eigenfunction expansion method. Application of analytical formula is an efficient way to predict the settlement of the AVP soft foundation. However, there is a quite deviation from the previous analytical solution (Shen et al. [26,28]) from the site measured result in the later half period when the air booster is working. The main reason is that they use the general solution through separation of variables which is usually for homogeneous equations; therefore, the initial and boundary conditions are difficult to adapt to the changing process of pore water pressure in nonhomogeneous equations of AVP soft foundation. As shown in Figure 3, the aim of this study is to (1) introduce the governing equations and the initial and boundary conditions based on the radio consolidation assumptions proposed by Barron [30] and Hansbo [31]; (2) to propose a new solving method of eigenfunction expansion which is more adapted to the nonhomogeneous equations than that of the previous study (Shen et al. [26,28]); (3) to compare the newly proposed solution and the previous solution; and finally (4) to investigate the main influential factors on the AVP consolidation by parametric study, which could provide some suggestions for the application of the AVP method in a deep soft foundation.

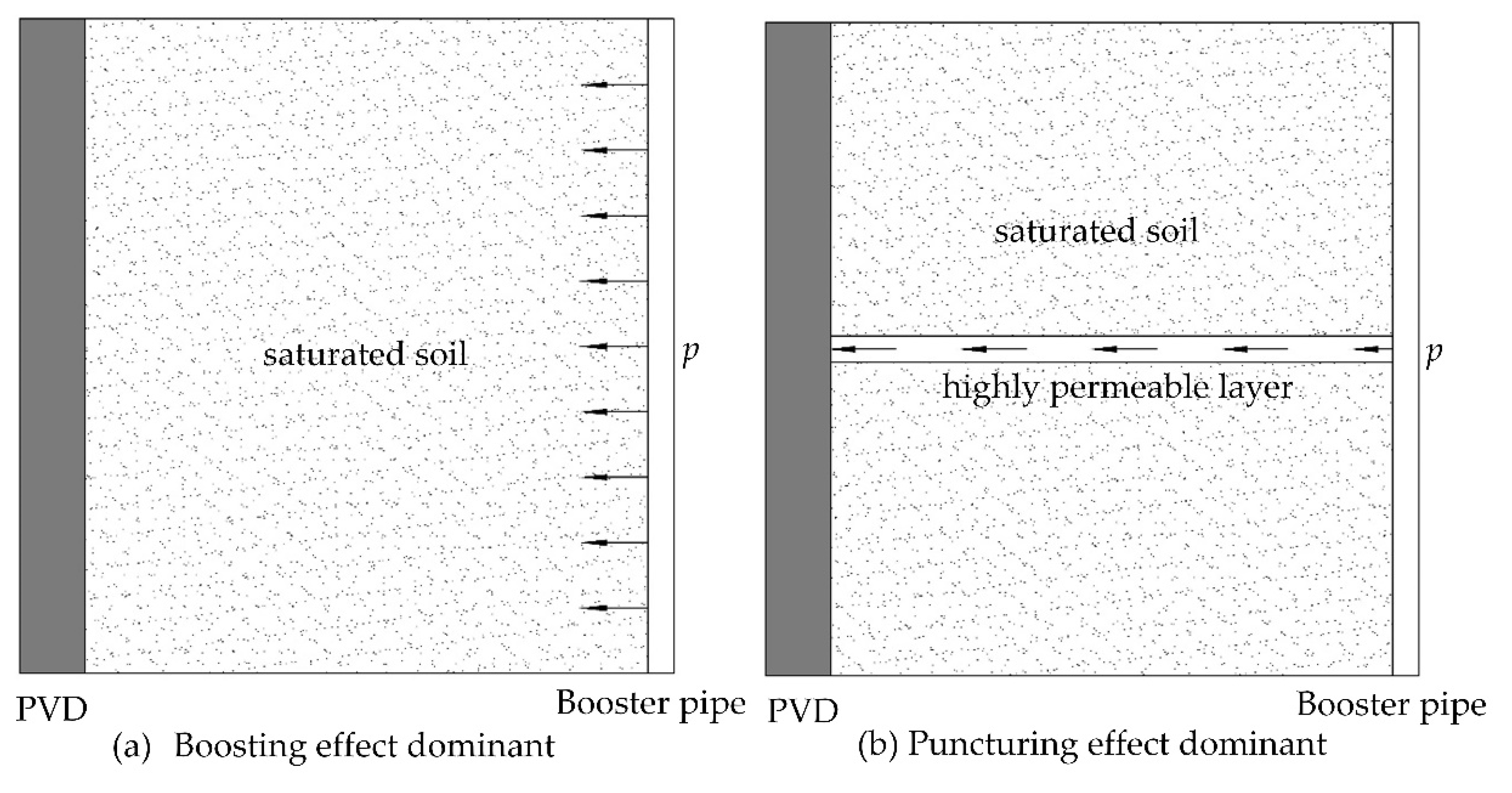
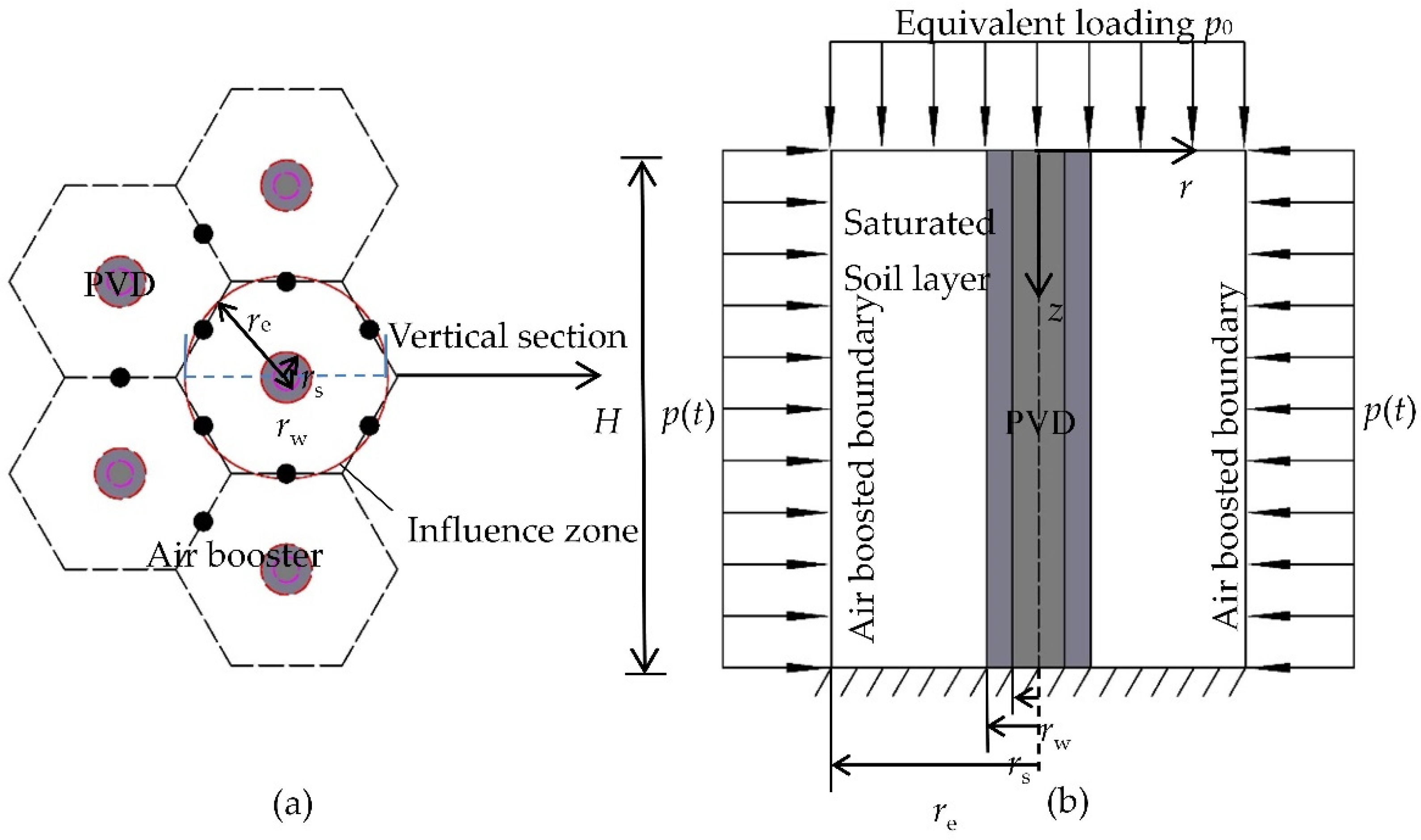
2. Mathematical Modeling

2.1. Governing Equations

Working in association with air boosters, prefabricated vertical drains (PVDs) are usually arranged in a triangular pattern, as shown in Figure 4a. Figure 4b illustrates the simplified elevation of a typical system with air boosters that penetrates a saturated soil stratum. This system consists of a typical drain with the radius of r_w, the smear zone with the radius of r_s, and its influence zone with the radius of r_e. The thickness of this system is H. On the top surface of this system, the vacuum pressure, equivalent to p₀, is applied uniformly. The top surface of this system is considered to be pervious, while the bottom base is assumed to be impervious. During the mathematical derivations, this study adopts assumptions that are similar to those proposed by Barron [30] and Hansbo [31]. It was assumed that:

(1) Equal strain conditions were satisfied, i.e., for every point at the same depth, the vertical deformation was equal.

(2) Lateral deformation was ignored.

(3) Only the radial seepage was considered.

(4) Darcy’s law was valid.

(5) The undisturbed soil and smear area properties were the same, but the permeability coefficients differed.

(6) The radial seepage and pore pressure change along the radial direction in the vertical drain were neglected.

(7) When PVDs were the drainage channels, they were equivalent to the simplified vertical drain and obtained the equivalent vertical drain diameter (d_w) using Equation (1) [31].

$$d_{\mathrm{w}}=\frac{2\left(b+\delta \right)}{\pi }$$

(1)

where b and δ are the interfacial width and the thickness of the PVDs, respectively.

In addition, with the air booster installed between the PVDs, the air booster injects the high–pressure air into the soil, which is equivalent to applying a radial pressure (p(t) in Figure 4b) on the outer radius of the influence zones of the drains. The pressure p(t) is the function of time, as described in Equation (2).

$$p\left(t\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{p}{t_1}t& t<t_1\end{array}\\ \begin{array}{cc}p& t\ge t_1\end{array}\end{array}\right.$$

(2)

where t₁ is when the confining pressure reaches p caused by the boosted air; after t₁, p(t) remains stable as p.

The governing equation of radial consolidation under equal strain assumption is as follows [32]:

$$\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}=-\frac{1}{E_{\mathrm{s}}}\frac{\partial {\overline{u}}_{\mathrm{r}}}{\partial t}$$

(3)

$$-\frac{k_{\mathrm{s}}}{{\gamma }_{\mathrm{w}}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{\mathrm{r}}}{\partial r}\right)=\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}\begin{array}{cc}& r_{\mathrm{w}}\le r\end{array}\le r_{\mathrm{s}}$$

(4)

$$-\frac{k_{\mathrm{h}}}{{\gamma }_{\mathrm{w}}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{\mathrm{r}}}{\partial r}\right)=\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}\begin{array}{cc}& r_{\mathrm{s}}\le r\end{array}\le r_{\mathrm{e}}$$

(5)

$$\frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}=-\frac{2k_{\mathrm{s}}}{r_{\mathrm{w}}{k}_{\mathrm{w}}}\frac{\partial u_{\mathrm{r}}}{\partial r}\left|{}_{r=r_{\mathrm{w}}}\right.$$

(6)

where E_s is the modulus of compressibility of the soil, ε_v is the volumetric strain of the soil in the influence zone, t is time, ${\overline{u}}_{\mathrm{r}}$ is the average pore water pressure in the soil, u_r and u_w are the pore water pressure within the influence zone, and the vertical drain at any point considered radial seepage only, respectively. k_h, k_s are the horizontal permeability coefficients of the soil in the undisturbed area and the smear zone, respectively, k_w is the permeability coefficient of the PVDs, r is the radial coordinate, r_w, r_s, r_e represent the radius of the vertical drain, the smear zone, and the influence zone, respectively, and γ_w is the unit weight of water.

2.2. Definite Conditions

As the governing equation is known, some general but definite conditions were necessary to solve it. According to the assumptions, initial conditions and boundary conditions were:

$$u_r\left|{}_{r=r_{\mathrm{e}}}\right.=p\left(t\right)$$

(7)

$$u_r\left|{}_{r=r_{\mathrm{w}}}\right.=u_{\mathrm{w}}$$

(8)

$$k_{\mathrm{h}}\frac{\partial u_{\mathrm{e}}}{\partial r}\left|{}_{r=r_{\mathrm{s}}}\right.=k_{\mathrm{s}}\frac{\partial u_{\mathrm{s}}}{\partial r}\left|{}_{r=r_{\mathrm{s}}}\right.$$

(9)

$$u_{\mathrm{s}}\left|{}_{r=r_{\mathrm{s}}}\right.=u_{\mathrm{e}}\left|{}_{r=r_{\mathrm{s}}}\right.$$

(10)

$${\overline{u}}_{\mathrm{r}}\left|{}_{t=0}\right.=u_0=p_0$$

(11)

$$u_{\mathrm{w}}\left|{}_{z=0}\right.=0$$

(12)

$$\frac{\partial u_{\mathrm{w}}}{\partial z}\left|{}_{z=l}\right.=0$$

(13)

where u_e, u_s are the pore water pressure in the influence zone and the smear zone at any depth, respectively, when considering radial seepage alone, u₀ is the initial pore water pressure, and l is the maximum distance of vertical drains. Equations (7)–(13) have their physical meaning. Equation (7) defines the boundary pressure at the influence zone as the same as that of the boosted air. Similarly, Equation (8) indicates that the pore water pressure is continuous at the junction of the vertical drain and the soil. Equations (9) and (10) show that the flow and pore water pressure are identical in the influence and smear zones. Equation (11) was the initial condition; that is, the initial average pore water pressure was equal to the equivalent vacuum pressure p₀; Equations (12) and (13) represent drainage boundary and nondrainage boundary, respectively. All the physical meanings of the above symbols are in the list of nomenclature.

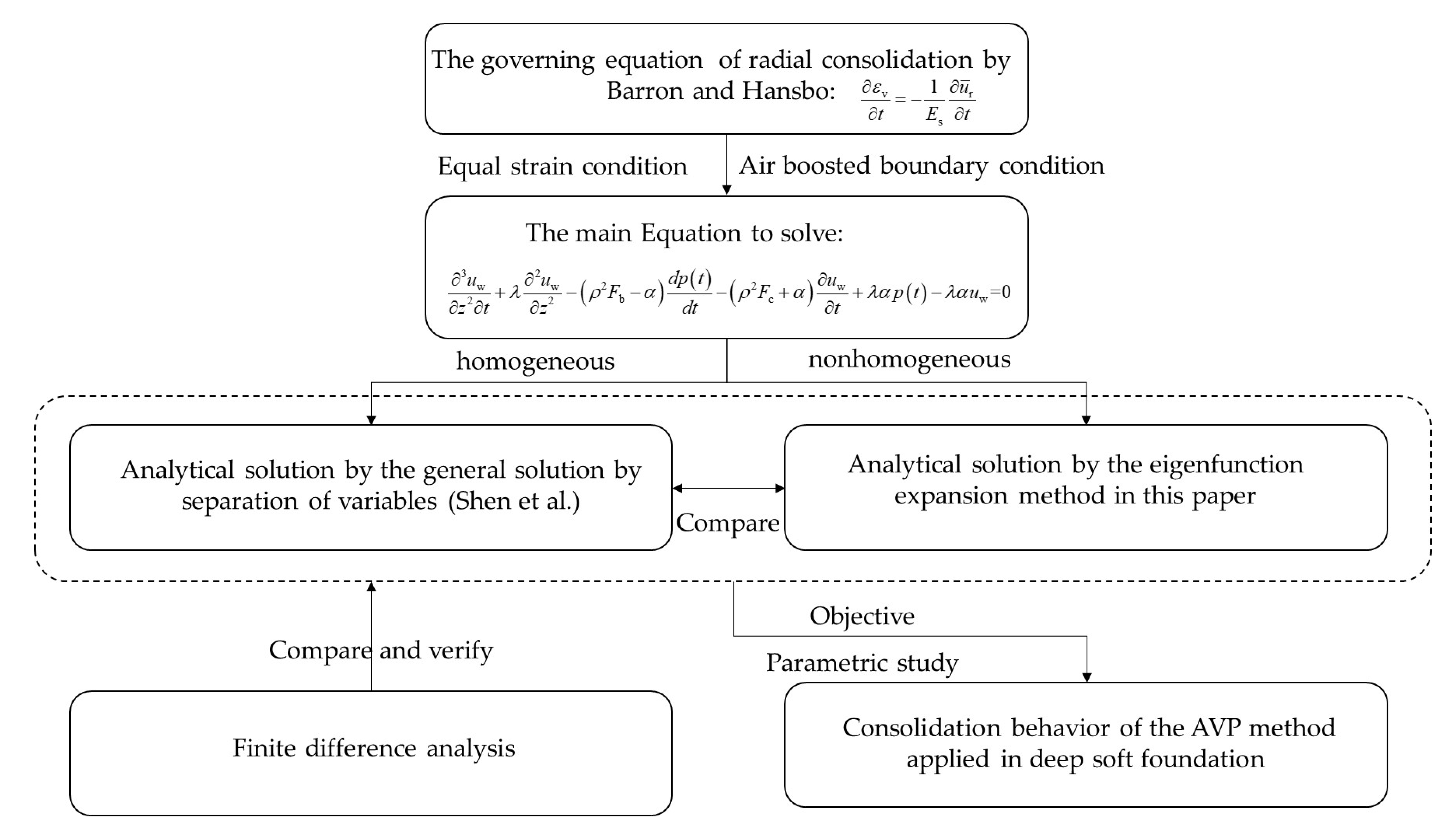
3. Solutions

No matter which method is used to obtain the analytical solution for air–boosted vacuum consolidation of saturated soil, the solution procedure is the same, that is, finding the relationship between ${\overline{u}}_{\mathrm{r}}$ and u_w based on the governing equations, then eliminating ${\overline{u}}_{\mathrm{r}}$, establishing the relationship among u_w, z, t, and p(t), finally back calculating ${\overline{u}}_{\mathrm{r}}$ and u_r.

3.1. The Analytical Solution of Shen et al.

By integrating Equations (4) and (5) with respect to r and using the boundary conditions Equations (7)–(10), Equations (14)–(17) can be obtained:

$$\frac{\partial u_{\mathrm{r}}}{\partial r}=-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{s}}}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}\frac{r}{2}+\frac{p\left(t\right)-u_{\mathrm{w}}}{\eta r}+\frac{-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{s}}}\frac{r_{\mathrm{w}}{}^2-r_{\mathrm{s}}{}^2}{4}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{h}}}\frac{r_{\mathrm{s}}{}^2-r_{\mathrm{e}}{}^2}{4}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}}{\eta r}\begin{array}{cc}& r_{\mathrm{w}}\le r\end{array}\le r_{\mathrm{s}}$$

(14)

$$\frac{\partial u_{\mathrm{r}}}{\partial r}=-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{h}}}\frac{r}{2}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\left[\frac{p\left(t\right)-u_{\mathrm{w}}}{\eta r}-\frac{-\frac{{\gamma }_{\mathrm{w}}}{k_s}\frac{r_{\mathrm{w}}{}^2-r_{\mathrm{s}}{}^2}{4}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{{\gamma }_{\mathrm{w}}}{k_h}\frac{r_{\mathrm{s}}{}^2-r_{\mathrm{e}}{}^2}{4}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}}{\eta r}\right]\begin{array}{cc}& r_{\mathrm{s}}\le r\end{array}\le r_{\mathrm{e}}$$

(15)

$$u_{\mathrm{r}}=-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{s}}}\left(\frac{r^2-r_{\mathrm{w}}^2}{4}+\frac{r_{\mathrm{w}}^2-r_{\mathrm{s}}^2}{4\eta }\ln \left(\frac{r}{r_{\mathrm{w}}}\right)\right)\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{h}}}\frac{r_{\mathrm{e}}^2-r_{\mathrm{s}}^2}{4\eta }\ln \left(\frac{r}{r_{\mathrm{w}}}\right)\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{p\left(t\right)-u_{\mathrm{w}}}{\eta }\ln \left(\frac{r}{r_{\mathrm{w}}}\right)+u_{\mathrm{w}}\begin{array}{cc}& r_{\mathrm{w}}\le r\end{array}\le r_{\mathrm{s}}$$

(16)

$$\begin{array}{l}{u}_{\mathrm{r}}=-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{s}}}\left(\frac{r_{\mathrm{s}}^2-r_{\mathrm{w}}^2}{4}+\frac{r_{\mathrm{w}}^2-r_{\mathrm{s}}^2}{4\eta }\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \left(\frac{r}{r_{\mathrm{s}}}\right)+\ln \left(\frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right)\right)\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}-\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{h}}}\left(\frac{r^2-r_{\mathrm{s}}^2}{4}-\frac{r_{\mathrm{e}}^2-r_{\mathrm{s}}^2}{4\eta }\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \left(\frac{r}{r_{\mathrm{s}}}\right)+\ln \left(\frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right)\right)\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}\\ \begin{array}{cc}& +\frac{p\left(t\right)-u_{\mathrm{w}}}{\eta }\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \left(\frac{r}{r_{\mathrm{s}}}\right)+\ln \left(\frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right)+u_{\mathrm{w}}\begin{array}{cc}& r_{\mathrm{s}}\le r\end{array}\le r_{\mathrm{e}}\end{array}\end{array}$$

(17)

where $\eta =\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln n+\left(1-\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\right)\ln s$, $s=\frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}$ is the ratio of the radius of the smear zone to the vertical drain, $n=\frac{r_{\mathrm{e}}}{r_{\mathrm{w}}}$ is the ratio of the radius of the influence zone to the vertical drain.

The average pore water pressure at any depth in the soil is:

$${\overline{u}}_{\mathrm{r}}=\frac{1}{\pi \left(r_{\mathrm{e}}^2-r_{\mathrm{w}}^2\right)}{\displaystyle {\int }_{r_{\mathrm{w}}}^{r_{\mathrm{e}}}2\pi r{u}_{\mathrm{r}}}dr$$

(18)

Substituting Equations (16) and (17) into Equation (18) yields:

$${\overline{u}}_{\mathrm{r}}=\frac{{\gamma }_{\mathrm{w}}{r}_{\mathrm{e}}^2}{4k_{\mathrm{h}}}{F}_{\mathrm{a}}\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+F_{\mathrm{b}}p\left(t\right)+F_{\mathrm{c}}{u}_{\mathrm{w}}$$

(19)

where

$$\begin{array}{l}{F}_{\mathrm{a}}=\frac{1}{n^2\left(n^2-1\right)}\left[-\frac{1}{2}{\left(n^2-s^2\right)}^2\right]+\frac{n^2-s^2}{\left(n^2-1\right)\eta }·\\ \left\{\left[\ln s+\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\left(\ln \frac{n}{s}-\frac{1}{2}\right)\right]+\frac{s^2}{2n^2}\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}-1\right)+\frac{1}{2n^2}\right\}+\\ \\ \frac{k_{\mathrm{h}}}{k_{\mathrm{s}}}\left\{\frac{1}{n^2\left(n^2-1\right)}\left(\frac{1}{2}{s}^4+n^2-s^2{n}^2-\frac{1}{2}\right)+\frac{s^2-1}{\left(n^2-1\right)\eta }·\right.\\ \left.\left[\ln s+\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\left(\ln \frac{n}{s}-\frac{1}{2}\right)\right]+\frac{s^2-1}{\left(n^2-1\right)\eta }·\left[\frac{s^2}{2n^2}\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}-1\right)+\frac{1}{2n^2}\right]\right\}\end{array}$$

(20)

$$F_b=\frac{1}{\eta \left(n^2-1\right)}\left[\frac{1}{2}\left(1-s^2\right)+n^2\ln s+\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\left(n^2\ln s+\frac{1}{2}{s}^2-\frac{1}{2}{n}^2\right)\right]$$

(21)

$$F_{\mathrm{c}}=1-F_{\mathrm{b}}$$

(22)

Substituting Equation (14) into Equation (6) yields:

$$\begin{array}{ll}\frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}& =-\frac{2k_{\mathrm{s}}}{r_{\mathrm{w}}{k}_{\mathrm{w}}}\frac{\partial u_{\mathrm{r}}}{\partial r}\left|{}_{r=r_{\mathrm{w}}}\right.\\ & =\frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{w}}}\left[1+\frac{1-s^2}{2\eta }+\frac{\left(n^2-s^2\right)k_{\mathrm{s}}}{2\eta k_{\mathrm{h}}}\right]\frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}+\frac{2k_{\mathrm{s}}}{\eta k_{\mathrm{w}}{r}_{\mathrm{w}}^2}{u}_{\mathrm{w}}-\frac{2k_{\mathrm{s}}}{\eta k_{\mathrm{w}}{r}_{\mathrm{w}}^2}p\left(t\right)\end{array}$$

(23)

By combining Equations (3), (19), and (23), the following relations can be known:

$$\frac{\partial {\overline{u}}_{\mathrm{r}}}{\partial t}=-\lambda \left[{\overline{u}}_{\mathrm{r}}-F_{\mathrm{b}}p\left(t\right)-F_{\mathrm{c}}{u}_{\mathrm{w}}\right]$$

(24)

$$\frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}=-{\rho }^2\left[{\overline{u}}_{\mathrm{r}}-F_{\mathrm{b}}p\left(t\right)-F_{\mathrm{c}}{u}_{\mathrm{w}}\right]-\alpha p\left(t\right)+\alpha u_{\mathrm{w}}$$

(25)

where

$$\lambda =\frac{4E_{\mathrm{s}}{k}_{\mathrm{h}}}{{\gamma }_{\mathrm{w}}{F}_{\mathrm{a}}{r}_{\mathrm{e}}^2}=\frac{16c_{\mathrm{h}}}{d_{\mathrm{e}}^2{F}_{\mathrm{a}}}$$

(26)

$${\rho }^2=\frac{4k_{\mathrm{h}}}{k_{\mathrm{w}}{F}_{\mathrm{a}}{r}_{\mathrm{e}}^2}\left[1+\frac{1-s^2}{2\eta }+\frac{\left(n^2-s^2\right)k_{\mathrm{s}}}{2\eta k_{\mathrm{h}}}\right]$$

(27)

$$\alpha =\frac{2k_{\mathrm{s}}}{k_{\mathrm{w}}\eta r_{\mathrm{w}}^2}$$

(28)

In Equation (26), $c_{\mathrm{h}}=\frac{E_{\mathrm{s}}{k}_{\mathrm{h}}}{{\gamma }_{\mathrm{w}}}$, d_e is the diameter of the influence zone by the vertical drain.

Equations (24) and (25) are combined, and ${\overline{u}}_{\mathrm{r}}$ eliminated:

$$\frac{{\partial }^3{u}_{\mathrm{w}}}{\partial z^2\partial t}+\lambda \frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}-\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)\frac{dp\left(t\right)}{dt}-\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)\frac{\partial u_{\mathrm{w}}}{\partial t}+\lambda \alpha p\left(t\right)-\lambda \alpha u_{\mathrm{w}}=0$$

(29)

According to the relationship of p(t) with t, the Equation (29) can be rewritten as:

$$\frac{{\partial }^3{u}_{\mathrm{w}}}{\partial z^2\partial t}+\lambda \frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}-\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)\frac{\partial u_{\mathrm{w}}}{\partial t}-\lambda \alpha u_{\mathrm{w}}=\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)\frac{p}{t_1}-\lambda \alpha \frac{p}{t_1}t$$

(30)

The homogeneous form of Equation (30) is:

$$\frac{{\partial }^3{u}_{\mathrm{w}}}{\partial z^2\partial t}+\lambda \frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}-\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)\frac{\partial u_{\mathrm{w}}}{\partial t}-\lambda \alpha u_{\mathrm{w}}=0$$

(31)

The solution of Equation (30) in Shen et al. [26,28] uses the separation method of variables based on the premise that Equation (30) is a homogeneous partial differential equation. Therefore, the composition of the analytical solution is the general solution of Equation (31) and a particular solution of Equation (30).

As the separation method of variables is used, the general solution of Equation (31) is:

$$u_{\mathrm{w}}=\left(A\sin \beta z+B\cos \beta z\right)\exp \left(-B_{\mathrm{r}}t\right)$$

(32)

where $A=\frac{2}{M{F}_{\mathrm{c}}}\frac{\lambda -B_{\mathrm{r}}}{\lambda }\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]$; $F=\frac{-p}{\lambda \alpha t_1}{\rho }^2$; $B=0$; $\beta =\frac{M}{l},M=\frac{2m+1}{2}\pi ,m=0,1,2,\cdots$; $B_{\mathrm{r}}=\frac{\lambda \left(\alpha +{\beta }^2\right)}{{\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2}$.

Therefore, the general solution of Equation (30) can be obtained as:

$$u_{\mathrm{w}}=A\sin \frac{M}{l}z\exp \left(-B_{\mathrm{r}}t\right)+\phi \left(t\right)$$

(33)

where $\phi \left(t\right)=\exp \left(-Dt\right)+Et+F$, $D=\frac{\lambda \alpha }{{\rho }^2{F}_{\mathrm{c}}+\alpha }$, $E=\frac{p}{t_1}$.

Substituting $l=H$ into Equation (33),

$$u_{\mathrm{w}}=\frac{2}{M{F}_{\mathrm{c}}}\frac{\lambda -B_{\mathrm{r}}}{\lambda }\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}+\phi \left(t\right)$$

(34)

And

$$\begin{array}{ll}{\overline{u}}_{\mathrm{r}}& =\frac{2}{M}\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}\\ & +\left(F_{\mathrm{b}}-\frac{\alpha }{{\rho }^2}\right)p\left(t\right)+\left(F_{\mathrm{b}}+\frac{\alpha }{{\rho }^2}\right)\phi \left(t\right)\end{array}$$

(35)

By combining Equations (3), (14)–(17), and (35), the analytical solution of u_r is obtained as:

$$\begin{array}{l}{u}_{\mathrm{r}}=\left[\frac{k_{\mathrm{h}}}{k_{\mathrm{s}}}\left(\frac{1}{n^2}-\frac{r^2}{r_{\mathrm{e}}^2}\right)+\left(\frac{k_{\mathrm{h}}}{k_{\mathrm{s}}}\frac{s^2-1}{\eta n^2}+\frac{n^2-s^2}{\eta n^2}\right)\ln \frac{r}{r_{\mathrm{w}}}\right]·\\ \left\{\frac{2}{M}\frac{B_{\mathrm{r}}}{\lambda F_{\mathrm{a}}}\right.\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}+\\ \left.\frac{F_{\mathrm{b}}+F_{\mathrm{c}}}{-\lambda F_{\mathrm{a}}}\frac{p}{t_1}+\frac{\alpha }{F_a\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)}\exp \left(-\frac{\lambda \alpha }{\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)}t\right)\right\}+\\ \left(1-\frac{1}{\eta }\ln \frac{r}{r_{\mathrm{w}}}\right)\left\{\frac{2}{M{F}_{\mathrm{c}}}\frac{\lambda -B_{\mathrm{r}}}{\lambda }\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]\right.·\\ \left.{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}+\phi \left(t\right)\right\}+\ln \frac{r}{r_{\mathrm{w}}}\frac{p\left(t\right)}{\eta }\begin{array}{cc}& r_{\mathrm{w}}\le r\le r_{\mathrm{s}}\end{array}\end{array}$$

(36)

$$\begin{array}{l}{u}_{\mathrm{r}}=\left\{\frac{k_{\mathrm{h}}}{k_{\mathrm{s}}}\left[\frac{1-s^2}{n^2}+\frac{s^2-1}{\eta n^2}\left(\frac{k_{\mathrm{h}}}{k_{\mathrm{s}}}\ln \frac{r}{r_{\mathrm{s}}}+\ln \frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right]\right.+\\ \left.\left[\frac{s^2}{n^2}-\frac{r^2}{r_{\mathrm{e}}^2}+\frac{n^2-s^2}{\eta n^2}\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \frac{r}{r_{\mathrm{s}}}+\ln \frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right]\right\}·\\ \left\{\frac{2}{M}\frac{B_{\mathrm{r}}}{\lambda F_{\mathrm{a}}}\right.\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}+\\ \left.\frac{F_{\mathrm{b}}+F_{\mathrm{c}}}{-\lambda F_{\mathrm{a}}}\frac{p}{t_1}+\frac{\alpha }{F_{\mathrm{a}}\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)}\exp \left(-\frac{\lambda \alpha }{\left({\rho }^2{F}_{\mathrm{c}}+\alpha \right)}t\right)\right\}+\\ \left(1-\frac{1}{\eta }\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \frac{r}{r_{\mathrm{s}}}+\ln \frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\right)\left\{\frac{2}{M{F}_c}\frac{\lambda -B_{\mathrm{r}}}{\lambda }\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)F\right]\right.·\\ \left.{\displaystyle \sum _{m=0}^{\infty }\sin \frac{M}{H}z\exp \left(-B_{\mathrm{r}}t\right)}+\phi \left(t\right)\right\}+\left(\frac{k_{\mathrm{s}}}{k_{\mathrm{h}}}\ln \frac{r}{r_{\mathrm{s}}}+\ln \frac{r_{\mathrm{s}}}{r_{\mathrm{w}}}\right)\frac{p\left(t\right)}{\eta }\begin{array}{cc}& r_{\mathrm{s}}\le r\le r_{\mathrm{e}}\end{array}\end{array}$$

(37)

Equations (34)–(37) are the analytical solutions for soil consolidation under the AVP method from Shen et al. [26,28].

3.2. Improved Analytical Solution by Eigenfunction Expansion Method

The solutions by Shen et al. [26,28] do not satisfy all of the initial and boundary conditions:

(a). Equation (35) is the solution of ${\overline{u}}_{\mathrm{r}}$, and the initial condition is ${\overline{u}}_{\mathrm{r}}\left|{}_{t=0}\right.=u_0$. When substituting t = 0 into Equation (35), ${\overline{u}}_{\mathrm{r}}\left|{}_{t=0}\right.=u_0+\left(F_{\mathrm{b}}+\frac{\alpha }{{\rho }^2}\right)$, is not equal to u₀.

(b). Equation (34) is the solution of $u_{\mathrm{w}}$, and the boundary condition at z = 0 is $u_{\mathrm{w}}\left|{}_{z=0}\right.=0$. When substituting z = 0 into Equation (34), $u_{\mathrm{w}}=\phi \left(t\right)$, obviously, is not equal to zero.

Although some conclusions driven by Shen et al. [26,28] have reflected some truth of the consolidation of the soil foundation under the AVP method, the solution would not be accurate. Additionally, from the derivative process above, the main cause is the solution of Equation (30), which is the main equation that needs to be solved under these initial and boundary conditions to obtain the analytical solution of consolidation of the soil foundation under the AVP method. It should be noted that Equation (30) is a nonhomogeneous partial differential equation. Therefore, the method to solve Equation (30) as described above is not appropriate.

The eigenfunction expansion method is one of the most elegant techniques to solve the linear partial differential system considering the nonhomogeneous one, which is used to obtain the correct answer to Equation (30).

Taking both the radial and vertical boundary conditions (7) and (13) into account, herein we attempt to solve Equation (30) by proposing a solution of the following form as the same primary function as the general solution Equation (32):

$$u_{\mathrm{w}}={\displaystyle \sum _{m=0}^{\infty }{u}_m\left(t\right)}\sin \beta z$$

(38)

where $u_m\left(t\right)$ is an unknown function with the time that needs to be determined.

Meanwhile, the initial condition (11) and the nonhomogeneous part, i.e., the right part of Equation (30), should be rewritten with the same primary function to obtain the solution of $u_m\left(t\right)$:

$$\begin{array}{c}{\overline{u}}_r\left|{}_{t=0}\right.={\displaystyle \sum _{m=0}^{\infty }{F}_{\mathrm{c}}\left(\frac{\lambda }{\lambda -B_{\mathrm{r}}}\right)}\sin \beta z{u}_m\left(0\right)+\left(F_{\mathrm{b}}-\frac{\alpha }{{\rho }^2}\right)p\left(0\right)=u_0={\displaystyle \sum _{m=0}^{\infty }\frac{2}{M}{u}_0\sin \beta z}\\ u_m\left(0\right)=\frac{2u_0\left(\lambda -B_{\mathrm{r}}\right)}{M\lambda F_c}\end{array}$$

(39)

$$f\left(t\right)=-\lambda \alpha \frac{p}{t_1}t+\left({\rho }^2{F}_b-\alpha \right)\frac{p}{t_1}={\displaystyle \sum _{m=0}^{\infty }{f}_m\left(t\right)}\sin \beta z$$

(40)

where $f_m\left(t\right)=\frac{2}{l}{\displaystyle {\int }_0^l\sin \beta z·f}\left(t\right)dz=\frac{2}{M}f\left(t\right)=\frac{2}{M}\left(-\lambda \alpha \frac{p}{t_1}t+\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)\frac{p}{t_1}\right)$.

Substituting Equations (38) and (40) into Equation (30) yields:

$${u^{\prime }}_m\left(t\right)+\frac{\lambda \left(\alpha +{\beta }^2\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}{u}_m\left(t\right)=\frac{-f_m\left(t\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}$$

(41)

Let

$$B_{\mathrm{r}}=\frac{\lambda \left(\alpha +{\beta }^2\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}=\frac{\frac{16c_{\mathrm{h}}\left(M^2+\alpha l^2\right)}{d_{\mathrm{e}}^2{F}_{\mathrm{a}}{l}^2}}{\alpha +\frac{M^2}{l^2}+\frac{4k_{\mathrm{h}}}{k_{\mathrm{w}}{F}_{\mathrm{a}}{r}_{\mathrm{e}}^2}\left[1+\frac{1-s^2}{2\eta }+\frac{\left(n^2-s^2\right)k_{\mathrm{s}}}{2\eta k_{\mathrm{h}}}\right]G}$$

(42)

$$Q_m\left(t\right)=\frac{-f_m\left(t\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}=\frac{2}{M}\frac{-f\left(t\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}$$

(43)

wherein $G=\frac{k_{\mathrm{h}}}{k_{\mathrm{w}}}{\left(\frac{l}{d_{\mathrm{w}}}\right)}^2$ in Equation (42) is a well resistance factor and $Q_m\left(t\right)$ is a piecewise function, expressed as:

$$Q_m\left(t\right)=\left\{\begin{array}{cc}\frac{2}{M}\frac{-\left(-\lambda \alpha \frac{p}{t_1}t+\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)\frac{p}{t_1}\right)}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}& t\le t_1\\ \frac{2}{M}\frac{\lambda \alpha p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)}& t>t_1\end{array}\right.$$

(44)

Thus, the expression of $u_m\left(t\right)$ can be obtained based on Equations (39) and (41), when t ≤ t₁:

$$\begin{array}{l}{u}_m\left(t\right)=\frac{2}{M}\left(\frac{\lambda \alpha pt}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}-\frac{\lambda \alpha p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}^2}-\frac{\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}\right)\\ \begin{array}{cc}& +\end{array}\left\{\frac{2}{M}\left(\frac{\lambda \alpha p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}^2}+\frac{\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}\right)+\frac{2u_0\left(\lambda -B_{\mathrm{r}}\right)}{M\lambda F_{\mathrm{c}}}\right\}{e}^{-B_{\mathrm{r}}t}\end{array}$$

(45)

Let $u\left(t\right)$ be as follows:

$$\begin{array}{l}u\left(t\right)=\left(\frac{\lambda \alpha pt}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}-\frac{\lambda \alpha p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}^2}-\frac{\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}\right)\\ \begin{array}{cc}& +\end{array}\left(\frac{\lambda \alpha p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}^2}+\frac{\left({\rho }^2{F}_{\mathrm{b}}-\alpha \right)p}{\left({\rho }^2{F}_{\mathrm{c}}+\alpha +{\beta }^2\right)t_1{B}_{\mathrm{r}}}+\frac{u_0\left(\lambda -B_{\mathrm{r}}\right)}{\lambda F_{\mathrm{c}}}\right)e^{-B_{\mathrm{r}}t}\end{array}$$

(46)

Therefore, the term $u_{\mathrm{w}}$ can be expressed as:

$$u_{\mathrm{w}}={\displaystyle \sum _{m=0}^{\infty }\frac{2}{M}u\left(t\right)}\sin \frac{M}{H}z$$

(47)

Then, the expression of ${\overline{u}}_{\mathrm{r}}$ is:

$${\overline{u}}_{\mathrm{r}}={\displaystyle \sum _{m=0}^{\infty }\frac{2}{M}{F}_{\mathrm{c}}\frac{\lambda }{\lambda -B_{\mathrm{r}}}}\sin \frac{M}{H}z·u\left(t\right)+\left(F_{\mathrm{b}}-\frac{\alpha }{{\rho }^2}\right)\frac{p}{t_1}t$$

(48)

The solutions for $u_{\mathrm{w}}$ and ${\overline{u}}_{\mathrm{r}}$ are valid when 0 ≤ t ≤ t₁.

Shen et al. [26,28] have the potential assumption that the whole consolidation time t < t₁; however, as the p(t) was equal to a constant p, i.e., the relationship of p(t) and t is described in Equation (2), the Equations (34)–(37) are not valid when the consolidation time t > t₁. Therefore, the solutions of $u_m\left(t\right)$, $u\left(t\right)$, and ${\overline{u}}_{\mathrm{r}}$ when the time t > t₁ is:

$$\begin{array}{l}{u}_m\left(t\right)=\frac{2}{M}\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)B_r}+\left\{\left(-\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r^2}-\frac{\left({\rho }^2{F}_b-\alpha \right)p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r}\right)\right.\frac{2}{M{e}^{-B_r{t}_1}}\\ \begin{array}{cc}& \end{array}\left.+\frac{2}{M}\left(\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r^2}+\frac{\left({\rho }^2{F}_b-\alpha \right)p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r}\right)+\frac{2u_0\left(\lambda -B_r\right)}{M\lambda F_c}\right\}{e}^{-B_{r}t}\end{array}$$

(49)

$$\begin{array}{l}u\left(t\right)=\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)B_r}+\left\{\left(-\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r^2}-\frac{\left({\rho }^2{F}_b-\alpha \right)p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r}\right)\right.\frac{1}{e^{-B_r{t}_1}}\\ \begin{array}{cc}& \end{array}\left.+\frac{\lambda \alpha p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r^2}+\frac{\left({\rho }^2{F}_b-\alpha \right)p}{\left({\rho }^2{F}_c+\alpha +{\beta }^2\right)t_1{B}_r}+\frac{u_0\left(\lambda -B_r\right)}{\lambda F_c}\right\}{e}^{-B_{r}t}\end{array}$$

(50)

$${\overline{u}}_{\mathrm{r}}={\displaystyle \sum _{m=0}^{\infty }\frac{2}{M}{F}_{\mathrm{c}}\frac{\lambda }{\lambda -B_{\mathrm{r}}}}\sin \beta z·u\left(t\right)+\left(F_{\mathrm{b}}-\frac{\alpha }{{\rho }^2}\right)p$$

(51)

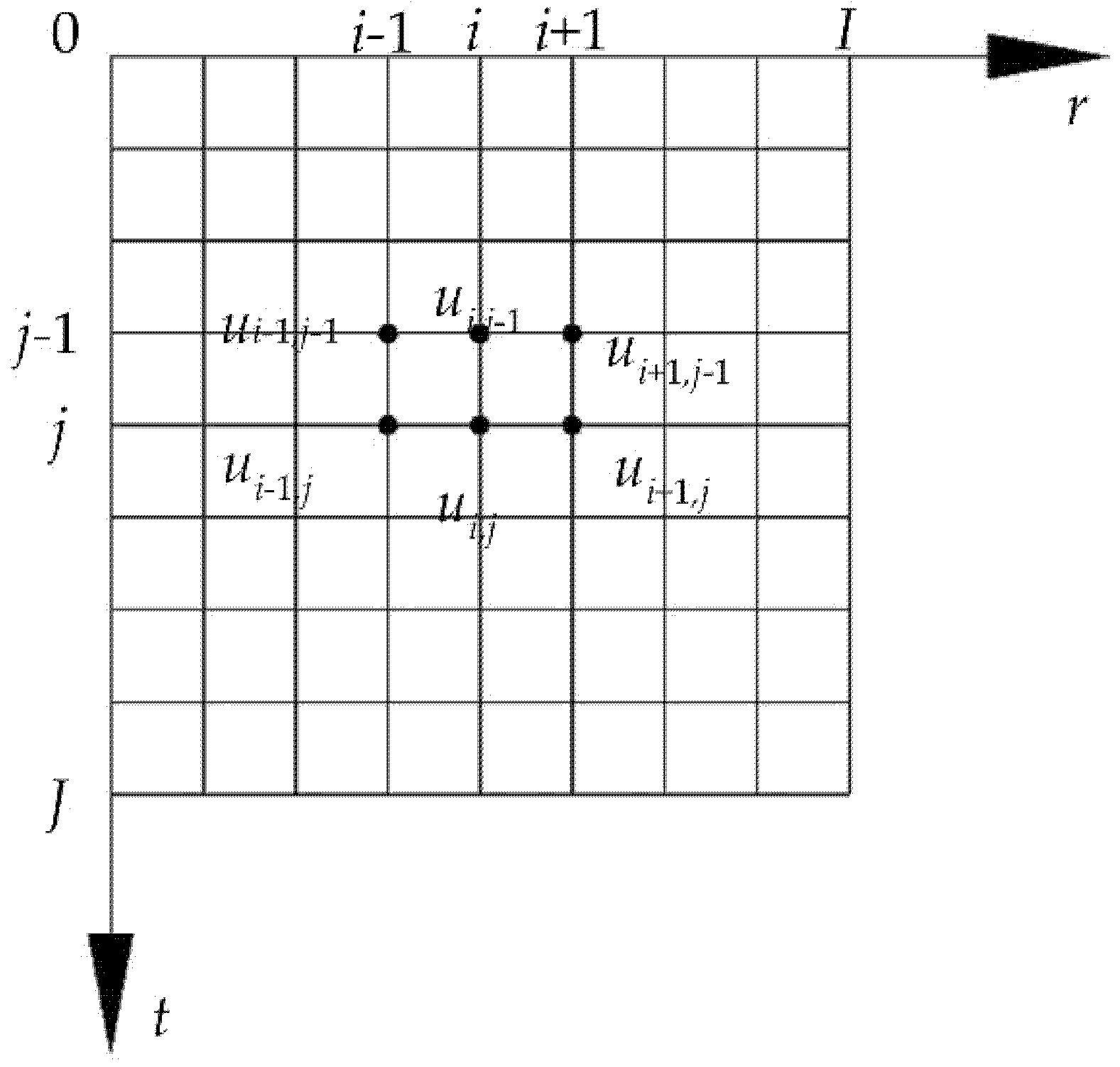
3.3. Finite Difference Analysis

Based on the basic principle of the finite difference method, with the radius r (the radial difference $r_{\mathrm{e}}-r_{\mathrm{w}}$) as the horizontal axis and time t as the vertical axis, a calculation for soil foundation consolidation analysis that considers only the radial seepage is established. The radius r was divided into I equal divisions, where I₁ was the dividing point of the undisturbed zone and the smeared zone, and the time T was divided into J equal divisions so that a different method calculation grid was established. As shown in Figure 5, the node in the grid represents the pore water pressure u, where u_i,j represents the value of the pore water pressure at the radius $i\frac{r_{\mathrm{e}}-r_{\mathrm{w}}}{I}$ between the influence radius r_e and the radius of vertical drain r_w at time $j\frac{T}{J}$.

If the vertical seepages were ignored, the initial and boundary conditions represented by Equations (12) and (13) would also be ignored so that other Equations (7)–(11) in the difference equation may be transformed as:

$$\left\{\begin{array}{c}{u}_{j,I}=p\left(t\right)\\ u_{j,1}=0\\ k_{j,I_1-1}\frac{u_{j,I_1}-u_{j,I_1-1}}{\Delta r}=k_{j,I_1+1}\frac{u_{j,I_1+1}-u_{j,I_1}}{\Delta r}\\ u_{0,i}=p_0\end{array}\right.$$

(52)

For the governing Equation (4) or (5), the central difference format discretizes the following difference format:

$$\begin{array}{ll}\frac{u_{j,i}-u_{j-1,i}}{\Delta t}& =c_{\mathrm{h}}{}_{\left(j-1,i\right)}\frac{\left(u_{j-1,i+1}-2u_{j-1,i}+u_{j-1,i-1}\right)}{{\left(\Delta r\right)}^2}\\ & +\frac{c_{\mathrm{h}}{}_{\left(j-1,i\right)}}{r_{\mathrm{w}}+\left(i-1\right)\Delta r}\frac{u_{j-1,i+1}-u_{j-1,i-1}}{2\Delta r}\end{array}$$

(53)

where $\Delta t=t/J$, $\Delta r=\left(r_{\mathrm{e}}-r_{\mathrm{w}}\right)/I$. Additionally, the straightforward solution is adopted because it is more convenient to compute for accuracy.

4. Solution Verification

Soil consolidation when k_w→∞, G = 0, and B_r = λ, is known as consolidation without well resistance. When the smear effects are also ignored, a particular case for consolidation without well resistance is called consolidation with an ideal well.

The calculated parameters of the soil layer are taken as Shen et al. [26]: r_w = r_s = 0.05 m, r_e = 0.5 m, k_h = k_s = 2.0 × 10⁻⁹ m/s, E_s = 2.49 × 10³ kPa, k_w = 1.0 × 10⁻² m/s, u₀ = 80 kPa, and p = 20 kPa.

Based on the consolidation with an ideal well and the parameters of the soil layer, the finite difference solution and the existing analytical solution are presented and discussed to verify the correctness of the developed analytical solution.

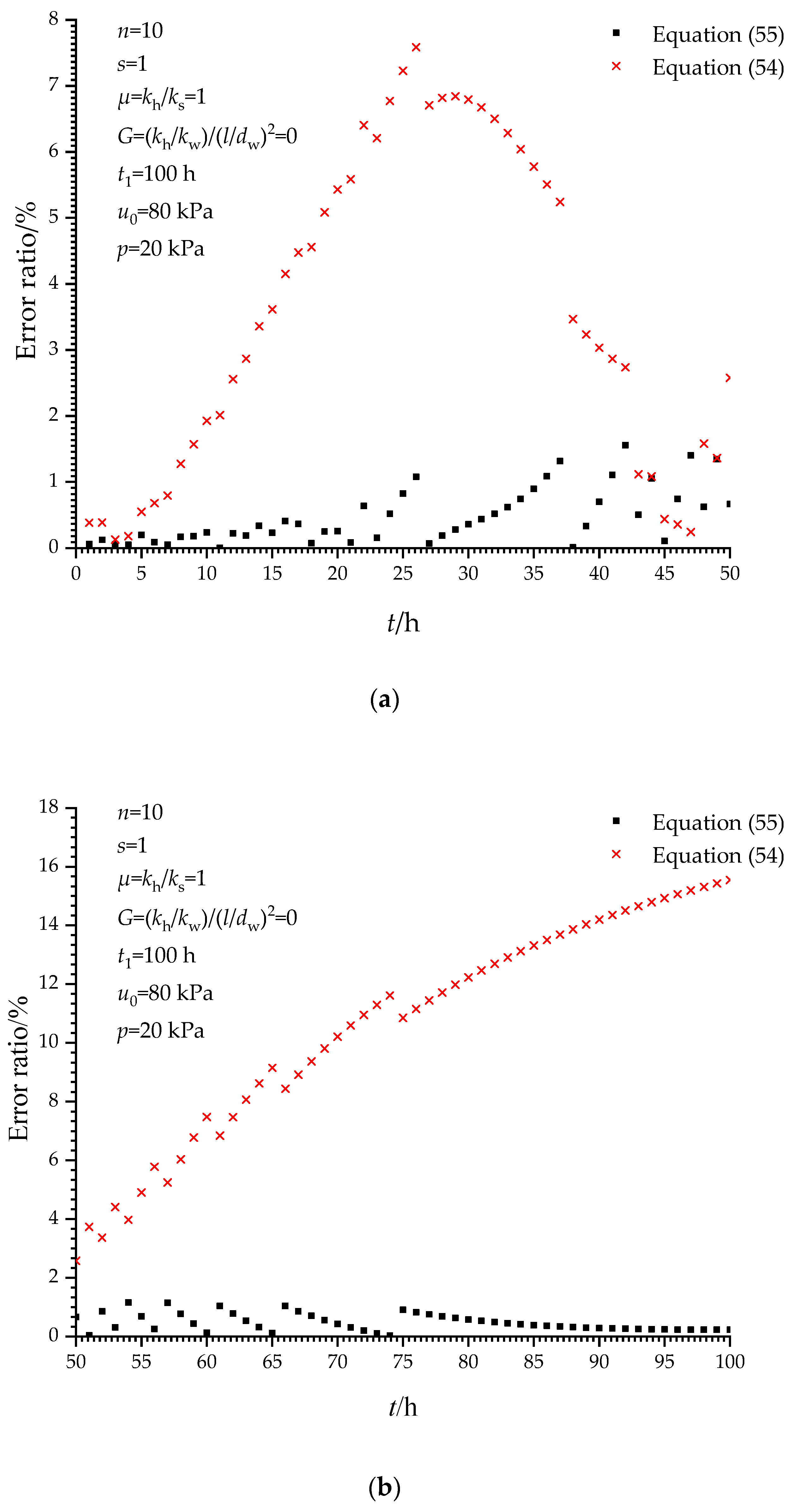
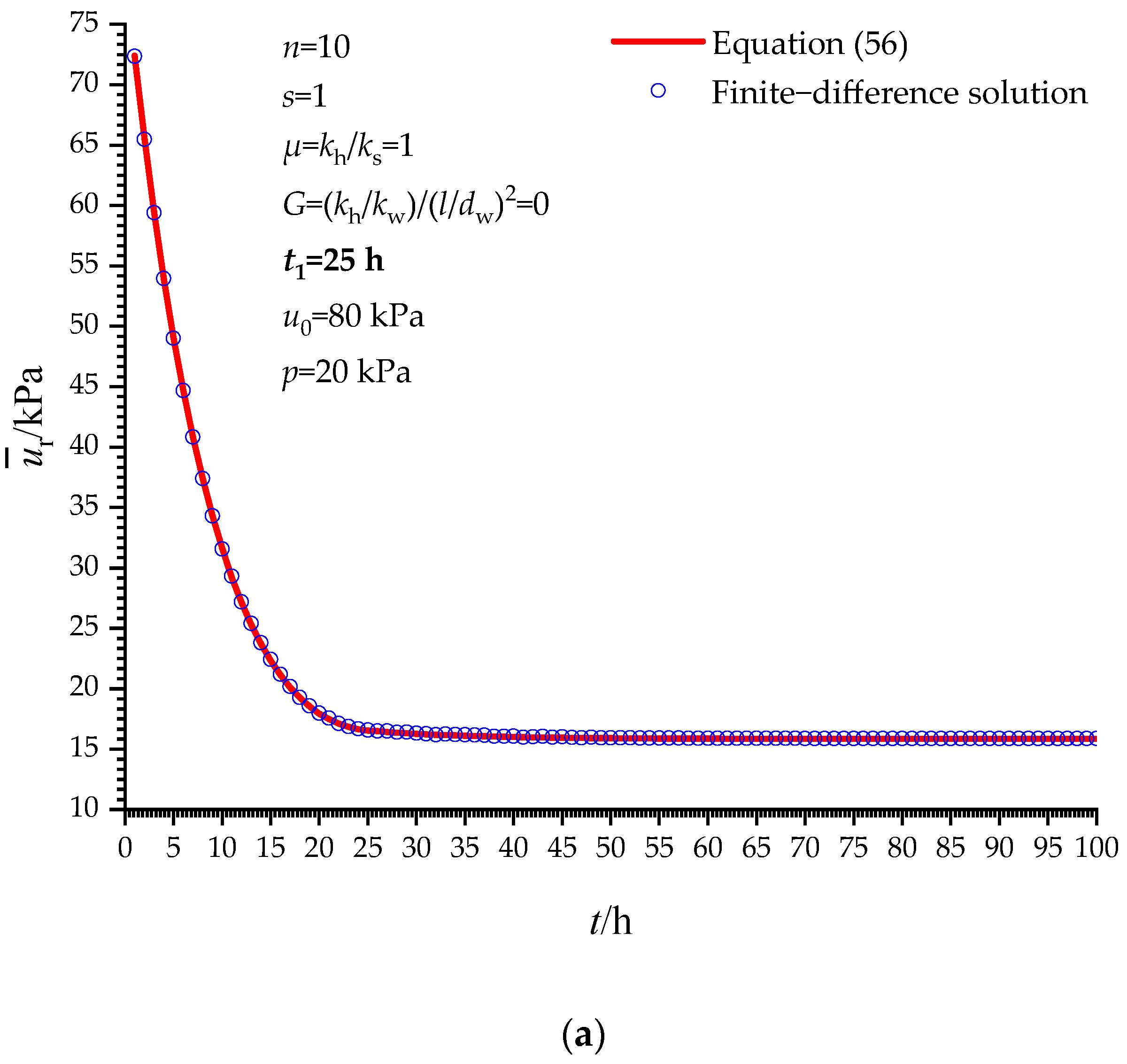
4.1. Verification When t ≤ t₁

When the condition of the consolidation with an ideal well is substituted to Equations (35) and (51), the solutions of ${\overline{u}}_{\mathrm{r}}$ can be obtained using the solution of Shen et al. [26,28] and the improved solution by the eigenfunction expansion method, respectively, when the consolidation time t < t₁:

$$\begin{array}{ll}{\overline{u}}_{\mathrm{r}1}& =\left[u_0-\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)\frac{-p}{\lambda \alpha t_1}{\rho }^2\right]\exp \left(-\lambda t\right)+\left(F_{\mathrm{b}}-\frac{\alpha }{{\rho }^2}\right)\frac{p}{t_1}t\\ & +\left(F_{\mathrm{c}}+\frac{\alpha }{{\rho }^2}\right)\left(\exp \left(-\frac{\lambda \alpha }{{\rho }^2{F}_{\mathrm{c}}+\alpha }t\right)+\frac{p}{t_1}t+\frac{-p}{\lambda \alpha t_1}{\rho }^2\right)\end{array}$$

(54)

$${\overline{u}}_{\mathrm{r}2}=\left(\frac{F_{\mathrm{b}}pt}{t_1}-\frac{F_{\mathrm{b}}p}{t_1\lambda }\right)+\left(\frac{F_{\mathrm{b}}p}{t_1\lambda }+u_0\right)e^{-\lambda t}$$

(55)

where ${\overline{u}}_{\mathrm{r}1}$ is the solution of Shen et al. [26,28] and ${\overline{u}}_{\mathrm{r}2}$ is the solution in this paper.

By using the parameters of the soil layer and t₁ = 100 h, the average pore pressures are calculated from Equations (54) and (55), and the results are illustrated in Figure 6. As a comparison, the result using the finite difference method is also plotted in Figure 6. Additionally, the deviation of average pore water pressure between the analytical solutions and the finite difference solution are plotted in Figure 7, where the error ratio is the difference between analytical solutions and the finite difference solution to the finite difference solution.

As shown in Figure 6a and Figure 7a, when t ≤ 50 h, the results provided by the above analytic solutions are in good agreement with that of the finite difference method, but the newly improved analytic solution (Equation (55)) is closer to the finite difference solution with the maximum error ratio < 2%, which is smaller than that of the analytic solution by Shen et al. (7.5%) [26]. It can be seen from Figure 6b and Figure 7b that when t > 50 h, the analytical solution by Equation (55) is still in good agreement with that of the finite difference solution with the error ratio less than 2%; however, the analytical solution by the general method of separation of variables (Equation (54)) is largely deviating from the numerical solution with the error ratio up to 16%. That means the formula solution of Equation (55) solved by the eigenfunction expansion method can reflect variations in the pore water pressure during the entire consolidation period when the air booster is working, whereas Equation (54) could not reflect these variations well, especially in the later half period.

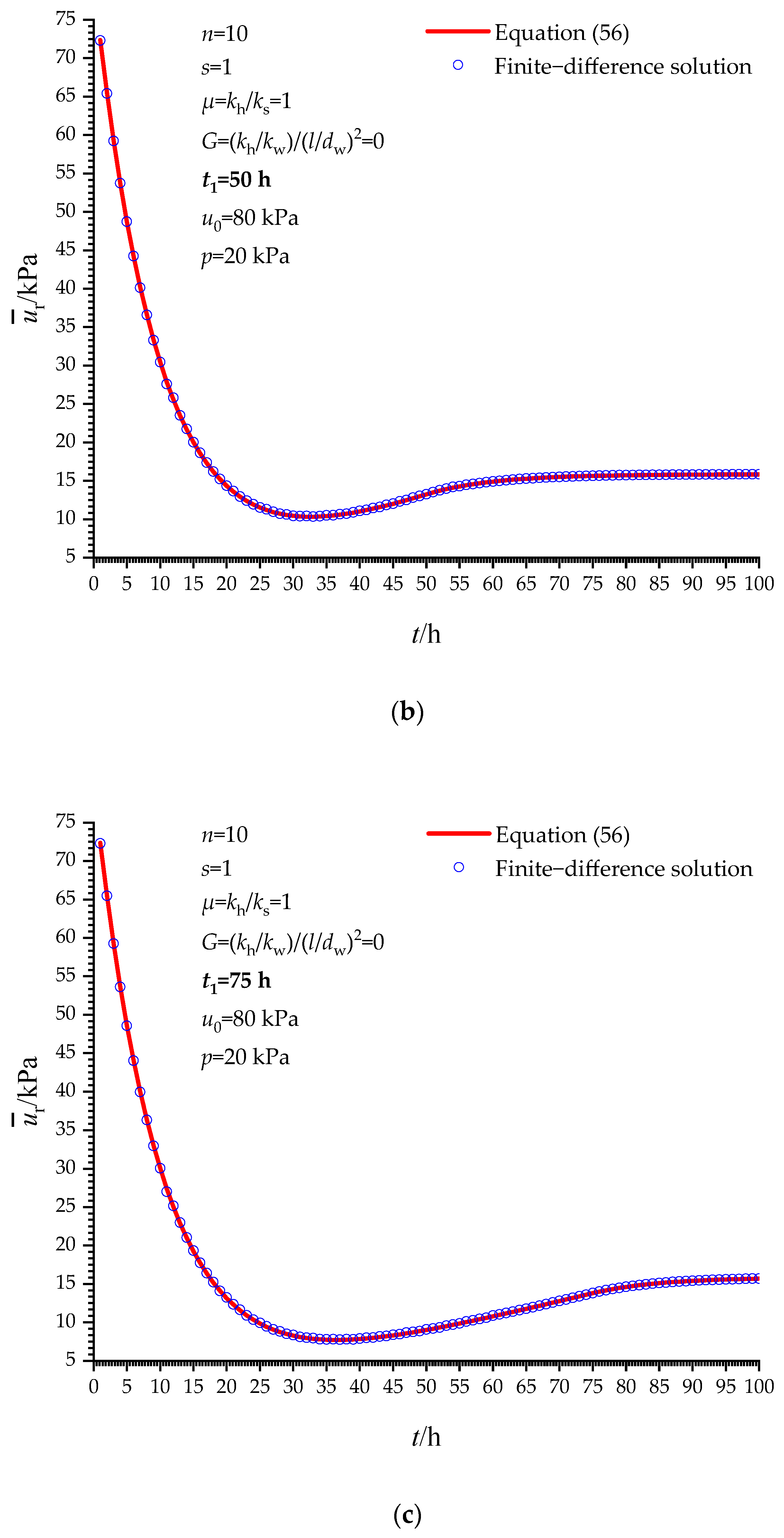
4.2. Verification When t > t₁

Although Shen et al. [26,28] mentioned the function of p(t) with t, the analytical solution for the consolidation of the AVP method in Shen et al. [26,28] is missing when t > t₁. Therefore, in this paper, the analytical solution for the consolidation with an ideal well of the AVP method is given shown as Equation (56) when t > t₁ and the finite difference solution is given to compare.

$${\overline{u}}_{\mathrm{r}2}=F_{\mathrm{b}}p+\left[-\frac{F_{\mathrm{b}}p}{t_1\lambda }\frac{1}{e^{-\lambda t_1}}+\frac{F_{\mathrm{b}}p}{t_1\lambda }+u_0\right]e^{-\lambda t}$$

(56)

The results calculated from Equations (55) and (56) corresponding to t₁ = 25, 50, and 75 h are shown in Figure 8. Additionally, the finite difference solutions are plotted in it.

As seen, the results given by the developed analytical solution using the eigenfunction expansion method are in excellent agreement with those from the finite difference solution, powerfully indicating that the improved analytical solution is correct.

Through the above comparison and analysis, the advantage of the newly improved analytical solution is that it improves the accuracy of predicting the consolidation of the soil by air–boosted vacuum preloading, particularly in the late period when the air booster is working, the error ratio is reduced from 16% to 2%. Additionally, the analytical solution for the consolidation of the AVP method when t > t₁ is provided and verified correctly as well.

5. Parametric Study

In the practical engineering application of the AVP method, the pressure of the boosted air and the ratio of influence zone radius to vertical drain radius would be essential to the consolidation effect by the AVP method, while the time t₁ has a small effect. Therefore, the effects of the pressure of the boosted air (p), and the ratio of influence zone radius to vertical drain radius (n) are investigated using Equations (54) and (55) with t₁ = 100 h. Additionally, according to the previous conclusion, the variation in average pore water pressure during the time 0 < t < 50 h is presented.

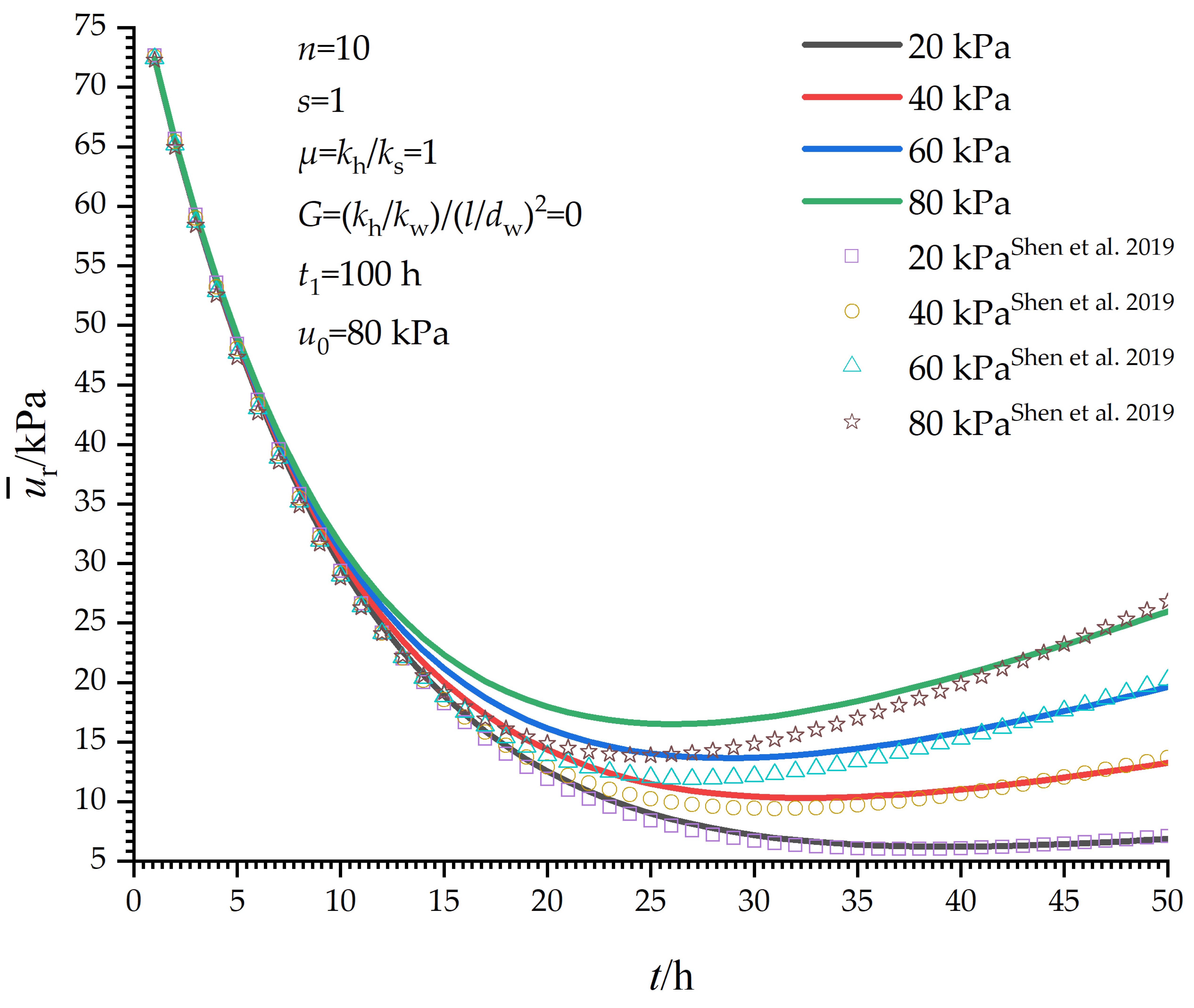
5.1. Influence of p

Figure 9 shows the results from Equations (54) and (55) due to the difference in the pressure of the boosted air (p). The dissipation rate of pore water pressure decreased as the pressure of the boosted air (p) increased, in which the pore water pressure is relevant to the settlement of the foundation, that is, higher pore water pressure means less settlement. Thus, adequate pressure is needed to assist the consolidation of vacuum preloading, which is suggested as 20~40 kPa.

With the increasing pressure of the boosted air, the deviation between Equations (54) and (55) (demonstrated to be close to finite difference solution before) increases during the early period (5–35 h in this paper). The cause of that might be the solution to Equation (30). That Equation (30) is taken as a homogeneous partial differential equation results in a solution that is overly sensitive to the pressure of the boosted air.

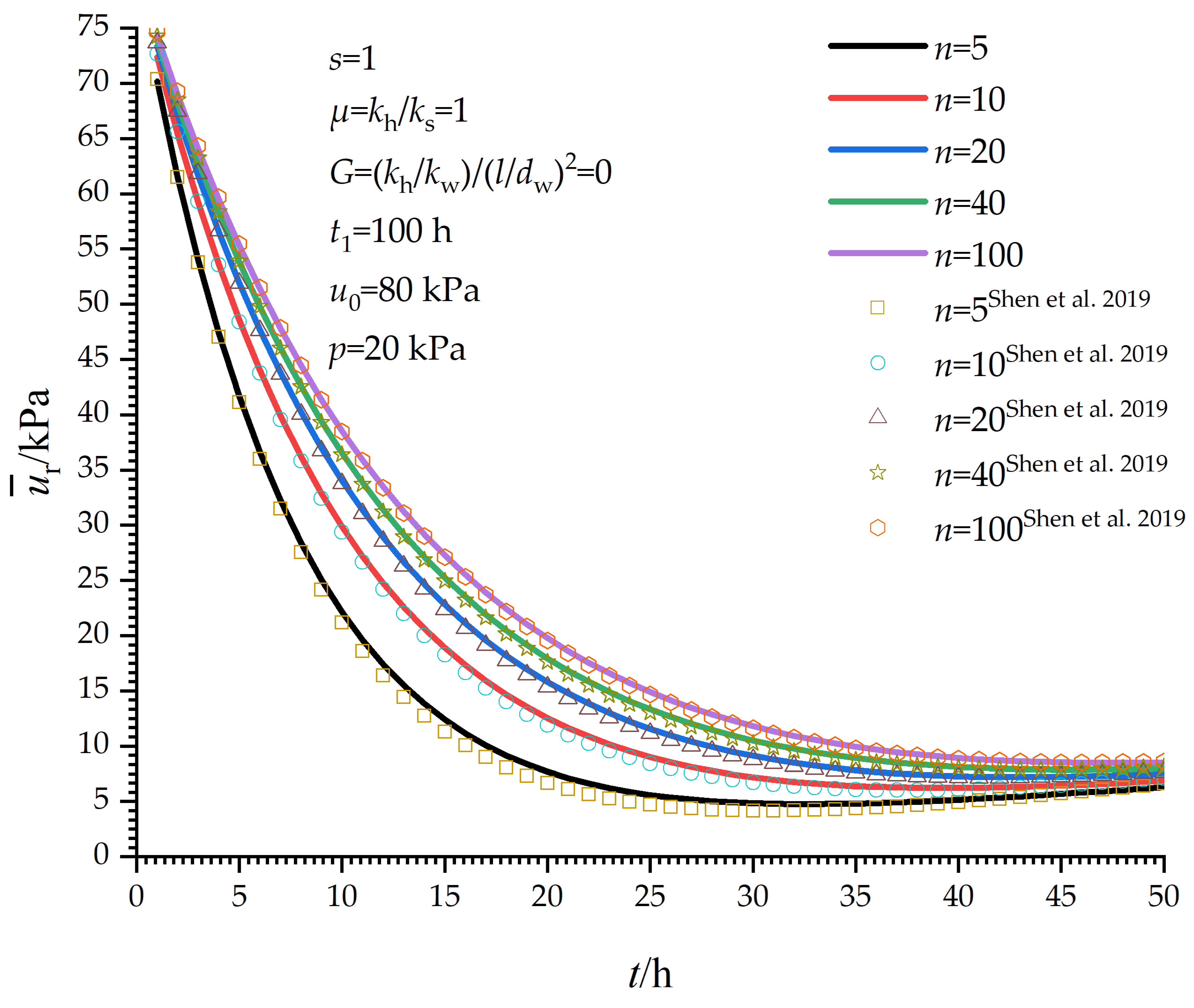
5.2. Influence of n

Figure 10 shows the results from Equations (54) and (55) with the ratio of influence zone radius to vertical drain radius n. Both the analytical solutions indicate that the consolidation characteristics of the soil using the AVP method show that the rate of dissipation of pore water pressure decreases as n increases, and the rate of decrease of pore water pressure when n > 20 is significantly less than that n < 20. In the conventional vacuum preloading method, when the prefabricated drains are used, the ratio n is always taken as between 15 and 22, so the suggested n would be 15~20.

6. Discussion

Compared with the analytical solution using the general solution by separation of variables, there are several advantages of the improved analytical solution: (i) from the solution form, the form of the improved analytical solution (Equations (50) and (55)) exhibits a beauty of symmetry and simplicity; (ii) from prediction accuracy, the error ratio of the improved analytical solution always remains under 2%; (iii) from the sensitivity, the improved analytical solution can better reflect the changed situation caused by the influential factors.

The difference between the two analytical solutions is because of the different treatment of Equation (30). Equation (30) is a nonhomogeneous partial differential equation, while it is treated as a homogeneous one in Shen et al. [26,28], which makes the solution more sensitive to the change in influential factors, as shown in Figure 6 and Figure 9.

7. Conclusions

In previous studies, the analytical solution for one–dimensional consolidation of soil foundation treatment by the AVP method was derived based on the solution for the homogeneous partial differential equations; however, those equations are nonhomogeneous. A new solving method of the eigenfunction expansion was used in this study to adapt the nonhomogeneous equations more accurately. This new solving method and the newly derived analytical solution were validated by the finite difference method and verified to be more accurate with a significantly reduced error ratio compared with that of the previous studies. The effects of p and n were investigated. Results show that the analytical solution agrees well with the numerical solution, and the following conclusions were drawn:

(1) Based on the fact that the partial differential equations solved for consolidation of the saturated soil under the AVP method are nonhomogeneous, the solution using the eigenfunction expansion method considering the whole consolidation time (including t > t₁) is proposed, which has a simpler and more symmetrical form, and higher accuracy than the general solution by the solving method of separating variables, in which the error ratio is less than 2%.

(2) In this newly derived analytical solution, the settlement when t > t₁ is estimated, which the previous analytical solution fails to calculate.

(3) Two essential parameters of the consolidation engineering of deep soil foundation, that are the pressure of the boosted air (p) and the ratio of influence zone radius to vertical drain radius (n), are suggested with p = 20~40 kPa and n = 15~20 in this paper.