An Attention and Wavelet Based Spatial-Temporal Graph Neural Network for Traffic Flow and Speed Prediction
Abstract
:1. Introduction
- A spatial-temporal graph neural network (STAGWNN) for traffic flow prediction was proposed. In it, a wavelet-based graph neural network (GWNN) combined with a graph convolutional neural network with a learnable location attention mechanism were fused to dynamically capture the local and global spatial topology of traffic flow data.
- We proposed to fuse a gated TCN and temporal attention mechanism to extract the local and global temporal features of traffic flow data.
- The proposed model was tested on two real traffic datasets, and the results showed that it outperformed all baseline networks.
2. Related Work
2.1. Traffic Flow Prediction
2.2. Graph Convolution Network
3. Methodology
3.1. Preliminaries
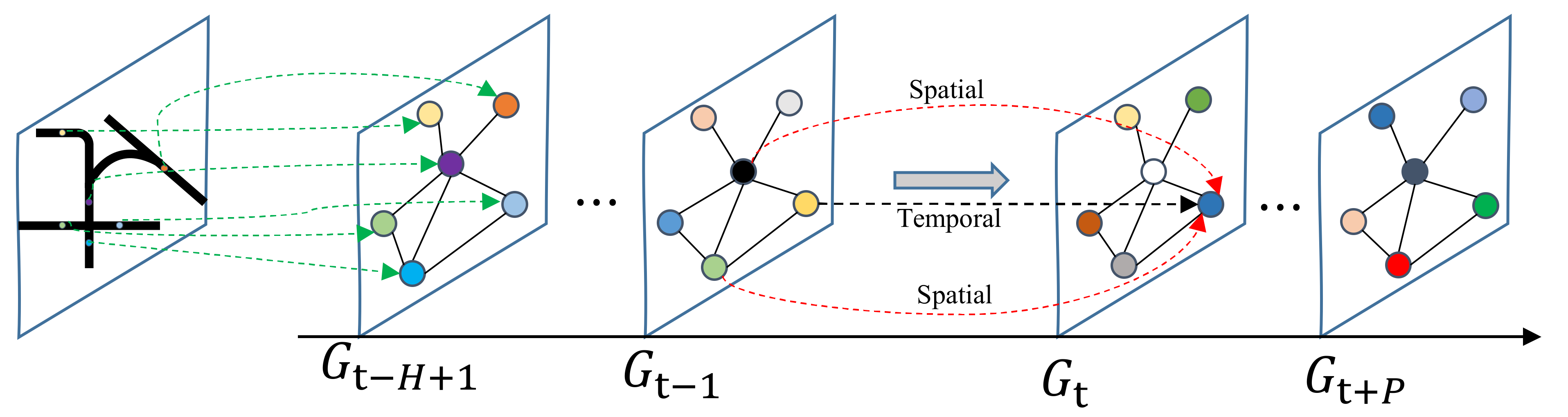
3.1.1. Spatial-Temporal Graph Prediction of Traffic Flow
3.1.2. Graph Convolution
3.2. Methodology
3.2.1. Framework of STAWGNN
3.2.2. Spatial Feature Fusion Convolutional Layer
3.2.3. Temporal Feature Fusion Convolutional Layer
3.2.4. Prediction Output Layer
4. Experiment
4.1. Dataset Details
4.2. Experimental Settings
4.3. Evaluation Indicators and Comparison Models
- STGCN: Spatial-temporal graph convolutional network [10], which applied ChebNet graph convolution and 1D convolution to extract spatial and temporal correlation.
- ARIMA: Autoregressive integrated moving average model with Kalman filtering [15].
- FC-LSTM: LSTM encoder-decoder predictor model [37] that employed a recurrent neural network with fully connected LSTM hidden units.
- DCRNN: Diffusion convolutional recurrent neural network [22] that used diffusion graph convolutional network and RNN to learn the representation of spatial dependencies and temporal relations.
- LSGCN: Long short-term graph convolutional network [23] that proposed a spatial gated block where a new graph attention network called cosAtt and GCN were integrated into a gated form to capture the spatial features of traffic flow data.
- SLCNN: A spatial-temporal graph learning neural network [24] that learned the spatial features of traffic flow data through local and global pairs.
- ASTGCN: Attention-based spatial-temporal graph convolutional network [38] that used two attention layers to capture the dynamic associations in both spatial and temporal dimensions.
- FC-GAGA: Fully connected gated graph network [39] that performed traffic prediction without using prior knowledge of graph structure but learned spatial dependencies through gated graph modules.
4.4. Result
4.4.1. Performance Comparison
4.4.2. Performance Analysis of Graph Wavelet Neural Network
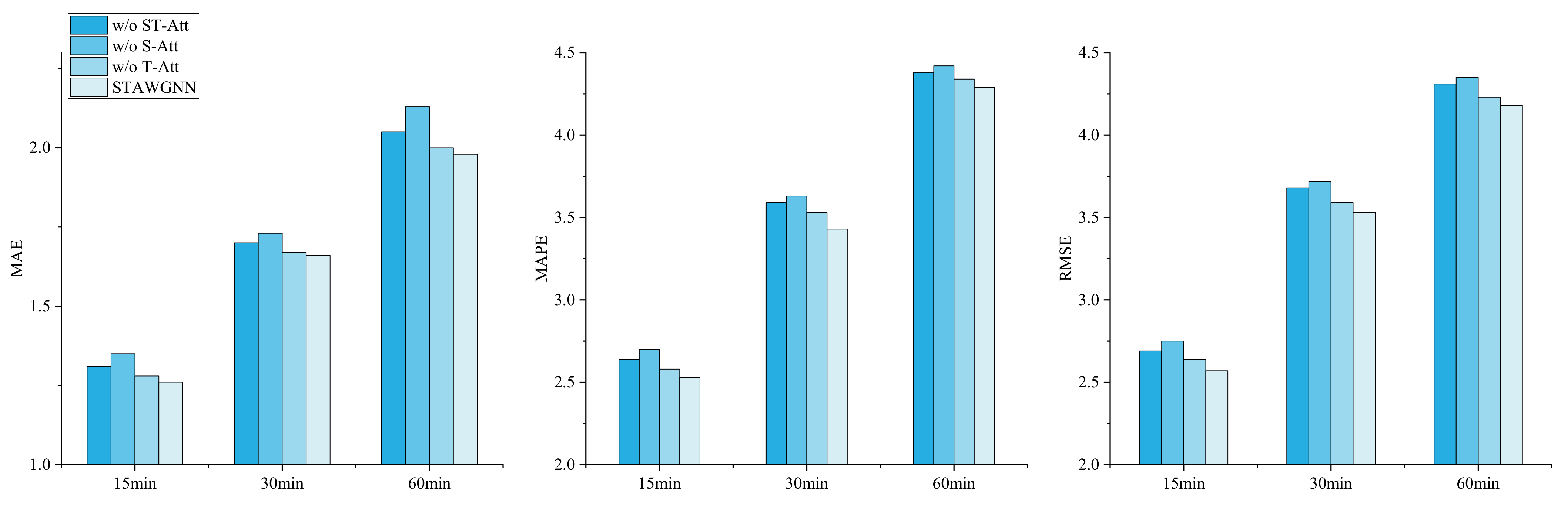
4.4.3. Influence of Attention Mechanism
- w/o ST-Att: STAWGNN without spatial and temporal attention mechanisms.
- w/o S-Att: STAWGNN without spatial attention mechanism. Only graph wavelet networks are used in spatial feature extraction to capture the local spatial features hidden in the traffic flow data.
- w/o T-Att: STAWGNN without temporal attention mechanism. Gated TCNs are only used to capture local temporal features in traffic flow data.
4.4.4. Traffic Flow Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuen, M.; Ng, S.C.; Leung, M.F. A competitive mechanism multi-objective particle swarm optimization algorithm and its application to signalized traffic problem. Cybern. Syst. 2020, 52, 73–104. [Google Scholar] [CrossRef]
- Huang, K.W.; Chen, G.W.; Huang, Z.H.; Lee, S.H. Anomaly Detection in Airport based on Generative Adversarial Network for Intelligent Transportation System. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics-Taiwan, Taiwan, China, 6–8 July 2022; pp. 311–312. [Google Scholar]
- Yang, S.; Lu, H.; Li, J. Multifeature Fusion-Based Object Detection for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2022, 1–8. [Google Scholar] [CrossRef]
- Nagy, A.M.; Simon, V. Survey on traffic prediction in smart cities. Pervasive Mob. Comput. 2018, 50, 148–163. [Google Scholar] [CrossRef]
- Han, S.; Kim, J. Video scene change detection using convolution neural network. In Proceedings of the 2017 International Conference on Information Technology, Singapore, 27–29 December 2017; pp. 116–119. [Google Scholar]
- Quamer, W.; Jain, P.K.; Rai, A.; Saravanan, V.; Pamula, R.; Kumar, C. SACNN: Self-attentive convolutional neural network model for natural language inference. Trans. Asian Low-Resour. Lang. Inf. Processing 2021, 20, 50. [Google Scholar] [CrossRef]
- Caliwag, E.M.F.; Caliwag, A.; Baek, B.K.; Jo, Y.; Chung, H.; Lim, W. Distance Estimation in Thermal Cameras Using Multi-Task Cascaded Convolutional Neural Network. IEEE Sens. J. 2021, 21, 18519–18525. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Syst. Appl. 2022, 207, 117921. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the KDD ‘20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual, San Diego, CA, USA, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Chen, Y.; Wu, L.; Zaki, M. Iterative deep graph learning for graph neural networks: Better and robust node embeddings. Adv. Neural Inf. Processing Syst. 2020, 33, 19314–19326. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph wavenet for deep spatial-temporal graph modeling. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019. [Google Scholar]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef]
- Cai, L.; Zhang, Z.; Yang, J.; Yu, Y.; Qin, J. A noise-immune Kalman filter for short-term traffic flow forecasting. Phys. A Stat. Mech. Its Appl. 2019, 536, 122601. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Keller J, M.; Gray M, R.; Givens J, A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 4, 580–585. [Google Scholar] [CrossRef]
- Yu, R.; Li, Y.; Shahabi, C.; Demiryurek, U.; Liu, Y. Deep learning: A generic approach for extreme condition traffic forecasting. In Proceedings of the 2017 SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017; pp. 777–785. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X. DNN-based prediction model for spatio-temporal data. In Proceedings of the SIGSPATIAL’16: 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Burlingame, CA, USA, 31 October–3 November 2016; pp. 1–4. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Huang, R.; Huang, C.; Liu, Y.; Dai, G.; Kong, W. LSGCN: Long Short-Term Traffic Prediction with Graph Convolutional Networks. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence and Seventeenth Pacific Rim International Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 2355–2361. [Google Scholar]
- Zhang, Q.; Chang, J.; Meng, G.; Xiang, S.; Pan, C. Spatio-temporal graph structure learning for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1177–1185. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Qiu, Y.; Cheng, X. Graph wavelet neural network. In Proceedings of the IJCAI, Macau, China, 10–16 August 2019. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Ma, X.; Wang, Y. Learning traffic as a graph: A gated graph wavelet recurrent neural network for network-scale traffic prediction. Transp. Res. Part C Emerg. Technol. 2020, 115, 102620. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 5165–5175. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N.V. Heterogeneous graph neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 793–803. [Google Scholar]
- Xie, Z.; Chen, J.; Peng, B. Point clouds learning with attention-based graph convolution networks. Neurocomputing 2020, 402, 245–255. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, C.; Li, L.; Zhou, J.; Li, X.; Song, L.; Qi, Y. Geniepath: Graph neural networks with adaptive receptive paths. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 4424–4431. [Google Scholar]
- Li, R.; Wang, S.; Zhu, F.; Huang, J. Adaptive graph convolutional neural networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Processing Syst. 2017, 30. [Google Scholar] [CrossRef]
- Roy, A.; Roy, K.K.; Ali, A.A.; Amin, M.A.; Rahman, A.M. Unified spatio-temporal modeling for traffic forecasting using graph neural network. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Li, M.; Zhu, Z. Spatial-temporal fusion graph neural networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, CA, USA, 2–9 February 2021; Volume 35, pp. 4189–4196. [Google Scholar]
- Li, F.; Feng, J.; Yan, H.; Jin, G.; Yang, F.; Sun, F.; Li, Y. Dynamic graph convolutional recurrent network for traffic prediction: Benchmark and solution. ACM Trans. Knowl. Discov. Data (TKDD) 2021. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2014; Volume 27. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27–28 January 2019; Volume 33, pp. 922–929. [Google Scholar]
- Oreshkin, B.N.; Amini, A.; Coyle, L.; Coates, M. FC-GAGA: Fully connected gated graph architecture for spatio-temporal traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, CA, USA, 2–9 February 2021; pp. 9233–9241. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations, Banff, AL, Canada, 14–16 April 2014. [Google Scholar]







| Dataset | Node | Edge Number | Time Steps | Time Interval | Long | Unit |
|---|---|---|---|---|---|---|
| PEMS-BAY | 325 | 2369 | 52,116 | 5 min | 12 | km/h |
| PEMSD7(M) | 228 | 832 | 12,672 | 5 min | 12 | km/h |
| Dataset | Batch Size | Epochs | Learning Rate | Dropout Rate | S | Optimizer |
|---|---|---|---|---|---|---|
| PEMS-BAY | 32 | 100 | 0.0001 | 0.5 | 0.05 | Adam |
| PEMSD7(M) | 32 | 100 | 0.0001 | 0.5 | 0.05 | Adam |
| PMDS-BAY | 15 min | 30 min | 60 min | ||||||
| MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | |
| HA | 2.88 | 6.80% | 5.59 | 2.88 | 6.80% | 5.59 | 2.88 | 6.80% | 5.59 |
| ARIMA | 1.62 | 3.50% | 3.30 | 2.33 | 5.40% | 4.76 | 3.38 | 8.30% | 6.50 |
| FC-LSTM | 2.05 | 4.80% | 4.19 | 2.20 | 5.20% | 4.55 | 2.37 | 5.70% | 4.96 |
| DCRNN | 1.38 | 2.90% | 2.95 | 1.74 | 3.90% | 3.97 | 2.07 | 4.90% | 4.74 |
| STGCN | 1.37 | 2.95% | 2.98 | 1.85 | 4.22% | 4.34 | 2.49 | 5.81% | 5.70 |
| ASTGCN | 1.52 | 3.22% | 3.13 | 2.01 | 4.48% | 4.27 | 2.61 | 6.00% | 5.42 |
| LSGCN | 1.42 | 2.87% | 2.71 | 2.02 | 4.13% | 4.15 | 3.13 | 6.11% | 6.16 |
| SLCNN | 1.44 | 3.00% | 2.90 | 1.73% | 4.10% | 3.81 | 2.03 | 4.80% | 4.53 |
| FC-GAGA | 1.34 | 2.82% | 2.82 | 1.66 | 3.71% | 3.75 | 1.93 | 4.48% | 4.40 |
| STAWGNN | 1.26 | 2.53% | 2.57 | 1.66 | 3.43% | 3.53 | 1.98 | 4.29% | 4.18 |
| PMDS7(M) | 15 min | 30 min | 45 min | ||||||
| MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | |
| HA | 4.01 | 10.61% | 7.20 | 4.01 | 10.61% | 7.20 | 4.01 | 10.61% | 7.20 |
| ARIMA | 5.55 | 12.92% | 9.00 | 5.86 | 13.94% | 9.13 | 6.68 | 16.78% | 9.68 |
| FC-LSTM | 3.57 | 8.60% | 6.20 | 3.92 | 9.55% | 7.03 | 4.16 | 10.10% | 7.51 |
| DCRNN | 2.37 | 5.54% | 4.21 | 3.31 | 8.06% | 5.96 | 4.01 | 9.99% | 7.13 |
| STGCN | 2.25 | 5.26% | 4.04 | 3.03 | 7.33% | 5.70 | 3.57 | 8.69% | 6.77 |
| ASTGCN | 2.85 | 7.25% | 5.15 | 3.35 | 8.67% | 6.12 | 3.96 | 10.56% | 7.20 |
| LSGCN | 2.22 | 5.14% | 3.98 | 2.96 | 7.18% | 5.47 | 3.43 | 8.51% | 6.39 |
| SLCNN | 2.22 | 5.21% | 4.07 | 2.88 | 7.17% | 5.50 | 3.27 | 8.20% | 6.28 |
| FC-GAGA | 2.18 | 5.29% | 4.15 | 2.80 | 7.06% | 5.58 | 3.31 | 8.47% | 6.66 |
| STAWGNN | 2.18 | 5.07% | 3.95 | 2.88 | 6.95% | 5.28 | 3.31 | 7.99% | 6.03 |
| Dataset | Total Number of Elements | The Number of Non-Zero Value | Proportion of Non-Zero Valued |
|---|---|---|---|
| PEMS-BAY | 104,329 | 22,707 | 21.7% |
| PEMSD7(M) | 50,350 | 9667 | 19.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Xing, S.; Mao, G. An Attention and Wavelet Based Spatial-Temporal Graph Neural Network for Traffic Flow and Speed Prediction. Mathematics 2022, 10, 3507. https://doi.org/10.3390/math10193507
Zhao S, Xing S, Mao G. An Attention and Wavelet Based Spatial-Temporal Graph Neural Network for Traffic Flow and Speed Prediction. Mathematics. 2022; 10(19):3507. https://doi.org/10.3390/math10193507
Chicago/Turabian StyleZhao, Shihao, Shuli Xing, and Guojun Mao. 2022. "An Attention and Wavelet Based Spatial-Temporal Graph Neural Network for Traffic Flow and Speed Prediction" Mathematics 10, no. 19: 3507. https://doi.org/10.3390/math10193507
APA StyleZhao, S., Xing, S., & Mao, G. (2022). An Attention and Wavelet Based Spatial-Temporal Graph Neural Network for Traffic Flow and Speed Prediction. Mathematics, 10(19), 3507. https://doi.org/10.3390/math10193507





