Growth and Debt: An Endogenous Smooth Coefficient Approach
Abstract
1. Introduction
2. Empirical Methodology
2.1. The Augmented Solow Growth Model
2.2. An Endogenous Smooth Coefficient Model
3. Data
4. Estimation Results
4.1. Homogeneous Models and Mean Parameter Estimates
4.2. Parameter Heterogeneity
4.2.1. Including the Period 2010–2014
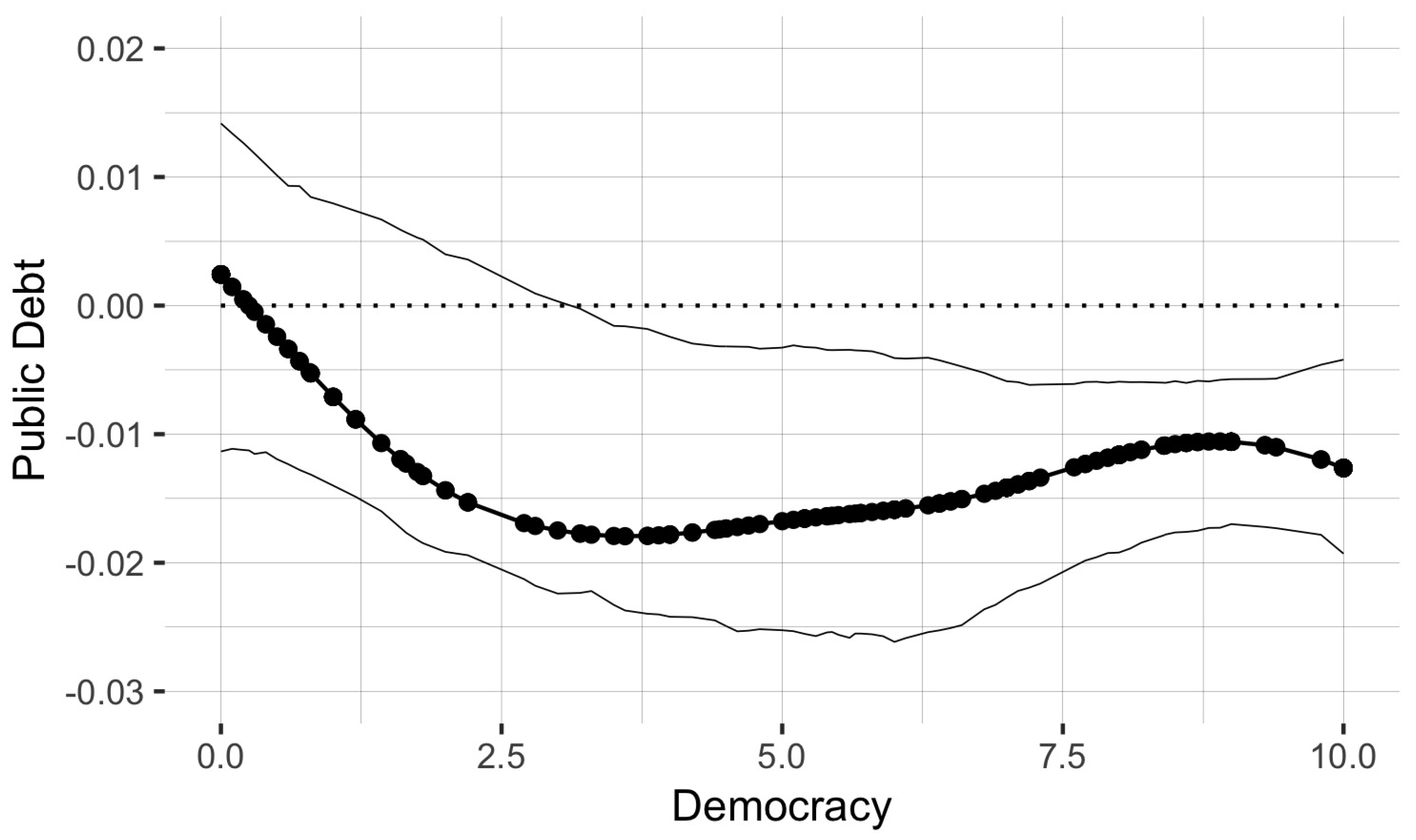
4.2.2. Policy Implications
4.2.3. Parameter Heterogeneity in the Relationship between Growth and Other Regressors
5. Robustness Checks
5.1. Influential Countries
5.2. Alternative Measure for Democracy
5.3. Additional Control Variables
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
| Mean | Std. Dev. | Min | Max | |
|---|---|---|---|---|
| Panel A. Penn World Table 7.0 (1980–2009) | ||||
| Growth | 0.014 | 0.023 | −0.099 | 0.083 |
| Initial income | 8.42 | 1.27 | 5.87 | 10.71 |
| Lag of initial income | 8.34 | 1.23 | 5.78 | 10.55 |
| Investment rate | 3.05 | 0.35 | 1.87 | 3.89 |
| Lag of investment rate | 3.05 | 0.39 | 1.74 | 4.31 |
| Population growth rate | −2.71 | 0.16 | −3.23 | −2.38 |
| Lag of population growth rate | −2.69 | 0.16 | −3.08 | −2.28 |
| Government consumption | 2.19 | 0.44 | 1.06 | 3.56 |
| Lag of government consumption | 2.19 | 0.48 | 1.01 | 3.69 |
| Trade openness | 66.51 | 36.49 | 9.77 | 199.86 |
| Lag of trade openness | 61.01 | 35.80 | 9.70 | 180.09 |
| Panel B. Penn World Table 9.0 (1980–2014) | ||||
| Growth | 0.025 | 0.029 | −0.061 | 0.114 |
| Initial income | 8.77 | 1.17 | 6.42 | 11.20 |
| Investment rate | 2.96 | 0.45 | 0.65 | 3.92 |
| Population growth rate | −2.71 | 0.15 | −3.07 | −2.38 |
| Schooling | 0.77 | 0.32 | 0.036 | 1.31 |
| Panel C. World Bank | ||||
| Inflation rate | 2.30 | 1.17 | −1.95 | 7.57 |
| Lag of inflation rate | 2.34 | 1.19 | −1.46 | 8.26 |
| Life expectancy | 4.17 | 0.17 | 3.63 | 4.41 |
| Lag of life expectancy | 4.14 | 0.18 | 3.63 | 4.38 |
| Fertility | 3.62 | 1.73 | 1.21 | 7.78 |
| Lag of fertility | 4.06 | 1.89 | 1.17 | 7.82 |
| Panel D. IMF | ||||
| Public debt | 4.08 | 0.61 | 2.17 | 6.33 |
| Lag of public debt | 3.92 | 0.73 | 1.12 | 6.46 |
| Panel E. Barro and Lee (2000) | ||||
| Schooling | 0.60 | 0.77 | −2.18 | 1.97 |
| Lag of schooling | 0.32 | 0.90 | −2.66 | 1.90 |
| Panel F. Polity IV | ||||
| Democracy | 5.74 | 3.83 | 0.00 | 10.00 |
| Lag of democracy | 5.02 | 4.17 | 0.00 | 10.00 |
| Executive constraints | 4.96 | 2.05 | 1.00 | 7.00 |
| Lag of executive constraints | 4.51 | 2.33 | 1.00 | 7.00 |
| Panel G. Freedom House | ||||
| Political rights | 4.82 | 1.93 | 1.00 | 7.00 |
| Lag of political rights | 4.53 | 2.08 | 1.00 | 7.00 |
| Civil liberties | 4.67 | 1.68 | 1.00 | 7.00 |
| Lag of civil liberties | 4.45 | 1.77 | 1.00 | 7.00 |
| Variable | Source | Definition |
|---|---|---|
| Growth | PWT 7.0 & 9.0 | Growth rate of real per capita GDP in chain series for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). |
| Initial income | PWT 7.0 & 9.0 | Logarithm of real per capita GDP in chain series at 1980, 1990, 2000, and 2010 (for extended data). Lagged values correspond to 1975, 1985, 1995, and 2005 (for extended data). |
| Investment rate | PWT 7.0 & 9.0 | Logarithm of average ratios over each period of investment to real GDP per capita for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Population growth rate | PWT 7.0 & 9.0 | Logarithm of average population growth rates plus 0.05 for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Schooling | Barro and Lee (2000) | Logarithm of average years of male secondary and tertiary school attainment for ages above 25 in 1980, 1990, 1999, and 2010 (for extended data). Lagged values correspond to 1975, 1985, 1995, and 2005 (for extended data). |
| Public debt | IMF, Debt Database Fall 2011 Vintage | Logarithm of average percentages over each period of public debt to GDP for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Fertility | World Bank | Logarithm of average total fertility rate in 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Life expectancy | World Bank | Logarithm of average average life expectancy at birth for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Trade openness | PWT 7.0 & 9.0 | Average ratios for each period of exports plus imports to real GDP per capita for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Government consumption | PWT 7.0 & 9.0 | Logarithm of average ratios for each period of government consumption to real GDP per capita for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Inflation rate | World Bank | Logarithm of average inflation plus 1 for the periods 1980–1989, 1990–1999, 2000–2009, and (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Democracy | Polity IV | An index ranges from 0 to 10 where higher values equals a greater extent of institutionalized democracy. Average for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Executive constraints | Polity IV | An index ranges from 1 to 7 where higher values equals a greater extent of institutionalized constraints on the power of chief executives. Average for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, 2005–2009 (for extended data). |
| Political rights | Freedom House | An index ranges from 1 to 7 where higher values equals a greater extent of institutionalized constraints on the power of chief executives. Average for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Civil liberties | Freedom House | An index ranges from 1 to 7 where higher values equals a greater extent of institutionalized constraints on the power of chief executives. Average for the periods 1980–1989, 1990–1999, 2000–2009, and 2010–2014 (for extended data). Lagged values correspond to 1975–1979, 1985–1989, 1995–1999, and 2005–2009 (for extended data). |
| Negative and Significant | Insignificant | ||
|---|---|---|---|
| ≤1 | ≥7.6 & ≤9 | ≥9 | |
| Algeria (1980, 1990) | Argentina (2000) | Australia (1980, 1990, 2000) | Argentina (1980, 1990) |
| Bangladesh (1980) | Bolivia (1990, 2000) | Austria (1980, 1990, 2000) | Benin (1990, 2000) |
| Benin (1980) | Botswana (2000) | Belgium (1980, 1990, 2000) | Bangladesh (1990, 2000) |
| Burundi (1980, 1990) | Brazil (1990, 2000) | Canada (1980, 1990, 2000) | Bolivia (1980) |
| Cameroon (1980, 1990, 2000) | Chile (1990, 2000) | Costa Rica (1980, 1990, 2000) | Botswana (1980, 1990) |
| Central African Republic (1980) | Colombia (1980, 1990) | Cyprus (1980, 1990, 2000) | Brazil (1980) |
| Chile (1980) | Dominican Republic (2000) | Denmark (1980, 1990, 2000) | Burundi (2000) |
| Cote’d Ivoire (1980, 1990) | Ecuador (1980, 1990) | Finland (1980, 1990, 2000) | Central African Republic (1990, 2000) |
| Egypt (1980, 1990, 2000) | France (1980) | France (1990, 2000) | Congo Republic (1990) |
| Gabon (1980, 1990, 2000) | Greece (1980) | Greece (1990, 2000) | Cote’d Ivoire (2000) |
| Gambia (2000) | Guatemala (2000) | Ireland (1980, 1990, 2000) | Colombia (2000) |
| Ghana (1980) | India (1980, 1990, 2000) | Italy (1980, 1990, 2000) | Dominican Republic (2000) |
| Guyana (1980) | Republic of Korea (2000) | Israel (1980, 1990, 2000) | Ecuador (2000) |
| Indonesia (1980, 1990) | Lesotho (2000) | Jamaica (1980, 1990, 2000) | Gambia (1980, 1990) |
| Iran (1980) | Mexico (2000) | Japan (1980, 1990, 2000) | Ghana (1980, 1990) |
| Kenya (1980, 1900) | Panama (1990, 2000) | Netherlands (1980, 1990, 2000) | Guatemala (1990) |
| Lesotho (1980) | Paraguay (2000) | New Zealand (1980, 1990, 2000) | Guyana (1990, 2000) |
| Malawi (1980) | Peru (2000) | Norway (1980, 1990, 2000) | Honduras (1980, 1990, 2000) |
| Mali (1980) | Philippines (2000) | Portugal (1980, 1990, 2000) | Kenya (2000) |
| Mauritania (1980, 2000) | Senegal (2000) | Spain (1980, 1990, 2000) | Lesotho (1990) |
| Morocco (1980, 1990, 2000) | South Africa (1990, 2000) | Sweden (1980, 1990, 2000) | Malaysia (1980, 2000) |
| Nicaragua (1980, 1990) | Thailand (1990) | United Kingdom (1980, 1990, 2000) | Malawi (1990, 2000) |
| Niger (1980) | Trinidad & Tobago (1990, 2000) | United States (1980, 1990, 2000) | Mali (1990, 2000) |
| Panama (1980) | Turkey (1990, 2000) | Uruguay (1990, 2000) | Mexico (1980, 1990) |
| Paraguay (1980) | Venezuela (1980, 1990) | Nepal (1980, 1990, 2000) | |
| Sierra Leone (1980) | Nicaragua (1990) | ||
| Swaziland (1980, 1990, 2000) | Niger (1990, 2000) | ||
| Syria (1980, 1990, 2000) | Pakistan (1980, 1990, 2000) | ||
| Togo (1980, 1990, 2000) | Papua New Guinea (1980, 1990, 2000) | ||
| Tunisia (1980, 1990, 2000) | Paraguay (1990) | ||
| Zambia (1980) | Republic of Korea (1980, 1990) | ||
| Zimbabwe (1990) | Peru (1980, 1990) | ||
| Sierra Leone (1980, 2000) | |||
| South Africa (1980) | |||
| Sri Lanka (1980, 1990, 2000) | |||
| Thailand (2000) | |||
| Turkey (1980) | |||
| Venezuela (2000) | |||
| Zambia (1990, 2000) | |||
| Zimbabwe (1980, 2000) |
| Paper | Sample | Empirical Methodology | Debt Measure | Instrumental Variable | Findings |
|---|---|---|---|---|---|
| Caner et al. (2010) | 101 developing and developed countries (1980–2008) | Cross-section; Threshold Least Squares | General government gross debt (% GDP) from IMF | No instruments | Significant negative effect; debt threshold is 77% for all countries; 64% for the sample of developing countries only |
| Cecchetti et al. (2011) | 18 OECD countries (1980–2010) | Panel data; FE; panel threshold; LSDV | General government debt from IMF | No instruments | Significant negative effect; threshold level is 85% |
| Checherita-Westphal and Rother (2012) | 12 Euro area countries (1970–2008) | Panel data; FE; 2SLS; GMM | Gross government debt (% GDP) from AMECO | Lagged debt-to-GDP ratio up to the 5th lag; average of the debt levels of the other countries in the sample | Significant negative effect; debt turning point is in between 90% and 100% |
| Minea and Parent (2012) | 20 advanced countries as in Reinhart and Rogoff (2010) (1945–2009) | Panel data; panel smooth threshold regression | Public debt from IMF | No instruments | Negative effect below the threshold level of 115%; positive effect beyond this level of debt |
| Baum et al. (2013) | 12 Euro area countries (EMU) (1990–2007/2010) | Panel data (yearly); non-/dynamic panel threshold model; OLS; GMM | Public debt from AMECO | No instrument for debt variable | Significant positive effect below the threshold level of 67% for the period 1990–2007; insignificant effect beyond that threshold; significant negative effect beyond the threshold level of 95% for the period 1990–2010 |
| Kourtellos et al. (2013) | 82 countries (1980–2009) | Panel data (10-year averages); structural threshold regression; 2SLS; GMM | Public debt (% of GDP) from IMF | Lag of public debt | Threshold variable is democracy; significant negative effect for low-democracy regime countries; insignificant effect for countries in high-democracy regime |
| Paper | Sample | Empirical Methodology | Debt Measure | Instrumental Variable | Findings |
|---|---|---|---|---|---|
| Wright and Grenade (2014) | 13 Caribbean countries (1990–2012) | Panel data; PDOLS | Debt/GDP from IMF | No instruments | 61% is the threshold level |
| Eberhardt and Presbitero (2015) | 118 countries (1961–2012) | Unbalanced panel data; panel time series approach; ECM | Gross general government debt from WDI and IMF | No instruments | No common threshold level of public debt for all countries; evidence for differences in debt-growth relationship across countries |
| Égert (2015) | 20 advanced and 21 emerging economies (1946–2009) | Panel data; threshold regression | Central government debt from the same source in Reinhart and Rogoff (2011) | No instruments | Little evidence on 90% threshold level; some evidence for lower threshold level |
| Woo and Kumar (2015) | 38 advanced and emerging economies (1970–2008) | Panel data; BE; pooled OLS; FE; SGMM | Gross government debt (% of GDP) from IMF | 5 lag of debt variable | Significant negative effect; threshold level of 90%, beyond which debt has a negative effect |
References
- Acemoglu, Daron, Simon Johnson, and James A. Robinson. 2001. The colonial origins of comparative development: An empirical investigation. American Economic Review 91: 1369–401. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Simon Johnson, James A. Robinson, and Pierre Yared. 2005. From education to democracy? American Economic Review 95: 44–49. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Suresh Naidu, Pascual Restrepo, and James A. Robinson. 2015. Democracy does cause growth. Journal of Political Economy. [Google Scholar] [CrossRef]
- Acemoglu, Daron, and James A. Robinson. 2012. Why Nations Fail: The Origins of Power, Prosperity, and Poverty. New York: Currency. [Google Scholar]
- Allen, Franklin, Elena Carletti, Itay Goldstein, and Agnese Leonello. 2015. Moral hazard and government guarantees in the banking industry. Journal of Financial Regulation 1: 1–21. [Google Scholar] [CrossRef]
- Azariadis, Costas, and Allan Drazen. 1990. Threshold externalities in economic development. The Quarterly Journal of Economics 105: 501–26. [Google Scholar] [CrossRef]
- Barro, Robert J., and Xavier I. Salai-Martin. 1995. Economic Growth. New York: McGraw-Hill. [Google Scholar]
- Baum, Anja, Cristina Checherita-Westphal, and Philipp Rother. 2013. Debt and growth: New evidence for the euro area. Journal of International Money and Finance 32: 809–21. [Google Scholar] [CrossRef]
- Bernal, Raquel, and Michael P. Keane. 2011. Child care choices and children’s cognitive achievement: the case of single mothers. Journal of Labor Economics 29: 459–12. [Google Scholar] [CrossRef]
- Bohn, Henning. 1995. The sustainability of budget deficits in a stochastic economy. Journal of Money, Credit and Banking 27: 257–71. [Google Scholar] [CrossRef]
- Cai, Zongwu, Mitali Das, Huaiyu Xiong, and Xizhi Wu. 2006. Functional coefficient instrumental variables models. Journal of Econometrics 133: 207–41. [Google Scholar] [CrossRef]
- Cai, Zongwu, and Qi Li. 2008. Nonparametric estimation of varying coefficient dynamic panel data models. Econometric Theory 24: 1321–42. [Google Scholar] [CrossRef]
- Caner, Mehmet, Thomas Grennes, and Fritzi Koehler-Geib. 2010. Finding the Tipping Point-When Sovereign Debt Turns Bad. Technical Report. Washington, DC: The World Bank. [Google Scholar]
- Cecchetti, Stephen G., Madhusudan S. Mohanty, and Fabrizio Zampolli. 2010. The Future of Public Debt: Prospects and Implications. Technical Report. Basel: Bank for International Settlements. [Google Scholar]
- Cecchetti, Stephen G., Madhusudan S. Mohanty, and Fabrizio Zampolli. 2011. The Real Effects of Debts. Technical Report. Basel: Bank for International Settlements. [Google Scholar]
- Checherita-Westphal, Cristina, and Philipp Rother. 2012. The impact of high government debt on economic growth and its channels: An empirical investigation for the euro area. European Economic Review 56: 1392–405. [Google Scholar] [CrossRef]
- Chen, Xiaohong. 2007. Large sample sieve estimation of semi-nonparametric models. In Handbook of Econometrics. Edited by James J. Heckman and Edward E. Leamer. New York: Springer, vol. 6B, pp. 5549–32. [Google Scholar]
- Chudik, Alexander, Kamiar Mohaddes, Hashem M. Pesaran, and Mehdi Raissi. 2017. Is there a debt-threshold effect on output growth? The Review of Economics and Statistics 99: 135–50. [Google Scholar] [CrossRef]
- Das, Mitali. 2005. Instrumental variables estimators for nonparametric models with discrete endogenous variables. Journal of Econometrics 124: 335–61. [Google Scholar] [CrossRef]
- Delgado, Michael S., Deniz Ozabaci, Yiguo Sun, and Subal C. Kumbhakar. 2015. Smooth Coefficient Models With Endogenous Environmental Variables. Technical Report. West Lafayette: Purdue University. [Google Scholar]
- Durlauf, Steven N., Andros Kourtellos, and Artur Minkin. 2001. The local solow growth model. European Economic Review 45: 928–40. [Google Scholar] [CrossRef]
- Eberhardt, Markus, and Andrea F. Presbitero. 2013. This Time They Are Different: Heterogeneity and Nonlinearity in The Relationship Between Debt and Growth. Technical Report. Washington, DC: IMF. [Google Scholar]
- Eberhardt, Markus, and Andrea F. Presbitero. 2015. Public debt and growth: heterogeneity and non-linearity. Journal of International Economics 97: 45–58. [Google Scholar] [CrossRef]
- Égert, Balázs. 2015. Public debt, economic growth and nonlinear effects: Myth or reality? Journal of Macroeconomics 43: 226–38. [Google Scholar] [CrossRef]
- Elmendorf, Douglas W., and N. Gregory Mankiw. 1999. Government debt. In Handbook of Macroeconomics. Edited by John B. Taylor. Oxford: Taylor and Michael Woodford. [Google Scholar]
- Glaeser, Edward L., Rafael La Porta, Florencio Lopez-De-Silanes, and Andrei Shleifer. 2004. Do institutions cause growth? Journal of Economic Growth 9: 271–303. [Google Scholar] [CrossRef]
- Gonzáles, Andrés, Timo Teräsvirta, and Dick VanDijk. 2005. Panel Smooth Transition Regression Models. Technical Report. Stockholm: Stockholm School of Economics. [Google Scholar]
- Härdle, Wolfgang, and Steve J. Marron. 1991. Bootstrap simultaneous error bars for nonparametric regression. The Annals of Statistics 19: 778–96. [Google Scholar] [CrossRef]
- Henderson, Daniel J., Subal C. Kumbhakar, and Christopher F. Parmeter. 2012. A simple method to visualize results in nonlinear regression models. Economics Letters 117: 578–81. [Google Scholar] [CrossRef]
- Henderson, Daniel J., Chris Papageorgiou, and Christopher F. Parmeter. 2011. Growth empirics without parameters. The Economic Journal 122: 125–54. [Google Scholar] [CrossRef]
- Henderson, Daniel J., and Christopher F. Parmeter. 2015. Applied Nonparametric Econometrics. New York: Cambridge University Press. [Google Scholar]
- Jalles, Joao T. 2011. The impact of democracy and corruption on the debt-growth relationship in developing countries. Journal of Economic Development 36: 41–72. [Google Scholar]
- Ketteni, Elena, Theofanis P. Mamuneas, and Thanasis Stengos. 2007. Nonlinearities in economic growth: A semiparametric approach applied to information technology data. Journal of Macroeconomics 29: 555–68. [Google Scholar] [CrossRef]
- Kourtellos, Andros. 2011. Modeling parameter heterogeneity in cross-country regression models. In Economic Growth and Development (Frontiers of Economics and Globalization). Edited by O. de La Grandville. Bingley: Emerald Group Publishing Limited, pp. 579–604. [Google Scholar]
- Kourtellos, Andros, Thanasis Stengos, and Chih Ming Tan. 2013. The effect of public debt on growth in multiple regimes. Journal of Macroeconomics 38: 35–43. [Google Scholar] [CrossRef]
- Kourtellos, Andros, Thanasis Stengos, and Chih Ming Tan. 2016. Structural thresold regression. Econometric Theory 32: 827–60. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., and Kai Sun. 2012. Estimation of tfp growth: A semiparametric smooth coefficient approach. Empirical Economics 43: 1–24. [Google Scholar] [CrossRef]
- Li, Qi, Cliff J. Huang, Dong Li, and Tsu-Tan Fu. 2002. Semiparametric smooth coefficient models. Journal of Business and Economic Statistics 20: 412–22. [Google Scholar] [CrossRef]
- Liu, Zhenjuan, and Thanasis Stengos. 1999. Non-linearities in cross-country growth regressions: A semiparametric approach. Journal of Applied Econometrics 14: 527–38. [Google Scholar] [CrossRef]
- Mamuneas, Theofanis P., Andreas Savvides, and Thanasis Stengos. 2006. Economic development and the return to human capital: A smooth coefficient semiparametric approach. Journal of Applied Econometrics 21: 111–32. [Google Scholar] [CrossRef]
- Marshall, Monty G., Ted R. Gurr, and Keith Jaggers. 2016. Polity Iv Project: Dataset Users’ Manual. Technical Report. Vienna: Center for Systemic Peace. [Google Scholar]
- Minea, Alexandru, and Antoine Parent. 2012. Is High Public Debt Always Harmful to Economic Growth? Reinhart And Rogoff and Some Complex Nonlinearities. Technical Report. Clermont-Ferrand: Centre d’Études et de Recherches sur le Développement International. [Google Scholar]
- Minier, Jenny A. 2007. Institutions and parameter heterogeneity. Journal of Macroeconomics 29: 595–611. [Google Scholar] [CrossRef]
- Newey, Whitney K., and James L. Powell. 2003. Instrumental variable estimation of nonparametric models. Econometrica 71: 1565–78. [Google Scholar] [CrossRef]
- Newey, Whitney K., James L. Powell, and Francis Vella. 1999. Nonparametric estimation of triangular simultaneous equations models. Econometrica 67: 565–603. [Google Scholar] [CrossRef]
- Ozabaci, Deniz, Daniel J. Henderson, and Liangjun Su. 2014. Additive nonparametric regression in the presence of endogenous regressors. Journal of Business & Economic Statistics 32: 555–75. [Google Scholar]
- Panizza, Ugo, and Andrea F. Presbitero. 2014. Public debt and economic growth: is there a causal effect. Journal of Macroeconomics 41: 21–41. [Google Scholar] [CrossRef]
- Racine, Jeffrey S., and Qi Li. 2004. Nonparametric estimation of regression functions with both categorical and continuous data. Journal of Econometrics 119: 99–130. [Google Scholar] [CrossRef]
- Reinhart, Carmen M., Vincent R. Reinhart, and Kenneth S. Rogoff. 2012. Public debt overhangs: advanced-economy episodes since 1800. Journal of Economic Perspectives 26: 69–86. [Google Scholar] [CrossRef]
- Reinhart, Carmen M., and Kenneth S. Rogoff. 2010. Growth in a Time of Debt. NBER Working Paper No. 15639. Cambridge, MA, USA: NBER. [Google Scholar]
- Temple, Jonathan. 1999. The new growth evidence. Journal of Economic Literature 37: 112–56. [Google Scholar] [CrossRef]
- Vaona, Andrea, and Stefano Schiavo. 2007. Nonparametric and semiparametric evidence on the long-run effects of inflation on growth. Economics Letters 94: 452–58. [Google Scholar] [CrossRef]
- Woo, Jaejoon, and Manmohan S. Kumar. 2015. Public debt and growth. Economica 82: 705–39. [Google Scholar] [CrossRef]
- Wright, Alan, and Kari Grenade. 2014. Determining optimal public debt and debt-growth dynamics in the caribbean. Research in Applied Economics 6: 87–115. [Google Scholar] [CrossRef]
- Yener, Haluk, Thanasis Stengos, and Ege M. Yazgan. 2015. Survival Maximizing Leverage of an Economy: The Case of Greece. Technical Report, Discussion Paper. Guelph: University of Guelph. [Google Scholar]
- Yener, Haluk, Thanasis Stengos, and Ege M. Yazgan. 2017. Analysis of the seeds of the debt crisis in europe. The European Journal of Finance 23: 1589–610. [Google Scholar] [CrossRef]
| 1. | In another paper Newey and Powell (2003), the conditional mean of disturbances given instruments was assumed to be zero without imposing an additive structure for the endogenous variables. |
| 2. | The authors used B-spline smoothing in the first two steps assuming the domain of the basis functions over the closed interval. |
| 3. | Excluded countries are Guyana, Nicaragua, Papua New Guinea, and Syria. Guyana and Papua New Guinea are excluded since they were not reported in PWT 9.0. Data for Syria were not available in the IMF public debt database beyond 2010. |
| 4. | Acemoglu et al. (2001) evaluated the difference between OLS and 2SLS estimates of the democracy variable using executive constraints as an instrument. They expected that using this variable as an instrument would not solve the endogeneity problem, but that it would correctly address the measurement error if it was properly measured. The estimated effect of the institutions variable from the 2SLS method was 0.87 and highly significant. They concluded that measurement error in the institutions variable could be the primary difference between the OLS and 2SLS estimates. |
| 5. | Henderson et al. (2012) suggest to plot gradient estimates in a 45o plot to expose parameter heterogeneity that exists in the estimates. Their suggestion is useful especially when covariate vector is more than one dimension. Since in our model estimation the coefficients vary with respect to only one variable, from the graphical point of view it is better to plot coefficient estimates on a Cartesian coordinate system. |
| 6. | These countries are the Central African Republic and Malawi for the year 1990. |
| 7. | The figures and detailed results obtained in this section are available upon request from the author. |


| Variable | OLS | 2SLS | SPSCM-IV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| Intercept | 0.0355 | 0.0258 | −0.0203 | −0.0126 | 0.0236 | −0.0068 | −0.0068 | 0.0409 | 0.0196 | −0.0171 |
| 0.0143 | 0.0143 | 0.0437 | 0.0450 | 0.0144 | 0.0444 | 0.0457 | 0.005 | 0.0391 | 0.0346 | |
| Public Debt | −0.0080 | −0.0067 | −0.0060 | −0.0058 | −0.0064 | −0.0058 | −0.0055 | −0.0071 | −0.0073 | −0.0053 |
| 0.0034 | 0.0033 | 0.0033 | 0.0033 | 0.0033 | 0.0033 | 0.0033 | 0.0011 | 0.0025 | 0.0023 | |
| Democracy | 0.0012 | 0.0014 | 0.0014 | 0.0015 | 0.0022 | 0.0021 | —– | —– | —– | |
| 0.0004 | 0.0006 | 0.0006 | 0.0004 | 0.0007 | 0.0007 | |||||
| Initial Income | −0.0049 | −0.0051 | −0.0060 | −0.0061 | −0.0097 | −0.0081 | ||||
| 0.0035 | 0.0035 | 0.0021 | 0.0034 | 0.0024 | 0.0024 | |||||
| Investment Rate | 0.0178 | 0.0176 | 0.0183 | 0.0181 | 0.0077 | 0.0077 | ||||
| 0.0053 | 0.0053 | 0.0053 | 0.0053 | 0.004 | 0.0039 | |||||
| Population Growth Rate | −0.0111 | −0.0102 | −0.0073 | −0.0069 | −0.0283 | −0.028 | ||||
| 0.0248 | 0.0248 | 0.0247 | 0.0248 | 0.0142 | 0.014 | |||||
| Schooling | 0.0050 | 0.0051 | 0.0047 | 0.0048 | 0.0090 | 0.0090 | ||||
| 0.0039 | 0.0040 | 0.0039 | 0.0040 | 0.0029 | 0.003 | |||||
| Inflation Rate | −0.0015 | −0.0017 | −0.0028 | |||||||
| 0.0012 | 0.0012 | 0.0011 | ||||||||
| Trend | 0.0054 | 0.0041 | 0.0023 | 0.0017 | 0.0038 | 0.0019 | 0.0013 | |||
| 0.0018 | 0.0019 | 0.0023 | 0.0018 | 0.0020 | 0.0017 | 0.0018 | ||||
| In-Sample | 0.0832 | 0.1211 | 0.2093 | 0.2154 | 0.1191 | 0.2025 | 0.2094 | 0.1744 | 0.3799 | 0.4257 |
| Out-of-Sample | 0.0982 | 0.1399 | 0.2684 | 0.2767 | 0.1379 | 0.2600 | 0.2698 | 0.1187 | 0.3099 | 0.3411 |
| ASPE | 0.00048 | 0.00046 | 0.00044 | 0.00044 | 0.00047 | 0.00073 | 0.00074 | 0.00049 | 0.00041 | 0.00040 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koroglu, M. Growth and Debt: An Endogenous Smooth Coefficient Approach. J. Risk Financial Manag. 2019, 12, 23. https://doi.org/10.3390/jrfm12010023
Koroglu M. Growth and Debt: An Endogenous Smooth Coefficient Approach. Journal of Risk and Financial Management. 2019; 12(1):23. https://doi.org/10.3390/jrfm12010023
Chicago/Turabian StyleKoroglu, Mustafa. 2019. "Growth and Debt: An Endogenous Smooth Coefficient Approach" Journal of Risk and Financial Management 12, no. 1: 23. https://doi.org/10.3390/jrfm12010023
APA StyleKoroglu, M. (2019). Growth and Debt: An Endogenous Smooth Coefficient Approach. Journal of Risk and Financial Management, 12(1), 23. https://doi.org/10.3390/jrfm12010023




