Contribution to the Valuation of BRVM’s Assets: A Conditional CAPM Approach

Abstract

The conditional capital asset pricing model (CAPM) theory postulates that the systematic risk ($\beta$) of an asset or portfolio varies over time. Several dynamics are thus given to systematic risk in the literature. This article looks for the dynamic that seems to best explain the returns of the assets of the Regional Stock Exchange of West Africa (BRVM) by comparing two dynamics: one by the Kalman filter (assuming that the $\beta$ follow a random walk) and the other by the Markov switching (MS) model (assuming that $\beta$ varies according to regimes) for four portfolios of the BRVM. Having found a link between the beta of the market portfolio and the size criterion (measured by capitalization), the two previous models were re-estimated with the addition of the SMB (Small Minus Big) variable. The results show according to the RMSE criterion that the estimation by the Kalman filter fits better than MS, which suggests that investors cannot anticipate systematic risk because of its high volatility.

1. Introduction

In the world of finance, the evaluation of the return of financial assets is governed by the well-known theory of the capital asset pricing model (CAPM). This theory, introduced by Sharpe (1964), Lintner (1965), and Black (1972), states that the risk premium of an asset is equal to the product of the systematic asset risk (beta) and the market portfolio. The beta is approximately equal to the covariance between asset returns and market returns. However, there are several criticisms based on the CAPM hypothesis. The most important criticism is from Fama and French (1992)1, which stipulated that the beta of the portfolio market alone was not enough to explain the return of an asset. However, another criticism, and not the least, concerns the postulation of the CAPM, which considers one period. In other words, the beta obtained was based on only one period. This is how the conditional CAPM appeared.

The conditional CAPM postulates that the simple CAPM theory holds from period to period. Thus, agents review their beta (systematic risk) from period to period. Two branches of conditional CAPM currently exist. The first takes into account the addition of a new factor (implying another beta), while the second models the beta of the market portfolio as a system evolving over time. For the last one, several formulations exist regarding the dynamics of the beta. Some authors model it as a random walk, others as a random coefficient, and others as a learning process of an investor. All these forms of modeling are based on precise assumptions about investor behavior. However, among all the formulations of systematic beta risk, which one is more suitable?

The aim of this work is first to investigate the formulation of the beta and thus the behavior of the investors who best explain the return of Regional Stock Exchange (BRVM) assets2. Two main hypotheses are evaluated in this work:

• Investors cannot predict the systematic risk of assets because it is highly volatile.
• Investors change their behaviors over a given period, so the asset’s beta takes different values according to these periods.

The first hypothesis is based on the conditional CAPM’s formulation postulating the non-stability of the beta of the assets over time. It is therefore assumed a non-stationarity of the betas. The second hypothesis comes from a large list of works3 in the literature of Markov switching (MS) models regarding the beta estimate.

To our knowledge, no study of the BRVM has focused on such a subject.

The results suggest that Hypothesis 1 is more plausible when considering the RMSE criterion.

2. Materials and Methods

The idea of conditional models is to generalize the CAPM to more than two periods making them more in line with reality. They thus raise the hypothesis of a simple periodicity of the CAPM. Indeed, in the CAPM as established, the investor makes a decision at a period following the observed beta. When changing periods, he can revise his behavior. The example given by Jagannathan and Wang (1996) is that in a recession, the leverage effect of low-performing firms is expected to increase sharply relative to other firms, resulting in an increase in their systematic risk (beta). Thus, the beta obtained from the simple CAPM is a conditional beta as shown by the following equation:

$$\mathbb{E}(R_{it}/I_{t-1})=r_f+{\beta }_{t-1}\mathbb{E}(R_{mt}-r_f/I_{t-1})$$

(1)

where $R_{it}$ represents the returns, $r_f$ the risk-free interest rate, $R_{mt}$ the returns of market portofolio and $I_{t-1}$ the information available up to t-1. Several approaches are used in conditional models: those with several factors (Jagannathan and Wang (1996); Lettau and Ludvigson (2001)), those with covariances varying over time (Harvey et al. (1992); Bollerslev et al. (1988)), and those with beta4 varying in time. Although the first two approaches are widely used, the approach allowing a variation of beta over time is regaining interest, particularly with the work of Adrian and Franzoni (2009) and Caia and Renb (2012). Prior to this work, the most commonly used methods for estimating time-varying beta are mainly state space models (Kalman filter estimation), recursive least squares, window regressions, etc. In this vast literature, we distinguish the works of Groenewold and Fraser (1999), Park (2004), and Abdymomunov and Morley (2011).

Groenewold and Fraser (1999) investigated the beta estimate of conditional CAPM with time-varying beta on monthly assets in Australia for 23 sectors over the period 1979–1994. After estimating the betas by the recursive least squares, and by the Kalman filter, they tested the stationarity of the estimated beta and found it to be non-stationary, which reinforces the idea of using such models. Park (2004) examined the relationship between returns and systematic beta risks on US assets. He first estimated the simple CAPM (simple computation of the betas by the covariance between returns and market portfolio) and showed by means of a Cusum test that betas were not stable over time. Based on the fact that the betas are not stable over time, they evaluated the relationship between return and beta using the Kalman filter for 10 portfolios classified by size (capitalization) and 12 others constructed using the classification of Breeden et al. (1989) and Ferson and Harvey (1991), and the results show that the small portfolios have higher beta and reciprocally. They explain it by the fact that these portfolios are generally less diversified. The author has also estimated a conditional CAPM, where it distinguishes two types of beta according to the sign of the risk premium of the market portfolio beta and the return on portfolios. This result is consistent with the implication that beta is a useful measure of systematic risk in time. Abdymomunov and Morley (2011) have proposed a beta estimate using the Markov change regime method. Their results suggest that the use of the MS model improves the explanation of asset return at the moment when the simple CAPM is invalid.

The previous models do not take investor learning into account. Indeed, it would not be wrong to think that investors do not know the long-term level of systematic risk and therefore learn rationally from observations of expected returns. It is on this base that Adrian and Franzoni (2009) modeled the returns on US assets. To take investors knowledge of systematic risk into account, they introduced variables such as “the term spread,” representing the difference between the yields of US 10-year and 3-month treasury bills, “the value spread” and the CAY variable of Lettau and Ludvigson (2001), capturing innovations in the cointegration relationships between consumption, market portfolio, and labor income. The results suggest that the insertion of learning and estimation by Kalman filters reduce pricing errors.

Recently, Caia and Renb (2012) proposed a new approach for estimating the CAPM with time-varying beta. Namely, they used a regression model with a functional coefficient with beta varying over time. The innovation here is certainly due to the consideration of different windows in the estimation of beta (nonparametric estimation) but also of a different learning in each window. The results show that this model better explains the return of assets than the simple CAPM.

2.1. Conditional Estimation of Systematic Risk ($\beta$)

The previous section helps one to understand the necessity of using conditional CAPM and mainly those that vary the beta over time. From Equation (1), it will be necessary to give a specification to the form of beta. It should be specified that a small modification is made to the specification of Equation (1) to retain the following equation:

$$\mathbb{E}\left(R_{it}\right)=r_f+{\beta }_{t-1}\mathbb{E}{(R_{mt}-r_f)}^5.$$

(2)

Two specifications are used for this study. For each specification, two variants will be estimated depending on whether SMB (Small Minus Big) is introduced as a factor from the Fama and French three-factor model.

2.1.1. Specification 1: $\beta$ Varies According to a Random Walk

Variant 1: The $\beta$ of Market Portfolio Follows a Random Walk

The first variant of Specification 1 relating to Equation (2) is to consider that the beta of the market portfolio follows a random walk. The equation can then be written as

$${\beta }_t^m={\beta }_{t-1}^m+{\eta }_t$$

(3)

where ${\eta }_t\sim N(0,{\sigma }_{\eta }^2)$, and ${\beta }_t^m$ refers to the beta associated with the market portfolio. The idea underlying this choice is that the beta variance of the market portfolio varies over time. In other words, it is not stationary. Thus, we make the assumption, unlike Adrian and Franzoni (2009), that agents do not know the long-term level of beta risk associated with the market portfolio. The beta cannot be predicted by its past value and varies randomly from period to period. This specification has been retained in several studies (Marti (2006) and Park (2004)). The general model can therefore be written as follows:

$$\begin{array}{c}{R}_{it}=r_f+{\beta }_{t-1}^m(R_{mt}-r_f)+{ϵ}_{it}\\ {\beta }_t^m={\beta }_{t-1}^m+{\eta }_t\end{array}.$$

(4)

Variant 2

The second variant consists in introducing an additional variable into the estimation of the returns of the assets. This is the SMB variable6. The latter represents the difference (Minus) of profitability between small (Small) and large (Big) assets sorted by capitalization. We assume that the beta associated with SMB is not stable. The latter is also assumed to follow a random walk. This choice is justified by the work of Huang and Hueng (2009). They have shown that taking into account a change in the coefficients of the additional factors of the simple CAPM could significantly reduce the price error. The general model is thus written as follows:

$$\begin{array}{c}{R}_{it}=r_f+{\beta }_{t-1}^m(R_{mt}-r_f)+{\beta }_{t-1}^{SMB}SM{B}_t+{ϵ}_{it}\\ {\beta }_t^m={\beta }_{t-1}^m+{\eta }_t^1\\ {\beta }_t^{SMB}={\beta }_{t-1}^{SMB}+{\eta }_t^2\end{array}.$$

(5)

Equations (4) and (5) are estimated by the Kalman filter. Indeed, these equations are special cases of Equation (A1) (see Appendix A), presenting the general form of the state space model estimated by the Kalman filter. Equation (4) is obtained by setting $Z_t=\left(1R_{mt}\right)$, ${\alpha }_t={\left(r_f{\beta }_{it}^m\right)}^{\prime }$, $T_t=I_2$, where $I_2$ denotes the identity matrix of order 2 and $R_t={\left(01\right)}^{\prime }$. Equation (5) is obtained by setting $Z_t=\left(1R_{mt}SM{B}_t\right)$, ${\alpha }_t={\left(r_f{\beta }_{it}^m{\beta }_{it}^{SMB}\right)}^{\prime }$, $T_t=I_3$, where $I_3$ denotes the identity matrix of order 3 and $R_t={\left(011\right)}^{\prime }$.

Choosing the Initialization Parameters for the Kalman Filter

The state space model estimated by the Kalman filter distinguishes four initialization parameters. This is $a_1$, $P_1$, $H_t$, and $Q_t$ (see Appendix A). Although the parameters $a_1$ and $P_1$ are important in the initialization, they are not determinative since, whatever the value of these parameters, the filter will always tend to find its equilibrium value around the series by error correction (Durbin and Koopman (2012)), “Time Series Analysis by State Space Methods”, pp. 32–33). The most important parameters are $H_t$ and $Q_t$ since they can drastically change the estimates obtained. Durbin and Koopman propose an estimate of these parameters by the maximum likelihood.

The parameter $Q_t$ is the one that acts on the beta estimated by the Kalman filter. Although it is estimated by the maximum likelihood, the obtained value may not minimize other criteria concerning the quality of the model, in particular the RMSE (root mean squared error). Thus, unlike the Durbin and Koopman approach, we propose the determination of the $Q_t$ minimizing the RMSE criterion.

2.1.2. Specification 2: The $\beta$ Varies According to Regime

Variant 1: Only the Market Portfolio Is Included as an Explanatory Variable

This variant takes into account the returns of the market portfolio as the only explanatory variable. The specification for the beta of the market portfolio is allowed to take different values according to regime. This type of model has already been used in the literature to estimate the beta of the market portfolio in Guidolin and Timmermann (2005) and Abdymomunov and Morley (2011). The number of regimes (states) is a priori unknown. For the case of two states, the model can be written as follows:

$$\begin{array}{c}{R}_{it}=r_f+{\beta }_{S_t}^m(R_{mt}-r_f)+{\sigma }_{S_t}{ϵ}_{it}\\ {\beta }_{S_t}^m=\left\{\begin{array}{cc}{\beta }_1^m\hfill & \mathrm{si}{S}_t=1\hfill \\ {\beta }_2^m\hfill & \mathrm{si}{S}_t=2\hfill \end{array}\right.\\ {\sigma }_{S_t}=\left\{\begin{array}{cc}{\sigma }_1\hfill & \mathrm{si}{S}_t=1\hfill \\ {\sigma }_2\hfill & \mathrm{si}{S}_t=2\hfill \end{array}\right.\\ \end{array}$$

(6)

where $S_t$ denotes a discrete random variable taking the value 1 when in the first state and 2 in the second state; ${\beta }_1^m$ and ${\beta }_2^m$ are the beta values corresponding to the different states. We also assume that the standard error deviation ${\sigma }_{St}$ (associated to the white noise ${ϵ}_{it}$ in Equation (6)) varies from one regime to another. Thus, ${\sigma }_1$ and ${\sigma }_2$ designate the values of the standard deviation according to the two states.

Variant 2: Adding the SMB Factor

This variant is obtained by adding the SMB in Equation (6) and by varying its coefficient according to different states. The general model is thus written:

$$\begin{array}{c}{R}_{it}=r_f+{\beta }_{S_t}^m(R_{mt}-r_f)+{\beta }_{S_t}^{SMB}SM{B}_t+{\sigma }_{S_t}{ϵ}_{it}\\ {\beta }_{S_t}^m=\left\{\begin{array}{cc}{\beta }_1^m\hfill & \mathrm{if}{S}_t=1\hfill \\ {\beta }_2^m\hfill & \mathrm{if}{S}_t=2\hfill \end{array}\right.\\ {\beta }_{S_t}^{SMB}=\left\{\begin{array}{cc}{\beta }_1^{SMB}\hfill & \mathrm{if}{S}_t=1\hfill \\ {\beta }_2^{SMB}\hfill & \mathrm{if}{S}_t=2\hfill \end{array}\right.\\ {\sigma }_{S_t}=\left\{\begin{array}{cc}{\sigma }_1\hfill & \mathrm{if}{S}_t=1\hfill \\ {\sigma }_2\hfill & \mathrm{if}{S}_t=2\hfill \end{array}\right.\end{array}.$$

(7)

Equations (6) and (7) are placed in the Goldfield and Quandt (1973) (see Appendix B) model of the Markovian switching (MS) model. These models will therefore be estimated by the MS.

2.2. Bootstrap Analysis of the Comparison

In order to strengthen the results of our comparison, we provide an additional bootstrap analysis. Thus, we will make a bootstrap with a replacement obtained after 1000 RMSE replications of the Kalman filter models and MS according to the one-factor or the two-factor model. Thus, the distributions of these RMSE will be compared.

2.3. Data Source

The data used comes from the Regional Stock Exchange (BRVM). The disposable variables are the daily prices of 45 assets and their capitalization, market portfolio values (composite BRVM), and sector portfolios covering the period 1999 to 2017. Since the number of observations per asset was different, the data were aggregated at the monthly level, and the returns on the different assets were calculated.

On the basis of these 45 assets, four portfolios were constructed according to the size of the capitalizations7. They are named, respectively, portfolios 1, 2, 3, and 4 in ascending order of capitalization. The SMB (Small Minus Big) variable was obtained by differentiating the returns of small-cap portfolios from large-cap portfolios. For the risk-free asset rate, the rate at which AFD issued a good AAA rated bond for the period 2008–2016 was taken as a proxy. This annual rate is 5.25%. Having monthly data, this rate has been converted to a monthly rate.

3. Results

In this section, we first present the result of the one-factor model and then the two-factor model.

3.1. Estimation of Unconditional and Conditional CAPM with One Factor

The unconditional CAPM estimate on the different portfolios yields poor results. Indeed, after estimates, the residuals of all the portfolios were not normal, so we carried out the Wald test to check the significance of the coefficients. More importantly, the Wald test results show that beta is not significant for any portfolio. In such a situation, Jagannathan and Wang (1996) suggest moving directly to the conditional CAPM estimate.

3.1.1. Portfolios Description

Table 1. Descriptive statistics of portfolios.

	Obs	Min	Mean	Standard-dev	Max
Portfolio 1	219	−39.57	4.02	31.30	294.24
Portfolio 2	219	−27.45	4.38	26.11	208.88
Portfolio 3	219	−18.04	2.52	19.86	169.50
Portfolio 4	219	−140.20	0.32	11.33	30.99

Source: author’s computations.

presents the summary statistics of the four portfolios. Thus, over the entire period, Portfolio 2 has the highest average monthly return. Indeed, it stood at 4.38% with a dispersion of 26.11% around this average. This portfolio is followed by Portfolios 1, 3, and 4 with average monthly returns of 4.02, 2.52, and 0.32%, respectively. In addition, it should be noted that large-cap portfolios are the least risky in terms of variance.

3.1.2. $\beta$ Estimation with Kalman Filter

Table 2. The one-factor model estimated by the Kalman filter and Markov switching (MS).

	Kalman Filter			Markov Switching
	rf	${\mathit{\beta }}_{\mathit{M}}$	${\mathit{\sigma }}_{{\mathit{\beta }}_{\mathit{M}}}$	rf	State 1	State 2
					${\mathit{\beta }}_{\mathit{M}}$	${\mathit{\beta }}_{\mathit{M}}$
P1	−0.93	22.47	21.42	−1.70 ***	16.93 **	55.16
P2	−0.33	32.10	17.13	−0.65 *	39.40 ***	−46.19 **
P3	0.60	98.36	40.65	−0.15	48.23 ***	55.09
P4	1.37	93.26	43.94	0.91 ***	102.42 ***	71.07 ***

Source: author’s computation. * p < 0.1; ** p < 0.05; *** p < 0.01.

presents the results of the beta estimate with the Kalman filter and the MS model using the one-factor model. The results of the Kalman filter show that the average systematic risk (beta) of the portfolio increases with the size of the portfolio, except for Portfolio 4. Thus, the average beta of Portfolio 1 is 22.47% with a variability of 21.42%, while Portfolio 3 is 98.36% with a variability of 40.65%. In addition, it should be noted that the risk-free asset ratio is negative for the two smaller portfolios. 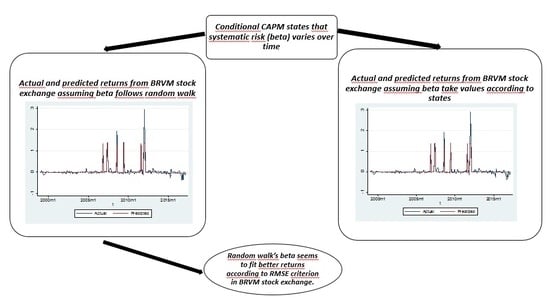The Figure 1 shows the adequacy of the yields predicted by the Kalman filter to the true yields.

3.1.3. $\beta$ Estimation with the Markov Switching Model

The MS model reveals that the behavior of portfolio returns is governed by two states. The results of the beta estimate by the MS model yield negative and significant risk-free interest rates for the two smaller-sized portfolios like with the Kalman filter. However, the risk-free interest rateof Portfolio 3 is also negative. The states governing the performance of the portfolios differ in terms of volatility (low and high volatility states can be identified). In periods of low volatility (State 1), systematic portfolio risks increase with portfolio size and the change in rating has a significant positive impact on portfolio’s performance. The systematic risk of the market increases from 16.93 for Portfolio 1 to 102.42% for the 4. Finally, during periods of high volatility (State 2), the performance of the market portfolio have no significant effect on the returns, regardless of the portfolios.

3.2. Integration of the SMB Factor of Fama and French

The summary of results from the estimation of the two-factor models are shown in the

Table 3. $\beta$ estimation with the SMB factor.

	Kalman Filter					Markov Switching
	rf	${\mathit{\beta }}_{\mathit{M}}$	${\mathit{\sigma }}_{{\mathit{\beta }}_{\mathit{M}}}$	${\mathit{\beta }}_{\mathit{SMB}}$	${\mathit{\sigma }}_{{\mathit{\beta }}_{\mathit{SMB}}}$	rf	State 1		State 2
							${\mathit{\beta }}_{\mathit{M}}$	${\mathit{\beta }}_{\mathit{SMB}}$	${\mathit{\beta }}_{\mathit{M}}$	${\mathit{\beta }}_{\mathit{SMB}}$
P1	0.13	−45.38	30.78	92.37	26.84	0.25	57.80 ***	69.15 ***	−44.11	73.63 ***
P2	−1.20	631.80	99.52	104.08	490.47	−0.70 **	39.10 ***	3.81 **	−65.49	−8.21
P3	5.07	74.38	4.04	74.37	4.04	−0.22	48.52 ***	1.40	63.71 **	−7.96
P4	0.13	80.40	34.70	1.09	26.39	0.98 ***	105.07 ***	−3.35 ***	70.37 ***	−1.82

Source: author’s computation. p < 0.1; ** p < 0.05; *** p < 0.01.

.

3.2.1. Estimation by the Kalman Filter

The introduction of the size factor has increased the systematic risk of all portfolios in absolute value, except for 3 and 4. However, the growth of this risk with the size of the portfolios is, respectively, observed firstly for Portfolios 1 and 2 and secondly for 3 and 4. It should be noted that the systematic risk of Portfolio 1 is negative. As a result, the market beta stood at −45.38% with a variability of 30.78% for Portfolio 1, 631.80% with a variability of 99.52% for Portfolio 2, 74.38% with a variability of 4.04% for Portfolio 3, and 80.40% with a variability of 34.70% for Portfolio 4.

On the other hand, the average risk linked to the size factor (SMB) decreases with the size of the portfolios, except for Portfolio 1. It went from 104.08% for Portfolio 2 to 1.09% for Portfolio 4, with respective variabilities of 490.47 and 26.39%. The Figure 2 shows the predicted returns with the model with the size factor and actual returns.

3.2.2. The Markov Switching Model Estimation

The MS model yields different results according to the states. Indeed, during periods of low volatility, portfolio returns are both explained by the market portfolio and the size factor, except for Portfolio 3. For the latter, the SMB factor is not significant. The SMB factor introduction hardly changes the systematic risk of Portfolios 3 and 4 during periods of low volatility, whereas those of Portfolios 1 and 2 vary significantly by 40.87 and 40.10 percentage points, respectively, compared to the model without the SMB factor.

4. Discussion

After estimation of the different models, we proceed in this section to their comparison according to the RMSE criterion.

Table 4. RMSE of different estimation.

	RMSE
	One Factor Model		Model with SMB Factor
	FK	MS	FK	MS
Portfolio 1	0.1492	0.1498	0.0213	0.0882
Portfolio 2	0.1200	0.1205	0.0000	0.1213
Portfolio 3	0.0595	0.0646	0.3062	0.0646
Portfolio 4	0.0360	0.0453	0.0152	0.0689

Source: author’s computation.

presents the RMSE of the different models according to the portfolios. The results show that, generally, the Kalman filter is better. Indeed, when considering the one-factor model, the Kalman filter has the smallest RMSE compared to the MCRM for all portfolios. It should be noted, however, that the gap remains small. For the two-factor model, the Kalman filter performs better than the MS model for Portfolios 1, 2, and 4. The beta of Portfolio 3 seems to be more governed by states than by a random work.

To reinforce these results, according to our methodology, we compare below the bootstrap distributions of the RMSE of Kalman filter and MS models after 1000 replications. Figure 3 gives the bootstrap distributions of the RMSE following the one-factor model. The results show, with the exception of Portfolio 1, that the RMSE distribution obtained by the MS model dominates that of the Kalman filter. This means that the model obtained by the Kalman filter outperforms the MS model. For Portfolio 1, we cannot draw conclusions because distributions are crossing.

Figure 4 shows the bootstrap distributions of the RMSE following the one-factor model. At this level, the conclusions are similar to the case of the one-factor model for Portfolios 1 and 4. For Portfolios 2 and 3, we cannot draw conclusions.

Thus, our results converge more toward the fact that the systematic risk beta follows a random walk, since the model obtained by the Kalman filter generally dominates that with a change in regime.

5. Conclusions

The literature on conditional CAPM has seen much development. As such, a multitude of models exist today for systematic risk modeling ($\beta$). Based on two assumptions, we estimated the systematic risk according to two models: the Kalman filter and the MS model for four BRVM portfolios, constructed by sorting the assets according to their capitalization and considering the quartiles. Two types of models were evaluated: the first with a market beta as an explanatory variable (a one-factor model) and the second when adding the SMB (Small Minus Big) factor.

The results show that, according to the RMSE criterion, the Kalman filter model is more efficient for both the one- and two-factor estimation.

Following these results, conjectures can be made regarding the behavior of investors in the BRVM market. These conjectures stem directly from the study assumptions. The Kalman filter model provides better predictions than MS. This means that when choosing a portfolio, managers are more likely to expect an uncontrolled risk than a risk varying according to periods.

It is important to remember that our results only apply to the assets of the BRVM and in the context of portfolios built according to criteria concerning the size of capitalizations.

Some of the hypotheses in this study can be released to provide a basis for future research. In this study, only one additional factor was taken into account due to a lack of data. Additional analysis that could be an extension of this study would be to integrate other factors such as HML or B/M. Another extension is the choice of the risk-free asset rate. The rate chosen for our study is only a proxy. An approach that models the risk-free asset would be appropriate.