The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market
Abstract
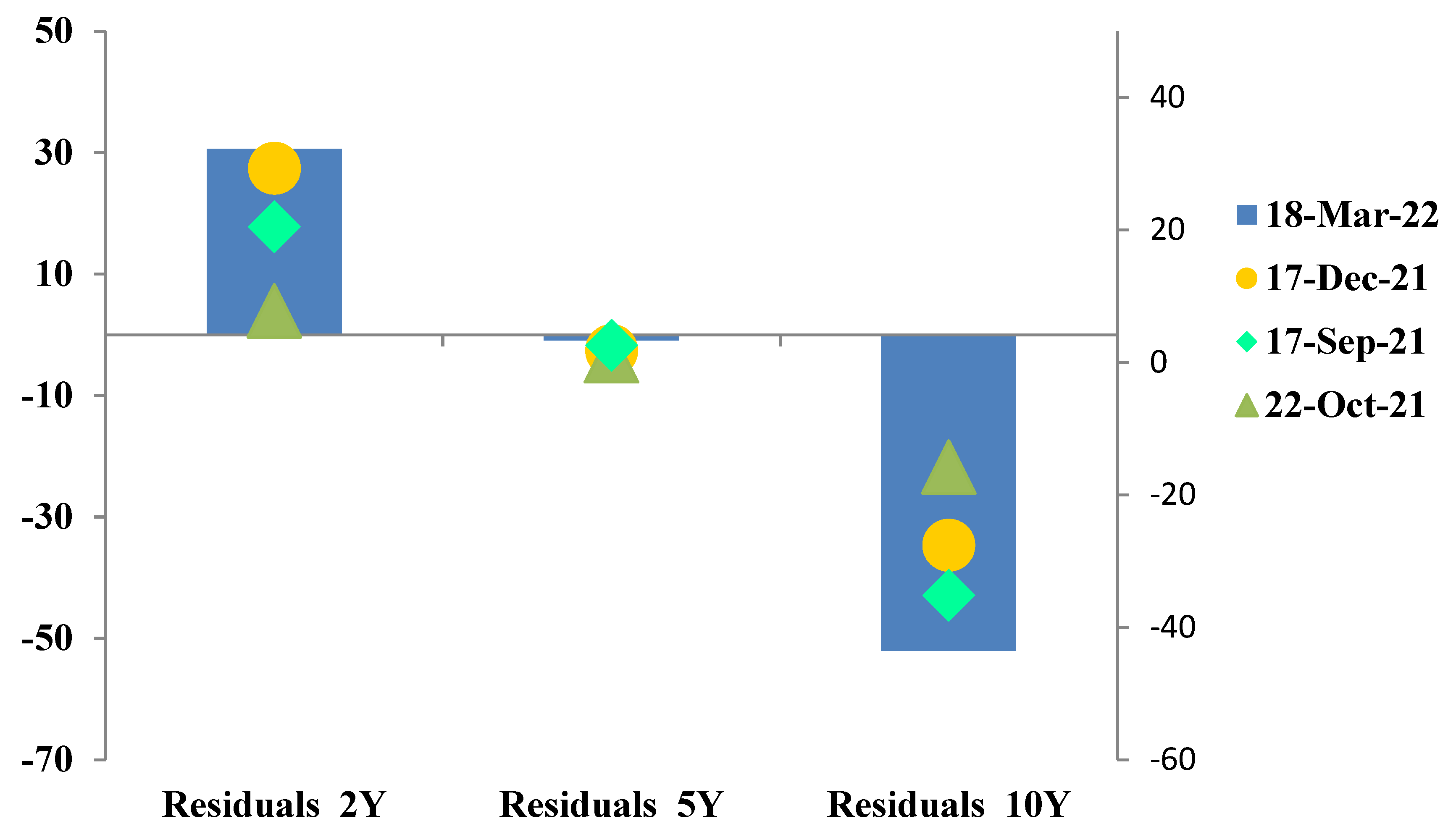
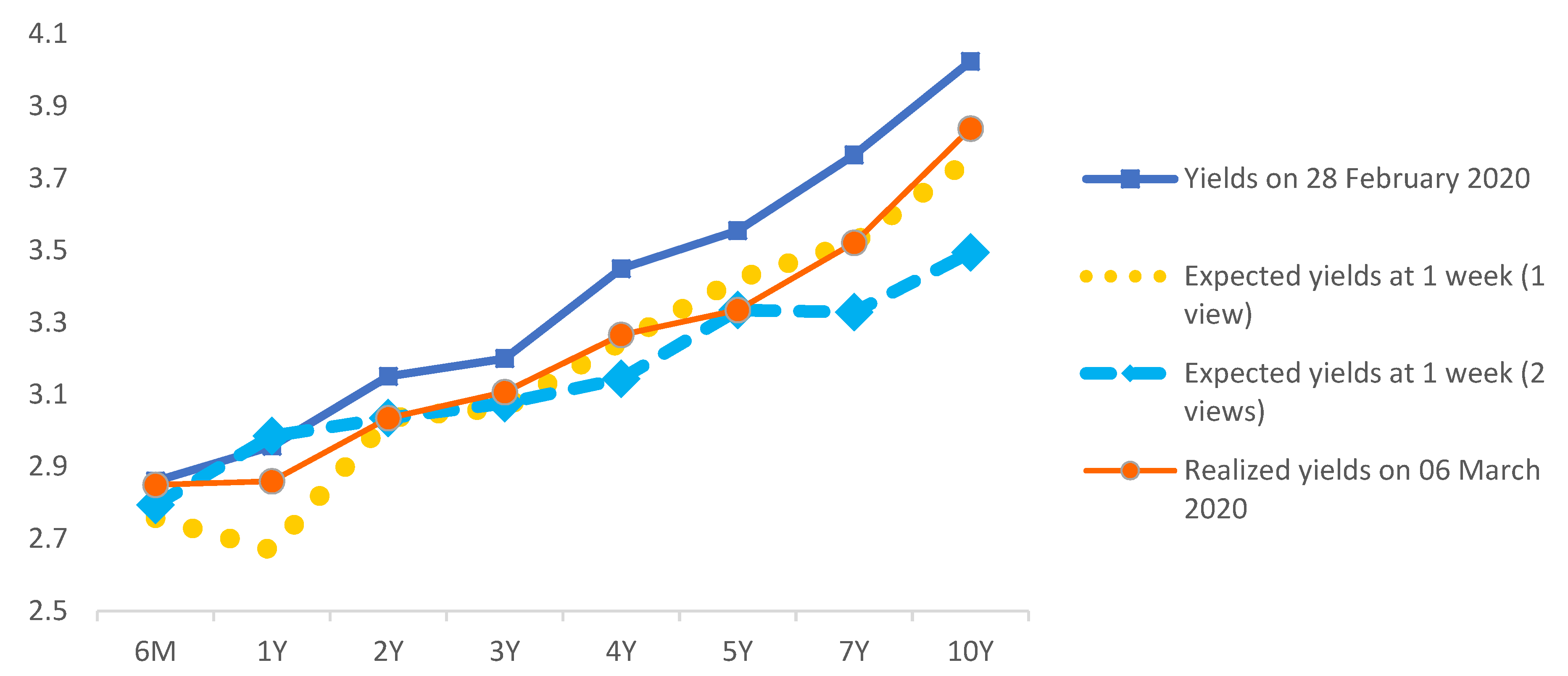
:1. Introduction
2. Literature Review
3. Principal Component Analysis
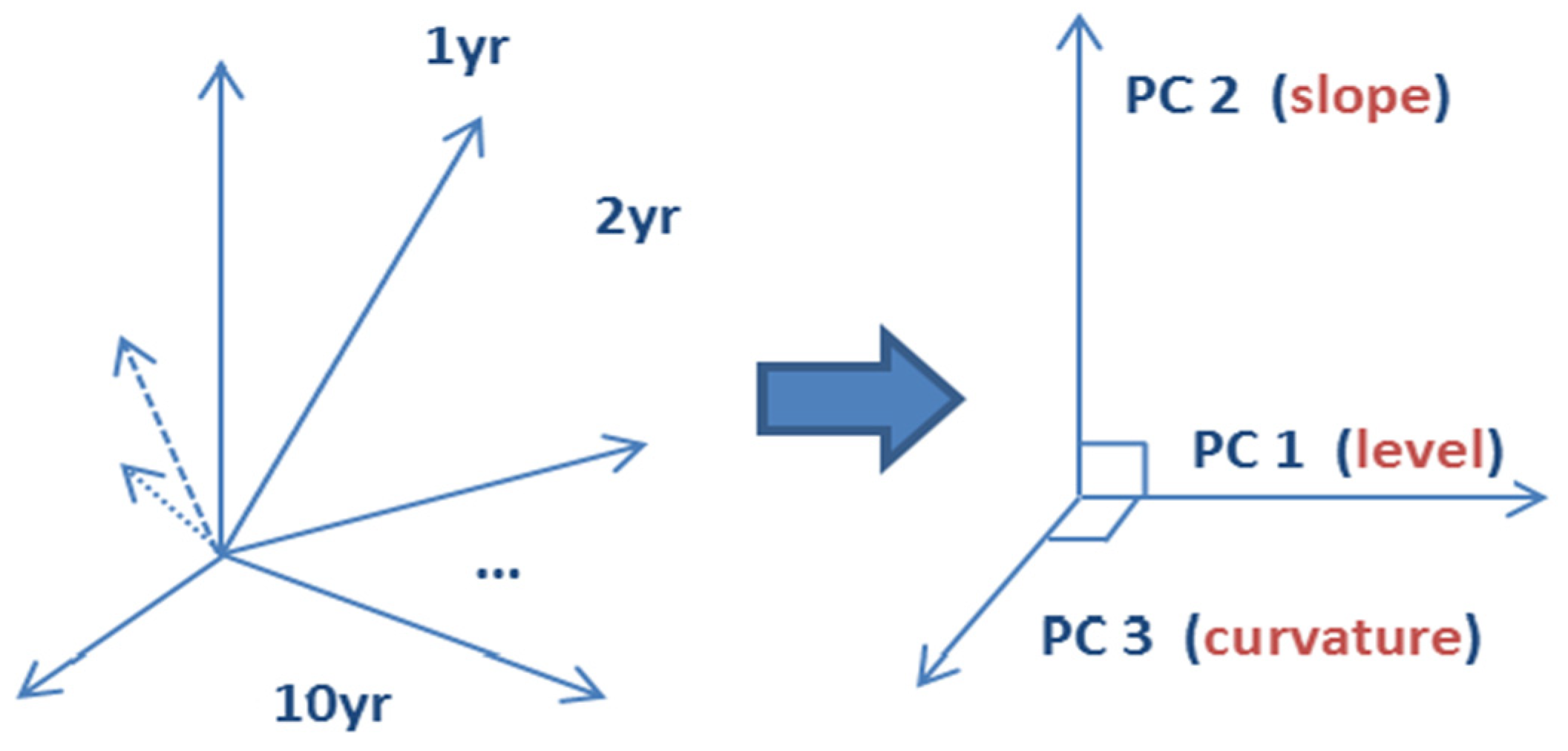
3.1. Key Rates versus Principal Components
3.2. PCA Methodology
- The vector λ = () of the variances of principal components;
- The matrix of the factor loadings associated with the principal components.
4. Building Yield Curve Shocks of Deterministic Probability
4.1. The Probabilistic Framework of Interest Rate Scenarios
4.2. Measures of Historical Plausibility of Yield Curve Shocks (Explanatory Power, Magnitude Plausibility, and Shape Plausibility)
- 1.
- The representation of any yield curve shock as a set of principal components’ realizations;
- 2.
- The ranking of principal components given by their explanatory powers .
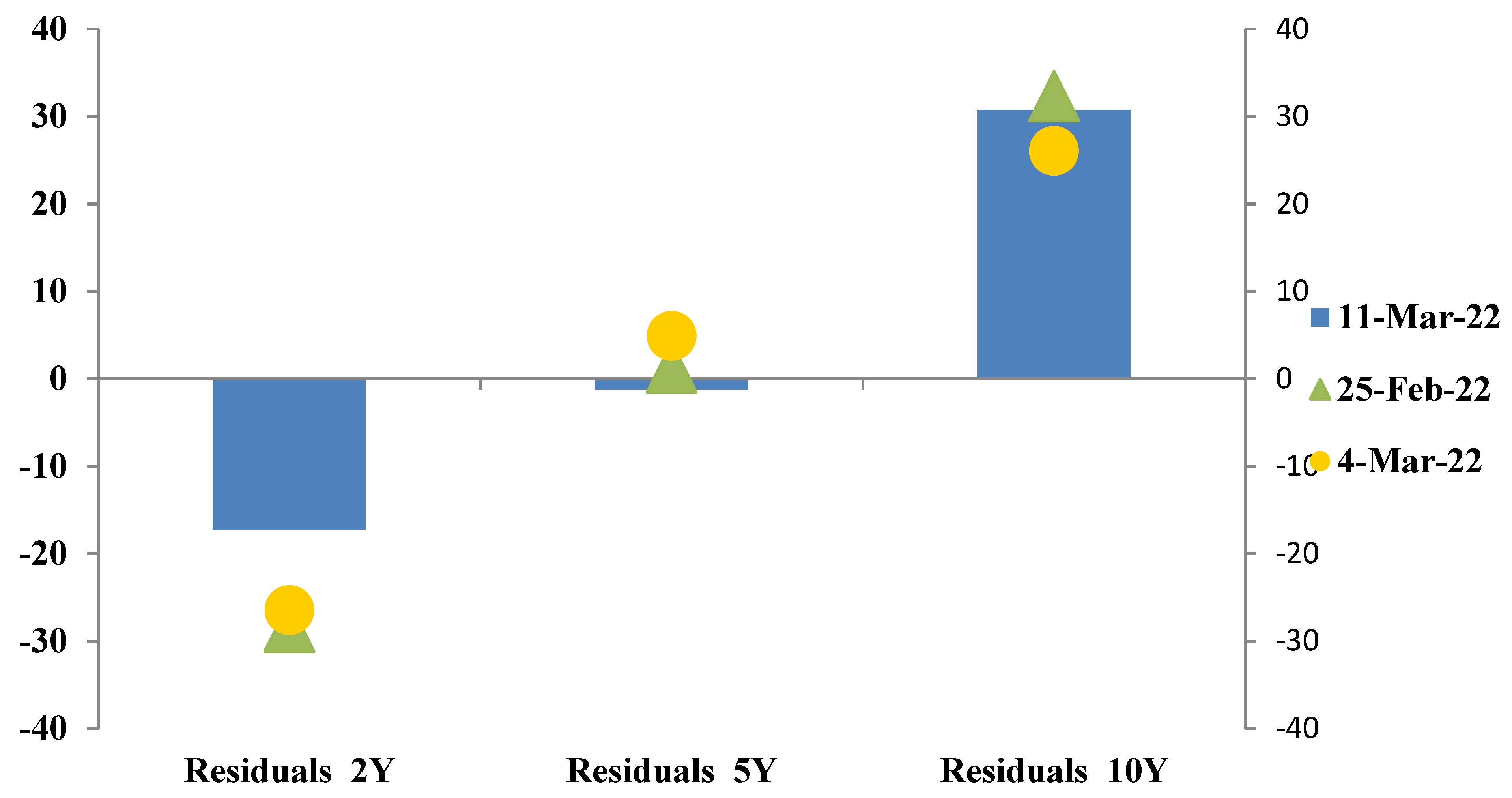
4.3. Incorporating Trader’s View into Yield Curve Forecasts
5. PCA Applied to the Romanian Government Bond Market
5.1. Explanatory Powers of Principal Components
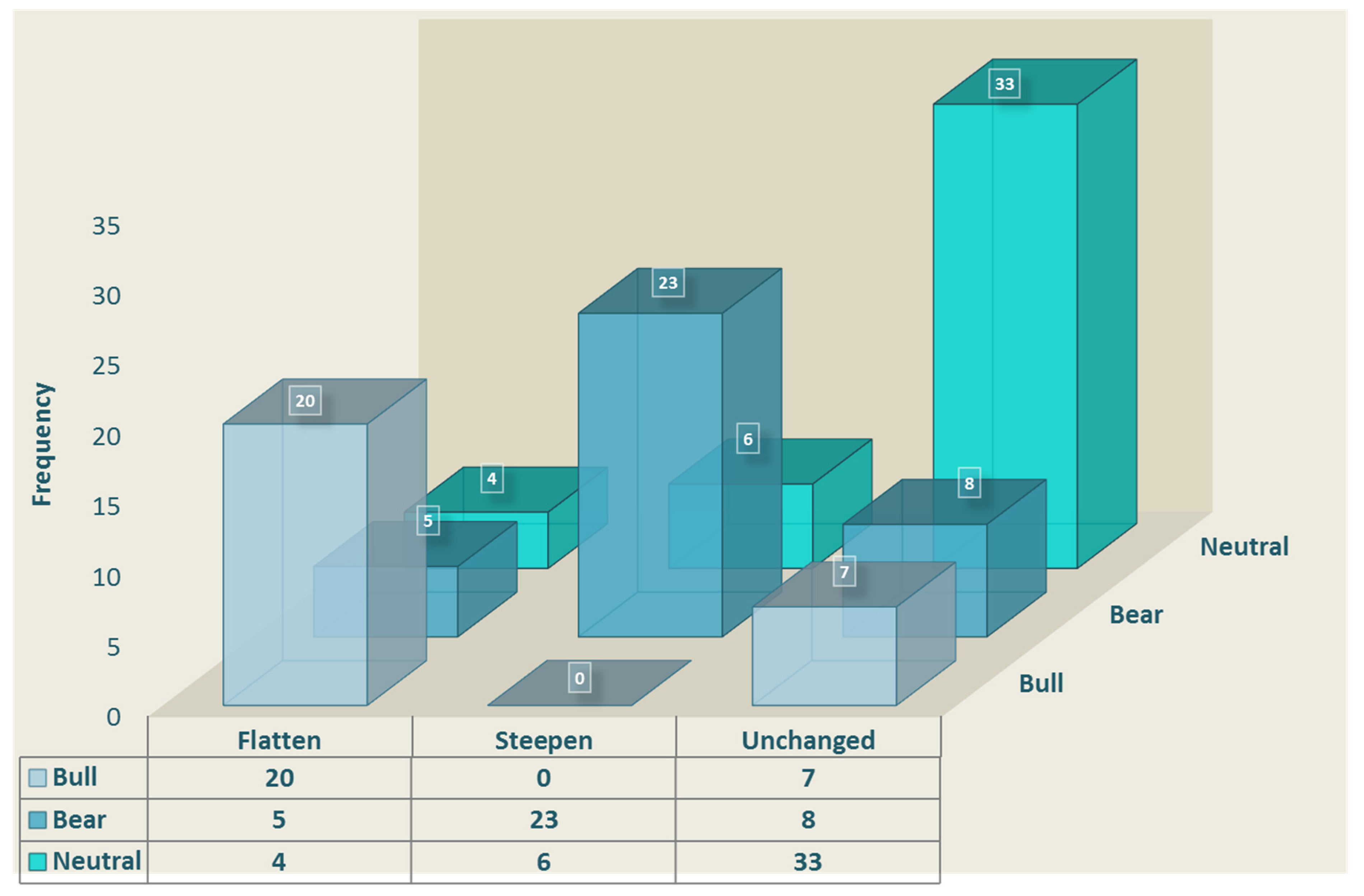
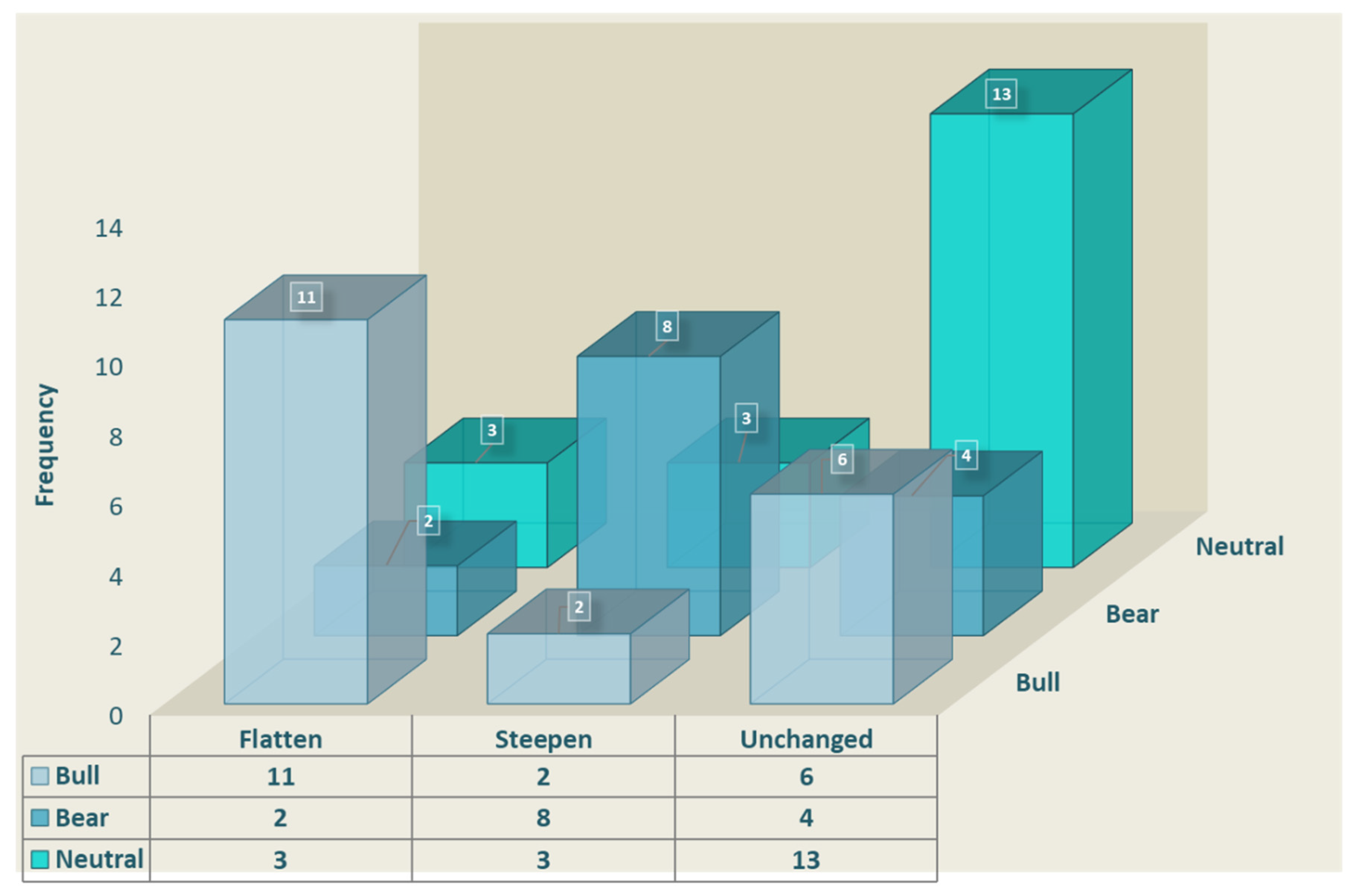
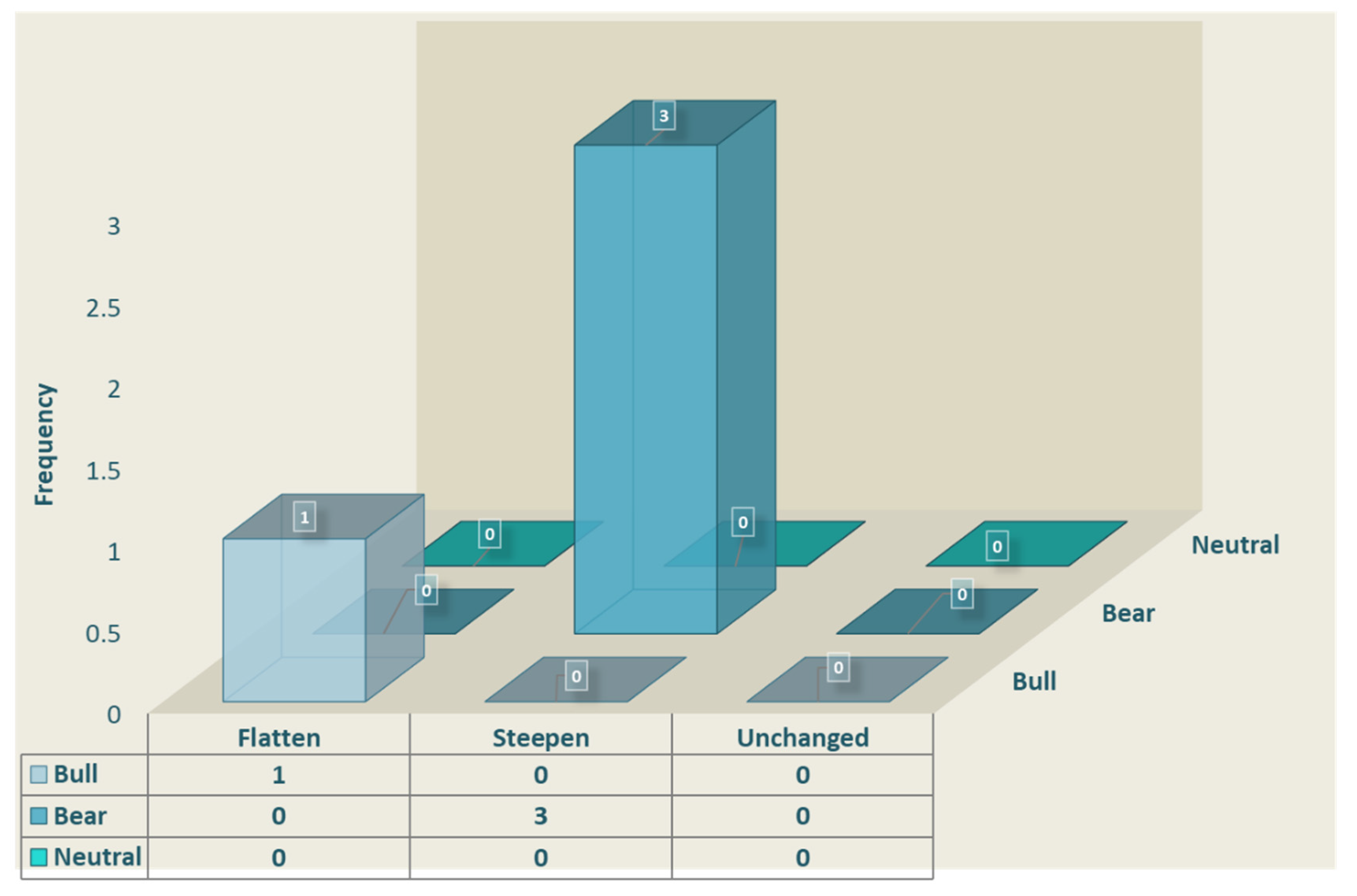
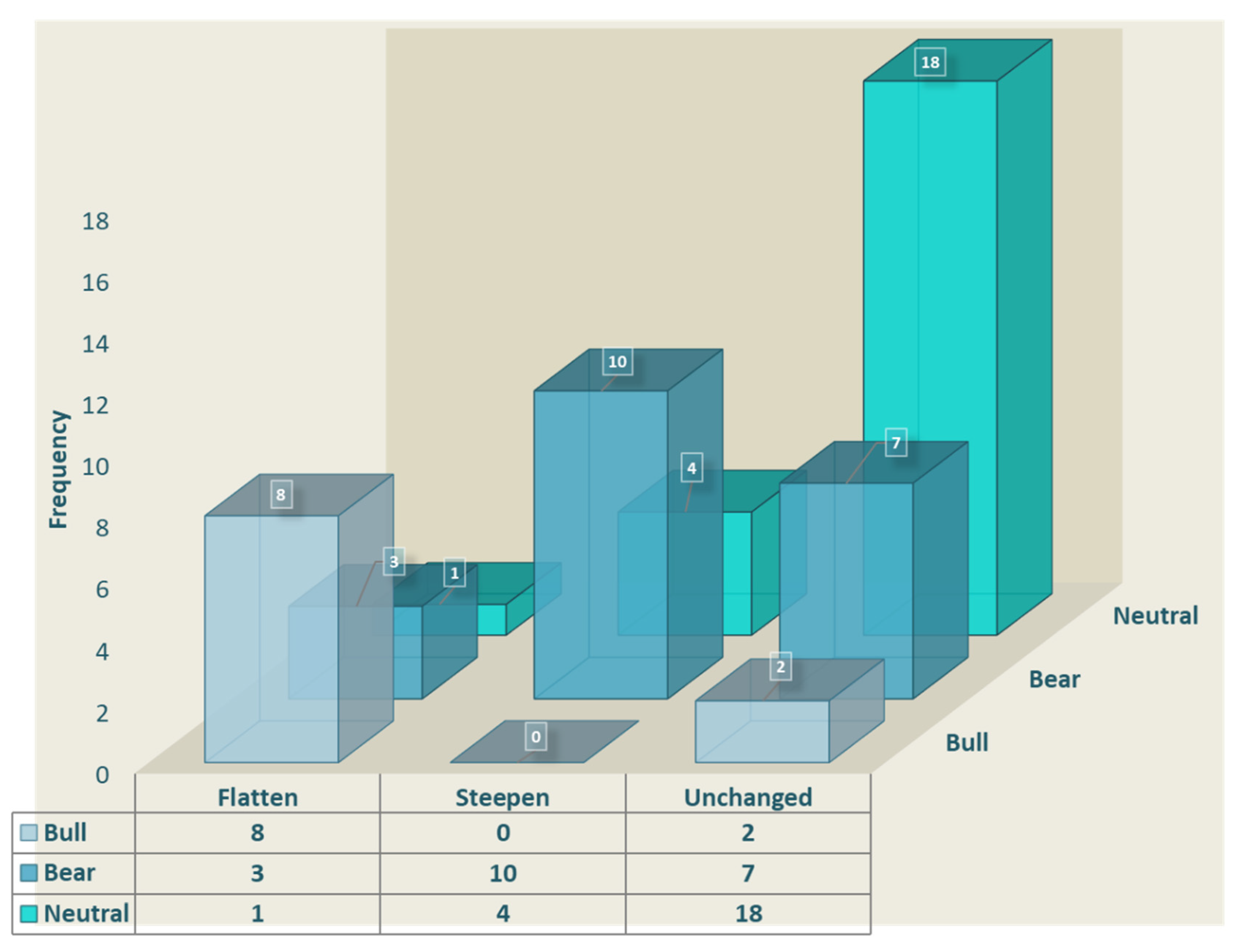
5.2. Steepeners and Flatteners of the Romanian Sovereign Yield Curve: The Use of PCA in Identifying Relative-Value Trading Opportunities
5.3. Developing Romanian PCA Yield Curve Scenarios: Examples from the Outbreak of the COVID-19 Pandemic and the Start of the Russian–Ukrainian War
5.3.1. Plausibility Measures of Interest Rate Shocks for Romanian Government Bonds
5.3.2. Incorporating Trader’s View to Derive Romanian PCA Yield Curve Forecasts
- i.
- The Romanian 2-year yield to increase from 4.48% to 4.62%;
- ii.
- The Romanian 5-year yield to increase from 5.12% to 5.38%;
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

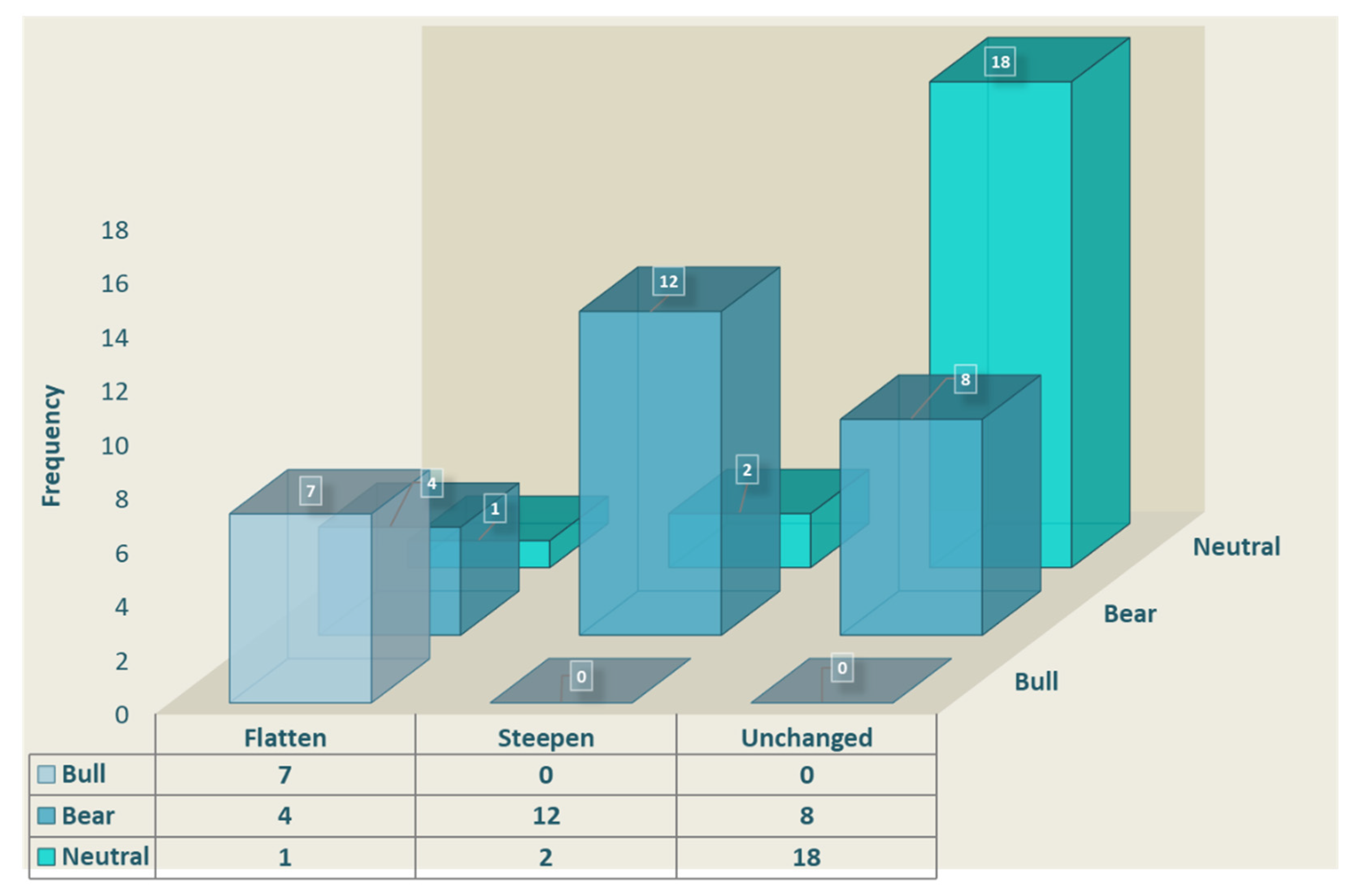
| Annualized Shock (bps) | 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y | Contribution (Explanatory Power) |
|---|---|---|---|---|---|---|---|---|---|
| PC1 shock | 78 | 64 | 138 | 139 | 148 | 172 | 200 | 209 | 80.83% |
| PC2 shock | 65 | 28 | 57 | 71 | 36 | −1 | −61 | −84 | 11.16% |
| PC3 shock | 78 | 46 | −37 | −19 | −19 | −1 | −40 | 8 | 4.88% |
| Parallel Shock | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 73.33% |
| YC PCAs Shock | 221 | 138 | 158 | 165 | 170 | 149 | 133 | 221 | 96.87% |
| YC Annualized Shock (bps.) | Corresp. STDEV | Likelihood |
|---|---|---|
| 50 | 0.35 | 36.32% |
| 144 | 1.00 | 15.87% |
| 100 | 0.69 | 24.51% |
| 150 | 1.04 | 14.92% |
| 200 | 1.39 | 8.23% |
| 225 | 1.56 | 5.94% |
| 250 | 1.73 | 4.18% |
| Annualized Shock of Same Shape (bps) | 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y |
|---|---|---|---|---|---|---|---|---|
| PC1 shock | 155 | 129 | 275 | 278 | 297 | 343 | 401 | 417 |
| PC2 shock | 130 | 56 | 115 | 141 | 72 | −1 | −121 | −169 |
| PC3 shock | 156 | 91 | −73 | −39 | −39 | −1 | −80 | 17 |
| Parallel Shock | 289 | 289 | 289 | 289 | 289 | 289 | 289 | 289 |
| YC PCAs Shock | 441 | 276 | 317 | 330 | 341 | 297 | 266 | 441 |
| PC1 | 99.97% | 97.78% | 0.00% | 0.00 | 0.96 |
| PC2 | 0.01% | 1.22% | 0.00% | 0.00 | 0.00 |
| PC3 | 0.02% | 0.66% | 0.00% | 0.00 | 0.00 |
| PC4 | 0.00% | 0.19% | 0.00% | 0.00 | 0.00 |
| PC5 | 0.00% | 0.07% | 0.00% | 0.00 | 0.00 |
| PC6 | 0.00% | 0.04% | 0.00% | 0.00 | 0.00 |
| PC7 | 0.00% | 0.02% | 0.00% | 0.00 | 0.00 |
| PC8 | 0.00% | 0.01% | 100.00% | 0.00 | 1.00 |
| Sum of Squares | 0.03 | 1.40 | |||
| Shape Plausibility | 98.15% |
| 1 | By the time Golub and Tilman wrote the book Risk Management: Approaches for Fixed Income Markets in 2000, there were only a few proprietary and government trading desks that used principal component durations in weighting butterfly yield curve trades and in other portfolio management and trading decisions. |
| 2 | Due to the outbreak of the COVID-19 pandemic in 2020, the second half of March in particular was marked by extreme market movements on the government bond market, with yields increasing by up to 150 basis points across the sovereign yield curve within only 2 weeks. |
| 3 | In unsupervised learning, models are trained to find patterns or methods for data subgrouping or categorization based on variables and observations. Such unsupervised learning techniques include principal component analysis (PCA) and a range of clustering methods. On the other hand, in supervised learning, predictive models are developed through the use of classification and regressions (logistic regression and neural networks, to name a few). While supervised learning models are trained by comparing their output against known true observations, in unsupervised learning, no correct answer is provided throughout the training phase. |
| 4 | Obtained from RiskMetrics® (monthly data set). |
| 5 | That day was market by a dramatic increase in U.S. interest rates as a result of the credit and liquidity crisis in 1998. The shock was characterized by a day-on-day 10-basis-point increase in the 3-month yield, an approximately 20-basis-point move in the intermediate zone of the yield curve, and an about 7-basis-point change in the 30-year spot rate. |
| 6 | By definition, a standard normal variable N(0,1) has a mean of 0 and a standard deviation of 1. |
| 7 | Generally 1 year. |
| 8 | Unlike the factor models developed by Nelson and Siegel (1987) and Diebold et al. (2008), where factors have an intuitive interpretation (level, slope, curvature) but calibration is nonlinear, so models lose part of their tractability. |
| 9 | For an extensive review of Nogueira’s model, see the chapter “Expressing Views” in his work “Updating the Yield Curve to Analyst’s Views”, specified in Note 19 in this article. |
| 10 | |
| 11 | With lambda set at 0.8, in order to capture the effects of very recent market dynamics, especially around extremely stressful events, such as the start of the COVID-19 pandemic or the start of the Russian military invasion of Ukraine. |
| 12 | Available at https://learn.bowdoin.edu/excellaneous/#downloads, accessed on 21 March 2022. |
| 13 | Due to the start of the COVID-19 pandemic in 2020, the second half of March in particular was marked by extreme market movements on the government bond market, with yields increasing by up to 150 basis points across the sovereign yield curve within only 2 weeks. |
| 14 | Similar to the one performed by Golub and Tilman (2000) on the U.S. Treasury curve, 105. |
| 15 | In November 2021, the offshore exposure to ROMGBs reached 16.5%, a 3.6 percentage points drop from the 20.1% level registered in December 2020. By the end of February 2022, the offshore share in Romanian local debt further decreased to 15.7%, suggesting an underweight position. |
| 16 | In the months preceding this event, demand for ROMGBs increased, given that investors had been gradually pricing in the rising chances for early elections; also, until that moment, the demand for Romanian government bonds was sustained by supportive liquidity conditions on the market. |
| 17 | The 10-year Romanian government bond yield reached 6.41% on 11 March 2022. |
| 18 |
References
- Alexander, Carol. 2008. Market Risk Analysis—Quantitative Methods in Finance. Chichester: John Wiley & Sons Ltd., vol. 1, pp. 59–65. [Google Scholar]
- Annaert, Jan, Anouk G. P. Claes, Marc. J. K. De Ceuster, and Hairui Zhang. 2012. Estimating the Yield Curve Using the Nelson-Siegel Model: A Ridge Regression Approach. Brussels: University of Antwerp, pp. 2–6. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2054689 (accessed on 21 March 2022).
- Asare, Sekyere. A. 2019. Yield Curve Modelling: A Comparison of Principal Components Analysis and the Discrete-Time Vasicek Model. Ph.D. thesis, Concordia University, Montreal, QC, Canada; pp. 25–26, 62. Available online: https://spectrum.library.concordia.ca/id/eprint/985642/1/SekyereAsare_MSc_S2020.pdf (accessed on 21 March 2022).
- Bank of International Settlements. 2005. Zero-coupon yield curves-technical documentation. BIS Paper 25: 1–37. Available online: https://www.bis.org/publ/bppdf/bispap25.htm (accessed on 20 September 2021).
- Barrett, W. Brian, Thomas F. Gosnell Jr., and Andrea. J. Heuson. 1995. Yield curve shifts and the selection of immunization strategies. Journal of Fixed Income 5: 5–64. [Google Scholar] [CrossRef]
- Bliss, Robert, and Eugen Fama. 1987. The information in long-maturity forward rates. American Economic Review 77: 680–92. Available online: http://www.jstor.org/stable/1814539 (accessed on 16 May 2021).
- Bolder, David Johnson, Grahame Jamieson, and Adam Metzler. 2004. An Empirical Analysis of the Canadian Term Structure of Zero-Coupon Interest Rates. Bank of Canada Working Papers, SSRN 1082833. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1082833 (accessed on 23 May 2021).
- Coroneo, Laura, Ken Nyholm, and Rositsa Vidova-Koleva. 2008. How Arbitrage-free is the Nelson-Siegel Model? ECB Working Paper No. 874. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1091123 (accessed on 15 January 2022).
- Cox, John C., Jonathan. E. Ingersoll, and Stephen. A. Ross. 1985. A Theory of the Term Structure of Interest Rates. Econometrica 53: 385–407. Available online: https://www.jstor.org/stable/1911242 (accessed on 12 October 2021). [CrossRef]
- Credit Suisse Securities Research and Analytics, Fixed Income Research. 2012. PCA Unleashed. pp. 11–16. Available online: https://research-doc.credit-suisse.com/docView?language=ENG&format=PDF&source_id=csplusresearchcp&document_id=1001969281&serialid=EVplkK6oNi2Oum067aSBs%2Bp%2F04%2F3pgbDBc%2B1pGHrQ0U%3D&cspId=null (accessed on 7 February 2022).
- Diebold, Francis X., Canlin Li, and Vivian Z. Yue. 2008. Global Yield Curve Dynamics and Interactions: A Generalized Nelson-Siegel Approach. Journal of Econometrics 146: 35–60. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0304407608001127 (accessed on 30 April 2021). [CrossRef] [Green Version]
- Dullmann, Klaus, and Marliese Uhrig-Homburg. 2000. Profiting Risk Structure of Interest Rates: An Empirical Analysis for Deutschemark-Denominated Bonds. European Financial Management 6: 367–88. [Google Scholar] [CrossRef]
- Erste Group Research. 2020. Navigating Storm with One Engine Gone. CEE Country Macro Outlook, April 2, 4. [Google Scholar]
- Erste Group Research. 2021. Twin Deficits in Spotlight with Political Noise in Background. CEE Country Macro Outlook, September 10, 4. [Google Scholar]
- European Central Bank. 2020. The new euro area yield curves. Monthly Bulletin. February, pp. 95–103. Available online: https://www.ecb.europa.eu/stats/financial_markets_and_interest_rates/euro_area_yield_curves/html/index.en.html#data (accessed on 10 December 2021).
- Fabozzi, Frank J., Lionel Martellini, and Philippe Priaulet. 2005. Predictability in the shape of the term structure of interest rates. Journal of Fixed Income 15: 40–53. [Google Scholar] [CrossRef]
- Farid, Jawwad A., and F. Salahuddin. 2010. Interest Rate Modeling. Karachi: Alchemy Software Pvt Limited, pp. 43–45. Available online: http://FourQuants.com (accessed on 5 March 2021).
- Golub, Bennett W., and Leo M. Tilman. 2000. Risk Management: Approaches for Fixed Income Markets. Hoboken: John Wiley & Sons, pp. 93–120, 211–37. [Google Scholar]
- Heath, David, Robert Jarrow, and Andew Morton. 1992. Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation. Econometrica 60: 77–105. [Google Scholar] [CrossRef]
- Hodges, Stewart D., and Naru Parekh. 2006. Term Structure Slope Risk. Journal of Fixed Income 16: 54–59. [Google Scholar] [CrossRef]
- Hull, John, and Alan White. 1990. Pricing Interest Rate Derivatives Securities. Review of Financial Studies 3: 573–92. Available online: http://www.ressources-actuarielles.net/EXT/ISFA/1226.nsf/0/3853d6e3a251918ec1257917004418f0/$FILE/Pricing%20interest-rate-derivative%20securities.pdf (accessed on 10 August 2021). [CrossRef]
- Kumar, Vinayak. 2019. Risk Premia in the Yield Curve. Philadelphia: University of Pennsylvania, pp. 4–5. Available online: https://repository.upenn.edu/cgi/viewcontent.cgi?article=1076&context=joseph_wharton_scholars (accessed on 11 April 2022).
- Litterman, Robert, and Jose Scheinkman. 1991. Common factors affecting bond returns. Journal of Fixed Income 1: 54–61. Available online: https://jfi.pm-research.com/content/1/1/54 (accessed on 15 September 2021). [CrossRef]
- Martellini, Lionel, and Jean Christophe Meyfredi. 2007. A copula approach to value-at-risk estimation for fixed-income portfolios. Journal of Fixed Income 17: 5–15. Available online: https://risk.edhec.edu/sites/risk/files/EDHEC_Working_Paper_A_Copula_Approach_to_Value-at-Risk_Estimation.pdf (accessed on 20 September 2021). [CrossRef]
- Moody’s Analytics. 2014. Principal Component Analysis for Yield Curve Modeling—Reproduction of Out-of-Sample Yield Curves. Available online: https://www.moodysanalytics.com/-/media/whitepaper/2014/2014-29-08-PCA-for-Yield-Curve-Modelling.pdf (accessed on 20 April 2022).
- Nelson, Charles, and Andrew F. Siegel. 1987. Parsimonious modeling of yield curves. Journal of Business 60: 473–89. Available online: https://www.jstor.org/stable/2352957 (accessed on 12 November 2021). [CrossRef]
- Nogueira, Leonardo M. 2008. Updating the Yield Curve to Analyst’s Views’, Central Bank of Brazil—Foreign Reserves Department; University of Reading—ICMA Centre, pp. 2–7. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1107653 (accessed on 12 April 2022).
- Piazessi, Monika. 2010. Afine Term Structure Models. Stanford: Elsevier, p. 703. Available online: https://web.stanford.edu/~piazzesi/s.pdf (accessed on 11 April 2022).
- Piazzesi, Monika, Moritz Lenel, and Martin Schneider. 2019. The Short Rate Disconnect in a Monetary Economy. Journal of Monetary Economics 106: 59–77. Available online: https://doi.org/10.1016/j.jmoneco.2019.07.008 (accessed on 14 November 2021).
- Ronn, Ehud I. 1996. The Impact of Large Changes in Asset Prices on Intra-Market Correlations in the Stock and Bond Markets. Working Paper. Austin: University of Texas at Austin, p. 2. [Google Scholar]
- Svensson, Lars E. O. 1994. Estimating and Interpreting forward Interest Rates: Sweden 1992–1994. IMF Working Paper, WP/94/114. Available online: https://www.elibrary.imf.org/view/journals/001/1994/114/001.1994.issue-114-en.xml (accessed on 21 October 2021).
- Svensson, Lars E. O. 1996. Estimating the term structure of interest rates for monetary policy analysis. Scandinavian Journal of Economics 98: 163–83. Available online: https://doi.org/10.2307/3440852 (accessed on 10 December 2021).
- Vasicek, Oldrich. 1977. An Equilibrium Characterisation of the Term Structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Yau, Roland. 2012. Principal Components Analysis and Interest Rate Modeling. Available online: https://www.risklatte.xyz/Videos/video21.php (accessed on 15 November 2021).

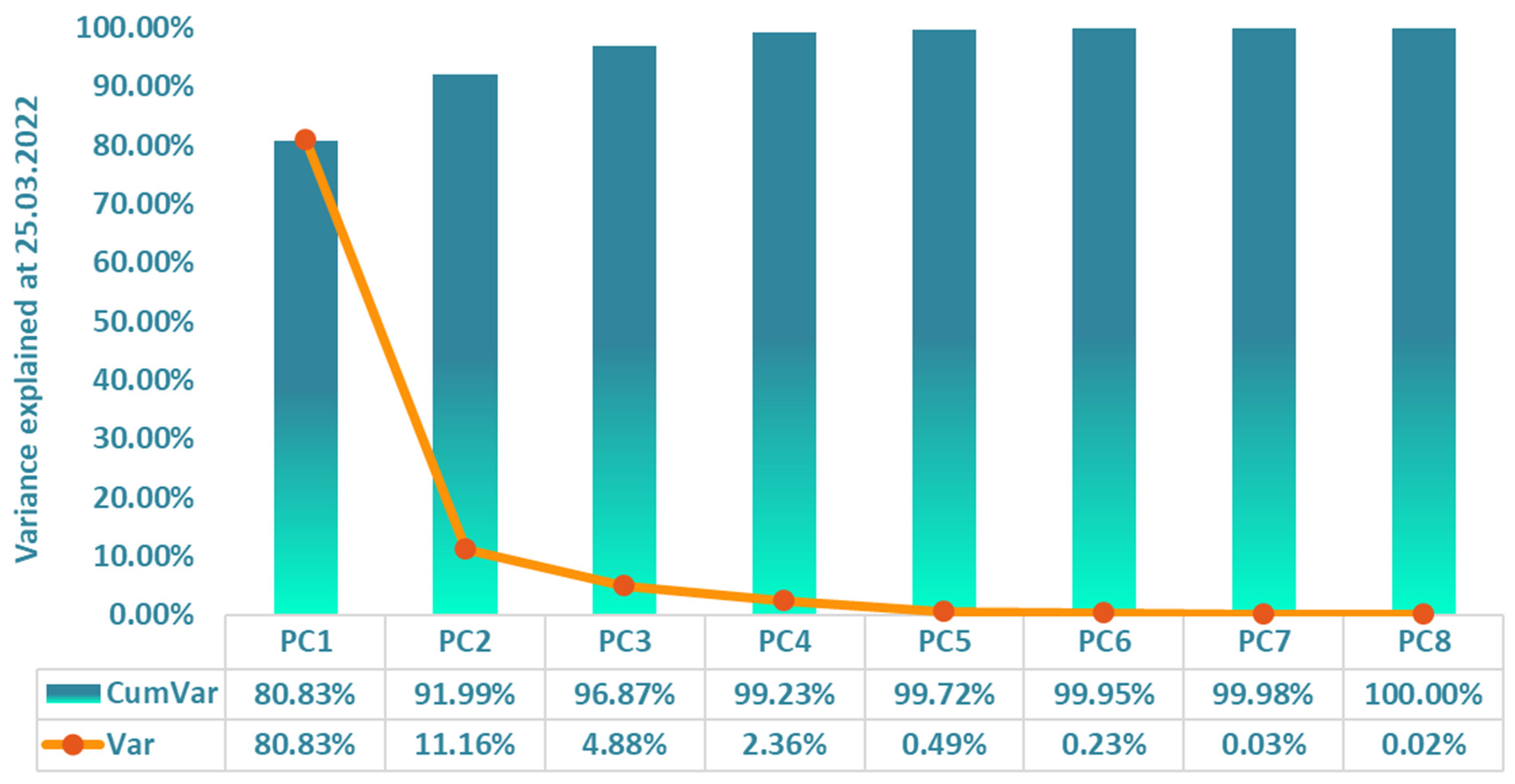
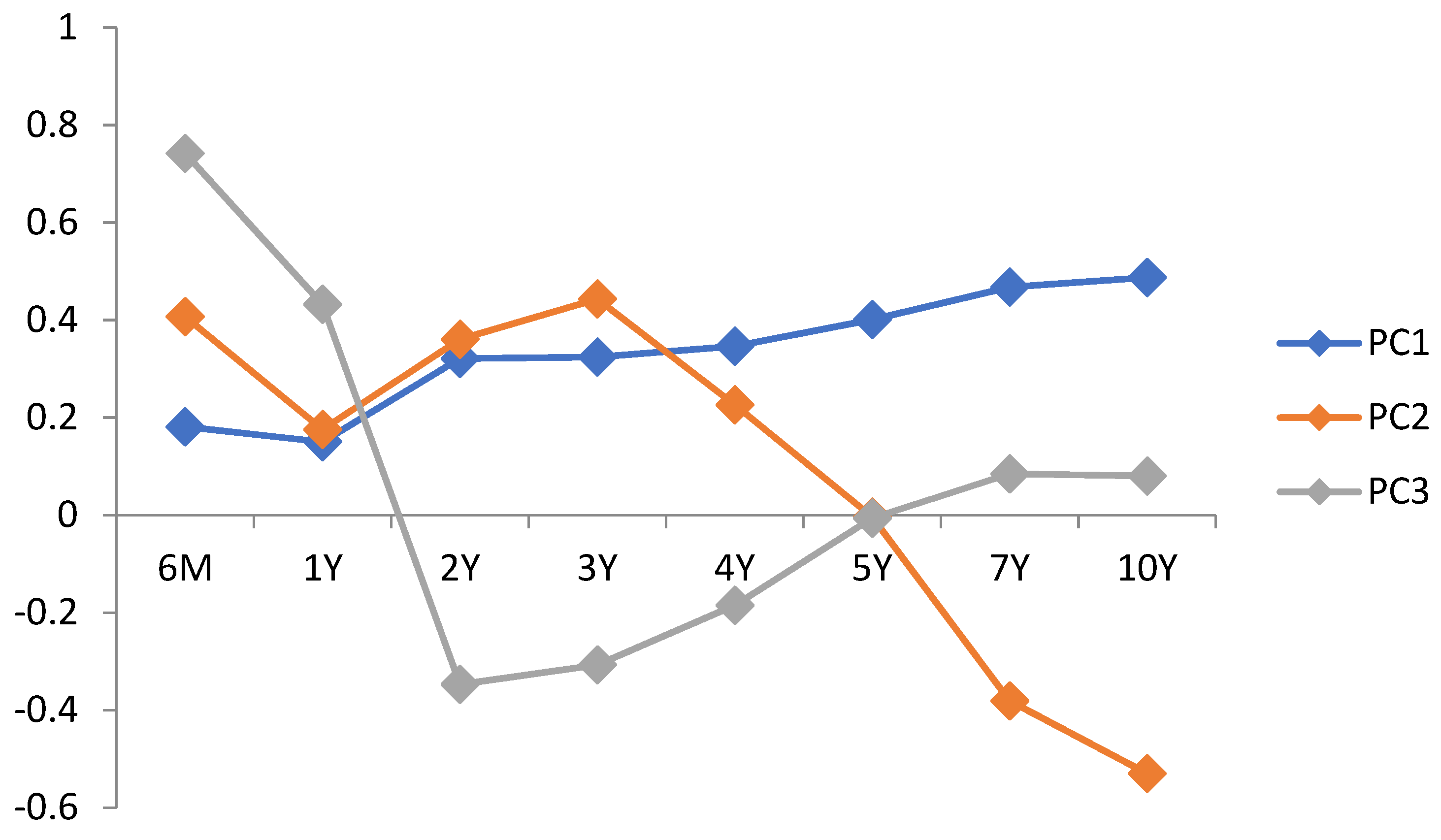

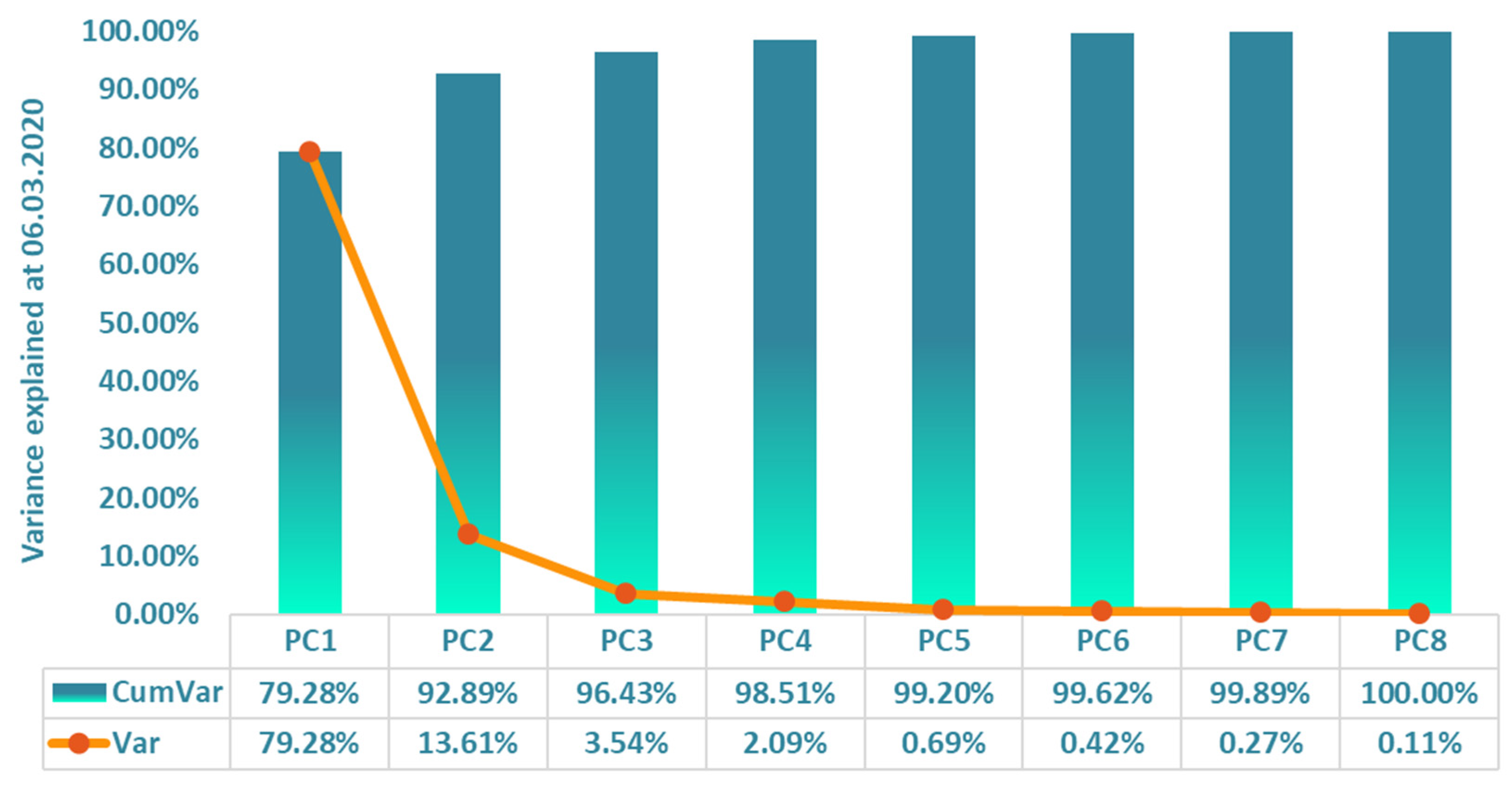





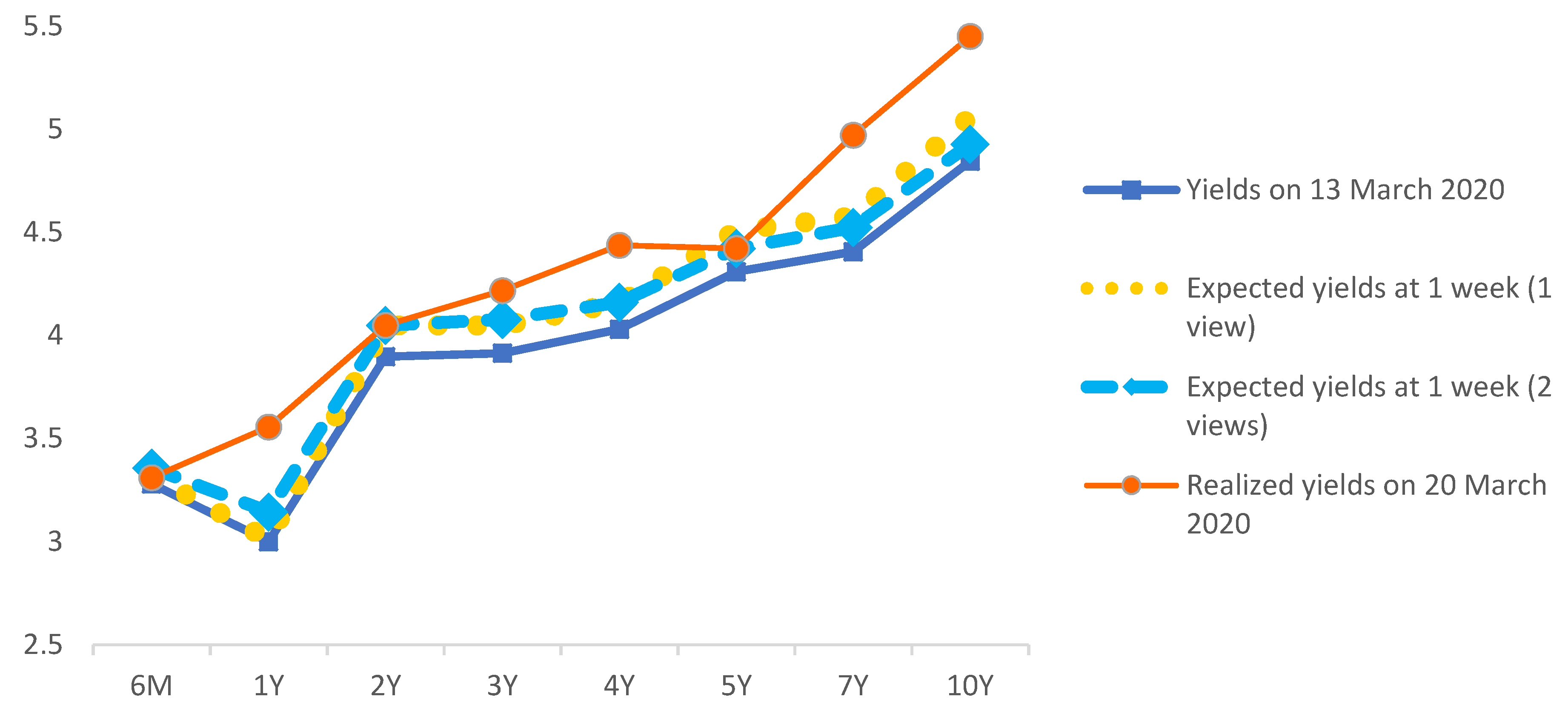
| CumVar | 80.83% | 91.99% | 96.87% | 99.23% | 99.72% | 99.95% | 99.98% | 100.00% |
| Var | 80.83% | 11.16% | 4.88% | 2.36% | 0.49% | 0.23% | 0.03% | 0.02% |
| EigVal | 3531.13 | 487.69 | 213.29 | 103.15 | 21.36 | 9.97 | 1.27 | 0.85 |
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| 6M | 0.1810 | 0.4069 | 0.7419 | 0.4945 | 0.0381 | 0.0115 | 0.0413 | 0.0583 |
| 1Y | 0.1501 | 0.1756 | 0.4322 | −0.8577 | 0.1513 | 0.0318 | −0.0072 | −0.0165 |
| 2Y | 0.3210 | 0.3603 | −0.3472 | 0.0666 | 0.6010 | 0.1689 | −0.4461 | 0.2311 |
| 3Y | 0.3243 | 0.4433 | −0.3073 | −0.0078 | −0.0768 | 0.2143 | 0.5462 | −0.5038 |
| 4Y | 0.3465 | 0.2261 | −0.1851 | −0.0886 | −0.4217 | −0.3655 | 0.1984 | 0.6602 |
| 5Y | 0.4008 | −0.0038 | −0.0061 | 0.0056 | −0.3370 | −0.4117 | −0.5689 | −0.4823 |
| 7Y | 0.4674 | −0.3811 | 0.0846 | 0.0162 | −0.3107 | 0.7073 | −0.1139 | 0.1384 |
| 10Y | 0.4871 | −0.5300 | 0.0800 | 0.0848 | 0.4697 | −0.3481 | 0.3536 | −0.0392 |
| Corell. | 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y |
|---|---|---|---|---|---|---|---|---|
| 6M | 1 | 0.445185 | 0.267383 | 0.271843 | 0.219032 | 0.252181 | 0.232288 | 0.263297 |
| 1Y | 0.445185 | 1 | 0.372053 | 0.428519 | 0.277162 | 0.233198 | 0.235828 | 0.18192 |
| 2Y | 0.267383 | 0.372053 | 1 | 0.804901 | 0.61661 | 0.569723 | 0.560736 | 0.514846 |
| 3Y | 0.271843 | 0.428519 | 0.804901 | 1 | 0.863154 | 0.784579 | 0.800367 | 0.779038 |
| 4Y | 0.219032 | 0.277162 | 0.61661 | 0.863154 | 1 | 0.894921 | 0.916332 | 0.891449 |
| 5Y | 0.252181 | 0.233198 | 0.569723 | 0.784579 | 0.894921 | 1 | 0.886539 | 0.899717 |
| 7Y | 0.232288 | 0.235828 | 0.560736 | 0.800367 | 0.916332 | 0.886539 | 1 | 0.960033 |
| 10Y | 0.263297 | 0.18192 | 0.514846 | 0.779038 | 0.891449 | 0.899717 | 0.960033 | 1 |
| Corell. | 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y |
|---|---|---|---|---|---|---|---|---|
| 6M | 1 | 0.372496 | 0.63688 | 0.617435 | 0.567352 | 0.628632 | 0.547862 | 0.568978 |
| 1Y | 0.372496 | 1 | 0.394008 | 0.499355 | 0.504074 | 0.318997 | 0.512123 | 0.481065 |
| 2Y | 0.63688 | 0.394008 | 1 | 0.944869 | 0.868314 | 0.902138 | 0.817978 | 0.824703 |
| 3Y | 0.617435 | 0.499355 | 0.944869 | 1 | 0.949967 | 0.91885 | 0.916332 | 0.925064 |
| 4Y | 0.567352 | 0.504074 | 0.868314 | 0.949967 | 1 | 0.920361 | 0.971006 | 0.966721 |
| 5Y | 0.628632 | 0.318997 | 0.902138 | 0.91885 | 0.920361 | 1 | 0.898622 | 0.909081 |
| 7Y | 0.547862 | 0.512123 | 0.817978 | 0.916332 | 0.971006 | 0.898622 | 1 | 0.987694 |
| 10Y | 0.568978 | 0.481065 | 0.824703 | 0.925064 | 0.966721 | 0.909081 | 0.987694 | 1 |
| Weekly Shocks (bps) | 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y | Realization | Contribution (Explanatory Power) |
|---|---|---|---|---|---|---|---|---|---|---|
| PC1 shock | 11 | 9 | 19 | 19 | 21 | 24 | 28 | 29 | 59.42 | 80.83% |
| PC2 shock | 9 | 4 | 8 | 10 | 5 | 0 | −8 | −12 | 22.08 | 11.16% |
| PC3 shock | 11 | 6 | −5 | −4 | −3 | 0 | 1 | 1 | 14.60 | 4.88% |
| Parallel Shock | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 56.60 | 73.33% |
| YC First 3 PCAs Shock | 31 | 19 | 22 | 23 | 24 | 21 | 18 | 31 | 96.87% |
| YC Weekly Shock (bps.) | Corresponding Standard Deviation | Likelihood |
|---|---|---|
| 10 | 0.50 | 30.85% |
| 20 | 1.00 | 15.87% |
| 25 | 1.25 | 10.56% |
| 30 | 1.50 | 6.68% |
| 40 | 2.00 | 2.28% |
| 50 | 2.50 | 0.62% |
| 60 | 3.00 | 0.13% |
| YC Weekly Shock (bps.) | Corresp. STDEV | Likelihood |
|---|---|---|
| 5 | 0.59 | 28.76% |
| 8 | 1.00 | 15.87% |
| 15 | 1.77 | 3.84% |
| 20 | 2.36 | 0.91% |
| 25 | 2.95 | 0.16% |
| YC Weekly Shock (bps.) | Corresp. STDEV | Likelihood |
|---|---|---|
| 17 | 0.50 | 30.85% |
| 34 | 1.00 | 15.87% |
| 43 | 1.25 | 10.56% |
| 51 | 1.50 | 6.68% |
| 68 | 2.00 | 2.28% |
| 85 | 2.50 | 0.62% |
| 102 | 3.00 | 0.13% |
| YC Weekly Shock (bps.) | Corresp. STDEV | Likelihood |
|---|---|---|
| 5 | 0.56 | 28.77% |
| 9 | 1.00 | 15.87% |
| 15 | 1.69 | 4.55% |
| 20 | 2.25 | 1.22% |
| 25 | 2.82 | 0.24% |
| YC Weekly Shock (bps.) | Corresp. STDEV | Historical likelihood |
|---|---|---|
| 6 | 0.50 | 30.85% |
| 12 | 1.00 | 15.87% |
| 15 | 1.25 | 10.56% |
| 18 | 1.50 | 6.68% |
| 24 | 2.00 | 2.28% |
| 30 | 2.50 | 0.62% |
| 36 | 3.00 | 0.13% |
| 2Y | 3Y | 4Y | 5Y | 7Y | 10Y | |
|---|---|---|---|---|---|---|
| Yields on 18 February 2022 | 4.48 | 4.68 | 4.88 | 5.12 | 5.30 | 5.62 |
| Expected yields at 1 week (1 view) | 4.62 | 4.80 | 5.06 | 5.50 | 5.92 | 6.22 |
| Expected yields at 1 week (2 views) | 4.62 | 4.79 | 5.12 | 5.38 | 5.93 | 6.24 |
| Realized yields on 25 February 2022 | 4.62 | 4.86 | 5.07 | 5.38 | 5.70 | 5.92 |
| Square error (1 view) | 0.00 | 0.00 | 0.00 | 0.01 | 0.05 | 0.09 |
| Square error (2 views) | 0.00 | 0.00 | 0.00 | 0.00 | 0.06 | 0.11 |
| 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y | |
|---|---|---|---|---|---|---|---|---|
| Yields on 28 February 2020 | 2.86 | 2.96 | 3.15 | 3.20 | 3.45 | 3.56 | 3.77 | 4.02 |
| Expected yields at 1 week (1 view) | 2.76 | 2.67 | 3.03 | 3.06 | 3.25 | 3.42 | 3.52 | 3.76 |
| Expected yields at 1 week (2 views) | 2.79 | 2.99 | 3.03 | 3.08 | 3.14 | 3.33 | 3.33 | 3.49 |
| Realized yields on 6 March 2020 | 2.85 | 2.86 | 3.03 | 3.11 | 3.27 | 3.33 | 3.52 | 3.84 |
| Square error (1 View) | 0.01 | 0.04 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 |
| Square error (2 Views) | 0.00 | 0.02 | 0.00 | 0.00 | 0.01 | 0.00 | 0.04 | 0.12 |
| 6M | 1Y | 2Y | 3Y | 4Y | 5Y | 7Y | 10Y | |
|---|---|---|---|---|---|---|---|---|
| Yields on 13 March 2020 | 3.28 | 3.00 | 3.90 | 3.91 | 4.03 | 4.31 | 4.41 | 4.84 |
| Expected yields at 1 week (1 view) | 3.32 | 3.01 | 4.05 | 4.05 | 4.16 | 4.51 | 4.58 | 5.06 |
| Expected yields at 1 week (2 views) | 3.36 | 3.14 | 4.05 | 4.08 | 4.16 | 4.42 | 4.52 | 4.93 |
| Realized yields on 20 March 2020 | 3.31 | 3.56 | 4.05 | 4.22 | 4.44 | 4.42 | 4.97 | 5.45 |
| Square error (1 View) | 0.00 | 0.30 | 0.00 | 0.03 | 0.08 | 0.01 | 0.16 | 0.15 |
| Square error (2 Views) | 0.00 | 0.17 | 0.00 | 0.02 | 0.08 | 0.00 | 0.20 | 0.27 |
| CumVar | 70.52% | 90.35% |
| Var | 70.52% | 19.83% |
| EigVal | 592.25813 | 166.55078 |
| PC1 | PC2 | |
| 6M | 0.2377 | 0.2096 |
| 1Y | 0.3926 | 0.7628 |
| 2Y | 0.2862 | 0.1059 |
| 3Y | 0.3102 | 0.1535 |
| 4Y | 0.3963 | −0.1365 |
| 5Y | 0.3099 | −0.1718 |
| 7Y | 0.4177 | −0.3202 |
| 10Y | 0.4286 | −0.4344 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oprea, A. The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market. J. Risk Financial Manag. 2022, 15, 247. https://doi.org/10.3390/jrfm15060247
Oprea A. The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market. Journal of Risk and Financial Management. 2022; 15(6):247. https://doi.org/10.3390/jrfm15060247
Chicago/Turabian StyleOprea, Andreea. 2022. "The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market" Journal of Risk and Financial Management 15, no. 6: 247. https://doi.org/10.3390/jrfm15060247
APA StyleOprea, A. (2022). The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market. Journal of Risk and Financial Management, 15(6), 247. https://doi.org/10.3390/jrfm15060247





