A Threshold GARCH Model for Chilean Economic Uncertainty
Abstract
1. Introduction
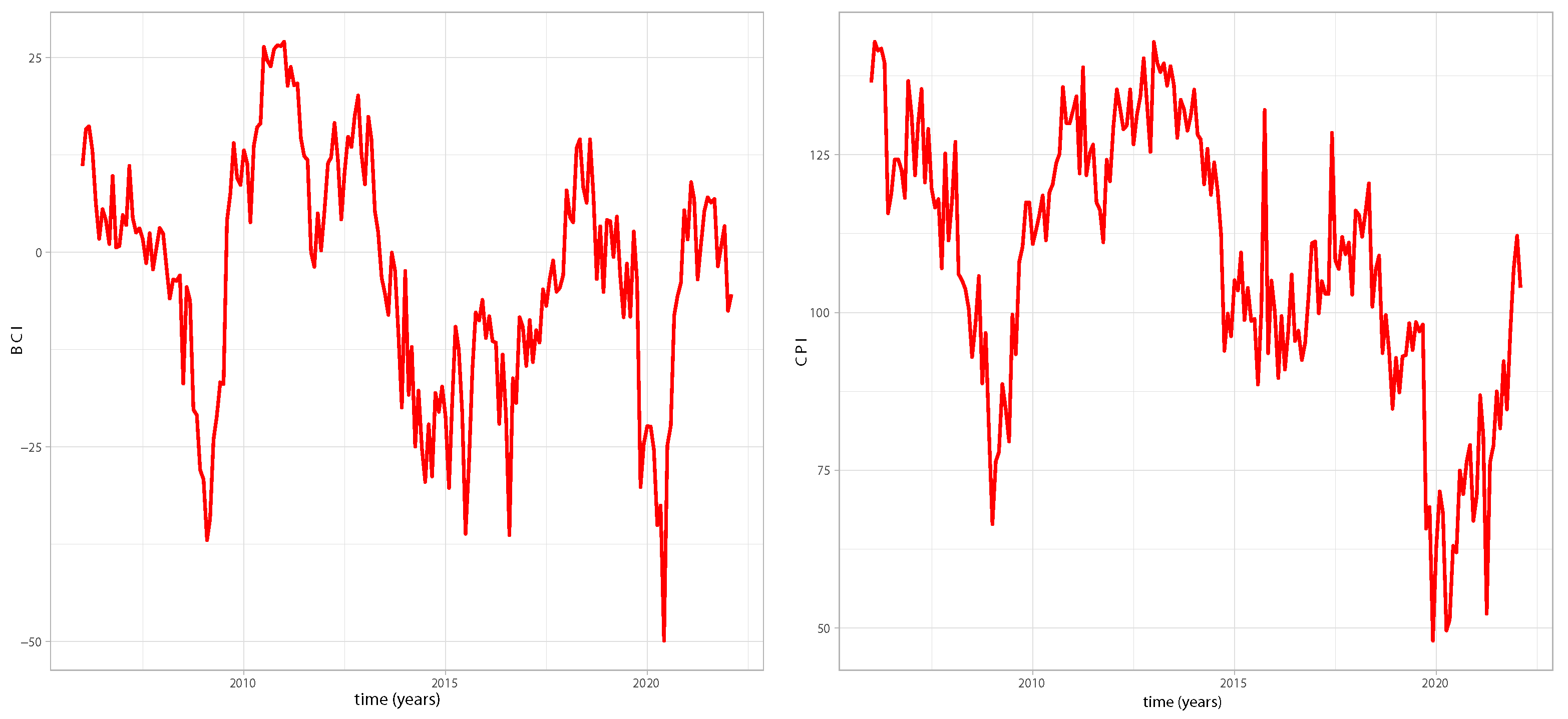
2. Data
2.1. Business Confidence Index
2.2. Consumer Perception Index
- Current economic situation compared to the previous year: Would you say that your current economic situation is worse, the same, or better?
- Current unemployment in relation to the previous year: Today, unemployment in the country is higher, equal, or lower?
- Future economic situation: Would you say that in a year or more your economic situation will be worse, the same, or better?
- Future unemployment: Would you say that in a year or more unemployment in the country will be higher, the same, or lower?
- Future income: Do you think your total family income in the next year will be more, the same, or less?
3. Statistical Modeling
3.1. ARIMA Model
3.2. TAR Model
3.2.1. Model Identification
3.2.2. Ordinary Least Square Error Estimation Method
3.3. TGARCH Model
3.3.1. Quasi-Maximum Likelihood Estimation
3.3.2. ARMA-TGARCH Model with Skew-t Innovations
3.4. Model Selection Criteria
3.5. Computational Implementation
4. Results
4.1. ARIMA and SARIMA Models
4.2. TAR Model
4.3. ARMA-TGARCH Models
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | A methodological note about building this index is available at https://ceen.udd.cl/estudios-y-publicaciones/ice/ (accessed on 12 November 2022). |
| 2 | A methodological note about building this index is available at https://ceen.udd.cl/estudios-y-publicaciones/ipeco/ (accessed on 12 November 2022). |
| 3 | Constructed through the percentage of participation with respect to each sector’s GDP. |
References
- Abid, Salah H., Uday J. Quaez, and Javier E. Contreras-Reyes. 2021. An information-theoretic approach for multivariate skew-t distributions and applications. Mathematics 9: 146. [Google Scholar] [CrossRef]
- Acuña, Guillermo. 2017. Assessing the Predictive Power of the Consumer Perception Index. MPRA Paper No. 83154. Santiago: Universidad del Desarrollo. Available online: https://mpra.ub.uni-muenchen.de/83154/ (accessed on 12 November 2022).
- Arnold, Matthias, and Roland Günther. 2001. Adaptive parameter estimation in multivariate self-exciting threshold autoregressive models. Communications in Statistics-Simulation and Computation 30: 257–75. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Box, George E. P., Gwilym M. Jenkins, Gregory C. Reinsel, and Greta M. Ljung. 2015. Time Series Analysis: Forecasting and Control. Hoboken: John Wiley & Sons. [Google Scholar]
- Barbu, Cătălin Mihail, Dorian Laurenţiu Florea, Dan-Cristian Dabija, and Mihai Constantin Răzvan Barbu. 2021. Customer Experience in Fintech. Journal of Theoretical and Applied Electronic Commerce Research 16: 1415–33. [Google Scholar] [CrossRef]
- Cámara Chilena de la Construcción. 2022. Informe de Macroeconomía y Construcción (MACh 62). Santiago: Gerencia de Estudios y Políticas Públicas, Cámara Chilena de la Construcción (CChC), September, Available online: https://cchc.cl/uploads/archivos/archivos/informe-mach-62.pdf (accessed on 12 December 2022).
- Cao, Charles Q., and Ruey S. Tsay. 1992. Nonlinear time-series analysis of stock volatilities. Journal of Applied Econometrics 7: S165–S185. [Google Scholar] [CrossRef]
- Cerda, Rodrigo, Alvaro Silva, and José Tomás Valente. 2016. Economic Policy Uncertainty Indices for Chile. Economic Policy Uncertainty Working Paper. Santiago: CLAPES-UC, Pontificia Universidad Católica de Chile. [Google Scholar]
- Contreras-Reyes, Javier E. 2022. Rényi entropy and divergence for VARFIMA processes based on characteristic and impulse response functions. Chaos, Solitons & Fractals 160: 112268. [Google Scholar]
- Contreras-Reyes, Javier E. 2023. Information quantity evaluation of nonlinear time series processes and applications. Physica D: Nonlinear Phenomena 445: 133620. [Google Scholar] [CrossRef]
- Contreras-Reyes, Javier E., and Wilfredo Palma. 2013. Statistical analysis of autoregressive fractionally integrated moving average models in R. Computational Statistics 28: 2309–31. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimates for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Djeddour, Khedidja, and Yakoub Boularouk. 2013. Application of threshold autoregressive model: Modeling and forecasting using us export crude oil data. American Journal of Oil and Chemical Technologies 1: 1–11. [Google Scholar] [CrossRef][Green Version]
- Ghalanos, Alexios. 2022. Introduction to the Rugarch Package. Version 1.4-3. Seattle: Twitter. [Google Scholar]
- Gibson, David, and Darfiana Nur. 2011. Threshold Autoregressive Models in Finance: A Comparative Approach. Wollongong: University of Wollongong. Available online: https://ro.uow.edu.au/asearc/26/ (accessed on 12 November 2022).
- Hansen, Bruce E. 2011. Threshold autoregression in economics. Statistics and Its Interface 4: 123–27. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Yeasmin Khandakar. 2007. Automatic time series for forecasting: The forecast package for R. Journal of Statistical Software 27: 122. [Google Scholar]
- ICARE. 2004. Indicador Mensual de Confianza Empresarial. Informe encuesta mayo 2004. Santiago: Universidad Adolfo Ibáñez, pp. 1–16. Available online: https://www.icare.cl/imce/ (accessed on 12 November 2022).
- Idrovo-Aguirre, Byron J., and Javier E. Contreras-Reyes. 2019. Backcasting cement production and characterizing cement’s economic cycles for Chile 1991–2015. Empirical Economics 57: 1829–52. [Google Scholar] [CrossRef]
- Idrovo-Aguirre, Byron J., and Javier E. Contreras-Reyes. 2021a. The response of housing construction to a copper price shock in Chile (2009–2020). Economies 9: 98. [Google Scholar] [CrossRef]
- Idrovo-Aguirre, Byron J., and Javier E. Contreras-Reyes. 2021b. Monetary fiscal contributions to households and pension fund withdrawals during the COVID-19 pandemic: An approximation of their impact on construction labor supply in Chile. Social Sciences 10: 417. [Google Scholar] [CrossRef]
- Idrovo-Aguirre, Byron J., Francisco J. Lozano, and Javier E. Contreras-Reyes. 2021. Prosperity or Real Estate Bubble? Exuberance probability index of the Real Price of Housing in Chile. International Journal of Financial Studies 9: 51. [Google Scholar] [CrossRef]
- Jara-Labarthé, Vanessa, and César A. Cisneros Puebla. 2021. Migrants in Chile: Social crisis and the pandemic (or sailing over troubled water...). Qualitative Social Work 20: 284–88. [Google Scholar] [CrossRef]
- Kliestik, Tomas, Katarina Valaskova, George Lazaroiu, Maria Kovacova, and Jaromir Vrbka. 2020. Remaining Financially Healthy and Competitive: The Role of Financial Predictors. Journal of Competitiveness 12: 74–92. [Google Scholar] [CrossRef]
- Korap, Levent. 2011. Threshold GARCH modeling of the inflation & inflation uncertainty relationship: Historical evidence from the Turkish economy. Istanbul Journal of Economics 60: 157–72. [Google Scholar]
- Lahiri, Kajal, George Monokroussos, and Yongchen Zhao. 2016. Forecasting Consumption: The Role of Consumer Confidence in Real Time with many Predictors. Journal of Applied Econometrics 31: 1254–75. [Google Scholar] [CrossRef]
- Ljung, Greta M., and George E. P. Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Lyu, Yongjian, Peng Wang, Yu Wei, and Rui Ke. 2017. Forecasting the VaR of crude oil market: Do alternative distributions help? Energy Economics 66: 523–34. [Google Scholar] [CrossRef]
- Maleki, Mohsen, Darren Wraith, Mohammad R. Mahmoudi, and Javier E. Contreras-Reyes. 2020. Asymmetric heavy-tailed vector auto-regressive processes with application to financial data. Journal of Statistical Computation and Simulation 90: 324–40. [Google Scholar] [CrossRef]
- Mena, Gonzalo E., Pamela P. Martinez, Ayesha S. Mahmud, Pablo A. Marquet, Caroline O. Buckee, and Mauricio Santillana. 2021. Socioeconomic status determines COVID-19 incidence and related mortality in Santiago, Chile. Science 372: 934. [Google Scholar] [CrossRef]
- Moreno, Edna, and Fabio H. Nieto. 2014. TAR models in financial time series. Comunicaciones en Estadistica 7: 223–43. [Google Scholar]
- Nelson, Daniel B. 1990. Stationarity and persistence in the GARCH(1,1) model. Econometric Theory 6: 318–34. [Google Scholar] [CrossRef]
- Pérez, Fredy, and Hermilson Velásquez. 2004. Análisis de cambio de régimen en series de tiempo no lineales utilizando modelos TAR. Lecturas de Economia 61: 101–19. [Google Scholar]
- Petruccelli, Joseph D. 1986. On the consistency of least squares estimators for a threshold AR (1) model. Journal of Time Series Analysis 7: 269–78. [Google Scholar] [CrossRef]
- Petruccelli, Joseph D., and Samuel W. Woolford. 1984. A threshold AR(1) model. Journal of Applied Probability 21: 270–86. [Google Scholar] [CrossRef]
- R Core Team. 2022. A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Ramírez-Parietti, Ignacio, Javier E. Contreras-Reyes, and Byron J. Idrovo-Aguirre. 2021. Cross-sample entropy estimation for time series analysis: A nonparametric approach. Nonlinear Dynamics 105: 2485–508. [Google Scholar] [CrossRef]
- Shum, Wai Yan. 2020. Modelling conditional skewness: Heterogeneous beliefs, short sale restrictions and market declines. North American Journal of Economics and Finance 51: 101070. [Google Scholar] [CrossRef]
- Tong, Howell. 1993. Non-Linear Time Series: A Dynamical System Approach. Oxford Statistical Science Series; Oxford: Clarendon Press. [Google Scholar]
- Tsay, Ruey S. 1989. Testing and modeling threshold autoregressive processes. Journal of the American Statistical Association 84: 231–40. [Google Scholar] [CrossRef]
- Uribe Bravo, Adán. 2015. Pronósticos en Modelos con Umbrales. Guanajuato: CIMAT. Available online: https://repositorioslatinoamericanos.uchile.cl/handle/2250/2257038 (accessed on 12 November 2022).
- Vătămănescu, Elena-Mădălina, Vlad-Andrei Alexandru, Andreea Mitan, and Dan-Cristian Dabija. 2020. From the Deliberate Managerial Strategy towards International Business Performance: A Psychic Distance vs. Global Mindset Approach. Systems Research and Behavioral Science 37: 374–87. [Google Scholar] [CrossRef]
- Verbesselt, Jan, Rob Hyndman, Glenn Newnham, and Darius Culvenor. 2010. Detecting trend and seasonal changes in satellite image time series. Remote sensing of Environment 114: 106–15. [Google Scholar] [CrossRef]
- Wu, Jing. 2010. Threshold GARCH Model: Theory and Application. London: The University of Western Ontario, pp. 1–42. Available online: http://publish.uwo.ca/~jwu87/files/JobMarketPaper_JingWu.pdf (accessed on 12 November 2022).
- Yang, Yung-Lieh, and Chia-Lin Chang. 2008. A double-threshold GARCH model of stock market and currency shocks on stock returns. Mathematics and Computers in Simulation 79: 458–74. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]
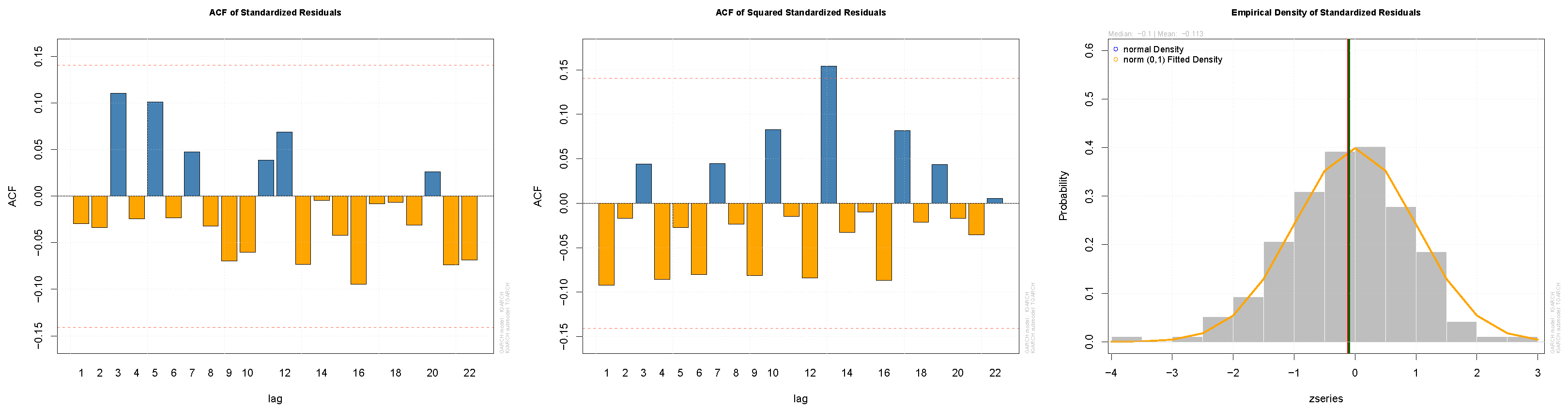


| Category | Interval |
|---|---|
| Extraordinarily optimistic | ≥45 |
| Very optimistic | |
| Optimistic | |
| Moderately optimistic | |
| Slightly optimistic | |
| Neutral | |
| Slightly pessimistic | |
| Moderately pessimistic | |
| Very pessimistic | |
| Extraordinarily pessimistic | <−45 |
| Parameter | BCI Estimates | CPI Estimates |
|---|---|---|
| 0.926 (0.030) | 0.965 (0.019) | |
| −0.189 (0.075) | −0.400 (0.067) | |
| 0.097 (0.074) | – | |
| −0.202 (0.077) | – |
| BCI | CPI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AIC | AIC | AIC | ||||||||
| 1 | 1 | 1 | 736.6063 | 2 | 1 | 1 | 735.6555 | 1 | 1 | 849.3376 |
| 1 | 1 | 2 | 738.6053 | 2 | 1 | 2 | 737.6545 | 1 | 2 | 842.3831 |
| 1 | 1 | 3 | 736.4068 | 2 | 1 | 3 | 735.4560 | 1 | 3 | 831.2180 |
| 1 | 1 | 4 | 731.8181 | 2 | 1 | 4 | 730.8673 | 1 | 4 | 828.2918 |
| 1 | 1 | 5 | 729.6451 | 2 | 1 | 5 | 728.6943 | 1 | 5 | 826.5194 |
| 1 | 2 | 1 | 737.2708 | 2 | 2 | 1 | 736.3200 | 2 | 1 | 845.1154 |
| 1 | 2 | 2 | 739.2698 | 2 | 2 | 2 | 738.3190 | 2 | 2 | 844.0723 |
| 1 | 2 | 3 | 737.0713 | 2 | 2 | 3 | 736.1205 | 2 | 3 | 832.9071 |
| 1 | 2 | 4 | 732.4827 | 2 | 2 | 4 | 731.5319 | 2 | 4 | 829.9810 |
| 1 | 2 | 5 | 730.3096 | 2 | 2 | 5 | 729.3588 | 2 | 5 | 828.1809 |
| BCI | CPI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AIC | AIC | AIC | AIC | ||||||||
| 1 | 1 | 6.6832 | 3 | 5 | 6.7260 | 1 | 1 | 7.3196 | 3 | 5 | 7.3439 |
| 1 | 2 | 6.6842 | 4 | 1 | 6.7270 | 1 | 2 | 7.3305 | 4 | 1 | 7.3415 |
| 1 | 3 | 6.6956 | 4 | 2 | 6.7265 | 1 | 3 | 7.3405 | 4 | 2 | 7.3180 |
| 1 | 4 | 6.7073 | 4 | 3 | 6.7323 | 1 | 4 | 7.3501 | 4 | 3 | 7.3621 |
| 1 | 5 | 6.7126 | 4 | 4 | 6.7426 | 1 | 5 | 7.3163 | 4 | 4 | 7.3396 |
| 2 | 1 | 6.7034 | 4 | 5 | 6.7466 | 2 | 1 | 7.3018 | 4 | 5 | 7.3646 |
| 2 | 2 | 6.7048 | 5 | 1 | 6.7467 | 2 | 2 | 7.2869 | 5 | 1 | 7.3607 |
| 2 | 3 | 6.7257 | 5 | 2 | 6.7475 | 2 | 3 | 7.3249 | 5 | 2 | 7.3389 |
| 2 | 4 | 6.7279 | 5 | 3 | 6.7513 | 2 | 4 | 7.2992 | 5 | 3 | 7.3743 |
| 2 | 5 | 6.7328 | 5 | 4 | 6.7616 | 2 | 5 | 7.3103 | 5 | 4 | 7.3609 |
| 3 | 1 | 6.7051 | 5 | 5 | 6.7611 | 3 | 1 | 7.3258 | 5 | 5 | 7.3698 |
| 3 | 2 | 6.7039 | 3 | 2 | 7.3046 | ||||||
| 3 | 3 | 6.7095 | 3 | 3 | 7.3345 | ||||||
| 3 | 4 | 6.7220 | 3 | 4 | 7.3190 | ||||||
| Parameter | Estimation | Std. Error | t-Value | p-Value | |
|---|---|---|---|---|---|
| BCI | 0.940 | 0.034 | 28.014 | 0.001 | |
| −0.162 | 0.084 | −1.924 | 0.054 | ||
| 0.497 | 0.332 | 1.499 | 0.134 | ||
| 0.081 | 0.033 | 2.422 | 0.016 | ||
| 0.857 | 0.066 | 12.939 | 0.001 | ||
| CPI | 0.994 | 0.009 | 106.930 | 0.001 | |
| −0.411 | 0.059 | −6.920 | 0.001 | ||
| 0.005 | 0.061 | 0.075 | 0.940 | ||
| 0.001 | 0.001 | 0.007 | 0.994 | ||
| 0.031 | 0.021 | 1.437 | 0.151 | ||
| 0.931 | 0.001 | 3972.814 | 0.001 | ||
| 0.001 | 0.012 | 0.001 | 0.999 | ||
| 0.888 | 0.076 | 11.645 | 0.001 | ||
| m | 4.951 | 1.505 | 3.290 | 0.001 |
| Standardized Residuals | Standardized Squared Residuals | |||||
|---|---|---|---|---|---|---|
| Lag | Statistic | p-Value | Lag | Statistic | p-Value | |
| BCI | 1 | 0.170 | 0.681 | 1 | 1.674 | 0.196 |
| 5 | 2.260 | 0.887 | 5 | 2.571 | 0.491 | |
| 9 | 3.834 | 0.729 | 9 | 3.978 | 0.593 | |
| CPI | 1 | 0.351 | 0.553 | 1 | 0.817 | 0.366 |
| 5 | 1.468 | 0.998 | 11 | 6.085 | 0.424 | |
| 9 | 2.592 | 0.943 | 19 | 9.299 | 0.528 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chávez, D.; Contreras-Reyes, J.E.; Idrovo-Aguirre, B.J. A Threshold GARCH Model for Chilean Economic Uncertainty. J. Risk Financial Manag. 2023, 16, 20. https://doi.org/10.3390/jrfm16010020
Chávez D, Contreras-Reyes JE, Idrovo-Aguirre BJ. A Threshold GARCH Model for Chilean Economic Uncertainty. Journal of Risk and Financial Management. 2023; 16(1):20. https://doi.org/10.3390/jrfm16010020
Chicago/Turabian StyleChávez, Diego, Javier E. Contreras-Reyes, and Byron J. Idrovo-Aguirre. 2023. "A Threshold GARCH Model for Chilean Economic Uncertainty" Journal of Risk and Financial Management 16, no. 1: 20. https://doi.org/10.3390/jrfm16010020
APA StyleChávez, D., Contreras-Reyes, J. E., & Idrovo-Aguirre, B. J. (2023). A Threshold GARCH Model for Chilean Economic Uncertainty. Journal of Risk and Financial Management, 16(1), 20. https://doi.org/10.3390/jrfm16010020








