An Investigation of the Predictability of Uncertainty Indices on Bitcoin Returns
Abstract
:1. Introduction
2. Literature
3. Methodology
3.1. Random Forest Algorithm
3.2. Cross-Validation
4. Empirical Results
4.1. Data and Summary Statistics
4.2. The Feature Importance
4.3. Robustness Checks
4.4. Model Accuracy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Description | Data Frequency | |
|---|---|---|---|
| Business Investment and Sentiment | BIS | Based on the counts of newspaper articles containing the keywords in the category—business investment and sentiment from eleven major U.S. newspapers, multiplying the contemporaneous equity market volatility tracker value that moves with the CBOE Volatility Index and the realized volatility of returns on the S&P 500. | Monthly |
| BBD Measuring Economic Policy Uncertainty Index | BMPU | The Baker-Bloom-Davis MPU, based on access to the world news indices for the United States, implements the approach developed for measuring economic policy uncertainty. | Monthly |
| Exchange Rates | ER | Based on the counts of newspaper articles containing the keywords in the category—exchange rates from eleven major U.S. newspapers, multiplying the contemporaneous equity market volatility tracker value that moves with the CBOE Volatility Index and the realized volatility of returns on the S&P 500. | Monthly |
| Financial Crises | FC | Based on the counts of newspaper articles containing the keywords in the category—financial crises from eleven major U.S. newspapers. | Monthly |
| Financial Regulation | FR | Based on the counts of newspaper articles containing the keywords in the category–financial regulation from eleven major U.S. newspapers, multiplying the contemporaneous equity market volatility tracker value that moves with the CBOE Volatility Index and the realized volatility of returns on the S&P 500. | Monthly |
| Interest Rates | IR | Based on the counts of newspaper articles containing the keywords in the category—interest rates. | Monthly |
| Japan Economic Policy Uncertainty Index | JEP | The index consists of the articles in four major Japanese newspapers. | Monthly |
| Macroeconomic News and Outlook | MNEMV | The index is based on the counts of newspaper articles containing the keywords in the category—macroeconomic news and outlook from eleven major U.S. newspapers, multiplying the contemporaneous equity market volatility tracker value that moves with the CBOE Volatility Index and the realized volatility of returns on the S&P 500. | Monthly |
| Overall Equity Market Volatility | OEMV | Based on the average of the standardized scaled counts of newspaper articles containing the keywords to match the mean value of the CBOE Volatility Index. The index tracks the overall equity market volatility for eleven major U.S. newspapers. | Monthly |
| Singapore Economic Policy Uncertainty Index | SEPU | A trade-weighted average of national EPU indices for 21 countries. | Monthly |
| New South Korean Economic Policy Uncertainty Index | SKE | The New South Korean Economic Policy Uncertainty (EPU) Index uses six major newspapers in South Korea. | Monthly |
| Twitter-based Economic Uncertainty Index | TEU | The index extracts all messages (tweets) in English sent on Twitter since June 2011 that contain keywords related to Uncertainty and the Economy. | Daily |
| World Trade Uncertainty Index | WTUI | It measures trade uncertainty globally using the Economic Intelligence Unit country reports. | Quarterly |
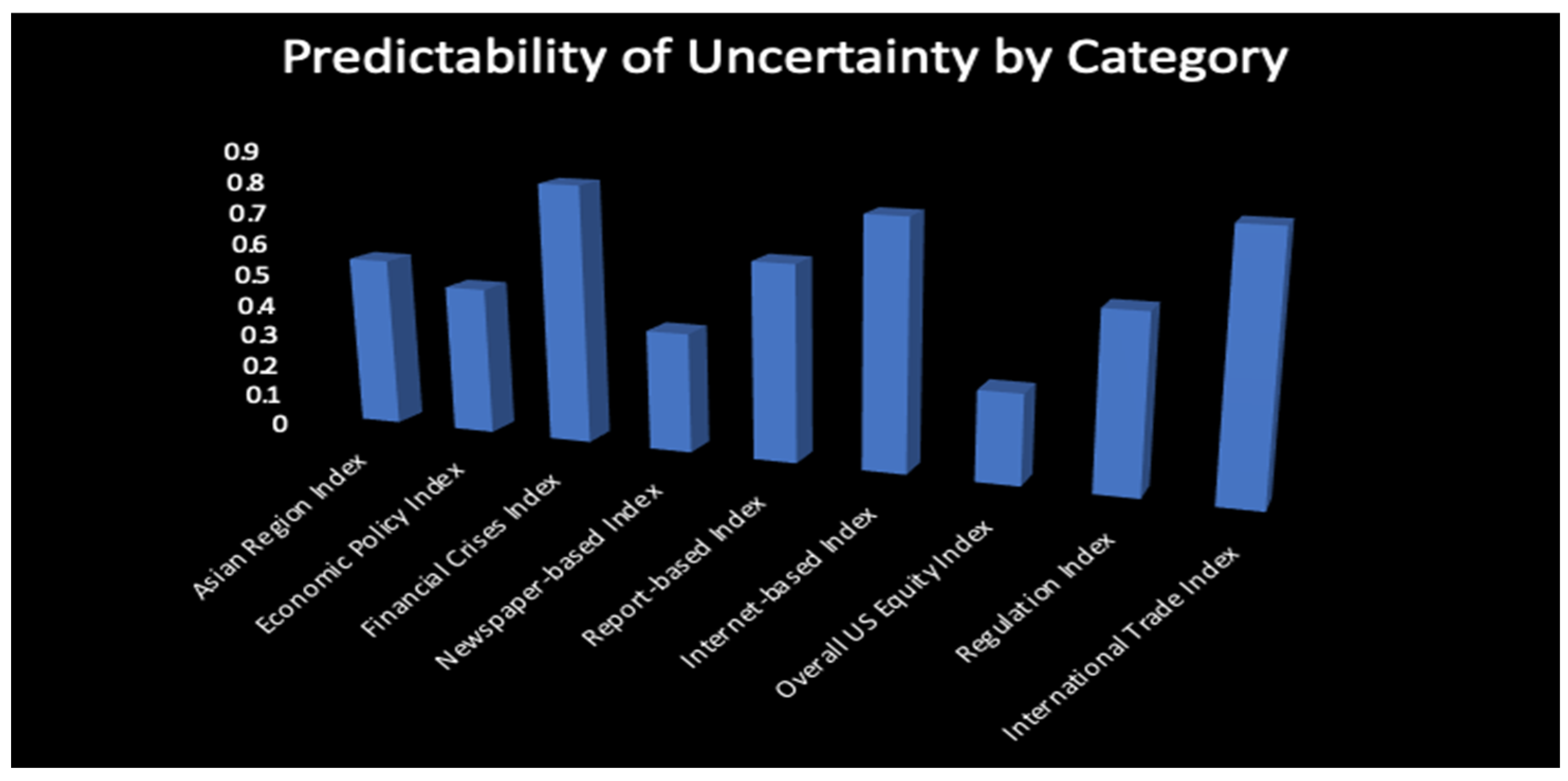
| Category | Feature |
|---|---|
| Asian Region Index | SEPU, SKE, JEP |
| Economic Policy Index | BIS, BMPU, ER, FC, IR, JEP, MNEMV, OEMV, SEPU, SKE), TEU, WTUI |
| Financial Crises Index | FC |
| Newspaper-based Index | BIS, BMPU, ER, FC, FR, IR, JEP, MNEMV, OEMV, SKE |
| Report-based Index | WTUI |
| Internet-based Index | TEU |
| Overall US Equity Index | OEMV |
| Regulation Index | FR |
| International Trade Index | SEPU, WTUI |
| Mean | Median | Maximum | Minimum | Std. Dev. | Skewness | Kurtosis | Jarque-Bera | |
|---|---|---|---|---|---|---|---|---|
| BIS | 0.496348 | 0.348 | 3.9517 | 0 | 0.543014 | 3.151029 | 17.71081 | 1131.213 *** |
| BMPU | 74.84245 | 58.08498 | 304.0693 | 18.68333 | 51.09273 | 1.840589 | 7.544355 | 151.0599 *** |
| BTC | 0.08203 | 0.064265 | 1.562375 | −0.470078 | 0.285 | 1.641923 | 9.688176 | 245.1928 *** |
| ER | 0.245037 | 0.14665 | 3.8576 | 0 | 0.440176 | 5.786614 | 44.95514 | 8365.932 *** |
| FC | 3.950982 | 3.451 | 20.4663 | 1.6502 | 2.207639 | 4.272334 | 31.03031 | 3792.633 *** |
| FR | 2.408818 | 2.4325 | 5.6821 | 0.7559 | 0.932568 | 0.704123 | 3.784667 | 11.4783 *** |
| IR | 5.284479 | 4.6696 | 19.0173 | 1.7408 | 2.744067 | 2.319844 | 9.788747 | 298.6276 *** |
| JEP | 114.818 | 108.8493 | 212.6997 | 62.28234 | 31.8555 | 1.044502 | 4.070694 | 24.33725 *** |
| OEMV | 19.14626 | 17.01115 | 63.3638 | 9.5696 | 7.656087 | 2.560262 | 12.82233 | 541.9162 *** |
| SEPU | 179.1436 | 153.8134 | 407.7419 | 82.86535 | 77.13623 | 0.880181 | 2.834384 | 13.80784 *** |
| SKE | 161.363 | 137.604 | 538.1768 | 55.90073 | 79.98659 | 1.74158 | 7.292713 | 134.9724 *** |
| TEU | 87.959 | 71.87471 | 445.7241 | 24.56089 | 67.18413 | 3.105647 | 16.07644 | 925.6157 *** |
| WTUI | 19.95698 | 1.43 | 174.34 | 0.04 | 39.57344 | 2.240248 | 6.887645 | 155.4164 *** |
| MNEMV | 13.62065 | 12.23125 | 46.6632 | 6.9832 | 5.732917 | 2.656577 | 13.19266 | 583.5295 *** |
| 1 | China banned cryptocurrencies on 6/2009, 11/2013, 4/2014, 2/2017, 9/2017 and 5/2021. In September of 2021, China’s central bank and its National Development and Reform Commission harshly banned crypto mining and crypto transactions. (source: http://www.gov.cn/zhengce/zhengceku/2021-10/08/content_5641404.htm, accessed in October 2021). |
| 2 | The features were selected based on the findings of the existing literature and the availability of the data. A full list of features can be seen in Table A1 of Appendix A. |
| 3 | Table A2 in Appendix A lists nine categories. |
| 4 | The quarterly earnings report was released by Twitter Inc. on 2 October 2022. https://investor.twitterinc.com/financial-information/quarterly-results/default.aspx, accessed in October 2022. |
| 5 | https://www.businessofapps.com/data/twitter-statistics/ (accessed on 2 October 2022). |
| 6 | Data source is from “Bitcoin market capitalization quarterly 2013–2022”, https://www.statista.com. |
| 7 | https://www.statista.com/statistics/1195753/bitcoin-trading-selected-countries/ (accessed on 2 October 2022). |
References
- Al-Yahyaee, Khamis, Mobeen Ur Rehman, Walid Mensi, and Idries Mohammad Wanas Al-Jarrah. 2019. Can uncertainty indices predict Bitcoin prices? A revisited analysis using partial and multivariate wavelet approaches. The North American Journal of Economic Finance 49: 47–56. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Bertomeu, Jeremy, Edwige Cheynel, Eric Floyd, and Wenqiang Pan. 2021. Using machine learning to detect misstatements. Review of Accounting Studies 26: 468–519. [Google Scholar] [CrossRef]
- Bouri, Elie, and Rangan Gupta. 2021. Predicting Bitcoin returns: Comparing the roles of newspaper- and internet-based measures of uncertainty. Finance Research Letters 38: 101398. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random Forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Bryzgalova, Svetlana, Jiantao Huang, and Christian Julliard. 2023. Bayesian solutions for the factor zoo: We just ran two quadrillion models. The Journal of Finance 78: 487–557. [Google Scholar] [CrossRef]
- Burman, Prabir. 1989. A comparative study of ordinary cross-validation, v-fold cross-validation and the repeated learning-testing methods. Biometrika 76: 503–14. [Google Scholar] [CrossRef]
- Bzdok, Danilo, Naomi Altman, and Martin Krzywinski. 2018. Statistics versus machine learning. Nature Methods 15: 233–34. [Google Scholar] [CrossRef]
- Cochrane, John H. 2011. Presidential address: Discount rates. Journal of Finance 66: 1047–108. [Google Scholar] [CrossRef]
- Demir, Ender, Giray Gozgor, Chi Keung Marco Lau, and Samuel A. Vigne. 2018. Does economic policy uncertainty predict the Bitcoin returns? An empirical investigation. Finance Research Letters 26: 145–49. [Google Scholar] [CrossRef]
- French, Joseph. 2021. #Bitcoin, #COVID-10: Twitter-based uncertainty and Bitcoin before and during the pandemic. International Journal of Financial Studies 9: 28. [Google Scholar]
- Gozgor, Giray, Aviral Kumar Tiwari, Ender Demir, and Sagi Akron. 2019. The relationship between Bitcoin returns and trade policy uncertainty. Finance Research Letters 29: 75–82. [Google Scholar] [CrossRef]
- Geisser, Seymour. 1975. The predictive sample reuse method with applications. Journal of the American Statistical Association 70: 320–28. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 2017. Presidential address: The scientific outlook in financial economics. The Journal of Finance 72: 1399–440. [Google Scholar] [CrossRef]
- Li, Zheng-Zheng, Chi-Wei Su, and Meng Nan Zhu. 2022. How Does Uncertainty Affect Volatility Correlation between Financial Assets? Evidence from Bitcoin, Stock and Gold. Emerging Markets Finance & Trade 58: 2682–94. [Google Scholar]
- Li, Zhiyong, Yifan Wan, Tianyi Wang, and Mei Yu. 2023. Factor-timing in the Chinese factor zoo: The role of economic policy uncertainty. Journal of International Financial Markets, Institutions & Money 85: 101782. [Google Scholar]
- Liu, Mingxi, Guowen Li, Jianping Li, Xiaoqian Zhu, and Yinhong Yao. 2021. Forecasting the price of Bitcoin using deep learning. Finance Research Letters 40: 101755. [Google Scholar] [CrossRef]
- Nguyen, Khanh Quoc. 2021. The correlation between the stock market and Bitcoin during COVID-19 and other uncertainty periods. Finance Research Letters 46: 102284. [Google Scholar] [CrossRef]
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2019. The effects of markets, uncertainty and search intensity on bitcoin returns. International Review of Financial Analysis 63: 220–42. [Google Scholar] [CrossRef]
- Scagliarini, Tomas, Giuseppe Pappalardo, Alessio Emanuele Biondo, Alessandro Pluchino, Andrea Rapisarda, and Sebastiano Stramaglia. 2022. Pairwise and high-order dependencies in the cryptocurrency trading network. Scientific Reports 12: 18483. [Google Scholar] [CrossRef]
- Smith, Simon. 2022. Time-variation, multiple testing, and the factor zoo. International Review of Financial Analysis 84: 102394. [Google Scholar] [CrossRef]
- Stone, M. 1974. Cross-validatory choice and assessment of statistical predictions. Journal of Royal Statistical Society, Series B 36: 111–47. [Google Scholar] [CrossRef]
- Stone, M. 1977. An asymptotic equivalence of choice of model by cross-validation and Akaike’s criterion. Journal of Royal Statistical Society, Series B 39: 44–47. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, Chi Xie, Danyan Wen, and Longfeng Zhao. 2019. When Bitcoin meets economic policy uncertainty (EPU): Measuring risk spillover effect from EPU to Bitcoin. Finance Research Letters 31: 489–97. [Google Scholar] [CrossRef]
- Wang, Jinghua, and Geoffrey M. Ngene. 2020. Does Bitcoin still own the dominant power? An intraday analysis. International Review of Financial Analysis 71: 101551. [Google Scholar] [CrossRef]
- Witten, Ian H., Eibe Frank, Mark A. Hall, and Christopher Pal. 2005. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed. Burlington: Morgan Kaufmann. [Google Scholar]
- Wu, Chang-Che, Shu-Ling Ho, and Chih-Chiang Wu. 2021. The determinants of Bitcoin returns and volatility: Perspectives on global and national economic policy uncertainty. Financial Research Letters 45: 202175. [Google Scholar] [CrossRef]
- Zhang, Ping. 1993. Model selection via multifold cross validation. The Annals of Statistics 21: 299–313. [Google Scholar] [CrossRef]
- Zhu, Lin, Dafeng Qiu, Daji Ergu, Cai Ying, and Kuiyi Liu. 2019. A study on predicting loan default based on the random forest algorithm. Procedia Computer Science 162: 503–13. [Google Scholar] [CrossRef]

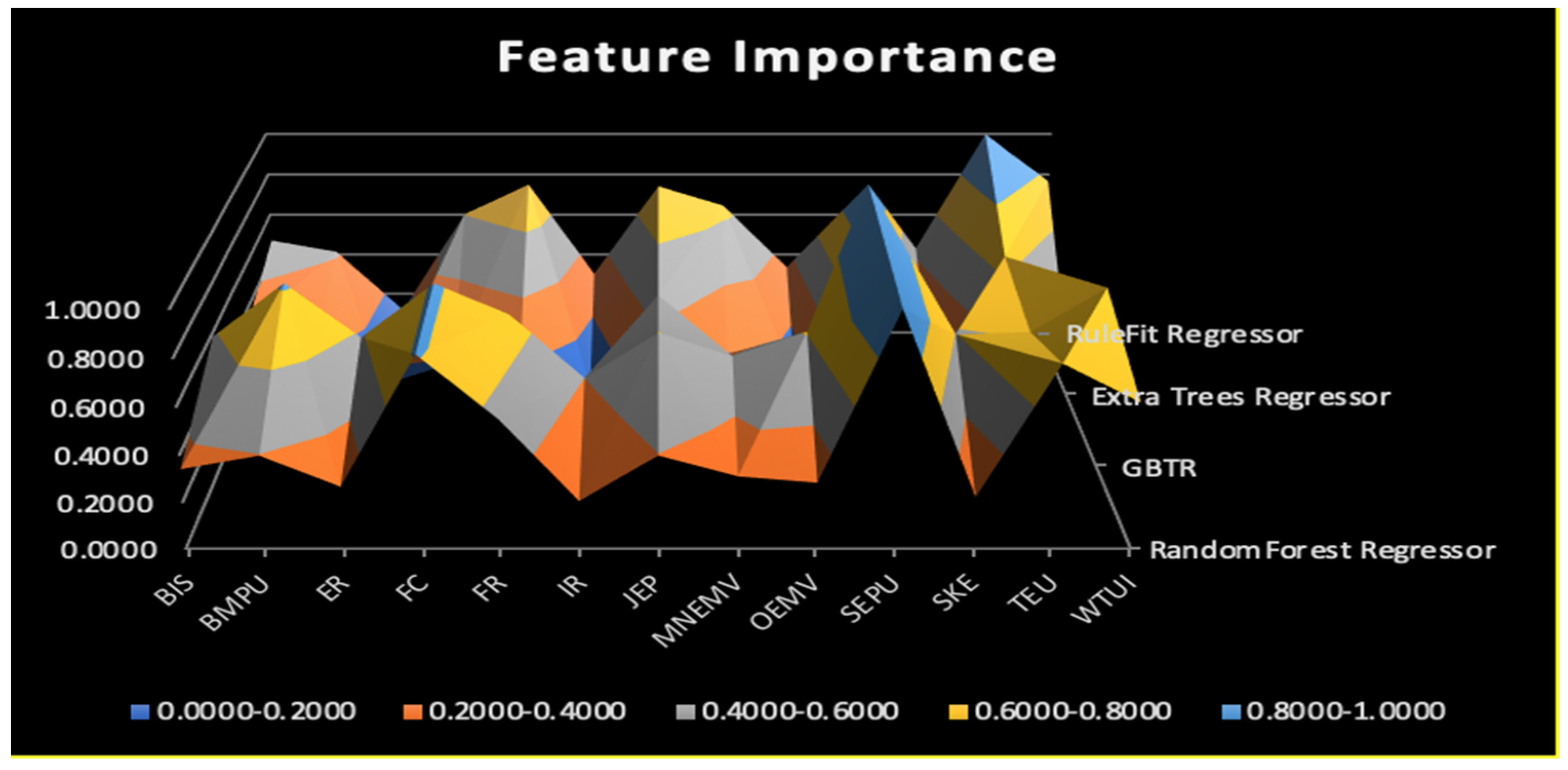
| Feature | Random Forest Model | GBTR Model | Extra Tree Model | Rule Fit Model |
|---|---|---|---|---|
| BIS | 0.3392 | 0.5840 | 0.3261 | 0.4712 |
| BMPU | 0.3967 | 0.8196 | 0.2291 | 0.4131 |
| ER | 0.2643 | 0.5815 | 0.0541 | 0.1173 |
| FC | 0.8167 | 0.8188 | 0.1558 | 0.6016 |
| FR | 0.5504 | 0.6834 | 0.2910 | 0.7521 |
| IR | 0.2046 | 0.4005 | 0.0472 | 0.3028 |
| JEP | 0.3972 | 0.6025 | 0.4807 | 0.7437 |
| MNEMV | 0.3084 | 0.4979 | 0.1981 | 0.6465 |
| OEMV | 0.2819 | 0.6073 | 0.0908 | 0.3359 |
| SEPU | 1.0000 | 1.0000 | 1.0000 | 0.5150 |
| SKE | 0.2208 | 0.5958 | 0.1234 | 0.4311 |
| TEU | 0.7781 | 0.6054 | 0.6635 | 1.0000 |
| WTUI | 0.6177 | 0.8007 | 0.1625 | 0.7677 |
| Model | Random Forest Model | GBTR Model | Extra Tree Model | Rule Fit Model |
|---|---|---|---|---|
| Sample Size | 64.15% | 64.15% | 64.15% | 64.15% |
| RMSE (Cross Validation) | 0.2734 | 0.2915 | 0.2859 | 0.3553 |
| Residual Mean | 0.0095 | 0.0053 | −0.1501 | −0.1878 |
| 0.1391 | 0.0212 | 0.0462 | −0.0979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ngene, G.M.; Shi, Y.; Mungai, A.N. An Investigation of the Predictability of Uncertainty Indices on Bitcoin Returns. J. Risk Financial Manag. 2023, 16, 461. https://doi.org/10.3390/jrfm16100461
Wang J, Ngene GM, Shi Y, Mungai AN. An Investigation of the Predictability of Uncertainty Indices on Bitcoin Returns. Journal of Risk and Financial Management. 2023; 16(10):461. https://doi.org/10.3390/jrfm16100461
Chicago/Turabian StyleWang, Jinghua, Geoffrey M. Ngene, Yan Shi, and Ann Nduati Mungai. 2023. "An Investigation of the Predictability of Uncertainty Indices on Bitcoin Returns" Journal of Risk and Financial Management 16, no. 10: 461. https://doi.org/10.3390/jrfm16100461
APA StyleWang, J., Ngene, G. M., Shi, Y., & Mungai, A. N. (2023). An Investigation of the Predictability of Uncertainty Indices on Bitcoin Returns. Journal of Risk and Financial Management, 16(10), 461. https://doi.org/10.3390/jrfm16100461









