On the Measurement of Hedging Effectiveness for Long-Term Investment Guarantees
Abstract
:1. Introduction
2. Modeling Framework
2.1. GMMB Variable Annuity Product
2.2. Market Dynamics
2.3. Hedging Strategy
2.4. Projection of the Insurer’s Loss
3. Statistical Framework for Measuring the Effectiveness of Dynamic Hedges
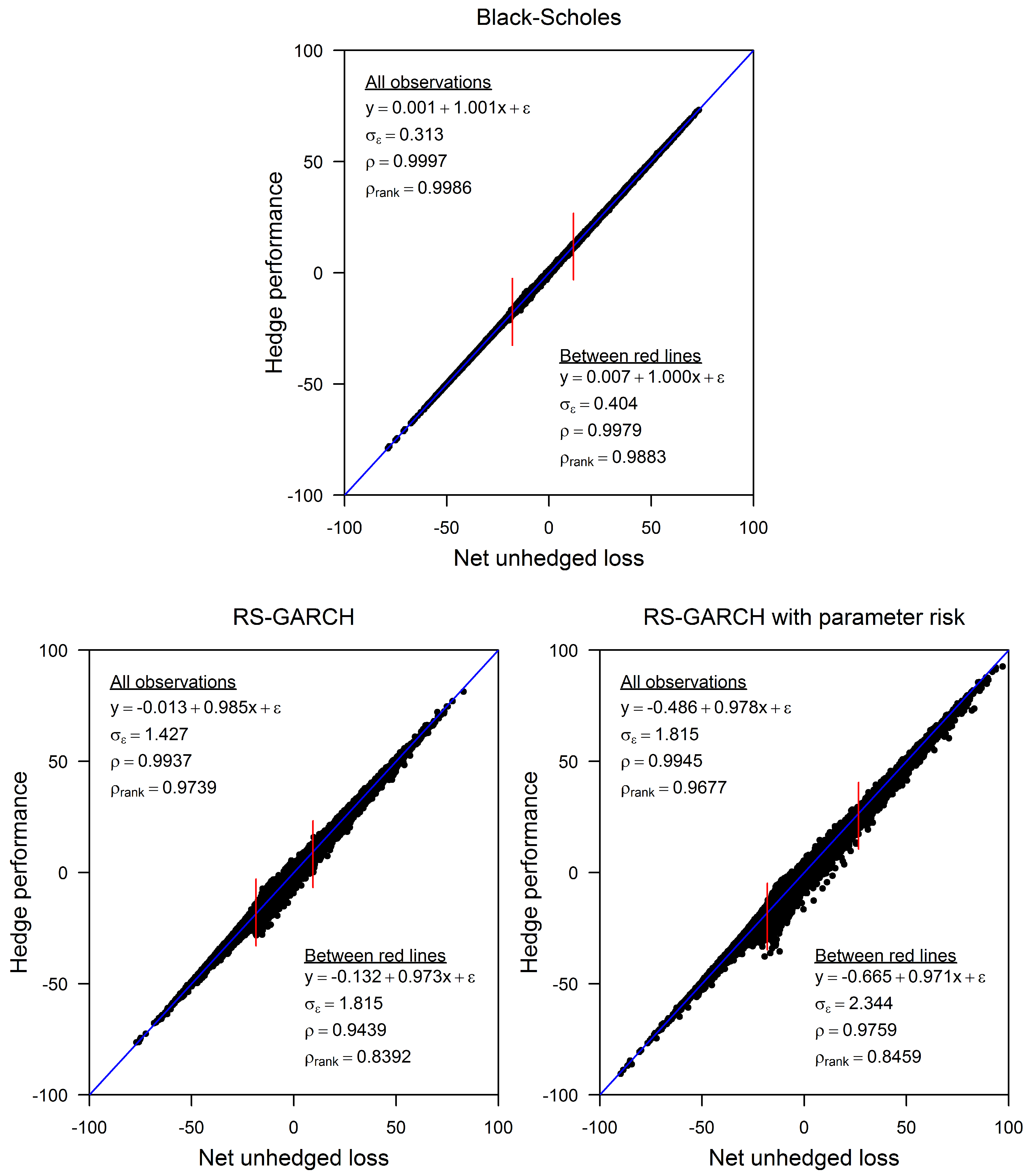
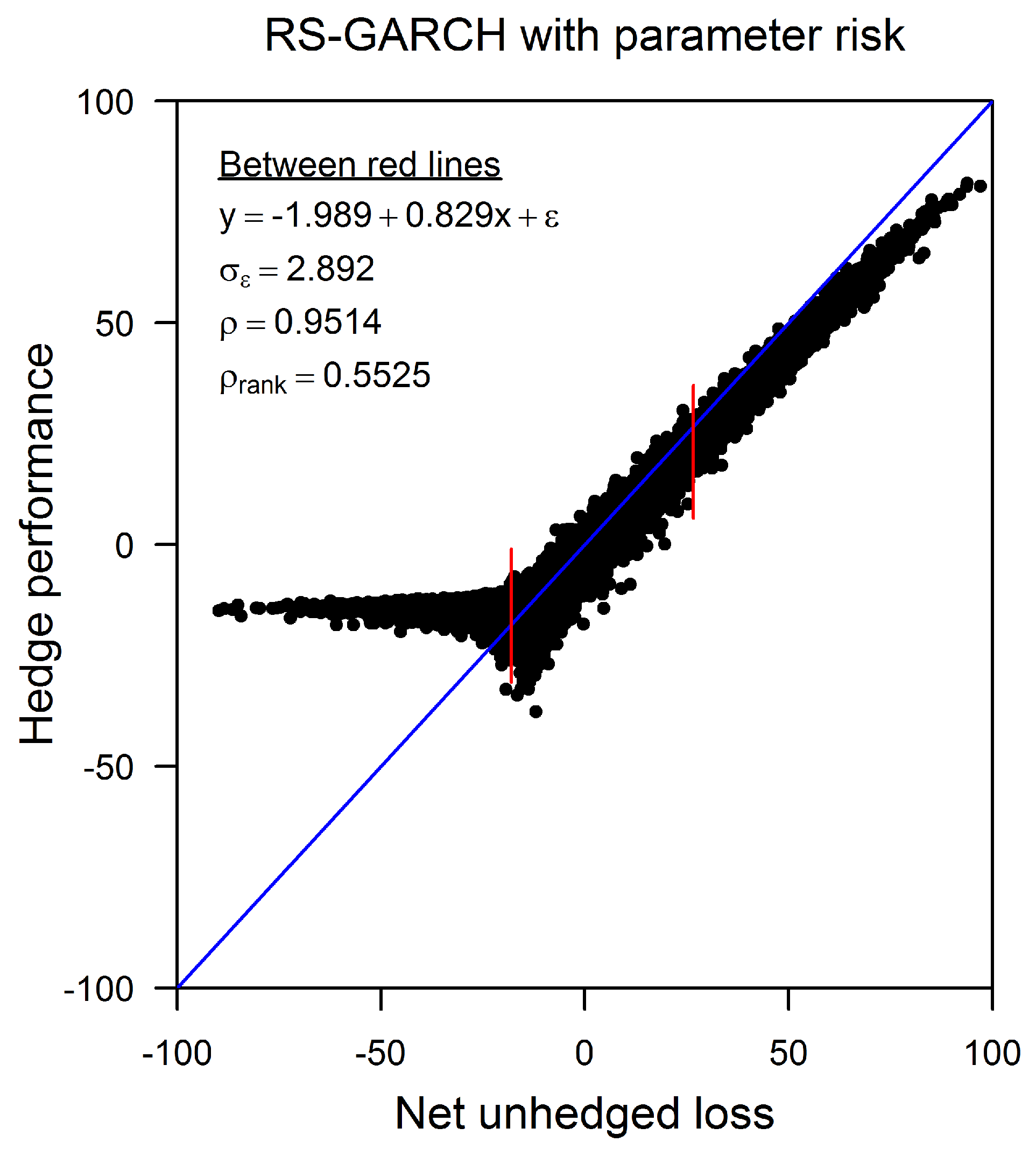
3.1. Relationship between Y and X
3.2. Relationship between and X
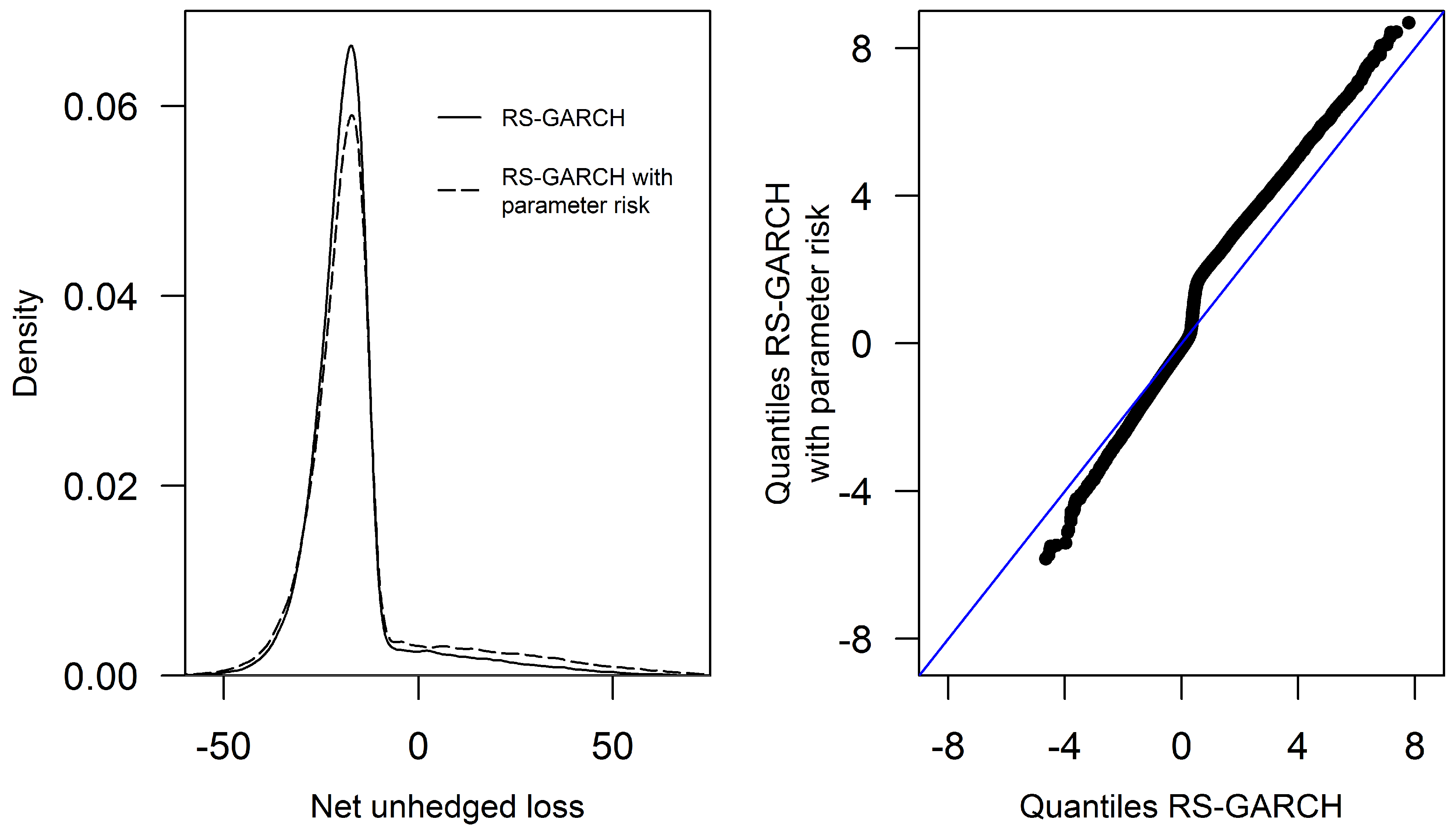
3.3. Distributions of X and
3.4. Risk Measures
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Branger et al. (2012) and Kaeck (2013) improved on the methodology to measure hedging effectiveness by comparing the distributions of anticipated and realized hedging errors. Anticipated hedging errors are those obtained when the model used to determine the hedge coincides with the data generating process. Realized hedging errors correspond to those that are observed when the hedging strategy is implemented on empirical data or on simulated data based on a data generating process that is not consistent with the model used for hedging. If the distributions of anticipated and realized hedging errors differ significantly, this suggests some form of model misspecification in the hedge. |
| 2 | The interest of the accounting literature for measuring hedging effectiveness is due to Statements of Financial Accounting Standards No. 133, Accounting for Derivative Instruments and Hedging Activities, commonly known as FAS 133. FAS 133, which came into effect in the U.S. at the turn of the century, requires that all derivatives entered into by a corporation must be marked to market and changes in their values reported in the income statement. This accounting treatment can create earnings volatility when derivatives are used for risk management purposes as the timing of gains and losses on the hedged items may not be matched with those on the corresponding hedging derivatives. To remedy this problem, FAS 133 allows corporations to match the timing of these gains and losses, provided that they demonstrate and document that the hedge is highly effective in offsetting changes in fair value for the risks being hedged. FAS 133 does not endorse any specific testing methodology, but recommends the use of statistical tests. A good overview of approaches proposed in the accounting literature for measuring hedging effectiveness is given by Charnes et al. (2003), Finnerty and Grant (2002), and Hailer and Rump (2005). |
| 3 | The “Report of the Task Force on Segregated Fund Liability and Capital Methodologies” produced by the Canadian Institute of Actuaries states that “typically delta and rho are hedged while vega and gamma are only monitored” (see Canadian Institute of Actuaries 2010). A survey performed by Watson (2013) also indicates that U.S. insurers mainly hedge delta and rho risks from their variable annuity portfolio. Although we did not include interest rate risk in our modeling framework for simplicity, our approach to measure hedging effectiveness can be applied to more general modeling settings and hedging strategies. |
| 4 | The switching mean does not necessarily generate a jump in returns, but there is a high likelihood of observing a significant negative return when the model enters the crisis regime. When jump-diffusion models are discretized, the occurrence of a negative jump is equivalent to observing a large negative return in a given time interval. |
| 5 | In our study, we suppose for simplicity that one can buy and sell shares of the investment portfolio tracked by the variable annuity. In practice, variable annuities invest in mutual funds which are relatively illiquid and cannot be shorted. As a result, insurers must construct their hedging strategies using financial instruments that are both liquid and highly correlated with the mutual fund. This exposes the hedging strategy to basis risk: the risk that price fluctuations in the underlying asset cannot be perfectly replicated by trading in available instruments. Recent studies showed that basis risk significantly affects hedging effectiveness, notably in the context of variable annuities (see, e.g., Ankirchner et al. 2014; Bauer 2020; Li et al. 2022; Trottier et al. 2018). |
| 6 | Alternative approaches can be considered to determine the volatility parameter in the Black–Scholes model. For example, it can be set based on forward-looking measures of volatility such as the implied volatility surface extracted from option price data. Previous empirical studies have showed that the variance risk premium is typically negative (see, e.g., Bakshi and Kapadia 2003; Carr and Wu 2006, 2009; Clark and Dickson 2019; Israelov and Klein 2016), which implies that the risk–neutral volatility is expected to be larger than the real-world volatility. Although a higher volatility leads to higher option prices, it is unclear whether the use of a volatility assumption inferred from derivative prices is more effective in a variable annuity hedging context. For instance, Augustyniak and Boudreault (2017) compared hedging effectiveness using a historical volatility estimate to a calibration based on a measure of the VIX and found that “forward-looking measures of volatility may not lead to better volatility inputs than measures based on historical data.” We refer to Section 5.8 in Augustyniak and Boudreault (2017) for a detailed discussion on the calibration of the volatility parameter. |
| 7 | Given n sampled values from a random variable Z, denoted by , the AAD is given by
|
References
- Alexander, Carol, and Andreas Kaeck. 2012. Does model fit matter for hedging? Evidence from FTSE 100 options. Journal of Futures Markets 32: 609–38. [Google Scholar] [CrossRef]
- Alexander, Carol, Andreas Kaeck, and Leonardo M. Nogueira. 2009. Model risk adjusted hedge ratios. Journal of Futures Markets 29: 1021–49. [Google Scholar] [CrossRef]
- Alexander, Carol, and Leonardo M. Nogueira. 2007. Model-free hedge ratios and scale-invariant models. Journal of Banking & Finance 31: 1839–61. [Google Scholar] [CrossRef]
- Alexander, Carol, Alexander Rubinov, Markus Kalepky, and Stamatis Leontsinis. 2012. Regime-dependent smile-adjusted delta hedging. Journal of Futures Markets 32: 203–29. [Google Scholar] [CrossRef]
- Ankirchner, Stefan, Judith C. Schneider, and Nikolaus Schweizer. 2014. Cross-hedging minimum return guarantees: Basis and liquidity risks. Journal of Economic Dynamics and Control 41: 93–109. [Google Scholar] [CrossRef]
- Augustyniak, Maciej. 2014a. Estimation du modèle GARCH à changement de régimes et son utilité pour quantifier le risque de modèle dans les applications financières en actuariat. Ph.D. thesis, Université de Montréal, Montréal, QC, Canada. Available online: http://hdl.handle.net/1866/10826 (accessed on 22 November 2022).
- Augustyniak, Maciej. 2014b. Maximum likelihood estimation of the Markov-switching GARCH model. Computational Statistics & Data Analysis 76: 61–75. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, and Alexandru Badescu. 2021. On the computation of hedging strategies in affine garch models. Journal of Futures Markets 41: 710–35. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, Alexandru Badescu, and Jean-François Bégin. 2021. A discrete-time hedging framework with multiple factors and fat tails: On what matters. Journal of Econometrics 232: 416–44. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, and Mathieu Boudreault. 2012. An out-of-sample analysis of investment guarantees for equity-linked products: Lessons from the financial crisis of the late 2000s. North American Actuarial Journal 16: 183–206. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, and Mathieu Boudreault. 2017. Mitigating interest rate risk in variable annuities: An analysis of hedging effectiveness under model risk. North American Actuarial Journal 21: 502–25. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, Mathieu Boudreault, and Manuel Morales. 2018. Maximum likelihood estimation of the Markov-switching GARCH model based on a general collapsing procedure. Methodology and Computing in Applied Probability 20: 165–88. [Google Scholar] [CrossRef]
- Augustyniak, Maciej, Frédéric Godin, and Clarence Simard. 2017. Assessing the effectiveness of local and global quadratic hedging under GARCH models. Quantitative Finance 17: 1305–18. [Google Scholar] [CrossRef]
- Babaoğlu, Kadir, Peter Christoffersen, Steven Heston, and Kris Jacobs. 2018. Option valuation with volatility components, fat tails, and nonmonotonic pricing kernels. Review of Asset Pricing Studies 8: 183–231. [Google Scholar] [CrossRef]
- Badescu, Alexandru, Zhenyu Cui, and Juan-Pablo Ortega. 2017. Non-affine GARCH option pricing models, variance-dependent kernels, and diffusion limits. Journal of Financial Econometrics 15: 602–48. [Google Scholar] [CrossRef]
- Badescu, Alexandru, Robert J. Elliott, and Juan-Pablo Ortega. 2014. Quadratic hedging schemes for non-Gaussian GARCH models. Journal of Economic Dynamics & Control 42: 13–32. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 1997. Empirical performance of alternative option pricing models. The Journal of Finance 52: 2003–49. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 2000. Pricing and hedging long-term options. Journal of Econometrics 94: 277–318. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, and Nikunj Kapadia. 2003. Delta-hedged gains and the negative market volatility risk premium. Review of Financial Studies 16: 527–66. [Google Scholar] [CrossRef]
- Bauer, Jan. 2020. Hedging of variable annuities under basis risk. Asia-Pacific Journal of Risk and Insurance 14: 20190040. [Google Scholar] [CrossRef]
- Bauwens, Luc, Arie Preminger, and Jeroen V. K. Rombouts. 2010. Theory and inference for a Markov switching GARCH model. The Econometrics Journal 13: 218–44. [Google Scholar] [CrossRef] [Green Version]
- Bégin, Jean-François, Christian Dorion, and Geneviève Gauthier. 2020. Idiosyncratic jump risk matters: Evidence from equity returns and options. Review of Financial Studies 33: 155–211. [Google Scholar] [CrossRef]
- Branger, Nicole, Eva Krautheim, Christian Schlag, and Norman Seeger. 2012. Hedging under model misspecification: All risk factors are equal, but some are more equal than others. Journal of Futures Markets 32: 397–430. [Google Scholar] [CrossRef]
- Broadie, Mark, Mikhail Chernov, and Michael Johannes. 2007. Model specification and risk premia: Evidence from futures options. The Journal of Finance 62: 1453–90. [Google Scholar] [CrossRef]
- Canadian Institute of Actuaries. 2010. Report of the Task Force on Segregated Fund Liability and Capital Methodologies. Document 210053. Ottawa: Canadian Institute of Actuaries. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2006. A tale of two indices. The Journal of Derivatives 13: 13–29. [Google Scholar] [CrossRef]
- Carr, Peter, and Liuren Wu. 2009. Variance risk premiums. Review of Financial Studies 22: 1311–41. [Google Scholar] [CrossRef]
- Charnes, John M., Paul Koch, and Henk Berkman. 2003. Measuring hedge effectiveness for FAS 133 compliance. Journal of Applied Corporate Finance 15: 95–103. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Christian Dorion, Kris Jacobs, and Yintian Wang. 2010. Volatility components, affine restrictions, and nonnormal innovations. Journal of Business & Economic Statistics 28: 483–502. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Steve Heston, and Kris Jacobs. 2006. Option valuation with conditional skewness. Journal of Econometrics 131: 253–84. [Google Scholar] [CrossRef]
- Christoffersen, Peter, and Kris Jacobs. 2004. Which GARCH model for option valuation? Management Science 50: 1204–21. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Kris Jacobs, Chayawat Ornthanalai, and Yintian Wang. 2008. Option valuation with long-run and short-run volatility components. Journal of Financial Economics 90: 272–97. [Google Scholar] [CrossRef] [Green Version]
- Clark, Steven P., and Mike Dickson. 2019. Performance expectations of basic options strategies may be different than you think. Journal of Asset Management 20: 91–102. [Google Scholar] [CrossRef]
- Coleman, Thomas F., Yohan Kim, Yuying Li, and Maria-Cristina Patron. 2007. Robustly hedging variable annuities with guarantees under jumps and volatility risks. The Journal of Risk and Insurance 74: 347–76. [Google Scholar] [CrossRef]
- Coleman, Thomas F., Yuying Li, and Maria-Cristina Patron. 2006. Hedging guarantees in variable annuities under both equity and interest rate risks. Insurance: Mathematics & Economics 38: 215–28. [Google Scholar] [CrossRef]
- Cont, Rama. 2006. Model uncertainty and its impact on the pricing of derivative instruments. Mathematical Finance 16: 519–47. [Google Scholar] [CrossRef]
- Dumas, Bernard, Jeff Fleming, and Robert E. Whaley. 1998. Implied volatility functions: Empirical tests. The Journal of Finance 53: 2059–106. [Google Scholar] [CrossRef]
- Eraker, Bjorn, Michael Johannes, and Nicholas Polson. 2003. The impact of jumps in volatility and returns. The Journal of Finance 58: 1269–300. [Google Scholar] [CrossRef]
- Feng, Runhuan, Guojun Gan, and Ning Zhang. 2022. Variable annuity pricing, valuation, and risk management: A survey. Scandinavian Actuarial Journal 2022: 867–900. [Google Scholar] [CrossRef]
- Finnerty, John D., and Dwight Grant. 2002. Alternative approaches to testing hedge effectiveness under SFAS No. 133. Accounting Horizons 16: 95–108. [Google Scholar] [CrossRef]
- François, Pascal, and Lars Stentoft. 2021. Smile-implied hedging with volatility risk. Journal of Futures Markets 41: 1220–40. [Google Scholar] [CrossRef]
- Francq, Christian, Michel Roussignol, and Jean-Michel Zakoïan. 2001. Conditional heteroskedasticity driven by hidden Markov chains. Journal of Time Series Analysis 22: 197–220. [Google Scholar] [CrossRef]
- Hailer, Angelika C., and Siegfried M. Rump. 2005. Evaluation of hedge effectiveness tests. Journal of Derivatives Accounting 2: 31–51. [Google Scholar] [CrossRef]
- Hardy, Mary R. 2003. Investment Guarantees: Modeling and Risk Management for Equity-Linked Life Insurance. Hoboken: John Wiley & Sons. [Google Scholar]
- Hull, John, and Alan White. 2017. Optimal delta hedging for options. Journal of Banking & Finance 82: 180–90. [Google Scholar] [CrossRef]
- Israelov, Roni, and Matthew Klein. 2016. Risk and return of equity index collar strategies. The Journal of Alternative Investments 19: 41–54. [Google Scholar] [CrossRef]
- Kaeck, Andreas. 2013. Hedging surprises, jumps, and model misspecification: A risk management perspective on hedging S&P 500 options. Review of Finance 17: 1535–69. [Google Scholar] [CrossRef]
- Kim, In Joon, and Sol Kim. 2004. Empirical comparison of alternative stochastic volatility option pricing models: Evidence from Korean KOSPI 200 index options market. Pacific-Basin Finance Journal 12: 117–42. [Google Scholar] [CrossRef]
- Kling, Alexander, Frederik Ruez, and Jochen Ruß. 2011. The impact of stochastic volatility on pricing, hedging and hedge efficiency of withdrawal benefit guarantees in variable annuities. Astin Bulletin 41: 511–45. [Google Scholar]
- Lassance, Nathan, and Frédéric Vrins. 2018. A comparison of pricing and hedging performances of equity derivatives models. Applied Economics 50: 1122–37. [Google Scholar] [CrossRef]
- Li, Wenchu, Thorsten Moenig, and Maciej Augustyniak. 2022. Basis Risk in Variable Annuities. Working Paper, SSRN eLibrary. Available online: http://https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3531307 (accessed on 22 November 2022).
- Nandi, Saikat. 1998. How important is the correlation between returns and volatility in a stochastic volatility model? Empirical evidence from pricing and hedging in the S&P 500 index options market. Journal of Banking & Finance 22: 589–610. [Google Scholar] [CrossRef]
- Trottier, Denis-Alexandre, Frédéric Godin, and Emmanuel Hamel. 2018. Local hedging of variable annuities in the presence of basis risk. Astin Bulletin 48: 611–46. [Google Scholar] [CrossRef]
- Watson, Towers. 2013. Variable Annuity Hedging Survey: Sophistication Gains, Challenges Remain. Insights, August. [Google Scholar]


| Daily RS-GARCH | |||||||
| 0.544 | 0.042 | 0.936 | 0.980 | 0.339 | |||
| (0.010) | (0.20) | (0.0013) | (0.087) | (0.006) | (0.006) | (0.004) | (0.083) |
| Weekly RS-GARCH | |||||||
| 0.0431 | 2.527 | 0.041 | 0.905 | 0.948 | 0.316 | ||
| (0.064) | (0.54) | (0.0185) | (0.518) | (0.018) | (0.024) | (0.022) | (0.105) |
| Rebalancing | Mean | StDev | AAD | 95% CTE | 99% VaR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| B-S | RSG | B-S | RSG | B-S | RSG | B-S | RSG | B-S | RSG | |
| Unhedged | 13.0 | 17.6 | 19.4 | 20.9 | 27.4 | 42.9 | 37.2 | 53.7 | ||
| Annual | 1.5 | 2.4 | 5.5 | 5.9 | 4.4 | 4.7 | 14.5 | 17.4 | 16.8 | 20.3 |
| Monthly | 0.1 | 0.9 | 1.5 | 2.8 | 1.1 | 2.0 | 3.4 | 8.6 | 4.0 | 10.2 |
| Weekly | 0.0 | 0.6 | 0.7 | 2.2 | 0.5 | 1.6 | 1.7 | 6.8 | 2.0 | 8.0 |
| Daily | 0.0 | 0.2 | 0.3 | 1.9 | 0.2 | 1.3 | 0.7 | 5.2 | 0.9 | 6.3 |
| Rebalancing | Mean | StDev | B | 95% CTE | 99% VaR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| D | W | D | W | D | W | D | W | D | W | |
| Unhedged | 17.6 | 23.4 | 20.9 | 21.2 | 42.9 | 62.0 | 53.7 | 71.9 | ||
| Annual | 2.4 | 1.8 | 5.9 | 6.6 | 4.7 | 4.8 | 17.4 | 19.4 | 20.3 | 23.1 |
| Monthly | 0.9 | 0.7 | 2.8 | 3.5 | 2.0 | 2.4 | 8.6 | 10.7 | 10.2 | 12.7 |
| Weekly | 0.6 | 0.1 | 2.2 | 2.9 | 1.6 | 2.0 | 6.8 | 8.3 | 8.0 | 9.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augustyniak, M.; Badescu, A.; Boudreault, M. On the Measurement of Hedging Effectiveness for Long-Term Investment Guarantees. J. Risk Financial Manag. 2023, 16, 112. https://doi.org/10.3390/jrfm16020112
Augustyniak M, Badescu A, Boudreault M. On the Measurement of Hedging Effectiveness for Long-Term Investment Guarantees. Journal of Risk and Financial Management. 2023; 16(2):112. https://doi.org/10.3390/jrfm16020112
Chicago/Turabian StyleAugustyniak, Maciej, Alexandru Badescu, and Mathieu Boudreault. 2023. "On the Measurement of Hedging Effectiveness for Long-Term Investment Guarantees" Journal of Risk and Financial Management 16, no. 2: 112. https://doi.org/10.3390/jrfm16020112
APA StyleAugustyniak, M., Badescu, A., & Boudreault, M. (2023). On the Measurement of Hedging Effectiveness for Long-Term Investment Guarantees. Journal of Risk and Financial Management, 16(2), 112. https://doi.org/10.3390/jrfm16020112









