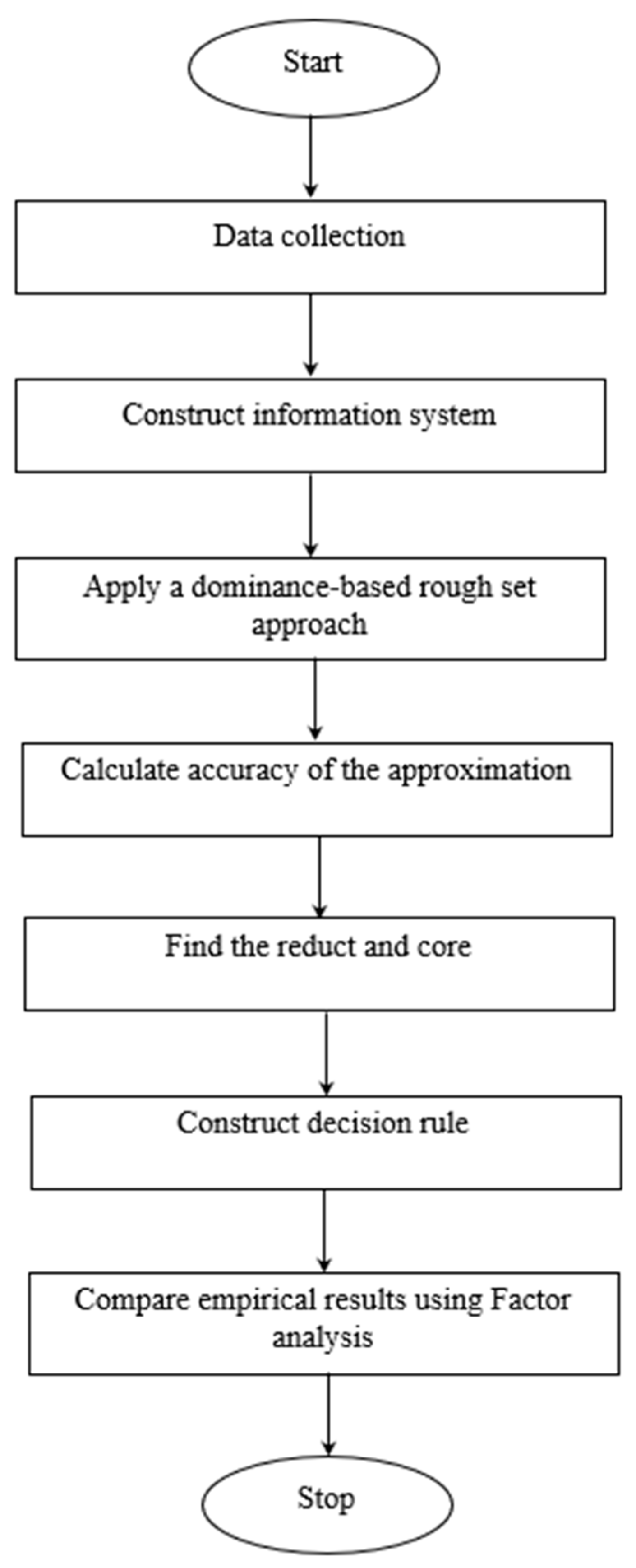
Criteria Selection of Housing Loan Based on Dominance-Based Rough Set Theory: An Indian Case

Abstract

Because India has one of the world’s fastest-growing economies, the Indian banking sector is essential to the country’s reform. The approval of home loans to customers is one of the crucial tasks carried out by Indian banks. The risk of loan repayment outside of the agreed-upon time frame can be reduced by accurately estimating the customer’s loan need. The majority of earlier studies on the development of banking lacked a methodical approach to analyze qualitative data. Even though the traditional multivariate statistically based factor analysis approach is a great way to categories data in qualitative analysis, the technique cannot be used without any statistical presumptions and additional information about the data. This study handles the banking attributes related to home loans using the Dominance-based Rough Set Approach (D-RSA). In order to categorize the customer’s attributes, this study suggests using a preference-based “if … then” decision rule. This rule can aid decision makers in understanding the risk factors associated with loan factors for a financial organization.

1. Introduction

One of the crucial industries that has a significant influence on a nation’s financial and economic development is banking. The banking sector has made a sizable contribution to employment opportunities and national income in developing nations such as India. Indian private and public banks have long been the most active and quickly growing institutions in the nation. The Indian banking system is essential for fostering the nation’s economic development. The banking industry has a number of suitable determinants despite being a significant contributor to the Indian economy. As we all know, the banking industry is made up of a variety of factors, including monthly income, education, etc. Indian bankers frequently struggle with decision making when it confronts problems involving client relationships. For business marketing to analyze the close connections between the various factors that are connected to the banking system, customer relationships are crucial. The key and initial steps in the planning process to comprehend the relationship between banking tasks and the decision system are the sanctioning of loans. Therefore, the goal of this study is to forecast how much money customers will be able to borrow from banks.

Mathematical functions are applied to endless techniques, and have been frequently used with banking sector studies where the data need quantitative analysis. The model of choice is based on drawbacks and presumptions such as independent variables, normal distribution, multicollinearity, and heteroscedasticity. As the banking industry predominantly deals with numbers, it does not always have numeric data. Qualitative attributes such as employee’s credentials, strategies related to business marketing, and types of loan facilities are quite prevalent. However, their nature makes it difficult to utilize the typical statistical methods of analysis.

The rough set theory developed by Z. Pawlak is an appropriate method that is utilized to understand data from a given information system (Pawlak 1982) The fundamental concept of the rough set theory lies in the indiscernibility relation, i.e., the entities in the given set will be similar to the pre-existing sets (Huang et al. 2016). The rough set theory utilizes zones for understanding the attributes and their relations; the zones are the upper and the lower approximation zone. The upper zone will deal with the attributes that are unknown, whereas the lower zone deals with the known facts. The middle ground contains imperceptible or uncertain attributes. Thus, the technique can deal with inadequate knowledge such as fuzzy theory, statistical techniques, discriminate analysis, and probability theory (Dubois and Prade 1990; Krusińska et al. 1992; Polkowski and Skowron 1994).

The fundamental notion of the rough set theory is of an attribute reduction. This is simply an attribute that possesses and safeguards the essential properties of the set. This is used to ease the demonstration of information systems by withdrawing the irrelevant attributes while simultaneously maintaining the feasibility to differentiate between varied entities. It provides a framework for dealing with incomplete and uncertain data, allowing for efficient analysis and decision-making in real-world scenarios where precise information may be lacking. It is a powerful data mining approach that is difficult to explore via standard statistical methods. Rough set theory has applications in various fields, including multi-criteria analysis (Greco et al. 2001; Baziki et al. 2022; Sharma et al. 2022; Chen and Tsai 2016), data envelopment analysis (DEA) (Shafiee and Shams-e-alam 2011), medical diagnosis (Hirano and Tsumoto 2005; Tsumoto 2007), signal processing (Xiao and Lai 2005), rough set clustering (Herawan et al. 2010), parallel computing (Li et al. 2015), and neural network (Lingras 1996).

However, the traditional rough set approach is inefficient in dealing with preference-ordered relationships arising from attributes such as service strategies, product quality, debt ratio (Błaszczyński et al. 2007), and business indicators (Couto and Gaiado 2015). Therefore, this study proposes an approach that applies the Dominance-based Rough Set Approach (D-RSA) for solving preference-ordered situations. Greco et al. (2002) developed the D-RSA to handle preference-ordered mining. It is an effective tool for reducing attributes in a batch of qualitative-based dominance that has been successful in many fields. Chakhar and Saad (2012) proposed a rough set technique for groups based on dominance in the multi-criteria class study. The model is applied in (Augeri et al. 2015) dominance-based rough set technique to set the speed constraints for cars in speed-restricted areas. Based on a number of case studies, the D-RSA is utilized to construct rules to examine multi-criteria group decision making (Chakhar et al. 2016). In (Sawicki and Żak 2014), D-RSA based analysis is performed on transportation problems by producing decision rules depending on customer views and expectations. The D-RSA model is used to define airline service strategies for customer satisfaction (Liou and Tzeng 2010). Zhai et al. (2009) applied the D-RSA to improve effective consumer satisfaction in product design. The D-RSA method is also implemented to develop strategies for airline service in (Liou 2011).

To the best of our knowledge, the application of the D-RSA for customer loan prediction has not been studied in the literature. In this paper, we have considered a case study of the financial establishment (bank) of India. We have applied a dominance-based rough set approach to extract certain decision rules. These rules ultimately regulate whether a bank’s manager should continue to an application for considering a mortgage loan. The loan sanctioned by a bank manager depends on a few sensible parameters, viz., CIBIL score, credit risk (CR) rating, occupation, etc. The results are acquired by using the D-RSA. This study aims to propose an innovative extraction approach for preference ordering in banking. This study aims to comprehend the variables’ preferences by establishing an association between banking decisions and tasks. The paper employs the D-RSA as the primary data reduction tool. The major contributors of the research are:

(i)

The dominance-based rough set approach is applied on housing loan data to guide and aid the financial institution for loan sanction. This model focuses on decision making, which is further controlled by various “if … then” decision rules. The bank management defines these decision rules, which consider other relevant and important factors regarding housing loans.

(ii)

Factor analysis is used to consider the dataset and a comparative study is performed to analyze the performance of the factors.

The rest of the article is divided into the following sections. A brief summary of the ideas in rough set theory based on dominance is covered in Section 2. In Section 3, we have discussed the basic concept of the D-RSA. Section 4 presents how the data set is utilized and how the methodology is used in the test for different techniques. The related results are also explained in this section. Some of the issues related to the study are discussed in Section 5. Section 6 concludes the article.

2. Previous Works

In the last couple of decades, various studies have been employed in the modeling of a banking data set. Analysis and managing the system of financial banking, especially loan ratings, have been an active research area over the past three decades. The D-RSA is one of the most important soft computing techniques that has various applications in banking loan systems. The D-RSA has been widely applied in various domains, including data mining, machine learning, pattern recognition, and decision support systems (Chakhar and Saad 2012). It provides a flexible and robust framework for handling incomplete and uncertain data, extracting knowledge from complex datasets, and aiding in decision-making processes. The study of banking information systems has attracted the attention of authors. The financial banking loan system has made significant use of statistics and econometrics. In earlier research, the decision-making process of the banking information system was frequently carried out using multivariate statistical approaches such as correlation analysis, discriminant analysis, cumulative probability distribution approach, and logistic regression analysis. For instance, to predict creditworthiness in retail banking, the authors of (Abdou et al. 2016) used logistic regression, classification and regression tree, and correlation neural network. Chen (2012) uses a rough set approach based on cumulative probability distribution (CPD) to examine credit ratings for Asian banks. McCollum and Milcheva (2023) applied the cap rate and baseline models to simulate housing loan data. In (Baziki et al. 2022), the authors used a Log-t convergence test and Quantile regression to calculate the loan pricing of data related to the Turkish commercial banking sector.

Recently, economic and financial data analysts are utilizing soft computing methods for their data analysis. Artificial Immune Systems and Artificial Neural Networks were utilized for developing a risk-associated early warning system for individuals’ home loan credit (Abdou et al. 2016). The fuzzy method was utilized for evaluating the performance of public sector banks in India for the years from 2009 to 2011 (Puri and Yadav 2014). Similar soft computing methods such as evolutionary algorithms and fuzzy sets have reportedly been utilized for examining and evaluating banking data (Sreekumar et al. 2015). DEA (Date Envelope Analysis) was utilized for evaluating the relative efficiency of consistent decision making for the data of State Bank of Patiala in India (Puri and Yadav 2013).

3. Dominance Rough Set Approach

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, and the experimental conclusions that can be drawn. The Dominance-Based Rough Set approach is an alteration of the fundamental rough set theory that was introduced by Pawlak (1982) The classical approach provides a mathematical structure for evaluating and understanding the possibilities of uncertainty and lack of precision that can arise with decision-making problems. Greco et al. (2000) introduced a method to handle multifaceted data sets and furnish the precision of the decision rules. The DRSA deals with the dominant behavior/relation between the entities in the given dataset. Dominance is a binary relation that defines the superiority or inferiority of one object over another with respect to a set of attributes. In the DRSA, an object is said to dominate another object if it is better in all attributes or at least in one attribute and not worse in any other attributes. All the basic details of the D-RSA approach are explained in the following (Greco et al. 1998, 2001).

3.1. Information System

The information pertaining to the objects is frequently organized as an information table with columns referencing the various criteria or attributes taken into consideration and rows referencing specific actions (Pawlak 1982).

Example 1.

Table 1. Information system of cinema hall.

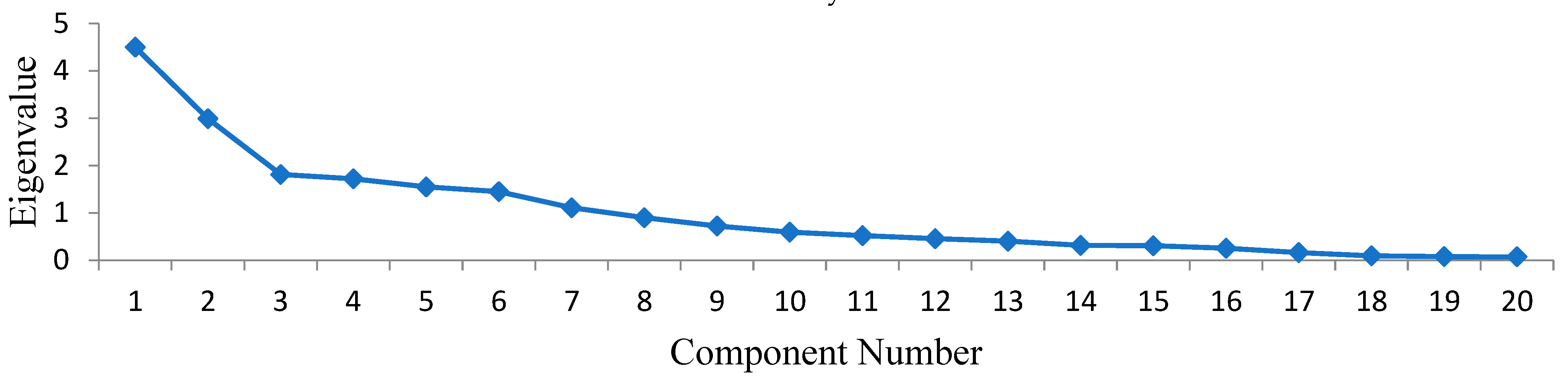
Audience	$\mathbf{Box} \mathbf{Office} \left({\mathit{\beta }}_1\right)$	$\mathbf{Audis} \left({\mathit{\beta }}_2\right)$	$\mathbf{Service} \left({\mathit{\beta }}_3\right)$	$\mathbf{Overall} \mathbf{Experience} \left({\mathit{\beta }}_4\right)$
Z1 Z2 Z3 Z4 Z5 Z6 Z7	Excellent Good Excellent Good Excellent Average Excellent	Medium High Medium High Low High High	Medium Excellent Good Excellent Medium Good Good	Good Average Good Excellent Good Average Excellent

consider an example of an information table of seven objects (audience) and four different attributes related to the cinema hall, in which three attributes are condition attributes $\left(C\right)$ and one decision attribute $\left(D\right).$

▪

Box office—${\beta }_1$;

▪

Audis—${\beta }_2$;

▪

Service—${\beta }_3$;

▪

Overall experience—${\beta }_4$.

In this example $U=\{Z_1,Z_2,Z_3,Z_4,Z_5,Z_6,Z_7\},C=\{{\beta }_1,{\beta }_2,{\beta }_3\}$ and $D=\left\{{\beta }_4\right\}.$

3.2. RST with Dominance Relation

For any pair of objects x and y, the dominance relation ${\nabla }_P$ allied with P is stated as follows: $x{\nabla }_{P}y⟺f\left(x,q\right)\succcurlyeq f\left(y,q\right),\forall q\in P.$ The letter “$\succcurlyeq$” for the criteria should be replaced with “$\preccurlyeq$” according to the diminishing preference. Every object $x\in U$ has a pair of sets associated with it. There are two types of P-dominating sets: (i) P-dominating set ${\nabla }_P^{+}\left(x\right)=\{y\in U:y{\nabla }_{P}x$} and (ii) set P-dominated set ${\nabla }_P^{-}\left(x\right)=\{y\in U:x{\nabla }_{P}y$} with x-dominating objects. The approximation decision classes are familiar to this pair of sets.

Example 2.

From the information in Table 1, condition attributes are randomly expressed and the attributes’ values are based on a preference-order scale. In this instance, object $Z_2$ dominates objects $Z_4$ and $Z_6$, $since f\left(Z_2,{\beta }_i\right)\preccurlyeq f\left(Z_h,{\beta }_i\right),h=4,6;i=1,2,3$, whereas there is not any dominance relationship between $Z_2$, $Z_1$, $Z_3$, $Z_5$, and $Z_7.$ The P-dominating and P-dominated sets related with $U$ were outlined in

Table 2. P-dominating and P-dominated sets.

Audience	P-Dominating Set	P-Dominated Set
Z1 Z2 Z3 Z4 Z5 Z6 Z7	${\nabla }_P^{+}\left(Z_1\right)=\{Z_1,Z_3{,Z}_7\}$  ${\nabla }_P^{+}\left(Z_2\right)=\{Z_2,Z_4\}$  ${\nabla }_P^{+}\left(Z_3\right)=\left\{Z_3,Z_7\right\}$  ${\nabla }_P^{+}\left(Z_4\right)=\{Z_2,Z_4\}$  ${\nabla }_P^{+}\left(Z_5\right)=\left\{Z_1,Z_3,Z_5,Z_7\right\}$  ${\nabla }_P^{+}\left(Z_6\right)=\left\{Z_2,Z_4,Z_6,Z_7\right\}$  ${\nabla }_P^{+}\left(Z_7\right)=\left\{Z_7\right\}$	${\nabla }_P^{-}\left(Z_1\right)=\{Z_1,Z_5\}$  ${\nabla }_P^{-}\left(Z_2\right)=\left\{Z_2,Z_4,Z_6\right\}$  ${\nabla }_P^{-}\left(Z_3\right)=\{Z_1,Z_3,Z_5\}$  ${\nabla }_P^{-}\left(Z_4\right)=\left\{Z_2,Z_4,Z_6\right\}$  ${\nabla }_P^{-}\left(Z_5\right)=\left\{Z_5\right\}$  ${\nabla }_P^{-}\left(Z_6\right)=\left\{Z_6\right\}$  ${\nabla }_P^{-}\left(Z_7\right)=\left\{{Z_1,Z_3,Z}_5,Z_6,Z_7\right\}$

.

In this example, however, ${\beta }_1,{\beta }_2,{\beta }_3$ are criteria and the classes are based on dominance relation. We have that:

▪

Concerning ${\beta }_1$, “excellent” is preferable than “good” and “good” is preferable than “average”;

▪

Concerning ${\beta }_2$, “high” is preferable than “medium” and “medium” is preferable than “low”;

▪

Concerning ${\beta }_3$, “excellent” is preferable than “good” and “good” is preferable than “medium”;

▪

Concerning ${\beta }_4$, “excellent” is preferable than “good” and “good” is preferable than “average”.

3.3. Rough Approximated Set through the Dominance Relation

The approximated sets are known as upward union and downward union of classes relative to dominated or dominating class, respectively, as

${Cl}_t^{\ge }=\bigcup _{s\ge t}{Cl}_s,{Cl}_t^{\le }=\bigcup _{s\le t}{Cl}_s,$ t = 1, …, n.

The declaration $x\in {Cl}_t^{\ge }$ means “x belongs at least to class ${Cl}_t$”, while $x\in {Cl}_t^{\le }$ means “x belongs at most to class ${Cl}_t$”.

Now, we can define P-lower and P-upper ${Cl}_t^{\ge }$ approximation, $t\in \{1,\dots ,n\}$, concerning $P\subseteq C$, respectively, representing $\underset{\_}{P}\left({Cl}_t^{\ge }\right)$ and $\overline{P}\left({Cl}_t^{\ge }\right)$, are described thus:

$\underset{\_}{P}\left({Cl}_t^{\ge }\right)=\{x\in U:{\nabla }_P^{+}(x)\subseteq {Cl}_t^{\ge }\}$;

$\overline{P}\left({Cl}_t^{\ge }\right)=\bigcup _{x\in {Cl}_t^{\ge }}{\nabla }_P^{+}\left(x\right)=\{x\in U:{\nabla }_P^{-}(x)\cap {Cl}_t^{\ge }\ne \varnothing \}$.

In a similar way, $\underset{\_}{P}\left({Cl}_t^{\le }\right)$ and $\overline{P}\left({Cl}_t^{\le }\right)$, are described as:

$\underset{\_}{P}\left({Cl}_t^{\le }\right)=\{x\in U:{\nabla }_P^{-}(x)\subseteq {Cl}_t^{\le }\}$;

$\overline{P}\left({Cl}_t^{\le }\right)=\bigcup _{x\in {Cl}_t^{\le }}{\nabla }_P^{-}\left(x\right)=\{x\in U:{\nabla }_P^{+}(x)\cap {Cl}_t^{\le }\ne \varnothing \}$.

Example 3.

From Table 1, in which $U=\left\{Z_1,Z_2,Z_3,Z_4,Z_5,Z_6,Z_7\right\}$ and all condition attributes $C=\{{\beta }_1,{\beta }_2,{\beta }_3\}$. The decision attributes domain $\left(D\right)$ has attributes values such as average, good, and excellent, for which U are categorized into three different dominance classes: ${Cl}_a=\left\{average\right\}$, ${Cl}_g=$ {good}, and ${Cl}_e=$ {excellent}. Therefore, the category of the decision class must be approximated as:

▪

${Cl}_a^{\le }$, i.e., overall evaluation of (at most) average cinema hall;

▪

${Cl}_g^{\le }$, i.e., overall evaluation of at most good cinema hall;

▪

${Cl}_g^{\ge }$, i.e., overall evaluation of at least good cinema hall;

▪

${Cl}_e^{\ge }$, i.e., overall evaluation of (at least) excellent cinema hall.

From Table 1, we compute the lower and upper approximation of these classes, i.e., evaluate $\underset{\_}{P}\left({Cl}_g^{\ge }\right)$. By using definition, we have $\underset{\_}{P}\left({Cl}_g^{\ge }\right)=\{Z\in U:{\nabla }_P^{+}(Z)\subseteq {Cl}_g^{\ge }$}. From Table 1, we obtain ${Cl}_g^{\ge }$ = {$Z_1,Z_3,Z_4,Z_5,Z_7$}. Applying the P-dominating sets stated in Table 2, $\underset{\_}{P}\left({Cl}_g^{\ge }\right)=\{Z_1,Z_3,Z_5,Z_7$}, since ${\nabla }_P^{+}\left(Z_J\right)\subseteq {Cl}_g^{\ge }$, J = 1, 3, 5, 7. Analogously, we can obtain other lower and upper approximation classes in

Table 3. Approximation set.

Lower Approximations	Upper Approximations
$\underset{\_}{P}\left({Cl}_a^{\le }\right)$$=\left\{Z_6\right\}$ $\underset{\_}{P}\left({Cl}_g^{\le }\right)$$=\{Z_1,Z_3,Z_5,Z_6$} $\underset{\_}{P}\left({Cl}_g^{\ge }\right)$$=\{Z_1,Z_3,Z_5,Z_7$} $\underset{\_}{P}\left({Cl}_e^{\ge }\right)$$=\{Z_7$}	$\overline{P}\left({Cl}_a^{\le }\right)$  $=\{Z_2,Z_4,Z_6\}$  $\overline{P}\left({Cl}_g^{\le }\right)=\{Z_1,Z_2,Z_3,Z_4,Z_5,Z_6\}$  $\overline{P}\left({Cl}_g^{\ge }\right)=\{Z_1,Z_2,Z_3,Z_4,Z_5,Z_7\}$  $\overline{P}\left({Cl}_e^{\ge }\right)=\{Z_2,Z_4,Z_7\}$

.

3.4. Accuracy of Approximation and Quality of Classification

The accuracy of the approximation of ${Cl}_t^{\ge }$ and ${Cl}_t^{\le }$ are described as follows:

$${\alpha }_P\left({Cl}_t^{\ge }\right)=\frac{card\left(\underset{\_}{P}\left({Cl}_t^{\ge }\right)\right)}{card\left(\overline{P}\left({Cl}_t^{\ge }\right)\right)},{\alpha }_P\left({Cl}_t^{\le }\right)=\frac{card\left(\underset{\_}{P}\left({Cl}_t^{\le }\right)\right)}{card\left(\overline{P}\left({Cl}_t^{\le }\right)\right)}$$

(1)

$$\mathrm{The} \mathrm{coefficient} {\gamma }_P\left(Cl\right)=\frac{card(U-((\bigcup _{t\in T}B{n}_P\left({Cl}_t^{\le }\right))\cup (\bigcup _{t\in T}B{n}_P\left({Cl}_t^{\ge }\right)\left)\right))}{card\left(U\right)}$$

(2)

is known as quality of approximation.

Example 4.

From the data in Table 1, applying Equations (1) and (2), the accuracy of approximation is 0.333 for decision class ($at most$) “average” and decision class ($at least$) “excellent” with an accuracy of 0.667 stated in

Table 4. Accuracy of approximation and quality of classification (Greco et al. 2002).

	At Most Average	At Most Good	At Least Good	At Least Excellent
Accuracy of approximation	0.333	0.667	0.667	0.333
Quality of classification	0.714

. While the quality of the classification is equal to 0.714. In this example, it contains only one reduction set, i.e., {Box-office, Audis} and it is also called the core.

3.5. Decision Rules

The D-RSA has been utilized for decision rule induction from data. The positive region derived from dominance relations serves as the basis for generating certain and possible decision rules, aiding in classification and prediction tasks. Different algorithms and techniques have been developed to extract decision rules from the D-RSA models. The D-RSA introduces the notion of a decision rule, which is a statement that relates a set of conditions (attributes) to a decision. Decision rules are expressed in the form of “if …, then …” decision rules. Decision rules are derived from the positive region of the dataset and are designed to be certain or possible. The algorithms for induction related to rules were acquired from (Dubois and Prade 1990; Greco et al. 2002).

Three different strategies can be used to evaluate all decision-making rules:

• $D_{\ge }$—Principles for making decisions that take the following form:
  If $f(x,q_1)\ge r_{q1}$ and $f(x,q_2)\ge r_{q2}$ and … $f(x,q_p)\ge r_{qp}$, then $x\in {Cl}_t^{\ge }$;
• $D_{\le }$—Principles for making decisions that take the following form:
  If $f(x,q_1)\le r_{q1}$ and $f(x,q_2)\le r_{q2}$ and … $f(x,q_p)\le r_{qp}$, then $\in {Cl}_t^{\le }$;
• $D_{\ge \le }$—Principles for making decisions that take the following form:
  If $f(x,q_1)\ge r_{q1}$ and $f(x,q_2)\ge r_{q2}$ and … $f(x,q_k)\ge r_{qk}$, and $f\left(x,q_{k+1}\right)\le r_{qk+1}$
  and … $f(x,q_p)\le r_{qp}$, then $x\in {Cl}_t\cup {Cl}_{t+1}\cup \dots {\cup Cl}_s$,
  where $P=\{q_1,q_2,\dots ,q_p\}\subseteq C$,($r_{q1},r_{q2},\dots r_{qp}$) $\in V_{q1}\times V_{q2}\times \dots \times V_{qp}$,
  and $t\in \{1,\dots ,n\}$.

3.6. Exploratory Data Analysis Approaches

The exploratory approach includes two methods: the principal component and factor analysis. The principal component constitutes an interpretation of the elementary data structures and a few uncorrelated variables. In order to identify the components and variables, extraction of the principal components is necessary. The aim of the principal component is to construct the set of variables that determine their corresponding variance–covariance structure using linear combinations of the variables. Factor analysis is used in the present study to epitomize the data covariance structure with a significantly smaller data dimension. However, determination of the underlying “factors” via factor analysis might illustrate the dimensions associated with large data variability.

4. Case Study

This case study’s primary objective is to separate the decision rules that show the banking features and categorize the various banking characteristics. An experimental analysis is used in this study to assist the banking service providers in expressing the effectiveness of the dominance-based rough set theory. We have gathered information about mortgage loans that customers have taken out from financial institutions and used it in our case study. The management will benefit from this study’s analysis of the home loan application. A good strategy for multi-attribute decision-making problems is the D-RSA. Banks must receive crucial information from the analysis in order for them to expand into new mortgage strategies and achieve their mortgage target. All the required steps of this model are interpreted in Figure 1.

4.1. Problem Discussion and Information Collection

This research was conducted on a financial institution of India and the data are related to mortgage loan applications. Financial establishments such as banks earn their major profit from housing loans. Hence, increasing numbers of housing loan applications is a prerequisite. The management system of financial establishments’ major focus is housing loans to extract more profit. In this study, attributes related to mortgage loans include (i) “loan request for”, “guarantor mean”, “title of Property”, “corporation permission for construction”, “security”, “loan required area”, “own house”, “loan required according project”, and “net worth level” (based on reserve bank of India guideline); (ii) “credit risk (CR) rating” (according to Moody’s Investor’s Service (2022)); (iii) “CIBIL Score” (source from credit information bureau India); (iv) “Age”, “occupation”, and “education” (based on Abdou et al. (2016)); (v) “gross monthly income”, “existing credit facility”, and “repayment period” (based on financial institution of India); and (vi) “permissible deductions” and “margin required” had been recommended based on a domain expert.

Table 5. List of attributes for mortgage selection study.

Mortgage Attributes	Interpretation	Literature, Another Source
(M1) Loan request for	Function for which mortgage is required	RBI guidelines
(M2) Loan required area	The place where borrower build a house (city/village)	RBI guidelines
(M3) Age	The age of the borrower at the time of lending	Financial institution
(M4) Occupation	Borrower’s job at the time of mortgage application	Financial institution
(M5) Education	Borrower’s highest academic instruction	Financial institution
(M6) Own house	Present living condition of the borrower (living with relative or rent)	RBI guidelines
(M7) Net worth level	Total wealth position of the borrower	RBI guidelines
(M8) Gross Monthly	Total earnings of the borrower in a month	Financial institution
Income (in thousands)
(M9) Permissible deductions (%)	Total deductions of borrowers in a month	Domain expert
(M10) Margin required (%)	Margin to be carried by using the borrower (margin based on basic project cost)	Domain expert
(M11) Repayment period	The initial period of the mortgage nationalized banks	Financial institution
(in year)
(M12) Loan required according project	Quantum of mortgage loan	RBI guidelines
(in Lakh)
(M13) Existing credit facility	Existing credit facility is a secured mortgage that takes precedence over unsecured earlier loans furnished through a lender other sources	Financial institution
(M14) Guarantor mean	Wealth position of the guarantor for borrower support	RBI guidelines
(M15) Title of Property	No objection certificate from the builder or developer (clearances from the builder)	RBI guidelines
(M16) Corporation permission	Required clearances from the government sovereignty	RBI guidelines
for construction
(M17) Security	Immovable property of borrowers as a security	RBI guidelines
(M18) CIBIL score	CIBIL Score is a credit history of the borrower	Credit information bureau India
(M19) Credit risk rating	A credit score rating is estimation of the credit risk (CR) of a potential mortgagor foreseeing their capability to pay mortgage returns	Moody’s investor’s service
Decision
(D) Ranking for loan approval	Evaluation of the borrower detail for mortgage	Financial institution

indicates a list of the attributes used to assess mortgage approval and related concept, example in the literature, or another source.

Data preprocessing was conducted to enhance the fine of the data set. In the dataset, a few attributes needed to be converted into a suitable format to aid significant analysis. For example, for attribute M18, the “CIBIL Score” was categorized into three classes according to credit information bureau India (CIBI) (https://www.creditninja.com). If the CIBIL Score of the borrower was less than 500, it was graded as “medium”; if CIBIL Score was between 500 and 750, the CIBIL Score was grouped as “high”; and if the CIBIL Score was greater than 750, it was graded as an “excellent” CIBIL Score. The attribute M19, “credit risk rating”, was classified into five categories. If the rating of the credit risk is very high, it was graded as “one”; if rating of the credit is high, it was categorized as “two”; if the credit risk rating is moderate, the rating of the credit risk was assigned as “three”; if the credit risk rating is low, it was allocated as “four”; and if rating of the credit risk is very low, the credit risk is assigned as “five”. After taking the advice of the manager, the decision attributes were divided into three classes according to the borrower’s situation.

Table 6. Description of attributes associated with borrowers’ applications.

Attributes	Domain Value	Value Set	Preference
Condition attribute (M1) Loan request for (M2) Loan required area (M3) Age (M4) Occupation (M5) Education (M6) Own house (M7) Net worth level (M8) Gross Monthly income (in thousand) (M9) Permissible deductions (%) (M10) Margin required (%) (M11) Repayment period (in year) (M12) Loan required according to project (in Lakh) (M13) Existing credit facility (M14) Guarantor mean (M15) Title of Property (M16) Corporation permission for construction (M17) Security (M18) CIBIL Score (M19) CR rating Decision (D) Ranking for loan approval	Construction of house; purchase of old house; purchase of flat Rural; urban Above 60; 50–60; 40–50; 30–40; Below 30 Others, businessman; private sector staff; government employee 10 + 2 and below; graduation; masters and above No; yes Low; medium; high Below 30; 30–50; above 50 65; 60 15; 20 10 and below; 20; 30 and above Below 20; 20–75; above 75 No; yes Low; medium; high Unclear; clear No; yes Plot and construction portion; flat; old house; flat and shop Medium; high; excellent Very high; high; moderate; low; very low Will not sanction; may be sanction; will certainly sanction	{1, 2, 3} {1, 2} {5, 4, 3, 2, 1} {1, 2, 3, 4} {1, 2, 3} {1, 2} {1, 2, 3} {1, 2, 3} {1, 2} {1, 2} {1, 2, 3} {1, 2, 3} {1, 2} {1, 2, 3} {1, 2} {1, 2} {1, 2, 3, 4} {2, 3, 4} {1, 2, 3, 4, 5} {1, 2, 3}	None Gain Gain Gain None Gain Gain Gain Gain Gain None Cost Gain Gain Gain Gain None Gain Gain Gain

shows the all the criteria/attributes for the mortgage data set and their preference.

The data are sourced through the financial institutions for further analysis to enhance the data consistency and quality. This step monotonously requires checking the data distribution, dealing with void values, eliminating inconsistent data, enriching data, and arranging the data to help modification of data into an analyzable structure. Furthermore, the sample size should be in a format that is enriched for further process. Subsequently, the RST analysis can be conducted on this well-furnished data for making decisions. The analytical approach of the data analyst with a domain expert will ensure the quality and usefulness of the extracted rules from the factual data.

4.2. D-RSA Analysis

Based on several studies of a financial institution, and the help of a bank manager, management team, reserve bank of India (RBI) guideline, and another domain expert, 20 essential criteria/attributes of 56 applications for a mortgage loan were selected to construct an information system; 20 attributes were looked into for analysis, 19 of which are referred to as condition criteria and 1 as decision criteria. We used the D-RSA technique for rule creation in the present study. The D-RSA toolkit JMAF (Blaszczynski et al. 2009) was used for constructing the decision rules.

The approximation accuracy for each decision class is provided in

Table 7. Accuracy of approximation for customer data.

	At Most 1	At Most 2	At Least 2	At Least 3
Lower approximation	7	28	45	23
Upper approximation	11	33	49	28
Boundary	4	5	4	5
Accuracy	0.636	0.848	0.918	0.821

. The outcomes suggest good accuracy for the distinct classes. If the quality of classification and accuracy of approximation have greater values, the criteria selected are usually sufficient to approximate the classification. The class “at most 1” refers to the class that is concerned with “loan will not be sanctioned”. The accuracy of the approximation for the decision class “at most 1” is 0.636. The decision class “at most 2” contains the two classes that are “not sanction” and “may be sanction” with an accuracy of approximation of 0.848. Additionally, the decision for class “at least 3” denotes a class that “will certainly sanction” having an accuracy of approximation of 0.821. Lastly, the class for decision value “at least 2” consists of two classes, “will certainly sanction” and “may be sanction”, with an accuracy of approximation of 0.839.

4.3. Rule Generation

The condition to determine support by considering the class allocation of the decision attributes and these conditions are used as the initial assessment approach in this article. The test data set’s customer applications are all examined to determine if they met either the condition criteria or both the condition and decision criteria of the decision rules. In this study, after a discussion with a domain expert from a financial institution, decision rules with their corresponding cover strength of $2$ or more were selected for a qualified certain minimal cover rule. The total qualified minimal cover rules are $18$, as listed in Table 3, including $2$ decision rules corresponding to at most class $1$, $7$ decision rules to at most class 2, $4$ rules belonging to at least decision class 2, and $5$ decision rules of at least class 3. The IF-THEN decision rules can be implemented to obtain the qualified minimal cover decision rules. Here is some examples to explain the $IF–THEN$ rules:

• $IF$ a customer’s gross monthly income is $above 30 Thousand$, $AND$ the CIBIL Score is $high$ or $excellent$, $AND$ the CR rating is rated as $high$ or $less$, $THEN$ the decision will be $at least may sanction$.
• $IF$ the existing credit facility is $yes$, $AND$ the CIBIL Score is $excellent$, and the CR rating is $low$ or $very low$, $THEN$ the decision for loan approval will be $certainly approve$.

We observe from

Table 8. List of the skilled certain decision rules.

Rule No.	Rule Interpretation	Cover Strength
S1	$IF$$\mathrm{existing} \mathrm{credit} \mathrm{facility} \mathrm{is} yes$$, AND$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} excellent$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} low or very low$$, THEN$$\mathrm{mortgage} \mathrm{loan} \mathrm{will} certainly sanction.$	12
S2	$IF$$\mathrm{education} \mathrm{of} \mathrm{customer} \mathrm{is} graduation$$, AND$$\mathrm{corporation} \mathrm{permission} \mathrm{for} \mathrm{construction} \mathrm{is} yes$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} moderate or low or very low$$, THEN$$\mathrm{mortgage} \mathrm{loan} \mathrm{will} \mathrm{be} certainly sanction.$	10
S3	$IF$$\mathrm{customer} \mathrm{working} \mathrm{as} \mathrm{a} government employee$$, AND$$\mathrm{existing} \mathrm{credit} \mathrm{facility} \mathrm{is} yes$$, THEN$$\mathrm{mortgage} \mathrm{loan} \mathrm{will} \mathrm{be}certainly sanction.$	7
S4	$IF$$\mathrm{customer} \mathrm{working} \mathrm{as} \mathrm{a} private$$\mathrm{or} government employee$$, \mathrm{A}ND$$\sec \mathrm{urity} \mathrm{for} \mathrm{a} \mathrm{mortgage} \mathrm{is} \mathrm{an} \mathrm{own} old house$$, THEN$$\mathrm{mortgage} \mathrm{loan} \mathrm{will} \mathrm{be} certainly sanction.$	5
S5	$IF$$\mathrm{mortgage} \mathrm{request} \mathrm{for} purchase of flat$$, AND$$\mathrm{customer} \mathrm{already} \mathrm{have} \mathrm{another} \mathrm{house}, AND$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} excellent$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} \mathrm{rated} \mathrm{as} high or less,$$THEN$$\mathrm{mortgage} \mathrm{loan} \mathrm{will} \mathrm{be} certainly sanction.$	8
S6	$IF$$\mathrm{CR} \mathrm{rating} \mathrm{is} \mathrm{less} \mathrm{than} \mathrm{or} \mathrm{equal} \mathrm{to} medium$$, THEN$$\mathrm{decision} \mathrm{will} \mathrm{be} at least may sanction.$	27
S7	$IF$$\mathrm{CIBIL} \mathrm{score} \mathrm{is}excellent$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} \mathrm{rated} \mathrm{as} high or less$$, THEN$$\mathrm{decision} \mathrm{will} \mathrm{be} \mathrm{at} least may sanction.$	30
S8	$IF$$\mathrm{customer}’\mathrm{s} \mathrm{gross} \mathrm{monthly} \mathrm{income} \mathrm{is} \mathrm{above} 30 Thousand$$, AND$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} high or excellen$$\mathrm{t}, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} \mathrm{rated} \mathrm{as} high or less$$, THEN$$\mathrm{decision} \mathrm{will} \mathrm{be} \mathrm{at} least may sanction.$	36
S9	$IF$$\mathrm{customer}’\mathrm{s} \mathrm{gross} \mathrm{monthly} \mathrm{income} \mathrm{is} \mathrm{above} 30 Thousand$$, AND$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} excellent$$, THEN$$\mathrm{decision} \mathrm{will} \mathrm{be} at least may sanction.$	36
S10	$IF$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} medium$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} high or very high$$, THEN$$\mathrm{loan} will not be a sanction.$	3
S11	$IF$$\mathrm{education} \mathrm{is} graduation$$, AND$$\mathrm{customer}’\mathrm{s} \mathrm{gross} \mathrm{monthly} \mathrm{income} \mathrm{is} \mathrm{below} 30 Thousand$$, THEN$$\mathrm{loan} will not be a sanction.$	2
S12	$IF \mathrm{corporation} \mathrm{permission} \mathrm{for} \mathrm{construction} \mathrm{is} no$$, \mathrm{T}HEN$$\mathrm{loan} \mathrm{will} at most may be a sanction.$	3
S13	$IF$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} medium or high$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} high or very high$$, THEN$$\mathrm{loan} \mathrm{will} at most may be a sanction.$	9
S14	$IF \mathrm{education} \mathrm{is} master and above$$, AND$$\mathrm{CIBIL} \mathrm{score} \mathrm{is} medium or high$$, THEN$$\mathrm{loan} \mathrm{will} \mathrm{be} at most may be a sanction.$	6
S15	$IF \mathrm{mortgage} \mathrm{request} \mathrm{for} \mathrm{purchase} \mathrm{of} flat$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} very high$$, THEN$$\mathrm{loan} \mathrm{will} at most may be a sanction.$	3
S16	$IF$$\mathrm{customer} \mathrm{occupation} \mathrm{is} other$$, AND$$\mathrm{CR} \mathrm{rating} \mathrm{is} high or very high$$, THEN$$\mathrm{loan} \mathrm{will} at most may be a sanction.$	7
S17	$IF$$\mathrm{customer} \mathrm{occupation} \mathrm{is} other$$, AND$$\mathrm{margin} \mathrm{required} \mathrm{is} 15\%$$, THEN$$\mathrm{loan} \mathrm{will} at most may be a sanction.$	5
S18	$IF$$\mathrm{education} \mathrm{is} master and above$$, AND$$\mathrm{net} \mathrm{worth} \mathrm{level} \mathrm{l}ow or medium$$, AND$$\mathrm{repayment} \mathrm{period} \mathrm{is} 20 year$$, THEN$$\mathrm{loan} \mathrm{will} at most may be a sanction$.	5

that, if a customer’s gross monthly income is $above 30 Thousand$, the CIBIL Score of the borrower is $high$ or $excellent$, and the rating of the credit risk is either $high$ or $moderate$ or $low$ or $very low$, then the decision of the financial institution is $at least may sanction$ and its cover strength is $36$ (cf. Rule $8$). This implies that the monthly income, CIBIL Score, and rating of the credit risk majorly influenced the decisions criteria. Rule 1 indicates that the mortgage loan will be certainly sanctioned when borrowers have an existing credit facility and an $excellent$ CIBIL Score with a credit risk either as $low$ or $very low$. From Rule 10, the financial institution will not approve the mortgage loan when the borrower’s CIBIL Score is $medium$ and the credit risk as $high$ or $very high$.

4.4. Variable Extraction

For the statistical analysis, we have used variables to represent both the condition and decision criteria. There are several factors that affect the banking loan system. Hence, we select the variables from $20$ interviewers with different backgrounds; $20$ essential criteria/attributes of $56$ applications for mortgage loan related to banking management have been considered in the process. In the questionnaire, the variables were arranged and then used for further analysis. The principal component and factor analysis are applied on these variables and eight common factors are obtained in terms of the uncorrelated variables. Here, the principal components are equal to the number of the total variables included in the empirical analysis. In the first method, the eigenvalues are calculated to condense the variance in a correlation matrix. The variance for eight common factors, respectively, are $14\%$, $11\%$, $11\%$, $10\%$, $10\%$, $8\%$, $6\%$, and $6\%$. The total variance of eight common factors is $80\%$, which implies that these eight common factors can be used to represent the information system of $20$ attributes. The results of the common factors are reported in

Table 9. Results of factor analysis after varimax rotation.

Attributes				Factors
	Factor1	Factor2	Factor3	Factor4	Factor5	Factor6	Factor7	Factor8	Communality
M1	0.041	0.02	−0.292	0.1	0.66	0.08	−0.096	0.533	0.832
M2	0.462	0.016	−0.732	0.239	0.157	−0.071	−0.107	−0.042	0.85
M3	0.326	0.515	0.284	−0.129	−0.503	0.05	0.36	0.179	0.886
M4	−0.069	−0.053	−0.823	0.023	0.11	0.33	0.02	−0.056	0.81
M5	0.175	−0.299	−0.778	−0.04	0.056	−0.196	0.212	0.019	0.814
M6	−0.052	0.006	0.031	−0.91	0.064	0.057	−0.028	0.094	0.849
M7	0.377	−0.622	−0.19	−0.467	0.139	−0.124	−0.026	0.17	0.848
M8	0.767	−0.22	−0.12	−0.076	−0.091	0.029	−0.086	0.137	0.692
M9	−0.272	−0.122	−0.191	0.04	0.027	0.014	0.843	0.041	0.84
M10	0.703	0.01	−0.145	−0.223	0.17	0.027	0.016	−0.055	0.599
M11	−0.322	−0.068	−0.288	0.505	0.297	0.015	−0.509	0.071	0.798
M12	0.773	−0.343	0.001	0.034	0.206	−0.009	−0.123	−0.119	0.788
M13	0.333	0.212	0.094	−0.714	−0.087	−0.096	0.042	−0.233	0.748
M14	0.19	−0.789	−0.076	0.28	−0.068	0.19	0.084	0.081	0.797
M15	−0.061	0.359	−0.085	0.044	−0.605	0.336	−0.369	0.053	0.76
M16	−0.039	−0.133	0.112	0.012	−0.009	−0.098	0.052	0.868	0.798
M17	0.299	0.014	−0.142	−0.052	0.824	0.282	−0.062	−0.055	0.878
M18	−0.337	−0.057	0.066	0.042	0.108	0.727	0.116	−0.357	0.805
M19	0.231	−0.729	−0.132	0.022	0.153	0.38	0.153	0.118	0.807
D	0.25	−0.28	−0.103	−0.015	0.046	0.813	−0.098	0.087	0.832
Variance	2.8311	2.3566	2.264	2.0421	2.0163	1.7631	1.3879	1.3709	16.032
Var %	14.2	11.8	11.3	10.2	10.1	8.8	6.9	6.9	80.2

. The second method is commonly used to identify the eigenvalues against the factors number in order to determine the principal data structure. A scree plot is depicted in Figure 2, which shows the eigenvalues related to a component or factors in descending order with respect to the number of the component or factors. In principal component analysis, the scree plot graphically interprets which component or factor determines most of the variability in the data.

5. Results and Discussion

In this research, a D-RSA-based application has been proposed to facilitate any financial institution while making decisions whether to sanction loans to customers. The proposed D-RSA model can be applied to applicant information (occupation, gross monthly income, repayment period, existing credit facility, guarantor mean, CR rating, etc.) that can be considered for loan sanction. Based on the outcome of the proposed model, any financial institution can develop a strategy to sanction loans to the customers. While designing the proposed D-RSA-based approach, certain superfluous attributes are removed that have no active role in the quality of classification. In this study, the data set is used to create 20 reductions and 4 core attributes. Table 7 depicts the precision of approximation as high as 0.918 for the loan applications, which suggests that the boundary region has quite few entities of the information system. Excessive high accuracy also implies that the entities of the class have better dependency amid all the condition attributes. The relevance of the condition attributes could be calibrated through the level of existence in the evaluated decision rules. In a managerial decision, the influential factor is identified through the frequency of usage of a condition attribute with minimum but higher cover rules. In total, certain least cover rules are 21, although there are 3 rules with a cover strength of less than 2. This implies that most of the derived data in the study can be segregated by 18 rules. When weighed against the fundamental rough set theory, it generated far too many rules that have quite little coverage; on the contrary, the D-RSA has the potential for obtaining efficient decision rules with mover cover strength. The possible reason might be that the D-RSA considers both attributes (criteria) and their related inconsistencies when too many rules are generated. Considering the proposed D-RSA model, it can be summarized from rules 7 to 9 that the CIBIL Score, gross monthly income, and CR rating are significant criteria with maximum cover strength, as far as the manager decisions on the sanction of loans are concerned.

The approach is applied to the survey data of a large information system of customers from a bank in India and its relative strength was evaluated. Compared with the empirical results of other statistical analysis, our results are significant. In this paper, a novel decision rule approach was employed in the banking market. In the present study, an approach that has new decision rule was applied in the banking market. In comparison to the conventional statistical techniques such as logistic regression and discriminant analysis, rough set theory prevails as it does not require many statistical assumptions that are associated with the distribution of variables. Additionally, the D-RSA efficiently tackles attributes that may or may not possess a preference identity. This approach also records the strong uniformity of the decision variable. Thus, the approach of this paper is to study the banking system with both quantitative and qualitative attributes with and without an order of preference. The pre-existing empirical reports depict that it is suitable and much needed to apply the D-RSA for the mining of data in the Indian Banking Sector

6. Conclusions and Future Research

Based on the Dominance-based rough set theory, this study proposed a multi-criteria decision-making model for financial institution loan disbursement. The decision rules provided by this model are derived from information on housing loans. The most important criteria of an information system that helps the concerned management make decisions are described by the decision rules. This model can then be utilized for potential inputs for financial institution decision making. The model we have presented in this paper, which is based on a rough dominance-based approach, will make it easier for financial institutions to release loans to clients. Due to their greater cover strengths, the information corresponding to the attributes, CIBIL Score, gross monthly income, and CR rating emerge as crucial input parameters while sanctioning customer loans.

The analysis suggests that, by determining whether to approve loans to customers, the D-RSA is a useful approach. It becomes crucial to describe the traits and components of the banking loan system in order to develop better decision-making guidelines. Since there are currently very few studies based on banking analysis, effective data mining tools can be created in the future to support various managerial decisions regarding various aspects of the banking domain. Additionally, by defining causal relationships that are applied to define dynamic systems of attributes, specific or accurate outcomes and characteristic values can be obtained using logistic regression, and more variable sets and larger sample sizes will be applied to authorize the model. This could be our future research focus.