Estimation of Optimal Hedge Ratio: A Wild Bootstrap Approach
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Background
3.2. Hedging with Wild Bootstrap Percentiles
- Step 1: Estimate the optimal hedge ratio given in (5) for the regression (4).
- Step 2: Draw a bootstrap sample () based on for each ith observation from 1 to T:where is resampled data of the spot returns, is a independent random variable with zero mean and unit variance, and is the transformed residual from the regression (4) robust to heteroskedasticity2.
- Step 3: Compute the new estimate of the hedge ratio with the bootstrap sample () (for i = 1, …, T) following the regression (4).
- Step 4: Repeat Steps 2 and 3 many times, say B, to form the bootstrap distribution of for .
- Step 5: The (1 − α)100% wild bootstrapping confidence interval is constructed with the lower limit and upper limits representing the 0.5α percentile and (1 − 0.5α) percentile, respectively, of the bootstrap distribution . The percentiles within the confidence interval can be estimated in a similar way. The number of bootstrap iterations B is set at 1000.
3.3. Hedging Based on the DCC-GARCH
3.4. Computational Details and Evaluation of Hedging Strategies
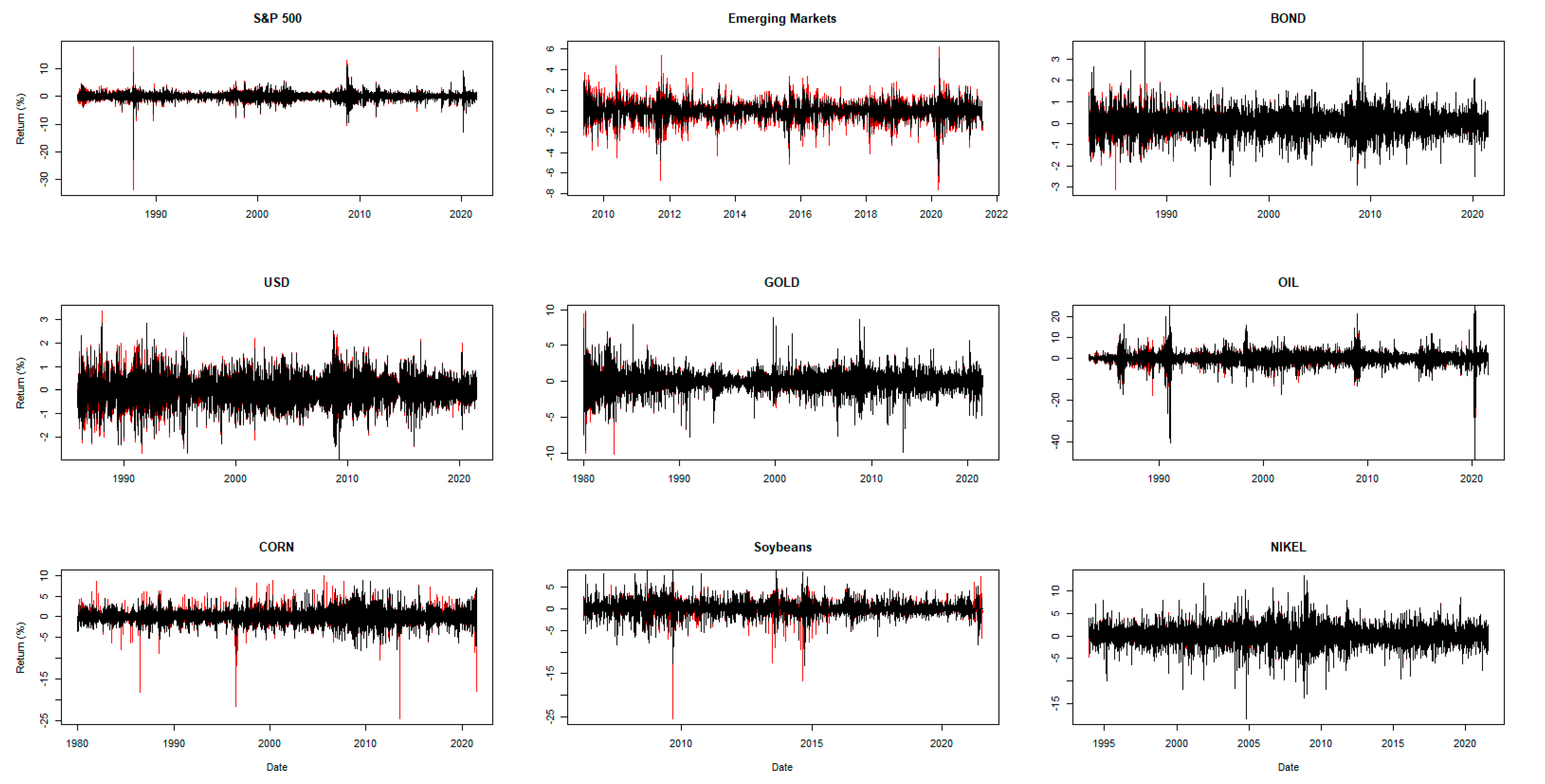
4. Data Details
5. Empirical Results
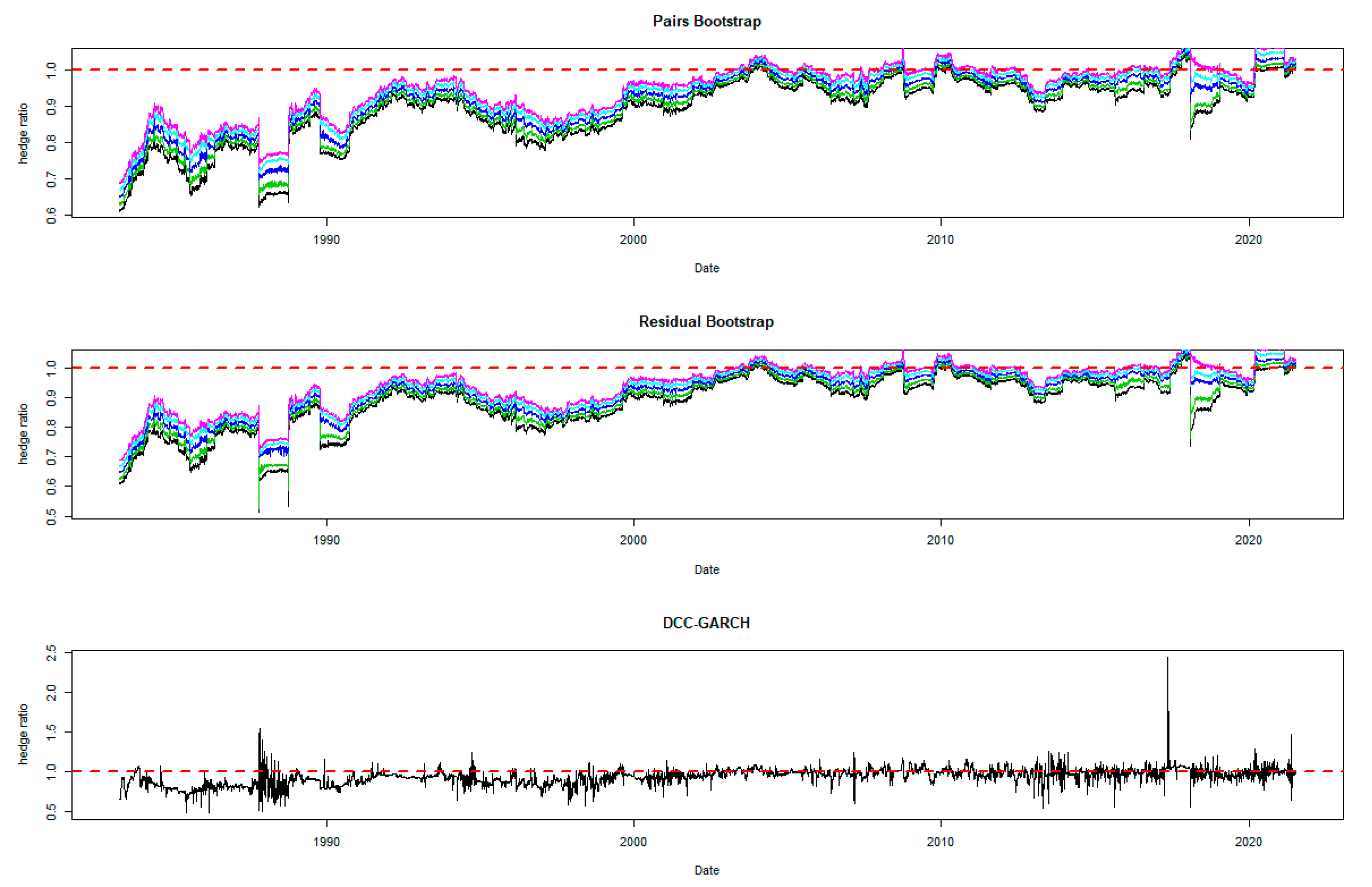
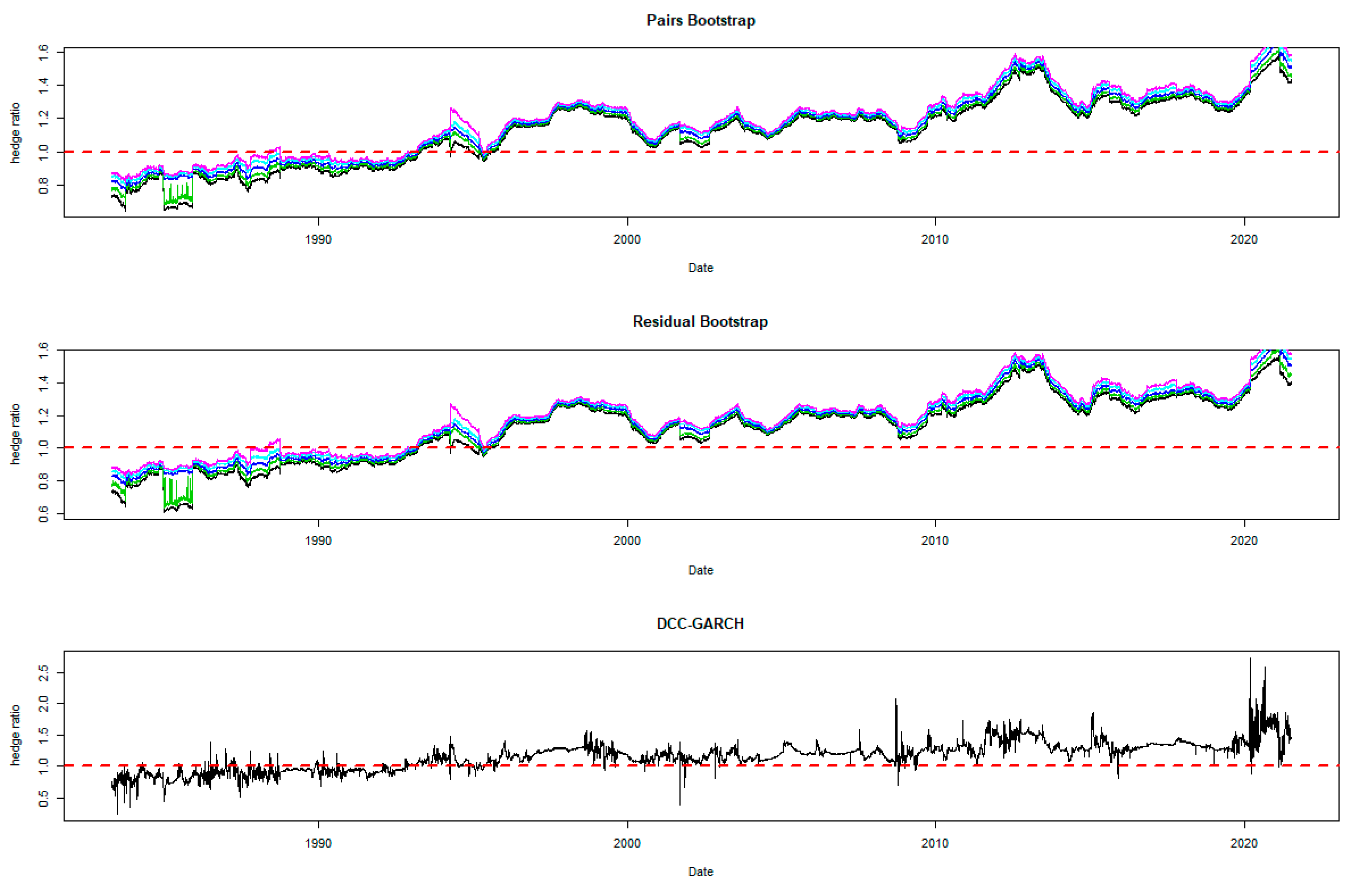
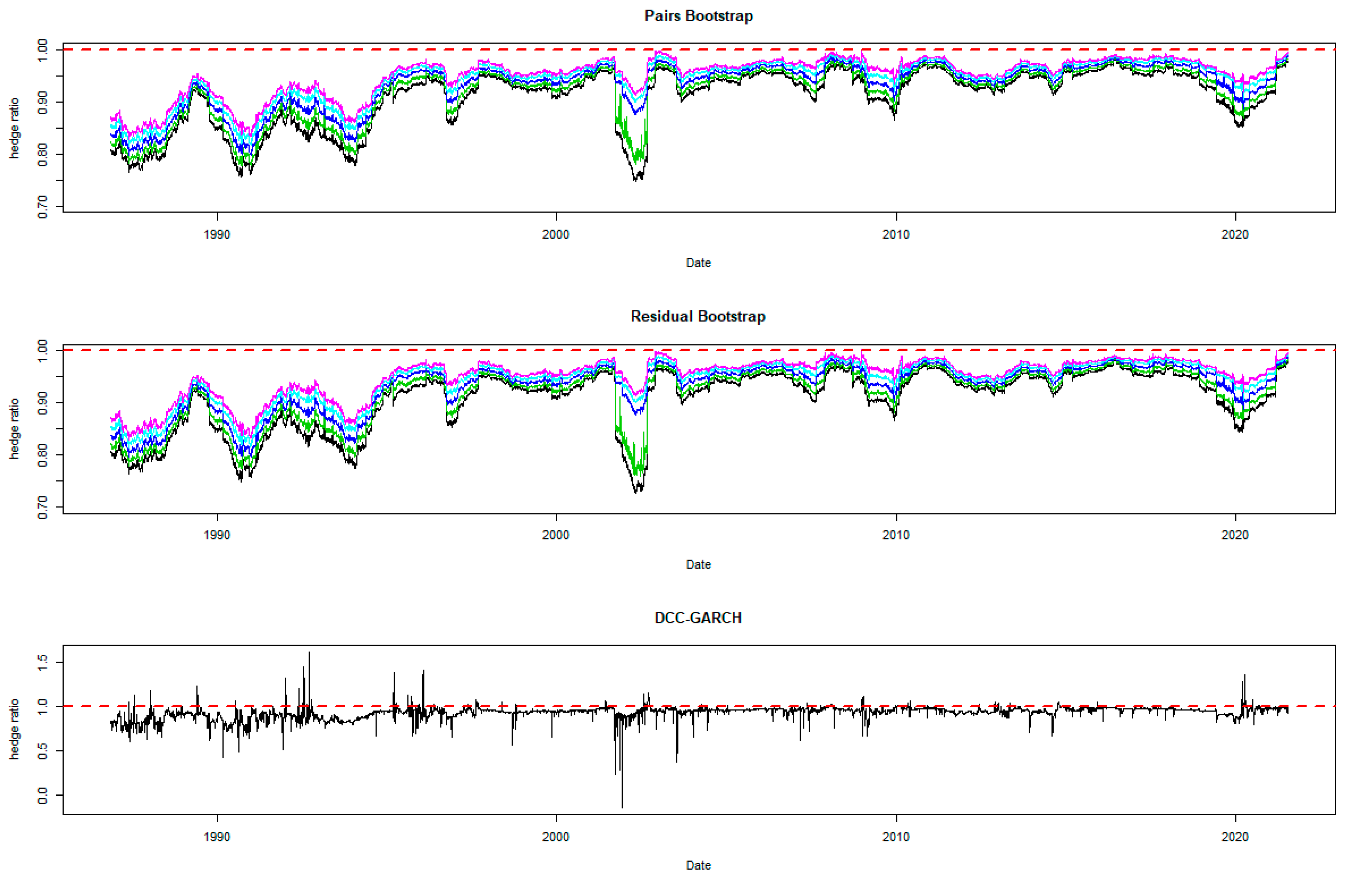
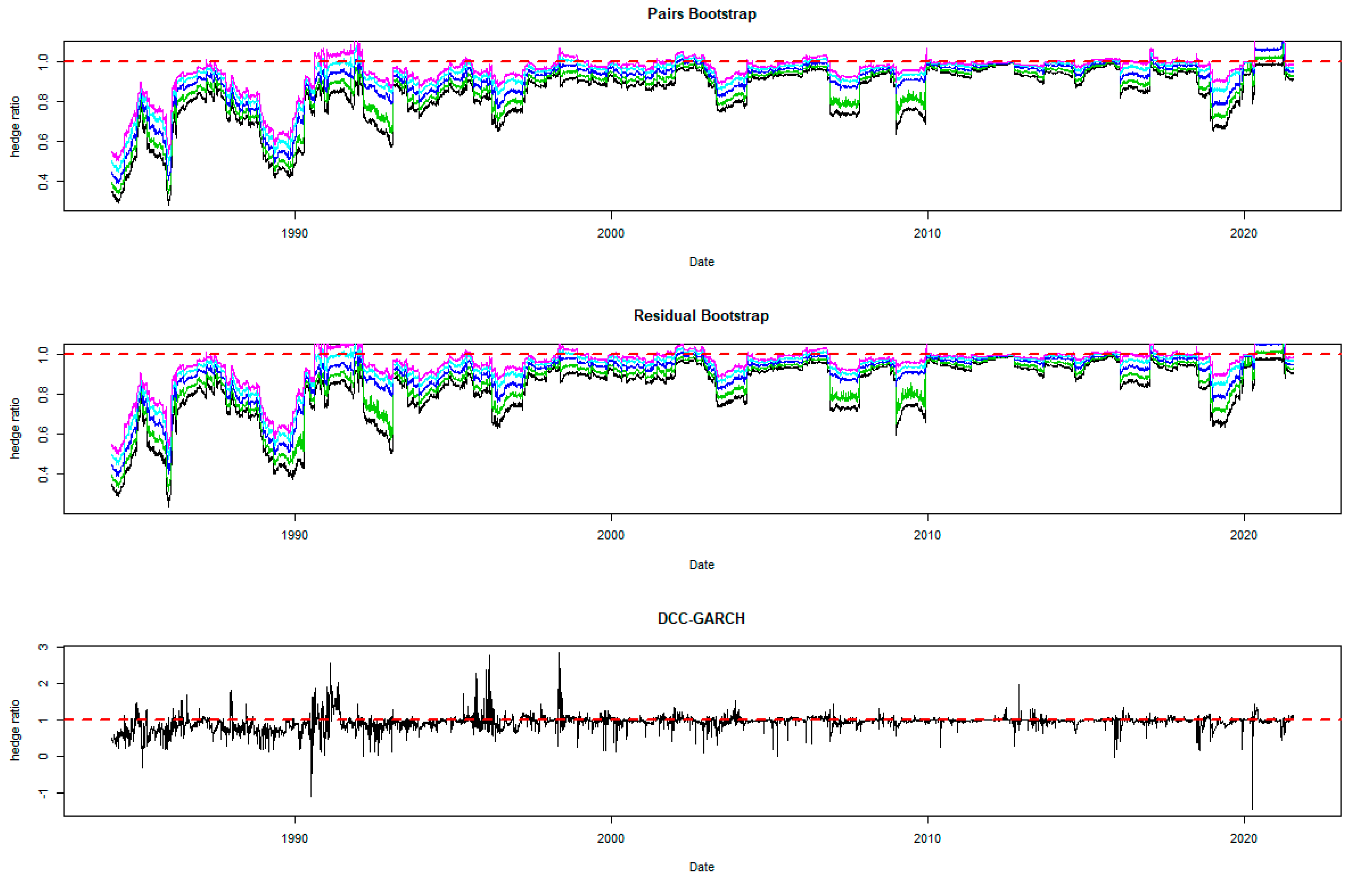
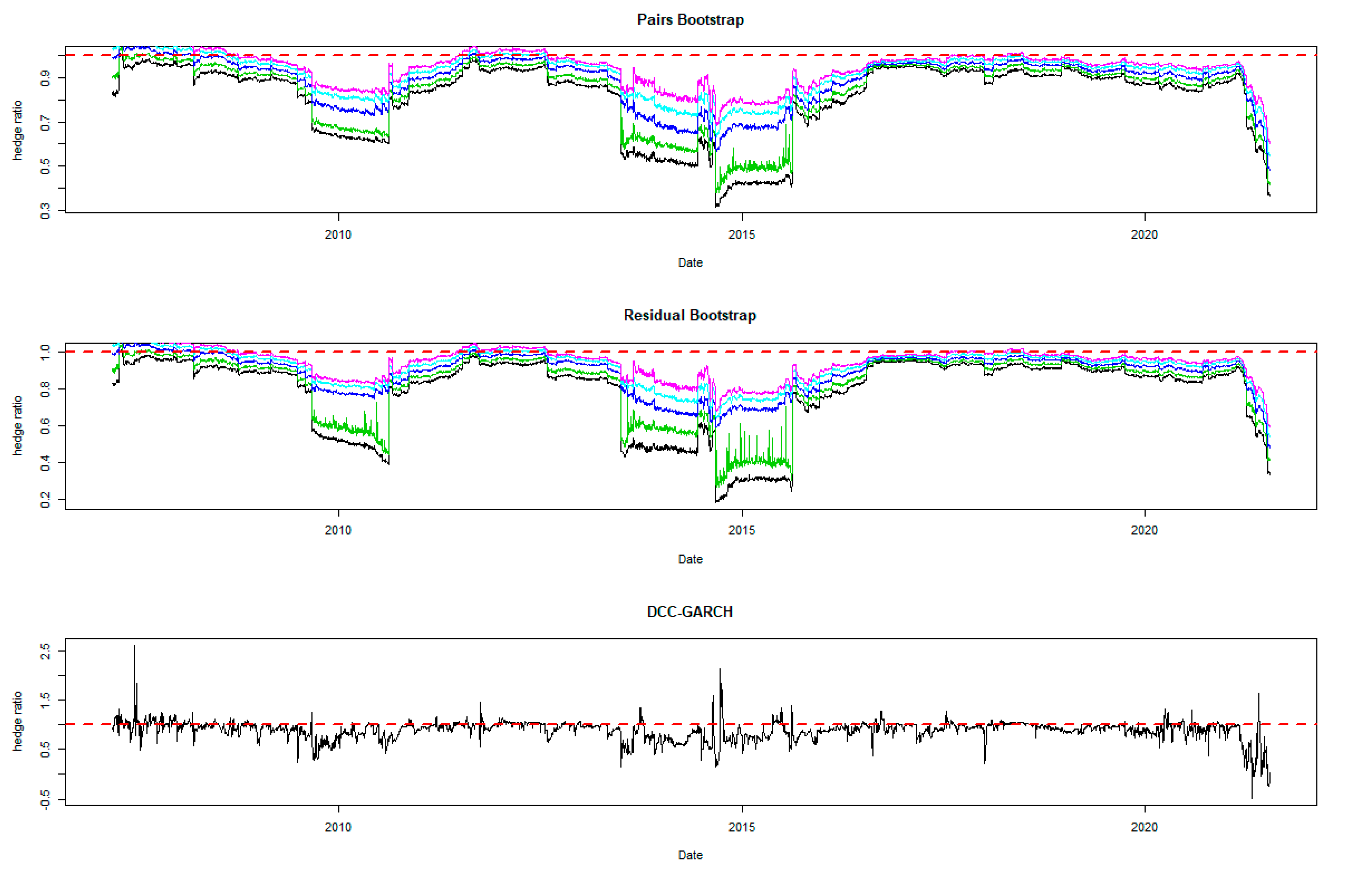
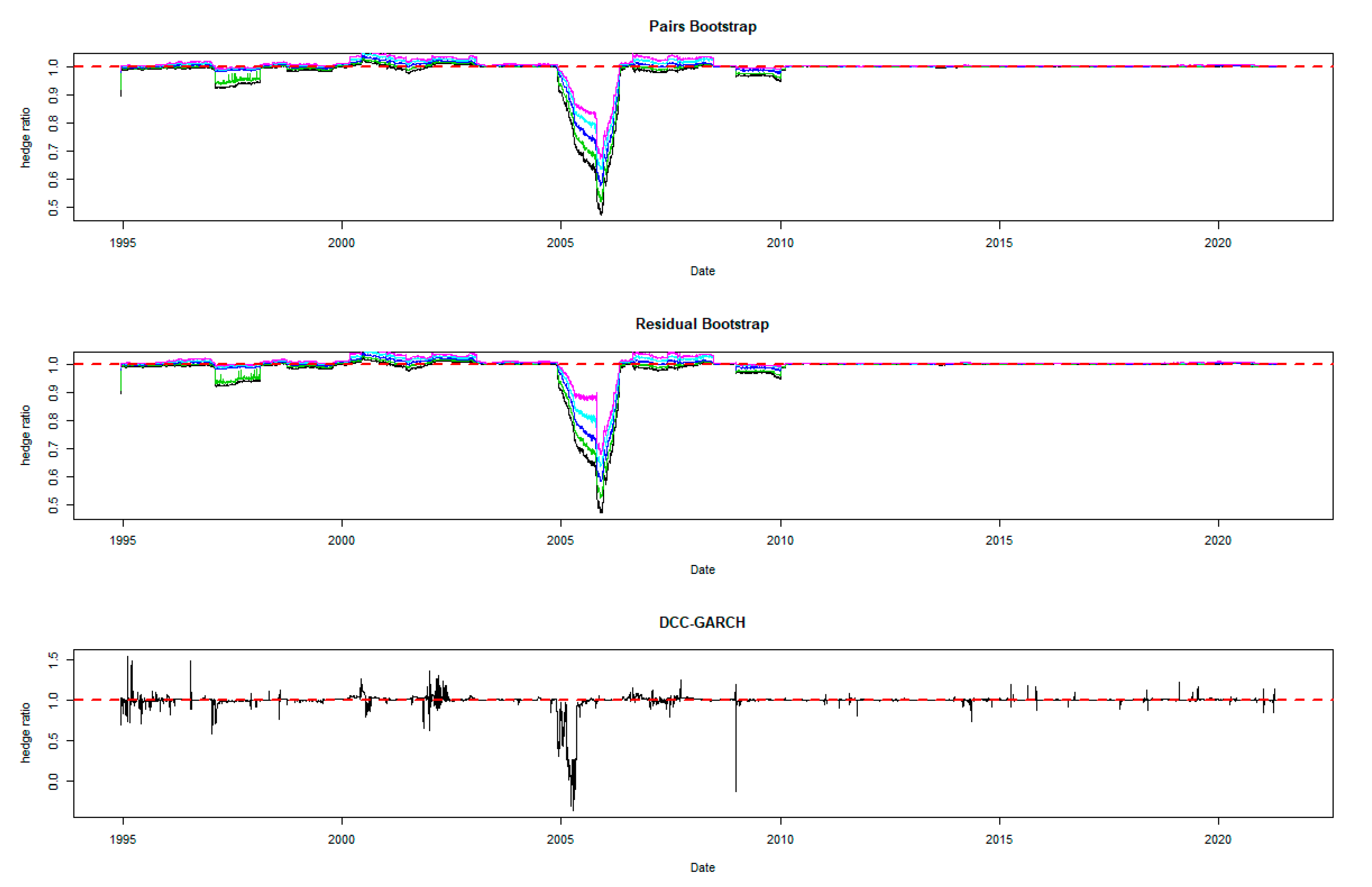
5.1. Optimal Hedge Ratio Estimates
5.2. Comparing the Hedging Effectiveness and the Robustness Checks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The naïve strategy is static with a hedge ratio of 1, taking a hedging position in a futures contract equal to the exact exposure in the spot market. |
| 2 | |
| 3 | The length of the time window is constructed for rebalancing needs of a portfolio for every 12 months when the portfolio manager can revise their hedging position based on the time-varying spot–futures relationship. Choosing the time window length also facilitates the convergence issue of the rolling DCC-GARCH model. |
| 4 | The US dollar index, which has existed since 1973, is a geometrically weighted average of a basket of six currencies against the US dollar, i.e., British pound, Canadian dollar, the Euro, Japanese yen, Swedish krona, and Swiss franc. Since the US dollar is freely floated against all other foreign currencies, the Federal Reserve Bank initiated the measure of the US dollar index to provide an external bilateral trade-weighted average of the US dollar. |
| 5 | The continuous futures indices are a perpetual series of futures prices, volumes, and open interest derived from individual futures contracts. They start at the nearest contract month, which forms the first price values for the continuous series until either the contract reaches its expiry date or until the first business day of the notional contract month, whichever is sooner. At this point, prices from the next trading contract month are taken. No adjustment for price differentials is made. Thomson Reuters DataStream provides the methodology. |
| 6 | Estimation of the MVHRs based on the proposed methods is processed in R. Interested readers can find the R codes by clicking on the linked Online Appendix. |
| 7 | As suggested by an anonymous referee, interested readers and practitioners are encouraged to try different percentiles other than the ones used in this paper to find the most suitable hedging position. It is subject to underlying assets, market conditions, estimation uncertainty, confidence level, and computing resources. |
| 8 | An alternative solution to the consequential effects of the outliers or leverage points is the robust regression technique (Knez and Ready 1997; Martin and Xia 2022). However, our wild bootstrap approach is more informative and effective by estimating a confidence interval of the optimal hedge ratio for various time windows and offering a range of possible alternatives based on the estimated percentiles. |
| 9 | Maximum entropy bootstrap (“meboot”) is a powerful alternative bootstrap method to deal with endogeneity issue in the relationship between non-stationary spot and futures return data (Zanjani et al. 2021). |
References
- Ai, Chunrong, Arjun Chatrath, and Frank Song. 2006. On the comovement of commodity prices. American Journal of Agricultural Economics 88: 574–88. [Google Scholar] [CrossRef]
- Akram, Q. Farooq. 2009. Commodity prices, interest rates and the dollar. Energy Economics 31: 838–51. [Google Scholar] [CrossRef]
- Alizadeh, Amir, and Nikos Nomikos. 2004. A Markov regime switching approach for hedging stock indices. Journal of Futures Markets 24: 649–74. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Ebens Heiko. 2001. The Distribution of Realized Stock Return Volatility. Journal of Financial Economics 61: 43–76. [Google Scholar]
- Barrett, Garry F., and Stephen G. Donald. 2003. Consistent tests for stochastic dominance. Econometrica 71: 71–104. [Google Scholar] [CrossRef]
- Black, Fischer. 1976. Studies of Stock Price Volatility Changes. In Proceedings of the 1976 Meetings of the American Statistical Association, Business and Economic Statistics. Washington, DC: American Statistical Association, pp. 177–81. [Google Scholar]
- Brooks, Chris, Alešs Černý, and Joelle Miffre. 2011. Optimal hedging with higher moments. Journal of Futures Markets 32: 909. [Google Scholar] [CrossRef]
- Büyükşahin, Bahattin, and Michel A. Robe. 2014. Speculators, commodities and cross-market linkages. Journal of International Money and Finance 42: 38–70. [Google Scholar] [CrossRef]
- Caporin, Massimiliano, Juan-Angel Jimenez-Martin, and Lydia Gonzalez-Serrano. 2014. Currency hedging strategies in strategic benchmarks and the global and Euro sovereign financial crises. Journal of International Financial Markets, Institutions & Money 31: 159. [Google Scholar]
- Chang, Chia-Lin, Juan-Ángel Jiménez-Martín, Esfandiar Maasoumi, and Teodosio Pérez-Amaral. 2015. A stochastic dominance approach to financial risk management strategies. Journal of Econometrics 187: 472–85. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, Lydia González-Serrano, and Juan-Angel Jimenez-Martin. 2013. Currency hedging strategies using dynamic multivariate GARCH. Mathematics and Computers in Simulation 94: 164–82. [Google Scholar] [CrossRef]
- Chatfield, Chris. 1993. Calculating interval forecasts. Journal of Business & Economic Statistics 11: 121–35. [Google Scholar]
- Chen, Chao-Chun, and Wen-Jen Tsay. 2011. A Markov regime-switching ARMA approach for hedging stock indices. Journal of Futures Markets 31: 165–91. [Google Scholar] [CrossRef]
- Chen, Rongda, Bo Wei, Chenglu Jin, and Jia Liu. 2021. Returns and volatilities of energy futures markets: Roles of speculative and hedging sentiments. International Review of Financial Analysis 76: 101748. [Google Scholar] [CrossRef]
- Chen, Sheng-Syan, Cheng-few Lee, and Keshab Shrestha. 2003. Futures hedge ratios: A review. Quarterly Review of Economics and Finance 43: 433–65. [Google Scholar] [CrossRef]
- Chen, Yi-Ting, Keng-Yu Ho, and Larry Y. Tzeng. 2014. Riskiness-minimizing spot-futures hedge ratio. Journal of Banking & Finance 40: 154–64. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 10: 407–432. [Google Scholar] [CrossRef]
- Cribari-Neto, Francisco, and Maria da Glória A. Lima. 2009. Heteroskedasticity-consistent interval estimators. Journal of Statistical Computation and Simulation 79: 787–803. [Google Scholar] [CrossRef]
- Cribari-Neto, Francisco, Tatiene C. Souza, and Klaus L. P. Vasconcellos. 2007. Inference Under Heteroskedasticity and Leveraged Data. Communications in Statistics—Theory and Methods 36: 1877–88. [Google Scholar] [CrossRef]
- Davidson, Russell, and Emmanuel Flachaire. 2008. The wild bootstrap, tamed at last. Journal of Econometrics 146: 162–69. [Google Scholar] [CrossRef]
- Ederington, Louis H. 1979. The hedging performance of the new futures markets. Journal of Finance 34: 157–70. [Google Scholar] [CrossRef]
- Efron, Bradley. 1979. Bootstrap Methods: Another Look at the Jackknife. The Annals of Statistics 7: 1–26. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Flachaire, Emmanuel. 2005. Bootstrapping heteroskedastic regression models: Wild bootstrap vs. pairs bootstrap. Computational Statistics & Data Analysis 49: 361–76. [Google Scholar]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Gorton, Gary B., Fumio Hayashi, and K. Geert Rouwenhorst. 2013. The fundamentals of commodity futures returns. Review of Finance 17: 35–105. [Google Scholar] [CrossRef]
- Groen, Jan J., and Paolo A. Pesenti. 2010. Commodity prices, commodity currencies, and global economic developments. In Commodity Prices and Markets. Chicago: University of Chicago Press. [Google Scholar]
- Hsu, Chih-Chiang, Chih-Ping Tseng, and Yaw-Huei Wang. 2008. Dynamic hedging with futures: A copula-based GARCH model. Journal of Futures Markets 28: 1095–116. [Google Scholar] [CrossRef]
- Johansen, Soren. 1991. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 59: 1551–80. [Google Scholar] [CrossRef]
- Kim, Jae H. 2006. Wild bootstrapping variance ratio tests. Economics Letters 92: 38–43. [Google Scholar] [CrossRef]
- Kim, Jae H., and Andrew P. Robinson. 2019. Interval-based hypothesis testing and its applications to economics and finance. Econometrics 7: 21. [Google Scholar] [CrossRef]
- Knez, Peter J., and Mark J. Ready. 1997. On the robustness of size and book-to-market in cross-sectional regressions. The Journal of Finance 52: 1355–82. [Google Scholar]
- Kroner, Kenneth F., and Jahangir Sultan. 1993. Time-Varying Distributions and Dynamic Hedging with Foreign Currency Futures. Journal of Financial and Quantitative Analysis 28: 535–51. [Google Scholar] [CrossRef]
- Ku, Yuan-Hung Hsu, Ho-Chyuan Chen, and Kuang-hua Chen. 2007. On the application of the dynamic conditional correlation model in estimating optimal time-varying hedge ratios. Applied Economics Letters 14: 503–9. [Google Scholar] [CrossRef]
- Lee, Hsiang-Tai. 2009. A copula-based regime-switching GARCH model for optimal futures hedging. Journal of Futures Markets 29: 946–72. [Google Scholar] [CrossRef]
- Lee, Hsiang-Tai. 2010. Regime switching correlation hedging. Journal of Banking & Finance 34: 2728–41. [Google Scholar] [CrossRef]
- Lee, Hsiang-Tai, and Jonathan K. Yoder. 2011. A bivariate Markov regime switching GARCH approach to estimate time varying minimum variance hedge ratios. Applied Economics 39: 1253–65. [Google Scholar] [CrossRef]
- Li, Ming-Yuan Leon. 2010. Dynamic hedge ratio for stock index futures: Application of threshold VECM. Applied Economics 42: 1403–17. [Google Scholar] [CrossRef]
- Lien, Donald. 2009. A note on the hedging effectiveness of GARCH models. International Review of Economics & Finance 18: 110–12. [Google Scholar] [CrossRef]
- Lien, Donald, and Keshab Shrestha. 2008. Hedging effectiveness comparisons: A note. International Review of Economics & Finance 17: 391–96. [Google Scholar] [CrossRef]
- Lien, Donald, Keshab Shrestha, and Jing Wu. 2016. Quantile estimation of optimal hedge ratio. Journal of Futures Markets 36: 194–214. [Google Scholar] [CrossRef]
- Lien, Donald, Yiu Kuen Tse, and Albert K. C. Tsui. 2002. Evaluating the hedging performance of the constant-correlation GARCH model. Applied Financial Economics 12: 791–98. [Google Scholar] [CrossRef]
- Liu, Regina Y. 1988. Bootstrap Procedures under some Non-I.I.D. Models. The Annals of Statistics 16: 1696–708. [Google Scholar] [CrossRef]
- Liu, Wei-han. 2016. A re-examination of maturity effect of energy futures price from the perspective of stochastic volatility. Energy Economic 56: 351–62. [Google Scholar] [CrossRef]
- Long, J. Scott, and Laurieh Ervin. 2000. Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model. The American Statistician 54: 217–24. [Google Scholar] [CrossRef]
- Maharaj, Elizabeth A., Imad Moosa, Jonathan Dark, and Param Silvapulle. 2008. Wavelet estimation of asymmetric hedge ratios: Does econometric sophistication boost hedging effectiveness? International Journal of Business and Economics 7: 213. [Google Scholar]
- Mammen, Enno. 1993. Bootstrap and Wild Bootstrap for High Dimensional Linear Models. The Annals of Statistics 21: 255–85. [Google Scholar] [CrossRef]
- Markopoulou, Chrysi E., Vasiliki D. Skintzi, and Apostolos-Paul N. Refenes. 2016. Realized hedge ratio: Predictability and hedging performance. International Review of Financial Analysis 45: 121–33. [Google Scholar] [CrossRef]
- Martin, R. Douglas, and Daniel Z. Xia. 2022. Efficient bias robust regression for time series factor models. Journal of Asset Management 23: 215–34. [Google Scholar] [CrossRef]
- Moosa, Imad A. 2017. Econometrics as a Con Art: Exposing the Limitations and Abuses of Econometrics. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Nguyen, Phong, and Wei-han Liu. 2017. Time-varying linkage of possible safe haven assets: A cross-market and cross-asset analysis. International Review of Finance 17: 43–76. [Google Scholar] [CrossRef]
- Park, Jin Suk, and Yukun Shi. 2017. Hedging and speculative pressures and the transition of the spot-futures relationship in energy and metal markets. International Review of Financial Analysis 54: 176–91. [Google Scholar] [CrossRef]
- Park, Sung Yong, and Sang Young Jei. 2010. Estimation and hedging effectiveness of time-varying hedge ratio: Flexible bivariate garch approaches. Journal of Futures Markets 30: 71. [Google Scholar] [CrossRef]
- Shrestha, Keshab, Ravichandran Subramaniam, Yessy Peranginangin, and Sheena Sara Suresh Philip. 2018. Quantile hedge ratio for energy markets. Energy Economics 71: 253–72. [Google Scholar] [CrossRef]
- Su, Yi-Kai, and Chun-Chou Wu. 2014. A New Range-Based Regime-Switching Dynamic Conditional Correlation Model for Minimum-Variance Hedging. Journal of Mathematical Finance 4: 207. [Google Scholar] [CrossRef]
- Tauchen, George, Harold Zhang, and Ming Liu. 1996. Volume, Volatility, and Leverage: A Dynamic Analysis. Journal of Econometrics 74: 177–208. [Google Scholar] [CrossRef]
- Waldmann, Elisabeth. 2018. Quantile regression: A short story on how and why. Statistical Modelling 18: 203–18. [Google Scholar] [CrossRef]
- Wang, Yudong, Chongfeng Wu, and Li Yang. 2015. Hedging with futures: Does anything beat the naïve hedging strategy? Management Science 61: 2870–89. [Google Scholar] [CrossRef]
- White, Halbert. 2000. A reality check for data snooping.(Statistical Data Included). Econometrica 68: 1097. [Google Scholar] [CrossRef]
- Wu, Feng, Zhengfei Guan, and Robert J. Myers. 2011. Volatility spillover effects and cross hedging in corn and crude oil futures. The Journal of Futures Markets 31: 1052–75. [Google Scholar] [CrossRef]
- Zanjani, Zeinab, Pedro Macedo, and Isabel Soares. 2021. Investigating Carbon Emissions from Electricity Generation and GDP Nexus Using Maximum Entropy Bootstrap: Evidence from Oil-Producing Countries in the Middle East. Energies 14: 3518. [Google Scholar] [CrossRef]



| S&P 500 | Emerging Markets | BOND | |||||
| SPOT | FUTURES | SPOT | FUTURES | SPOT | FUTURES | ||
| Mean | 0.035 | 0.035 | 0.0256 | 0.029 | 0.0071 | 0.0164 | |
| *** | *** | * | |||||
| Variance | 1.265 | 1.4626 | 0.6799 | 1.1316 | 0.2111 | 0.1601 | |
| *** | *** | *** | *** | *** | *** | ||
| Skewness | −1.1993 | −2.0849 | −0.6037 | −0.4749 | 0.0022 | 0.0439 | |
| Kurtosis | 27.4245 | 72.4538 | 5.2391 | 4.0391 | 3.4813 | 4.0891 | |
| J-B test | 323,194 | 2,246,131 | 3826.4 | 2279 | 5165.5 | 7129.9 | |
| *** | *** | *** | *** | *** | *** | ||
| ARCH test | 1255.3 | 985.37 | 766.1 | 616.63 | 739.07 | 880.7 | |
| *** | *** | *** | *** | *** | *** | ||
| Pearson Correlation | 0.96 *** | 0.94 *** | 0.94 *** | ||||
| USD | GOLD | OIL | |||||
| SPOT | FUTURES | SPOT | FUTURES | SPOT | FUTURES | ||
| Mean | −0.0033 | −0.0034 | 0.0101 | 0.0113 | 0.0081 | 0.0082 | |
| Variance | 0.2585 | 0.2861 | 1.2993 | 1.3455 | 7.2838 | 6.2511 | |
| *** | *** | *** | *** | *** | *** | ||
| Skewness | −0.0366 | −0.0083 | −0.1336 | −0.174 | −2.2866 | −1.2686 | |
| Kurtosis | 2.1446 | 2.0817 | 7.3637 | 8.5646 | 71.7029 | 29.2159 | |
| J-B test | 1784.2 | 1679.3 | 24,521 | 33,182 | 2,149,206 | 358,049 | |
| *** | *** | *** | *** | *** | *** | ||
| ARCH test | 234.01 | 217.65 | 1174.3 | 1289.4 | 1018.5 | 1403.8 | |
| *** | *** | *** | *** | *** | *** | ||
| Pearson Correlation | 0.97 *** | 0.99 *** | 0.87 *** | ||||
| CORN | SOYBEAN | NICKEL | |||||
| SPOT | FUTURES | SPOT | FUTURES | SPOT | FUTURES | ||
| Mean | 0.006 | 0.006 | 0.0176 | 0.0174 | 0.0192 | 0.0183 | |
| Variance | 2.1298 | 2.4919 | 3.153 | 3.0904 | 4.486 | 4.4166 | |
| *** | *** | *** | *** | *** | *** | ||
| Skewness | −0.0209 | −0.7041 | −0.2081 | −1.2622 | −0.1337 | −0.1333 | |
| Kurtosis | 3.0253 | 14.8187 | 5.4233 | 15.3669 | 4.0583 | 4.0288 | |
| J-B test | 4134.2 | 100,069 | 4921 | 40,338 | 4968.6 | 4896.8 | |
| *** | *** | *** | *** | *** | *** | ||
| ARCH test | 1167.84 | 1261.52 | 430.57 | 85.418 | 736.01 | 754.28 | |
| *** | *** | *** | *** | *** | *** | ||
| Pearson Correlation | 0.90 *** | 0.82 *** | 0.98 *** | ||||
| J-B Test | Box Test | ARCH Test | |
|---|---|---|---|
| S&P 500 | 1,939,712 | 1437.8 | 3164.6 |
| *** | *** | *** | |
| EMERGING MARKETS | 6283.7 | 277.38 | 429.31 |
| *** | *** | *** | |
| BOND | 532,811 | 501.67 | 693.74 |
| *** | *** | *** | |
| USD | 332,852 | 1002.5 | 765.13 |
| *** | *** | *** | |
| GOLD | 21,932,902 | 1231.8 | 2652.7 |
| *** | *** | *** | |
| OIL | 9,463,902 | 1153.1 | 1546.1 |
| *** | *** | *** | |
| CORN | 26,471,382 | 1115.1 | 154.2 |
| *** | *** | *** | |
| SOYBEAN | 271,734 | 216.95 | 575 |
| *** | *** | *** | |
| NICKEL | 4,258,932 | 1397.5 | 2540.9 |
| *** | *** | *** |
| S&P 500 | Mean | Variance | SV | HE | IQ | 95% Range |
| Unhedged | 0.0336 | 1.2636 | 1.1794 | 0.9469 | 4.3848 | |
| Naïve | 0 | 0.0976 | 0.3148 | 92.28% | 0.2288 | 1.0864 |
| DCC | 0.0039 | 0.0868 | 0.2975 | 93.13% | 0.2299 | 1.0730 |
| Resid10th | 0.0052 | 0.0747 | 0.2757 | 94.09% | 0.2350 | 1.0836 |
| Resid25th | 0.0047 | 0.0734 | 0.2723 | 94.19% | 0.2314 | 1.0548 |
| Resid50th | 0.0036 | 0.0748 | 0.2778 | 94.08% | 0.2276 | 1.0334 |
| Resid75th | 0.0031 | 0.0754 | 0.2790 | 94.03% | 0.2271 | 1.0291 |
| Resid90th | 0.0026 | 0.0765 | 0.2808 | 93.95% | 0.2276 | 1.0256 |
| Pair10th | 0.0047 | 0.0751 | 0.2791 | 94.06% | 0.2342 | 1.0775 |
| Pair25th | 0.0043 | 0.0741 | 0.2760 | 94.14% | 0.2310 | 1.0551 |
| Pair50th | 0.0037 | 0.0740 | 0.2755 | 94.14% | 0.2274 | 1.0348 |
| Pair75th | 0.0032 | 0.0745 | 0.2764 | 94.10% | 0.2269 | 1.0260 |
| Pair90th | 0.0027 | 0.0755 | 0.2782 | 94.03% | 0.2269 | 1.0243 |
| EMERGING | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0184 | 0.6626 | 0.8782 | 0.8454 | 3.2273 | |
| Naïve | −0.0001 | 0.1480 | 0.3637 | 77.66% | 0.3966 | 1.5015 |
| DCC | 0.0049 | 0.0733 | 0.2728 | 88.94% | 0.2887 | 1.0673 |
| Resid10th | 0.0045 | 0.0724 | 0.2768 | 89.07% | 0.2970 | 1.0455 |
| Resid25th | 0.0044 | 0.0709 | 0.2730 | 89.30% | 0.2903 | 1.0390 |
| Resid50th | 0.0043 | 0.0701 | 0.2696 | 89.42% | 0.2908 | 1.0426 |
| Resid75th | 0.0041 | 0.0702 | 0.2693 | 89.41% | 0.2898 | 1.0411 |
| Resid90th | 0.0040 | 0.0711 | 0.2684 | 89.27% | 0.2904 | 1.0552 |
| Pair10th | 0.0045 | 0.0719 | 0.2760 | 89.15% | 0.2971 | 1.0358 |
| Pair25th | 0.0044 | 0.0708 | 0.2726 | 89.31% | 0.2901 | 1.0392 |
| Pair50th | 0.0043 | 0.0701 | 0.2697 | 89.42% | 0.2910 | 1.0414 |
| Pair75th | 0.0042 | 0.0702 | 0.2695 | 89.41% | 0.2895 | 1.0361 |
| Pair90th | 0.0039 | 0.0710 | 0.2684 | 89.28% | 0.2912 | 1.0522 |
| BOND | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0056 | 0.2064 | 0.4534 | 0.5087 | 1.8519 | |
| Naïve | −0.0090 | 0.0245 | 0.1581 | 88.13% | 0.1412 | 0.6057 |
| DCC | −0.0096 | 0.0193 | 0.1400 | 90.65% | 0.1045 | 0.5289 |
| Resid10th | −0.0094 | 0.0193 | 0.1382 | 90.65% | 0.1074 | 0.5378 |
| Resid25th | −0.0097 | 0.0189 | 0.1368 | 90.84% | 0.1054 | 0.5344 |
| Resid50th | −0.0101 | 0.0184 | 0.1351 | 91.09% | 0.1043 | 0.5246 |
| Resid75th | −0.0103 | 0.0184 | 0.1355 | 91.09% | 0.1035 | 0.5171 |
| Resid90th | −0.0105 | 0.0186 | 0.1363 | 90.99% | 0.1040 | 0.5182 |
| Pair10th | −0.0095 | 0.0191 | 0.1378 | 90.75% | 0.1074 | 0.5335 |
| Pair25th | −0.0097 | 0.0188 | 0.1364 | 90.89% | 0.1057 | 0.5320 |
| Pair50th | −0.0101 | 0.0184 | 0.1352 | 91.09% | 0.1044 | 0.5251 |
| Pair75th | −0.0103 | 0.0184 | 0.1356 | 91.09% | 0.1033 | 0.5186 |
| Pair90th | −0.0105 | 0.0185 | 0.1362 | 91.04% | 0.1042 | 0.5184 |
| USD | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | −0.0018 | 0.2549 | 0.5166 | 0.5517 | 2.0872 | |
| Naïve | 0 | 0.0166 | 0.1383 | 93.49% | 0.0539 | 0.5393 |
| DCC | −0.0010 | 0.0149 | 0.1377 | 94.15% | 0.0568 | 0.5087 |
| Resid10th | −0.0005 | 0.0152 | 0.1340 | 94.04% | 0.0614 | 0.5105 |
| Resid25th | −0.0005 | 0.0149 | 0.1335 | 94.15% | 0.0586 | 0.5098 |
| Resid50th | −0.0004 | 0.0147 | 0.1330 | 94.23% | 0.0556 | 0.4982 |
| Resid75th | −0.0003 | 0.0147 | 0.1334 | 94.23% | 0.0535 | 0.4966 |
| Resid90th | −0.0003 | 0.0148 | 0.1340 | 94.19% | 0.0529 | 0.5028 |
| Pair10th | −0.0005 | 0.0151 | 0.1339 | 94.08% | 0.0613 | 0.5084 |
| Pair25th | −0.0005 | 0.0149 | 0.1332 | 94.15% | 0.0586 | 0.5081 |
| Pair50th | −0.0004 | 0.0147 | 0.1330 | 94.23% | 0.0557 | 0.4969 |
| Pair75th | −0.0003 | 0.0147 | 0.1334 | 94.23% | 0.0536 | 0.4977 |
| Pair90th | −0.0003 | 0.0148 | 0.1338 | 94.19% | 0.0531 | 0.5020 |
| GOLD | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0099 | 1.1599 | 1.0815 | 0.9389 | 4.4309 | |
| Naïve | −0.0009 | 0.0237 | 0.2560 | 97.96% | 0.0223 | 0.4043 |
| DCC | −0.0006 | 0.0261 | 0.2236 | 97.75% | 0.0308 | 0.4492 |
| Resid10th | −0.0011 | 0.0247 | 0.2250 | 97.87% | 0.0339 | 0.4789 |
| Resid25th | −0.0011 | 0.0240 | 0.2282 | 97.93% | 0.0315 | 0.4517 |
| Resid50th | −0.0010 | 0.0235 | 0.2328 | 97.97% | 0.0283 | 0.4197 |
| Resid75th | −0.0010 | 0.0234 | 0.2376 | 97.98% | 0.0265 | 0.4093 |
| Resid90th | −0.0010 | 0.0235 | 0.2379 | 97.97% | 0.0258 | 0.4059 |
| Pair10th | −0.0010 | 0.0245 | 0.2241 | 97.89% | 0.0339 | 0.4743 |
| Pair25th | −0.0010 | 0.0239 | 0.2279 | 97.94% | 0.0312 | 0.4475 |
| Pair50th | −0.0010 | 0.0235 | 0.2333 | 97.97% | 0.0283 | 0.4208 |
| Pair75th | −0.0010 | 0.0234 | 0.2377 | 97.98% | 0.0266 | 0.4096 |
| Pair90th | −0.0010 | 0.0235 | 0.2382 | 97.97% | 0.0260 | 0.4058 |
| OIL | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0079 | 7.4613 | 2.8111 | 2.2300 | 9.7561 | |
| Naïve | 0 | 1.8557 | 1.6861 | 75.13% | 0.0730 | 3.9421 |
| DCC | −0.0029 | 2.1846 | 1.5424 | 70.72% | 0.2155 | 4.2929 |
| Resid10th | 0.0003 | 1.9294 | 1.4405 | 74.14% | 0.3541 | 4.2156 |
| Resid25th | −0.0002 | 1.8729 | 1.4639 | 74.90% | 0.2909 | 4.0347 |
| Resid50th | −0.0015 | 1.8249 | 1.4464 | 75.54% | 0.2248 | 3.8982 |
| Resid75th | −0.0050 | 1.8364 | 1.5016 | 75.39% | 0.1819 | 3.9523 |
| Resid90th | −0.0061 | 1.8679 | 1.5424 | 74.97% | 0.1528 | 4.0073 |
| Pair10th | −0.0002 | 1.9219 | 1.4996 | 74.24% | 0.3474 | 4.1064 |
| Pair25th | −0.0006 | 1.8630 | 1.4610 | 75.03% | 0.2873 | 4.0370 |
| Pair50th | −0.0016 | 1.8227 | 1.4437 | 75.57% | 0.2263 | 3.8952 |
| Pair75th | −0.0035 | 1.8212 | 1.4804 | 75.59% | 0.1792 | 3.9072 |
| Pair90th | −0.0045 | 1.8398 | 1.5148 | 75.34% | 0.1530 | 3.9574 |
| CORN | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0038 | 2.1491 | 1.4207 | 1.5102 | 6.1754 | |
| Naïve | 0 | 0.4993 | 0.7173 | 76.77% | 0.0042 | 1.7181 |
| DCC | −0.0022 | 0.4823 | 0.7255 | 77.56% | 0.2464 | 2.1768 |
| Resid10th | −0.0069 | 0.6079 | 0.8125 | 71.71% | 0.3679 | 2.9273 |
| Resid25th | −0.0060 | 0.5782 | 0.7891 | 73.10% | 0.3093 | 2.7801 |
| Resid50th | −0.0012 | 0.4536 | 0.6716 | 78.89% | 0.2136 | 1.8796 |
| Resid75th | −0.0013 | 0.4615 | 0.6817 | 78.53% | 0.1641 | 1.7830 |
| Resid90th | −0.0013 | 0.4699 | 0.6928 | 78.14% | 0.1336 | 1.7441 |
| Pair10th | −0.0036 | 0.4870 | 0.7107 | 77.34% | 0.3457 | 2.4456 |
| Pair25th | −0.0036 | 0.4789 | 0.7030 | 77.72% | 0.2962 | 2.3239 |
| Pair50th | −0.0017 | 0.4534 | 0.6745 | 78.90% | 0.2168 | 1.9288 |
| Pair75th | −0.0018 | 0.4620 | 0.6852 | 78.50% | 0.1621 | 1.8273 |
| Pair90th | −0.0018 | 0.4691 | 0.6956 | 78.17% | 0.1311 | 1.7817 |
| SOYBEAN | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0155 | 3.1518 | 1.7304 | 1.7331 | 7.4145 | |
| Naïve | 0.0021 | 1.1470 | 0.9109 | 63.61% | 0.1308 | 3.7792 |
| DCC | −0.0011 | 1.0919 | 1.0180 | 65.36% | 0.2542 | 3.7704 |
| Resid10th | −0.0017 | 1.0829 | 1.0525 | 65.64% | 0.3742 | 3.9539 |
| Resid25th | −0.0017 | 1.0520 | 1.0283 | 66.62% | 0.3183 | 3.7859 |
| Resid50th | −0.0006 | 1.0056 | 0.9821 | 68.09% | 0.2409 | 3.5367 |
| Resid75th | −0.0007 | 1.0245 | 0.9763 | 67.49% | 0.1870 | 3.6052 |
| Resid90th | −0.0005 | 1.0475 | 0.9733 | 66.77% | 0.1489 | 3.6449 |
| Pair10th | −0.0013 | 1.0321 | 1.0231 | 67.25% | 0.3590 | 3.7438 |
| Pair25th | −0.0009 | 1.0213 | 1.0073 | 67.60% | 0.3085 | 3.6931 |
| Pair50th | −0.0005 | 1.0078 | 0.9846 | 68.02% | 0.2447 | 3.5657 |
| Pair75th | −0.0005 | 1.0256 | 0.9747 | 67.46% | 0.1898 | 3.6315 |
| Pair90th | −0.0006 | 1.0480 | 0.9720 | 66.75% | 0.1501 | 3.6661 |
| NICKEL | Mean | Variance | SV | HE | IQ | 95% range |
| Unhedged | 0.0115 | 4.5584 | 2.0992 | 2.3105 | 8.5971 | |
| Naïve | 0.0001 | 0.1727 | 0.4684 | 96.21% | 0.0296 | 0.6895 |
| DCC | 0.0007 | 0.1354 | 0.4047 | 97.03% | 0.0352 | 0.8080 |
| Resid10th | 0.0011 | 0.1758 | 0.4392 | 96.14% | 0.0388 | 0.9508 |
| Resid25th | 0.0009 | 0.1743 | 0.4428 | 96.18% | 0.0364 | 0.9208 |
| Resid50th | 0.0009 | 0.1735 | 0.4527 | 96.19% | 0.0347 | 0.8941 |
| Resid75th | 0.0010 | 0.1729 | 0.4547 | 96.21% | 0.0348 | 0.8680 |
| Resid90th | 0.0011 | 0.1733 | 0.4523 | 96.20% | 0.0358 | 0.8097 |
| Pair10th | 0.0011 | 0.1757 | 0.4389 | 96.15% | 0.0388 | 0.9442 |
| Pair25th | 0.0009 | 0.1742 | 0.4429 | 96.18% | 0.0365 | 0.9212 |
| Pair50th | 0.0009 | 0.1733 | 0.4522 | 96.20% | 0.0346 | 0.8921 |
| Pair75th | 0.0009 | 0.1730 | 0.4557 | 96.20% | 0.0348 | 0.8728 |
| Pair90th | 0.0009 | 0.1731 | 0.4541 | 96.20% | 0.0360 | 0.8413 |
| Panel A: Hedging for S&P 500 | |||||||
|---|---|---|---|---|---|---|---|
| Dominance | Naïve | DCC | Pair10th | Pair25th | Pair50th | Pair75th | Pair90th |
| Naïve | |||||||
| DCC | Inconclusive | ||||||
| Pair10th | |||||||
| Pair25th | Inconclusive | ||||||
| Pair50th | Inconclusive | Inconclusive | Inconclusive | ||||
| Pair75th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Pair90th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | Inconclusive | ||
| Dominance | Naïve | DCC | Resid10th | Resid20th | Resid50th | Resid75th | Resid90th |
| Naïve | |||||||
| DCC | Inconclusive | ||||||
| Resid10th | |||||||
| Resid25th | Inconclusive | ||||||
| Resid50th | Inconclusive | Inconclusive | Inconclusive | ||||
| Resid75th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Resid90th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Panel B: Hedging for Emerging Markets | |||||||
| Dominance | Naïve | DCC | Pair10th | Pair25th | Pair50th | Pair75th | Pair90th |
| Naïve | |||||||
| DCC | Inconclusive | ||||||
| Pair10th | Inconclusive | Inconclusive | |||||
| Pair25th | Inconclusive | Inconclusive | Inconclusive | ||||
| Pair50th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Pair75th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | Inconclusive | ||
| Pair90th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | Inconclusive | ||
| Dominance | Naïve | DCC | Resid10th | Resid20th | Resid50th | Resid75th | Resid90th |
| Naïve | |||||||
| DCC | Inconclusive | ||||||
| Resid10th | Inconclusive | Inconclusive | |||||
| Resid25th | Inconclusive | Inconclusive | Inconclusive | ||||
| Resid50th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Resid75th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | |||
| Resid90th | Inconclusive | Inconclusive | Inconclusive | Inconclusive | Inconclusive | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, P.M.; Henry, D.; Kim, J.H.; Colombage, S. Estimation of Optimal Hedge Ratio: A Wild Bootstrap Approach. J. Risk Financial Manag. 2024, 17, 310. https://doi.org/10.3390/jrfm17070310
Nguyen PM, Henry D, Kim JH, Colombage S. Estimation of Optimal Hedge Ratio: A Wild Bootstrap Approach. Journal of Risk and Financial Management. 2024; 17(7):310. https://doi.org/10.3390/jrfm17070310
Chicago/Turabian StyleNguyen, Phong Minh, Darren Henry, Jae H. Kim, and Sisira Colombage. 2024. "Estimation of Optimal Hedge Ratio: A Wild Bootstrap Approach" Journal of Risk and Financial Management 17, no. 7: 310. https://doi.org/10.3390/jrfm17070310
APA StyleNguyen, P. M., Henry, D., Kim, J. H., & Colombage, S. (2024). Estimation of Optimal Hedge Ratio: A Wild Bootstrap Approach. Journal of Risk and Financial Management, 17(7), 310. https://doi.org/10.3390/jrfm17070310








