Battery Pack Grouping and Capacity Improvement for Electric Vehicles Based on a Genetic Algorithm

Abstract

This paper proposes an optimal grouping method for battery packs of electric vehicles (EVs). Based on modeling the vehicle powertrain, analyzing the battery degradation performance and setting up the driving cycle of an EV, a genetic algorithm (GA) is applied to optimize the battery grouping topology with the objective of minimizing the total cost of ownership (TCO). The battery capacity and the serial and parallel amounts of the pack can thus be determined considering the influence of battery degradation. The results show that the optimized pack grouping can be solved by GA within around 9 min. Compared with the results of maximum discharge efficiency within a fixed lifetime, the proposed method can not only achieve a higher discharge efficiency, but also reduce the TCO by 2.29%. To enlarge the applications of the proposed method, the sensitivity to driving conditions is also analyzed to further prove the feasibility of the proposed method.

1. Introduction

Nowadays, consumption of fossil fuel and increment of greenhouse gas (GHG) emissions have become major challenges to environmental pollution. Vehicle electrification can mitigate these interactions by employing highly efficient motors to power vehicles [1,2]. Currently, electric vehicles (EVs), hybrid electric vehicles (HEVs), plug-in HEVs (PHEVs) and fuel cell vehicles represent the developing directions of vehicle electrification. Among all the dominant solutions, EVs attract wide attention due to their relatively simple vehicle configuration, high operating efficiency, qualified driving performance and relatively mature energy storage technologies [3,4]. In an EV, the energy storage system, usually a lithium-ion battery pack, becomes the essential and predominant component employed to drive the motor according to the driving demand. Therefore, it is considerably important and imperative to optimize the battery pack design with care to improve the vehicle economy.

For the battery pack in an EV, there exist hundreds of cells connected in series, parallel or even more complex topologies. These battery grouping technologies, including the series and parallel connected cell topologies, can greatly influence the whole pack specifications as well as the vehicle performance. Simply speaking, the series amount of all the cells can determine the vehicle rated voltage, which is related to the vehicle motor driving demands, and consequently, the parallel amount of the cells can influence the battery’s overall capacity and the internal resistance. More importantly, the cost of the lithium-ion batteries occupies about 30–50% of the total cost of an EV. For instance, in the Nissan Leaf, the cost of the battery pack accounts for nearly 38% of the total vehicle cost [5]. Given this, the battery capacity and its grouping topology, i.e., the amount in series and in parallel, should be considered with care to provide an optimal grouping solution to meet the driving power demand, while simultaneously ensuring the vehicle economy [6]. This consideration is the main research target in this paper.

Abundant research has been conducted on vehicle powertrain parameter optimization [7,8,9]. The main research target usually involves battery and motor matching and their coordinated control. In [5], the whole process to determine the battery pack capacity is investigated to obtain the minimum battery cost for manufacturers. In view of the driving range, the pack size is designed to minimize the whole operation cost; however, the battery degradation influence should be considered with care to match different driving ranges. In [10], the battery size for PHEVs and extended range EVs (EREVs) with respect to different user types and different annual mileages is optimized considering energy consumption, total cost and greenhouse gas emission. The authors also analyze the battery size determination induced by policy influences in Germany. In addition, the battery life model is set up to be 12 years without considering the influence of degradation. In [11], a suitable battery size for prolonging the battery lifetime and decreasing the operating cost of a vehicle is evaluated; however, an important task is neglected in that the connection mode of the battery pack is not fully taken into account. In [12], an accurate battery life model is chosen for estimating the battery lifetime over different depths of discharge (DOD). It should be noted that there exists a tradeoff between DOD and battery size, as well as battery life. Furthermore, to acquire the minimum total cost of ownership (TCO), a global optimization algorithm is indirectly applied to make a closed-loop controller to reach the minimum operating cost. In [13], a multi-objective optimization, including energy management and battery capacity, is conducted based on hybrid fuel cell vehicles. After comparing this optimization with the optimized consequences of dynamic programming under different battery capacities, a soft-run energy management strategy is proposed. Meanwhile, the battery lifetime is also optimized considering battery size and hydrogen consumption. In [14], a tank-to-wheel method is applied to analyze the efficiency of energy recuperation and output considering the efficiency of converting electrical energy into mechanical energy. Based on an energy control algorithm, the energy efficiency is analyzed in detail when the battery size changes. In [15], a novel cost-optimal method is adopted to evaluate the charging, power management and battery degradation mitigation of PHEVs. The cost of electricity charged from the grid, fuel cost and battery life are considered and minimized based on convex programming (CP). Nonetheless, the pack grouping has not been analyzed yet due to its different serial-parallel construction focuses.

To summarize, it is crucial to consider the battery grouping topology and battery degradation to optimize the TCO. This criticality motivates the authors to conduct research into it. Although the TCO interactions between battery size and lifetime have been studied substantially, to the authors’ best knowledge, researchers have seldom carried out studies taking the number of parallel modules and serial cells in a simplified connection pattern into account. Based on the above discussion, the overarching goal of this paper is herein proposed: to extend previous study by introducing a methodology for optimizing the lithium-ion battery pack grouping topology of EVs to satisfy customers’ expectations with consideration for the TCO and battery degradation influence.

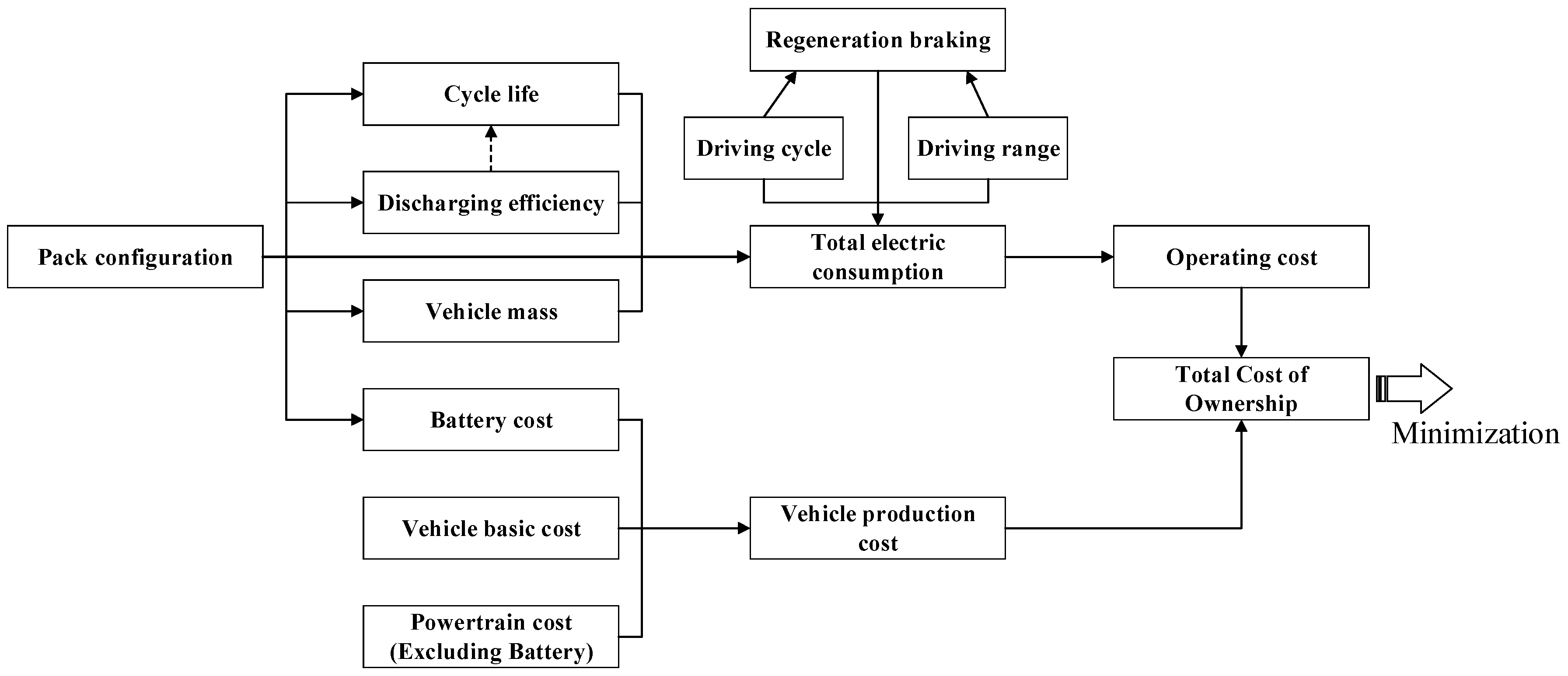
In order to optimize the TCO, it is imperative to analyze the vehicle powertrain, the battery degradation model, the daily operation cost, etc. The authors have considered all the related factors [16,17], as shown in Figure 1. The battery pack configuration can influence the cycle life, the discharging efficiency and the vehicle mass, and more directly, the battery cost, which is proportional to the battery capacity. Moreover, it can also determine the regeneration braking efficiency, and indirectly contribute to the operating cost. Therefore, these issues should be carefully taken into account to optimize the battery capacity and its grouping parameters.

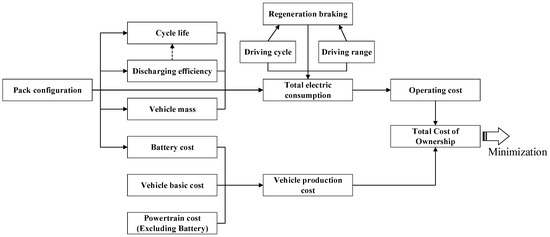
Figure 1. Structure of the battery combination optimization problem for BEVs.

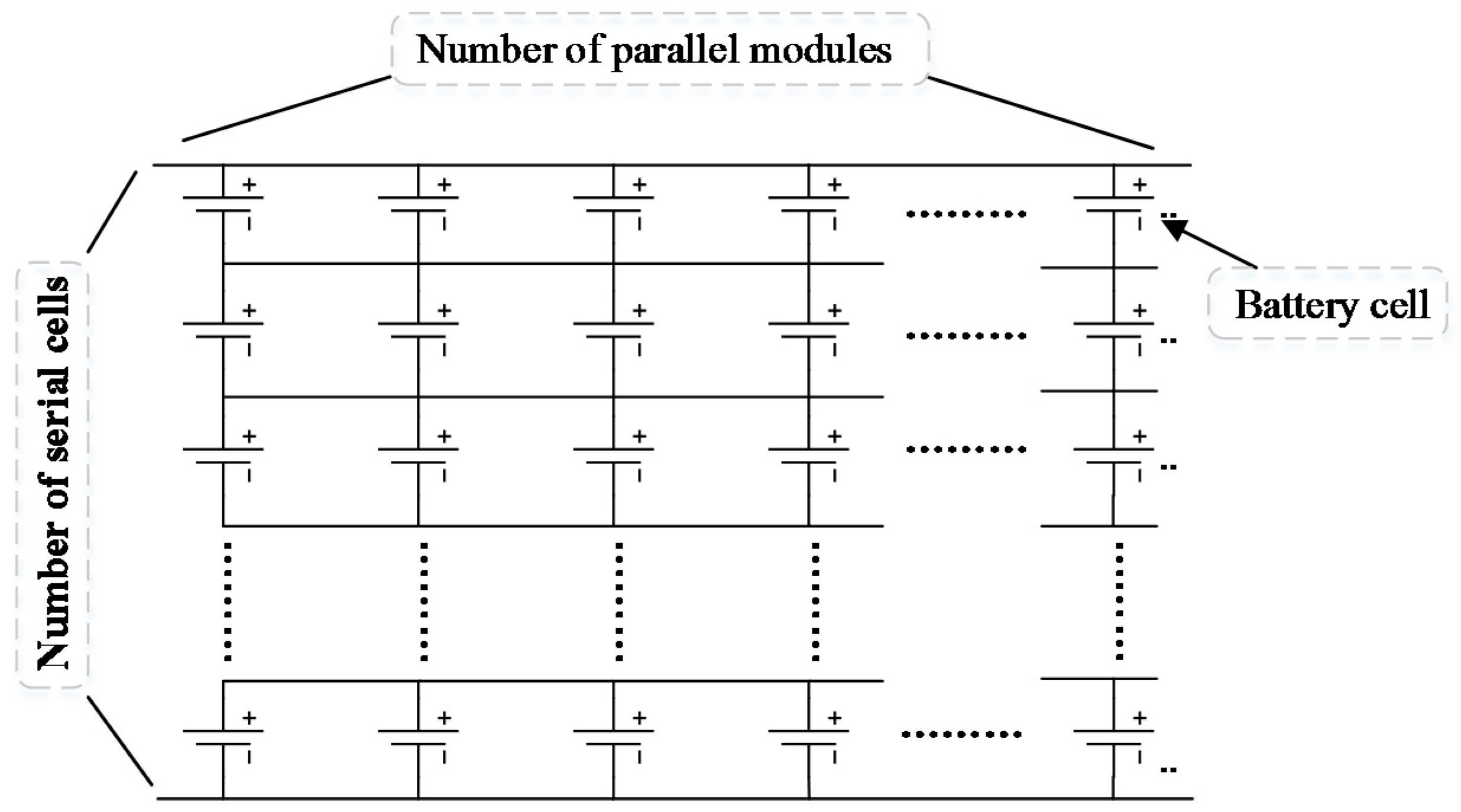
The proposed battery grouping topology is shown in Figure 2, in which the cell is a cylindrical lithium-ion battery. It can be observed that the number of parallel modules and the number of series modules should be determined. A commonly accepted design is that when the serial number increases, the voltage and internal resistance will consequently rise. Compared with the same power quantity, the battery current will decrease, thus improving the overall efficiency. In contrast, when the battery pack is short of voltage, the battery should release a larger current to satisfy the power demand, hence influencing the efficiency and cycle life [18]. On the other hand, the amount of cells connected in parallel can affect the current and the whole pack resistance. More cells connected in parallel will certainly produce higher efficiency, while contributing a heavier weight and more expensive cost [6,19,20]. Thus, a global optimization should be applied to determine these two topologies to minimize the battery lifetime cost and the total amount of all-life cost considering overall foregoing influences.

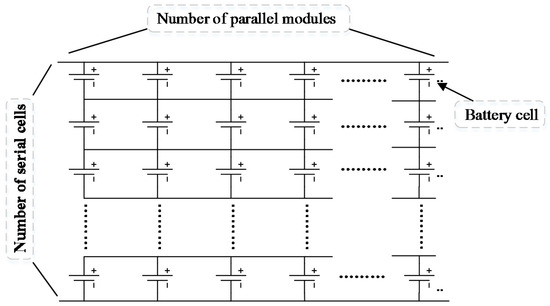
Figure 2. The battery pack in the parallel-series manner.

To achieve the abovementioned target, the related vehicle powertrain model and the battery degradation model should be built first. Then the optimal number of parallel modules and serial cells can be modeled for minimizing the TCO under objective driving cycles. Since the target problem is non-convex and highly nonlinear with series discrete variables and constraints, genetic algorithm (GA) is herein elaborated to overcome the defect and to find the optimal solution [21,22,23,24], as seen in Section 3. Due to the fact that the comparison results are sensitive to the driving cycles, the corresponding analysis is performed. Finally, the results are validated to prove the feasibility of the proposed algorithm, followed by the conclusion marked in the end.

2. Vehicle Modeling and Analysis

Based on the aforementioned statement [5,16], the target function for minimizing the TCO should be related to the battery grouping topology and the driving conditions, as well as the circumstance conditions, such as the electricity price, battery lifetime, etc. Therefore, the target function can be formulated:

$$\min TCO=f(N_{parallel},N_{series},Y_{driving\_cycle}(D),Z)$$

(1)

where $N_{parallel}$ equals the number of parallel modules and $N_{series}$ states the number of series cells in a pack module. $Y_{driving\_cycle}$, depicting the driving behavior under different driving cycles, is modeled in relation to the daily trip length $D$. $Z$ represents the underlying scenario assumptions, including the electricity price, the assumed battery lifetime, the production cost of batteries, motor cost, etc.

In order to determine the vehicle battery pack parameters, the vehicle model should be built first to provide the fundamental analysis of the demanded energy and power.

2.1. Vehicle Model

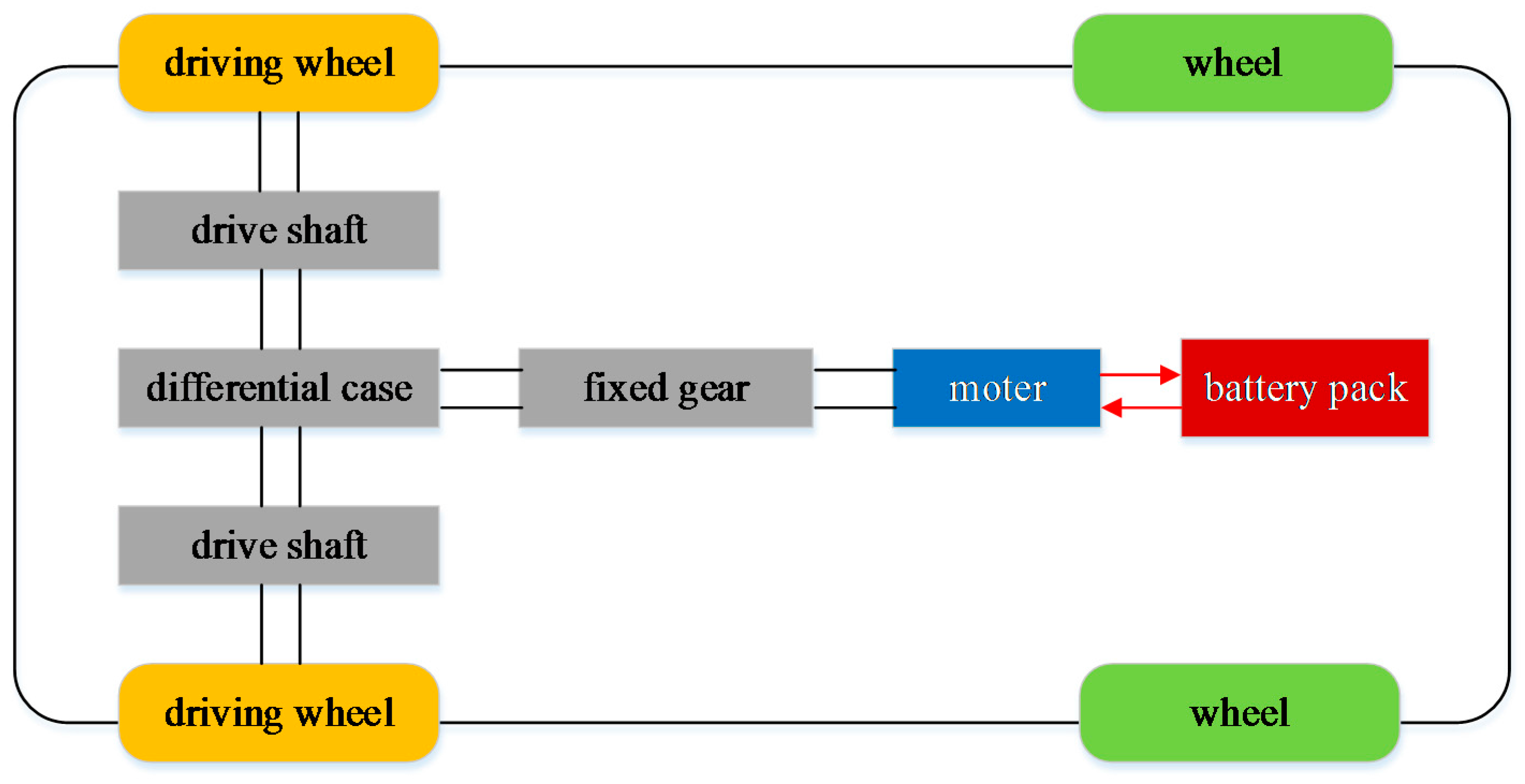
As shown in Figure 3, the powertrain structure of the proposed research target mainly comprises of a battery pack, a traction motor, a fixed gear, as well as a differential case [25,26]. In this paper, a permanent-magnet synchronous electric motor (PMSM) is harnessed to power the vehicle. The main parameters of the motor are shown in Table 1. The power density is supposed to be 2.5 kW/kg [27]. It can be found that the motor’s maximum power is 80 kW, and the mass is 32 kg. In this paper, a high power lithium-ion cylindrical battery cell AHR32113 (A123 Systems, Livonia, USA) [28,29] is selected to construct a battery pack, whose detailed parameters are listed in Table 2, from which we can see that the nominal capacity is 4.4 Ah, the rated cell voltage is 3.3 V, and the operating temperature ranges from −30 °C to 55 °C.

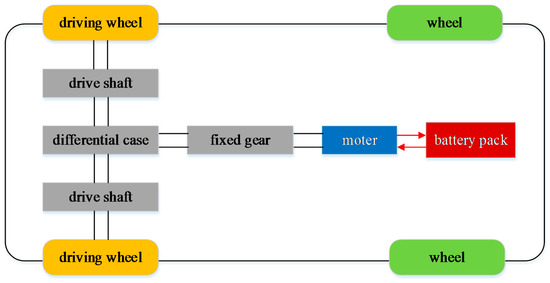
Figure 3. The EV powertrain topology of a central drive powertrain.

Table 1. The specifications of the baseline electric motor.

Motor Type	PMSM
Maximum Power	80 kW
Maximum Braking Torque	280 N m
Power Density	2.5 kW/kg
Energy Density	140 Wh/kg
Mass	32 kg

Table 2. AHR32113 Cell Specifications.

Cell Dimensions (mm)	Cell Weight (g)	Cell Capacity (Ah)	Voltage (V)	Operating Temperature (°C)
32 × 113	205	4.4	3.3	−30–55

With the battery cell specification, the weight of battery pack $m_{pack}$ can be formulated as:

$$m_{pack}=N_{bat}{m}_{bat}\phi$$

(2)

where $m_{cell}$ is the weight of the battery cells, $N_{bat}$ is the number of battery cells, and $\phi$ is the packaging coefficient, which is specified as 1.25 in this paper [30].

Now, the total vehicle mass $m_{total}$ can be calculated:

$$m_{total}=m_{veh}+m_{pack}+m_{mot}+m_{pc}$$

(3)

where $m_{veh}$ is the vehicle chassis mass, $m_{mot}$ is the electric motor mass, and $m_{pc}$ is the mass of the passengers and cargo and is specified to be 150 kg on average.

Based on the kinematic functions, the EV’s driving dynamics model can be formulated:

$$\{\begin{array}{l}P(t)=P_w(t)+P_f(t)+P_i(t)+P_j(t)+P_{acc}\hfill \\ P_w(t)={\rho }_{air}A{C}_D{v}^3(t)/2\hfill \\ P_f(t)=mgf\cos (\alpha (t))v(t)\hfill \\ P_i(t)=mg\sin (\alpha (t))v(t)\hfill \\ \begin{array}{l}{P}_j(t)=\delta mv(t)\frac{dv(t)}{dt}\\ J_{total}=\frac{{\displaystyle {\int }_{t_{initial}}^{t_{terminal}}(P(t)/({\eta }_{pack}\times {\eta }_{con}\times {\eta }_{mot}\times {\eta }_{fd}))dt}}{3600}\end{array}\hfill \end{array}$$

(4)

where $P(t)$ means the driving power, $P_w(t)$ equals the power of the aerodynamic drag force, and $P_f(t)$ represents the power of rolling resistance. $P_i(t)$ represents the gradient resistance power. $P_j(t)$ is the acceleration (or deceleration) power demand. $P_{acc}$, equaling 269 W, is the accessory power [31]. $g$ represents the gravitational acceleration, and equals 9.81 m/s². α namely the slope of the EV, is near zero most of the time. $J_{total}$ denotes the total energy consumption in each driving range in kWh. The remaining vehicle parameters are shown in Table 3.

Table 3. Vehicle parameters.

Parameters	Symbol	Value	Parameters	Symbol	Value
Frontal area	$A$	2.372 m3	Wheel radius	$r$	0.301 m
Aerodynamic drag coefficient	$C_D$	0.311	Converter efficiency	${\eta }_{con}$	0.97
Coefficient of rotating mass	$\delta$	1.02	Motor efficiency	${\eta }_{mot}$	0.96
Air density	${\rho }_{air}$	1.1985 kg/m3	Pack charge efficiency	${\eta }_{charging}$	0.95
Rolling resistance coefficient	$f$	0.015	Final drive efficiency	${\eta }_{fd}$	0.95

2.1.1. Regenerative Braking Model

For the EV, the regenerative braking system can automatically recover the braking energy. To optimize the battery capacity, the braking performance should be properly considered. To simplify the problem, the regenerative braking function can be indicated as:

$$W=\frac{\mu {\displaystyle {\int }_{t_{initial}}^{t_{terminal}}{m}_{total}{a}_k{v}_{k}dt}}{1000\times 3600}$$

(5)

where $W$ represents the regenerative braking energy in kWh, and $a_k$ and $v_k$ are the acceleration/deceleration in ${\mathrm{m}/\mathrm{s}}^2$ and velocity in m/s at moment $k$, respectively. $\mu$ denotes the factor of average energy recovery and equals 0.323, as discussed in [32]. $t_{initial}$ and $t_{terminal}$ state the initial time and terminal time of the braking operation.

2.1.2. Battery Model

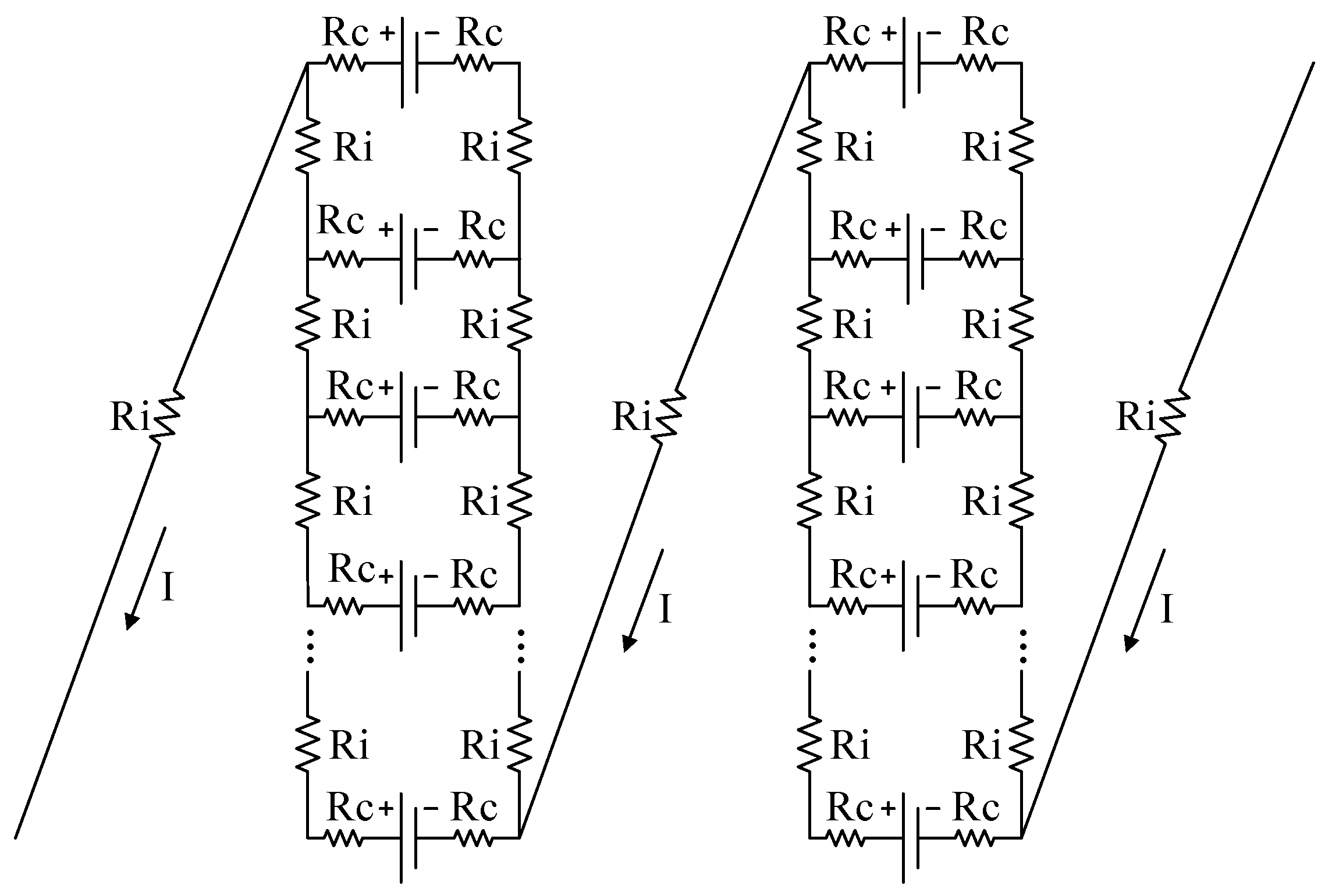
In order to study the interactions between the amount of series and parallel cells, the discharge efficiency influences induced by the resistance of the pack should be analyzed in advance. Given the amount of series and parallel units [33], the connected mode among each unit can be simplified and indexed, as shown in Figure 4. Each cell within a parallel unit connects with $R_i$, which is equal to the resistance of the copper conductors, and the contact resistor $R_C$ expresses the aluminum clamp resistance. Their values are specified to be 0.1 milliohm and 3 milliohm, respectively [34], and the cell resistor is set to be 10 milliohm. In this paper, the inconsistency of the pack is not taken into account for simplification. Therefore, the resistance function $R_{parallel\_unit}$ of the parallel unit can be furnished via the equivalent transformation between Y and ∆ connections, which is only determined by the parallel amount of cells after ensuring the aforementioned pre-set values:

$$R_{parallel\_unit}=g(N_{parallel})$$

(6)

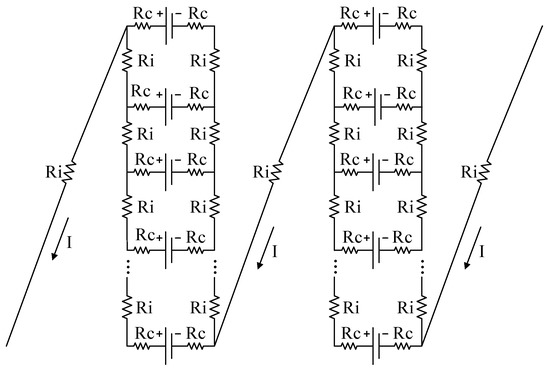
Figure 4. Schematic of series connection among each parallel unit.

Hence, the overall resistance $R_{pack}$ of the pack can be given as:

$$R_{pack}=(N_{series}+1)\times R_C+R_{parallel\_unit}\times N_{series}$$

(7)

The value of current $I$ and discharge efficiency ${\eta }_{discharge}$ can be described as:

$$\{\begin{array}{l}I=\frac{U-\sqrt{U^2-4R_{pack}{P}_{bat}}}{2R_{pack}}\hfill \\ {\eta }_{discharge}=\frac{U-I{R}_{pack}}{U}\hfill \end{array}$$

(8)

where $U$ is the open-circuit voltage of the battery pack and equals 3.3 × $N_{series}$ in this paper.

Traditionally, the widely adopted battery degradation model is calculated as an empirical function of the charge/discharge rate, DOD and battery capacity [35,36,37]. Indeed, the battery degradation model is rather complex and it is quite difficult to build a uniform relationship between it and the usage operation. This is not the research focus of this paper, and a simplified method, i.e., the Peterson model, is herein employed [38]. Considering one charge process per day, the battery energy consumption can be described as:

$$\{\begin{array}{ll}{w}_{discharge}=\frac{E_{dis}\times L_{day}}{{\eta }_{discharge}},\hfill & \mathrm{discharge}\\ w_{charge}=\frac{E_{dis}\times L_{day}}{{\eta }_{charge}},\hfill & \mathrm{charge}\end{array}$$

(9)

where $w_{charge}$ and $w_{discharge}$ are the energy processed for the daily charging and discharging respectively. ${\eta }_{discharge}$ represents the discharge efficiency. $L_{day}$ denotes the driving range per day. $E_{dis}$ means the electric energy consumption per kilometer in Wh/km under the identified driving cycle, and is proportional to the vehicle mass.

Consequently, by inputting (6) through (8) into (9), the battery lifetime $T_{bat}$ can be deduced:

$$T_{bat}=\frac{N_{bat}\times E_{cell}\times r_{EOL}}{({\alpha }_{discharge}{w}_{discharge}+{\alpha }_{charge}{w}_{charge})D_{drive}}$$

(10)

where $E_{cell}$ is a single battery cell’s energy capacity in kWh/cell. ${\alpha }_{discharge}$ and ${\alpha }_{charge}$ are the battery discharging and charging degradation factors and equal $3.46\times {10}^{-5}$ and $1.72\times {10}^{-5}$, respectively [39]. Note that $D_{drive}$ denotes the driving days per year and equals 300 days in this paper, and $r_{EOL}$ indexes the window function of DOD. In this paper, we suppose that when the battery capacity degrades to 80% rated values, the battery should be replaced [40].

2.2. Vehicle Cost Model

Based on the above discussion, the TCO consists of four parts: the vehicle body cost, powertrain cost, pack cost, as well as the operation cost. In this paper, an A00 class vehicle chassis is selected as the target platform, of which the mass is set to be 800 kg and the average cost is specified to be 2686 euros. The average price of a lithium-ion battery is specified to be 268.6 euros/kWh [27]. Now, the total cost of the battery cells $C_{pack}$ can be formulated:

$$C_{pack}=268.6\times N_{bat}\times E_{cell}$$

(11)

The average annual ownership cost $C_{year}$ for the EV can be calculated:

$$C_{year}=\frac{（J_{total}-W）\times P_e\times 300}{{\eta }_{discharge}}+\frac{C_{pack}+C_{basic\_vehicle}+C_p}{T_{veh}}$$

(12)

where $T_{veh}$ is the life cycle of both the vehicle and battery pack in years, $C_{basic\_vehicle}$ is the vehicle basic cost, $C_p$ is the powertrain cost and $P_e$, equaling 0.07 euros/kWh, represents the average electricity price based on investigation [41].

Based on the described model, GA is then applied to optimize the battery grouping configuration and to find the optimal solutions.

3. Optimization Framework

In this paper, GA is employed to optimize the battery pack grouping topology for EVs. GA is qualified to control the highly nonlinear system, and is strongly skilled in finding the optimal solutions. Typically, the process of GA includes encoding, selection, crossover and mutation operations [23]. During each generation, the individuals with a higher fitness value are elected to produce new individuals for the next offspring. The optimal populations are unchangeable and are directly considered as elitists for the next offspring. By selecting two individuals as parents to be hybridized, new offspring, namely children individuals, can be generated. The mutation process is integrated to reduce the possibility of converging into a local optimum by choosing a random element of a chromosome. After these steps, the whole process continuously iterates until meeting the terminal conditions [42,43]. Generally, the termination conditions include: (1) finding a satisfactory solution, (2) reaching the set fitness values, and (3) exceeding the budget time or number of generations.

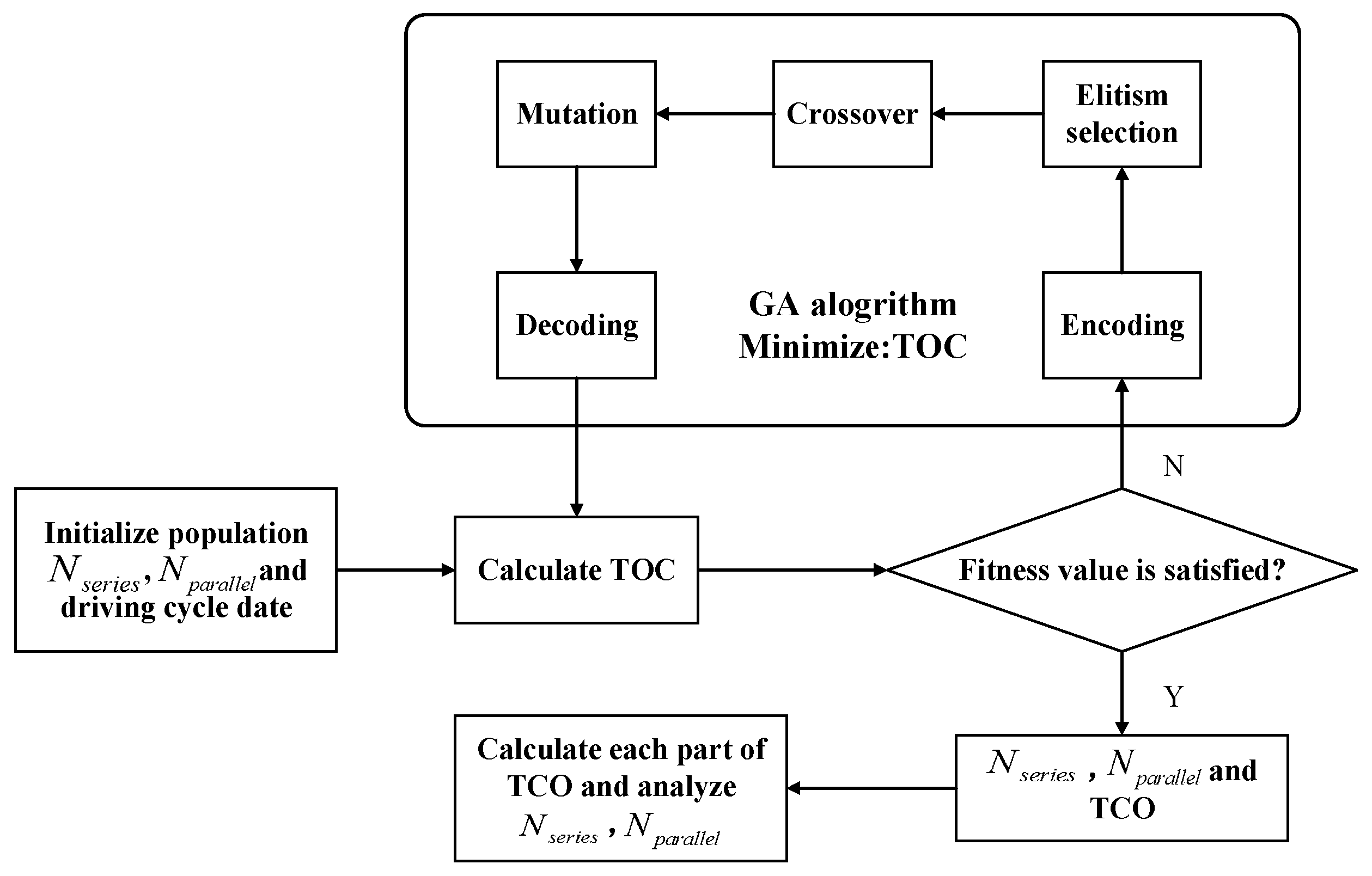
By optimization, the number of generations, population, crossover rate and mutation rate are set to be 60, 40, 0.8 and 0.2, respectively. The whole application is depicted in Figure 5. First, the initialization is set up, followed by calculating the TCO. Then, GA is applied to minimize the TCO until the termination conditions are achieved. Finally, the whole calculation process ends and the battery grouping information and TCO are determined.

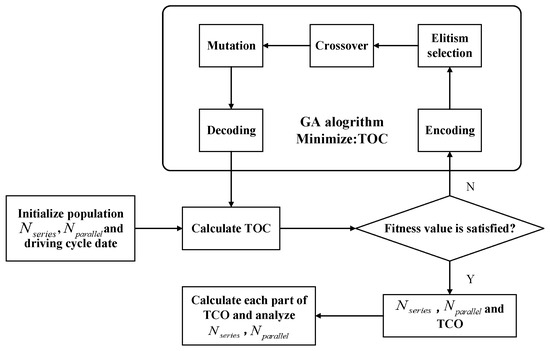
Figure 5. The optimization procedure using GA.

From the foregoing elaboration, the optimization can be processed with a series of optimal constraints. Due to the regulation that the most basic quality standard of battery life is 8 years [44], the limitation with respect to battery life is enforced to be more than 8 years considering its routine employment by a user. It is necessary to mention that due to the powering demand and voltage ratings of the motor and its driving system, the amount of series cells $N_{series}$ is set up to range from 80 to 120 to ensure the driving efficiency. In addition, the highest value of $N_{parallel}$ is limited to 100, since when the parallel amount is 100 and the series amount is 80, the total battery available capacity is approximately equal to 117 kWh, which should be enough to power the vehicle. Moreover, in view of the interaction between DOD and all-life cycles, the limited DOD ranges from 0 to 0.8. The other constraints relative to the vehicle components, e.g., maximum motor power, are regarded as common settings. To sum up, all the constraints can be formulated as:

$$\{\begin{array}{l}80\le N_{series}\le 120\\ 1\le N_{parallel}\le 100\\ 0<DOD\le 0.8\\ T_{veh}\ge 8\end{array}$$

(13)

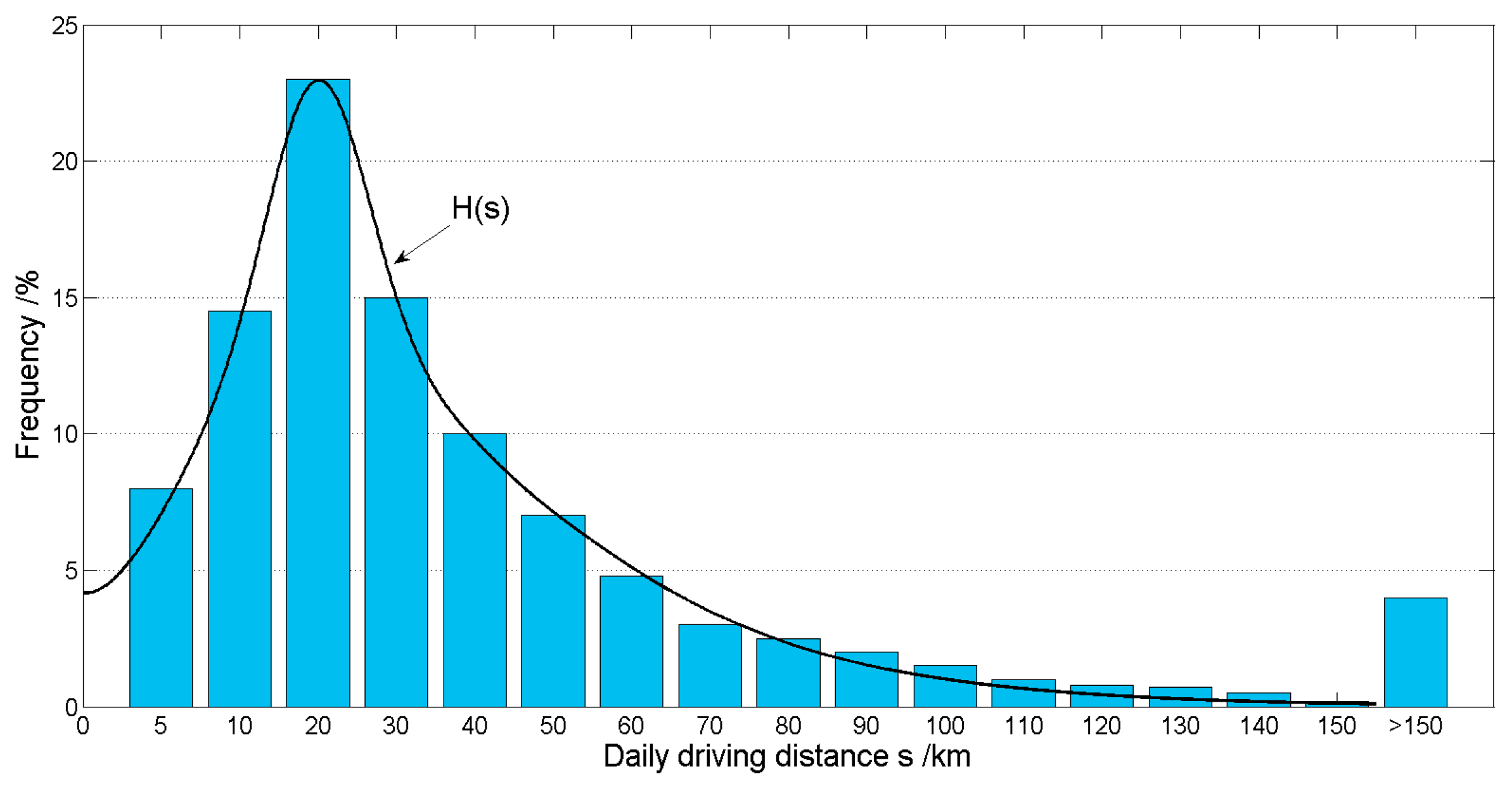
In order to optimize the battery size, the driving cycle should be determined with attention. In this paper, the driving pattern of users derived from Germany is adopted to simulate the daily driving distribution for automobiles, as shown in Figure 6 [45]. Here, a probability density function $H(s)$ can be fitted to calculate the average daily driving length, which will not interact with the investigative accuracy. The daily driving length $S_{daily}$ can be determined via integral operation:

$$S_{daily}={\displaystyle {\int }_{s}H(s)}sds$$

(14)

where $s$ denotes the daily driving distance. Based on Figure 6, the daily and annual driving lengths can be calculated, which are 41.22 km and 12366 km, respectively.

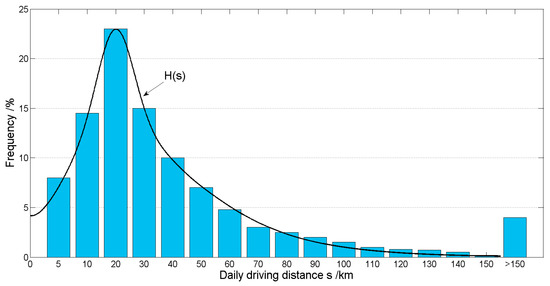
Figure 6. Distribution of daily driving distance.

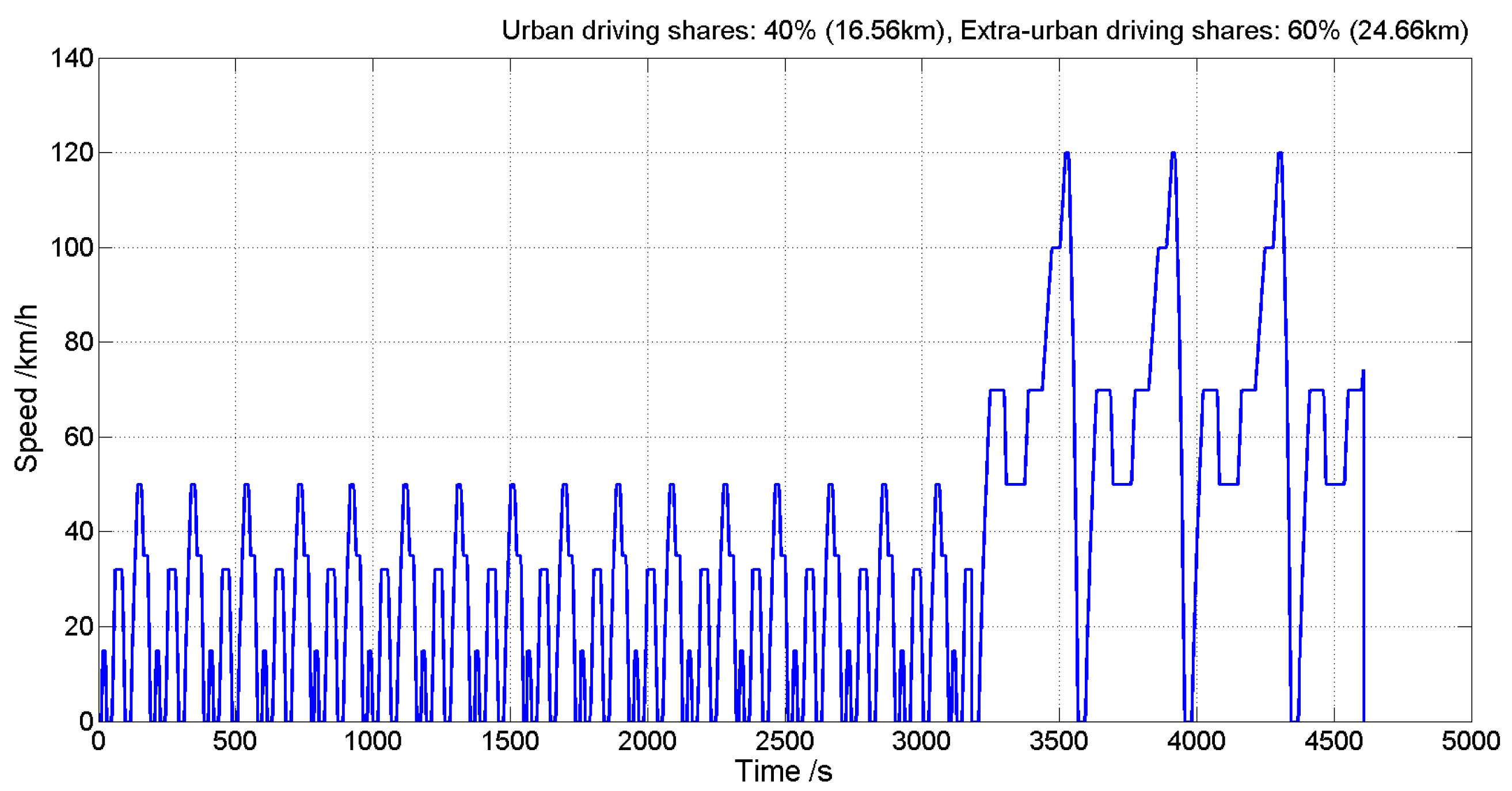
In this paper, a mixed driving cycle is employed to construct the daily driving conditions, which is composed of 40% urban cycle and 60% extra-urban cycle [10]. In [10], the authors calculated the weights of 40% and 60% through the average speed and average trip distance when driving 365 days per year; however, the situation of driving every day in a year rarely happens in the real world. Therefore, we propose that the share is still set to be 40% urban cycle and 60% extra-urban cycle but with 300 driving days per year. Here, based on the New European Driving Cycle (NEDC), exactly combined with the above two general kinds of portions, a mixed driving cycle is selected to simulate a typical cycle to estimate a real-world cycle, as indicated in Figure 7 [46]. Its average speed is 32.21 km/h, slightly lower than the 33.60 km/h under the NEDC cycle.

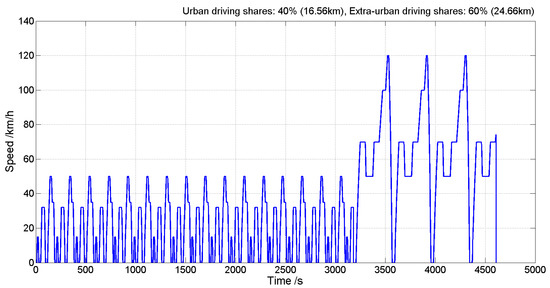
Figure 7. The mixture cycle based on NEDC.

Commonly, the basic driving performance requirement is the most pivotal portion of the whole cycle, and even the most attractive to the customers or manufacturers to some extent. In this paper, the basic EV performance requirements derived from China Battery Electric Passenger Cars Specifications (GB/T 28382-2012) [47] are implemented, as listed in Table 4. The acceleration time from 0 to 50 km/h is limited to 10 s, and the maximum grade ability is specified to be more than 20%. In addition, to satisfy the daily driving demand, the all-electric range (AER) should be more than 80 km.

Table 4. Vehicle performance requirements.

Vehicle Performance Index	Value
Acceleration time 0–50 km/h	≤10 s
Acceleration time 50–80 km/h	≤15 s
Gradeability during 60 km/h	≥4%
Gradeability during 30 km/h	≥12%
Maximum gradeability	≥20%
Maximum speed	≥80 km/h
All-electric range	≥80 km

The next step is to perform the corresponding analysis and results validation to prove the feasibility of the proposed method.

4. Results and Discussion

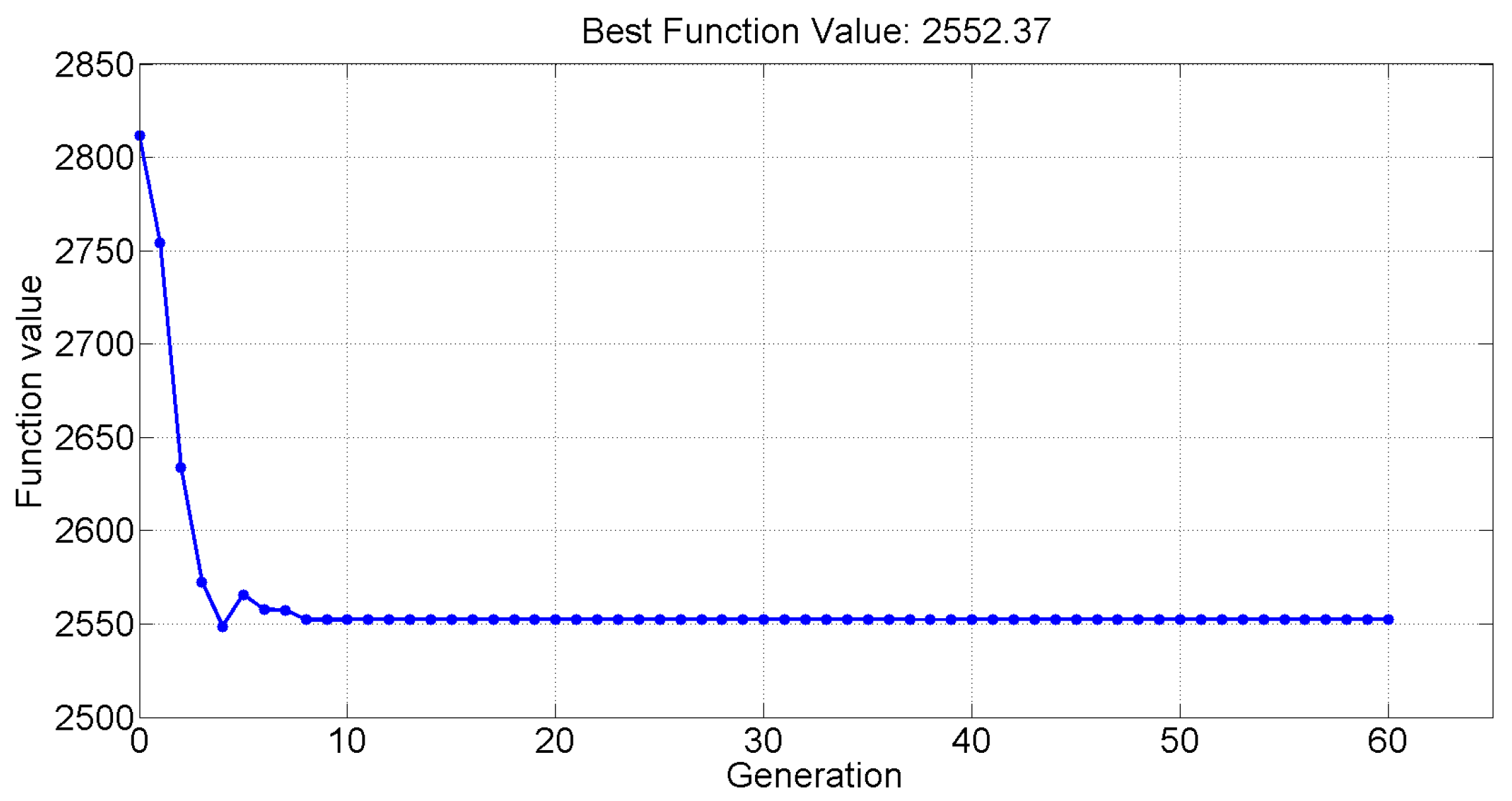
Due to the fact that the battery pack is a complicated system, an assumption is herein made that the temperature of the battery pack is consistent at 25 °C. Moreover, in order to ensure the accuracy of the modeling, the powertrain of the EV is taken from Autonomie, which is an effective and well-known simulation platform for EVs and PHEVs [48]. The whole validation is shown in Figure 8, yielding that the setting parameters are capable of obtaining a good result within 60 generations. The total calculation duration is within 9 min with a desktop computer using a Core i7 CPU and 8 gigabyte memory storage. The average TCO per year and the related results are exhibited in Table 5. After optimization, the parallel number of cells of the battery pack is 40, and the serial number is 113. The battery cost is 1687.93 euros, which occupies an overriding portion of 66.13% in the TCO and is apparently inverse to the sum of the operation cost and based vehicle cost (33.87%). In addition, the acceleration times to go from 0 to 50 km/h and from 0 to 80 km/h are 6.7 s and 10.6 s, respectively. The grade ability performance and maximum speed requirement can also be satisfied. In addition, the driving range is 298.96 km, reaching the design requirement.

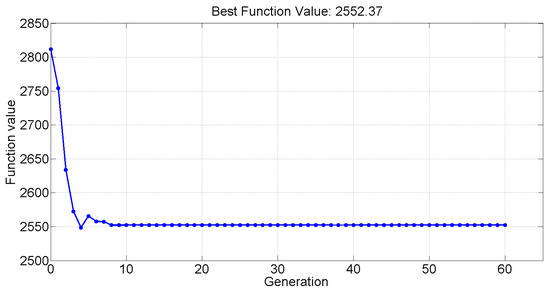
Figure 8. The GA method calculation process.

Table 5. The optimal solutions by genetic algorithm.

Variable	Optimal Solution
Parallel number	40
Serial number	113
Total vehicle mass	2140.25 kg
Battery cost	€1687.93 per year
Electricity cost	€166.76 per year
Based vehicle cost	€697.68 per year
Lifetime	10.09 years
Average discharge efficiency	90.39%
TCO	€2552.37 per year

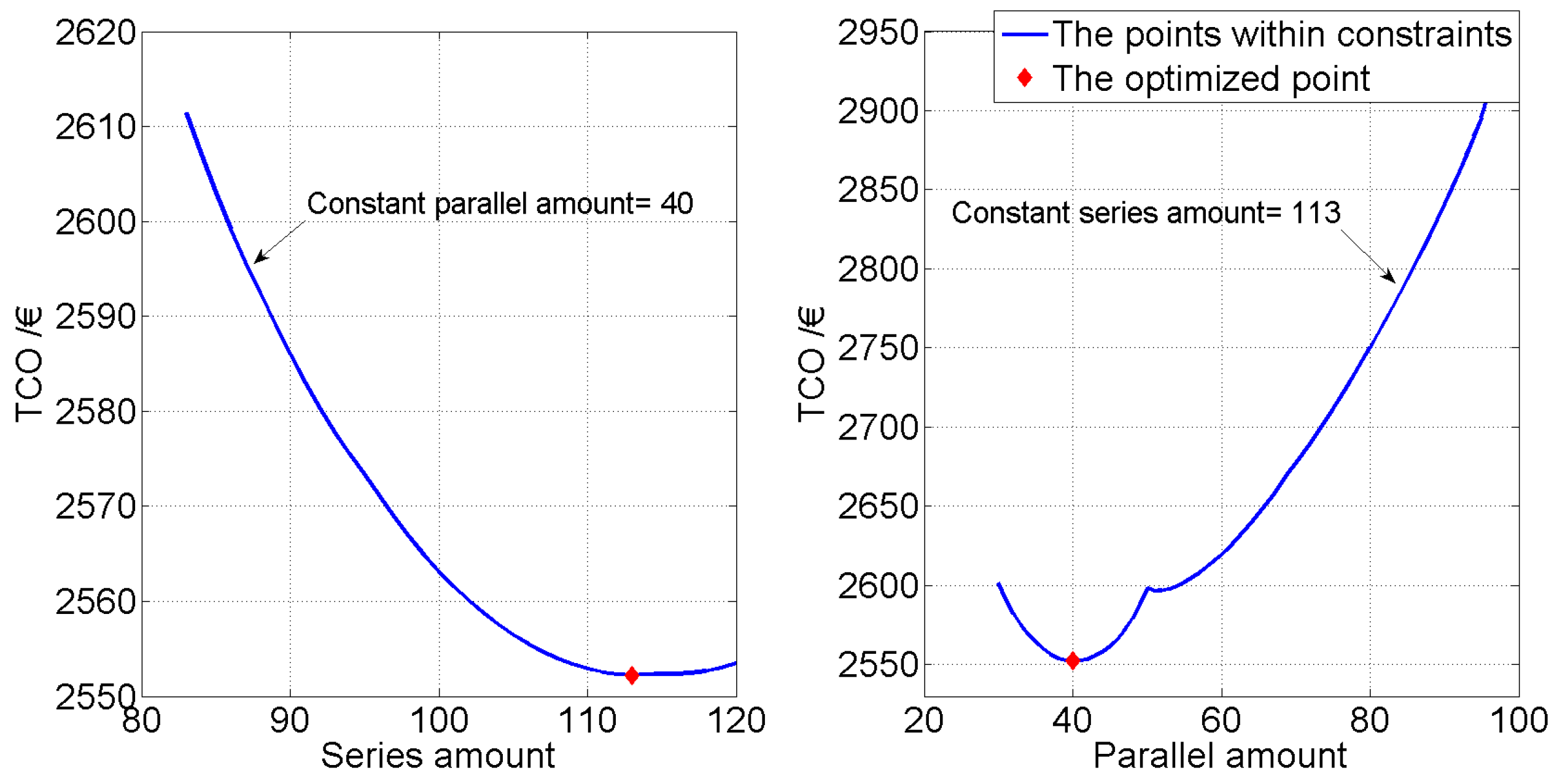
Figure 9 shows the TCO variations when the parallel and serial amounts of cells are supposed separately to be constant. It can be observed that when the parallel amount is set to be 40, the TCO reaches the minimum point when the serial amount is 113; similarly, when the serial amount is set to be 113, the TCO can achieve the minimum value of a parallel amount of 40. Thus, this observation proves that the grouping amounts of 113 and 40 reach the optimal solution and therefore justifies the feasibility of the proposed algorithm. Essentially, the main target of the proposed optimization method is to achieve the highest efficiency of the battery operation.

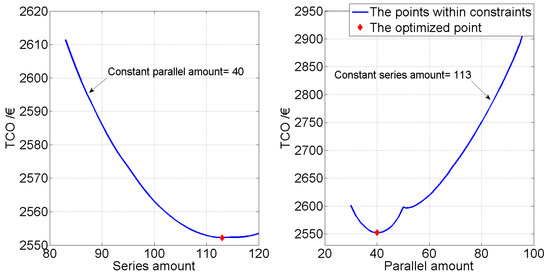
Figure 9. The results comparison.

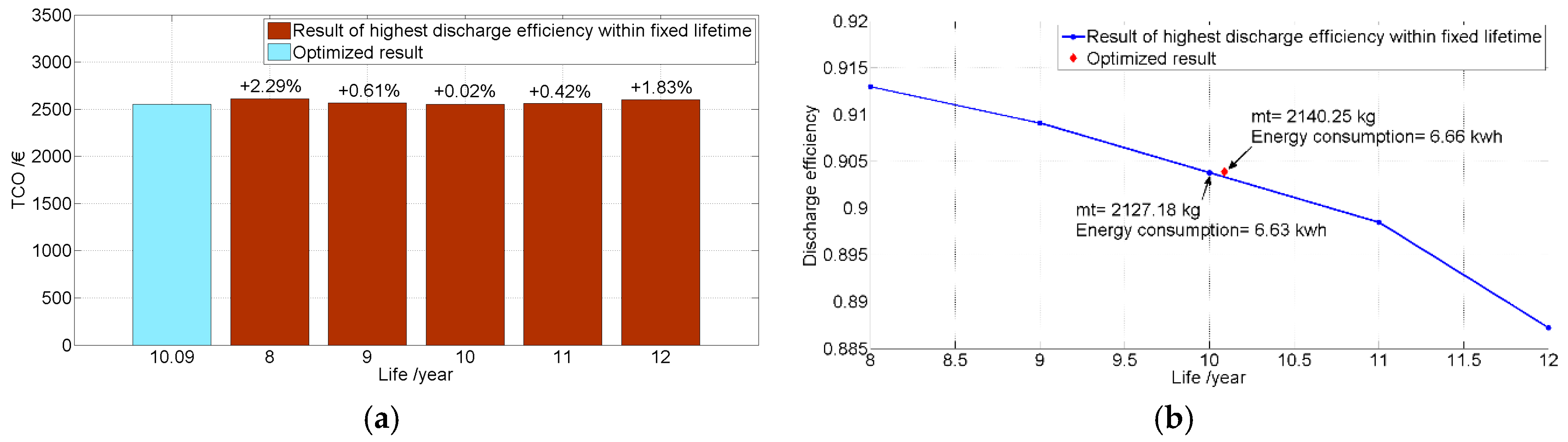
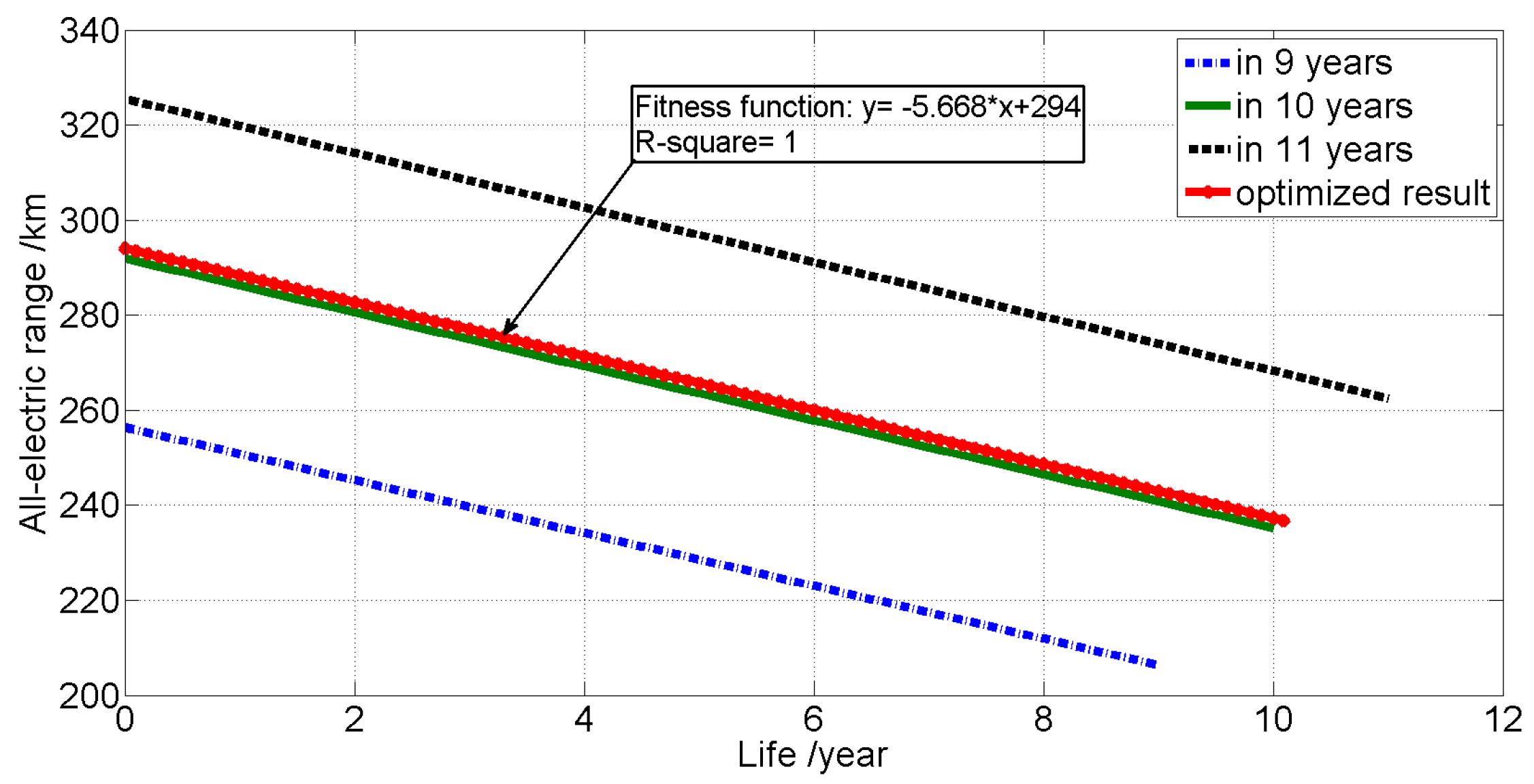
Based on the discussion in Section 2 above, the efficiency and lifetime of the battery pack are two key variables directly affecting the remaining variables. To further extend the analysis, these two variables are herein discussed. To easily compare these influences, the battery grouping topology is determined with regard to optimizing the highest efficiency with a fixed lifetime. The corresponding result is shown in Figure 10. It can be observed that the proposed solution can reduce the TCO by a maximum value of 2.29%, compared with those based on the constraint of fixed time. Now it can be proven that the determined topology can reach the highest efficiency by way of the proposed algorithm. To analyze the influences between the solutions and AER, an AER with increasing operation lifetime is taken into account, of which the groups are also selected by the aforementioned method, i.e., highest efficiency and constant pre-set lifetime, as shown in Figure 11. Apparently, the AER drops linearly, thus the function can be fitted with a linear function. In addition, it is necessary to note that the slopes of attenuation with rising operation lifetime are almost consistent and the differences between two lines is about 35 km.

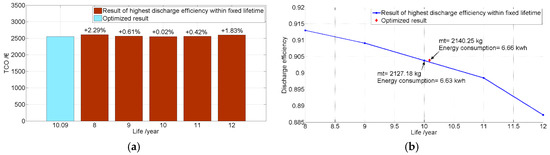
Figure 10. The comparison of TCO with the highest discharge efficiency and varying fixed lifetime. (a) The comparison of TCO; (b) The varied discharge efficiency.

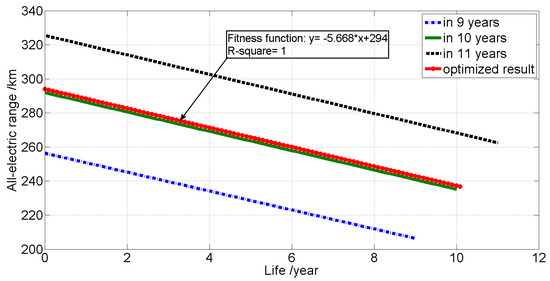
Figure 11. The varying all-electric range with increasing operation lifetime.

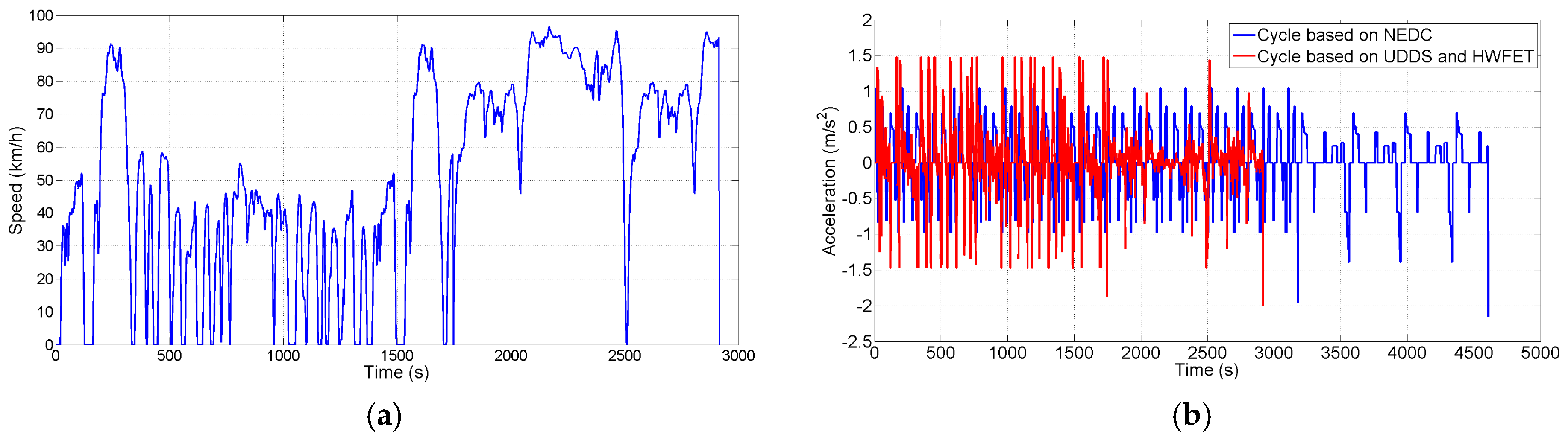
In order to extend the application of the optimized method, a sensitivity comparison is studied in this paper. It is difficult to adjust the pack grouped design with a varied driving cycle. In other words, there should be a fixed pack grouping configuration to satisfy the aforementioned driving pattern in practice. Here, a more aggressive cycle within irregular speed profiles, which combines with the Urban Dynamometer Driving Schedule (UDDS) and the Highway Fuel Economy Test (HWFET), sharing 40% of the urban cycle and 60% of the highway cycle, is employed to optimize the performance. UDDS is usually used to simulate an urban route with frequent accelerations and 31.53 km/h average speed; in contrast, HWFET is used to simulate a highway fuel economy with few stops and 77.23 km/h average speed, which is obviously more aggressive than the aforementioned proposed cycle. The speed and acceleration profiles of the mixed cycle are shown in Figure 12, with an average speed and average acceleration of 50.90 km/h and 0.24 m/s² respectively, which are higher than the 32.21 km/h and 0.15 m/s² under the foregoing cycle.

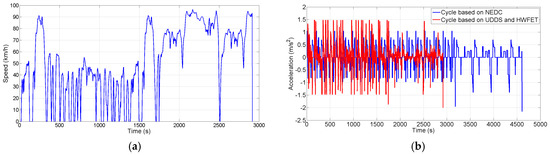
Figure 12. The new cycle based on driving patterns of users. (a) The speed profile of the new cycle; (b) The comparison of the acceleration under these two driving cycles.

As indexed in Table 6, the calculation shows that the optimal amount of series cells varies from 113 to 117, whereas the number of optimal parallel modules changes from 40 to 41. Due to its decreased lifetime and increased mass, each portion of the TCO has clearly risen; however, the variation of the discharge efficiency is almost unchanged, owing to the tradeoffs made by GA to decrease the TCO. Combined with the above discussion, the manufacturers can adaptively adjust the pack grouping parameters according to the actual demands in practice based on the proposed optimization method.

Table 6. The results under a mixed cycle combined with UDDS and HWFET cycles.

Variable	Optimal Solution
Parallel number	41
Serial number	117
Total vehicle mass	2211.23 kg
Battery cost	€2142.86 per year
Electricity cost	€239.92 per year
Based vehicle cost	€834.58 per year
Lifetime	8.73 years
Average discharge efficiency	90.14%
TCO	€3217.36 per year

5. Conclusions

This paper develops an optimization methodology for battery grouping configuration with the objective to minimize the TCO based on the driving patterns of users. Based on modeling the vehicle powertrain and the battery degradation, GA is applied to acquire the expected number of parallel modules and serial cells with the target of optimizing the TCO. The proposed approach is proven to be effective in optimizing the battery economy. In addition, aiming to implement this approach in practice, different cycles are employed to extend the applications so that manufacturers can adaptively regulate the pack grouping topologies according to the actual demand.

Currently, the driving cycles used in this paper are based on knowing the driving patterns. To enlarge the applications of the proposed method, an actual vehicle test and hardware-in-the-loop test need to be carried out as the next step. Additionally, further investigation of traveling habits and related factors, such as influences of the weather/climate and traffic information, should also be included in future studies.