Models for Flow Rate Simulation in Gear Pumps: A Review

Abstract

Gear pumps represent the majority of the fixed displacement machines used for flow generation in fluid power systems. In this context, the paper presents a review of the different methodologies used in the last years for the simulation of the flow rates generated by gerotor, external gear and crescent pumps. As far as the lumped parameter models are concerned, different ways of selecting the control volumes into which the pump is split are analyzed and the main governing equations are presented. The principles and the applications of distributed models from 1D to 3D are reported. A specific section is dedicated to the methods for the evaluation of the necessary geometric quantities: analytic, numerical and Computer-Aided Design (CAD)-based. The more recent studies taking into account the influence on leakages of the interactions between the fluid and the mechanical parts are explained. Finally the models for the simulation of the fluid aeration are described. The review brings to evidence the increasing effort for improving the simulation models used for the design and the optimization of the gear machines.

1. Introduction

In positive displacement pumps, the flow rate is generated by the cyclic variation of a number of variable volume chambers and the delivery port is ideally positively sealed from the inlet side. In gear machines the chambers are formed by the mating of two rotors, one of which is driven by the prime mover through a shaft. Merits of gear machines are the low cost due to the small number of components and the high reliability. Such kinds of pumps can be classified as external gear (also called spur gear) or internal gear. The former is constituted by two externally toothed rotors, normally identical, the latter by an internally toothed ring driven by an externally toothed rotor. In turn, the internal gear pumps can be classified as gerotor, if the difference between the number of teeth of the gears is one, and otherwise as crescent pumps, characterized by the presence of a fixed sealing element, the crescent.

The fields of application are simply countless. In general, gear machines are used as low-cost fixed displacement units for simple applications, above all in mobile hydraulics [1]. Some examples in automotive systems include lubricating pumps for internal combustion engines [2], fuel pumps [3], hydraulic power units for automatic [4], dual-clutch [5] and all-wheel-drive transmissions [6], pumps for steering units [7] and for exhaust gas after-treatment applications [8]. In the aeronautical field they are used for the lubrication of helicopter gearboxes [9] and aircraft gas turbine engines [10,11]. Other applications are in medical machines [12,13] and even in dispensers for sugar syrup [14].

Recently, due to the cost reduction of variable speed motors, gear pumps can be used as electrical variable flow units [15,16], with also some innovative solutions, such as the use of the outer gear as a driving rotor [17]. It must be highlighted that some examples of variable timing [18,19] and even real variable displacement machines have been conceived, both external gear and gerotor pumps [20,21]. For low pressure applications, the gears can be made also in plastic material [22,23].

In spite of their simplicity, the construction of the simulation model of a gear pump can be very intricate due to the complexity of the geometry of the variable volume chambers. An additional difficulty is due to the fact that the geometric quantities are strictly related to the particular type of profile used for the gears. The simulation model can be used to analyze many different aspects, such as the contact stresses, the wear or the noise. The analysis of all these features is beyond what is possible in a single article, hence this paper focuses only on the modelling of the real delivered flow rate that determines the volumetric efficiency. Moreover, the simulation of the instantaneous flow rate is a prerequisite for the evaluation of the pressure ripple and finally of the pump noise.

The aim of the review is to present and to contrast different modelling methods for the evaluation of the flow rate in gear pumps, in order to provide updated methodologies to researchers involved in the field of positive displacement machines. After a short description of the three types of machines analyzed—gerotor, internal gear (crescent) and external gear—the different simulation approaches, from 0D to 3D, are described. In particular, as far as the 0D models are concerned, two main topics are discussed: the way of selecting the control volumes and the equations used for the evaluation of the pressure and the flow rate, leakages included. Moreover, for all model types, the main commercial simulation products normally used for the implementation are also presented.

An important section of the paper is devoted to the analysis of the different methodologies for the calculation of the geometric quantities, which are used in most governing equations. Such methods have been classified in analytic, numerical and CAD-based, depending on the type of source used for the evaluation: analytic equations, look-up tables or CAD drawings respectively. In particular, the last method seems very interesting in view of its use in industrial field, since it can be implemented directly by CAD designers without specific competences in pump modelling.

Another crucial issue is represented by the capability of the model to take into account the variation of the clearances due to the micro-movements of the gears and to the elastic deformation of the fixed parts (balance plates, cover); this topic, representing a significant step forward in the simulation, is described in a section dedicated to the fluid-bodies interaction. Finally, a brief description of the models for the fluid aeration implemented in the commercial software products is also presented.

2. Examples of Gear Machines

In this section an example for each type of gear pump is briefly illustrated. In all figures the driving gear rotates clockwise and the delivery port is located on the upper side. Figure 1 shows a low pressure gerotor pump used in a lubricating circuit for internal combustion engines. Ideally, the conjugated profiles of the rotors have as many contact points as the number of teeth N of the outer gear.

Since the N variable volume chambers are identified by the space comprised between two consecutive teeth of the outer gear, they rotate more slowly than the inner rotor, according to the transmission ratio τ = (N − 1)/N; thus the total number of cycles per shaft revolution is N − 1. The rotors are mounted directly in the housing without any automatic compensation of the gaps. The shape of the port plate can be quite complex for improving the filling of the chambers at high speed [24].

In the crescent-type internal gear pumps the difference between the number of teeth of the gears is greater than one. For this reason to ensure the sealing between the suction and delivery volume, a fixed element, integral with the port plate, is needed. A medium pressure industrial pump in depicted in Figure 2.

In Figure 3 an example of an external gear pump is shown. The fluid is transported in the inter-teeth volumes (also called tooth-space volumes or carry-over volumes) along the periphery of the two gears. Two grooves are machined on the balance plates for avoiding trapped fluid in the meshing region. The balance plates house the bushings and are mounted with clearance on the casing so that a small axial movement is allowed. On the rear of the balance plates, the delivery pressure acts on a proper surface limited by a seal in order to generate a clamping force on the gears; in this way the compensation of the axial clearances is obtained.

3. Model Types

The simulation can be performed using different levels of detail in terms of phenomena taken into account, such as thermal effects, cavitation or micro-movements of the mechanical parts. Moreover it is possible to use different spatial discretizations, hence the models can be classified in 0D (lumped parameter), 1D or 2D-3D (CFD). Finally, mixed solutions can be also implemented, for instance, it is not so uncommon to couple a 0D model of a pump with a 1D model of the delivery pipe in order to reproduce the pressure ripple. Another example is represented by a 0D model for the simulation of the main flow and a 2D model of the gaps for the evaluation of the leakages if the geometry is quite complex. It is straightforward that the higher the number of dimensions, the higher the level of detail but also the computational time.

3.1. Lumped Parameter (0D) Models

The lumped parameter simulation consists in assuming that each control volume, into which the computational domain is split, has homogeneous properties, such as pressure and temperature. It is the most popular approach, since represents the best compromise between accuracy and computational time. Each control volume is simulated by a capacitive element, which calculates the pressure as function of the net ingoing flow rate. The control volumes are connected by resistive components calculating the flow rate as function of the pressure drop. The main resistive elements are represented by variable restrictors used for the simulation of the interface between the rotating variable chambers and the inlet/outlet volumes. In this case the flow regime is mainly turbulent. Additional resistive elements, simulated by laminar restrictors, are used for modelling the leakages through the clearances between the two gears and between a gear and the casing. Overall the pump is schematized as a sequence of capacitive and resistive components, some of them with variable geometry as function of the shaft angle.

3.1.1. Control Volumes

The choice of the control volumes has a consequence not only on the complexity of the model, but also on the results. Basically two different approaches are possible [25], hereinafter named single-chamber (SC) and multi-chamber (MC).

With the SC approach, a control volume is associated to each variable volume chamber, moreover there are at least two additional capacitive elements for the inlet/outlet volumes; however it is possible to have more components if it is necessary to split further the pipes.

With the MC approach all chambers connected to the same volume are lumped together, in order to obtain two main variable volumes (one for the inlet and the other for the outlet); moreover additional volumes are used for the isolated chambers and for the trapped volume.

The former approach is more detailed, mainly because it is possible to take into account the pressure drop across the port plate and between the teeth in the meshing zone, while in the latter, by definition, all non-isolated chambers have the same pressure that also coincides with the inlet or the outlet pressure. However, while in the gerotor machines the chambers are always well recognizable and therefore the application of the SC method is quite obvious, in crescent and external gear machines in some angular ranges two chambers are merged together, making the implementation of the SC method more intricate. For an external gear pump [26], the MC approach consists in defining the volumes as shown in Figure 4.

As described in the next section, the differential equation used for the evaluation of the pressure depends on the current value of the chamber volume. A difficulty in the implementation of the MC model is due to the fact that the volumes have discontinuities in correspondence of the aggregation or separation of a carry-over volume. Moreover the trapped volume is defined only when two contact points P₁ and P₂ exist, while it disappears, being merged with the outlet or inlet volume, when there is only one contact point. These discontinuities in the geometric functions must be properly handled to avoid numerical issues in the integration of the differential equations.

The main drawback of the MC method is due to the fact that it is not possible to simulate the pressure peak and the cavitation in the meshing region [27], while with the SC approach it is possible to follow each chamber along its travel from the inlet to the outlet. It means that with the MC method some aspects related to the noise or to the forces on the bearings cannot be reproduced with a good accuracy; nevertheless the simulation of the instantaneous delivered flow rate is normally weakly affected by such a simplification. Hence, if the main purpose of the simulation is only to study the interaction of the pump with the circuit in order to evaluate the pressure ripple, the MC method gives good results [28]. Moreover in case of crescent pumps (Figure 5), the trapped volume exists for a shorter angular range, with also a lower value of the derivative at equal geometry of the driving gear [29]. This represents a less critical issue with respect to the external gear machines, where the management of the trapped volume has a stronger impact on the pump performances.

The basic structure of the lumped parameter model valid for external gear and crescent pumps based on the MC approach is illustrated in Figure 6, where for ease of understanding, the variable volumes are represented as linear actuators. The carry-over volumes, indicated as fixed capacities, are connected one to each other and with the inlet and delivery volumes through laminar restrictors S_t representing the clearances on the tooth tip. Other restrictors S_a can be used for the leakages on the gear sides. The variable flow areas A_T simulate the connection of the trapped volume, when defined, with the inlet/outlet volume through the groove on the balance plates. Obviously, depending on the specific geometry, additional leakages can be considered.

For the SC method [30,31,32] the subdivision of the volumes in an external gear pump is reported in Figure 7. In this case, each control volume V_1,j and V_2,j for the driving and the driven gear respectively is always defined and remains constant with the exception of the meshing region.

In must be highlighted that for this kind of pump the inlet and delivery volumes do not remain constant. In fact the volume ${\mathrm{V}}_{\mathrm{out}}^{\prime }$ does not belong to the chamber 1,2 from which is separated by the flow area A_out1,2 but it must be merged to the delivery volume. In a similar way the variable volume ${\mathrm{V}}_{\mathrm{in}}^{\prime }$ must be aggregated to the inlet volume. The SC method represents the best way for the analysis of the pressure in the meshing zone in gear pumps; however the determination of the volume history implies complex procedures. The basic hydraulic models for external gear and gerotor machines are shown in Figure 8; in the former the number of chambers is equal to the sum of the teeth of the two gears, while in the latter is equal to the number of teeth of the outer rotor. In both cases the chambers are connected in parallel to the inlet and outlet volumes through variable restrictors A_in and A_out respectively.

In the external gear machines, since in the meshing region it is possible to have a connection between two chambers belonging to different gears due to the clearance on the flanks of the teeth (e.g., chambers 1,2 and 2,2 in Figure 7), the passageways through the variable restrictors A_b are also considered. However in some designs, a tooth can have the contact on both sides (dual-flank gear pumps). The gaps on the tooth tips are simulated with the orifices S_t. In general it is possible to have leakages directly between a variable chamber and the inlet/outlet volumes through the axial clearance between the gear side and the casing simulated by the restrictors S_in and S_out, shown only in Figure 8b for ease of representation. Finally, a direct leakage could occur in the internal gear machines due to the radial gap between the outer rotor and the casing (S_io), even if normally this contribution is quite negligible due to the high length of the passageway.

3.1.2. Governing Equations

In each control volume the equation derived from the mass conservation is applied and the pressure p is calculated by integration of the Equation (1):

$$\frac{dp}{dt}=\frac{\beta }{V}\left(\frac{\sum m_i}{\rho }-\frac{dV}{dt}+\alpha \cdot V\frac{dT}{dt}\right)$$

(1)

being V the volume, β the fluid bulk modulus, m_i the mass flow rate through the generic port i-th (positive if ingoing), ρ the density, T the temperature and α the volumetric expansion coefficient of the fluid. The first term in the parentheses represents the variation of the amount of fluid in the control volume, the second term the variation of the control volume itself and third the expansion of the fluid due to the temperature. For the determination of the last term, the conservation of the energy, expressed by the Equation (2), must be applied:

$$\frac{dT}{dt}=\frac{1}{\rho c_{p}V}\left(\dot{Q}+{\displaystyle \sum {\dot{h}}_i-h{\displaystyle \sum m_i+\alpha \cdot V\cdot T\cdot \frac{dp}{dt}}}\right)$$

(2)

where $\dot{Q}$ is the total heat flux, ${\dot{h}}_i$ is the enthalpy flow rate through the generic port i-th (positive if ingoing), c_p is the isobaric specific heat coefficient and h is the specific enthalpy. Hence, the pressure and the temperature for each control volume are calculated by solving the system of differential Equations (1) and (2). However, the pumps are usually tested at constant temperature, moreover the evaluation of the heat exchange ${\dot{Q}}_i$ is quite complex, therefore the simulation is normally performed considering only the dependence on the pressure. With such a simplification, in the Equation (1) it is possible to neglect the third term leading to the Equation (3):

$$\frac{dp}{dt}=\frac{\beta }{V\left(\phi \right)}\left(\sum Q_i-\omega \frac{dV}{d\phi }\right)$$

(3)

in which the geometric quantities, function of the shaft angle $\phi$, are highlighted, being Q_i the volumetric flow rate through the generic port i-th and ω the shaft angular speed.

For the evaluation of the main flow rates entering and leaving the chambers, the equation valid for turbulent flow is used:

$$Q_i=C_d{A}_i\left(\phi \right)\sqrt{\frac{2\left|\Delta p_i\right|}{\rho }}\mathrm{sgn}\left(\Delta p_i\right)$$

(4)

where A_i is the flow area, Δp_i is the pressure drop and C_d the discharge coefficient. However, when the pressure drop tends to zero, the derivative of the Equation (4) versus Δp_i tends to infinite, leading to critical to numerical issues. To solve this problem two solutions are possible. The simplest way is to define a critical pressure drop $\Delta p*$ in correspondence of which the transition between turbulent and laminar flow occurs. If the current pressure drop is higher than $\Delta p*$, then the Equation (4) is used, otherwise the flow rate is calculated with the Equation (5), expressing a linear relationship between the flow rate and the pressure drop:

$$Q_i=k\cdot A_i\left(\phi \right)\cdot \Delta p_i$$

(5)

The constant k is selected so that the Equations (4) and (5) give the same value in correspondence of $\Delta p*$:

$$k=C_d\sqrt{\frac{2}{\rho \Delta p*}}$$

(6)

A more efficient approach is to consider the dependence of the discharge coefficient with the flow number λ [33], which is conceptually similar to the Reynolds number and is defined as:

$$\lambda =\frac{d_h}{\nu }\sqrt{\frac{2\Delta p_i}{\rho }}$$

(7)

being d_h the hydraulic diameter and ν the kinematic viscosity. The discharge coefficient increases with the flow number and tends to a constant value as the flow regime becomes fully turbulent. In the popular simulation software product LMS Imagine.Lab Amesim^® the discharge coefficient is calculated by means of the Equation (8), in order to avoid discontinuities in the first derivative of the flow rate:

$$C_q=C_{q\max }\tanh \left(\frac{2\lambda }{{\lambda }_{crit}}\right)$$

(8)

where C_qmax is the maximum flow coefficient and λ_crit the critical flow number, which indicates the transition between laminar and turbulent regime. Nevertheless, a weak point of all 0D models is the uncertainty about the correct values of C_qmax and λ_crit, which can vary with the operating conditions and the rotor position.

In the leakage passageways the flow regime is typically laminar. With reference to a gap between two surfaces 1 and 2 with length L, width B and relative velocity ν_x (Figure 9a), the volumetric flow rate per unit width along the x axis is:

$$Q_x=\frac{v_{x}h}{2}-\frac{h^3}{12\mu }\cdot \frac{\partial p}{\partial x}$$

(9)

where μ is the dynamic viscosity. The two terms are called Couette and Poiseuille flow respectively.

In gear pumps there are two main leakages: on the tip and on the side of the teeth. For the former, in external gear and crescent pumps (Figure 9b), the geometry of the gap can be considered with constant height (even if such a height is variable with the shaft position) and the Equation (9) can be simplified as:

$$Q_x=\frac{v_{x}h}{2}+\frac{h^3}{12\mu L}\left(p_1-p_2\right)$$

(10)

being in this case ν_x is the peripheral velocity of the tooth tip. In gerotor pumps, the geometry of the gap has a variable height (Figure 9c), therefore it is necessary to integrate the pressure gradient from the Equation (9) and to apply the boundary conditions in order to obtain the solution (11) [34,35]:

$$Q_x=\frac{v_x}{2}\frac{I_1}{I_2}+\frac{p_1-p_2}{12\mu I_2};I_1={\displaystyle \underset{-a}{\overset{a}{\int }}\frac{1}{h^2}}dx;I_2={\displaystyle \underset{-a}{\overset{a}{\int }}\frac{1}{h^3}dx}$$

(11)

where ν_x in this case is the sliding velocity between the teeth and a is a distance far way enough from the point of minimum height. The relationship between the height and the coordinate x obviously depends on the specific profile of the gears. In case of outer gears with circular-shaped teeth (the most common type), it is possible to substitute the profile of the inner gear in correspondence of the minimum gap height h_min with the osculating circle with center C_i, so that both surfaces have a circular geometry with radii S and r_c that can be easily expressed analytically.

If the equations of the profiles are unknown, it is possible to use Equation (10) as an approximate solution using the minimum distance h_min between the gears for h and an equivalent length of the gap L* that must be properly tuned. Pellegri et al. [36] proposed to use the length L* for which the gap height is $\epsilon \approx 10\%$ higher than the minimum distance h_min.

For the leakages on the sides of the gears, the Equation (10) is normally used, where in this case L is an equivalent length; to a first approximation it can be chosen in correspondence to half the height of the tooth (Figure 10a). Such a length can be further reduced to take into account the shape of the port plate. The total leakage is then obtained by multiplying the Equation (10) by the height of the tooth, b_i or b_e. As alternative, knowing the equation of the gear profile, it is possible to define a geometric relationship expressing the tooth width L_i(r) of the inner rotor and L_e(r) for the outer as function of the radius [35,37], so that the Poiseuille flow rate can be calculated with the Equation (12), for the inner and outer gear respectively, in which it is possible to consider also the reduction of the tooth length due to the port plate shape (Figure 10b):

$$Q_i=\frac{h^3\left(p_1-p_2\right)}{12\mu }{\displaystyle \underset{Ri}{\overset{Ri+bi}{\int }}\frac{dr}{L_i\left(r\right)}};Q_e=\frac{h^3\left(p_1-p_2\right)}{12\mu }{\displaystyle \underset{\mathrm{Re}-be}{\overset{\mathrm{Re}}{\int }}\frac{dr}{L_e\left(r\right)}}$$

(12)

Also the evaluation of the Couette flow can be improved by considering that the relative velocity between the gear and the port plate is not constant along the entire tooth height, but it is function of the distance from the gear centre [35]. The technique of splitting the tooth side in several slices has been adopted also for external gears machines [38].

A different approach is used in the software GT-SUITE^® [39] for the evaluation of the flow rate in rectangular gaps. The method has been applied for the evaluation of the inter-teeth leakages in a gerotor pump [40]. The flow rate is calculated with the Equation (13):

$$Q=A\sqrt{\frac{2\left|\Delta p_i\right|}{\rho \left(1+C_f\frac{A_s}{A}\right)}}\mathrm{sgn}\left(\Delta p_i\right)$$

(13)

where the cross-sectional flow area is $A=H\cdot h$, H is the gear thickness, $C_f=24/\mathrm{Re}$ is the friction factor function of the Reynolds number and A_s the internal surface defined as:

$$A_s=2\left(H+h\right)L$$

(14)

Finally, in external gear pumps, the leakage through the radial clearance between the balance plates and the housing can also be considered [41] using the Poiseuille term of Equation (10); the flow occurs between the carry-over volume and the low or high pressure volume, depending on the gear position.

3.2. Distributed Parameter (1D) Models

In a 1D model, the pump is discretized into several volumes. In particular the suction and delivery ducts, simulated with a single capacitive component in a 0D model, are split in many volumes connected in series along the pipe axis. In each subvolume not only the compressibility, but also the friction and the inertia of the fluid are taken into account. This approach allows simulating the pressure waves in the pipes and it is necessary to evaluate the pressure ripple generated by the interaction between the flow oscillation of the pump and the circuit impedance. A 1D schematization is reasonable if the control volume develops along a preferred dimension, as such the axial direction of a duct. The variable chambers, due to their shape, continue to be simulated as 0D components. Most of the pump models described in the open literature have been implemented in LMS Amesim, where the pipes can be discretized in two different ways. The first approach considers N internal nodes forming the staggered grid shown in Figure 11 for the simulation of a pipe with length L and volume V, where each circle represents the capacitive effect and the rectangles the friction and the inertia. The former evaluate the pressure and the latter the flow rate for each node. If the thermal-hydraulic library is used, the temperature and the enthalpy flow rates are also calculated.

As alternative, it is possible to use a real 1D-CFD model based on a one-dimensional grid; in this case the continuity and momentum equations are computed using an independent solver with respect to the rest of the 0D model. With the thermal-hydraulic library also the energy equation is solved.

On the contrary, the flow model available in GT-SUITE is grounded always on a 1D discretization of the volumes (Figure 12a). Also in this case the equations of conservation of mass, momentum and energy are solved. The scalar variables are considered to be homogeneous in each volume, while the vector variables are evaluated at the boundaries. Also the junctions, in this case called flowsplits, are modelled as multiport volumes. With respect to LMS Amesim, not only the pipes, but also the inlet and delivery volumes of the pump can be discretized, typically in 2 or 3 parts. It means that, with reference to the Figure 12b, a pressure drop between the volumes V_OUT1, V_OUT2 and V_OUT3 can be taken into account. Obviously it is necessary to calculate the flow area for the connection between the variable chambers and each subvolume. Examples of gerotor pumps modelled with GT-SUITE can be found in the references [40,43].

3.3. Computational Fluid Dynamics (2D) Models

The 2D computational fluid dynamics (CFD) approach consists in solving the Navier-Stokes equations in a two-dimension domain. In case of limitations of the computational capabilities, this technique can be applied to a slice of pump for studying the flow only in a plane perpendicular to the shaft [44,45,46,47,48,49]. However nowadays the entire pump can be fully simulated in 3D, hence the 2D CFD is used mainly for the evaluation of the pressure distribution in the lateral gaps of the rotors, above all in external gear pumps. In fact, in this kind of machines the local pressure in the gap is important not only for a better evaluation of the leakages, but also for the calculation of the clamping force exerted by the balance plates on the rotors. If the Navier-Stokes equations are applied in a lubricated gap with incompressible Newtonian fluid (with the same reference frame as in Figure 9a) it is possible to neglect some terms:

• the inertial and convective forces,
• the pressure gradient and the velocity along the gap height (z axis),
• the velocity gradient along the gap length and width (x and y axes),

Moreover if steady state conditions are considered, the components of the pressure gradient are expressed by Equation (15):

$$\frac{\partial p}{\partial x}=\mu \frac{{\partial }^2{u}_x}{\partial z^2};\frac{\partial p}{\partial y}=\mu \frac{{\partial }^2{u}_y}{\partial z^2};\frac{\partial p}{\partial z}=0$$

(15)

The Reynolds Equation (16) is obtained by applying the mass conservation and assuming that the surface 2 representing the port plate is fixed:

$$\frac{\partial }{\partial x}\left(h^3\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(h^3\frac{\partial p}{\partial y}\right)=6\mu v_x\frac{\partial h}{\partial x}+6\mu v_y\frac{\partial h}{\partial y}$$

(16)

The integration of Equation (16) allows to obtain the 2D pressure distribution p(x, y). Starting from the Navier-Stokes equations, it is also possible to obtain the two components of the fluid velocity u_x and u_y along the x and y axes between the planes with relative velocity ν_x and ν_y:

$$u_x=\frac{z\left(z-h\right)}{2\mu }\cdot \frac{\partial p}{\partial x}+\frac{h-z}{h}{v}_x;u_y=\frac{z\left(z-h\right)}{2\mu }\cdot \frac{\partial p}{\partial y}+\frac{h-z}{h}{v}_y$$

(17)

Finally, the flow rate through the gap is calculated by the integration of the velocity along the z axis. The method has been applied in the last years with more and more levels of detail.

The basic approach is to consider a constant gap height [50,51], so that Equation (16) becomes simply ${\nabla }^{2}p=0$. In this way the pressure distribution depends only on the boundary conditions and on the geometry of the teeth and of the porting plate. In practice the obtained flow rate is an extension in 2D of Equation (10) used in the lumped parameter models.

A further step is to consider a constant tilt of the balance plate with respect to the face of the rotors in external gear pumps. In this way the so called “physical wedge” effect is taken into account. In fact a hydrodynamic pressure distribution is generated when the fluid is moving in a gap with decreasing height (the same working principle of the journal bearings). The influence of the tilt angle on the pressure distribution and on the leakage flow can be found in [52,53]. Additional improvements can be obtained by considering the movement of the balance plate (see Section 5.2).

3.4. Computational Fluid Dynamics (3D) Models

The 3D fluid dynamics simulation represents the most advanced method for the evaluation of the flow field in the pumps. In this case the Navier-Stokes equations are solved in a 3D domain discretized in a variable geometry mesh. The main issues for its application have always been the way for deforming and updating the mesh as the shaft rotates, the sliding interfaces and the grid refinement in the gaps. However, the advantages are the possibility to take into account the non-uniform distribution of the pressure in each variable chamber, due for instance to the centrifugal force, and to consider the shape effect and the orientation of the chambers with respect to the inlet and outlet volumes.

The first 3D simulations of an entire external gear and gerotor pump were performed about 20 years ago [54,55]. Due to the high computational times, many researchers have adopted different hybrid strategies, such as the simulation in 3D of only a portion of the pump (meshing region, leakages or pipes) in order to obtain data to be used as input for a lumped parameter model. Even when the pump is entirely simulated in 3D, the results are often used only for some specific research activities or for tuning a less detailed fast-running model.

In the last 5 years, most of the 3D CFD simulations of gear pumps have been performed with the dedicated software PumpLinx^® [56] based on templates available for the main types of pumps. However it is also possible to simulate hydraulic valves [57,58]. An example of 3D model of a gerotor pump is shown in Figure 13. The computational domain is generated starting from the surfaces in STL (STereo Lithography) format of the different components, such as rotors, port plate and so on. It is possible to generate an unstructured body-fitted Cartesian grid for the fixed volumes and also structured hexahedral cells for meshing the variable chambers and the gaps. The treatment of rotating and sliding components is managed automatically by the software. Further details can be found in the reference [56].

Some examples of studies performed with PumpLinx on gear machines are briefly described hereinafter. As far as the gerotor pumps are concerned, one of the first studies was carried out by Hsieh, who used the 3D simulation for analyzing the influence of the geometric parameters in a pump with epicycloid-hypocycloid profiles [59]. Later, the same author studied the effect of a novel variable clearance design [60]. Another example, where the CFD analysis is used for studying new gear profiles, is the work made by Hao et al. [61]; in this case the aim of the new design is to increase the average flow rate in low-speed conditions. A typical application of the 3D models is the determination of the volumetric efficiency in different operating conditions [62] and the optimization of the configuration of the port plate [63]. With reference to the delivered flow rate, in the reference [64] the influence of the geometric parameters on the filling capability of the pump at high speed has been studied. There are also some recent examples of comparison between 0D and 3D models [36] and a practical use of the CFD for tuning a lumped parameter model [65]. In general, a common application of the CFD is the evaluation of the discharge coefficients [66,67,68].

So far the only example of simulation of a crescent pump is the work written by Jiang et al. [69], where the authors determined the flow-speed characteristic up to the condition of cavitation.

Examples of gear pump models can be found in [7,70], while the approach used by Heisler et al. [71] for the simulation of helical gears considered as a series of thin gears rotated progressively in accordance with the helix angle is noteworthy. The software has been also used for simulating a variable displacement external gear pump [72] based on the principle of the sliding gears [20], but without the displacement control. Quite uncommon is the simulation of a gear flow meter [73]. Some authors performed a system-level simulation, since they studied in 3D not only an external gear lubricating pump, but also the entire automotive oil circuit [74], with a still reasonable number of 8 million cells for grid independent results.

Another popular CFD software used for the simulation of gear machines is ANSYS Fluent^®. Since it is a general purpose code, it does not provide specific templates for the simulation of pumps; hence the variable geometry mesh must be managed by the user by means of User Defined Functions (UDF). Although some authors simulated the entire pump [75,76,77], other studies focused only on a portion of the machine, as such only the meshing region in an external gear pump [78] or the tooth tip leakages in gerotor and external gear machines [79].

With reference to the clearances, Gamez-Montero et al. [80] developed a new boundary condition, named “viscous wall-cell” for a model of a gerotor pump in ANSYS Fluent. Such a condition, written in C++ language, is used to virtually increase the local fluid viscosity in the tooth tip gap in order to simulate the contact between the gears. The same approach has been used with the open source software OpenFOAM^® in an external gear pump [81] and in a mini-gerotor pump [82]. In this last case the authors have also tested a new boundary condition for maintaining a good mesh quality in the inter-teeth gaps.

Gerotor pumps have been simulated also with ANSYS CFX^® for contrasting the performance of profiles constituted by multiple curves [83]. The same software has been used by Yoon et al. [84] for the simulation of an external gear pump by means of the immersed boundary method [85]. With this technique it is not necessary to adapt the grid to the contour of the solid bodies and consequently the remeshing can be avoided if the bodies are moving. A Cartesian grid is used and the cells can be entirely or partially included is the solid parts. For the former the governing equations are not solved, for the latter the momentum equation is modified by adding a source term in order to force the fluid to move with the same velocity of the solid.

STAR-CD^® is a software product largely used for the 3D in-cylinder simulation in internal combustion engines; however it has been used also for the simulation of gerotor pumps [86]. In this case the grid was generated with the pre-processor PROSTAR^® and the rotation/deformation of the mesh was managed by means of a script. Another example is the work of Elayaraja et al. [87]. The same pre-processor was used by Zhang et al. [88] for generating the mesh used for a simulation of a gerotor pump in CFD-ACE+^®.

4. Evaluation of the Geometric Quantities

As shown in Section 3.1.2, the governing equations used in the 0D models require the law of variation of the volume along with its angular derivative and of the flow areas as a function of the shaft angle. In gear machines, the determination of such functions is particularly complex and depends on the type of profile used for the teeth. The most popular profile type for the external and crescent machines is represented by the involute of circle, while for the gerotor pumps by the circular arc. However, several other shapes have been studied in the last years.

In this paper the intricate aspects related to the mating of the gears will not be considered, but the general methodologies used for extracting the quantities of interest are reviewed. It must be highlighted that the angular derivative of the volumes is the most important quantity, since it is strictly related to the flow rate; hence its angular history must be assessed with a very good precision. It is straightforward that it would be better to calculate all quantities with the maximum accuracy, however from the Equation (3) it can be noted that an uncertainty on the value of the effective bulk modulus could make useless the correct evaluation of the chamber volume. This is particularly evident in the low pressure pumps where, due to the presence of small amounts of separated air, the effective bulk modulus can differ to a great extent from the value of the pure liquid [89]. In such operating conditions, the use of a constant value for the volume in the denominator of the Equation (3), instead of a function variable with the angle $\phi$, could give very similar results [28].

Analogously, a wrong value of the discharge coefficient can make ineffective a very precise calculation of the flow area with a strong influence on the flow rate supplied by the Equation (4). Basically, the different methods for the evaluation of the geometric quantities can be classified as analytic, numerical and CAD-based, hereinafter explained.

4.1. Analytic Methods

Analytic methods consist in starting from the equations of the profiles, of the line of contact and of the port plate geometry for finding the exact expression of the volumes, derivatives and flow areas. However only in a few simple cases it is possible to determine an analytic function, while normally a numerical integration is necessary. Nevertheless, some exact formulations can be found above all for the angular derivative of the control volume for both the MC and SC approaches. The volume is then calculated by numerical integration of the derivative.

The main advantage of the analytic procedure is the possibility to perform easily parametric studies. The drawback is the long implementation time and the fact that is valid only for a predetermined type of profile.

4.1.1. Direct Evaluation of the Derivative

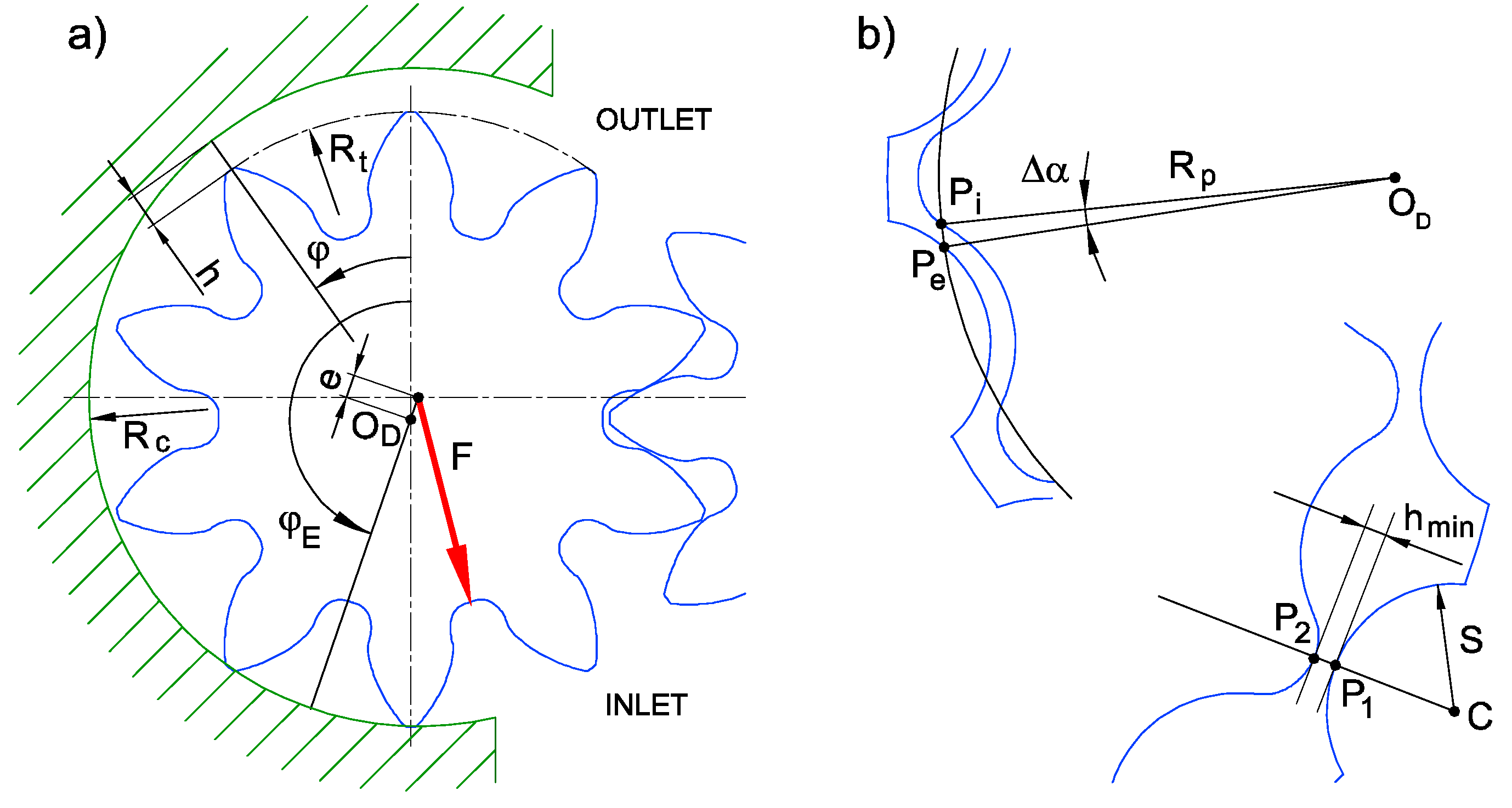
The vector-ray method allows calculating directly the angular derivative of the volume as function of the shaft angle starting only from the analytic expression of the line of contact. It can be applied for the determination of the derivative of a volume that is limited by the theoretical contact points between the gears or between a gear and the casing. Hence it can be used in all pumps simulated with the MC approach, since by definition in a positive displacement machine the delivery volume is always positively sealed from the inlet volume by at least a contact point. Moreover it can also be used in the gerotor pumps with the SC method, since in this kind of machine each chamber is ideally separated by the other chambers by two consecutive contact points.

With reference to the Figure 14, a vector-ray ${\rho }_D$ is a rotating segment joining the center O_D of the driving gear with a contact point 1 or 2, while ${\rho }_d$ refers to the center O_d of the driven rotor.

It is possible to demonstrate that the derivative of the volume limited by the contact points 1 and 2 (or 2’ and 2”) is given by the Equation (18), where H is the axial thickness and τ is the transmission ratio with sign, it means that in case of an external gear pump with identical rotors is equal to −1 [29]:

$$\frac{dV}{d\phi }=\frac{1}{2}H\left[\left({\rho }_{D1}^2-{\rho }_{D2}^2\right)+\tau \left({\rho }_{d2}^2-{\rho }_{d1}^2\right)\right]$$

(18)

Equation (18) can be obtained following different ways. The most used is to consider that the volume variation is the volume swept per unit angle by the vector-rays as the shaft rotates. An alternative point of view is that in an ideal pump the contribution of the torque on the shaft induced by the delivery pressure acting in a chamber is the product between the pressure and the angular derivative. With reference to the gerotor pump in Figure 15, the torque M_D per unit pressure on the inner gear can be expressed as the cross product between the force F_i on the gear and the position vector of its point of application A:

$$\frac{dV}{d\phi }=\frac{\left|M_D\right|}{p}=\frac{1}{p}\left|\overline{{\mathrm{O}}_{D}A}\times F_i\right|$$

(19)

Since both the force and the distance of the application point from the centre O_D can be expressed as function of the coordinates of the contact points 1 and 2, it is possible to rearrange Equation (19) in order to obtain the dependence on the square of the vector-rays. Since the torque on the shaft is also generated by the contribution of the force F_e on the driven gear modulated by the transmission ratio, Equation (18) is obtained.

A variant of this approach is to consider that in an ideal pump with incompressible fluid the input mechanical energy must be equal to the output hydraulic energy [1].

Regardless of the method, it is straightforward that the sum of the negative derivatives of all volumes supplies the instantaneous theoretical flow rate delivered by the pump per unit speed; therefore its mean value over the angular pitch Δ$\phi$ represents the displacement V_p of the machine:

$$V_p=-\frac{1}{\Delta \phi }{\displaystyle \underset{0}{\overset{\Delta \phi }{\int }}{\displaystyle \sum _i\min \left(\frac{d{V}_i}{d\phi },0\right)}}d\phi$$

(20)

Different authors have derived the expression (18) for gear pumps (but it can be used also for vane pumps [68]) for the evaluation of the volume derivative, of the kinematic flow ripple or of the flow irregularity index, in particular:

• Fabiani et al. [25] determined the derivatives for a gerotor pump to be used with both SC and MC approaches, moreover Equation (18) has been applied also for the evaluation of the flow area in case of a simple radial rim,
• Manring and Kasaragadda [90] calculated the theoretical flow ripple in external gear pumps with different numbers of teeth for the two rotors,
• Huang and Lian [91] obtained a closed solution of the kinematic flow rate for external gear pumps,
• the author of this paper [29] determined the expressions of the volume derivatives, displacement and flow ripple index for crescent pumps valid also for external gear machines,
• Zhou et al. [92] determined the kinematic flow rate of a crescent pump with conjugated involute gears,
• Song et al. [93] calculated the instantaneous flow rate and the trapped volume of a crescent pump with conjugated straight-line internal gear,
• Huang et al. [94] studied an external helical gear pump.

In particular, with reference to helical gears, Equation (18) must be generalized as follows:

$$\frac{dV}{d\phi }=\frac{1}{2}{\displaystyle \underset{0}{\overset{H}{\int }}\left[\left({\rho }_{D1}^2-{\rho }_{D2}^2\right)+\tau \left({\rho }_{d2}^2-{\rho }_{d1}^2\right)\right]}dz$$

(21)

In fact the vector-rays, for a given position $\phi$ of the shaft, are progressively rotated by an angle that depends on the axial coordinate z and on the helix angle, hence it is necessary to integrate the function along the entire axial height H. An example of simulation model of helical gear pump is given in [67].

4.1.2. Evaluation of the Volume

For crescent and external gear pumps, if the profile of the teeth is the very common involute-type, the analytic expression of the vector-rays as function of the shaft angle is given by a second-order polynomial. Consequently Equation (18) can be integrated analytically, although the integration’s constant must be determined numerically or graphically. In a gerotor pump, even with the classical circular arc profiles, it is not possible to obtain a closed-form of the integral of the Equation (18), which must be integrated numerically.

As an alternative, it is possible to obtain directly the volume history starting from the equations of the gear profiles. The easiest procedure consists in calculating the area subtended by the profiles expressed in polar coordinates between two consecutive contact points. Moreover, also the equation of the line of contact is necessary for determining the limits of integration.

With reference to a gerotor pump (Figure 16), the equations of the profiles of the inner and of the outer gears must be expressed in the form ${\rho }_i\left(\mathsf{\psi }\right)$ and ${\rho }_e\left(\mathsf{\psi }\right)$ respectively [25]. For a given position of the shaft, from the equation of the line of contact the initial and final angles ${\mathsf{\psi }}_{i1}$ and ${\mathsf{\psi }}_{i2}$ limiting the hatched slice of the inner gear are identified. In a similar way the angles ${\mathsf{\psi }}_{e1}$ and ${\mathsf{\psi }}_{e2}$ relative to the external gear can be determined.

The volume of the chamber limited by the contact points 1 and 2 is calculated with Equation (22):

$$V=\frac{1}{2}H\left({\displaystyle \underset{{\mathsf{\psi }}_{e2}}{\overset{{\mathsf{\psi }}_{e1}}{\int }}{\rho }_e^{2}d\mathsf{\psi }-{\displaystyle \underset{{\mathsf{\psi }}_{i2}}{\overset{{\mathsf{\psi }}_{i1}}{\int }}{\rho }_i^{2}d\mathsf{\psi }}}\right)$$

(22)

The same method can be used for the evaluation of the flow area in case of a simple radial rim of the port plate. In fact it is enough to substitute one of the rotating segments $\overline{{\mathrm{O}}_{D}1}$ or $\overline{{\mathrm{O}}_{D}2}$ with a fixed line representing the rim.

Another method adopted for gerotor machines consists in expressing the volume of the chamber as the algebraic summation of several elementary geometric figures, such as triangles and circular sectors [37,95] and of the area subtended by the profile of the inner gear. However this last term cannot be expressed in a closed-form and requires a numerical integration.

4.1.3. Teeth Clearance

As anticipated in Section 3.1.2, the gap on the tooth tip varies with the shaft position. In external gear and crescent pumps such a variation is generated by the movement of the rotor axis due to the clearance between the shaft and the bushings. In fact, with reference to the Figure 17a, the force F due to the pressure distribution on the gears moves the shafts downwards and the clearance on the tip of the first tooth leaving the inlet volume is recovered. As the inter-teeth volume rotates, the clearance increases up to the maximum value before the connection of the volume to the delivery side. The current eccentricity e and the corresponding direction ${\phi }_{\mathrm{E}}$ of the rotors can be calculated using the classical equations of the journal bearings as function of the current speed and load [50,96]. In order to take into account also the wear due to the running in process [66,97], the radius of the casing can be variable with the angle. The wear profile can be supplied as look-up table obtained by experimental measurements. The actual value of the tip clearance at a generic angle $\phi$ can be calculated with Equation (23) [50]:

$$h\left(\phi \right)=\left(R_c-R_t\right)-e\cdot \cos \left(\phi -{\phi }_E\right)$$

(23)

being R_t the external radius of the gear and R_c the radius of the housing.

In case of a gerotor pump, even if the ideal case of no clearance on the shaft bearings is assumed, the gap between the rotors is variable with the angular position. The clearance usually is generated by increasing the internal diameter of the outer gear. If the axes of both gears are assumed fixed, an angular backlash Δα must be recovered to have the contact between the gears. Hence in case of real gears only one or two pairs of teeth are in contact in the region in correspondence of the beginning of the suction phase, while for the remaining part of the rotation a variable clearance exists.

Some complex analytic methods, such as the Tooth Contact Analysis (TCA) [98], have been developed for the calculation of the real line of contact and also of the clearance between the pair of teeth not in contact [99,100,101]. As alternative, it is possible to use a less refined but effective procedure [34]. A generic point P_i integral to the inner gear moves along the circumference with radius R_p, which intersects the profile of the outer tooth in the point P_e (Figure 17b). The point P* such as $\overline{{\mathrm{P}}_{\mathrm{e}}\mathrm{P}*}=\min \left(\overline{{\mathrm{P}}_{\mathrm{e}}{\mathrm{P}}_{\mathrm{i}}}\right)$ will be the contact point. Knowing the equations of the profiles, it is possible to calculate numerically the coordinates of the point P*. The angular backlash is:

$$\Delta \alpha =\arcsin \left(\frac{\overline{{\mathrm{P}}_{\mathrm{e}}\mathrm{P}*}}{R_P}\right)$$

(24)

Once the inner gear has been rotated by the angle Δα, it is possible to calculate the distance between two teeth. In case of circular arc profiles, the common normal to the profiles in correspondence of the points P₁ and P₂ with minimum distance passes through the centre C of the outer rotor tooth. Hence the clearance h_min can be found numerically using Equation (25):

$$h_{min}=\min \left(\overline{{\mathrm{P}}_2\mathrm{C}}\right)-S$$

(25)

To a first approximation the angle Δα can be considered constant with good results. However if the variation of Δα with the shaft angle $\phi$ is also taken into account [35], it is possible to obtain the same accuracy of the more complex analytic methods.

It must be stressed that it should not be strictly necessary to know the relationship between the clearance and the angle for the entire revolution of the gears, since a pressure difference across the gap occurs only when two chambers are connected to two different volumes. In practice the clearance has an influence only around the positions of minimum and maximum volume of a chamber.

4.2. Numerical Methods

The numerical procedure consists in storing the X-Y coordinates of the gear profiles and of the contour of the port plate and to manipulate the data for obtaining all necessary quantities. It does not matter where the data come from, they can be generated analytically, from a CAD drawing or even from a measurement of the gears. To avoid confusion, it is worth to highlight that in this paper a “numerical method” is an approach that is not based on analytic definitions, while a procedure is considered “analytic” if some equations are need, even if they can be solved only by means of numerical methods. For the evaluation of the chamber quantities, the operations that must be performed for different angular positions $\phi$ of the shaft are:

• Positioning of the gears at the shaft angle $\phi$ using the well-known equations for the rotation of the reference frames (Figure 18a)
• Extraction of sub-vectors containing the coordinates of profile portions relative to a specific control volume (e.g., a chamber)
• Identification of the points P1 and P2 in correspondence of which the distance between the profiles of the gears or between a gear and the casing is minimum, ideally the contact points (Figure 18b)
• Creation of an ordered vector containing the contour of the entity (e.g., chamber surface, flow area) by cutting out the data whose coordinates are outside the points of minimum distance (Figure 18c)
• Calculation of the geometric quantities of the obtained closed polyline, such as area and hydraulic diameter.

For instance, if (x_i, y_i) are the generic coordinates of the points describing the contour of a chamber, the volume can be calculated with Equation (26):

$$V=\frac{1}{2}H{\displaystyle \sum _{i=1}^N\left(y_i+y_{i+1}\right)}\left(x_i-x_{i+1}\right)$$

(26)

If the coordinates of the gears are accurate enough, in step 3 it is also possible to evaluate the minimum distance representing the clearances that can be used for calculating the leakages. Moreover from the coordinates of the contact points, other geometric quantities can be measured, such as the direction of the force exerted by the fluid on the gear, useful for determining the components of the resultant force on the shaft.

A lumped parameter model of a gerotor pump grounded on a numerical approach for the determination of the geometric quantities is reported in [102], while an algorithm for determining the chamber volume history in external gear machines is described in [103].

The determination of the flow areas is more complicated, since it requires the evaluation of the intersection between the profile of the chamber and the contour of the port plate. The latter in some cases can be very complex, as in the gerotor pump shown in Figure 1b. A possible approach [104] consists in discretizing the region of interest and to count the number of “pixels” in common between the chamber and the port plate, both defined numerically (Figure 19a). In this way it does not matter if the total flow area is composed by different separated parts, as in Figure 19b.

As far as the flow areas are concerned, Gamez-Montero et al. [105] have developed a package called GEROLab written by using the open source software for numerical computation Scilab^®. Among the other features, GEROLab is also able to calculate the flow area of the chambers when a triangular or trapezoidal relief groove is present on the port plate rim [106].

4.3. CAD-Based Methods

This approach exploits the tools already available in commercial CAD software products. The method is becoming very attractive due to the fact that nowadays all components are designed directly in 3D parametric modellers, which allow performing automatic operations for tracking the geometric quantities as the shaft rotates. The main advantage is that no algorithm must be implemented and at least only some macros must be written for fully automating the evaluation of the quantities and for exporting the data in a proper format. The steps to be executed depend on the specific CAD software used, but basically can be synthesized as follows:

• If not already available, construction of the 3D CAD model with all mates properly set in order to match the degree of freedom of the real components.
• Creation of virtual parts representing the control volumes and the respective intersections for the flow areas.
• Definition of the features for the measurement of the volumes and of the flow areas and for exporting the data in a file with a proper format.
• Creation of multiple configurations of the assembly based on the shaft angle.
• Running of the simulation or of the macro that at each angular step calculates automatically the desired quantities.

In Figure 20 an example grounded on PTC Creo Elements/Pro^® is shown for a gerotor pump [107]. After the construction of the assembly, the surfaces of the profiles are used for the identification of the contact points. Then the chamber is isolated by cutting out the volume occupied by the gears from an auxiliary circular sector part (a). Additional virtual components are generated by extruding the timing rim profiles and the flow areas are formed by the intersections with the chambers; (b). Finally the virtual components are measured using specific features; (c). The procedure is repeated automatically for each angular step defined by the user. The same method has been applied to other machines [108]: external gear and roller pumps, orbit motors, single vane vacuum pumps.

A method based on the popular software Solidworks^® has been developed by Gherardini et al. [109] for different pumps, among which external gear and gerotor machines and by Jeong et al. [110] for gerotor pumps. Another example of CAD-based method is the procedure implemented in Catia^® by Kim et al. [111].

In most of the above-mentioned studies, the outcomes from the CAD procedure (volumes, derivatives and flow areas) have been used as input for a 0D model of the pump in the LMS Amesim environment, even if the generated data are software independent. On the contrary, the CAD-based tool GEM3D^® is a 3D graphical pre-processor of the software GT-SUITE. It allows, starting directly from the 3D geometry, not only to extract the necessary geometric quantities as function of the shaft angle, but also to build the 1D hydraulic model of the pump [40]. The CAD model in STL format can be imported directly in GEM3D or through ANSYS SpaceClaim^®.

5. Fluid-Bodies Interaction

The radial clearances between the rotors and the casing and between the shaft and the bushings are not only source of leakages, but are also responsible of the micro-movements of the gear axes. In a similar way, the axial clearance induces a translation and a tilt of the gears or of the balance plates. The movement is generated mainly by the radial and axial forces acting on the bodies due to the pressure distribution and by the contact forces exerted between the rotors. If the pump is well designed, the resultant of the forces on the rotors should be balanced by the pressure distribution in the gaps in order to work always in conditions of hydrodynamic lubrication. The fact that the rotors do not remain in their theoretical position implies asymmetric clearances, with a consequence on the evaluation of the leakages. Moreover, as already mentioned is Section 3.3, the lateral gaps should be considered with a variable height. Finally, even the hypothesis of perfectly rigid bodies under the action of the pressure forces could not be completely valid.

With the exception of the case of the tip clearance in Figure 17a, it is not easy to evaluate the movement of the gears, hence in most of the simulation models the only type of motion considered is the theoretical rotation of the rotors around their fixed axes. Therefore the major issue, known the overall clearance, is to establish a proper subdivision of the gap on the two sides of the gears, above all if the pump is not provided of balance plates, as in some low pressure machines. The same problem arises on the radial clearance. Tests performed on different gerotor pumps with both 0D and 3D simulation codes [64,65] have demonstrated that the hypothesis of symmetric clearance leads normally to an underestimation of the leakages. On the contrary the assumption that the gap is entirely recovered on one side is too pessimistic. The reason can be understood by considering a rectangular gap, whose flow rate is given by Equation (10): it is evident that the Poiseuille flow rate in two gaps with height h, is four times smaller than in a single gap with height 2h.

Normally, the best compromise is to use an intermediate position, even if it depends on both the oil temperature and the pump speed [65], which have an influence of the hydrodynamic lubrication: the consequence is that the same mean position is not suitable for all operating conditions. Hence, it is evident how the estimation of the real equilibrium position of the rotors represents a major breakthrough in the simulation of the gear pumps.

The importance of considering the variation of the clearances with the operating conditions increases in all cases where the leakages tend to be higher, in particular with high delivery pressure, low viscosity and wide temperature range. Therefore, pumps with a higher maximum working pressure are more sensitive to the current value of the clearance with respect to a low pressure pump (e.g., an external gear pump with respect to a gerotor). Nevertheless, in a gerotor fuel pump, in spite of the low delivery pressure, due to the extremely low viscosity of the working fluid the evaluation of the real position of the gears’ centres is a crucial aspect. Finally, in a lubricating pump for internal combustion engines, due to a very wide temperature range up to almost 200 °C, the clearances cannot be too tight, since the thermal expansion must be taken into account; hence in this application, the knowledge of the current gap is more important than in an industrial pump.

5.1. Radial Micro-Motion

There have been a few attempts at calculating the real position of the gear axes under operating conditions. Hua et al. [112] developed two modules in MATLAB^® running in cosimulation for crescent machines. The first one, starting from the equations of the profiles, calculates the position of the contact points and, for a given value of delivery pressure, evaluates the force on the outer rotor. The second module integrates the Reynolds equation in the radial clearance between the outer rotor and the housing and calculates the load capacity generated by the oil film. The current eccentricity and tilt of the outer rotor are given by the equilibrium of the above-mentioned forces.

Mucchi et al. [113] developed a model of an external gear pump where the position of the gear axes is calculated iteratively by the equilibrium of the radial forces on the shafts and of the bushing reactions. The leakages on the tooth tips are evaluated accordingly considering also the wear profile of the casing.

Pellegri and Vacca [114] evaluated the gear position using a CFD simulation for calculating the pressure distribution and, as a consequence, the load capacity of the shaft bushings. The same authors developed a lumped parameter model in LMS Amesim of a gerotor pump that takes into account the motion of the outer gear centre [115]. The model evaluates the geometric quantities with a numerical method (see Section 4.2) by means of a pre-processor. In particular, it generates a look-up table where several geometric features (volume, flow areas, clearance and so on) are function not only of the angular position, but also of the real coordinates of the outer rotor centre, considering all possible positions allowed by the clearance between the gears. During the simulation, the following forces on the outer gear are calculated:

• on the internal surface due to the pressure in all chambers,
• the contact force between the rotors,
• the hydrodynamic force of the oil film on the external diameter simulated as a short bearing (Ockvirk solution [116]).

Based on the equilibrium, the current coordinates of the outer gear centre are calculated. Finally the geometric functions, and in particular the inter-teeth clearances, are calculated by interpolation of the look-up table.

5.2. Variation of the Axial Clearances

Since the leakage flow depends on the cube of the gap height, the variation of the axial clearances due to the pressure field has a strong influence on the volumetric efficiency. In some cases the variation of the gap is due to a significant deformation of the pump cover, as in crankshaft mounted lubricating pumps, gerotor [117] and internal gear. Kini at al. used the flow solver and the stress model of the software product CFD-ACE+ for the evaluation of the cover deformation of a gerotor lubricating pump [118]. The deformation field calculated with ANSYS has been used to evaluate an equivalent stiffness used for correcting the gap height as function of the current delivery pressure in gerotor [65] and crescent pumps [28].

However, the axial movement of the mechanical parts is a typical problem of the external gears machines, due to the presence of the balance plates [1]. As already discussed in Section 3.3, the tilt of the balance plates generates a hydrodynamic pressure distribution on the lateral surface of the gears. However the current value of the tilt angle, as well as of the gap height, is the consequence of the moment and force equilibrium.

The method developed by Dhar and Vacca and implemented in the proprietary package HYGESim [119] allows to calculate the pressure distribution on the balance plate by means of a 2D CFD model in OpenFOAM, where the geometry of the gap is modified iteratively. In particular, for each angular step, the height of the gap and the tilt of the balance plate are adjusted up to the condition of static equilibrium. Since now the problem is no longer steady-state, an additional term proportional to the time derivative of the gap height, called “Normal Squeeze”, has to be also considered in the Reynolds equation.

Another aspect is related to the elastic deformation of the surfaces that leads to a local variation of the gap height (Elasto-Hydrodynamic Lubrication). Borghi and Zardin [120] used a commercial Finite Element Method (FEM) software for evaluating the deformation of the balance plate surface under the action of the pressure field calculated by integrating the Reynolds equation. The FEM analysis provides the stiffness matrix of the balance plates and of the pump casing, which is used to relate the pressure field and the deformation. The corrected gap height is then used for recalculating the new pressure field iteratively up to the convergence. The procedure takes into account also the variation of the viscosity with the pressure.

A further step is to calculate at the same time both the deformation and the instantaneous position, in terms of displacement and tilt, of the balance plate [121]. Finally, if the energy equation is also considered, along with the heat transfer (thermal-elasto-hydrodynamic lubrication), it is possible to take into account the influence on the gap height of the thermal deformation of the solid domain [122].

6. Cavitation and Fluid Aeration

The cavitation and aeration is a critical issue in all positive displacement machines, hence it is crucial that the simulation models could be able to reproduce these phenomena. Beside the effects related to the noise and to the wear, the presence of a gaseous phase implies a reduction of the volume of liquid displaced by the pump. In variable displacement pumps there is also a consequence on the pressure setting of the displacement control [123].

An important aspect is related to the air content. In fact a liquid can dissolve a volume fraction of gas, in this case air, which depends on the current pressure and temperature. For example, a mineral oil is able to dissolve at 20 degrees and atmospheric pressure in steady-state conditions up to 9% of air in volume. According to the Henry’s law, such a percentage is proportional to the current pressure. The practical consequence is the air separation in the suction side of the pump due to low pressure levels.

In gear machines, air and oil vapour can be present in the variable volume chambers at the beginning of the suction phase (meshing zone in external gear and crescent pumps) even at quite low speed. However, a major effect on the volumetric efficiency is due to the massive presence of gaseous fraction up to the end of the suction phase. In this case, when the connection of a chamber with the delivery volume is established, a backflow occurs due to the incomplete filling and the net delivered flow rate is reduced. Such a condition occurs at high speed and/or low suction pressure. Hence a model used for the evaluation of the flow rate cannot neglect the incomplete filling of the chambers. There is a vast literature on cavitation and aeration. With specific reference to the modelling of such phenomena in gear pumps, the approach used is to consider the working fluid as a mixture of liquid, vapour and air and the equivalent density is calculated as function of the corresponding fractions. Basically, for the aeration three different levels of detail can be considered. The simplest and most used methodology calculates the fraction of separated air based on the value of the Bunsen coefficient, of the total gas fraction and of the current pressure level by applying the Henry's law. Moreover it is assumed that the total gas fraction, namely the sum of the dissolved and separated (free) air, is constant in all parts of the circuit and the separation/aeration processes are instantaneous. All lumped parameter models of gear pumps developed in LMS Amesim so far have implemented this fluid model [124], even if not explicitly stated by the authors.

A more advanced model considers also the transport of the gas fraction along the pump, i.e., it is possible to have different fractions of total air in the capacitive components and to consider a local ingress of air. Finally the dynamics of the release and dissolution processes can be also taken into account. In fact the transition between dissolved and separated air is not instantaneous but it takes a certain amount of time. Recently a model with gas transport and dynamics has been added in the Thermal Hydraulic library of LMS Amesim [125], but examples of applications on gear pumps have not been published yet.

The influence of the air release/dissolution time constants in the meshing zone of an external gear pump was studied by Borghi et al. [126] with a modification of the Henry’s law. A customized fluid model in LMS Amesim that takes into account both gas transport and non-instantaneous release/dissolution has been developed by Zhou et al. [127] and applied to the simulation of external gear pumps. The software GT-SUITE also implements the most advanced model. A study on a gerotor pump operating in incomplete filling conditions can be found in [43].

In CFD models it is possible to simulate the non-homogeneous distribution of the air/vapour content in the variable chambers and to determine the regions where the air release and cavitation occurs. Also in this case different levels of detail can be considered, for instance separation/dissolution of the air fraction instantaneous or with time constants. In [128], del Campo at al. studied the cavitation in an external gear pump using a 2D model developed in Fluent.

The software PumpLinx implements the Full Cavitation Model developed by Singhal et al. [129]. An example of 3D simulation of a gerotor pump is reported in Figure 21a, where the gas volume fraction is shown for a specific position of the gears. The air release occurs at the beginning of the suction phase on the opposite side with respect to the port plate. The effect of massive air and vapour release at high speed is shown in the steady-state characteristic in Figure 21b. Experimental validations can be found in the open literature for gerotor pumps [56,64,65] and crescent machines [69].

It must be highlighted that the main difficulty in using advanced fluid models is the high number of parameters. In fact, not only the total amount of air present in the liquid under operating conditions is usually unknown, but also a rough estimation of the time constants for the air release/dissolution processes can be a challenge. However, due to the high time constant with respect to the release time, the dissolution process could be neglected in systems where fast pressure change occurs, such as in pumps [89].

It is worth to notice that, even without considering the release/dissolution transients, the ability of some 3D codes to assess the limit speed for which the incomplete filling begins represents, in general, a very important achievement in the simulation of the positive displacement pumps.

7. Conclusions

In this review paper the main techniques for the simulation of the gear machines have been analyzed. It was found that the external units are the most studied pumps, followed the by the gerotor, while the research activities on crescent pumps are quite limited. In general, the spread of commercial simulation tools has made the pump modelling more and more common, not only as academic activity, but also in industrial field. It is interesting to notice that one third of the references cited in this paper have been published starting from 2015. In particular during the last five years, 3D simulation has become an affordable method in terms not only of ease of use, but also in terms of computational time.

A typical industrial application of the simulation models is the optimization of the manufacturing tolerances, in order to reduce the clearances with a higher impact on the volumetric efficiency. Another use is the minimization of the pressure drops in the inlet side for avoiding the cavitation, for instance by choosing the correct diameter of the suction side or by shaping in a proper way the inlet volume and the port plate. Moreover, the optimization of the delivery side, e.g. the use of silencing grooves along with an appropriate delay of the beginning of the delivery phase, can lead to a reduction of pressure peaks and, as a consequence, of the pump noise.

An important innovation in the simulation of the positive displacement pumps, not only gear machines, is represented by the integrated use of different simulation products, in order to better understand the interaction between fluid domain and mechanical parts. However, it is likely that the simultaneous use of many simulation environments for 0D and 3D hydraulic models, FEM analysis and noise assessment could be mainly limited to the academic sphere, due to the significantly higher cost of the commercial licenses with respect to the educational ones that normally can be used also for non-profit research.

Even if in this review for reasons of conciseness only the models for the simulation of the flow rate (and implicitly of the volumetric efficiency) have been described, another important issue is represented by the models for the simulation of the friction, which are poorly discussed in the open literature and will deserve more attention.

With reference to the future, it is likely that next studies will focus on the axial and radial balancing of gerotor pumps, since the use of this kind of units is no longer limited to low pressure applications and the knowledge of the real positioning of the gears with respect to the casing has a strong influence on the volumetric efficiency. Other phenomena that it would be interesting to analyze are the thermal effects in the leakage passageways. In fact, due to the viscous friction between moving parts, the local temperature in the lubricated gaps will be higher than in the other control volumes, with a consequence on the calculation of the leakage flow.

Finally, another aspect that will be certainly examined more in depth is the air release/cavitation, thanks to the availability of advanced fluid models in the main commercial simulation products.